Gráfparaméterek, párosítások
Független ponthalmaz
A független ponthalmaz precíz definíciójára mindjárt kettő is van.
Íme az egyik:
Egy $G$ gráfban független csúcshalmaznak nevezzük a csúcsoknak az $A \subset V(G)$ részhalmazát, ha nincs olyan él, amelynek mindkét végpontja $A$-ban van.
És itt jön a másik:
Egy $G$ gráfban független csúcshalmaznak nevezzük a csúcsoknak az $A \subset V(G)$ részhalmazát, ha az $A$ által feszített részgráf nem tartalmaz élt.
Egy $G$ gráfban a független csúcsok maximális számát $\alpha(G)$-vel jelöljük.
Lefogó ponthalmaz
Egy $G$ gráfban a $T \subset V(G)$ ponthalmaz lefogó ponthalmaz, ha $G$ minden élének legalább az egyik végpontja $T$-ben van.
Egy gráfban a minimális méretű lefogó ponthalmaz elemszámát $\tau(G)$-vel jelöljük.
A maximális lefogó ponthalmaz pedig a gráf összes csúcsa, és elemszáma éppen $ \mid V(G) \mid = n $.
Gallai első tétele
Ha vesszük egy gráfban a maximális számú független pontokat és a minimális számú lefogó pontokat, akkor épp megkapjuk a gráf összes pontját.
Ezt hívjuk első Gallai tételnek:
\( \tau(G) + \alpha(G) = n \)
Független élhalmaz
Egy $G$ gráf éleinek $M$ részhalmaza független élhalmaz, ha $M$ semelyik két elemének nincs közös végpontja.
Egy gráf független éleinek maximális számát $\nu(G)$-vel jelöljük.
Lefogó élhalmaz
Egy $G$ gráf éleinek $R$ részhalmaza lefogó élhalmaz, ha a gráf minden csúcsa valamelyik $R$-beli él végpontja.
Egy $G$ gráfban a lefogó élek minimális számát $\rho(G)$-vel jelöljük.
Gallai második tétele
Ha vesszük egy gráfban a minimális számú lefogó éleket, és a maximális számú független éleket, akkor a gráf minden pontjához pontosan egy él fog tartozni.
Ez Gallai második tétele:
Ha egy $n$ csúcsú gráf nem tartalmaz izolált pontot, akkor
\( \rho(G) + \nu(G) = n \)
Gráfparaméterek közti összefüggések
\( \alpha(G) \leq \rho(G) \quad \nu(G) \leq \tau(G) \)
Tétel páros gráfokra
Egy $G$ gráf akkor és csak akkor páros, ha minden $G$-ben szereplő kör páros hosszúságú.
Párosítás
Egy $G$ gráfban az $E(G)$ élhalmaznak egy $M$ részhalmazát párosításnak nevezzük, ha $M$ semelyik két elemének nincs közös végpontja.
Párosítás javító útja
Egy $G$ gráfban az $e_1, e_2, e_3, \dots , e_n$ élsorozat az $M$ párosítás javító útja, ha
1) a megadott élsorozat egy páratlan hosszú út $G$-ben
2) az élek felváltva elemi $M$-nek:
$ e_{2k} \in M$ és $e_{2k+1} \notin M $
3) az út kezdő és végpontja nem illeszkedik semelyik $M$-beli élre sem
Teljes párosítás
Azokat a párosításokat nevezzük teljes párosításoknak, ami a gráf összes csúcsát lefedi.
Tutte-tétel
Egy gráfban akkor és csakis akkor létezik teljes párosítás, ha bárhogyan hagyunk el a gráfból néhány pontot, a megmaradt gráfban a páratlan komponensek száma nem több az elhagyott pontok számánál.
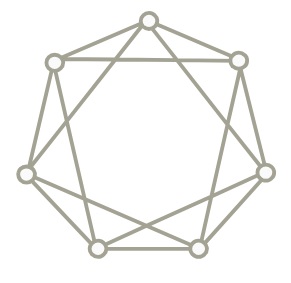
Adjuk meg az alábbi gráfban a maximális független ponthalmaz és minimális lefogó ponthalmaz számát.
Adjuk meg az alábbi gráf maximális független élhalmazának és minimális lefogó élhalmazának számát.
Próbáljuk megtalálni az alábbi gráfokban a maximális párosításokat.
a)
b)
c)
d)
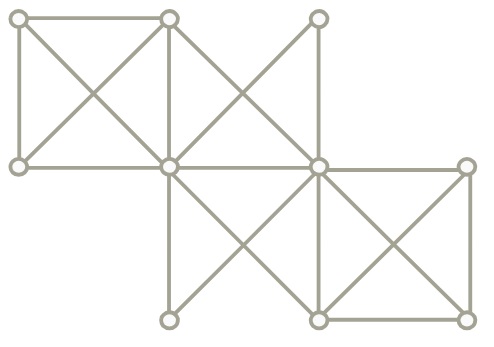
a) Adjuk meg a gráfparamétereit.
b) Adjuk meg a gráfparamétereit.
c) Adjuk meg a gráfparamétereit.
d) Adjuk meg a gráfparamétereit.
e) Egy gráfban $2n$ darab pont van, és minden pont foka legalább $n$. Legalább hány elemű egy lefogó élhalmaz a gráfban?
f) Egy 1001 pontú $G$ egyszerű gráfban $\tau{(G)}=1000$. Bizonyítsuk be, hogy $G$ teljes gráf.
a) Bizonyítsuk be, hogy minden $G$ egyszerű gráfra:
\( \chi{(G)} \cdot \alpha{(G)} \geq n \)
b) Bizonyítsuk be, hogy minden $G$ egyszerű gráfra:
\( 2\nu{(G)} \geq \tau{(G)} \)
c) Vajon minden $G$ egyszerű gráfban teljesül-e, hogy
\( \mid E(G) \mid \leq \Delta(G) \cdot \tau{(G)} \)
d) Bizonyítsuk be, hogy minden $G$ egyszerű gráfra:
\( \alpha{(G)} \left( \Delta(G)+1 \right) \geq n \)
e) Bizonyítsuk be, hogy bármely $G$ egyszerű gráfban:
\( \chi{(G)} + \alpha{(G)} \leq n +1 \)
f) Bizonyítsuk be, hogy bármely $G$ egyszerű gráfban:
\( \begin{pmatrix} \chi{(G)} \\ 2 \end{pmatrix} \leq \mid E(G) \mid \)
A $G$ gráf csúcshalmaza $V(G)=\{1,2, \dots, 30 \}$. Az $x,y \in V(G)$ csúcsok akkor legyenek szomszédosak $G$-ben, ha $x \neq y$ és $x \cdot y$ osztható 6-tal. Határozzuk meg $\nu(G)$ értékét!
Egy $G$ gráf csúcsai legyenek a 100-nál nem nagyobb pozitív egészek. Két különböző csúcs pontosan akkor szomszédos $G$-ben, ha a megfelelő egészek relatív prímek. Határozzuk meg a gráfparamétereket!
Egy $G$ gráf csúcsai legyenek a 100-nál nem nagyobb pozitív egészek. Két különböző csúcs pontosan akkor szomszédos $G$-ben, ha a hozzájuk tartozó számok szorzata osztható 4-gyel. Határozzuk meg $\alpha{(G)}$ és $\rho{(G)}$ értékeit!
Egy 1000 csúcsú gráfban $\tau{(G)}=400$. Igazoljuk, hogy $G$-ben nincs teljes párosítás.
