
A gazdasági folyamatokat leíró grafikonoktól a természet alkotta formációkon át a káoszelméletig egyre több helyen bukkanunk fraktálokra
Valahol az óceán partjának egy sziklás szakaszán különös háromszög-szerű kiszögellésre bukkantak. Egy földmérőt küldtek ki a partvonal alapos feltérképezésére, feladata az volt, hogy számítsa ki a partvonal hosszát. Amikor a földmérő megérkezett a partszakaszra, azt tapasztalta, hogy a part furcsa mintázatot követ. Ahogy elkezdett a part mentén sétálni, végigment egy 300 méter hosszú egyenes szakaszon, aminek a végén a part 60 fokos szögben háromszög-szerűen kiugrik az óceán felé. Folytatva útját a háromszög oldalán egy újabb 300 méteres egyenes szakasz következett, majd kiért a kiszögellés csúcsába. Itt újra 60 fokos szög, ezúttal a szárazföld irányába és megint 300 méternyi séta. Végül a parttal párhuzamosan újabb 300 méter.
A földmérő így összesen 300+300 métert sétált a parttal párhuzamosan és újabb 300+300 métert a kiszögellésen, vagyis a partvonal hossza éppen 1200 méter.
A séta közben azonban, ahogy lenézett a szikláról a víz felé, észrevette, hogy az egyenes szakaszokon is ugyanolyan furcsa háromszög-szerű kiszögellések láthatók, mint a teljes partszakaszon, így elhatározta, hogy másnap visszatér.
Ezúttal kijjebb merészkedett a szikla szélére és az előző nap 300 méter hosszúnak hitt egyenes szakaszról kiderült, hogy valójában 400 méter hosszú, mert a középső 100 méteren az előző napihoz hasonló, csak harmad akkora kiszögellést talált. Aztán ahogy továbbment a következő 300 hosszúnak és egyenesnek hitt szakaszra, ott is megtalálta a harmad akkora kiugrót és így erről a szakaszról is megállapította, hogy valójában 400 méter hosszú. Ahogyan mindegyikről, tehát előző napi feljegyzéseit átírva a partszakasz hossza 400+400+400+400 méter, vagyis 1600 méter. Tehát 1,25-ször annyi, mint előző nap gondolta.
A különös jelenség nem hagyta nyugodni a földmérőt, így a következő napon még pontosabb műszerekkel kezdte vizsgálni a partot és ezúttal az előző nap egyenesnek hitt partszakaszokon fedezte fel ugyanazokat a furcsa kiszögelléseket. Így meg kellett állapítania, hogy a part hossza megint 1,25-szerese az előző nap gondoltnak, és így már több mint másfélszerese az eredetileg képzeltnek.



Ha ez a mintázat a végtelenségig ismétlődik, nos akkor a part hossza az egyre pontosabb mérések során mindig a korábbinak az 1,25-szerese lesz és így az n-edik napon a földmérő már 1,25n-szer olyan hosszúnak fogja mérni, mint kezdetben. Nos, n=100 esetén ez már eléggé meglepő, ugyanis majdnem 5 milliárdszorosa az eredetileg mért hosszúságnak. Ez 5890 millió kilométer, ami a Nap-Föld távolság negyvenszerese.
És ahogy telnek a napok, a földmérőnek rá kell döbbennie, hogy a partszakasz hossza végtelen.
A természetben ennek az ismétlődésnek előbb utóbb fizikai gátat szabnak az anyagi tulajdonságok, amikor már homokszem méretű öblökről és kiszögellésekről beszélünk. Ám a matematika absztrakt világában ez az aprózódás tovább folytatható és így a partvonal hossza valóban végtelen.
Ha egy alakzatnak valamely részletébe belenagyítva éppen az eredeti alakzatot látjuk, akkor azt mondjuk, hogy az alakzat önhasonló. A belenagyítások sorozatát iterációnak nevezzük, az ilyen önhasonló alakzatokat pedig fraktálnak. Matematikai értelemben az önhasonlóság azt jelenti, hogy az alakzat bármilyen pici részletében is benne van a teljes alakzat. Ilyen például ez a képzeletbeli tengerpart, az úgynevezett Koch-görbe.
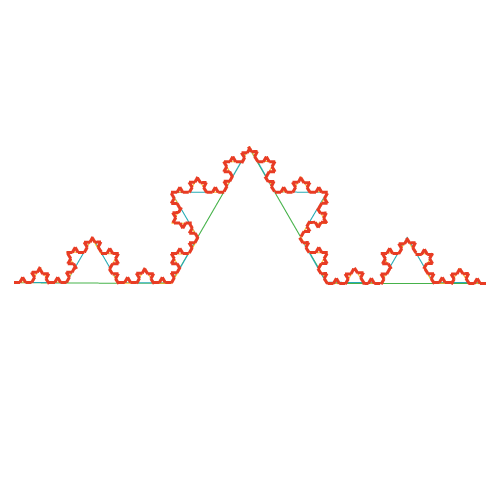

Fizikai értelemben viszont csak statisztikai önhasonlóságról beszélhetünk, mivel a belenagyítások, vagyis az iterációk száma általában véges, illetve maga az önhasonlóság sem teljesen tökéletes. A matematikai értelemben vett Koch-görbe fizikai megfelelője a random Koch-görbe.
A képzeletbeli tengerpartunkkal szemben a valódi tengerpartok nem szabályosan önhasonló és nem végtelenségig iterálható alakzatok. Ám bizonyos értelemben mégis fraktálok. Az, hogy mit is tekintünk fraktálnak, minél többet tudunk róluk annál nehezebb megmondani. A fraktál fogalmát Benoit Mandelbrot alkotta meg a latin fractus (megtört) szóból. Mandelbrot ezzel foglalkozó, egyszersmind az egész tudományágat megalapozó 1975-ös dolgozatát megelőzően a tőzsdei árfolyamok szabálytalan cikázását, a felhők formáit, a villámok útját vagy éppen a partvonal-problémát vizsgálva vett észre különös szabálytalanságokat és szabályszerűségeket és ezek vezették el a fraktál, mint fogalom megalkotásához. A partvonal-problémával már őt megelőzően az 1900-as évek elején Lewis Fry Richardson angol matematikus is foglalkozott, amikor térképészeti adatokat gyűjtött különböző országok határvonalainak hosszáról. Feltűnt neki, hogy például a Portugália és Spanyolország között húzódó határvonal hosszát a két ország térképészei más-más hosszúságúnak mérték. Vizsgálódásait folytatva arra jutott, hogy szinte alig van olyan eset, amikor a közös határvonalat a két szomszédos ország egyforma hosszúnak mérte volna és leírt egy különös jelenséget, amelyet azóta Richardson-effektusnak neveznek. Ennek lényege tulajdonképpen nem más, mint a képzeletbeli földmérőnk problémája a képzeletbeli tengerparton, nevezetesen az, hogy minél kisebb mérőrudakat használunk, a partvonal hosszának lemérésére, annál nagyobb érték jön ki. Richardson ezt gondolatkísérlettel szemléltette, amelyben megpróbálta lemérni a Britt sziget partvonalának hosszát. Ha 200 kilométer hosszú mérőrudakat használunk úgy, hogy a partvonalhoz illesztjük azokat, akkor 12 darabra van szükség és 2400 kilométer jön ki. Ha feleakkorákat, akkor azokból már 28 darab kell, és így azt kapjuk, hogy a partvonal hossza 2800 kilométer. Minél rövidebbek a rudak, annál nagyobb szám jön ki a partvonal hosszára, ami így lényegében végtelen.


Fölvetődhet a kérdés, hogy vajon ugyanezek a problémák miért nem merülnek föl például egy kör kerületének a meghatározásánál. Ha a mérőrudas példánkat egy 100 kilométer sugarú körre alkalmazzuk, akkor a mérés finomításával nem végtelen jön ki, hanem a jól ismert  ami a kör tényleges kerülete.
ami a kör tényleges kerülete.
A titok a fraktálok töredezettségében van. A kör ugyanis egy sima alakzat, minél jobban belenagyítunk, annál inkább hasonlít egy egyenes vonalra. Ezt a tulajdonságot a matematikában úgy nevezik, hogy differenciálható. A fraktálok viszont éppen arról híresek, hogy belenagyítva eszük ágában sincsen kiegyenesedni, ugyanolyan komplikáltan néznek ki, mint azelőtt. Vagyis valahogy annyira girbegurbák, hogy sűrűbbnek néznek ki, mint egy sima hétköznapi vonal.
Ilyen alakzatokat nem csak a papírlapon, hanem térben is képesek vagyunk előállítani, és ami azt illeti, a természet bővelkedik is ezekben. Itt van például egy fenyőfa. A fenyőfa lényegében egy kúp alakú test, ám ahelyett, hogy teljesen tömör lenne a belseje, ágak sokaságából áll, amik szétágaznak kisebb ágakra, hajtásokra, levelekre.
Ahogyan a képzeletbeli tengerpartunk egy végtelenül hosszú vonal, úgy a fenyőfa egy végtelenül szerteágazó felületű kúp. Nem ok nélkül természetesen. Az ember tüdejéhez hasonlóan a fenyőfa is azt szeretné, hogy a lehetőségekhez képest a legnagyobb legyen a felülete, és így a lehető leghatékonyabban legyen képes a levegővel érintkezve a légcserére. A fenyőfában, a tüdőben és a tengerpartunkban közös vonás, hogy valahogyan szeretnék úgy kitölteni a rendelkezésükre álló üres teret, hogy mindenütt jelen legyenek, de közben az üres tér is mindenütt jelen maradjon.
Ezt, hogy egy alakzat mennyire van jelen vagy épp mennyire nincs a rendelkezésére álló térben, jól szemlélteti az úgynevezett Sierpinski-féle szőnyeg. Ez úgy keletkezik, hogy egy egységnyi területű négyzetet felbontunk 9 kis négyzetre, majd a középsőt elhagyjuk.


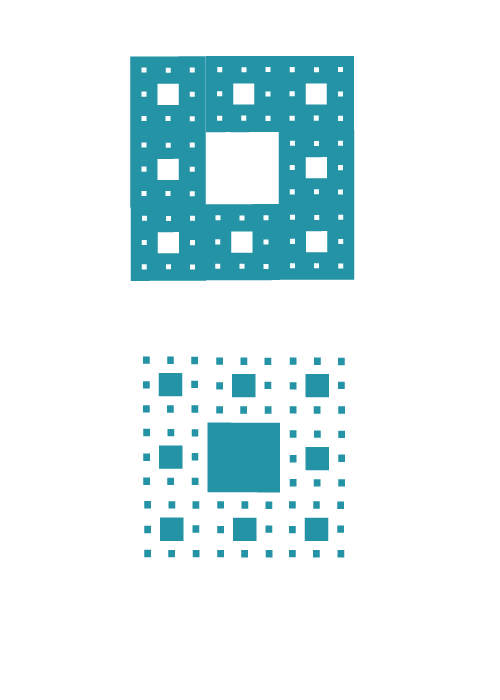
Ezek után a megmaradt 8 négyzetet újra felosztjuk 9 még kisebb négyzetre és mindegyiknek a közepét elhagyjuk. Ha a kivágott darabkákat elkezdjük gyűjteni, akkor ezek területe az eredeti négyzet területéhez képest 1/9, aztán 8/81 aztán 64/729 és így tovább. Egymás mellé téve őket a kapott terület az 1/9+8/81+64/729+… végtelen mértani sor összege. Közismert matematikai tény, hogy ha  akkor az
akkor az  végtelen mértani sor összege:
végtelen mértani sor összege:
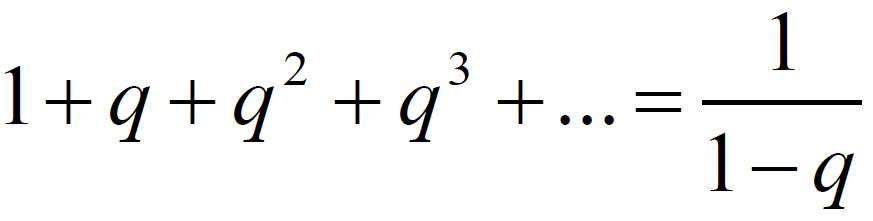
Lássuk csak, esetünkben mi a helyzet.
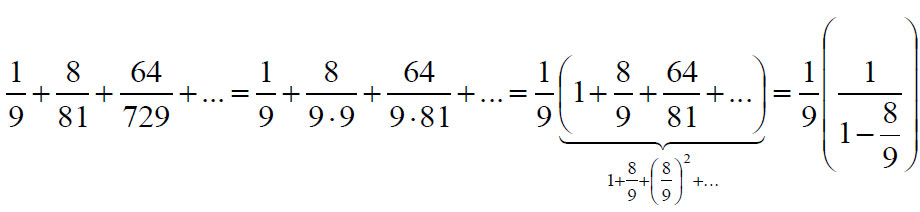
Ha beütjük a számológépbe az egyenlőség végén álló számot, akkor az jön ki… nos az jön ki, hogy 1.
Vagyis az eljárás végén az eredeti négyzetünk területe nullává válik, a kivágott darabkákból pedig újra képesek vagyunk összerakni az egységnyi területű négyzetet.
A Sierpinski –féle szőnyeg az eredeti egységnyi területű négyzetnek egy lecsupaszított, nulla területű csontváza. Mielőtt azonban azt gondolnánk, hogy ez a csontváz valójában nem is létezik, és az iteráció során nem marad semmi, érdemes belegondolni, hogy ez közel sincs így. A Sierpinski-féle szőnyeg ugyanis tartalmazza az eredeti négyzet mind a négy csúcsát, azoktól sehogyan sem tudjuk őt megfosztani. Sőt, tartalmazza a megmaradt 8 kisnégyzet mindegyik csúcsát is, sőt a 64 darab még kisebb négyzet mindegyik csúcsát, és így tovább.
A Sierpinski-szőnyeg és a Koch-görbe mindketten valahogy rendellenesen viselkednek. A Sierpinski-szőnyeg egy teljesen hétköznapi kétdimenziós alakzatból, egy négyzetből keletkezik, de közben elveszíti területét, és így, mintha a dimenziója is csökkenne. A Koch-görbe egy másik hétköznapi alakzatból egy egydimenziós vonalból keletkezik, de közben annyira besűrűsödik, hogy egyre inkább hasonlít egy területtel rendelkező kétdimenziós síkidomra.
Mindenki tudja, hogy egy kocka háromdimenziós, egy négyzetlap kétdimenziós és egy szakasz egydimenziós. Érdemes azonban egy kicsit közelebbről is megnézni, hogy pontosan mit is jelent a dimenzió fogalma. Ennek megértéséhez vegyünk egy egyszerű példát. Van egy szakaszunk, aminek a hossza 1 méter, és most szeretnénk egy olyan szakaszt, aminek a hossza kétszer akkora. Nos, ehhez nem kell mást tennünk, mint az eredeti szakaszt megdupláznunk.
Ha van egy négyzetünk, ami 1m X 1m nagyságú és szeretnénk egy kétszer akkora négyzetet, akkor viszont az eredeti négyzetből négy darab kell.
Ha van egy kockánk, ami 1m X 1m X1m nagyságú, és szeretnénk egy kétszer akkora méretű kockát, akkor az eredeti kockából 8 darabra van szükség.

Ha most nem kétszeresére, hanem k-szorosára akarjuk növelni az alakzatokat, akkor a szakasznál k darab, a négyzetnél k2 darab, míg a kockánál k3 darab kell ahhoz, hogy a kívánt alakzatot megépítsük.
Logikusnak tűnik tehát azt állítani, hogy a dimenzió tulajdonképpen nem más, mint a k-nak a kitevője.
Itt a k-nak igazából nincs sok szerepe, mert teljesen mindegy, hogy kétszer akkora kockát csinálunk 23 kiskockából, vagy 3-szor akkorát 33 darabból, egyedül az érdekes, hogy a kitevőben szereplő szám a 3.
A dimenzió tehát a következő érdekes módon definiálható. Van egy alakzatunk, amit szeretnénk k-szorosára nagyítani. Megszámoljuk, hogy célunk eléréséhez hány daraboot kell egymás mellé tenni az eredeti alakzatból, ez legyen N darab. Nos ekkor a dimenzió

Ha előveszünk egy számológépet és kiszámoljuk, hogy mi jön ki, mondjuk egy kocka megduplázásánál, amikor k=2 és N=8, vagy mondjuk mi jön ki egy négyszer akkora kockánál, amikor k=4 és N=64, azt tapasztaljuk, hogy a kapott eredmény 3, ami megnyugtató, mert a kockának a dimenziója tényleg 3 kell legyen. (Természetesen, aki járatos a logaritmus fogalmában, rögtön áthatja hogy tulajdonképpen a képletünk azt mondja, hogy a dimenzió  a ami éppen k-nak a kitevője.)
a ami éppen k-nak a kitevője.)
A dimenziónak ezt a szokatlan megközelítését egy Német matematikus, Felix Hausdorff találta ki és Hausdorff dimenziónak nevezzük. A Hausdorff dimenziónak megvan az a nagyon kellemes tulajdonsága, hogy a hétköznapi életünk során megszokott alakzatok dimenziói továbbra is a szokásosak, tehát 1, 2 vagy éppen 3, ugyanakkor lehetővé teszi nem egész dimenziók létezését is.
Nézzük meg például, hogy mekkora a Sierpinski-szőnyeg dimenziója. Ehhez azt a kérdést kell föltenni magunknak, hogy hány darab Sierpinski-szőnyegre van szükség egy háromszor akkora megalkotásához. Hát lássuk csak, belülre ugye nem kell, mert az üres, a szélekre pedig 8 darab.
Ezek szerint, ha k=3 akkor N=8 így a Sierpinski-szőnyeg Hausdorff dimenziója

Szemléletesen már korábban éreztük, hogy a kétdimenziós négyzet kiürítése valahogy egy picit csökkenti a dimenzióját is, és valóban, a Sierpinski-szőnyeg durván csak 1,9 dimenziós .
Lássuk most mi a helyzet a Koch-görbével. Itt szintén egy háromszor akkora Koch-görbét fogunk megalkotni, és ehhez szükségünk van 4 darab kisebb példányra.
Vagyis k=3 és N=4 így aztán a Koch-görbe dimenziója:
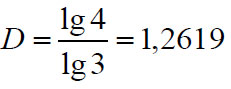
A Koch-görbe tehát sűrűbben tölti ki a síkot egy átlagos egydimenziós görbénél. Van azonban olyan görbe is, ami ennél sokkal meglepőbb dolgot tud. Előállításához a következő iterációkat kell végrehajtani:




Az így keletkező alakzatot Hilbert-görbének nevezzük. Számoljuk most ki a Hausdorff dimenzióját. Ahhoz, hogy egy kétszer akkora Hilbert görbénk legyen, négy kisebbet kell egymás mellé tennünk, tehát ha k=2 akkor N=4. A képlet szerint:
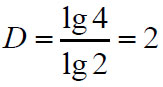
A Hilbert-görbe dimenziója tehát éppen kettő, így pontosan olyan sűrűn tölti ki a síkot, mint az a négyzetlap, amiben elhelyezkedik. Egy kevés számolással igazolható, hogy a Hilbert-görbe valóban teljesen hézagmentesen kitölti a négyzetlapot, vagyis annak minden egyes pontján áthalad, ugyanakkor minden pontjában folytonos is. Ez roppant különössé teszi, mivel így a görbe minden egyes pontjában sajátmagával határos. Ha képzeletben elindulunk a görbén, akkor hosszú kilométereken át kéne gyalogolnunk ahhoz, hogy eljussunk egy olyan pontjához, ami szó szerint egyetlen ugrásra van éppen mellettünk.
Az önhasonló vagy statisztikailag önhasonló alakzatok tehát hajlamosak arra, hogy dimenziójuk a megszokottnál magasabb legyen, vagy éppen alacsonyabb. Egy területtel nem rendelkező görbe az iteráció során képes kitölteni egy négyzetlapot, míg egy területtel rendelkező négyzetlap az iteráció során elveszítheti a területét.
A fraktálok diadalútja az 1900-as évek közepén kezdődött, amikor a dinamikai rendszerek úgynevezett kaotikus attraktorairól kiderült, hogy azok is fraktálszerűek. Maguk a dinamikai rendszerek tulajdonképpen matematikai konstrukciók, amelyek egy állapottérrel leírt rendszer bizonyos állapotainak rögzített szabályok szerinti (általában) időbeli változásával foglalkozik. Ilyen rendszer például az időjárás. Az 1940-es években a „valódi” komoly meteorológusok szemében az előrejelzés nem volt igazi tudomány. Inkább csak amolyan találgatásnak tekintették, a műszerek által mért pontos adatokból történő megérzésen alapuló jóslásnak. Egy matematikus gondolkodással és látásmóddal megáldott meteorológus, Edward Norton Lorenz azonban eltökélte, hogy ezt a jóslást a megérzések szintjéről a matematikai rendszerek világába emeli át. A számítógépek fejlődése lehetőév tette számára, hogy 1960-ra elkészítse bolygónk meteorológiai rendszerének egy végtelenül leegyszerűsített modelljét. A modell egész megbízhatónak bizonyult, mígnem egyik alkalommal egy több napra kiterjedő és roppant időigényes számítást úgy próbált meg lerövidíteni, hogy a gép által egyik napra már korábban kiszámított értékeket saját feljegyzései alapján kézzel táplálta be, megspórolva ezzel azt, hogy a gépnek kelljen újra kiszámítani azokat.
Az eredmény láttán először arra gondolt, hogy elromlott a gép, ugyanis teljesen más eredményeket kapott, mint korábban. Elkezdte hát kutatni a hiba okát. A gépet úgy alkotta meg, hogy számításait hat tizedes jegy pontossággal végezze, ám a végeredményt csak négy tizedes jegy pontosan írja ki. Amikor kézzel táplálta vissza a négy tizedes jegy pontosságú adatokat úgy gondolta, hogy ez a picike pontatlanság nem lesz jelentős hatással a teljes számolás végeredményére. Mint utóbb kiderült, ez az eltérés drámaian nagy hatással volt a végeredményre. Ezt a Lorenz által felfedezett jelenséget azóta pillangó-hatásnak nevezték el és lényege, hogy egyes rendszerek a kezdeti értékek parányi változtatása esetén drasztikusan eltérő lefutást produkálnak.
Képzeljünk el egy félgömb alakú tálat egy golyóval. Ha a tálba beleejtjük felülről a golyót, akkor az ide-oda gurulva előbb-utóbb megállapodik a tál közepén. Ha egy kicsit távolabbról, vagy egy kicsit más szögben ejtjük bele a golyót, az eredmény kicsit más lesz, de végül ugyanúgy megáll a tál közepén. Most fordítsuk fel a tálat és ejtsük rá a golyót így. Még akkor, ha egészen pontosan a tál középpontja felett engedjük el a golyót, sem tudjuk megjósolni, hogy vajon melyik oldalon fog legurulni, pláne azt nem tudjuk megmondani, hogy a golyó hol fog végül megállapodni. A kezdeti érték apró változtatásával pedig a golyó döntően eltérő pályákon fog mozogni.
Ha a tál bal oldalán leguruló golyó azt jelenti, hogy holnap esni fog az eső, a jobb oldalon leguruló, hogy sütni fog a nap, és a kezdeti érték – a mai napi mérési adatok – azt jelzik, hogy jobbra ejtjük le a golyót, akkor a meteorológus hátradőlhet székében és kijelentheti, hogy nem fog esni. Ha azonban a golyót a tál középpontja felett, vagy attól csak picit jobbra engedjük el, nos akkor a kimenetel eléggé bizonytalan.

Az időjárási előrejelzésekkel rokon vonást mutat, a tőzsdei árfolyamok vagy éppen a devizaárfolyamok előrejelzésének problémája. A pillangó-hatás itt is érvényesül, egy-egy cég vezetőjének elhalálozása, egy-egy váratlan ipari baleset beláthatatlan következményekkel lehet az árfolyamok alakulására, és a hatás tovagyűrűzve kihat az egész világ gazdaságára. Az árfolyamgörbék vizsgálata azért is érdekes, mert ezek a grafikonok maguk is fraktálok. Rendelkeznek a skálafüggetlenségnek nevezett tulajdonsággal, ami röviden annyit jelent, hogy ha a világ legtapasztaltabb brókere elé odateszünk skálázás nélkül egy árfolyamgörbét, nos még ő sem lesz képes megállapítani, hogy ez vajon egy hónap vagy egy 10 éves időszak árfolyammozgásait tartalmazza-e. Vagyis az árfolyam görbék statisztikailag önhasonlók, Hausdorff dimenziójuk általában 1,1 és 1,3 közé esik.


Az árfolyamgörbék vizsgálata és az erre épülő előrejelzés így aztán meglehetősen reménytelen vállalkozásnak tűnik. Ám éppen az ad lendületet a káoszelméletbeli kutatásoknak, hogy a káoszban is képesek legyünk észrevenni bizonyos törvényszerűségeket. Befejezésképpen nézzünk meg ezek közül egy egyszerűbbet. Harold Edwin Hurst a Nílus vízállásának adatait tanulmányozva figyelt föl arra a jelenségre, hogy egy nagyobb áradást rendszerint újra nagyobb áradás követ. Az adatok részletes statisztikai elemzésére kidolgozott egy érdekes mutatót, az úgynevezett Hurst-exponenst. Ez egyfajta fokmérője a mindennapi életből ismert pozitív és a negatív visszacsatolásnak. Ha a Hurst-exponens éppen 0,5 az azt jelenti, hogy a folyamat teljesen véletlenszerűen megy végbe, vagyis a golyót éppen a fejre állított üvegtál középpontja felett engedjük el. Ha a Hurst-exponens 0,5-nél nagyobb, akkor egyfajta pozitív visszacsatolás fedezhető fel, vagyis az árfolyamoknál maradva egy adott deviza erősödése újabb erősödést von maga után. Ha pedig ez a szám 0,5-nél kisebb, akkor negatív visszacsatolás van, tehát ha ma erősödik az árfolyam, akkor holnap gyengülni fog. Ezek a törvényszerűségek természetesen nagyon sérülékenyek és a sokat emlegetett pillangó-hatás következtében váratlanul el is tűnhetnek vagy épp az ellenkezőjébe fordulhatnak át. Ugyanakkor érdekes megemlíteni, hogy a hazai részvényindexnek, a BUX-nak a Hurst-exponense az utóbbi pár év adatai alapján 0,7 körül mozog. Vagyis, bár az árfolyam mozgása kaotikus, egy emelkedéssel záró nap után másnap is inkább emelkedésre, míg egy gyengüléssel záró nap után inkább gyengülésre számíthatunk. Ezek a Hurst-exponens értékek által uralt időszakok természetesen az árfolyammozgáshoz hasonlóan szintén sérülékenyek, tehát a Hurst-exponens értékének alakulása maga is fraktálszerű. Akár ebben a pillanatban is érkezhet egy pillangó, aki a 0,7 körüli értéket mondjuk 0,4-re változtatja.
