Koordinátarendszer, pontok koordinátái
Ennek a témakörnek a feladatai
Letöltöm az egész kurzus összes feladatát:
LetöltömLetöltöm ennek a témakörnek a feladatait:
LetöltömVálogass kedvedre a témakör feladatai között:
Rajzoljuk be ezeket a pontokat a koordinátarendszerbe:
$A(1,11)$
$B(5,10)$
$C(6,5 \;,8)$
$D(8,\; 6,5)$
$E(7,5 \;,4,5)$
$F(11,3)$
$G(12,5)$
Itt van a koordinátarendszerben ez a három pont.
Adjuk meg a negyedik pont koordinátáit úgy, hogy a négy pont egy téglalap négy csúcsa legyen.
a)
b)
c)
Egy téglalap három csúcsa A(1, -6), B(4, -4) és C(-2,5). Adjuk meg a negyedik csúcs koordinátáit.
d)
Egy téglalap két csúcsa A(4,2) és B(8,2). Adjuk meg a másik két csúcs koordinátáját, ha tudjuk, hogy a téglalap területe 24 területegység.
Keressük meg azokat a pontokat, amik ezt tudják:
a) $y=-x$
b) $x=2$
c) $x=3$
d) $y=2x$
e) $y=3x$
Itt ez az egyenes, ami átmegy az A(2,1) és B(6,3) pontokon.
a) Mennyi az y koordinátája annak a P pontnak, aminek az x koordinátája 8 és rajta van az egyenesen?
b) Mennyi az x koordinátája annak a Q pontnak, aminek az y koordinátája -3 és rajta van az egyenesen?
c) Mennyi az y koordinátája annak az R pontnak, aminek az x koordinátája -9 és rajta van az egyenesen?
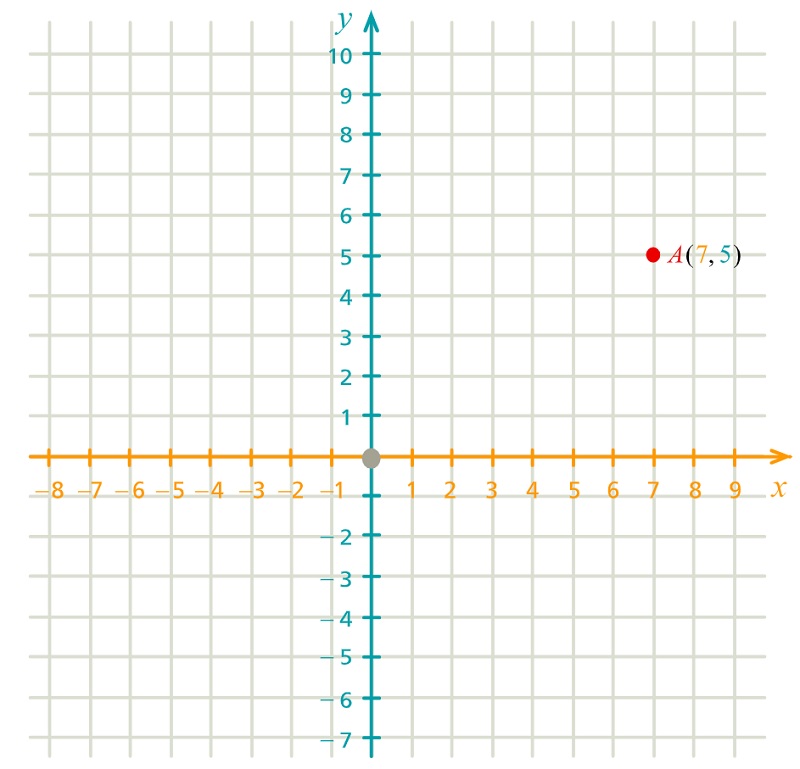
Adott a koordinátarendszerben az A(7,3) pont.
a) Tükrözzük az A pontot az x tengelyre, és hívjuk ezt a pontot B-nek.
b) Tükrözzük az A pontot az y tengelyre, és hívjuk ezt a pontot C-nek.
Egy háromszög csúcsainak koordinátái A(7,2), B(6,7) és C(2,3). Tükrözzük a háromszöget az x tengelyre, és adjuk meg az így keletkező háromszög csúcsainak koordinátáit.
Egy négyszög csúcsainak koordinátái A(6,4), B(7,8), C(3,9) és D(0,3). Tükrözzük a négyszöget az y tengelyre, és adjuk meg az így keletkező négyszög csúcsainak koordinátáit.
a) Tükrözzük az A pontot az origóra, és hívjuk ezt a pontot B-nek. Mik lesznek a B pont koordinátái?
b) Egy háromszög csúcsainak koordinátái A(7,2), B(6,7) és C(2,3). Tükrözzük a háromszöget az origóra, és adjuk meg az így keletkező háromszög csúcsainak koordinátáit.
c) Tükrözzük középpontosan a K pontra az A pontot.
d) Egy háromszög csúcsainak koordinátái A(8,4), B(7,8) és C(4,7). Tükrözzük a háromszöget a K(2,3) pontra és adjuk meg az így keletkező háromszög csúcsainak koordinátáit.
e) Egy négyszög csúcsainak koordinátái A(7,4), B(8,7), C(5,10) és D(2,9). Tükrözzük a négyszöget a K(2,3) pontra és adjuk meg az így keletkező négyszög csúcsainak koordinátáit.
Itt egy koordinátarendszer és benne egy háromszög. Számoljuk ki a háromszög területét.
a)
b) A háromszög csúcsai: A(7,1), B(8,5), C(4,5).
c) A háromszög csúcsai: A(3,8), B(-4,6), C(3,2).
d) A háromszög csúcsai: A(3,8), B(-4,6), C(5,2).
a) Egy négyzet egyik csúcsa A(5,2) és a négyzet szimmetrikus az x tengelyre. Mekkora a területe?
b) Egy háromszög egyik csúcsa A(3,2) és a háromszög szimmetrikus az y tengelyre. Adjuk meg a másik két csúcs koordinátáit, ha tudjuk, hogy a háromszög területe 15 területegység.
Az A(4,5) és a B(8,3) pontok az e egyenesen helyezkednek el.
a) A C és D pont is ezen az egyenesen van. A C pont második koordinátája 9, a D-nek pedig az első koordinátája -2. Adjuk meg a hiányzó koordinátákat.
b) Tükrözzük le az A pontot az x tengelyre, és az így keletkező tükörkép legyen E. Mekkora az ABE háromszög területe?
Az ABCD téglalap csúcsai betűzésének sorrendje A, B, C és D. A téglalap szimmetrikus az y tengelyre úgy, hogy az A csúcs tükörképe a B csúcs és a C csúcs tükörképe a D csúcs. A téglalap területe 24 területegység, és az A csúcs koordinátái: A(-4,3).
a) Adjuk meg a téglalap csúcsainak koordinátáit.
b) Tükrözzük a téglalapot az origóra, és adjuk meg a tükörkép csúcsainak koordinátáit is.
Egy moziban 192 szék van.
Hogyha beszámozzuk őket 1-től 192-ig, akkor a nézők elég nehezen találják meg az ülőhelyüket.
Hol keressük például a 114-es széket?
Valahol itt?
Vagy esetleg itt?
Ez így nagyon bonyolult…
Erre már a mozik is rájöttek, és kitaláltak valamit…
Minden sorban beszámozták a székeket 1-től 16-ig…
És aztán magukat a sorokat is beszámozták.
Így már elég könnyen megtaláljuk például az 5. sor és 7. széket…
Itt lépkedünk 6-ot…
És aztán erre 8-at.
És meg is van.
A matematikában ezt úgy hívjuk, hogy koordináta.
Adjuk meg például Bob koordinátáit…
Aki éppen itt ül.
Az első koordináta mindig az lesz, hogy hányadik sor…
A második koordináta, pedig a szék.
Ezek lesznek Bob koordinátái.
Hogyha most Bob átül ide…
Akkor nagyon könnyű megtalálni.
Erre lépünk 7-et…
Erre pedig 13-at…
És meg is van.
A dolog nem csak mozira működik…
Tegyünk ide egy számegyenest…
Meg ide is…
Ezt úgy hívjuk, hogy koordinátarendszer.
És a székek nem is kellenek…
A koordinátarendszerben minden pont egyértelműen megadható koordinátákkal.
Ez a P pont például…
Így adható meg:
A dolog fordítva is működik.
Itt van ez a Q pont:
És a koordinátái alapján egyértelműen berajzolható a koordinátarendszerbe.
Ezeknek a vonalaknak a metszéspontjában lesz a Q pont.
Rajzoljuk be ezeket a pontokat is a koordinátarendszerbe:
Hát, ez kész is.
De az izgalmak még csak most jönnek…
Ez itt egy koordinátarendszer.
Úgy készült, hogy vettünk egy számegyenest…
Meg ezt az előzőre merőleges másik számegyenest…
Aztán a nulla-pontjaiknál összeraktuk őket.
Léteznek olyan koordinátarendszerek is, ahol a tengelyek nem merőlegesek egymásra…
De most maradjunk inkább a merőleges verziónál.
Ezt derékszögű koordinátarendszernek nevezzük.
Van egy másik neve is: Descartes-féle koordinátarendszer.
Descartes egy ember volt, ő használta először a derékszögű koordinátarendszert.
Ezt a pontot, amely mindkét számegyenes nulla-pontja úgy hívjuk, hogy origó.
Az origó koordinátái:
A vízszintes tengelyt x tengelynek nevezzük.
A függőleges tengelyt pedig y-nak.
Hogyha itt van egy P pont a koordinátarendszerben…
Akkor az első koordinátája az x-koordináta…
És a második pedig az y.
x tengelynek nevezzük.
A dolog fordítva is működik…
Hogyha ismerjük egy pont koordinátáit:
Akkor a koordináták alapján pontosan meg tudjuk mondani, hogy hol van ez a pont.
És most itt jön egy nagyon fontos dolog…
Az x tengelyen lévő pontoknak van egy közös tulajdonsága.
Mindegyik ilyen pontnak a második koordinátája nulla.
És az y tengelyen lévő pontokban is van valami közös.
Ezeknek meg az első koordinátája nulla.
És ez a pont, amelyik mindkét tengelyen rajta van…
Ezt a pontot úgy hívjuk, hogy origó.
A koordinátatengelyek négy részre osztják a síkot.
Ezeket síknegyedeknek nevezzük.
Itt az első síknegyed…
Ez a második…
Itt van a harmadik…
Végül ez a negyedik.
Az első síknegyedben a pontok minkét koordinátája pozitív.
A második síknegyedben az első koordináta negatív, a második pozitív.
A harmadik síknegyedben mindkét koordináta negatív.
A negyedik síknegyedben pedig az első koordináta pozitív, de a második negatív.
És most lássuk, mik lehetnek ezeknek a pontoknak a koordinátái.
Kezdjük az A ponttal.
A pontok koordinátáit leolvasni nagyon egyszerű…
Húzunk egy párhuzamost az A ponton keresztül az y tengellyel…
És meg is van az x koordináta.
Hogyha az x tengellyel húzunk az A ponton keresztül egy egyenest…
Akkor pedig az y koordinátát kapjuk meg.
Aztán a C pont egy kicsit trükkös…
Az x tengellyel tudunk párhuzamost húzni…
És így az y koordinátát kapjuk meg.
Az x koordináta pedig…
Na igen, az nulla.
Hasonló a trükk a D-nél is.
Végül itt jön még az E és az F.
Ilyen egyszerű az egész…
