- Kombinatorika
- Halmazok, rendezett párok, leképezések
- Matematikai logika, ítéletkalkulus
- Gráfelméleti alapok
- Gráfok izomorfiája és síkbarajzolhatósága
- Gráfok bejárása és gráfalgoritmusok
- Kromatikus szám, klikk, perfekt gráfok
- Gráfparaméterek, párosítások
- Hálózatok
- Irányított gráfok, gráfalgoritmusok irányított gráfokban
- Lineáris leképezések
- Menger tételei, többszörös összefüggőség
- Páros gráfok, párosítások
- Sajátérték, sajátvektor, sajátfelbontás
- Teljes indukció
- Oszthatóság
- Euklideszi algoritmus & Diofantoszi egyenletek
- Kongruenciák
- Mátrixok
- Lineáris egyenletrendszerek
- Determináns, adjungált, kvadratikus alakok
- Komplex számok
- Polinomok
- Interpolációs polinomok
- Csoportok, gyűrűk, testek
Kromatikus szám, klikk, perfekt gráfok
Ennek a témakörnek a képletei
Letöltöm az egész kurzus összes képletét:
LetöltömLetöltöm ennek a témakörnek a képleteit:
LetöltömVálogass kedvedre a témakör képletei között:
Kromatikus szám
A legkevesebb színt, amivel egy gráf csúcsait kiszinezhetjük úgy, hogy a szomszédos csúcsok ne legyenek egyforma színűek, a gráf kromatikus számának nevezzük.
Jele: $\chi (G)$.
Klikk
Egy $G$ egyszerű gráfban klikknek nevezzük azokat a részgráfokat, amelyek teljes gráfok.
Klikkszám
Egy gráf klikkszáma a gráfban található maximális klikk elemszáma.
A $G$ gráf klikkszámát $\omega (G)$-vel jelöljük.
Minden gráfban a klikkszám alsó becslés a kromatikus számra:
\( \omega (G) \leq \chi (G) \)
Feszített részgráf
A $G$ gráfban a $G'$ részgráf feszített részgráf, ha bármely két csúcs a $G'$ gráfban pontosan akkor szomszédos, ha $G$-ben is szomszédos.
Perfekt gráf
Ha egy $G$ gráf minden $G'$ feszített részgráfjára igaz, hogy
\( \omega (G') = \chi (G') \)
akkor a $G$ gráfot perfekt gráfnak nevezzük.
Ha egy gráf perfekt, akkor a kromatikus száma egyenlő a klikkszámával. Az állítás fordítva nem igaz, abból, hogy $\omega (G') = \chi (G')$ még nem következik, hogy a gráf perfekt.
Kromatikus szám alsó és felső becslése
\( \omega(G) \leq \chi(G) \leq \Delta(G) + 1 \)
ahol $\omega(G)$ a gráf klikkszáma, $\chi(G)$ a kromatikus száma és $\Delta(G)$ a maximális fokszáma.
Mohó színezés
A mohó színezés egy algoritmus a gráfok színezésére.
Lényege, hogy sorba rakjuk a gráf csúcsait, és elkezdjük színezni úgy, hogy minden csúcs színezéséhez a lehető legkisebb sorszámú színt használjuk. Ezt addig folytatjuk, amíg az összes csúcs ki nem lesz színezve, és így elhasználunk legfeljebb $\Delta(G)+1$ darab színt.
Brooks-tétel
Ha $G$ nem teljes gráf, vagy páratlan csúcsú kör, akkor
\( \chi(G) \leq \Delta(G) \)
Élkromatikus szám
Egy $G$ gráfban azt a legkisebb számot, amire a gráfnak már van jó élszínezése, a $G$ gráf élkromatikus számának nevezzük.
Jele: $\chi_e$
Vizing-tétel
A Vizing-tétel a gráfok élkromatikus számára ad alsó és felső becslést:
\( \Delta(G) \leq \chi_e(G) \leq \Delta(G) + 1 \)
Vagyis a $G$ egyszerű gráfok két osztályba sorolhatók:
Első osztály: $\chi_e(G) = \Delta(G)$
Második osztály: $\chi_e(G) = \Delta(G)+1 $
Intervallumgráfok
Az intervallumgráf egy olyan gráf, melynek csúcsai megfeleltethetőek a valós számok egy-egy intervallumának, és két csúcs között akkor vezet él, ha a nekik megfeleltethető két intervallum metszete nem üres.
Az intervallumgráfok mindig perfekt gráfok.
Páros gráf
Egy $G$ gráfot páros gráfnak nevezünk, ha csúcsainak a $V(G)$ halmaza felbontható az $A$ és $B$ diszjunkt részhalmazokra, úgy hogy $A$-n és $B$-n belül nem vezetnek élek.
A páros gráfok kromatikus száma 2, élkromatikus számukra pedig König Dénesnek van egy remek tétele:
Ha $G$ páros gráf, akkor $ \chi_e(G) = \Delta(G) $
Mycielski-gráfok
Jan Mycielski lengyel matematikust nyugtalanította az a kérdés, hogy léteznek-e olyan gráfok, amelyeknek a kromatikus száma nagyon nagy, de a klikkszáma csak 2.
Létrehozott egy konstrukciót, amivel olyan gráfokat lehet alkotni, amelyek klikkszáma 2, a kromatikus számuk pedig bármilyen nagy lehet. Ezeket a gráfokat Mycielski-gráfoknak nevezzük.
Ennek a témakörnek a feladatai
Letöltöm az egész kurzus összes feladatát:
LetöltömLetöltöm ennek a témakörnek a feladatait:
LetöltömVálogass kedvedre a témakör feladatai között:
a) Színezzük ki a Svájccal határos országokat úgy, hogy két szomszédos ország nem lehet egyforma színű.
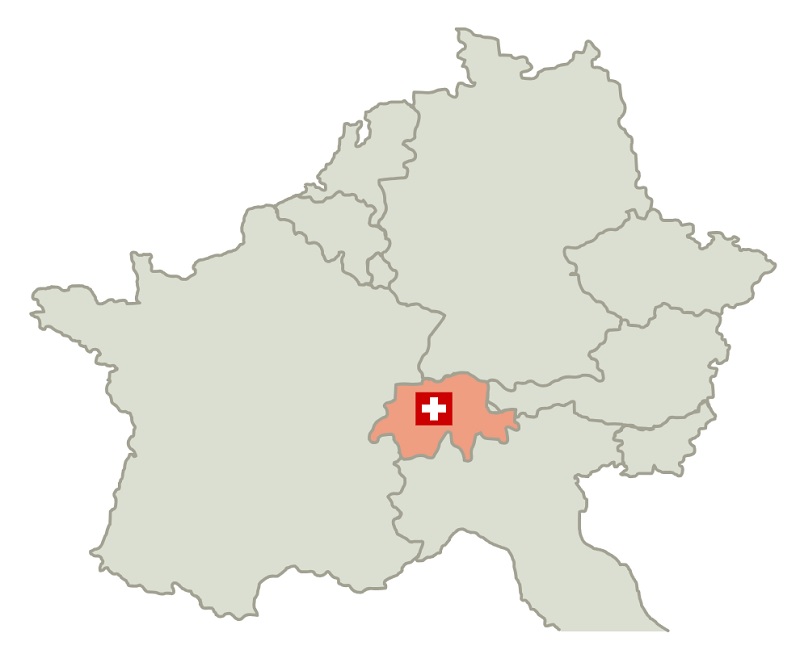
b) Színezzük ki a Luxemburggal határos országokat úgy, hogy két szomszédos ország nem lehet egyforma színű.

a) Mekkora a kromatikus száma ennek a gráfnak?

b) Mekkora a kromatikus száma ennek a gráfnak?

c) Mekkora a kromatikus száma ennek a gráfnak?
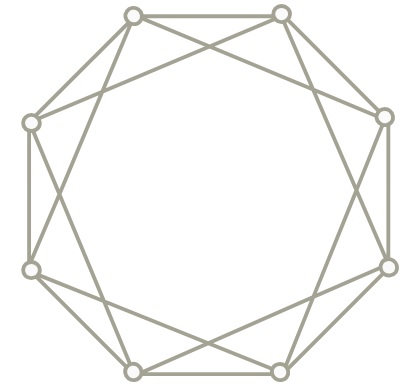
d) Egy $G$ gráfban 1000 darab csúcstól eltekintve minden pont foka legfeljebb 999. Bizonyítsuk be, hogy a gráf kromatikus száma legfeljebb 1000.
e) Egy $G$ gráf csúcshalmaza legyen a $V(G)=\{1,2,3,\dots,30\}$ és két csúcs akkor legyen szomszédos, ha a különbségük legalább 6. Mekkora ennek a gráfnak a kromatikus száma?
a) Mennyi a Petersen gráf élkromatikus száma?

b) Egy 1001 csúcsú gráf úgy keletkezik, hogy egy 1000 csúcsot tartalmazó kör minden pontját összekötjük az 1001-edik csúccsal. Mekkora ennek a gráfnak az élkromatikus száma?
a) Egy 2000 csúcsú G gráf két darab egyenként 1000 csúcsot tartalmazó körből készítettünk, úgy, hogy az egyik kör minden csúcsát összekötöttük a másik kör minden csúcsával.
Mekkora az így keletkező G gráf kromatikus száma és élkromatikus száma?
b) Számoljuk ki a Petersen gráf kromatikus számát.
c) Egy $G$ gráf csúcshalmaza legyen $V(G)=\{ 1,2,3,\dots, 30 \} $ és két csúcs akkor legyen szomszédos, ha a számok távolsága legalább 5. Mekkora ennek a gráfnak a kromatikus száma?
d) Egy másik gráf csúcshalmaza szintén a $V(G)=\{ 1,2,3,\dots, 30 \} $. A gráf $x,y \in V(G)$ csúcsai pontosan akkor legyenek szomszédosak, ha $ \mid x -y \mid = 4$ vagy $ \mid x - y \mid =6$. Határozzuk meg a gráf kromatikus számát.
Döntsük el, hogy az alábbi gráfok intervallum gráfok-e.
a)

b)

c)

d)
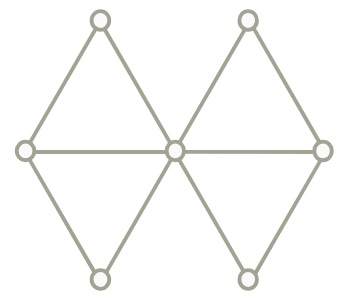
a) A $G$ gráf csúcshalmaza legyen a $V(G)=\{ 1, 2, 3, \dots, 30 \}$. Az $x,y \in V(G)$ csúcsok pontosan akkor legyenek szomszédosak $G$-ben, ha $ \mid x -y \mid = 3$ vagy $\mid x -y \mid = 5$. Határozzuk meg a $G$ gráf $\chi{(G)}$ kromatikus számát és $\chi_e{(G)}$ élkromatikus számát.
b) Egy 20 csúcsú fában 11 csúcs foka 1 és a maradék 9 csúcs foka is azonos. Határozzuk meg a fa élkromatikus számát.
c) Egy 1000 csúcsú gráfot úgy kaptunk, hogy vettünk két 500 pontú utat, és az egyik út minden pontját összekötöttük a másik út minden pontjával. Mekkora az így kelektező gráfnak a kromatikus száma és az élkromatikus száma?
d) Egy 1001 csúcsú $G$ gráfot két körből, egy 500 pontú és egy 501 pontú körből készítünk úgy, hogy az egyik kör minden csúcsát összekötjük a másik kör minden csúcsával. Mekkora az így keletkező gráf kromatikus száma és élkromatikus száma?
Egy 1000 csúcsú teljes gráfból elhagyjuk egy Hamilton-kör éleit. Mekkora lesz az így kapott gráf kromatikus száma?
A $G$ gráf csúcshalmaza $V(G)=\{1,2,\dots,100\}$. Az $x,y \in V(G)$ csúcsok akkor legyenek szomszédosak $G$-ben, ha $x \neq y$ és $10 \mid x \cdot y$.
Határozzuk meg $G$ kromatikus számát.
Egy 8 csúcsú teljes gráfból töröljük egy 6 csúcsú kör éleit. Határozzuk meg a kapott gráf kromatikus számát.
Egy 100 csúcsú teljes gráfból töröljük egy 50 csúcsú kör éleit. Határozzuk meg a kapott gráf kromatikus számát.
A $G$ gráf csúcshalmaza $V(G)=\{1,2,\dots,1000\}$. Az $x,y \in V(G)$ csúcsok akkor legyenek szomszédosak $G$-ben, ha $x \neq y$ és $(x,y) \geq 10$. Határozzuk meg $G$ kromatikus számát.
Határozzuk meg egy 6 csúcsú kör komplementerének élkromatikus számát.
Itt mindent megtudhatsz a gráfok kromatikus számáról. Elmeséljük, mit is jelent a kromatikus szám pontosan, hogyan kell kiszámolni, mire kell figyelni. Megnézzük, hogy mi az a klikk, és mi köze van a klikknek a kromatikus számhoz. Gyorsan és egyszerűen megtudhatod, hogy mi az a klikk, és mit jelent egy gráf klikkszáma. Megnézzük, hogyan kell kiszámolni, mi a kapcsolat a klikkszám és a kromatikus szám között, és kiderül, hogy vannak olyan perfekt gráfok, ahol a klikkszám és a kromatikus szám megegyezik. Megtudod, mit jelent az, hogy feszített részgráf, mik azok a perfekt gráfok, hogyan lehet őket felismerni. Megnézzük a perfekt gráfok klikkszámát és kromatikus számát, és kiderül néhány nagyon izgalmas dolog. Megnézheted, mit jelent a gráfok mohó színezése, hogyan kell elkészíteni egy gráf mohó színezését, és ez alapján becslést adni a kromatikus számra. A kromatikus szám alsó és felső becslése, példák. Az is kiderül, hogy mi az a Brooks-tétel. Megnézheted, mi az élkromatikus szám, hogyan lehet meghatározni egy gráf élkromatikus számát. Kiderül, hogyan működik a Vizing-tétel, és hogyan használhatjuk az élkromatikus szám kiszámolására. Élszínezés feladatok, megoldással, gráfok élkromatikus száma és élszínezése. Elmeséljük, mik azok az intervallumgráfok, hogyan keletkeznek, és mi az értelmük. Megnézzük az intervallumgráfok tulajdonságait, és azt, hogyan lehet egy gráfról eldönteni, hogy intervallumgráf-e vagy sem. Intervallumgráf feladatok megoldással. Ráadásul azt is megnézzük, hogyan kell kiszámolni egy páros gráf élkromatikus számát és kromatikus számát. Feladatok páros gráfok kromatikus számaival kapcsolatban, König Dénes tétele. Végezetül pedig röviden és szuper-érthetően elmeséljük, mi az a Mycielski-konstrukció, mi köze van a gráfok színezéséhez, a kromatikus számhoz és a klikkszámhoz. Mycielski gráfok, Grötzsch gráf.



