- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
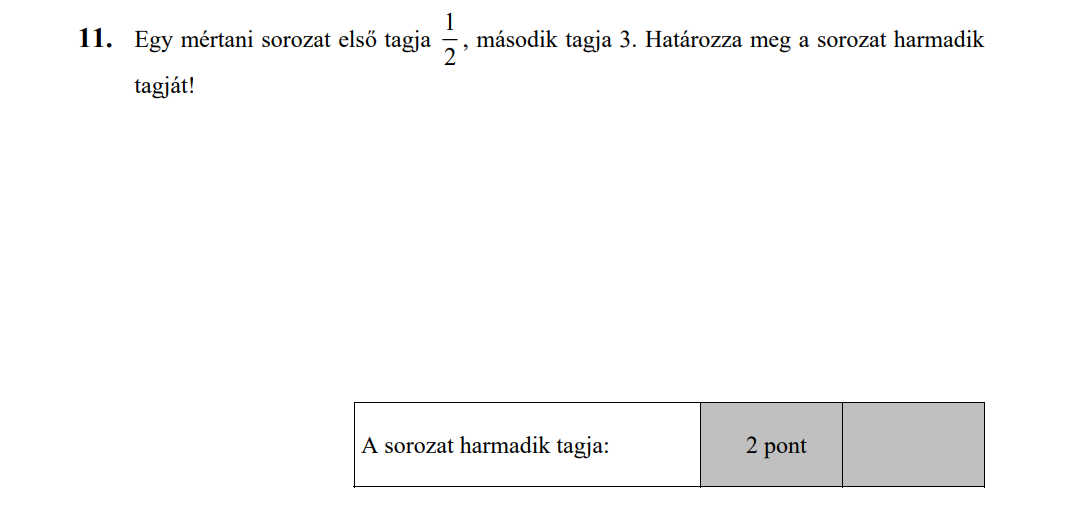
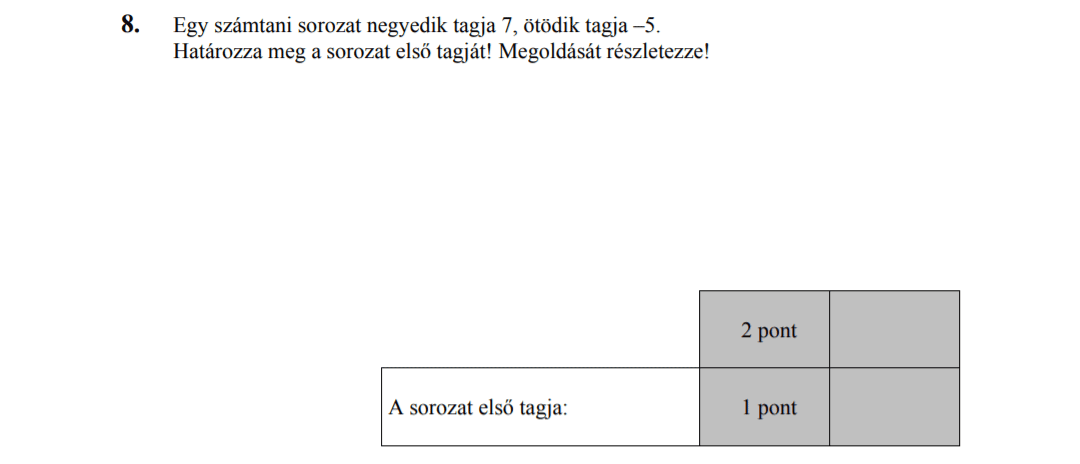
- Számtani és mértani sorozatok (16 pont)
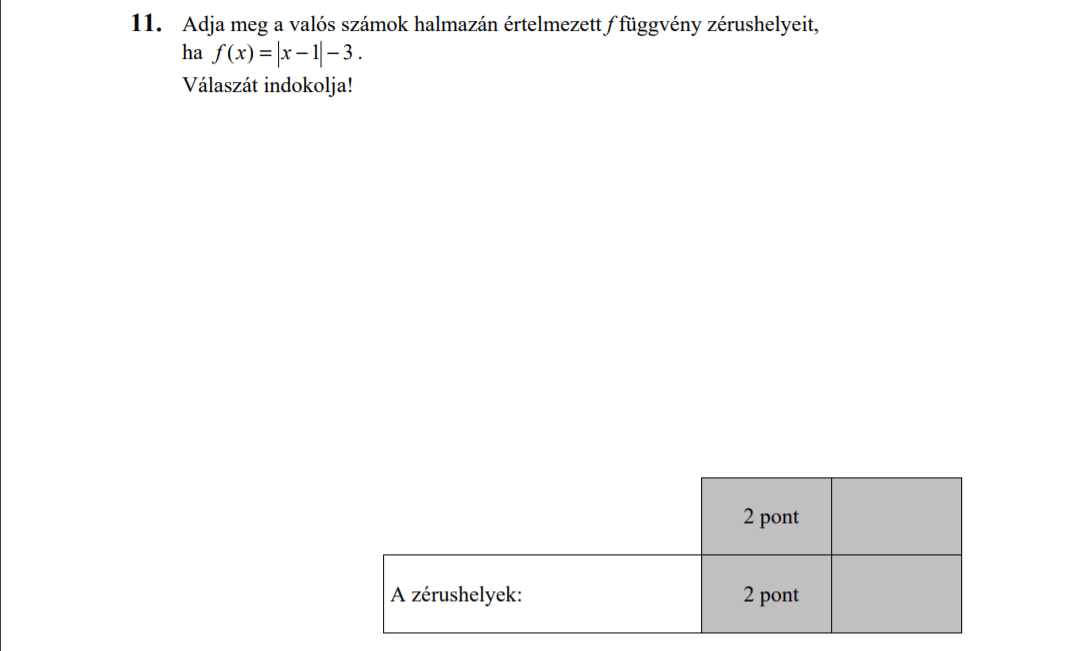
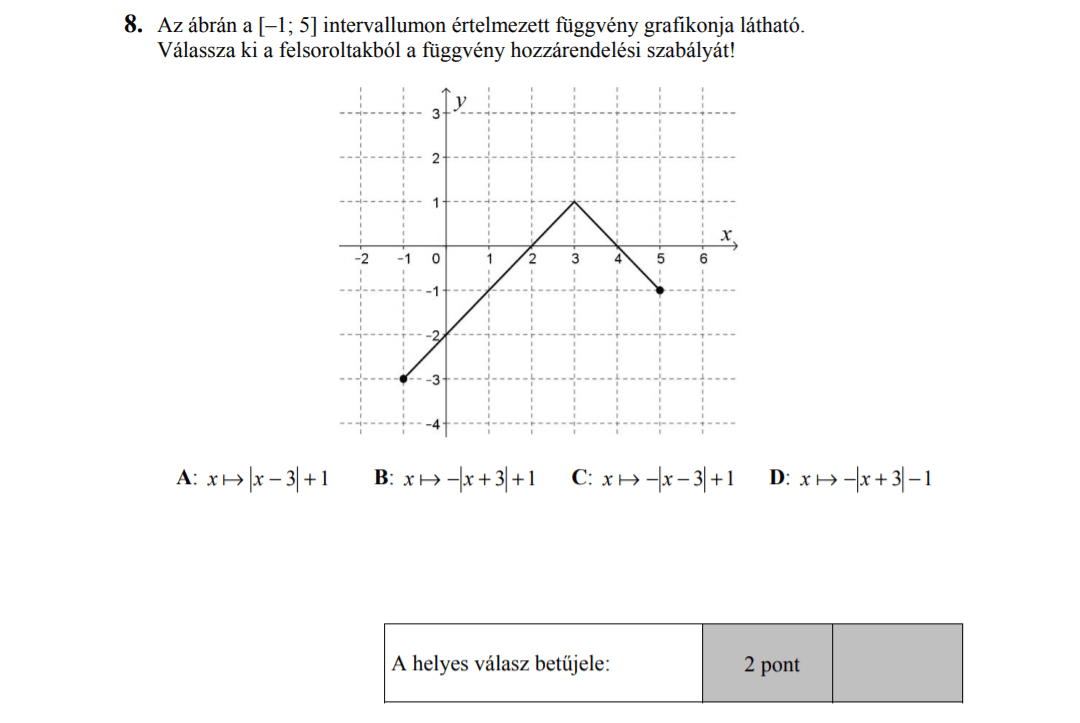
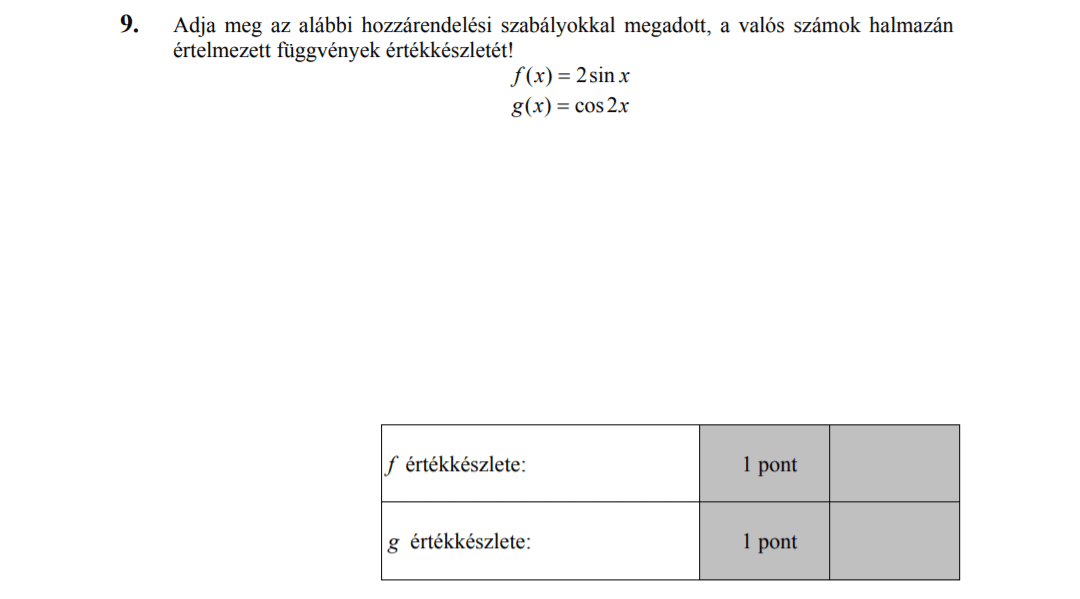
- Függvényekkel kapcsolatos feladatok (9,8 pont)
- Térgeometria (9,8 pont)
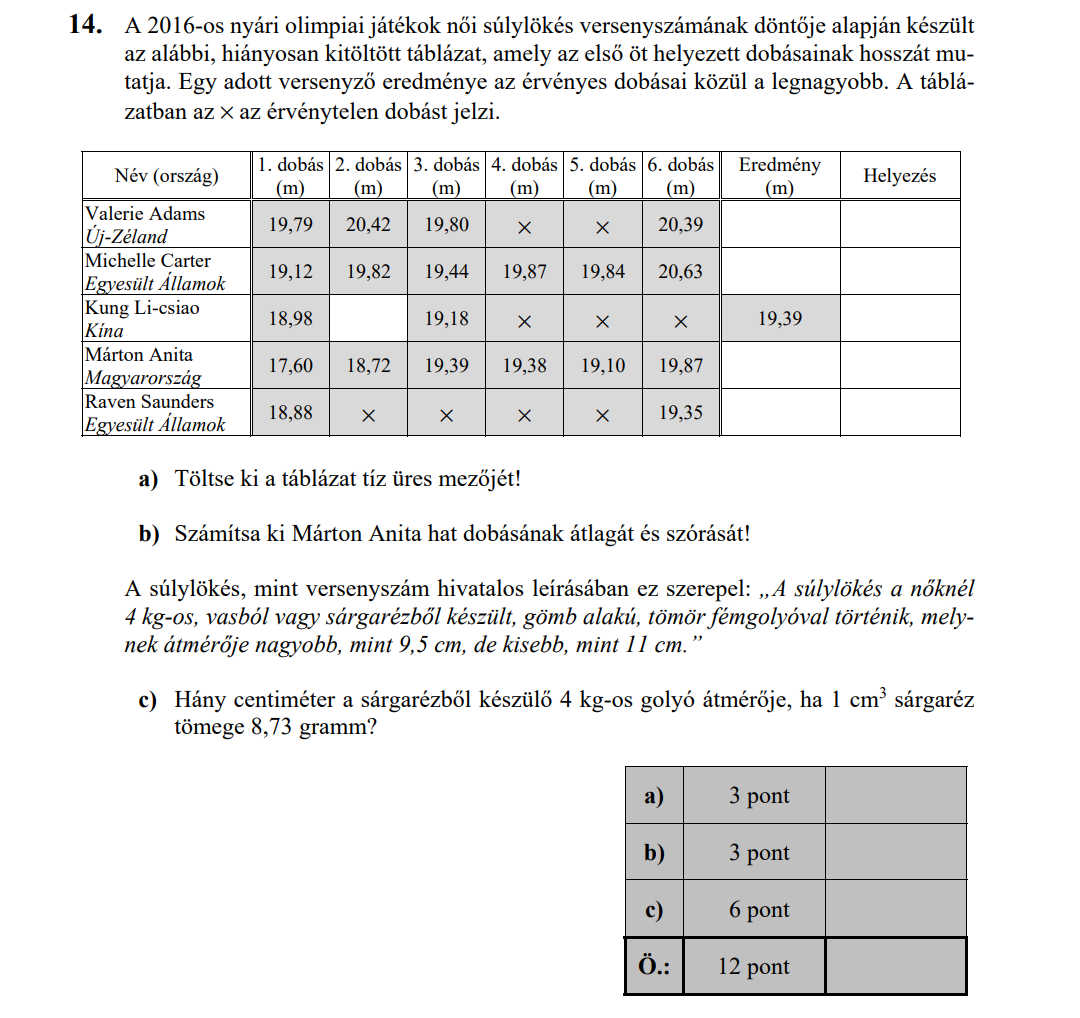
- Statisztika (9,3 pont)
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
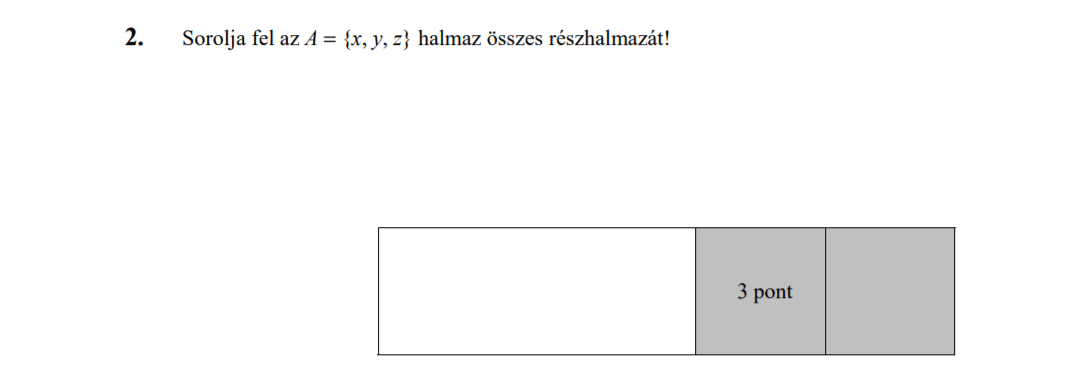
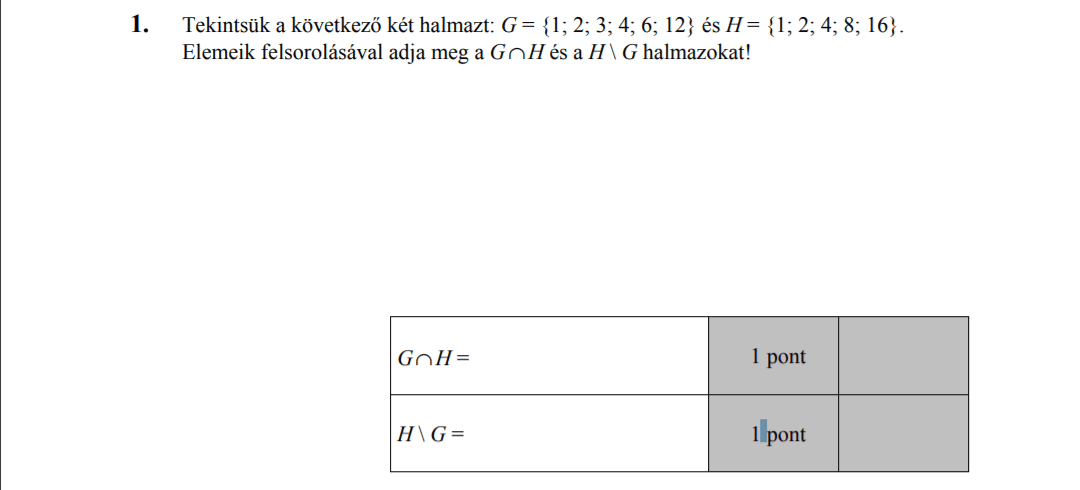
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
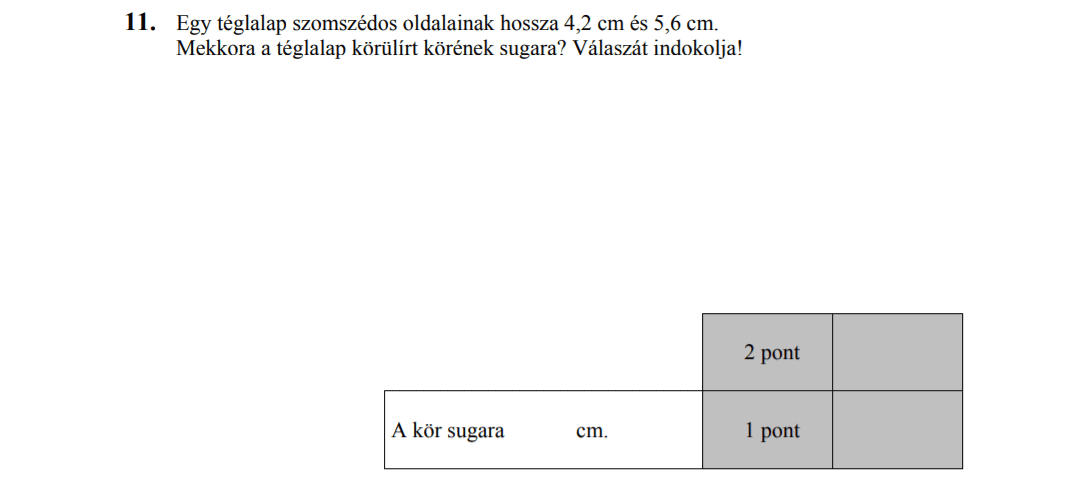
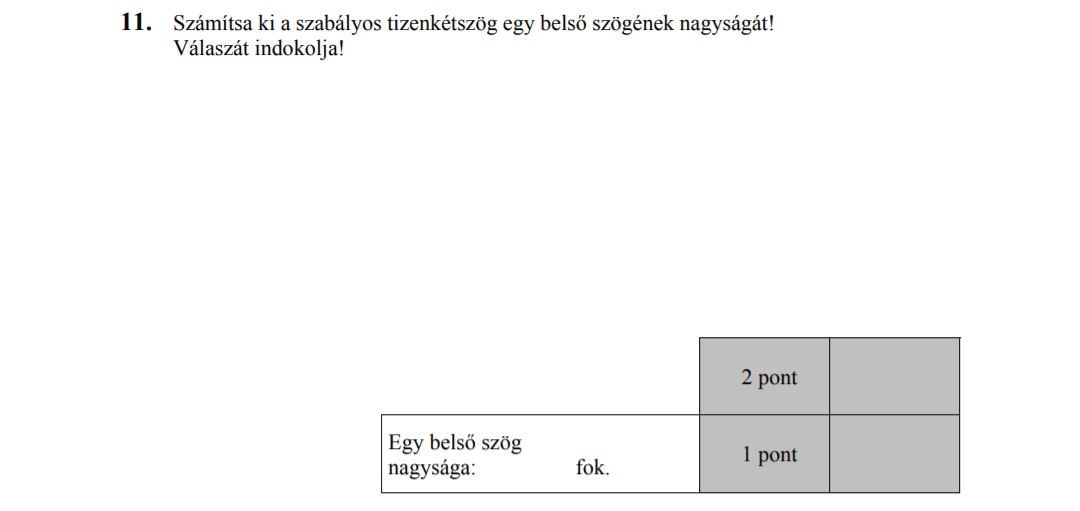
- Síkgeometria (4,5 pont)
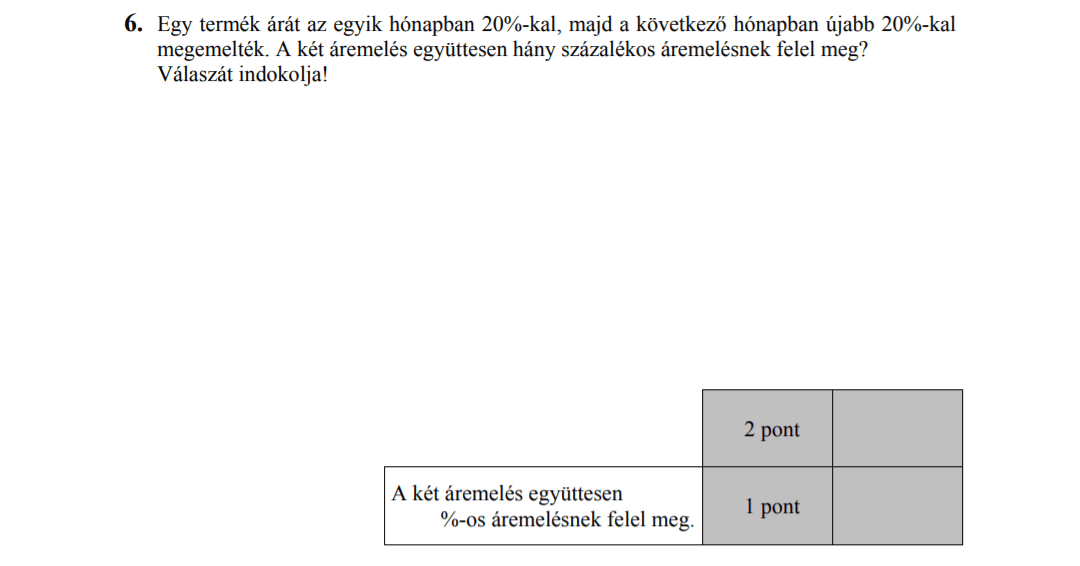
- Százalékszámítás (3,8 pont)
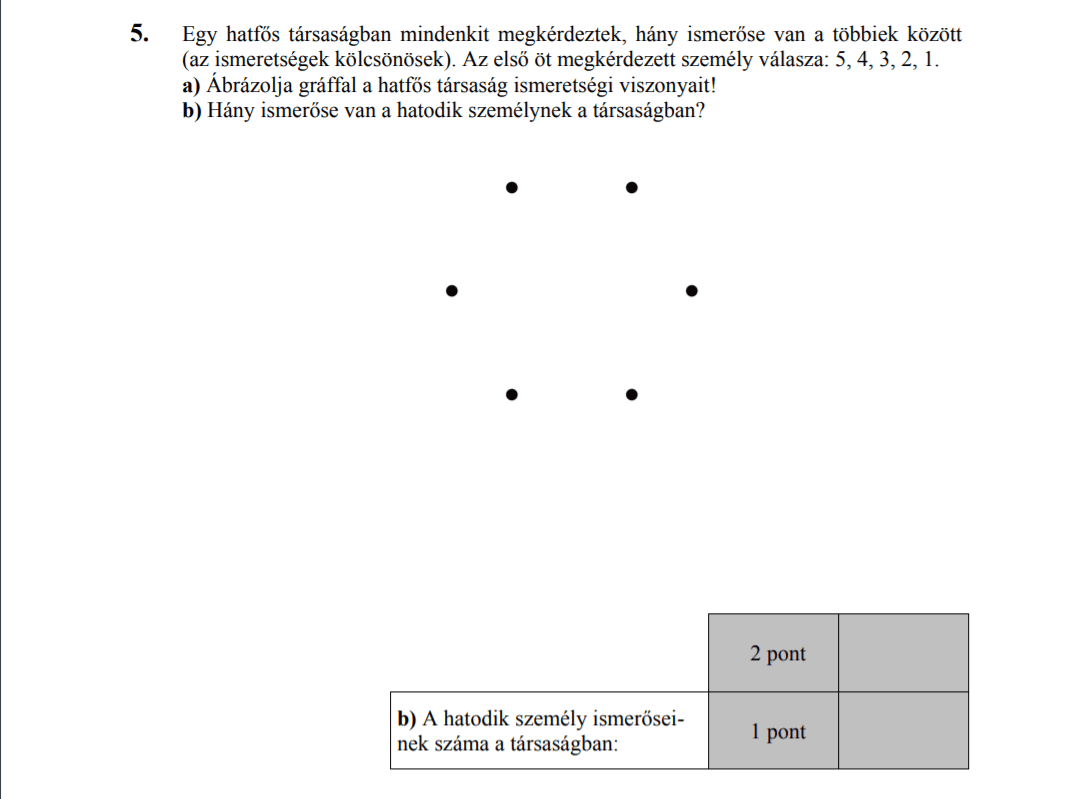
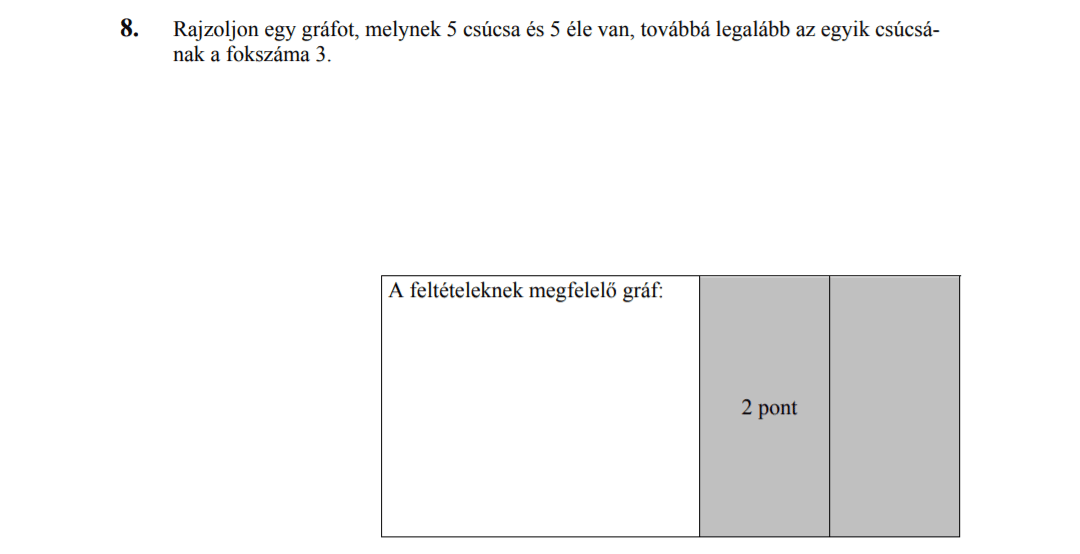
- Gráfok (3 pont)
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
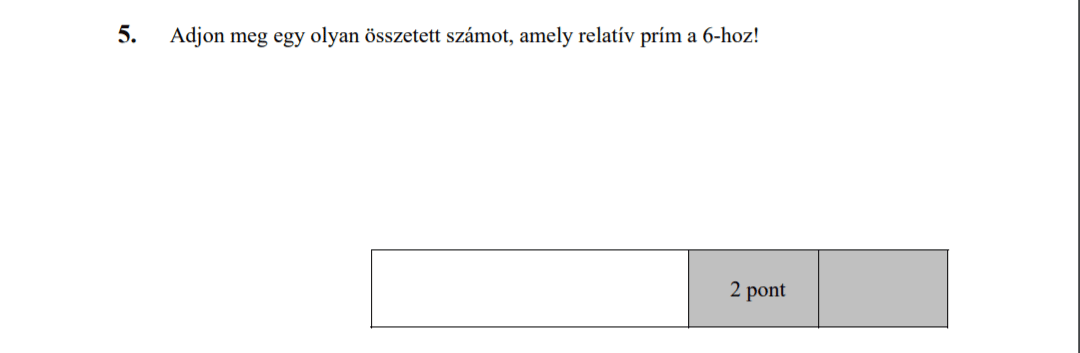
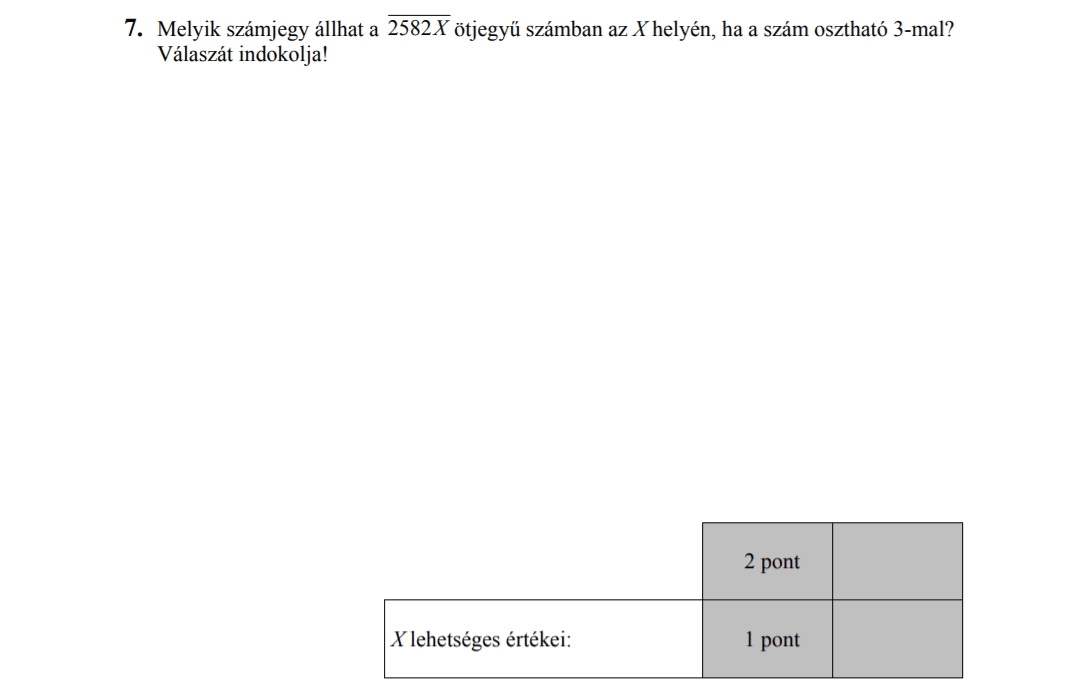
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Bizonyítási módszerek, matematikai logika
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


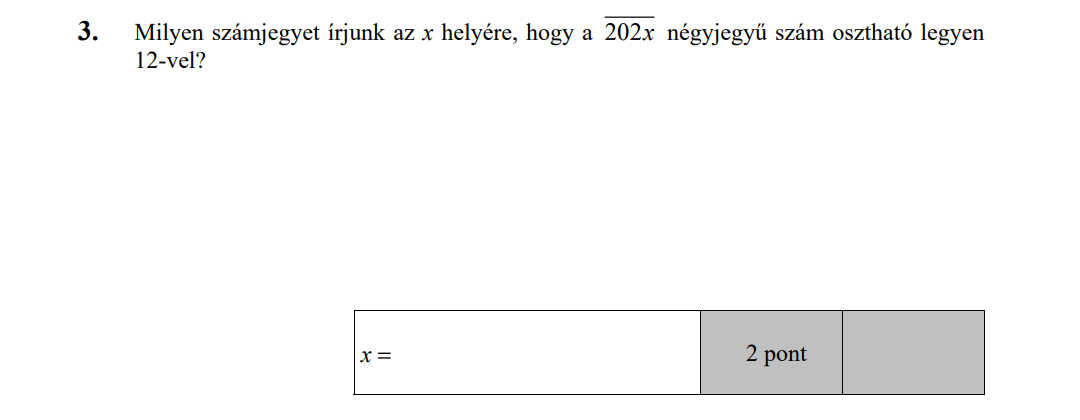
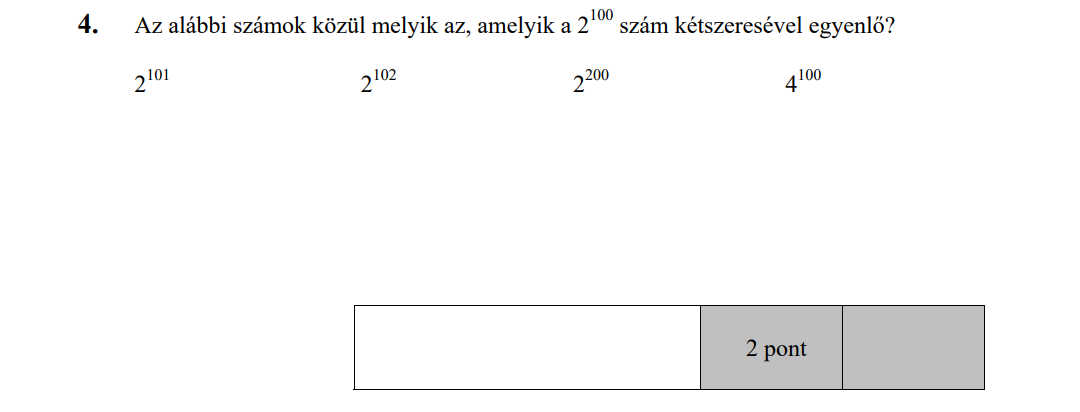



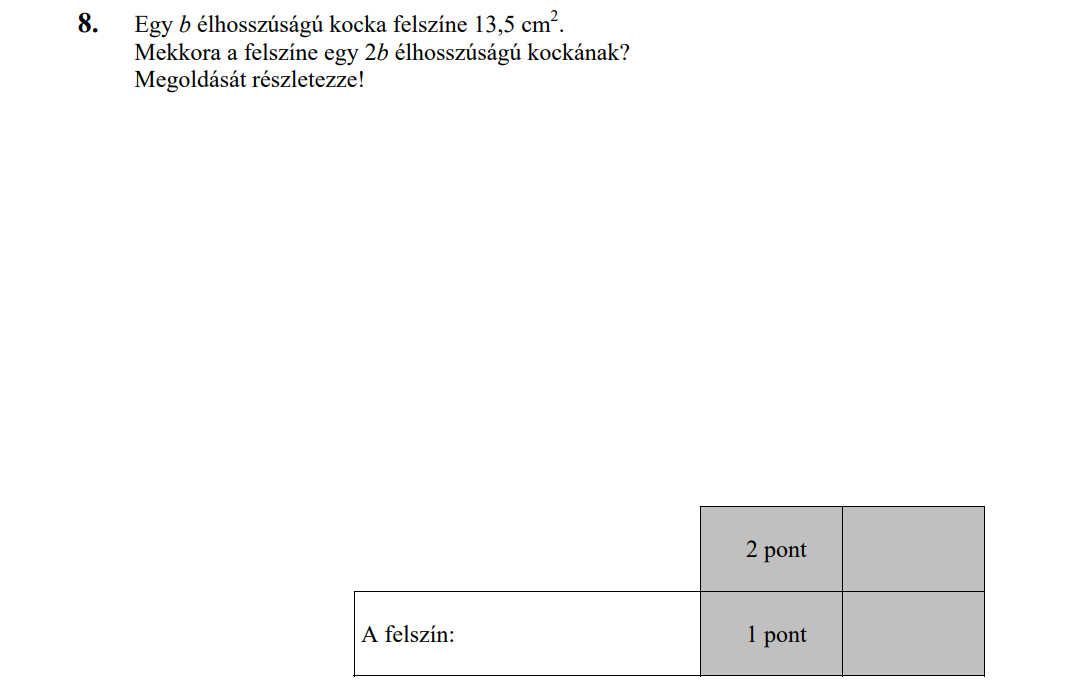




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
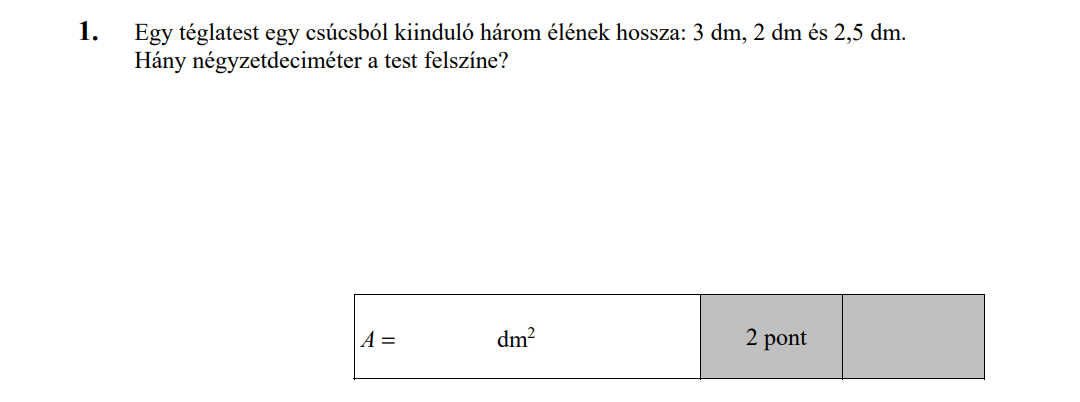
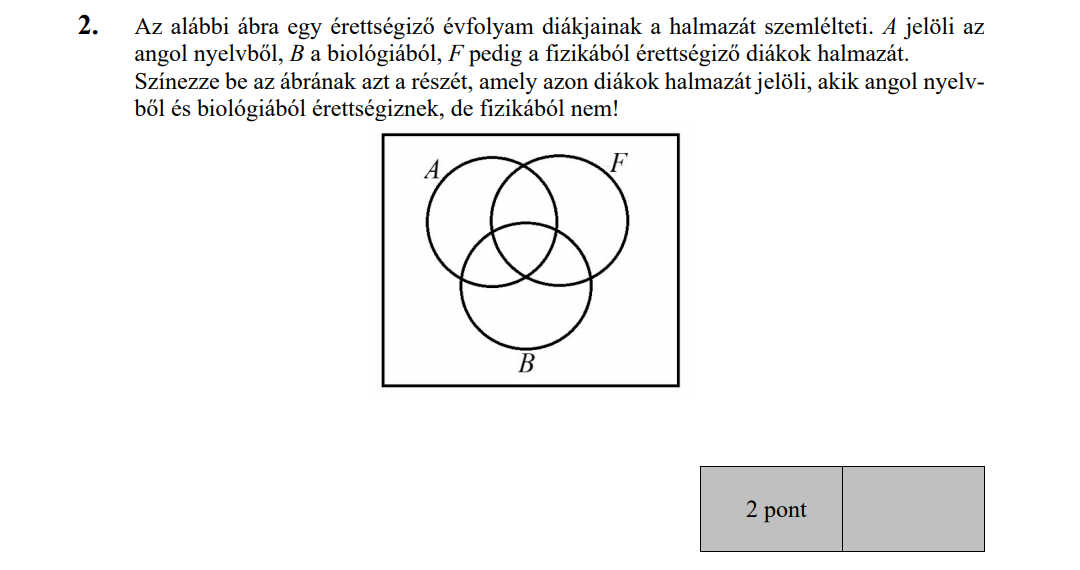

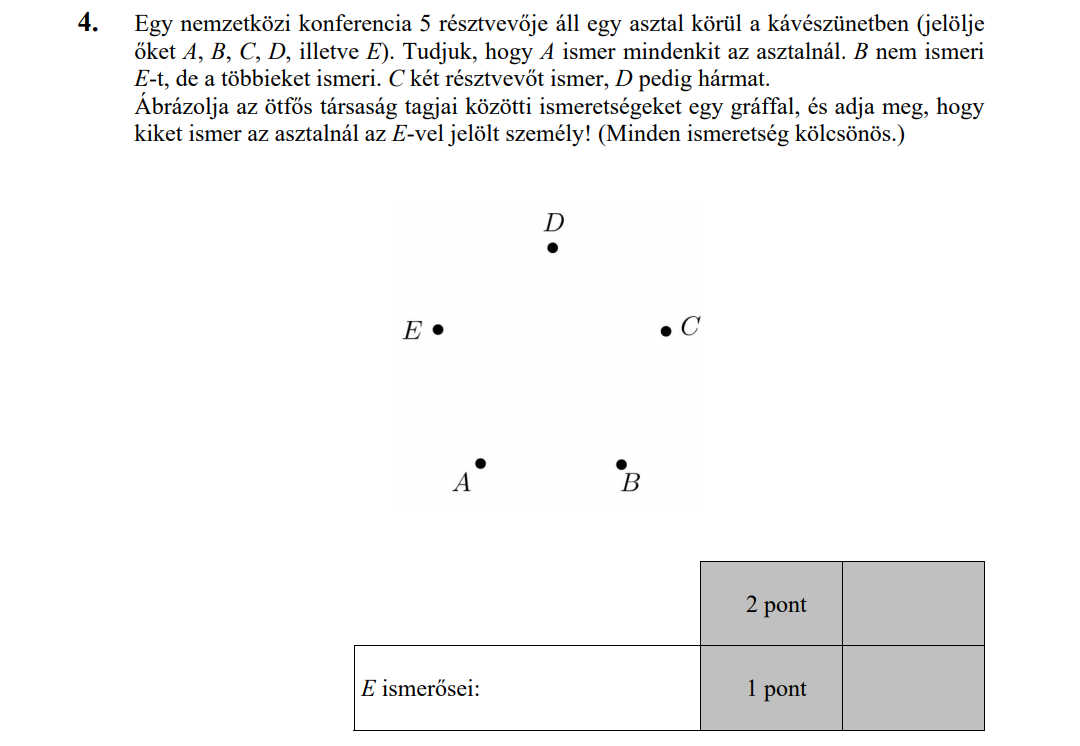

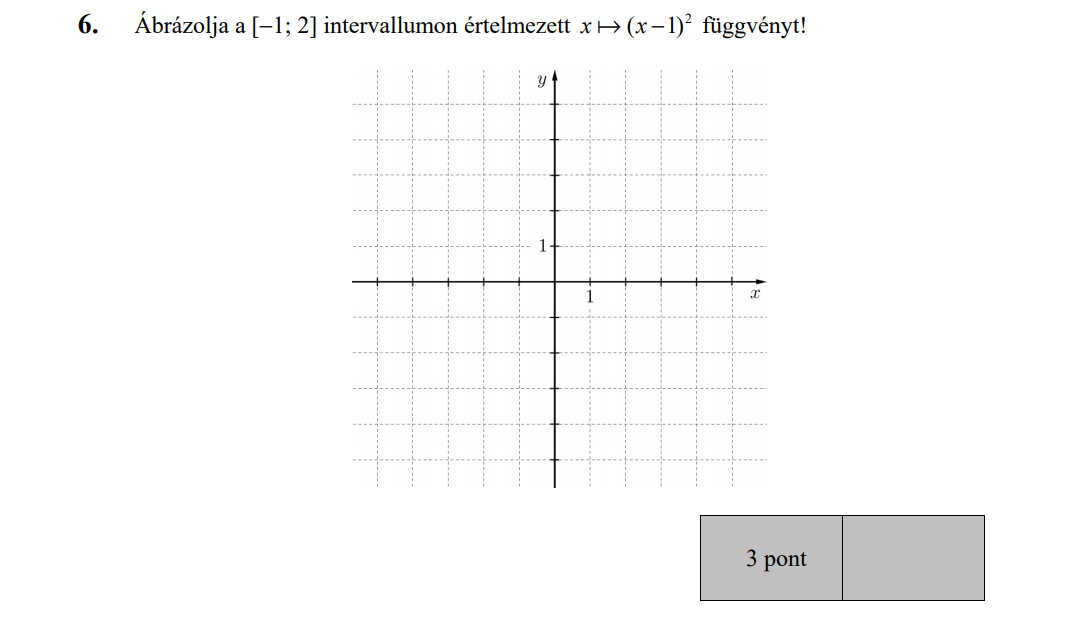



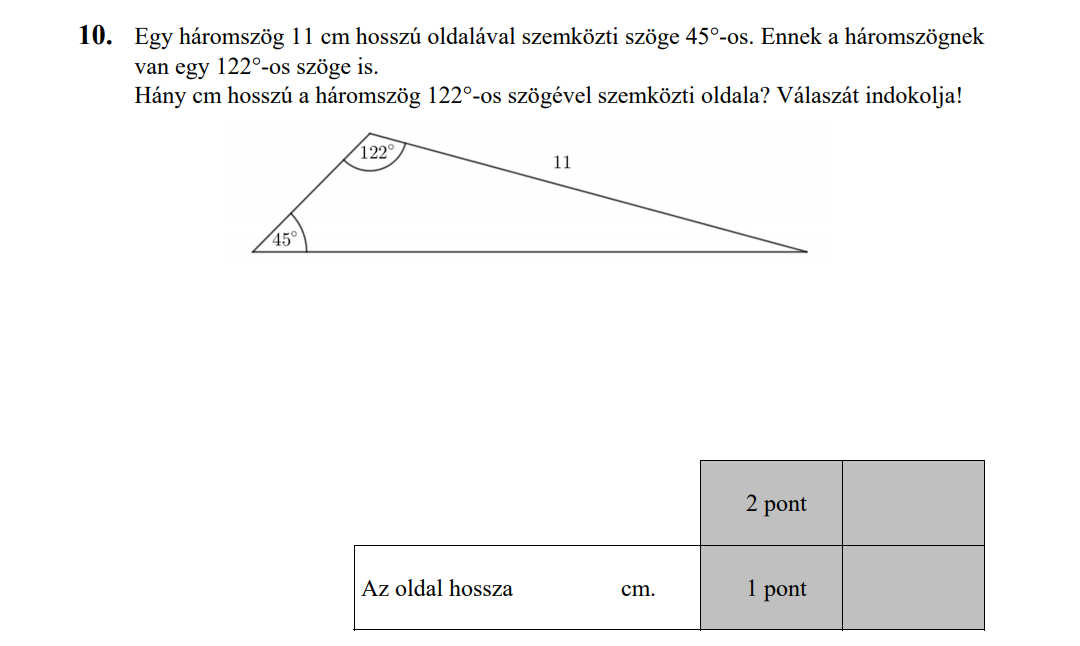

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



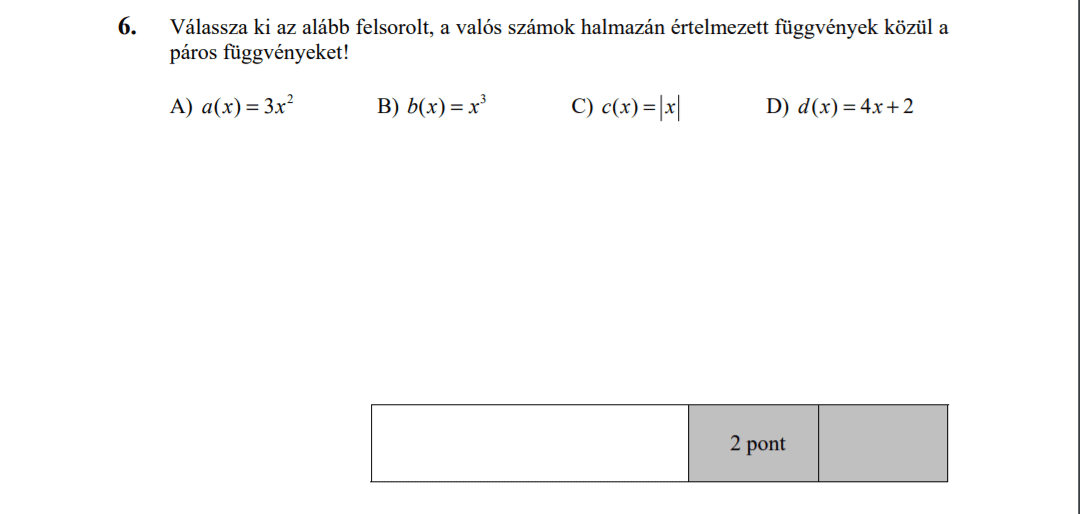
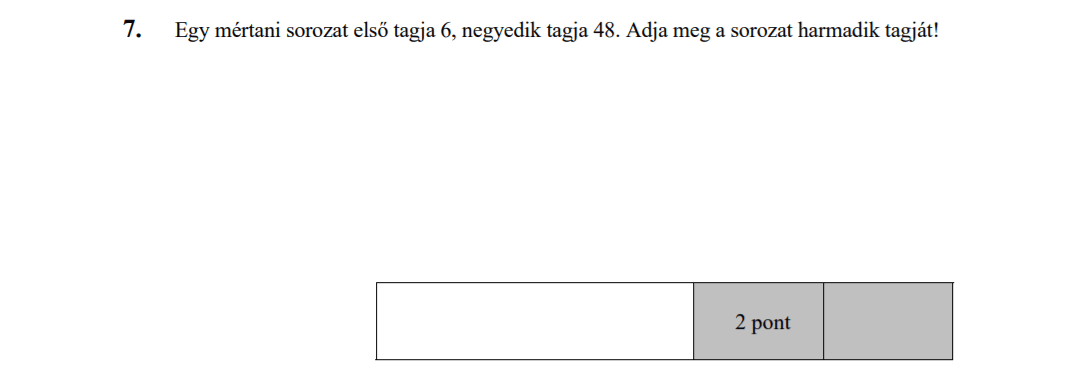



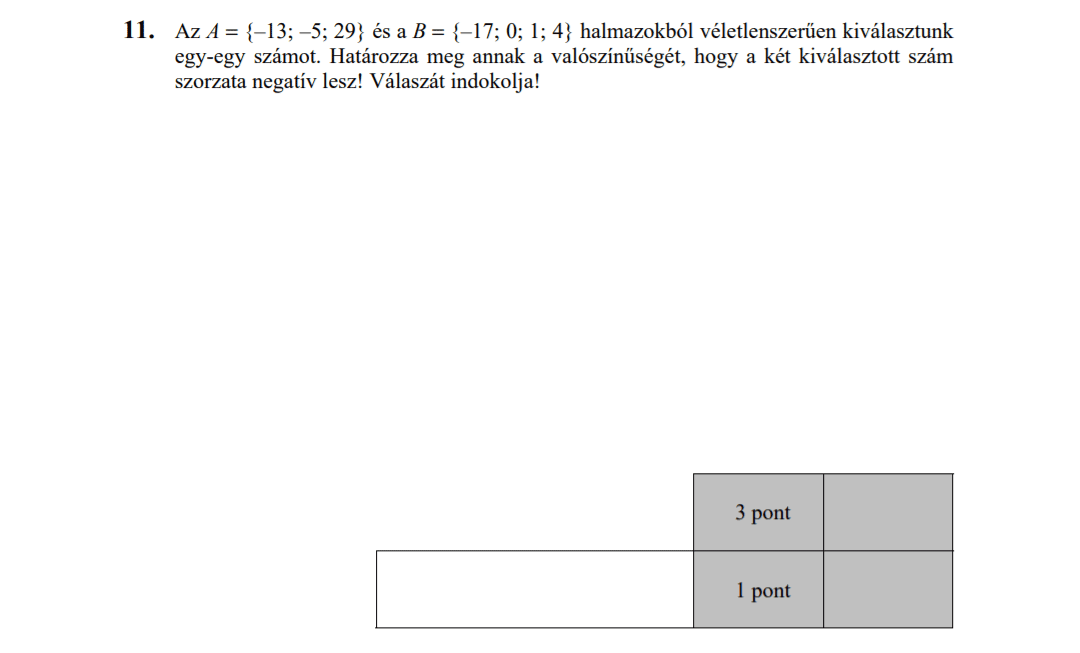

MÁSODIK RÉSZ


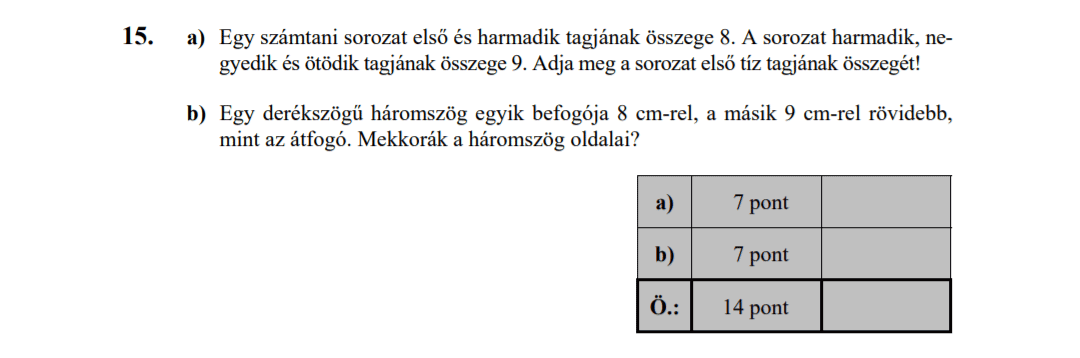



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






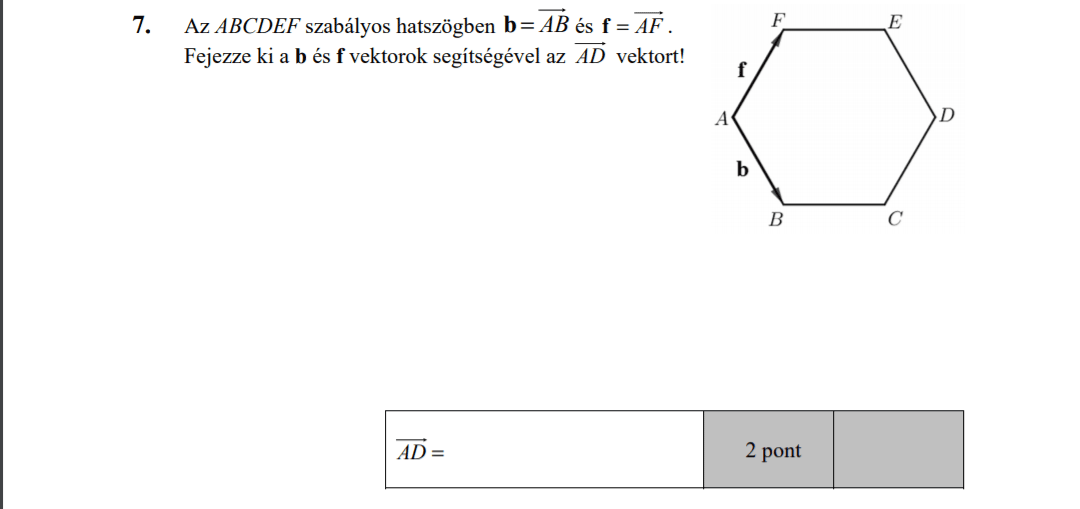



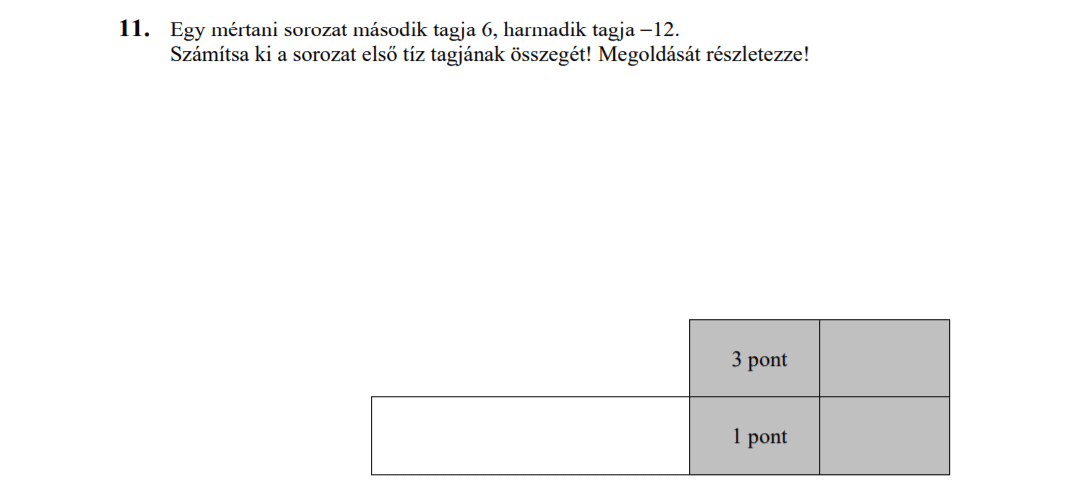

MÁSODIK RÉSZ

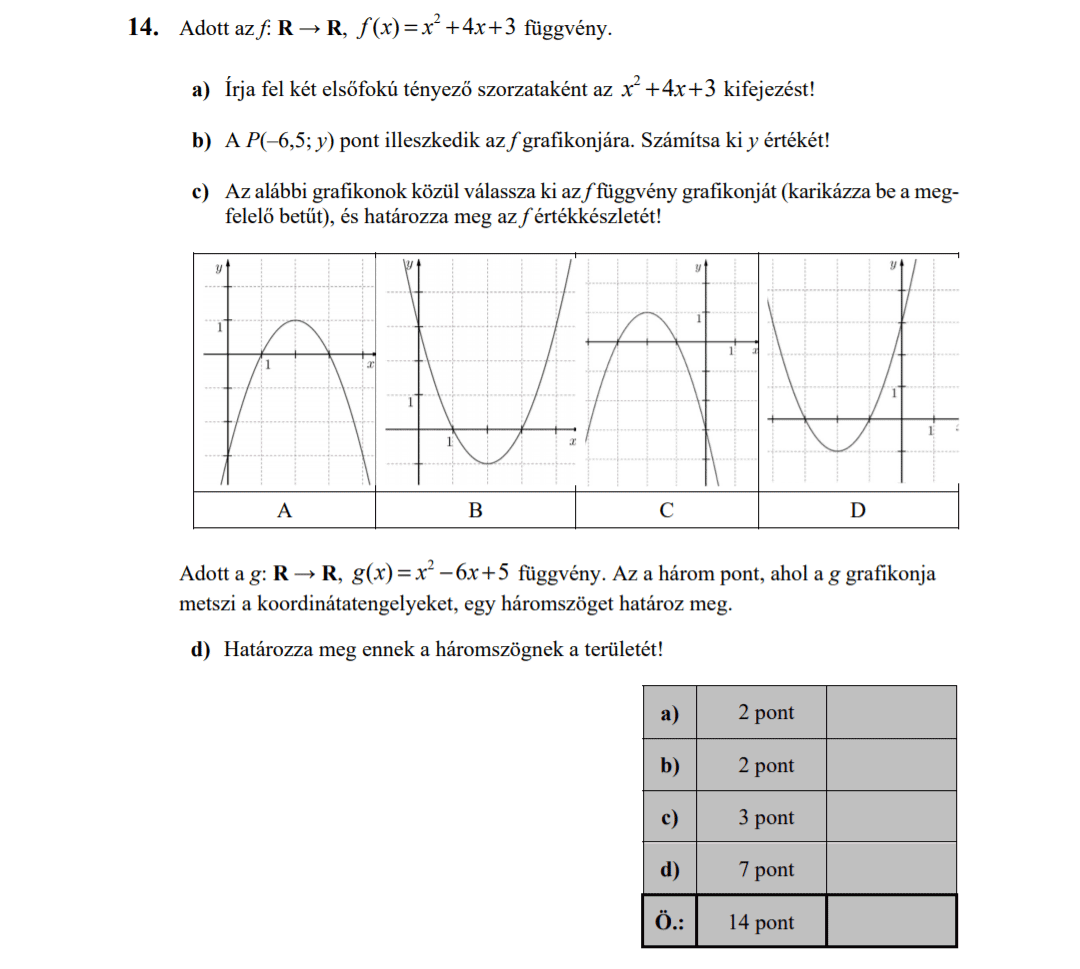




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



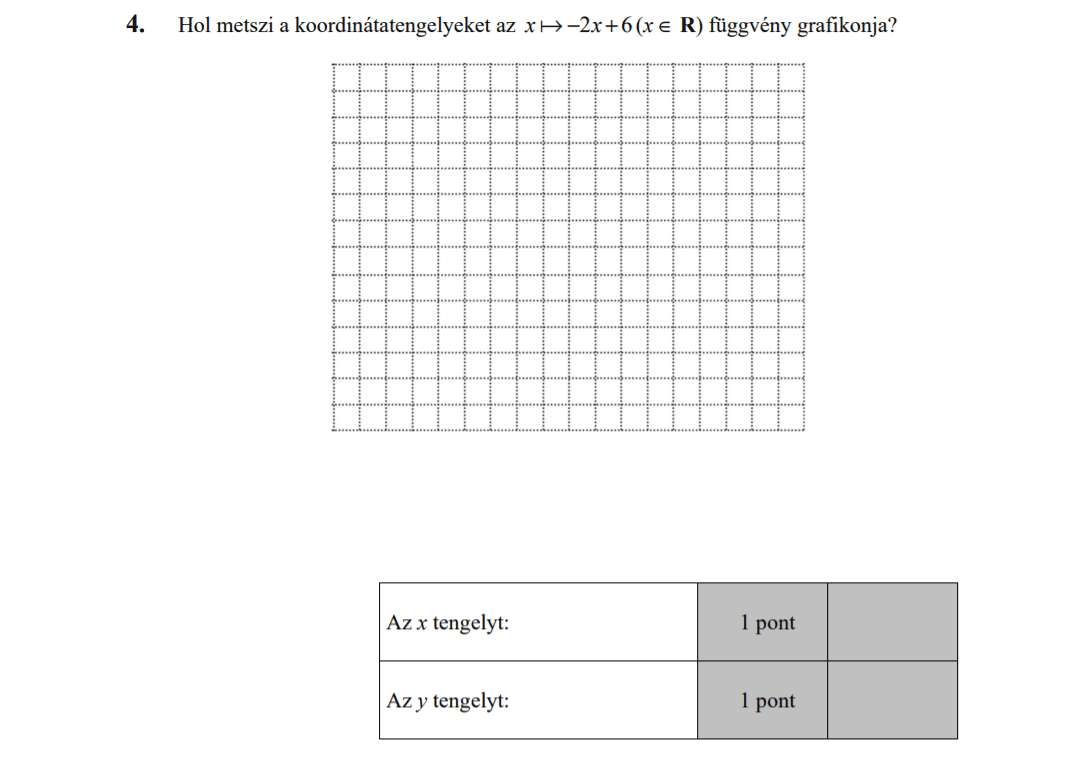

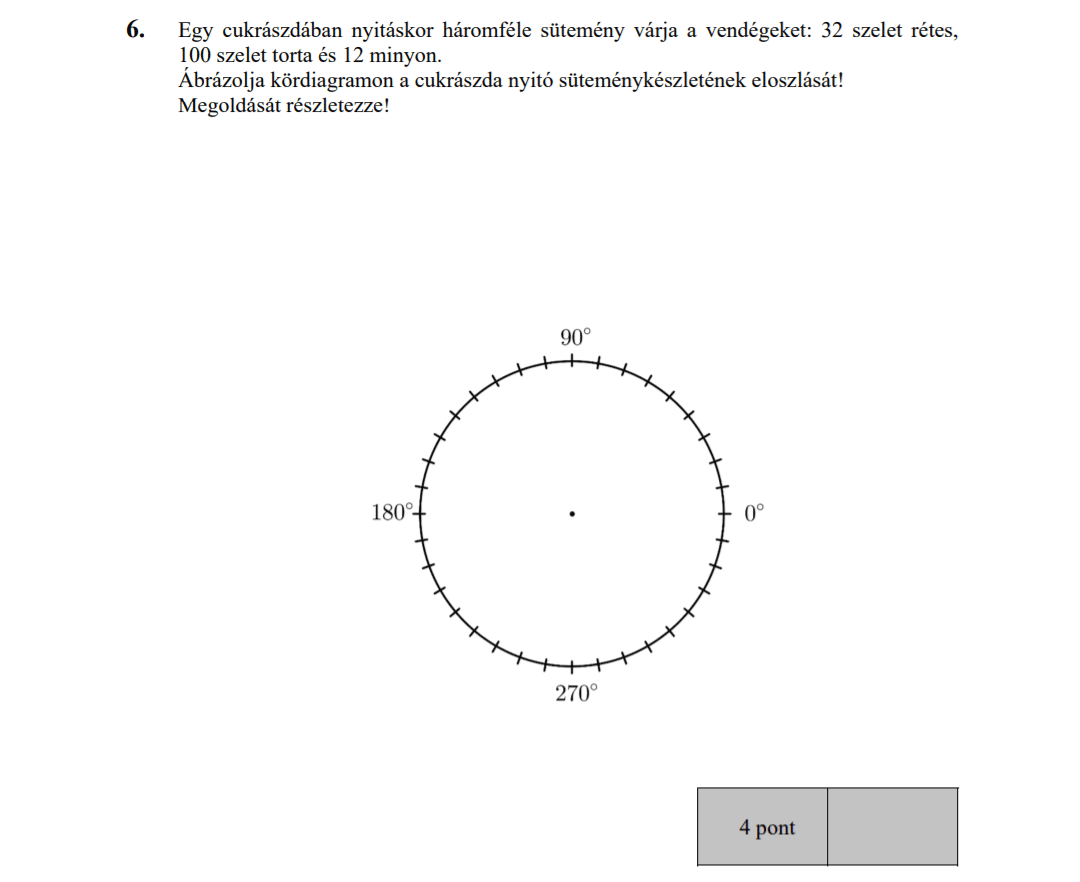






MÁSODIK RÉSZ

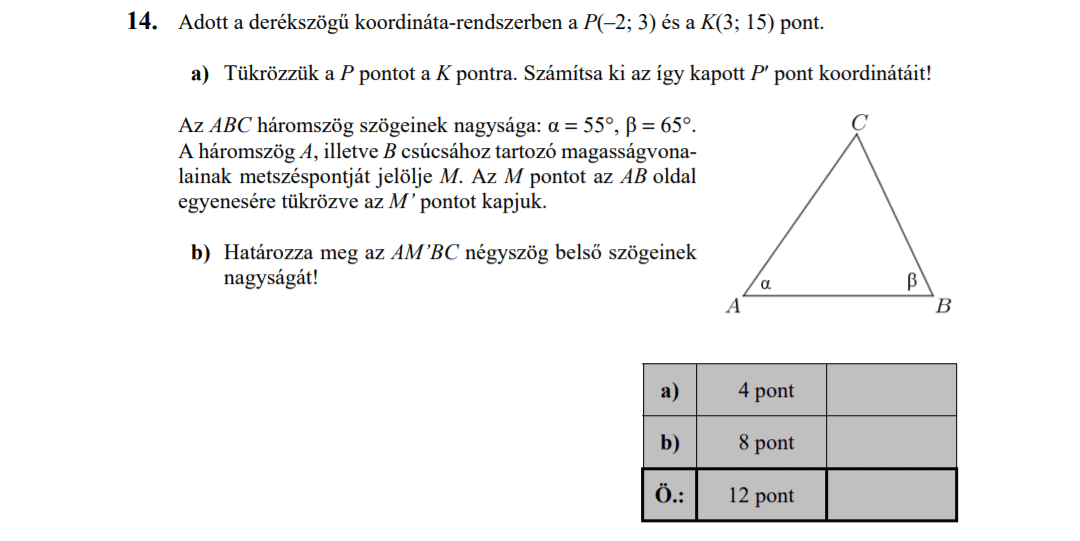




- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
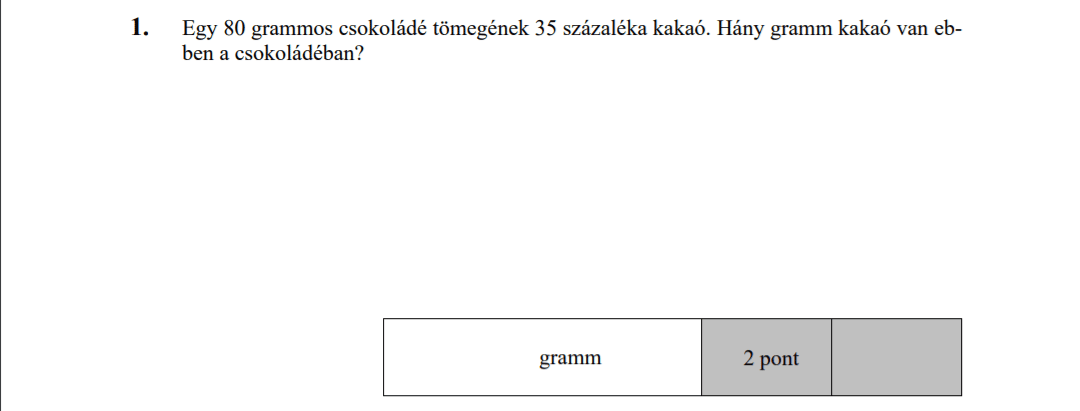

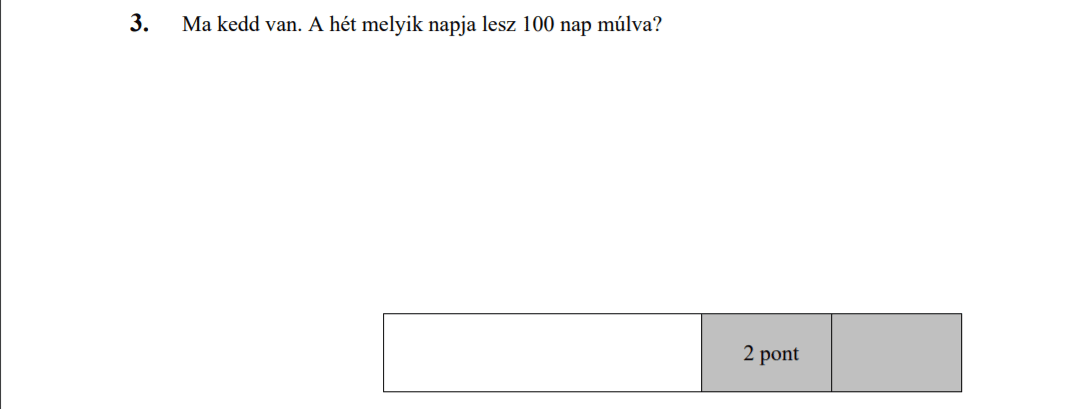
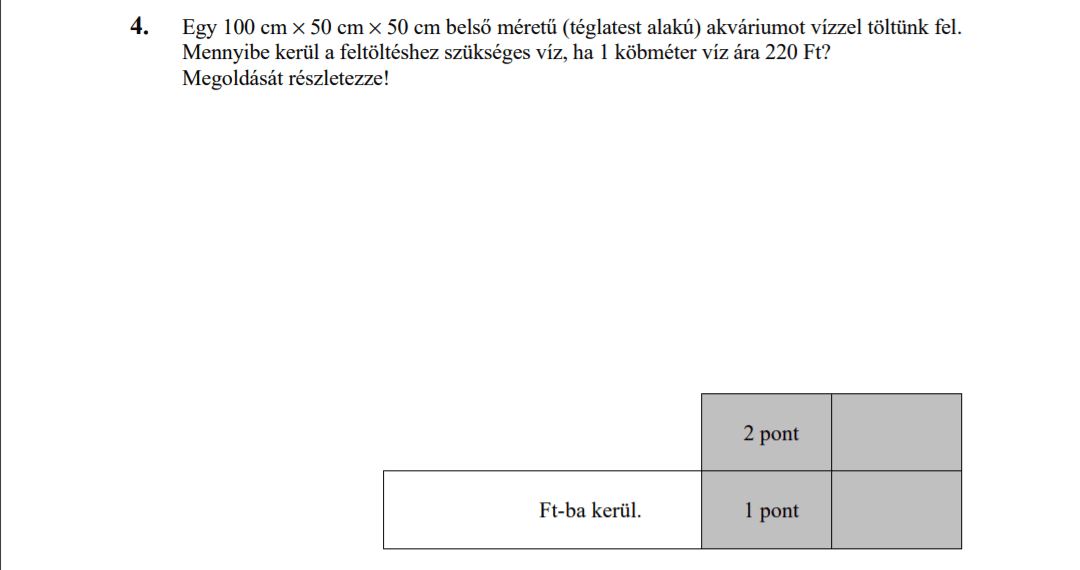
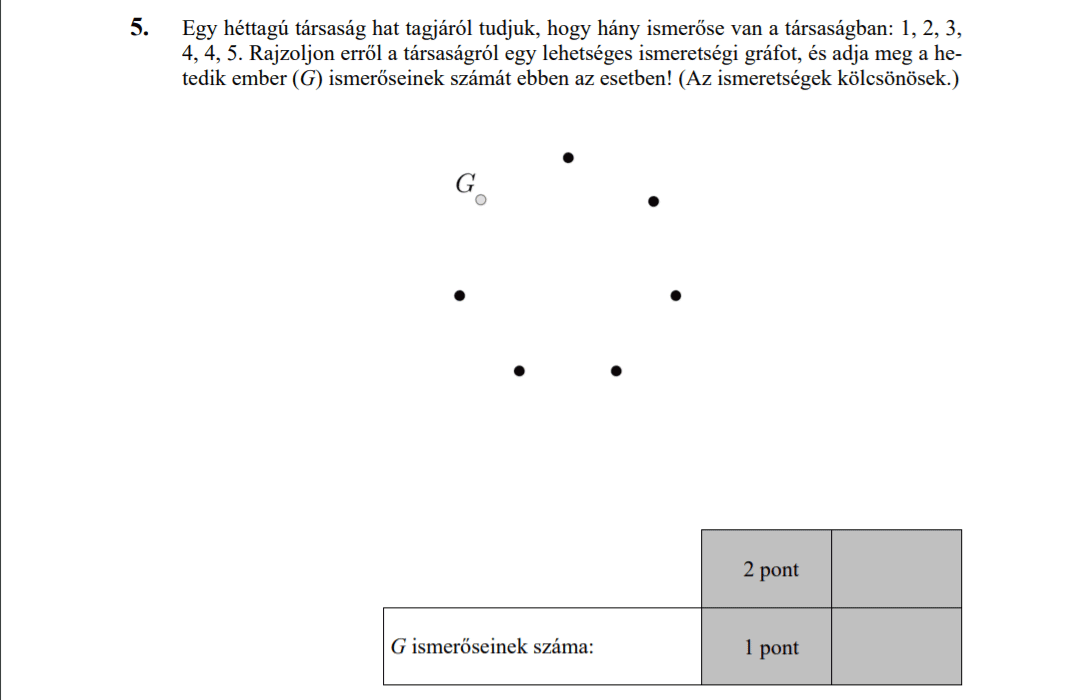







MÁSODIK RÉSZ
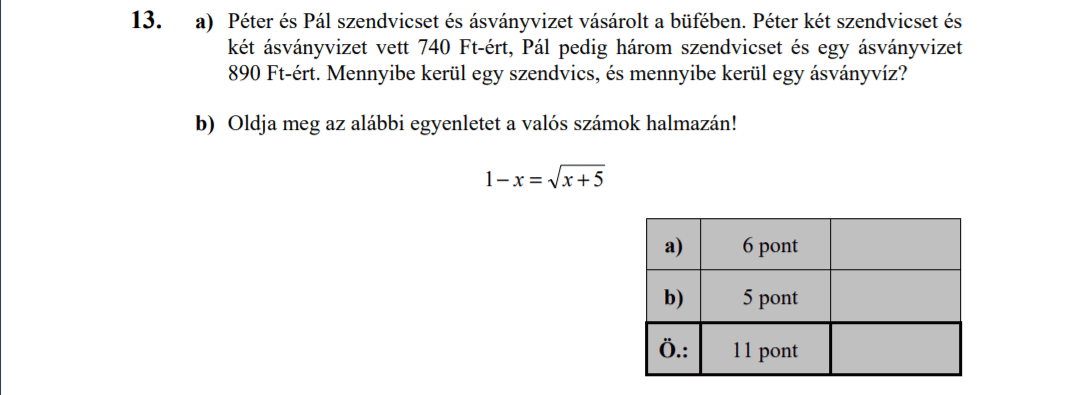
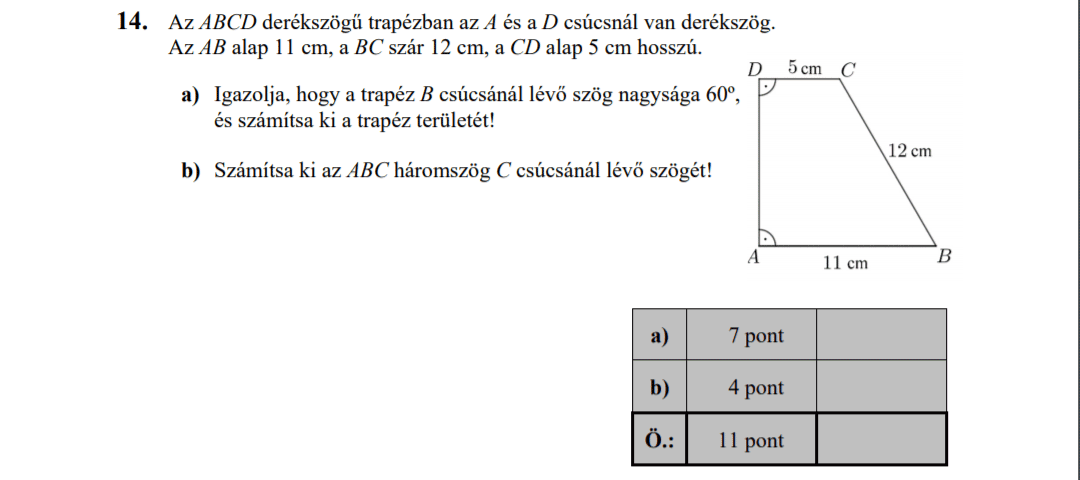



- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




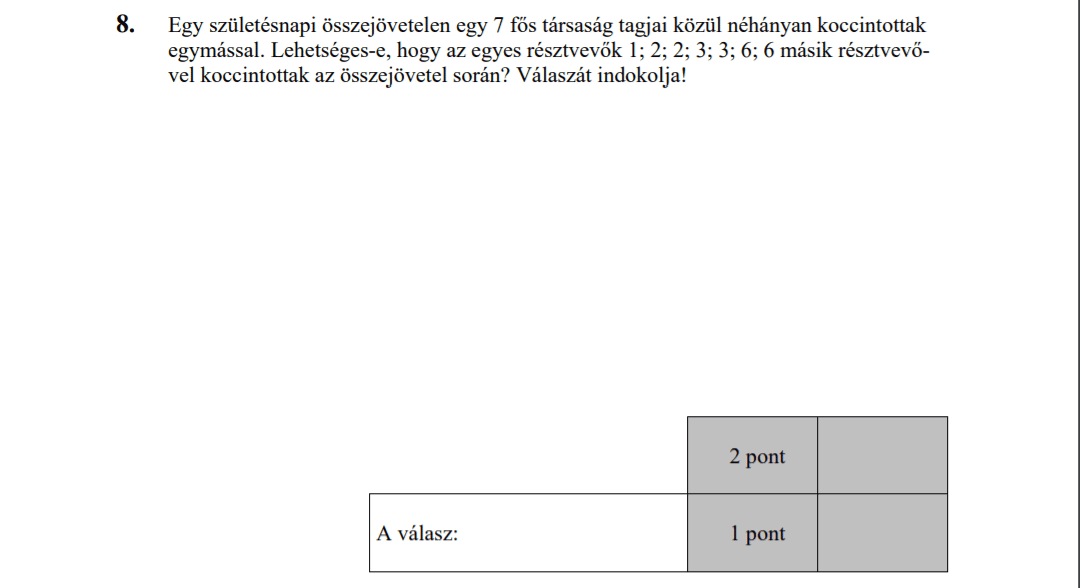



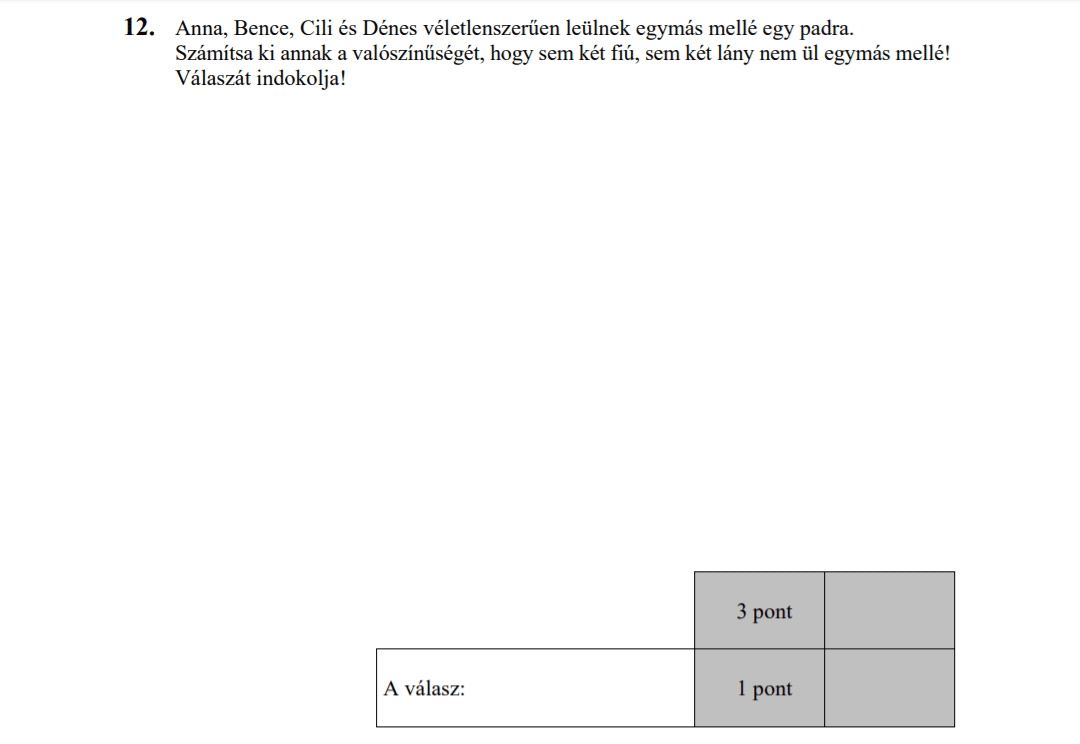
MÁSODIK RÉSZ

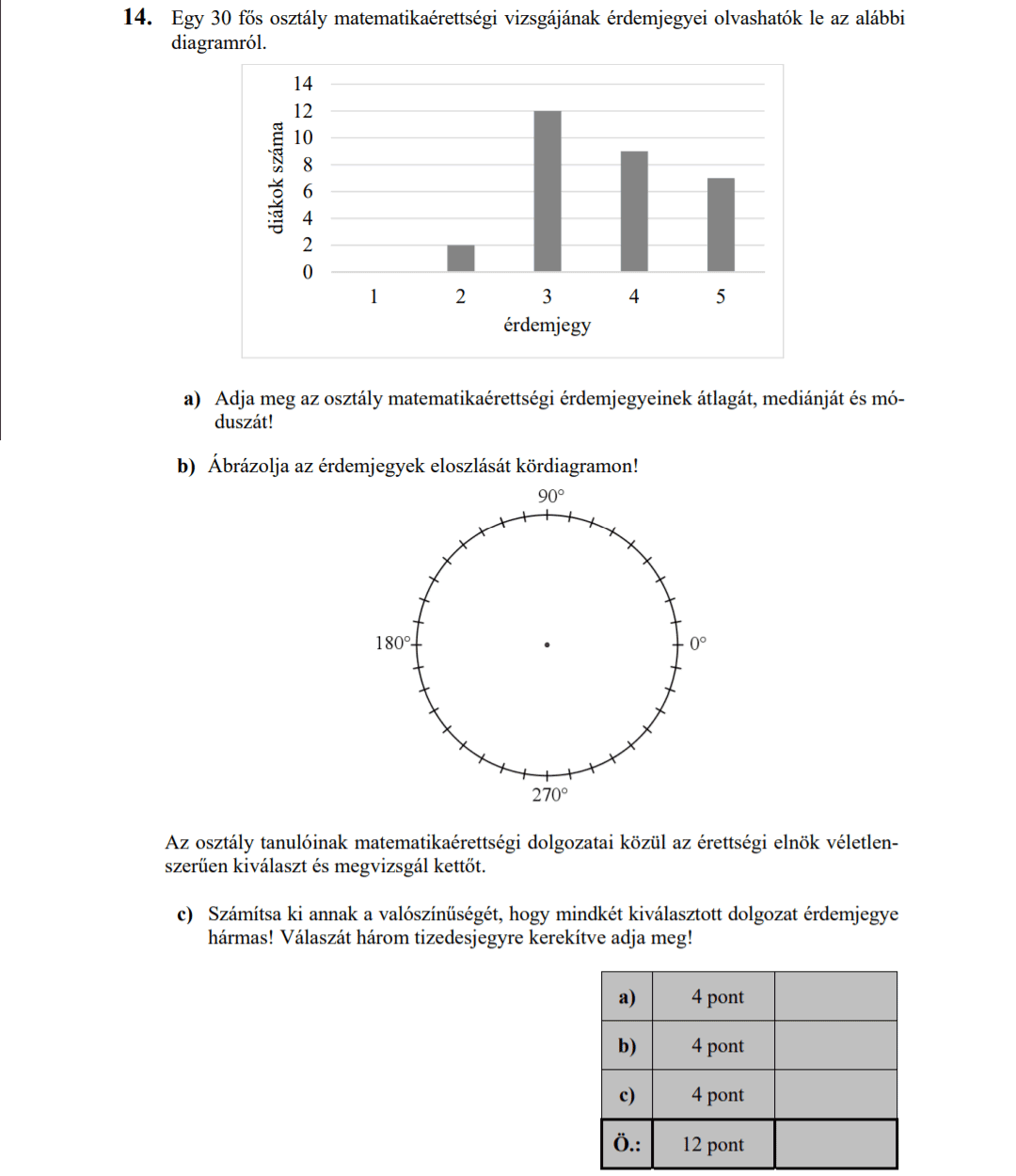
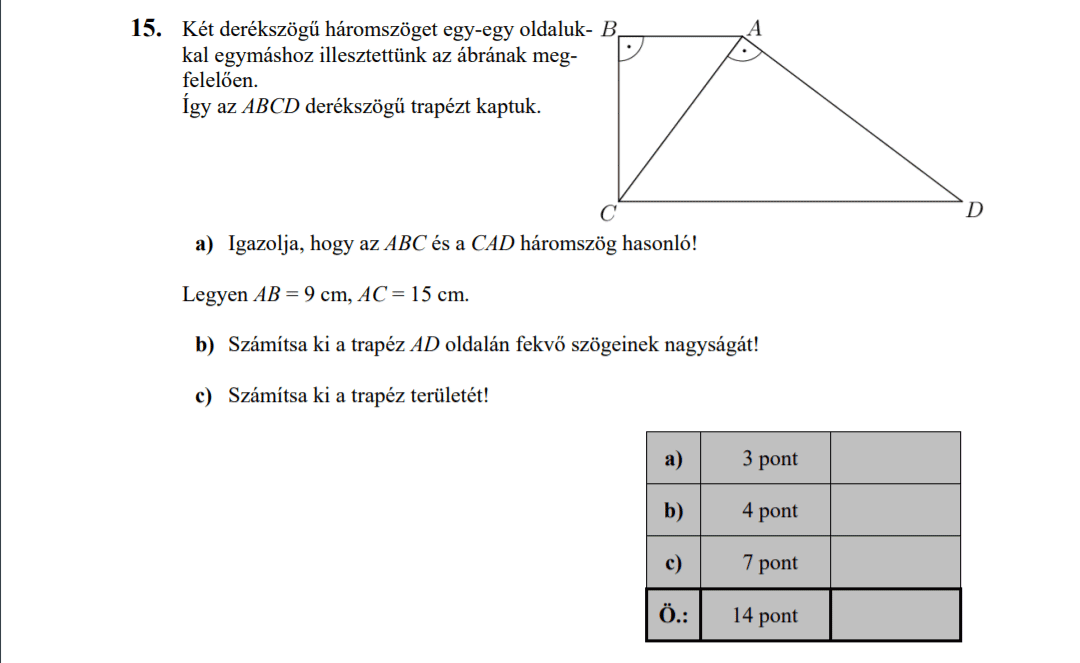



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


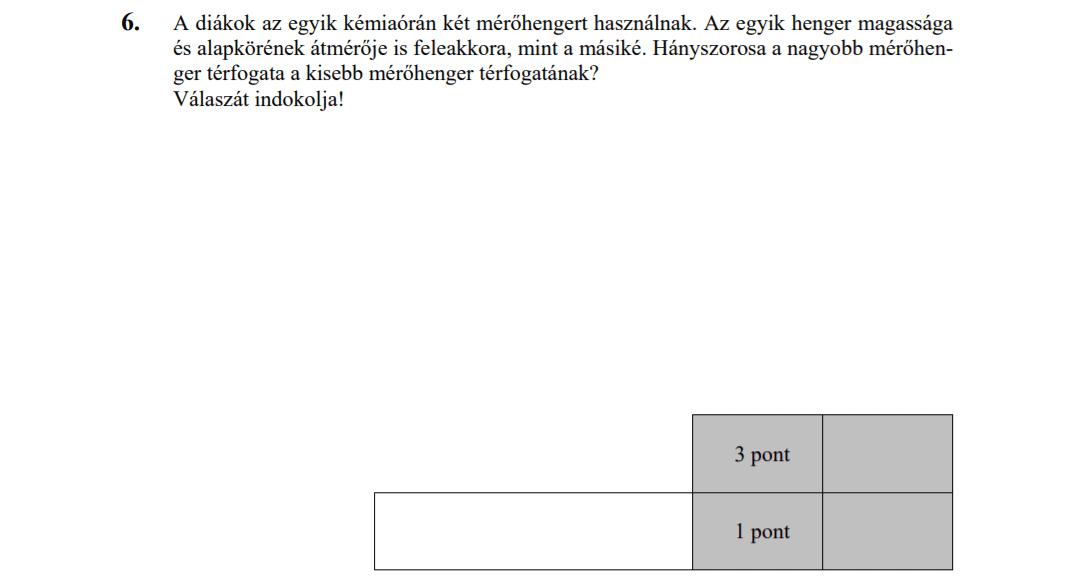
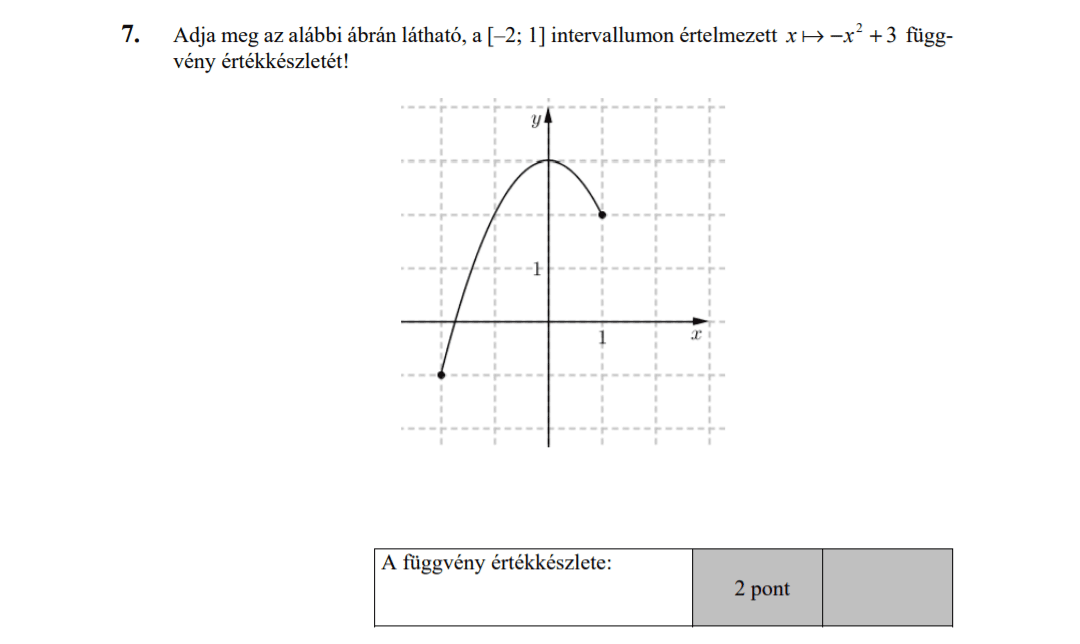

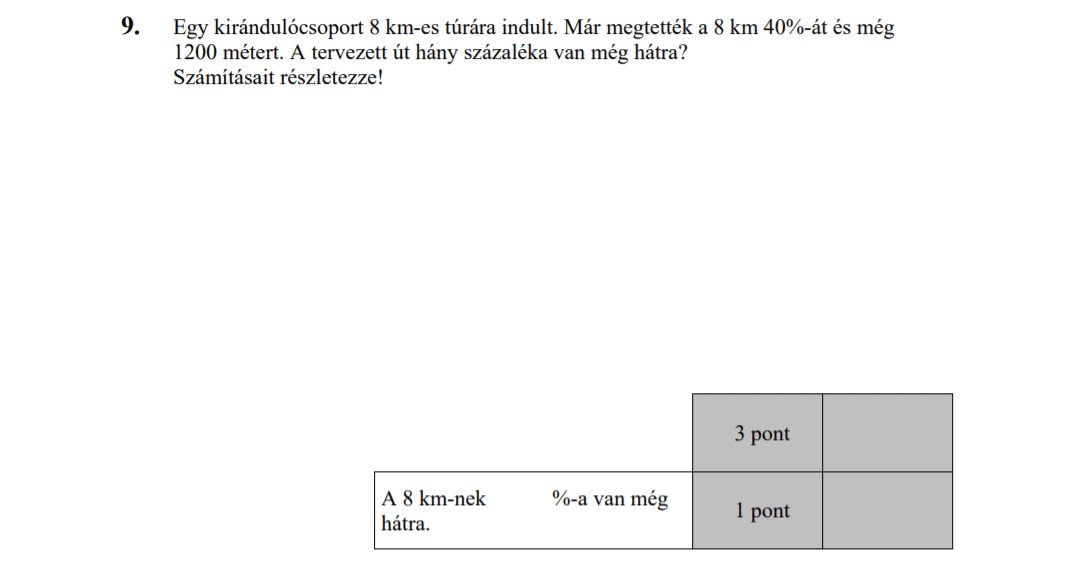
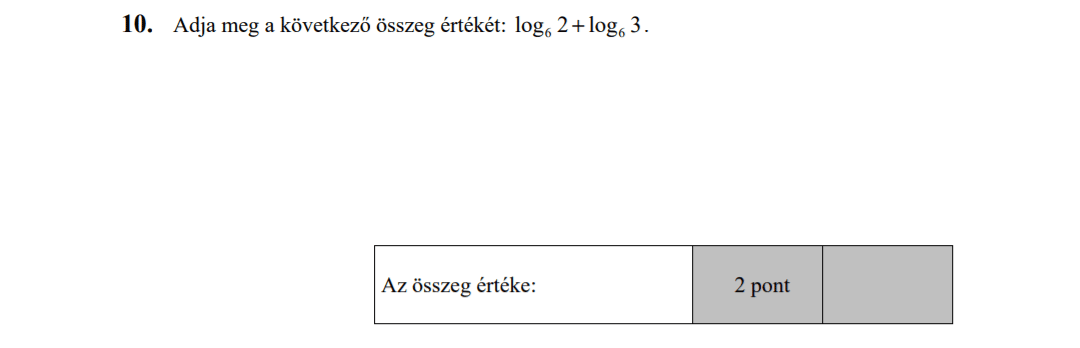

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






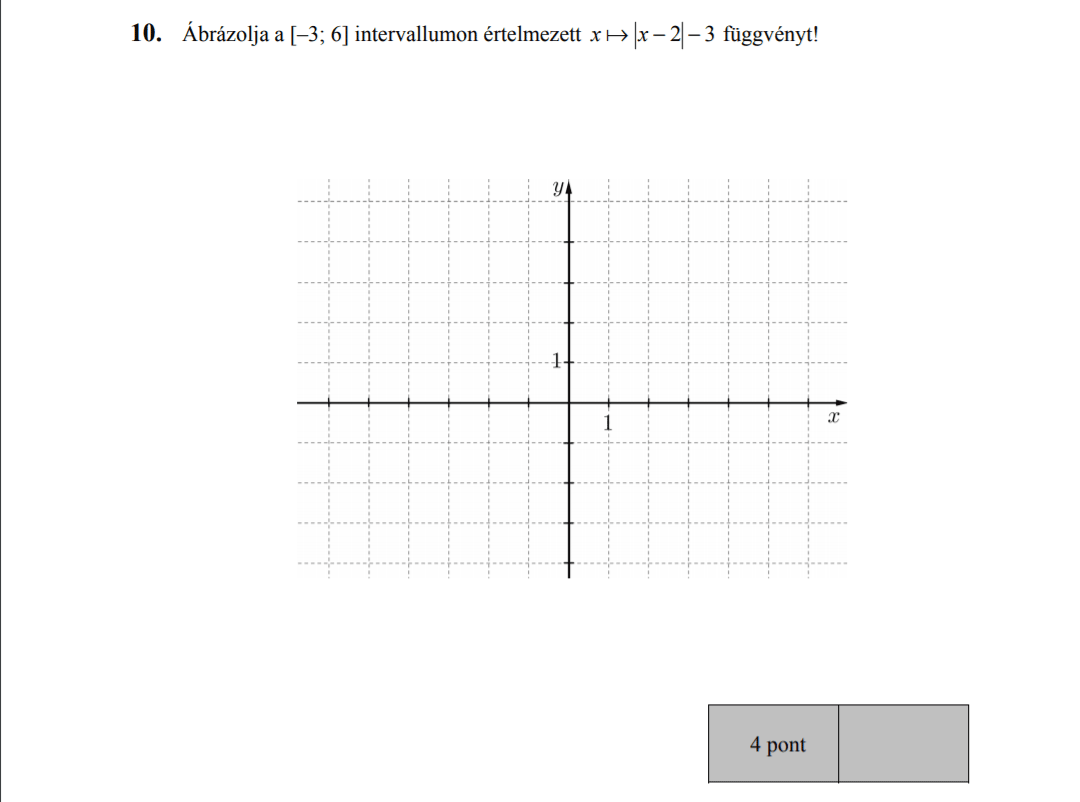

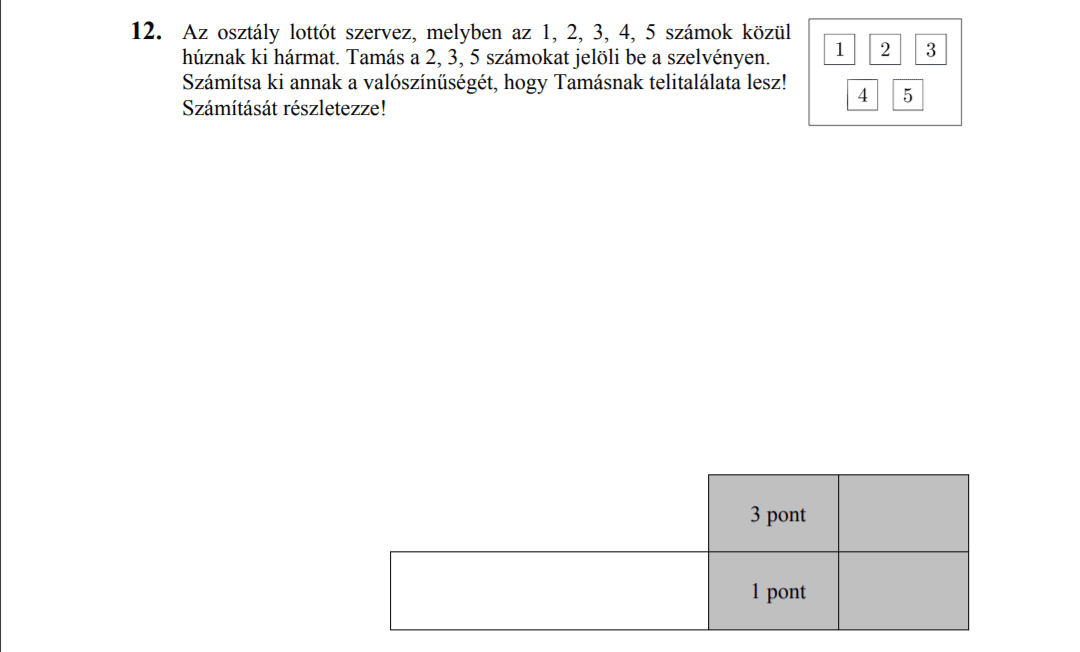
MÁSODIK RÉSZ

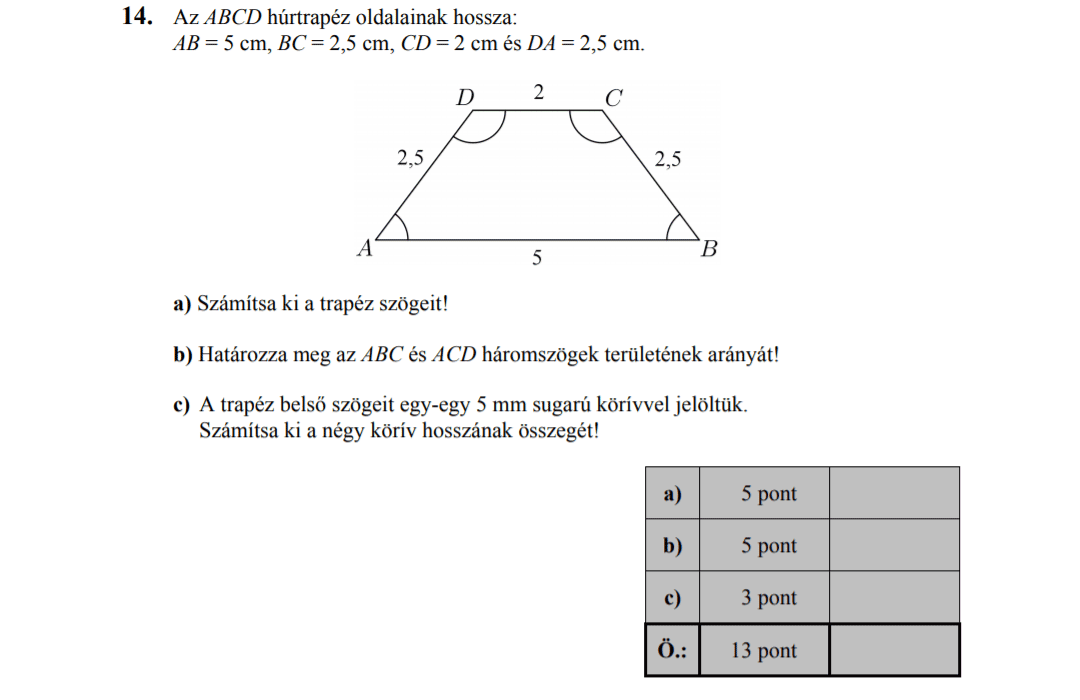

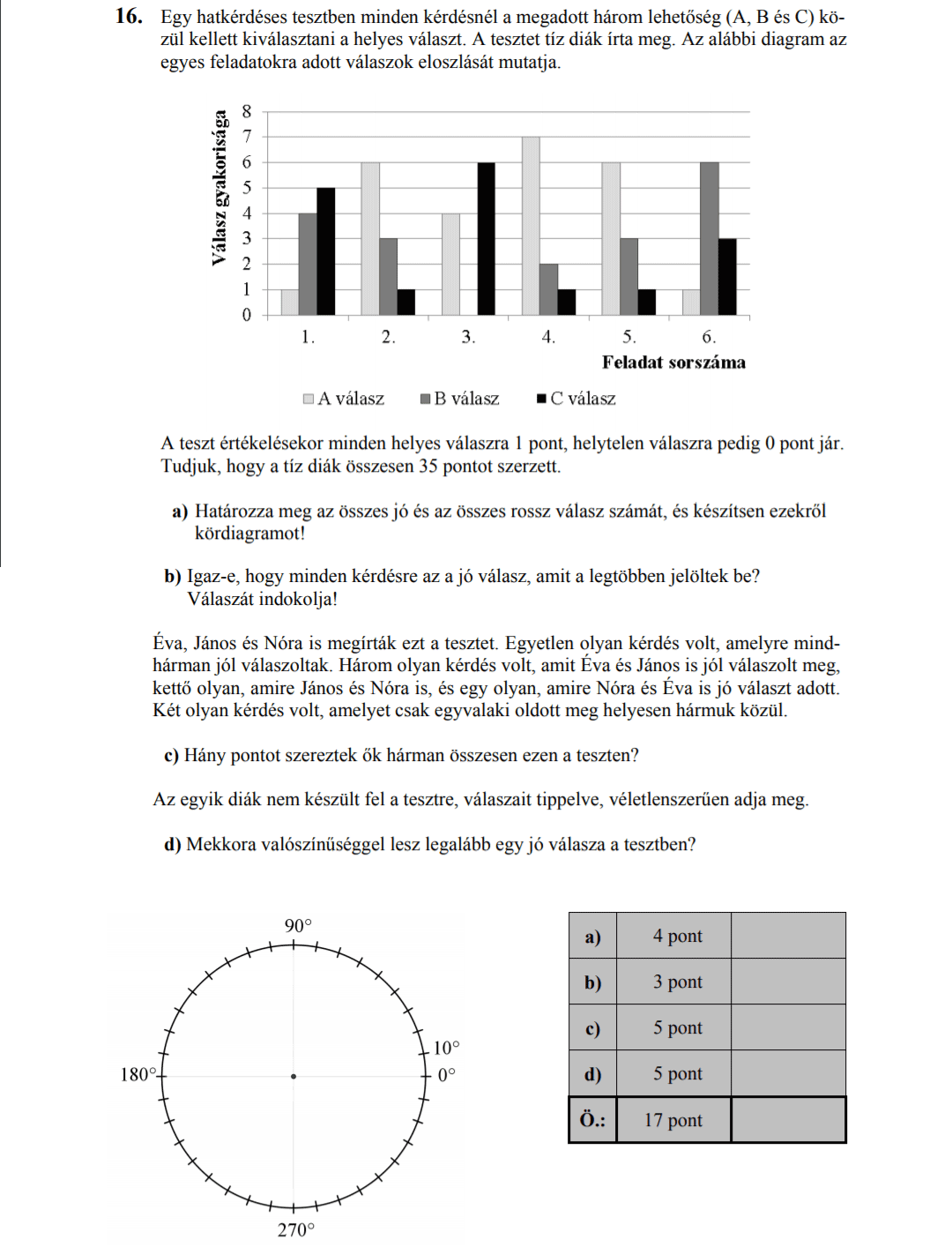


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

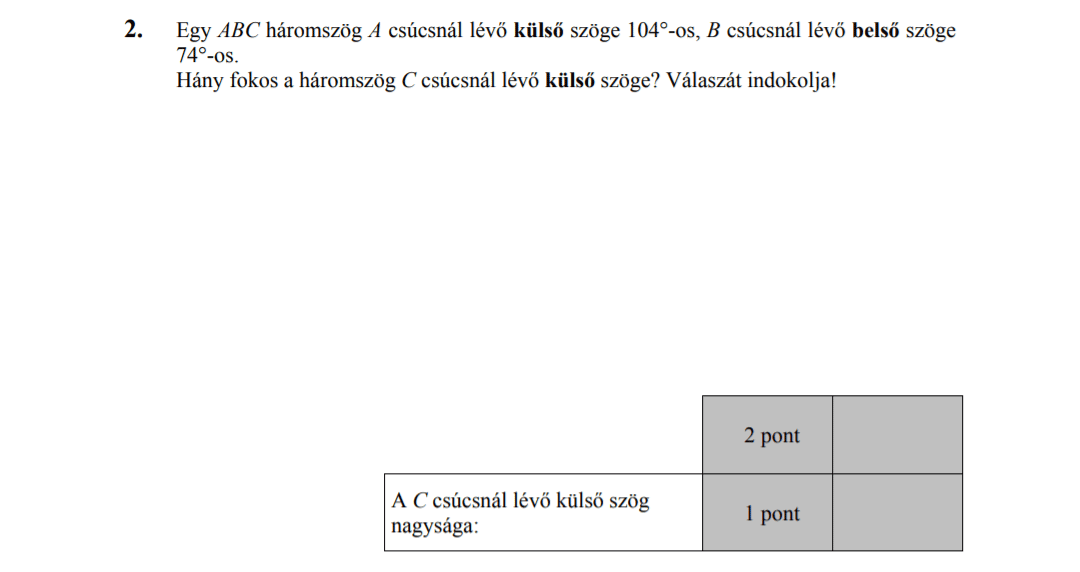





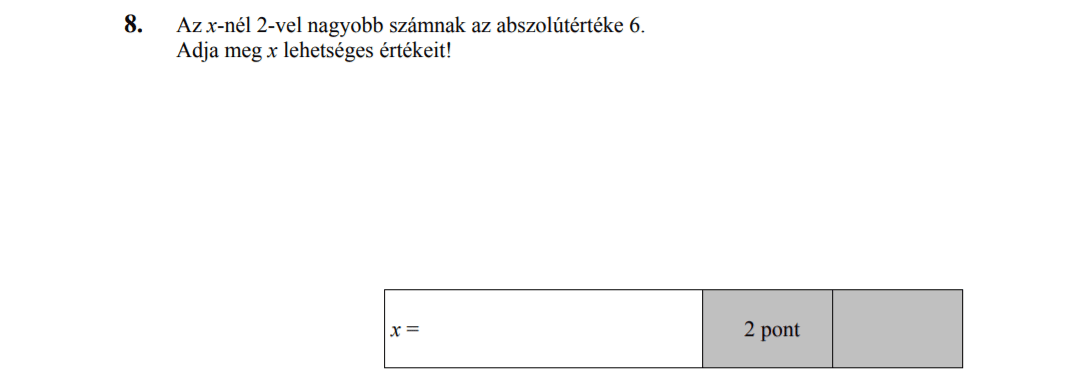

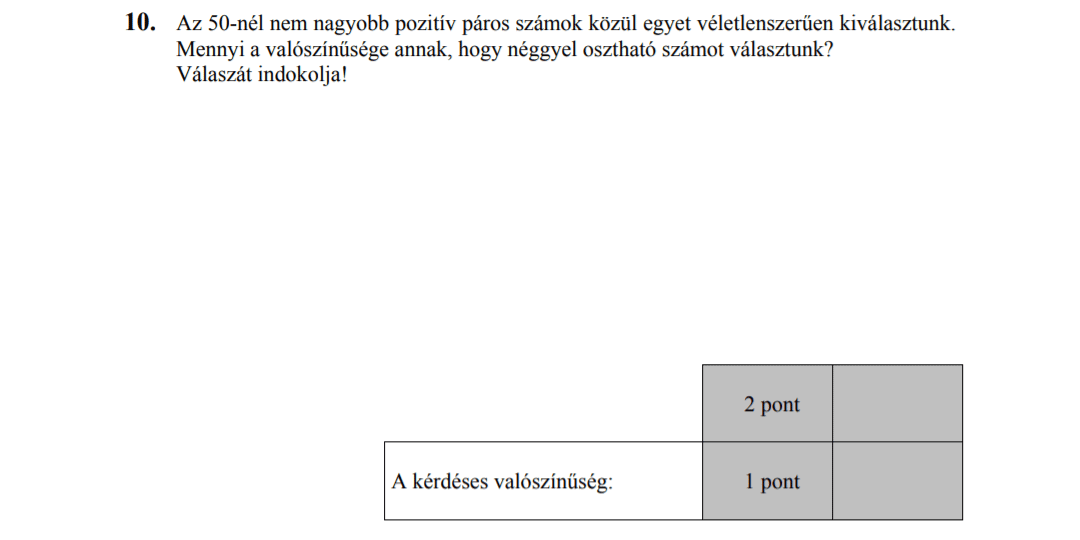


MÁSODIK RÉSZ

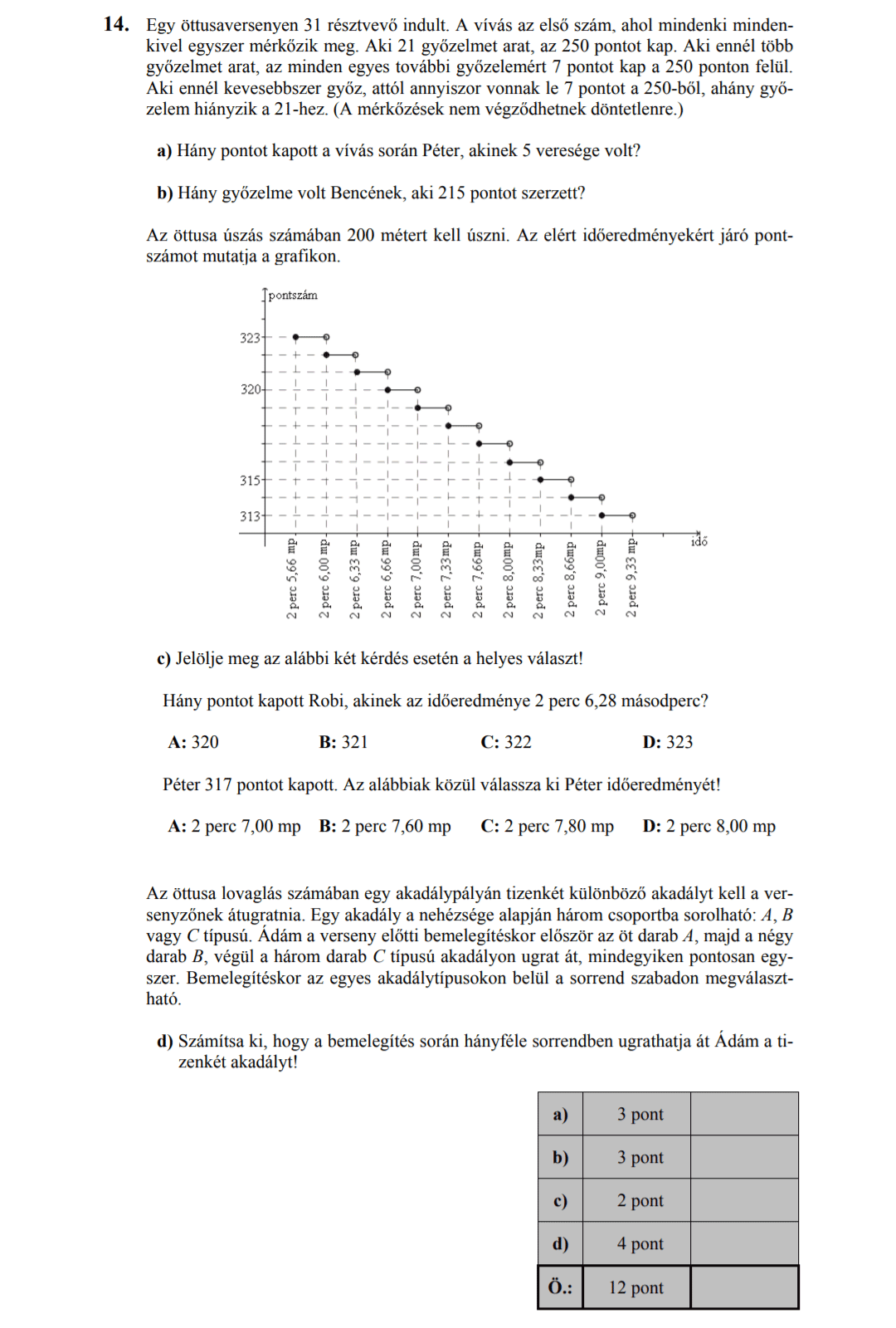
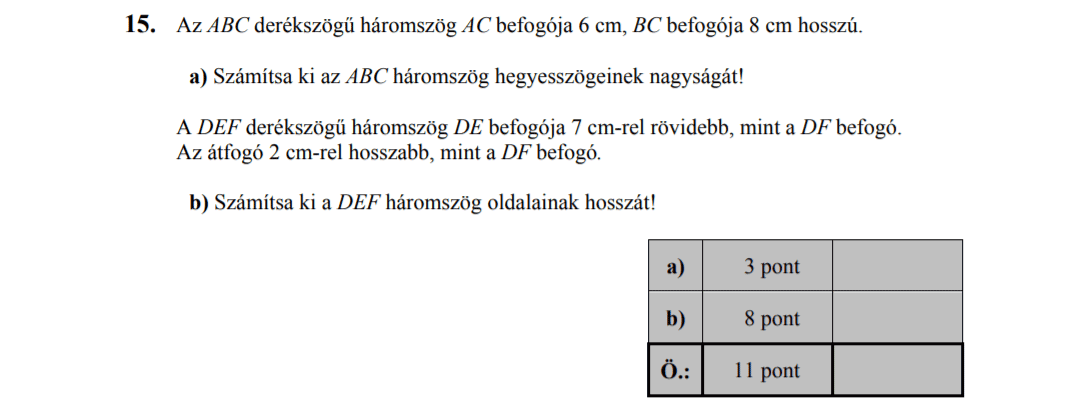



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

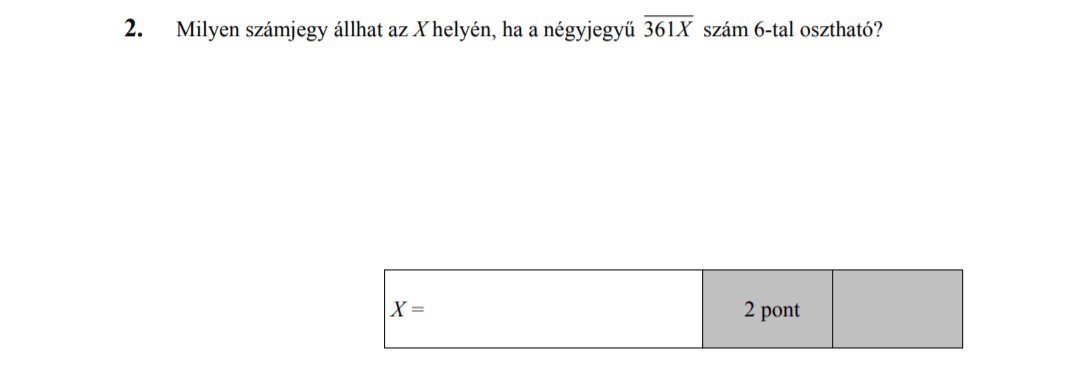



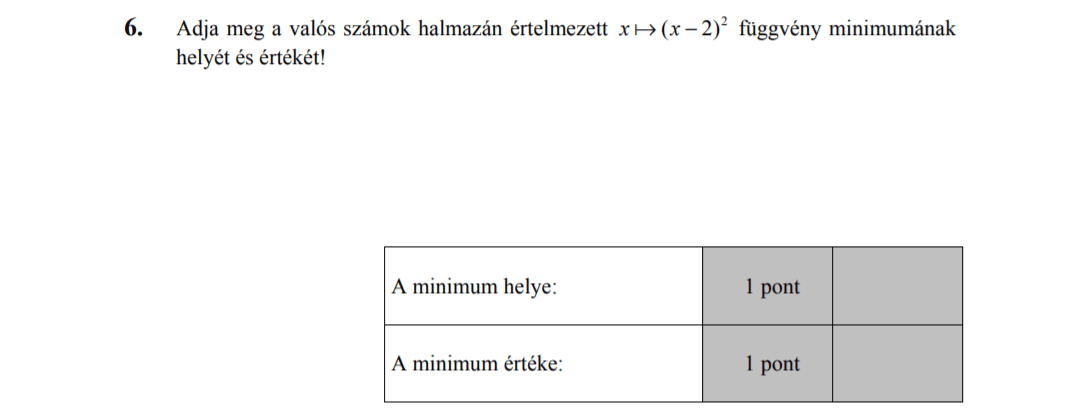

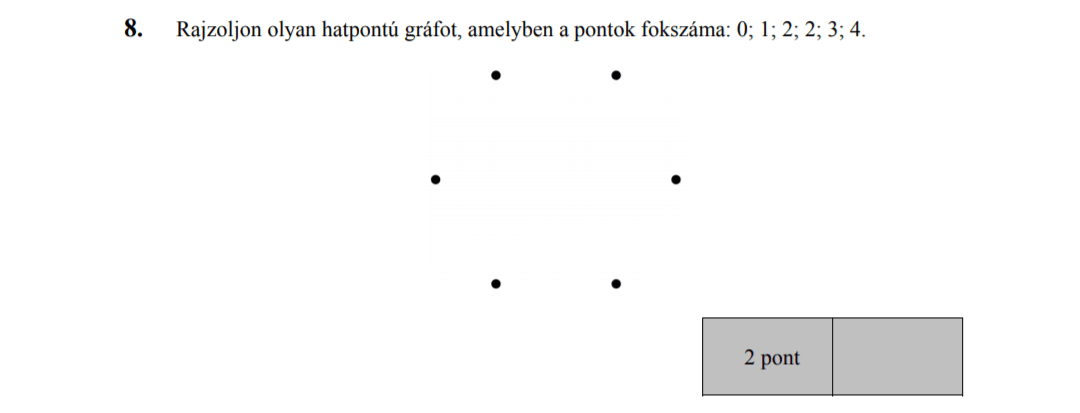


MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








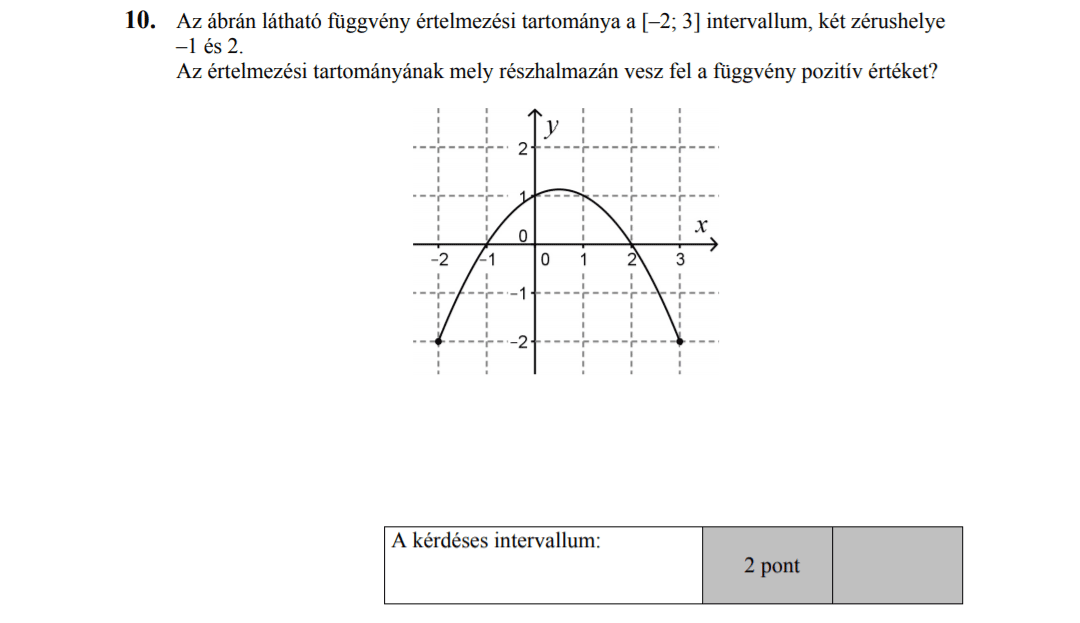


MÁSODIK RÉSZ


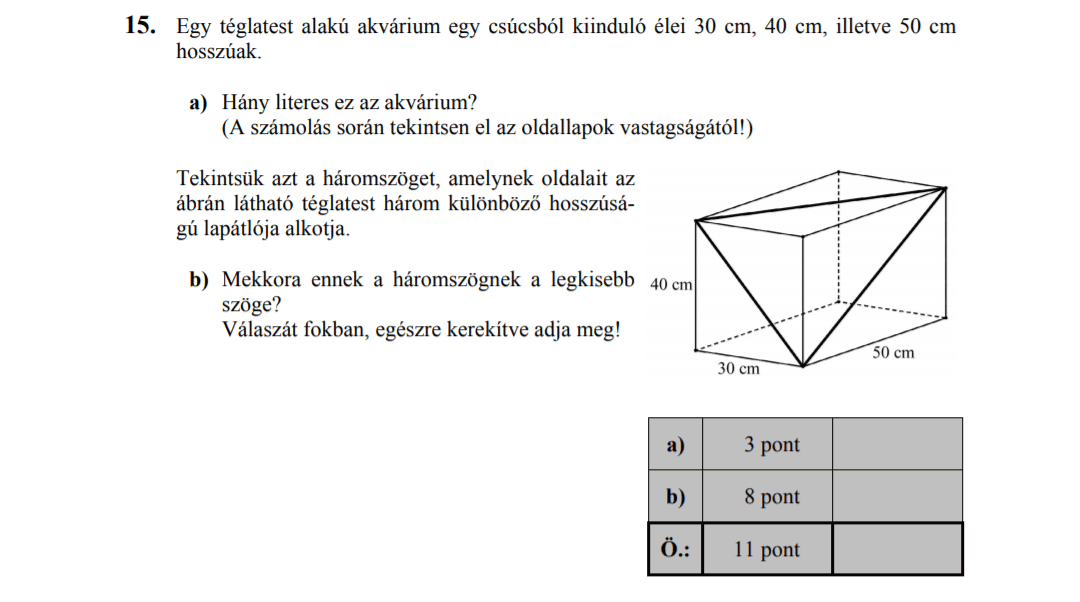

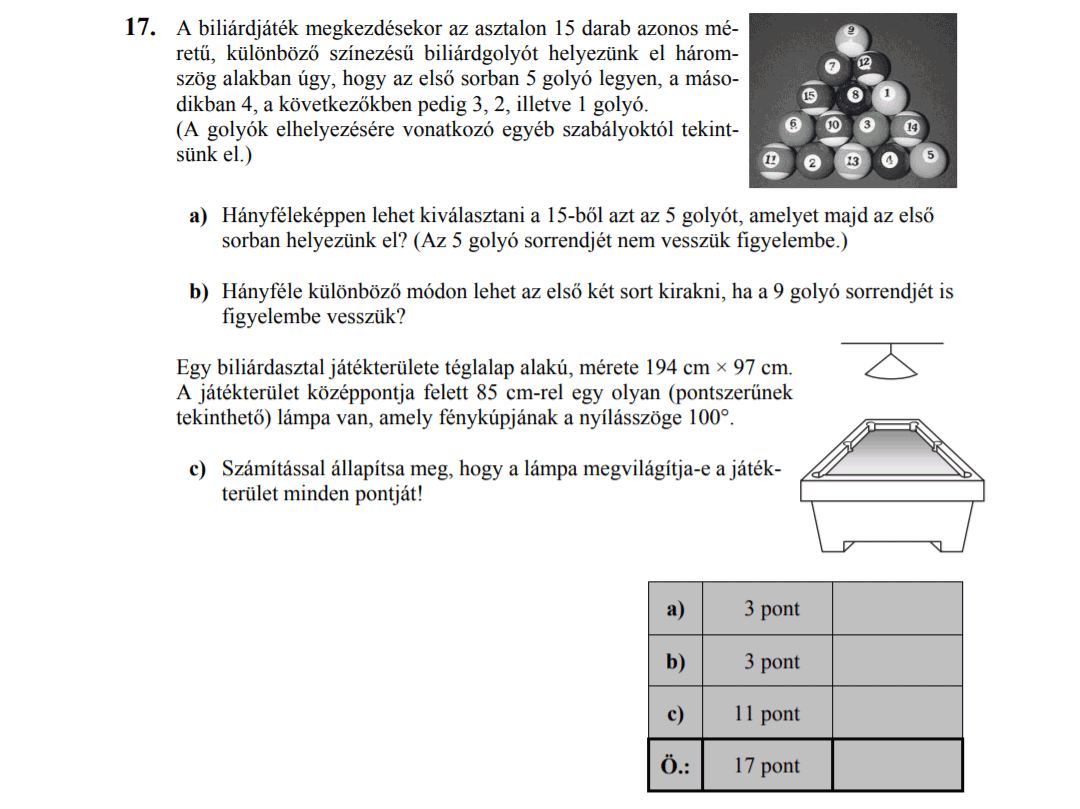

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


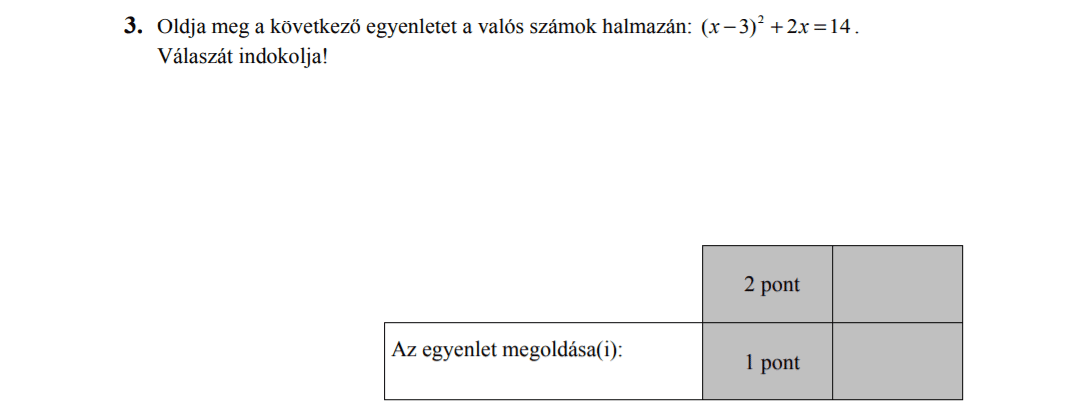





MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ

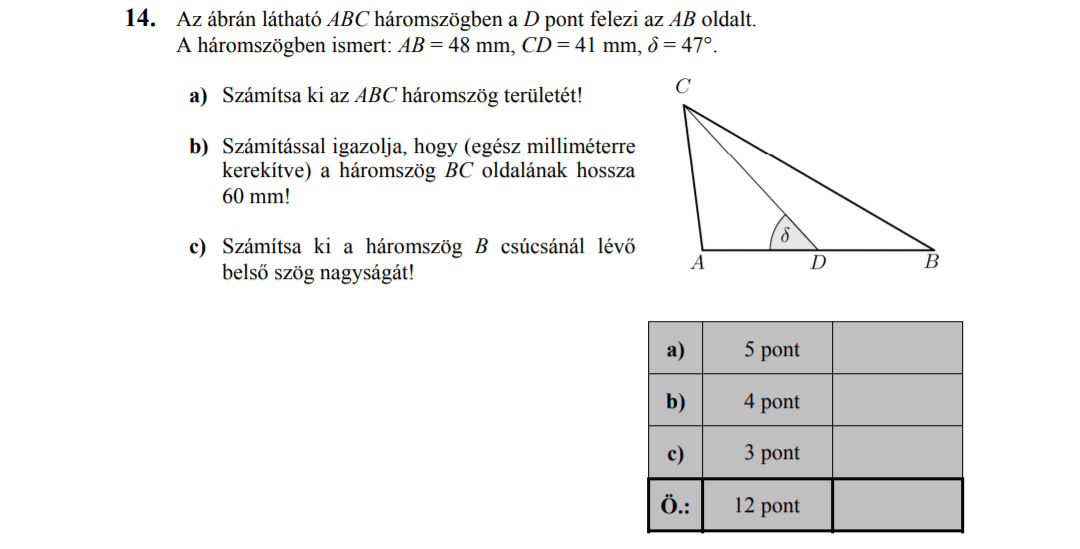




- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


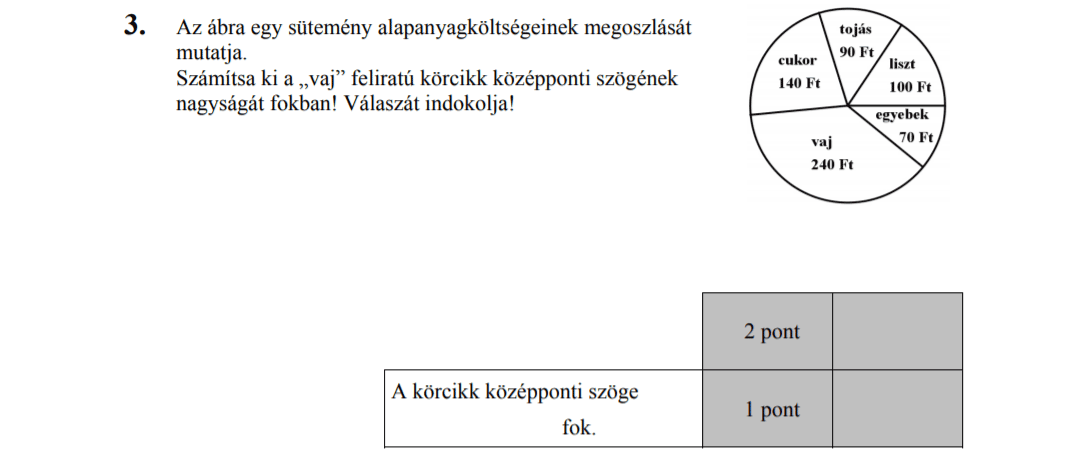
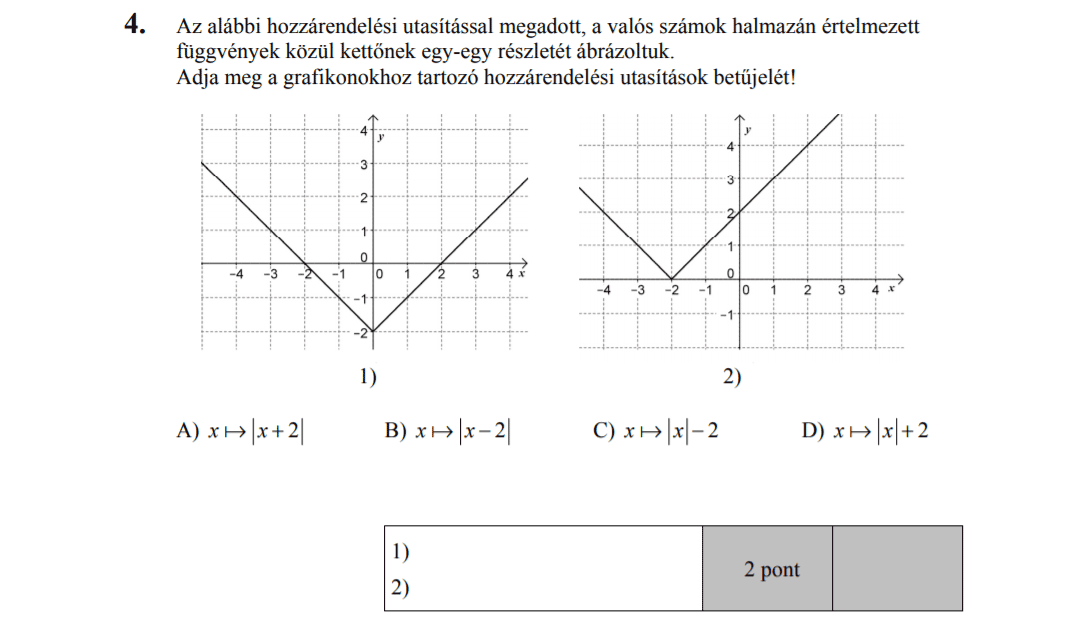
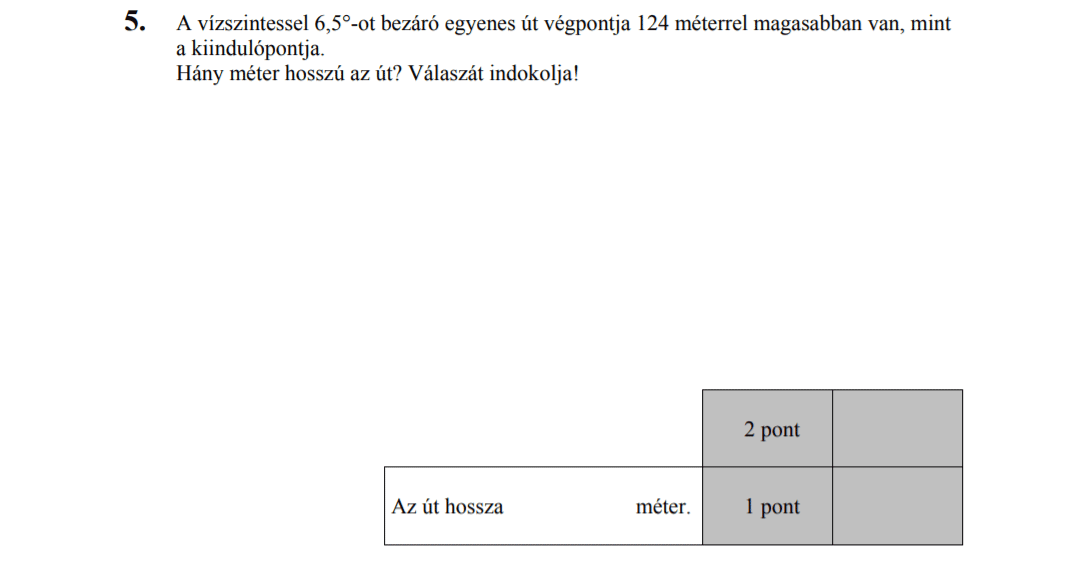





MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Univerzális kvantor
Az univerzális kvantor egy jelölése a "minden" kifejezésnek.
Jele: $\forall$
Egzisztenciális kvantor
Az egzisztenciális kvantor egy jelölése a "létezik" vagy "van olyan" kifejezésnek.
Jele: $\exists$
Logikai műveletek | Negáció
Az állítás negációja (vagy tagadása) egy egyváltozós művelet. Egy $A$ kijelentés negációja az a kijelentés, amely akkor igaz, ha $A$ hamis és akkor hamis, ha $A$ igaz.
Állítás
Az állítás (vagy kijelentés) olyan kijelentő mondat, amelyről egyértelműen eldönthetjük, hogy az igaz vagy hamis.
Végezzük el az alábbi feladatokat:
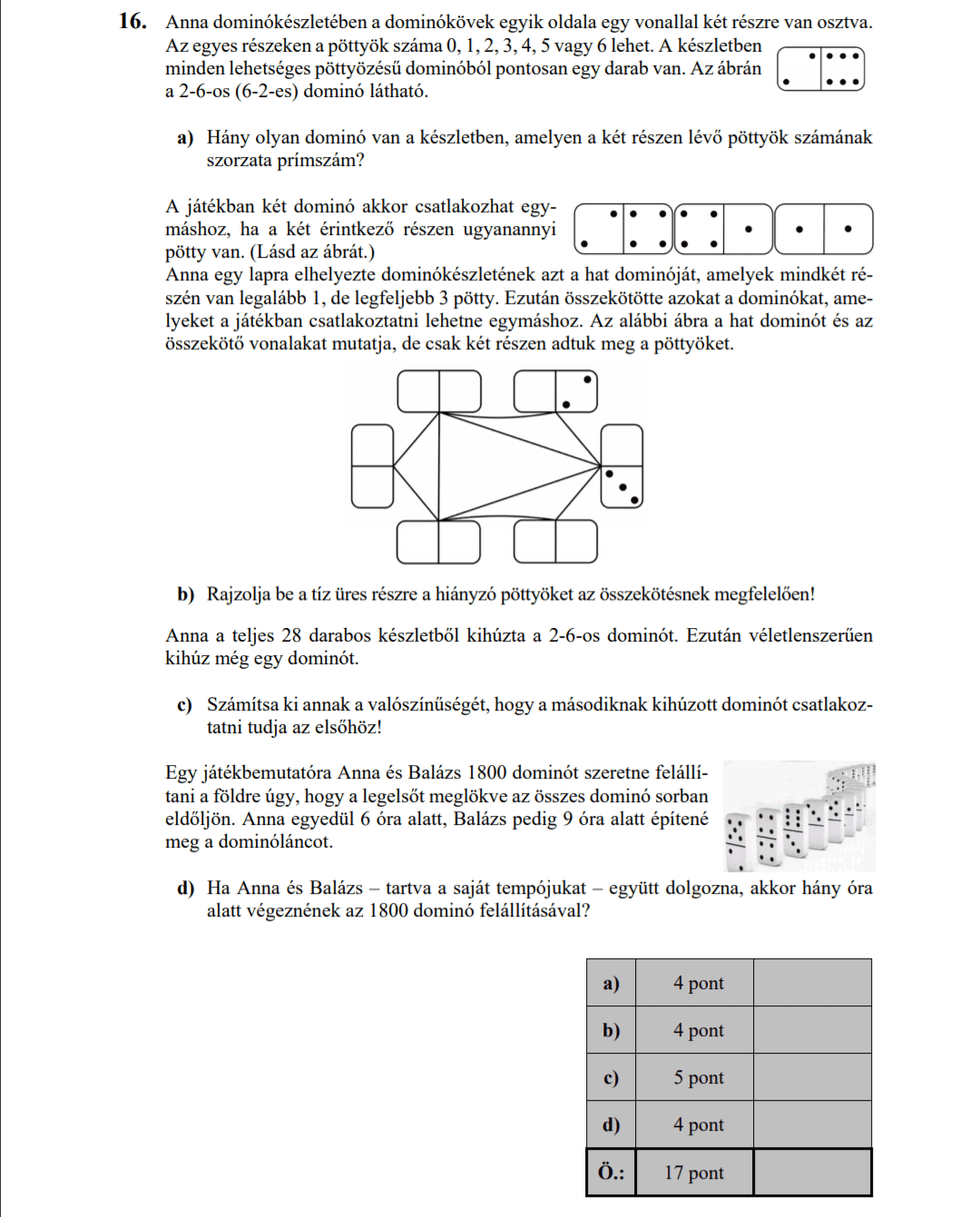
a) Egy vonaton 400-an utaznak. Bizonyítsuk be, hogy utazik rajta két olyan utas, akiknek ugyanazon a napon van a születésnapja.
b) Mi történik, ha felszáll újabb 333 utas?
c) És ha 1200-an utaznak a vonaton?
a) Egy 5 kocsiból álló vonaton 460-an utaznak. Bizonyítsuk be, hogy van olyan kocsi, amiben legalább 80 utas van.
b) Egy másik vonat szintén 5 kocsiból áll. Legalább hányan utaznak a vonaton, ha tudjuk, hogy biztosan van olyan kocsi, amiben legalább 40-en utaznak?
c) Az egyik kocsiban egy 10 tagú társaság utazik. Mindenki a társaságból legalább 7 másik embert ismer. Bizonyítsuk be, hogy bármely 3 embernek van közös ismerőse.
Van itt ez az állítás: "Minden mamut sárga."
Válasszuk ki innen azokat, amik az állítás tagadása:
Egyik mamut sem sárga.
Van olyan mamut, ami sárga.
Van olyan mamut, ami nem sárga.
A legtöbb mamut nem sárga.
Nem minden mamut sárga.
Egy vonaton 400-an utaznak. Bizonyítsuk be, hogy utazik rajta két olyan utas, akiknek ugyanazon a napon van a születésnapja.
Hát, ez így elsőre elég furán hangzik…
Mégis honnan kéne tudnunk, hogy kinek mikor van a születésnapja…
De pont ez a lényeg, hogy nem kell tudni.
Itt van például Bob.
És itt van 365 darab doboz, mert egy évben 365 nap van.
Sőt, legyen 366, mert néha szökőév is van.
Azt kell bizonyítani, hogy van két ember ugyanabban a dobozban.
Betesszük Bobot abba a dobozba, amelyik napon született.
Tegyük be, mondjuk ide.
Aztán itt van a következő utas.
Hogyha ugyanazon a napon született, mint Bob…
akkor meg is van a két ember ugyanabban a dobozban.
Ha viszont más napon született…
Hát igen, akkor még nem vagyunk kész.
Itt jönnek sorban az utasok.
Ha mindegyik utas más napon született, mint a többi…
akkor mindegyiket külön-külön dobozban helyezzük el.
Most járunk 366 darab utasnál.
És ekkor megjelenik a 367-edik utas…
Hová is tegyük?
Már nincsen üres doboz, tehát mindegy mikor született…
valakivel így is úgyis közös dobozba kerül.
Egészen biztos, hogy 367 darab utas nem fér el 366 dobozban.
Csak úgy, hogyha valamelyik dobozban ketten vannak.
Ezt a nem túl bonyolult gondolatot hívjuk skatulya-elvnek.
A skatulya a doboz régies elnevezése.
És ezt az elvet elég régen találták ki…
Ha a vonaton 367 ember, vagy ennél több utazik, akkor biztosan lesz két olyan utas, akik ugyanazon a napon születtek.
Most nézzük, mi történik akkor, hogyha fölszáll újabb 333 utas.
Ekkor a vonaton éppen 733-an utaznak.
A 733 pedig egy mágikus szám:
utast még éppen el tudunk úgy helyezni, hogy minden dobozban csak ketten legyenek.
De a plusz egy ember miatt valahol már biztosan hárman lesznek.
Hogyha 733 ember utazik a vonaton, egészen biztosan van köztük 3, akik ugyanazon a napon születtek.
És ha 1200-an utaznak a vonaton…
Ennyi utas már ki sem fér ide.
Szerencsére az ilyen esetekre is van egy matematikai módszer, amit úgy hívunk, hogy indirekt bizonyítás.
Rögtön folytatjuk…
Ha van öt darab labda és négy doboz…
Akkor a labdákat nem tudjuk úgy betenni a dobozokba, hogy mindegyikben csak egy labda legyen.
Valamelyik dobozban biztosan legalább két labda lesz.
Röviden összefoglalva erről szól a skatulya-elv.
Most pedig lássuk, mi ez az indirekt bizonyítás.
Egy 5 kocsiból álló vonaton 460-an utaznak. Bizonyítsuk be, hogy van olyan kocsi, amiben legalább 80 utas van.
Az indirekt bizonyítás lényege, hogy elképzeljük, mi történne, hogyha az állítás nem lenne igaz.
Vagyis tegyük föl, hogy mindegyik kocsiban 80-nál kevesebb utas van.
Ha minden kocsiban 80-nál kevesebb utas van, akkor lássuk csak, ![]() tehát az egész vonaton 400-nál kevesebben lennének.
tehát az egész vonaton 400-nál kevesebben lennének.
De ez lehetetlen, hiszen a vonaton 460-an vannak.
Vagyis lennie kell olyan kocsinak, ahol legalább 80-an vannak.
Egy másik vonat szintén öt kocsiból áll. Legalább hányan utaznak a vonaton, ha tudjuk, hogy biztosan van olyan kocsi, amiben legalább 40-en utaznak?
Hát, ez is valami skatulya-elvnek tűnik…
Csak most valahogy fordítva.
Hogyha mondjuk 100-an utaznak a vonaton, az valószínű kevés, mert simán lehet kocsinként 20 ember.
A 200 már határozottan biztatóbb.
Ha 200-an utaznak a vonaton, akkor biztosan van olyan kocsi, amiben legalább 40-en vannak.
Mert ha nem lenne, tehát minden kocsiban 40-nél kevesebben lennének, akkor az egész vonaton is 200-nál kevesebben lennének.
A 200 utas tehát már elég.
De a kérdés úgy szólt, hogy legalább hányan utaznak a vonaton, és előfordulhat, hogy már 200-nál kevesebb utas is jó lehet.
![]()
Ha 195-en utaznak a vonaton, akkor még előfordulhat, hogy minden kocsiban csak 39-en vannak.
De ha 196-an…
Akkor már kell lennie olyan kocsinak, amiben legalább 40-en vannak.
Hiszen, ha minden kocsiba csak 39-en lennének, akkor az egész vonaton is csak 195-en.
Tehát a válasz…
A vonaton legalább 196-an kell, hogy utazzanak.
Az egyik kocsiban egy 10 tagú társaság utazik. Mindenki a társaságból legalább 7 másik embert ismer. Bizonyítsuk be, hogy bármely 3 embernek van közös ismerőse.
Na, ez már egy izgalmasabb ügy.
Megint indirekten bizonyítunk, vagyis tegyük föl, hogy van 3 olyan ember, akiknek nincs közös ismerőse.
Hát, ha nincs közös ismerős, akkor itt bizony csak két ismertség lehet…
Sőt az is lehet, hogy kevesebb…
De az biztos, hogy legfeljebb kettő.
És itt is legfeljebb kettő…
Meg mindenhol.
Ebből a 7 emberből így legfeljebb 14 ismertség indulhat ki.
Mivel a társaságban mindenki legalább 7 másik embert ismer, hogyha embereink egymást ismerik...
akkor is még fejenként legalább 5 ismerősre van szükségük.
Így aztán legalább 15 ismertség indul ki innen.
Ez lehetetlen, mert azok ott heten legfeljebb 14 ismertséggel rendelkeznek.
Tehát ellentmondásra jutottunk.
Nem fordulhat elő, hogy van 3 ember, akinek nincs közös ismerőse.
Vagyis bármely 3 embernek van közös ismerőse.
Most, hogy ezt is megtudtuk, már csak egyetlen nyugtalanító kérdésre keressük a választ.
Arra, hogy mégis mit keres itt ez a rengeteg darázs?
Nem, valójában mégsem ez a kérdés…
Ez túlzottan életszerű lenne.
A kérdés úgy szól, hogy van itt ez a 7x7-es sakktábla és mindegyik mezőn egy darázs.
Egy adott pillanatban minden darázs átmászik valamelyik szomszédos mezőre.
A sarkuknál találkozó mezők nem számítanak szomszédosnak.
Lehetséges-e, hogy ekkor megint mindegyik mezőn pontosan egy darázs álljon?
Tegyük fel, hogy ez lehetséges.
Ez azt jelenti, hogy minden fekete mezőn álló darázsnak át kell másznia egy szomszédos fehér mezőre.
Fekete mezőből 25 darab van, fehérből meg csak 24 darab.
Nem tud a 25 darab fekete mezőn álló darázs átmászni a 24 fehér mezőre, csak úgy, ha lesz olyan mező, amin több darázs is van.
A nagy darázscserélő akció tehát lehetetlen.
A kvantorok. Hogy mik?
Minden ember utálja a matekot…
Azért ez így nem teljesen igaz, itt van ugyanis például Bob.
És Bob szereti a matekot.
![]()
Ez az állítás, hogy „Minden ember utálja a matekot.” tehát hamis.
Azért hamis, mert „Van olyan ember, aki szereti”.
Az egészből elég annyit megjegyezni, hogy Bobnak nehéz gyerekkora volt.
Nem, valójában ne ezt jegyezzük meg.
Hanem azt, hogy ez a két állítás egymás tagadása.
Nézzünk erre még egy példát és rögtön minden érthető lesz.
Itt van például ez az állítás:
Minden mamut piros.
Ennek az állításnak a tagadása:
Nem minden mamut piros.
Van olyan mamut, ami nem piros.
Tehát annak a tagadása, hogy „minden”…
így szól, hogy „van olyan, ami nem”.
A matematikában ezek a kifejezések meglehetősen gyakran előfordulnak.
Így aztán külön jelölés van rájuk forgalomban.
Ezt a jelet úgy hívják, hogy univerzális kvantor.
Ezt a másikat pedig úgy, hogy egzisztenciális kvantor.
![]()
Ezeknek a jeleknek a segítségével komplett kis titkosírásokat hozhatunk létre.
![]()
Ez például azt jelenti, hogy minden x-re létezik olyan y, hogy x+y=1.
A dolog igaznak tűnik, tényleg mindig létezik ilyen y.
![]()
Vagy itt van például egy másik:
![]()
Ami azt jelenti, hogy létezik olyan x, hogy minden y-ra x+y=1.
Na, ez már sajnos nem igaz.
Nem létezik olyan x szám, ami azt tudná, hogy bármilyen y-t adunk hozzá 1-et kapunk.
De visszatérve egy kicsit a mamutokra…
Van itt ez az állítás:
Minden mamut sárga.
Válasszuk ki innen azokat, amik az állítás tagadása:
Egyik mamut sem sárga.
Van olyan mamut, ami sárga.
Van olyan mamut, ami nem sárga.
A legtöbb mamut nem sárga.
Nem minden mamut sárga.
Hogyha még emlékszünk Bobra…
akkor talán rémlik valami, hogy a „minden” tagadása így szól: „van olyan, ami nem”.
Ez tehát biztosan jó.
Ez a másik pedig csak megtévesztésből van itt…
Hiányzik belőle a „nem” szócska.
Ócska kis trükk…
Aztán nyilván ez is az eredeti állítás tagadása…
Hiszen a mágikus „nem” szócskát őseink éppen a tagadás kifejezésére fejlesztették ki.
Ezek pedig nem tagadásai az eredeti állításnak, csak rá kell nézni itt lent a mamutokra és kiderül.
