- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
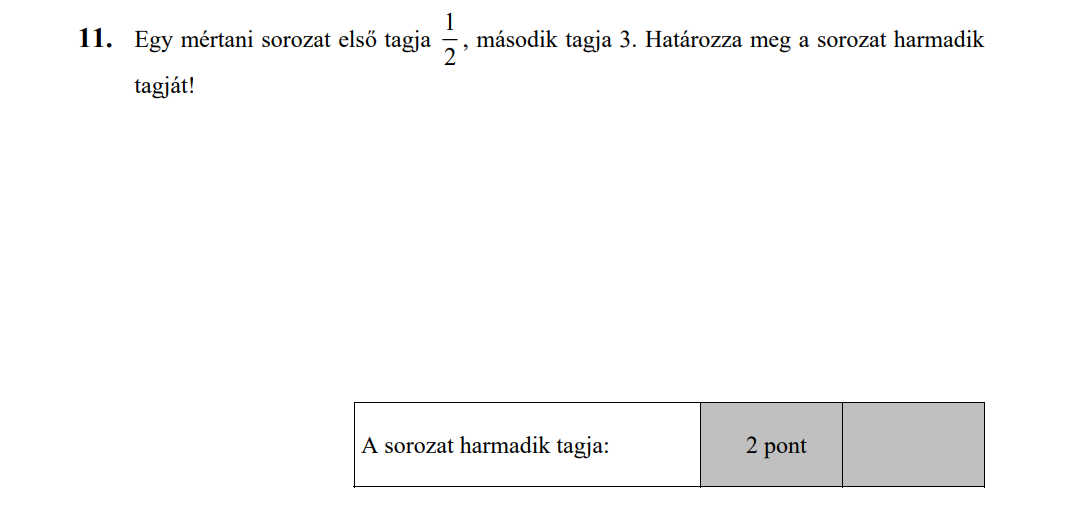
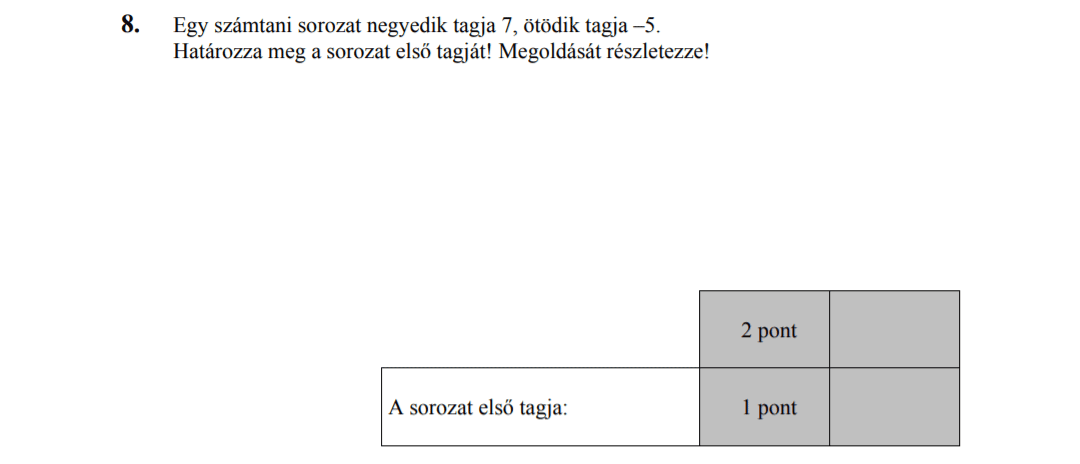
- Számtani és mértani sorozatok (16 pont)
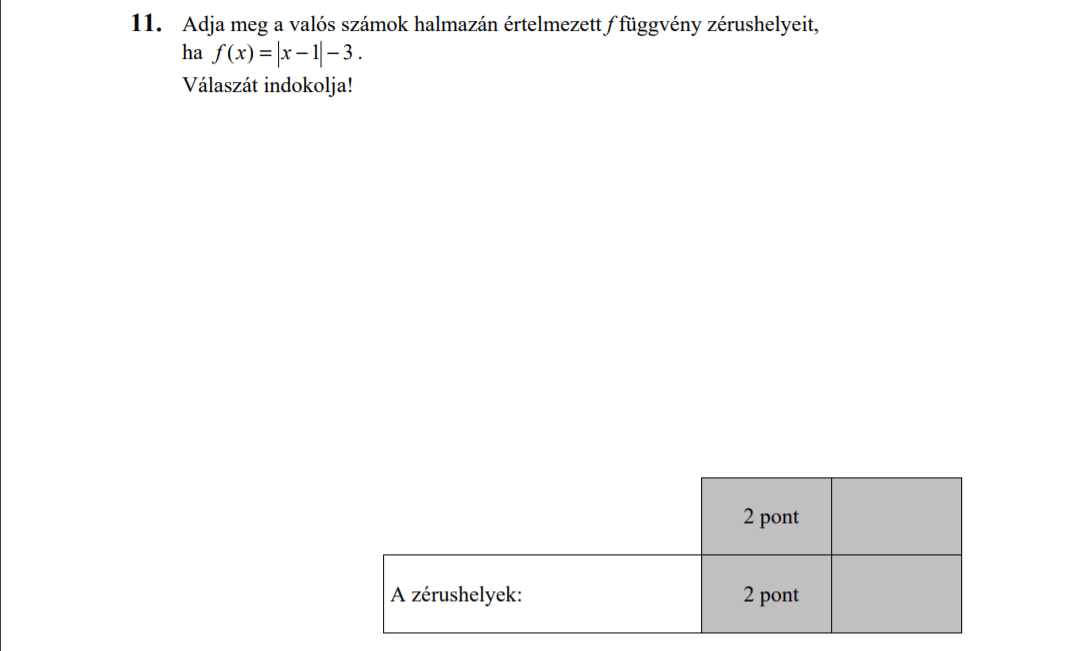
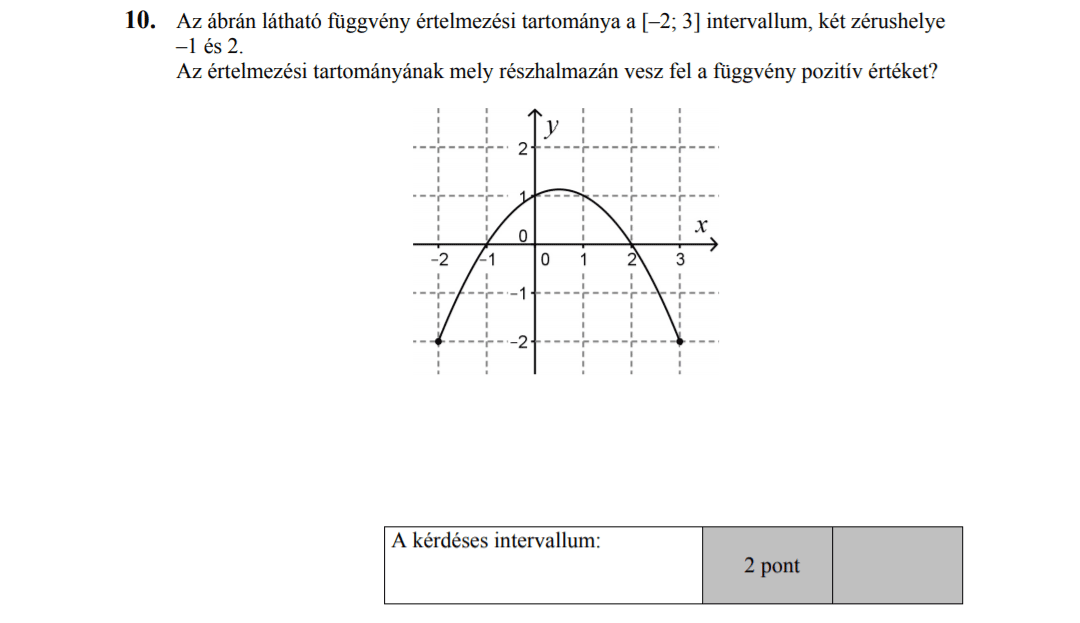
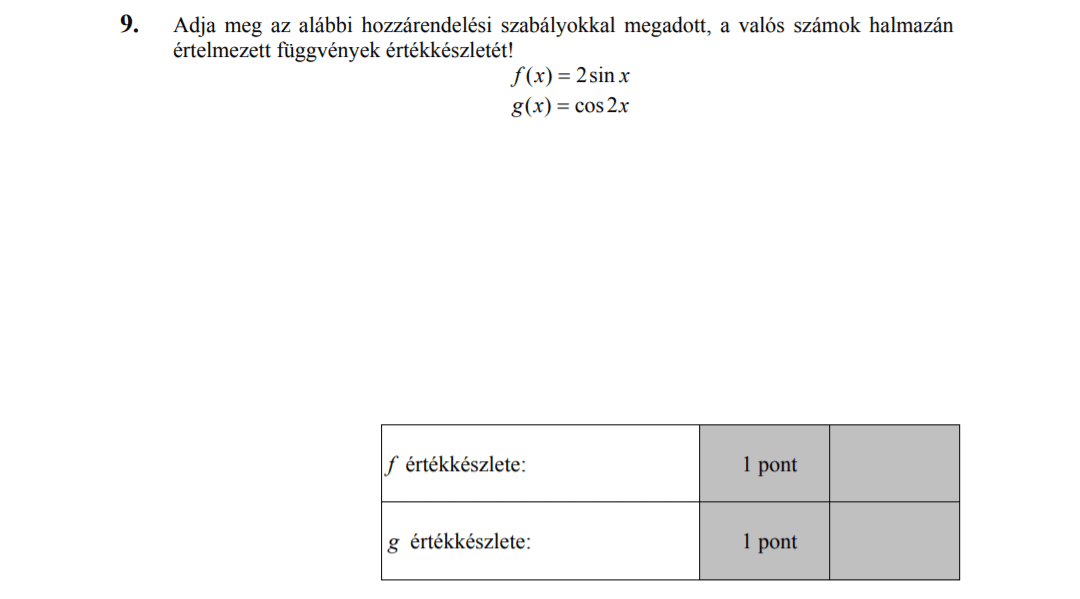
- Függvényekkel kapcsolatos feladatok (9,8 pont)
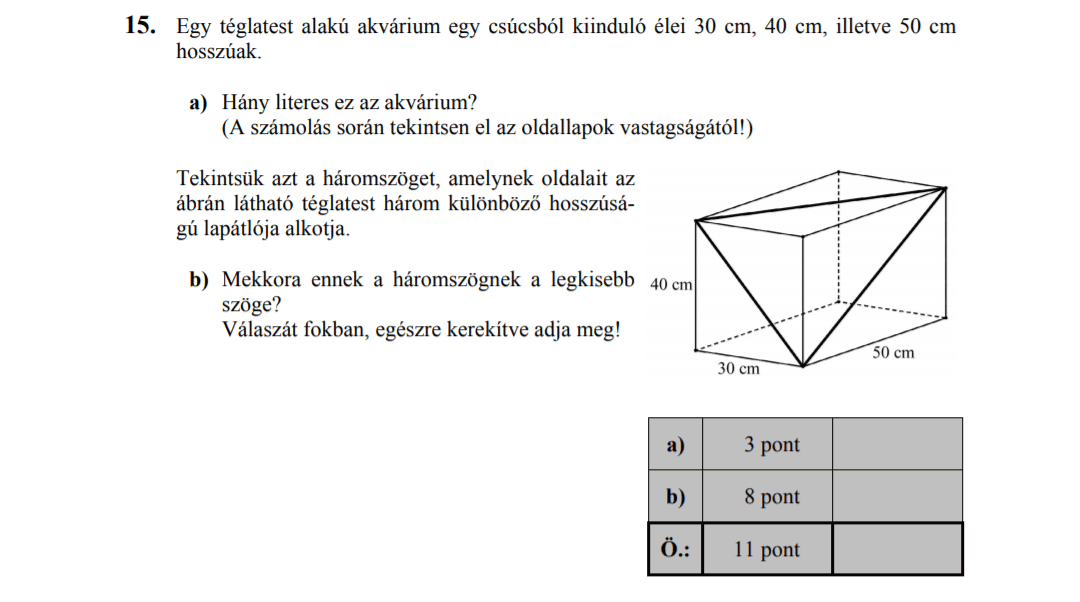
- Térgeometria (9,8 pont)
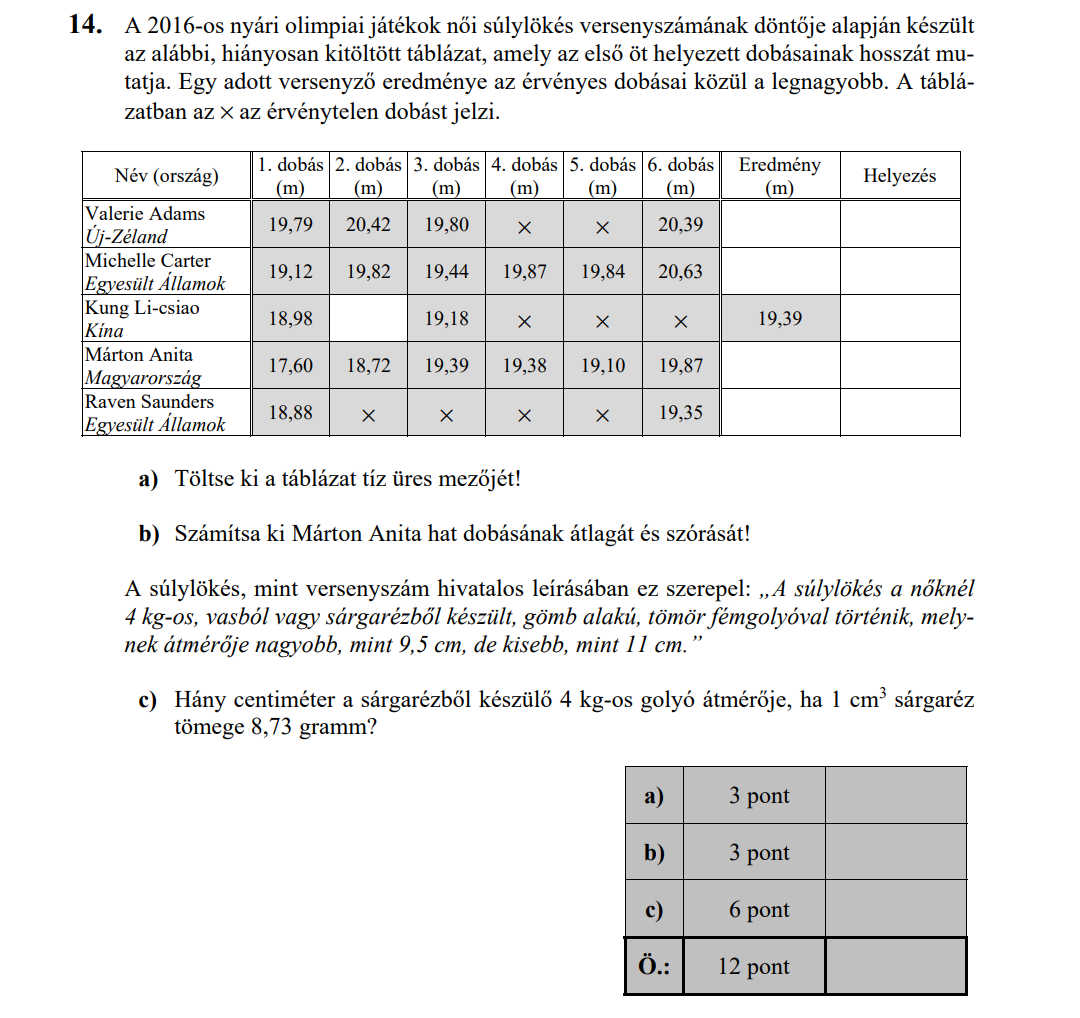
- Statisztika (9,3 pont)
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
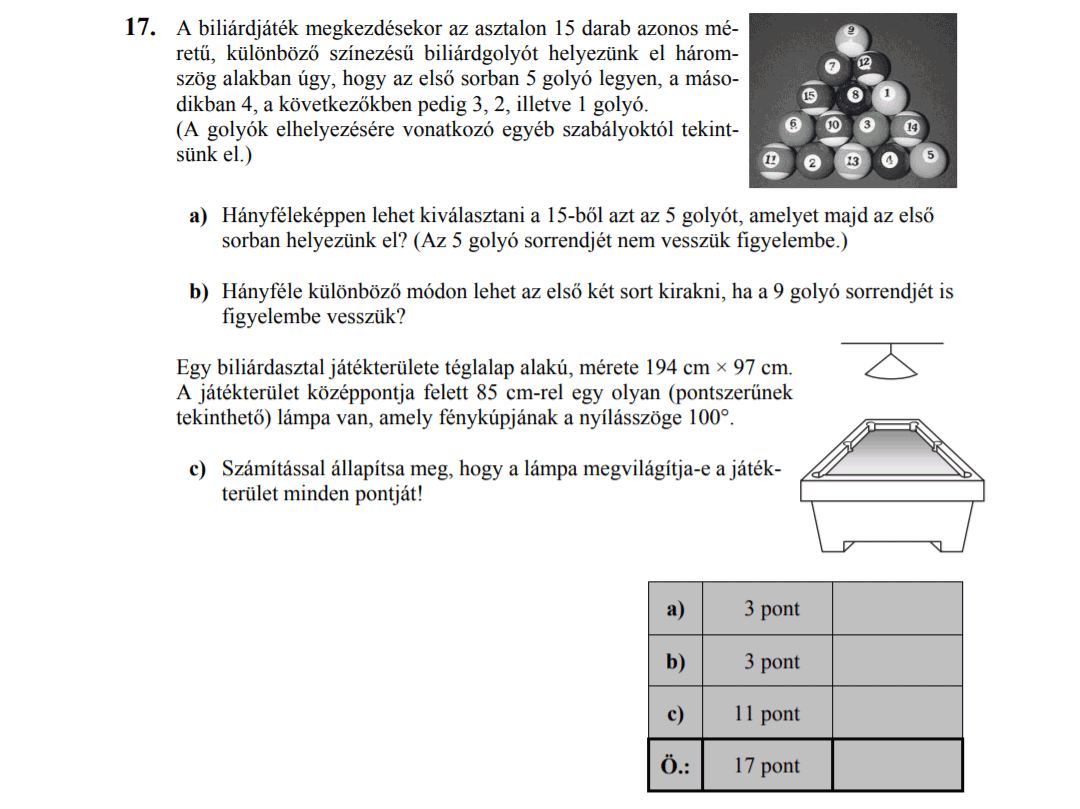
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
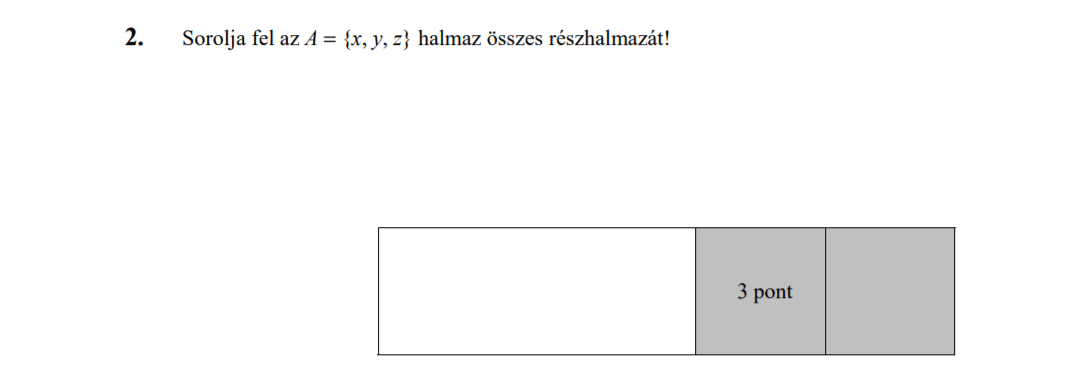
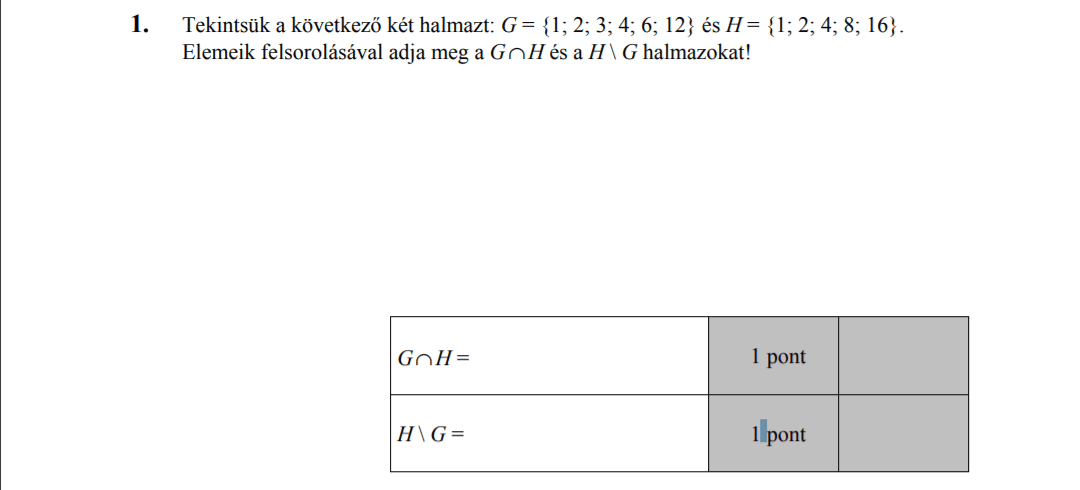
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
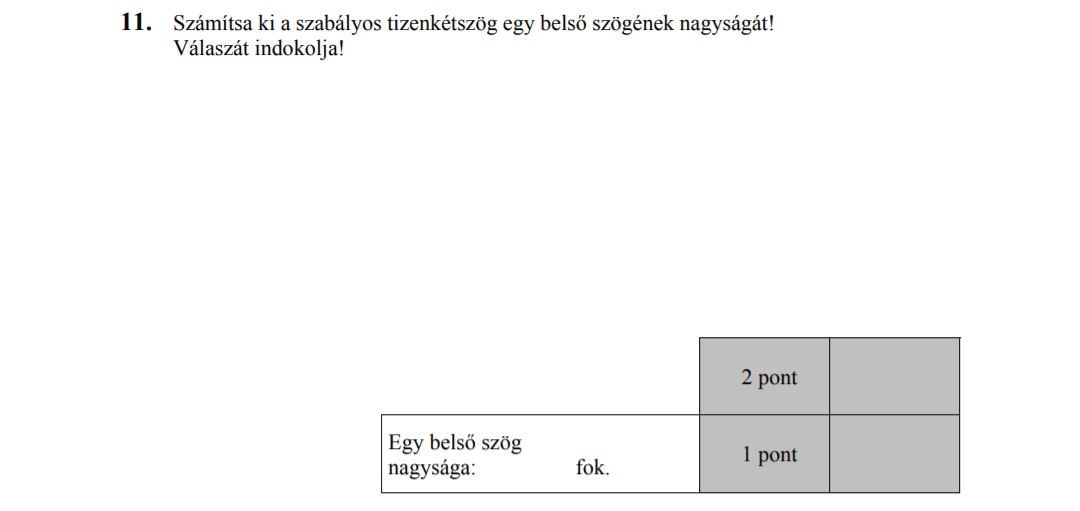
- Síkgeometria (4,5 pont)
- Százalékszámítás (3,8 pont)
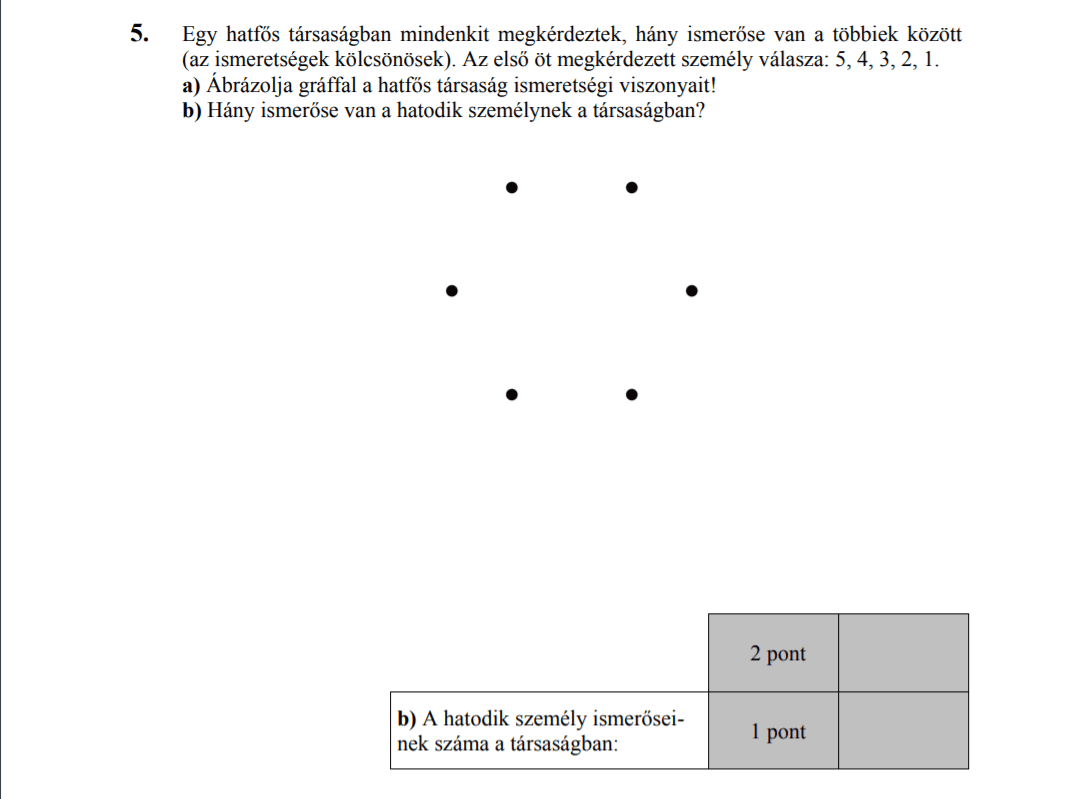
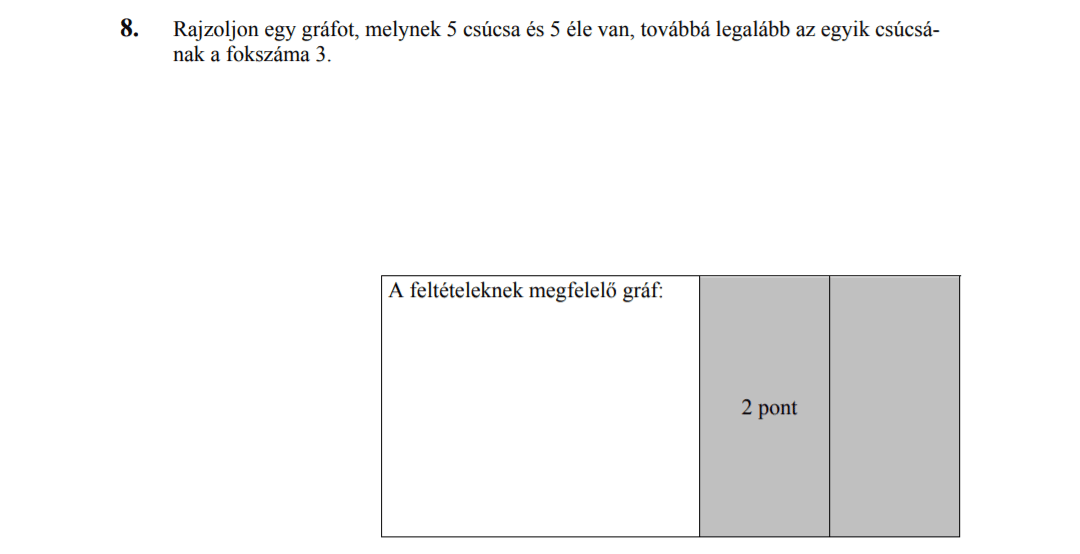
- Gráfok (3 pont)
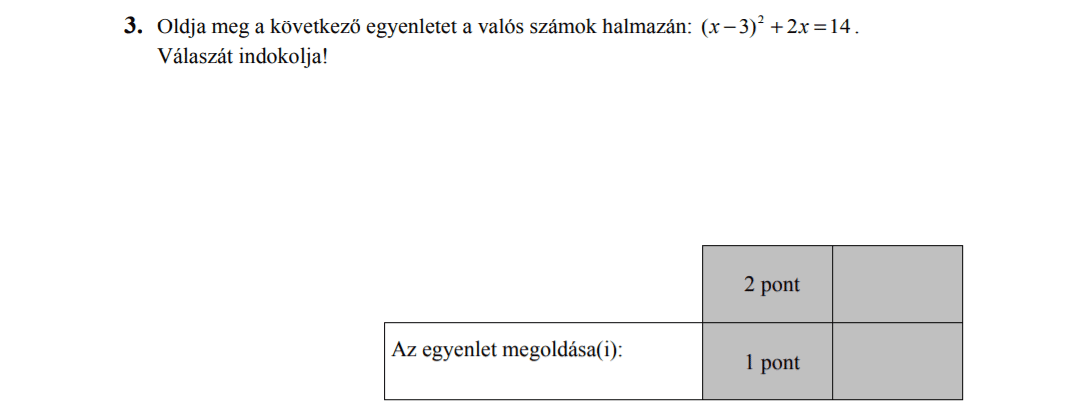
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
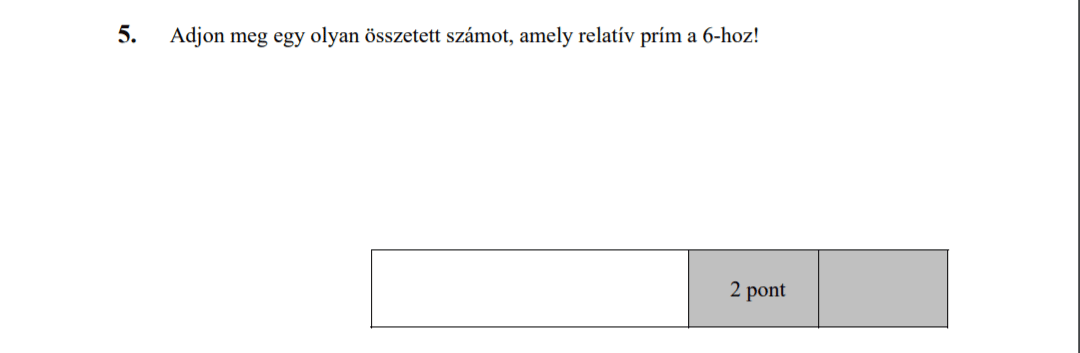
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Valószínűségszámítás (9,1 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


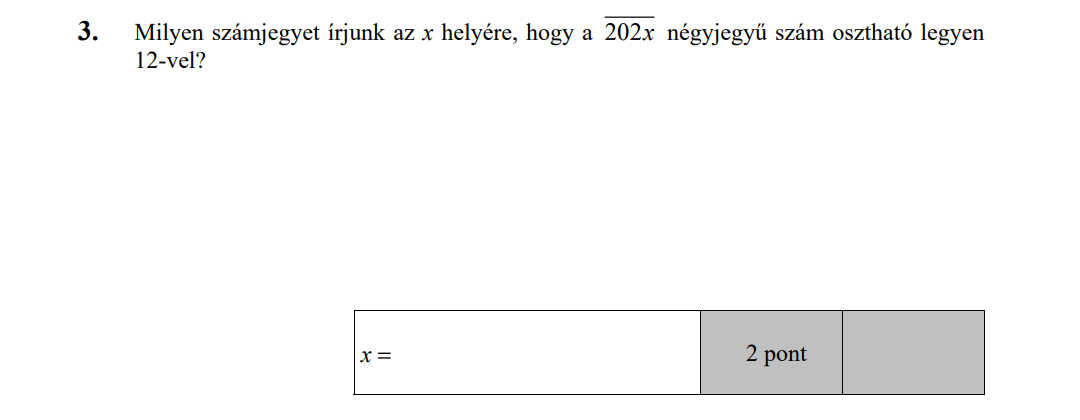
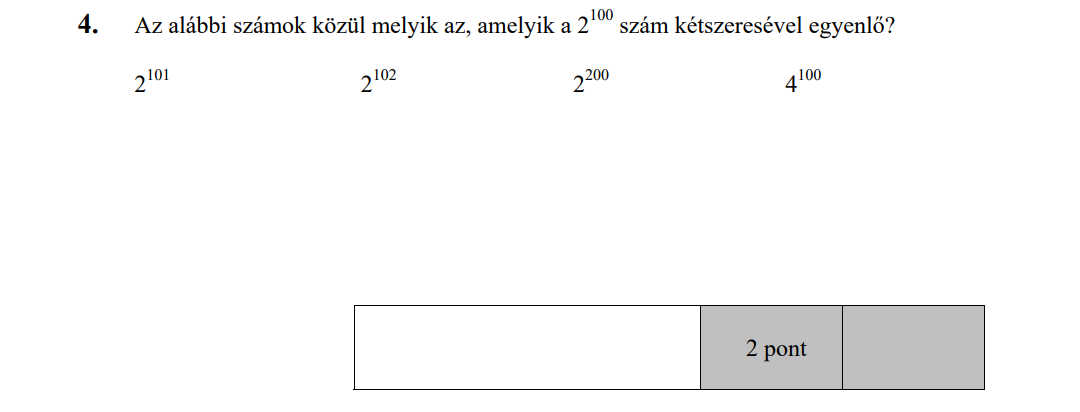



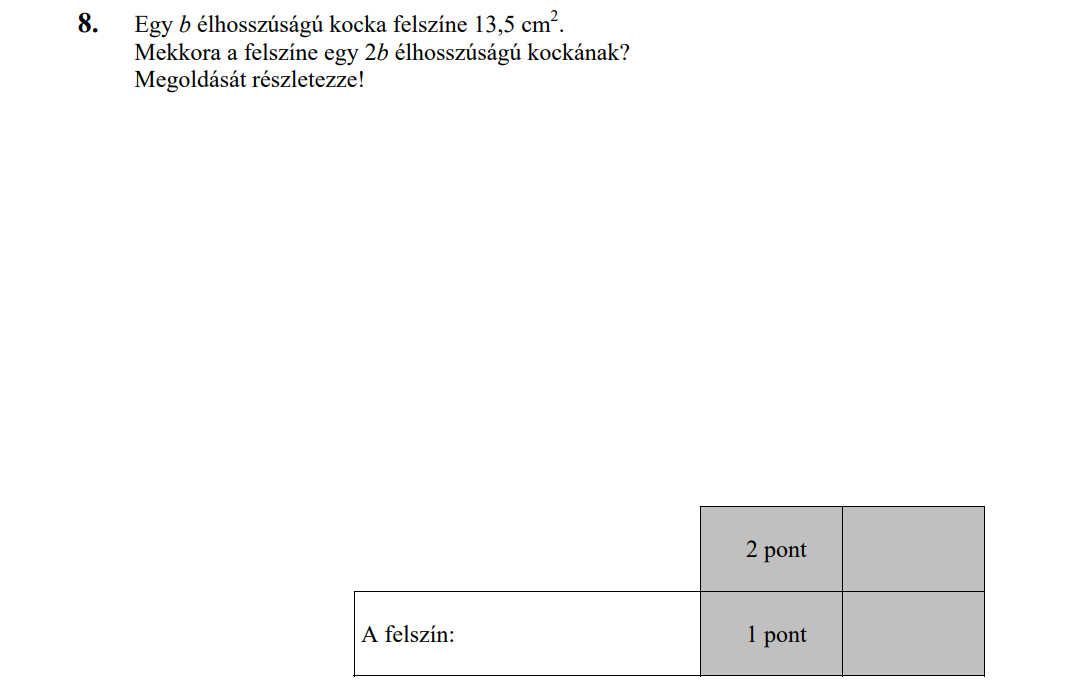




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
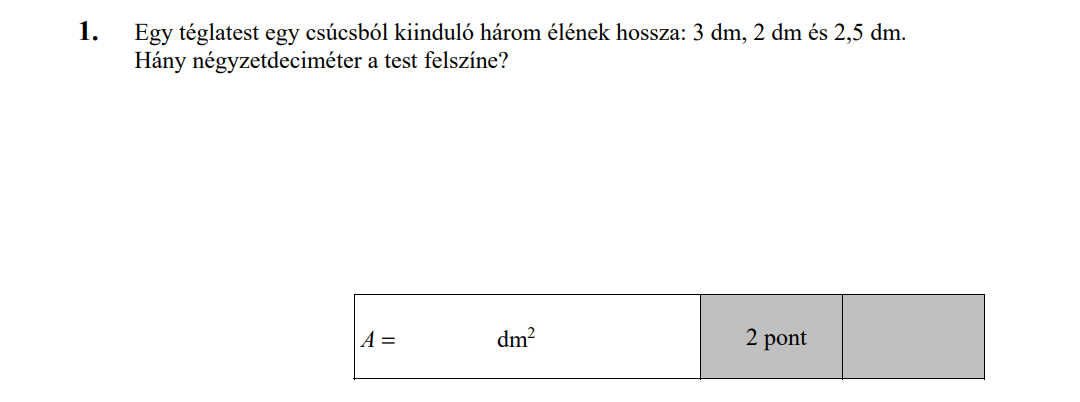
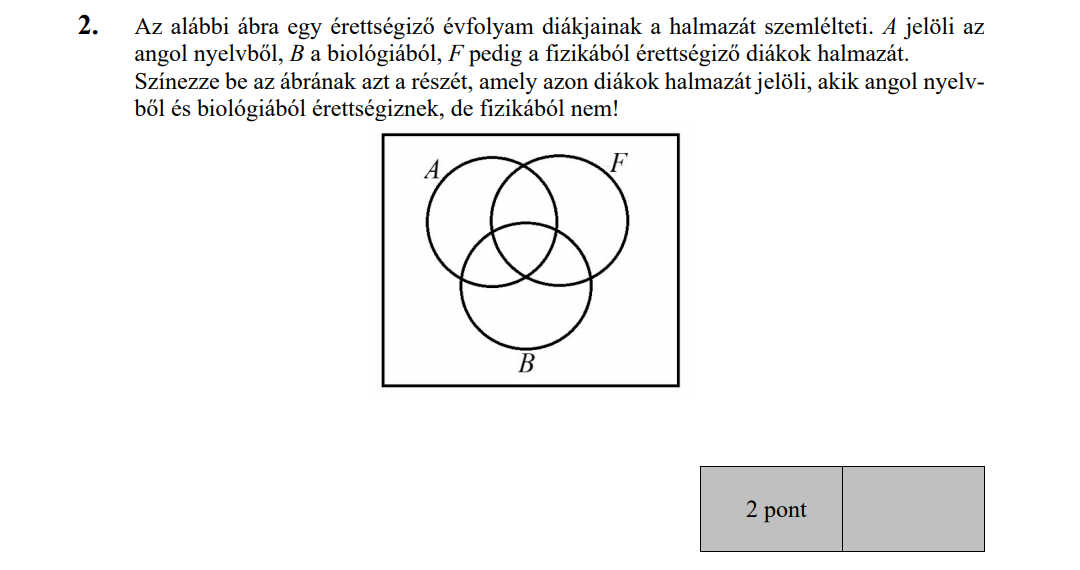

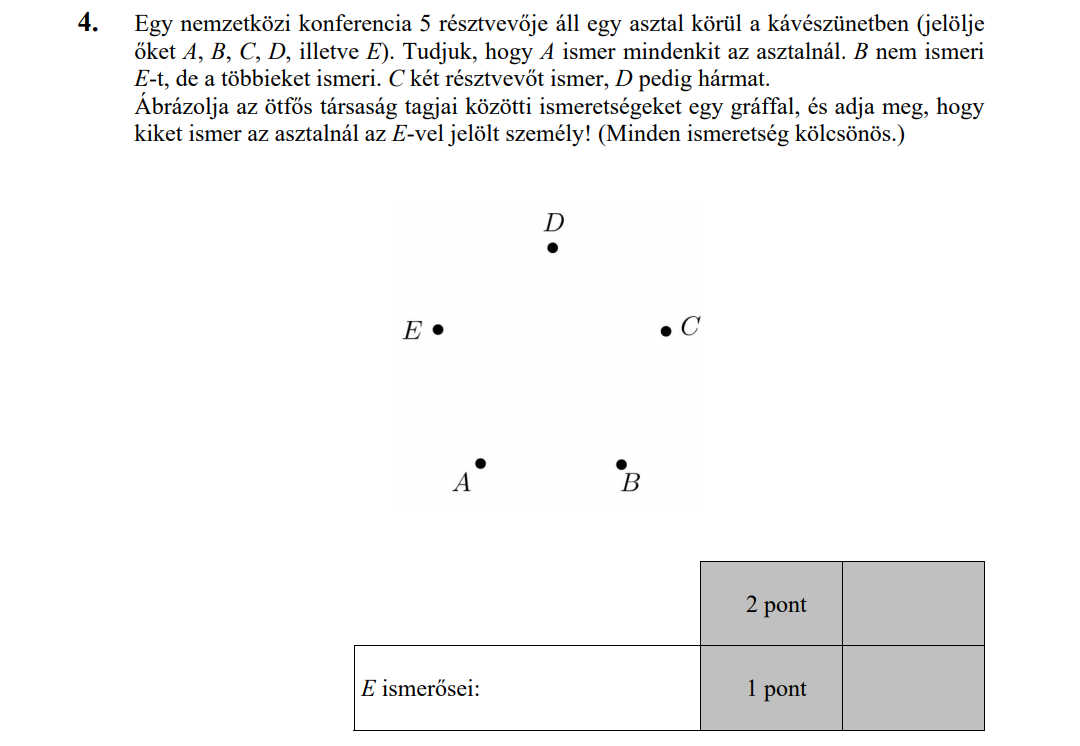

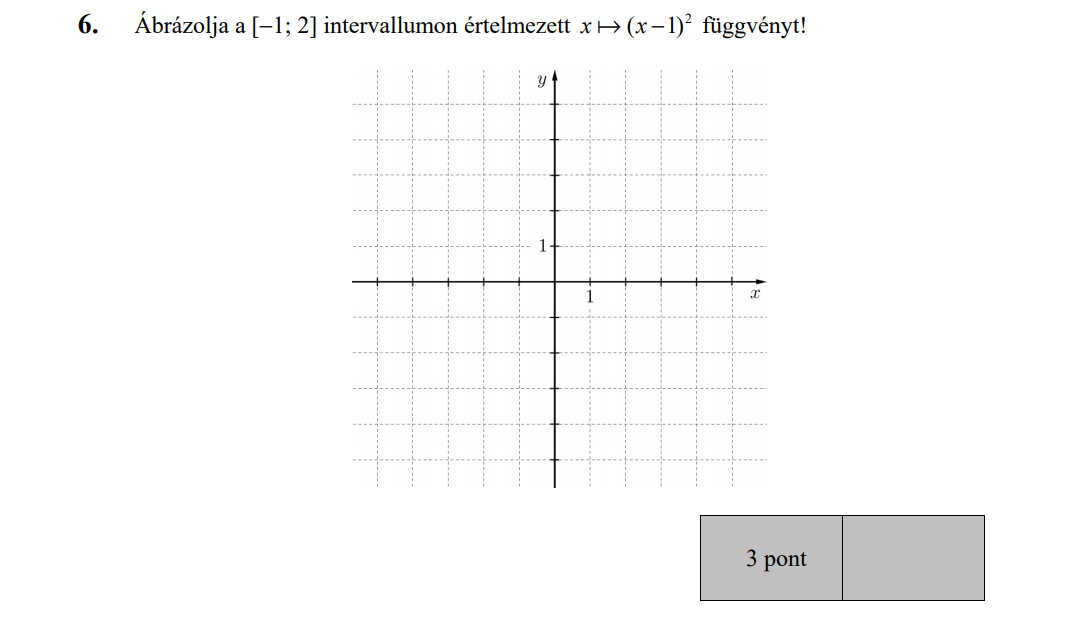



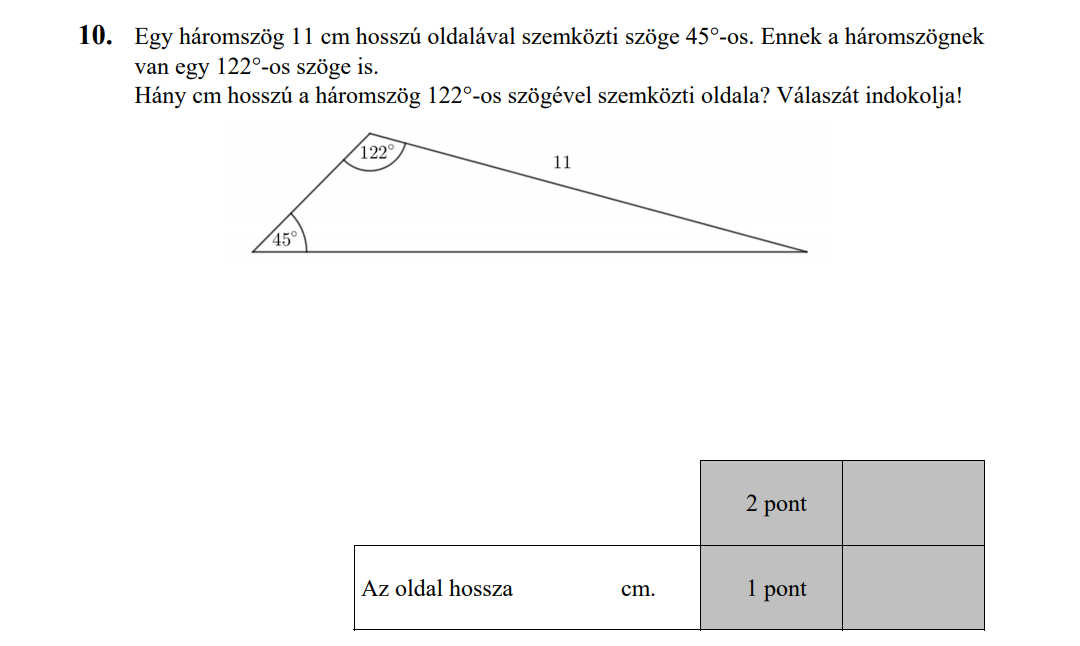

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



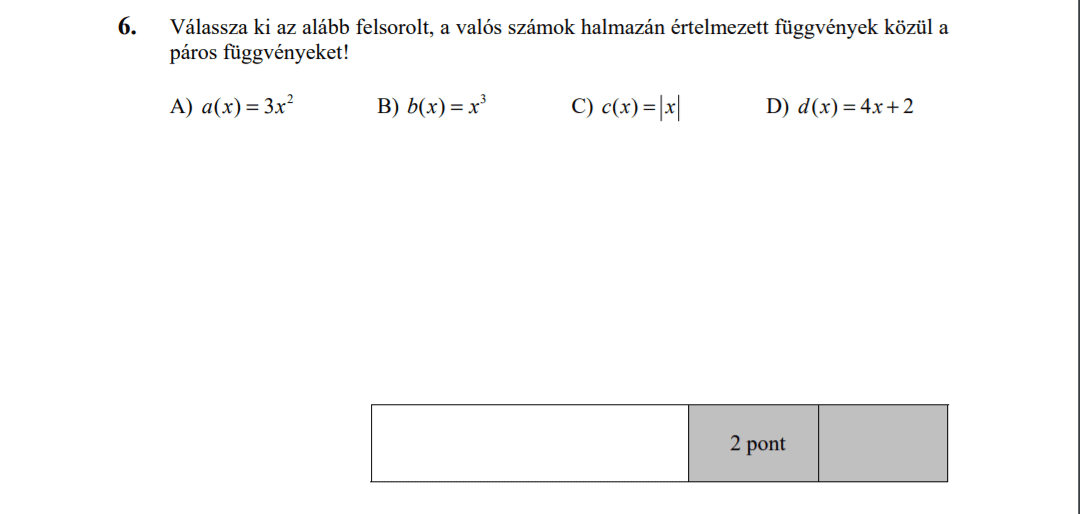
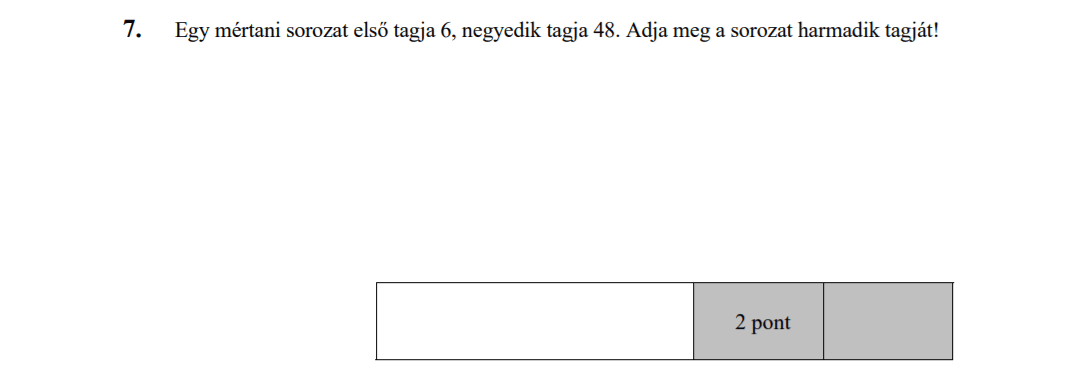



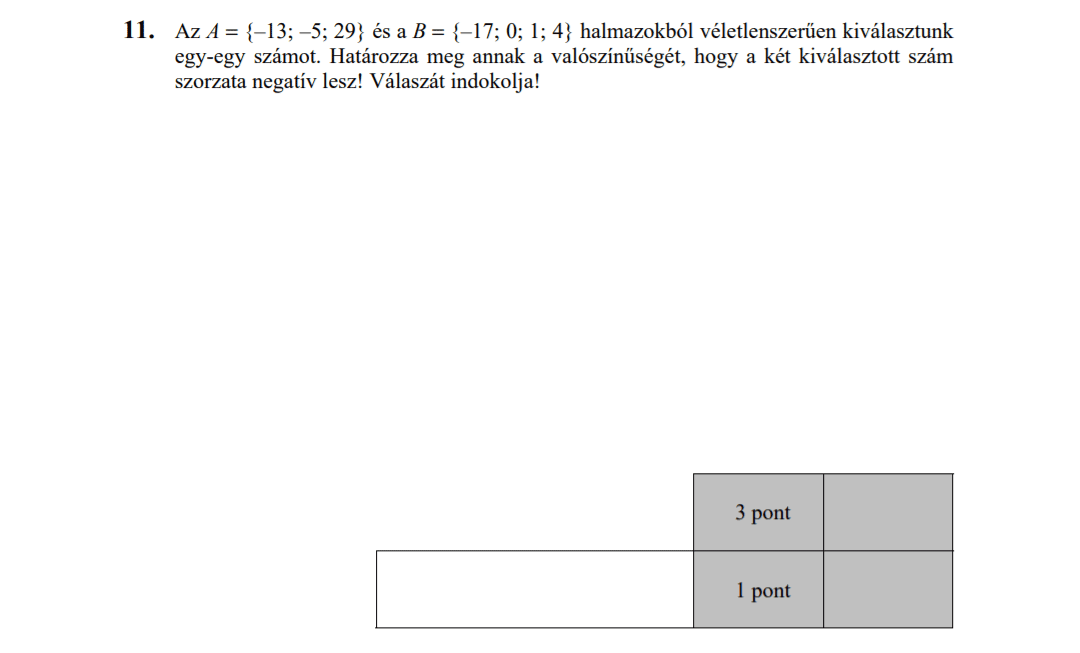

MÁSODIK RÉSZ


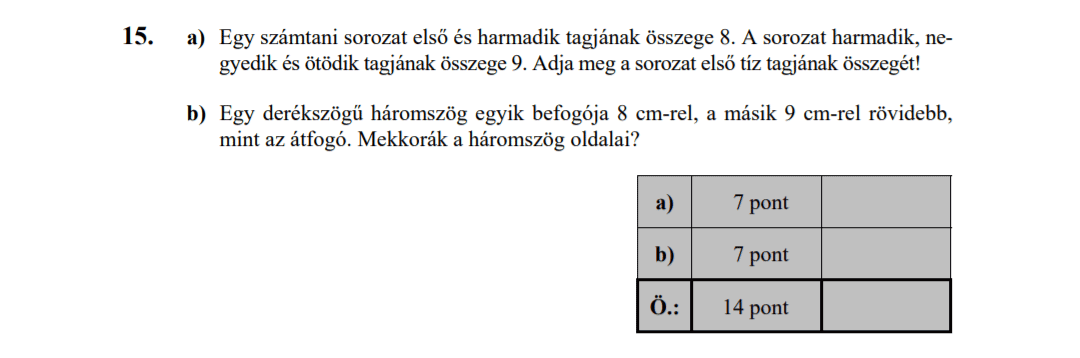



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






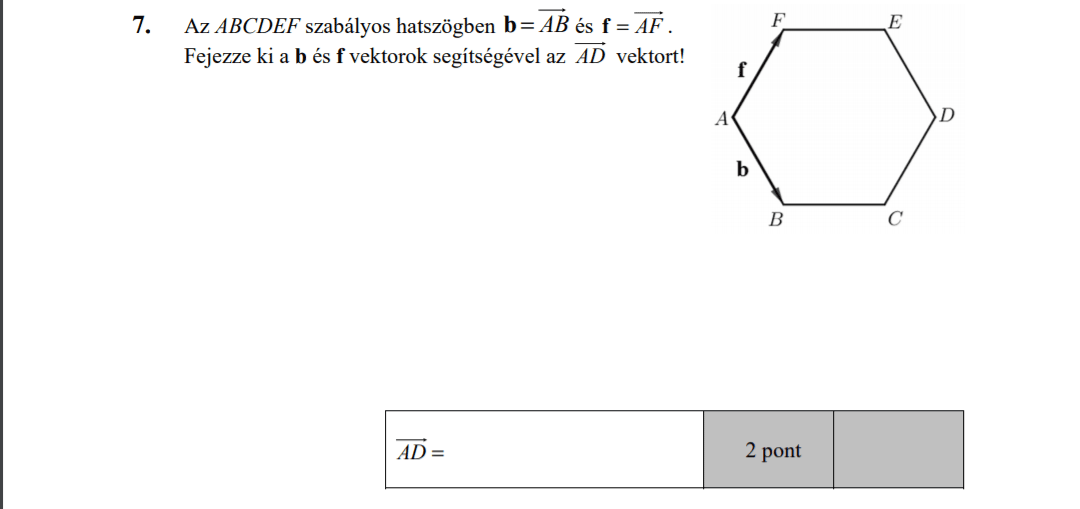



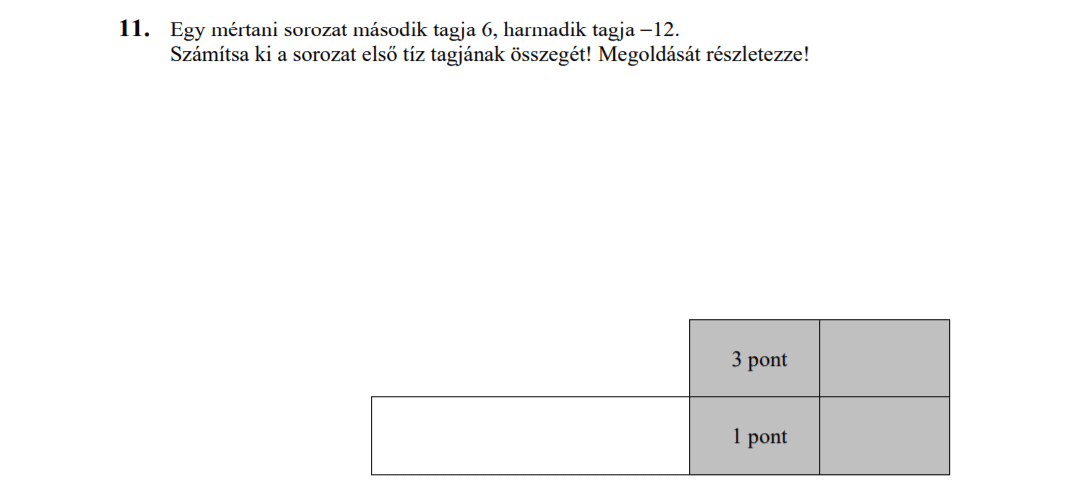

MÁSODIK RÉSZ

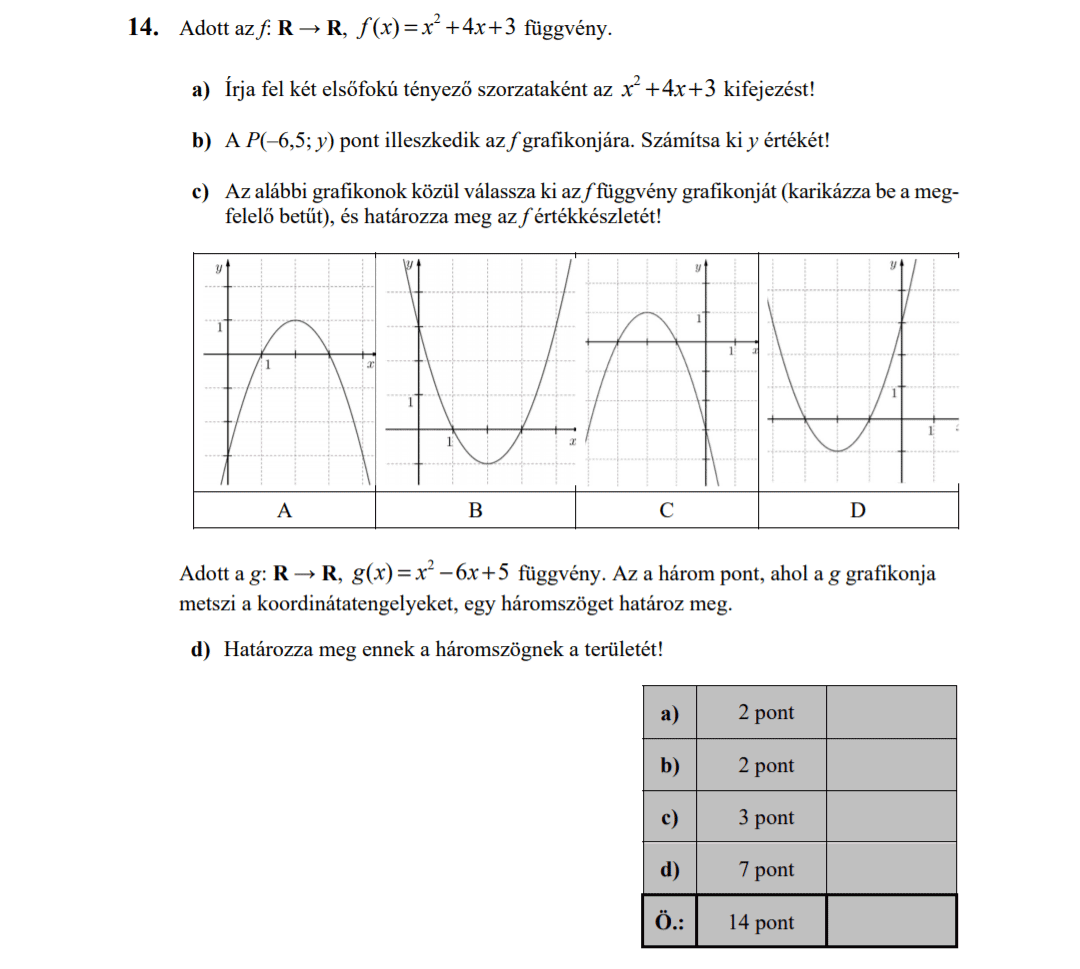




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



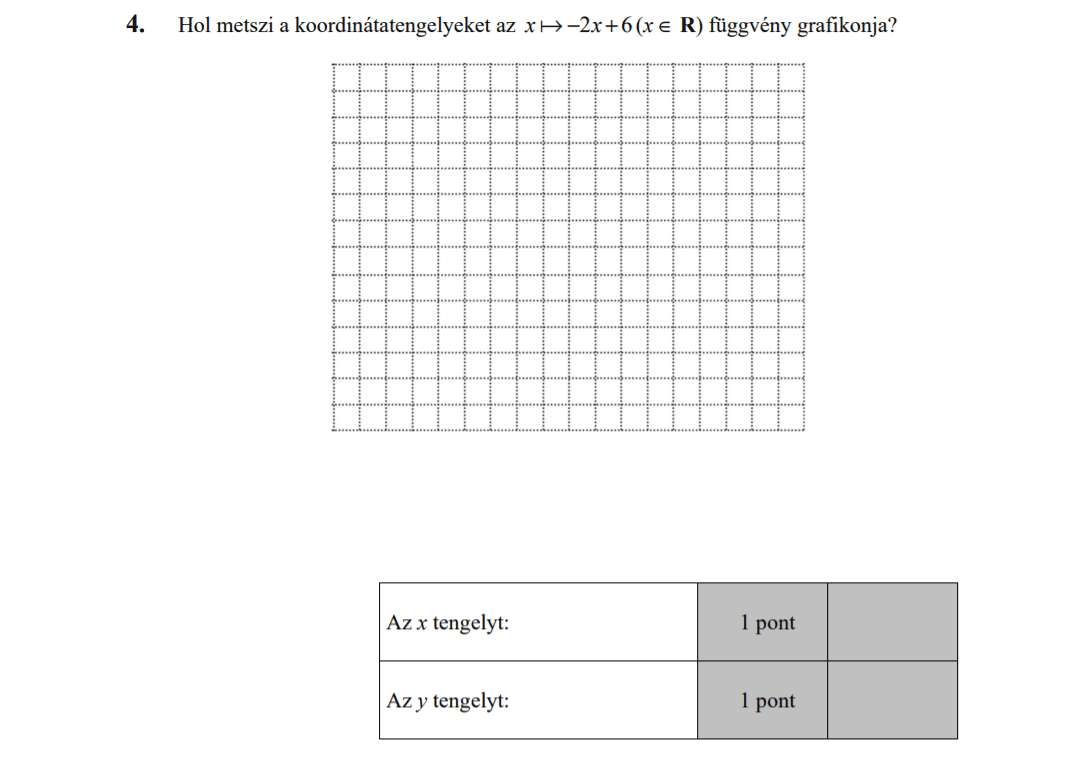







MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

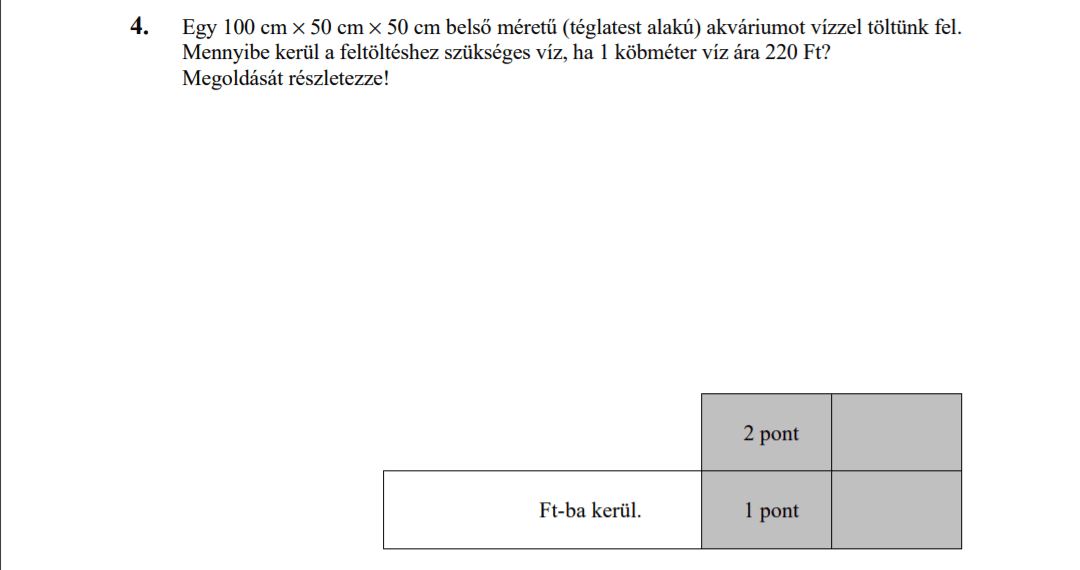
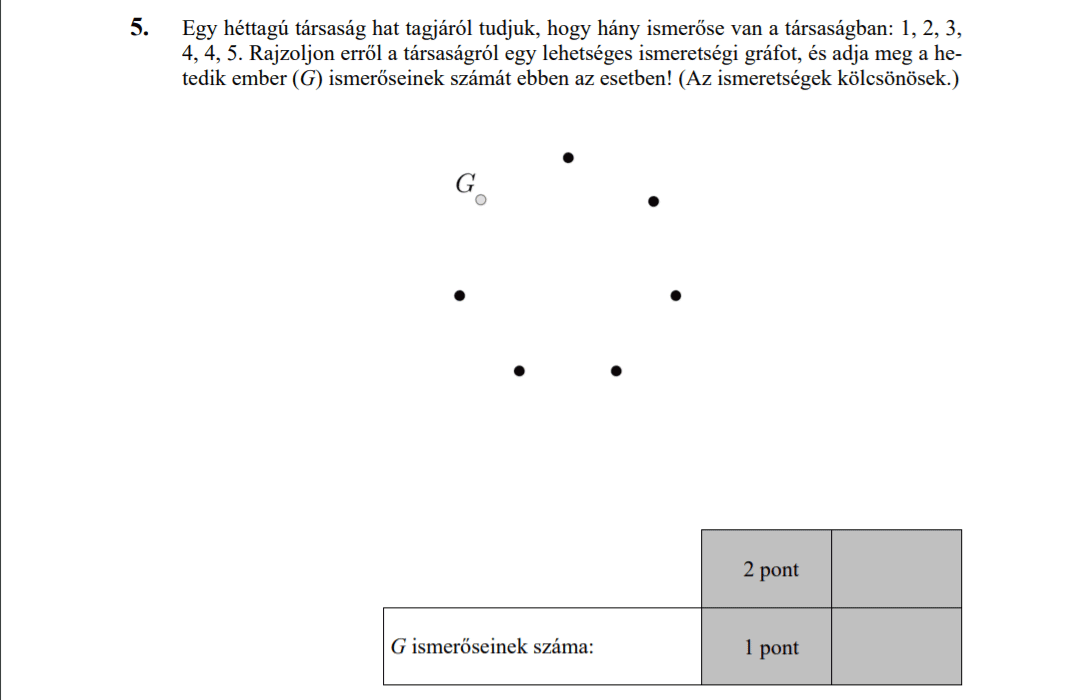







MÁSODIK RÉSZ
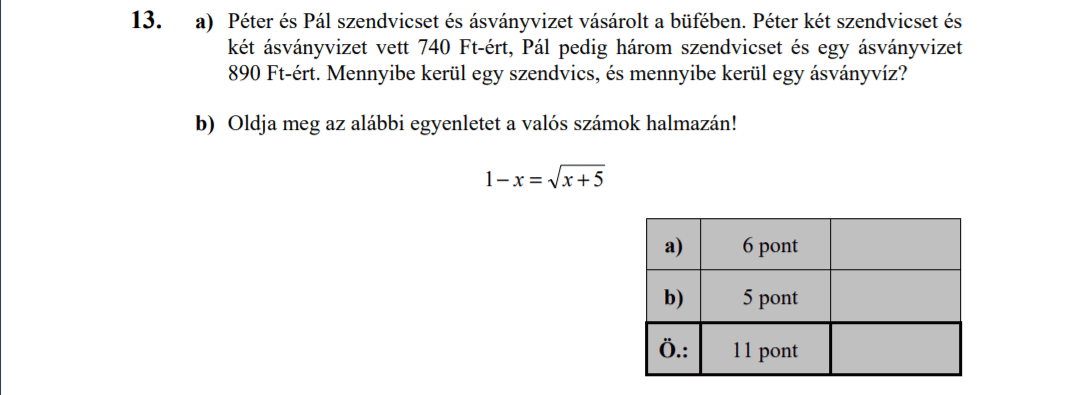
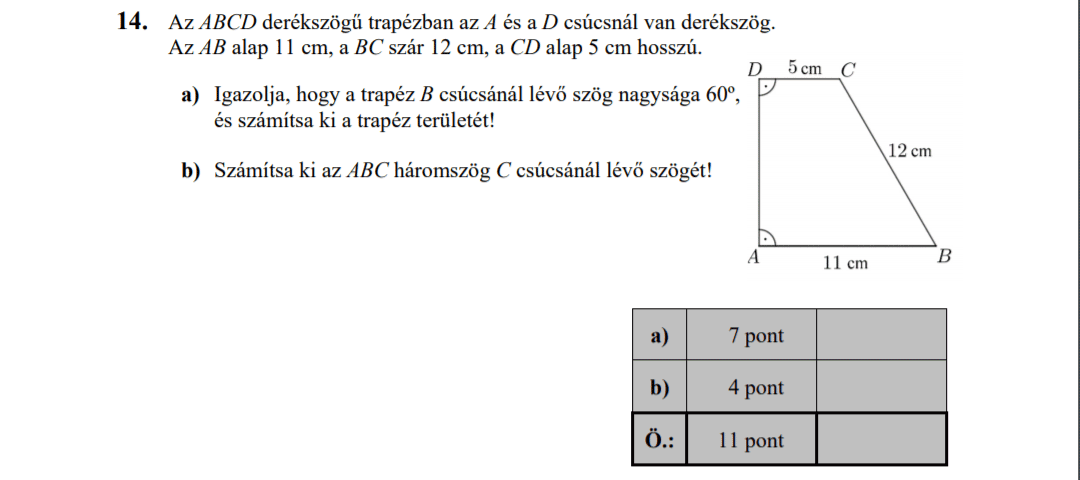



- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




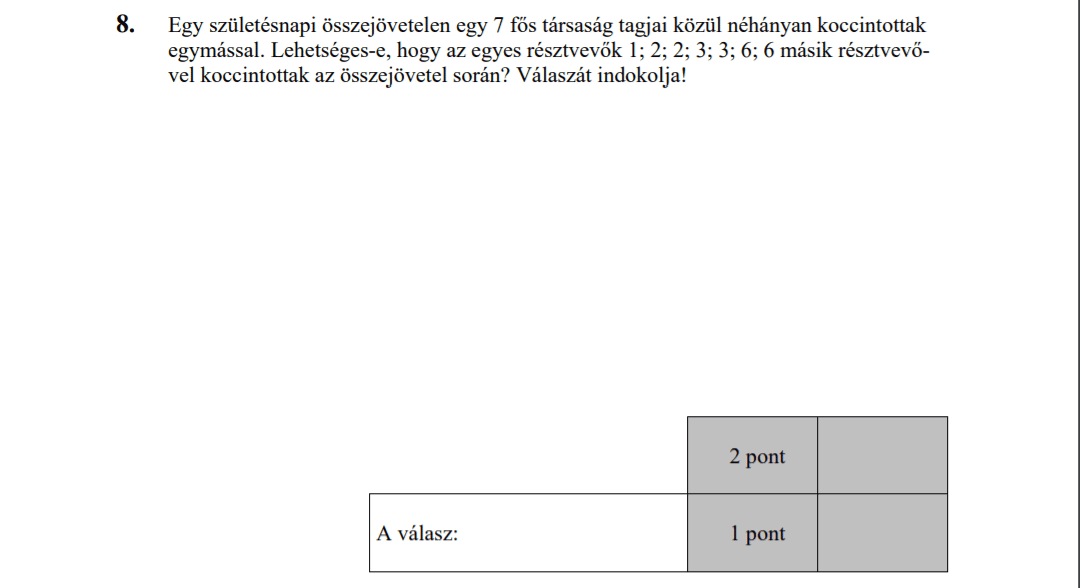



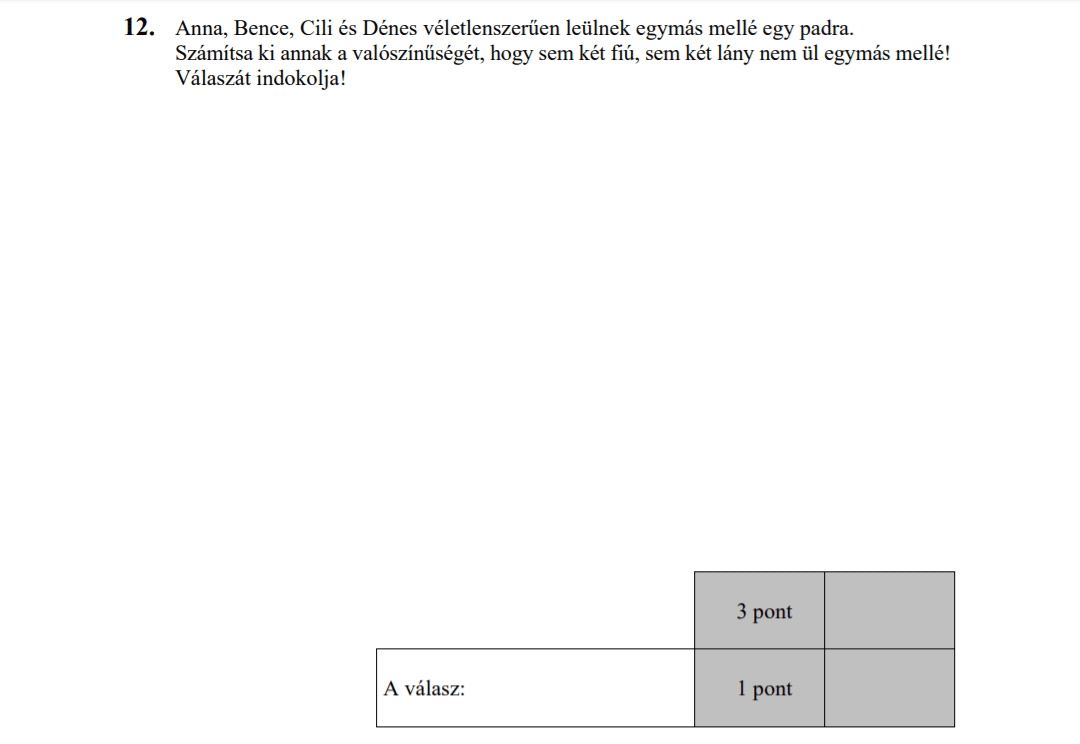
MÁSODIK RÉSZ

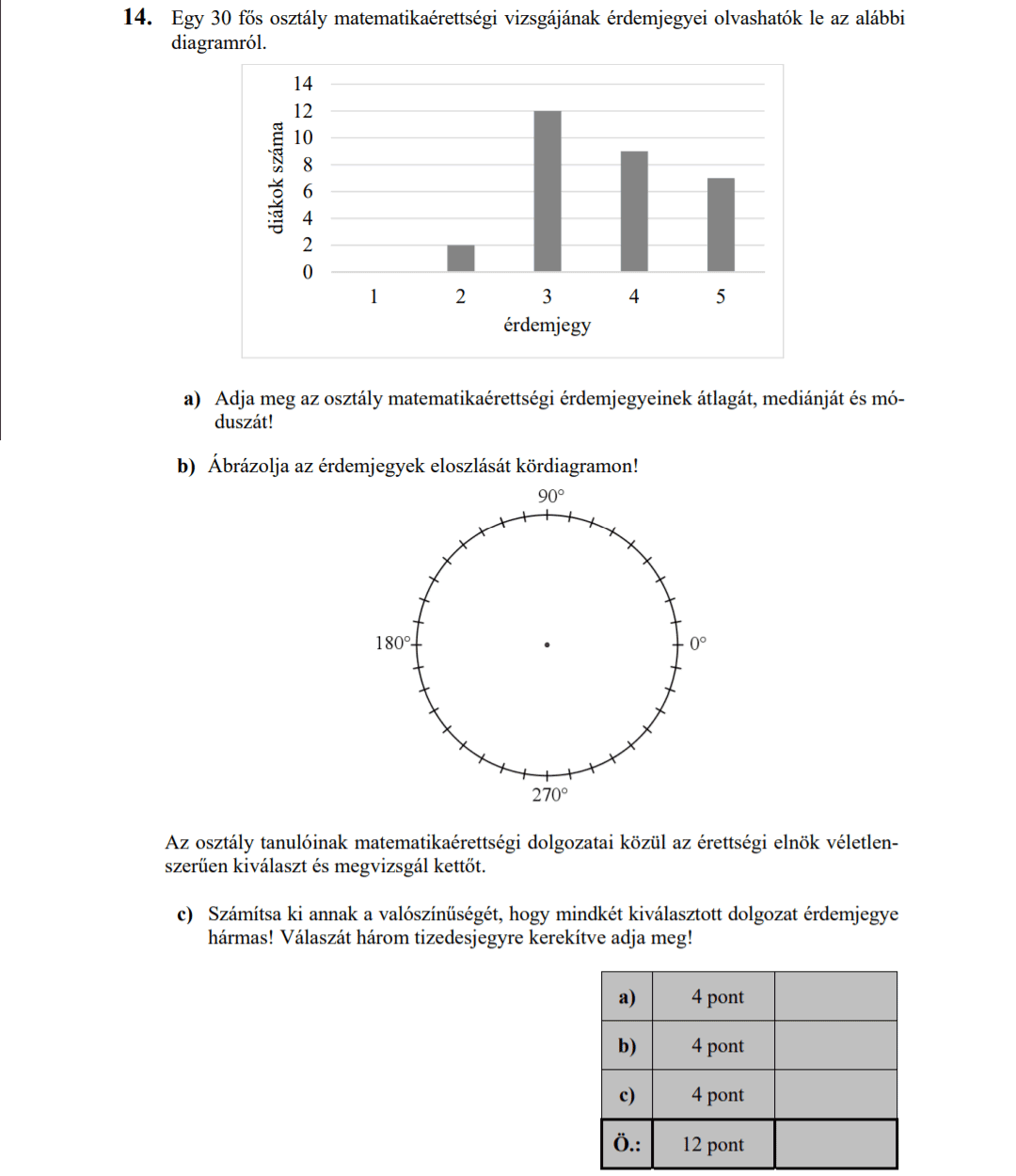
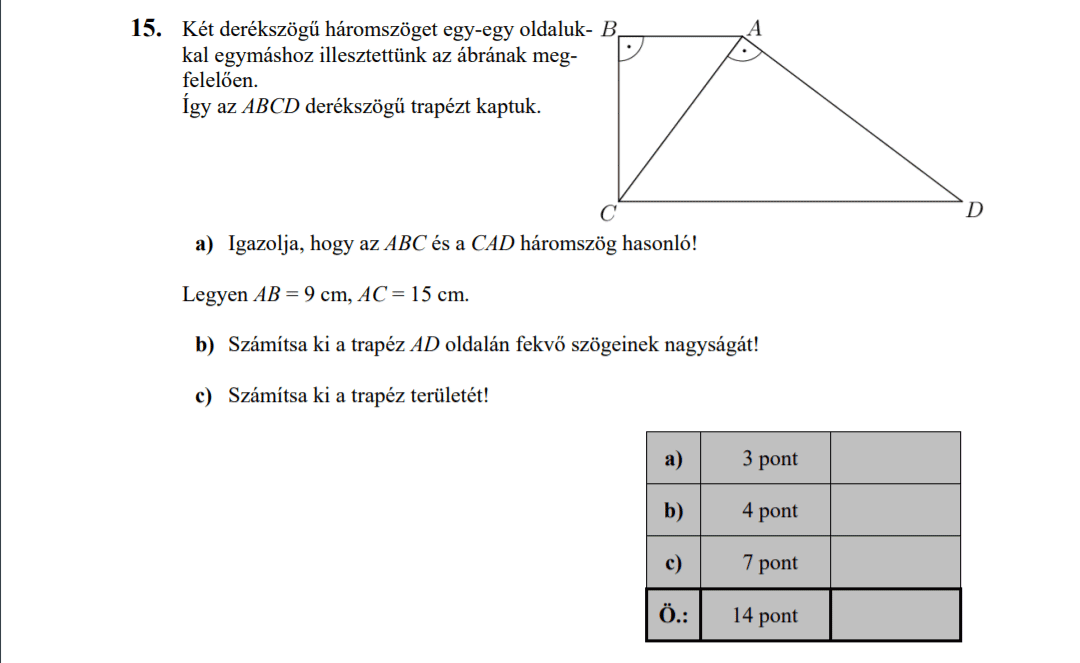



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


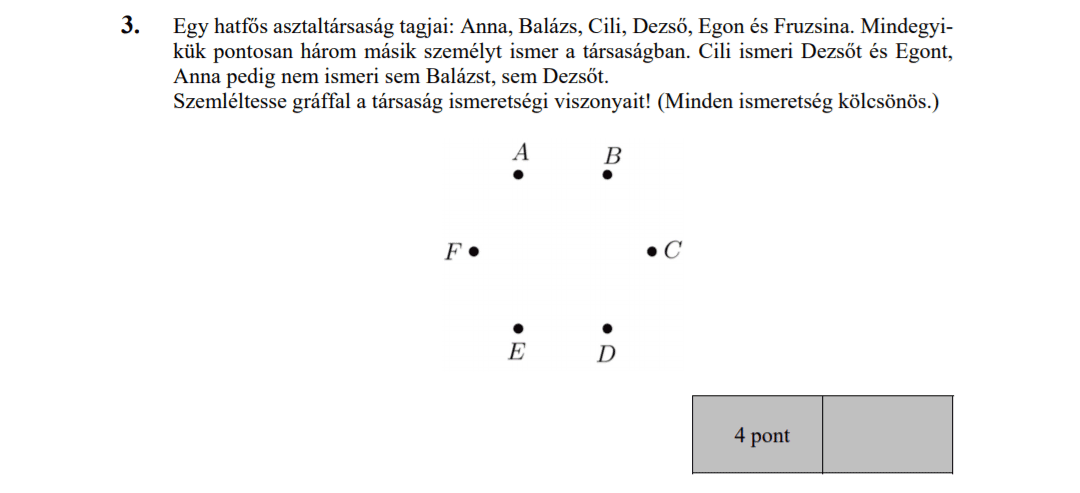


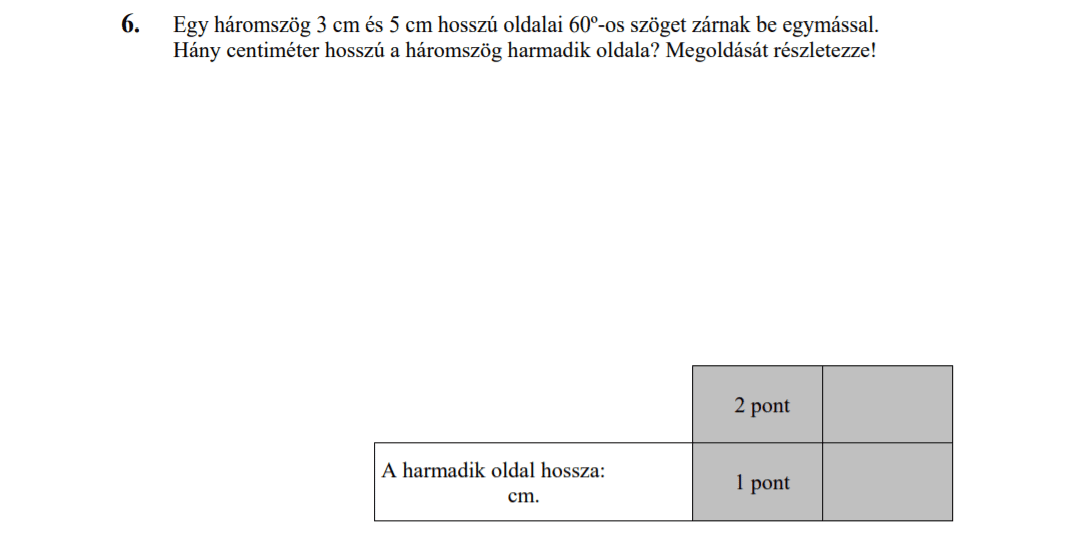

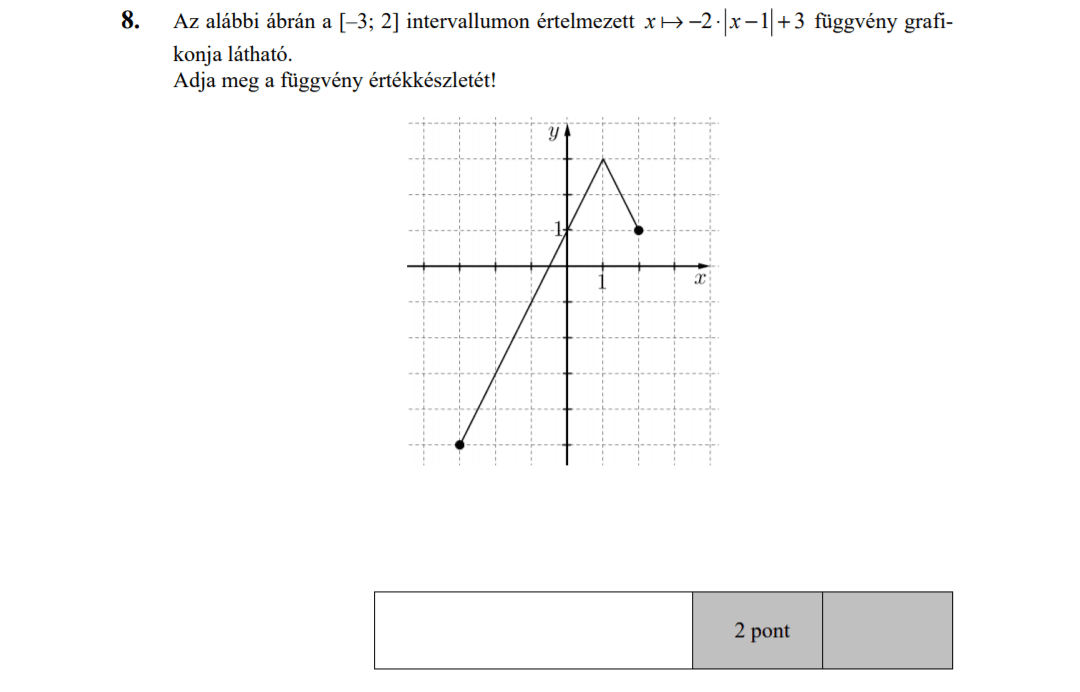

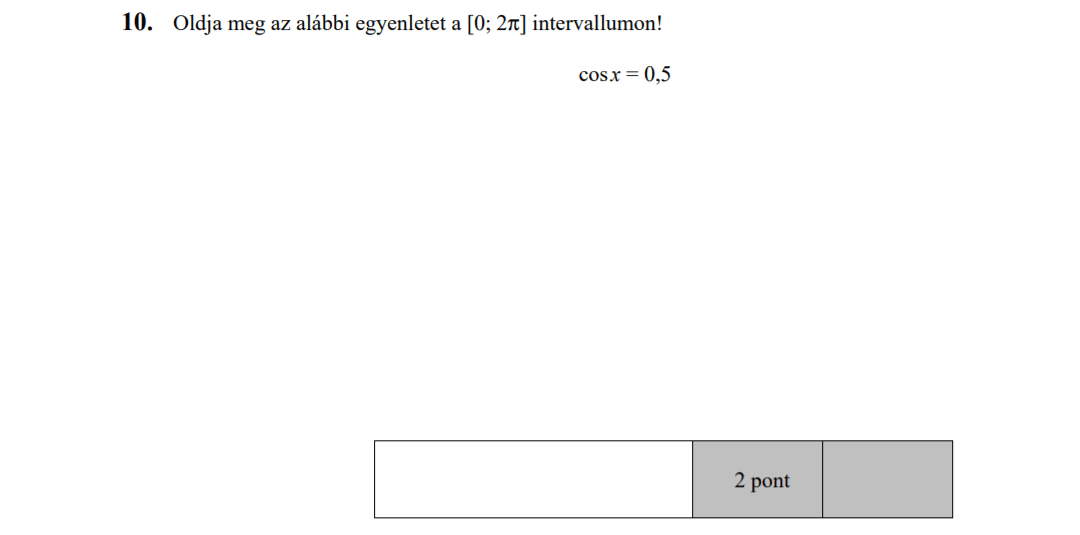

MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


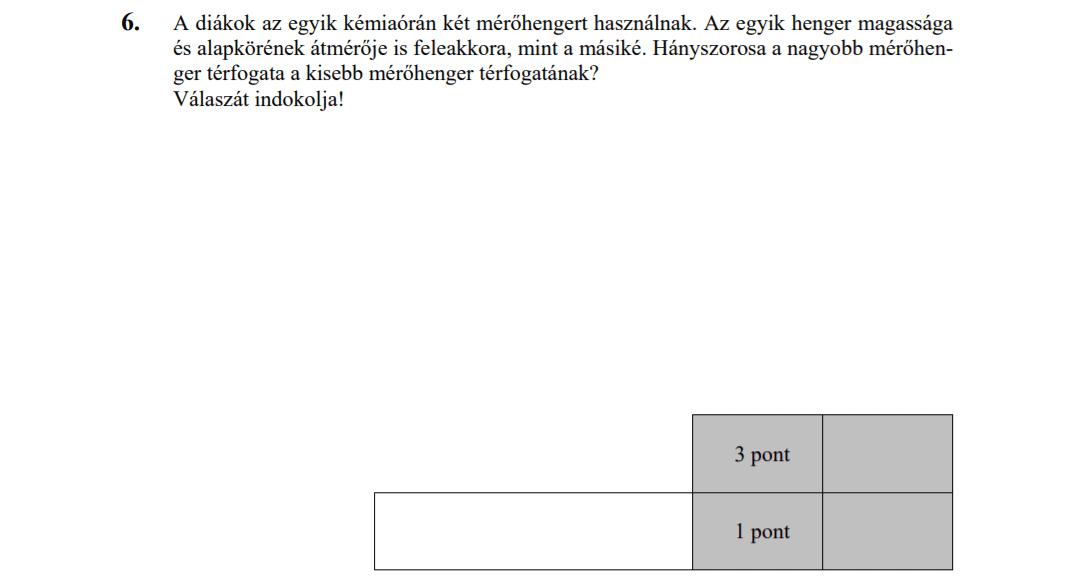
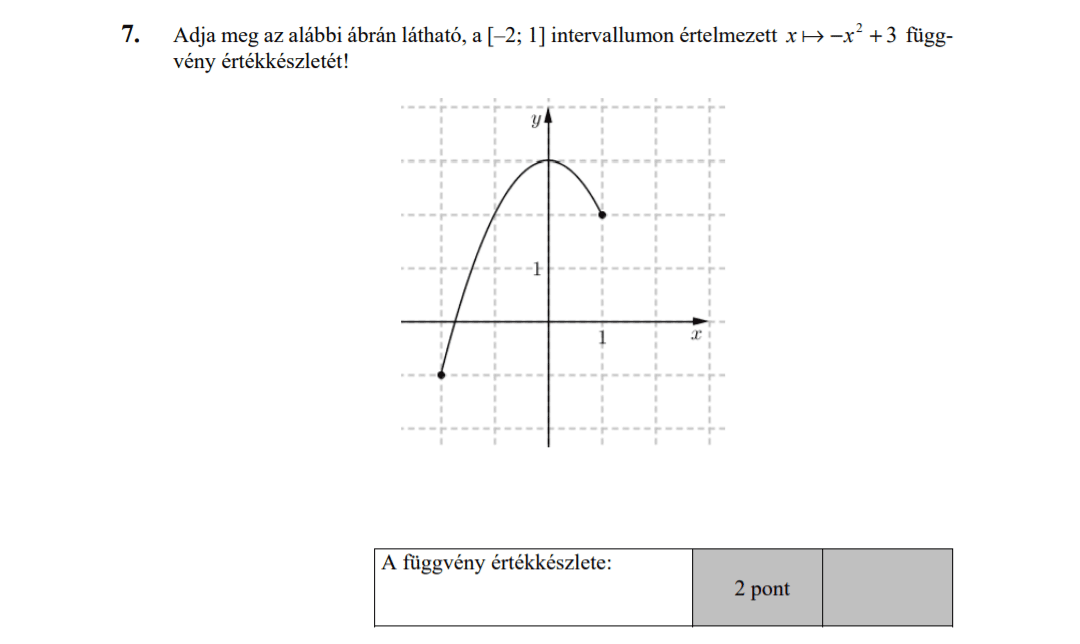

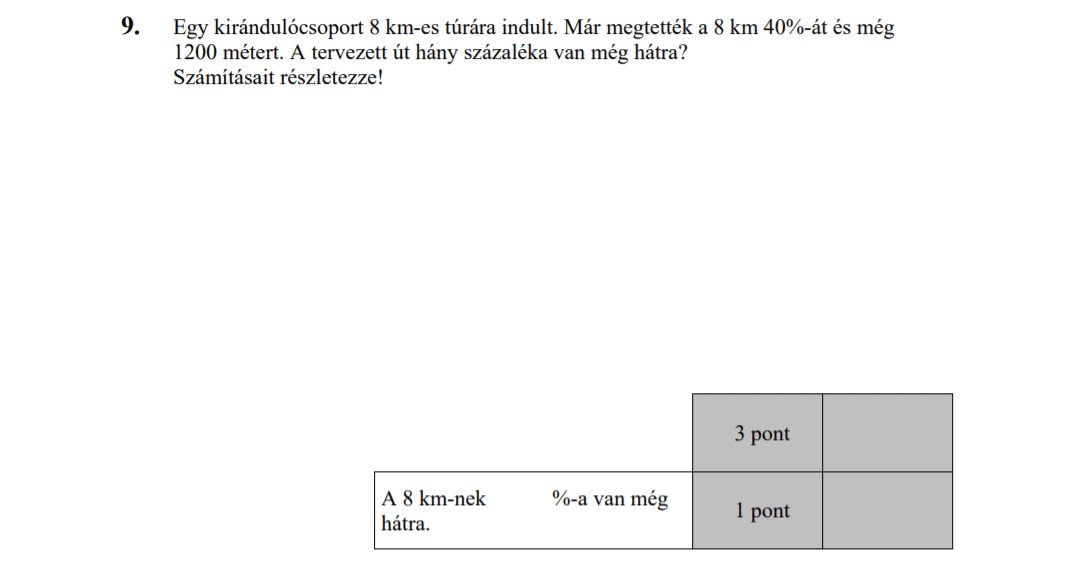
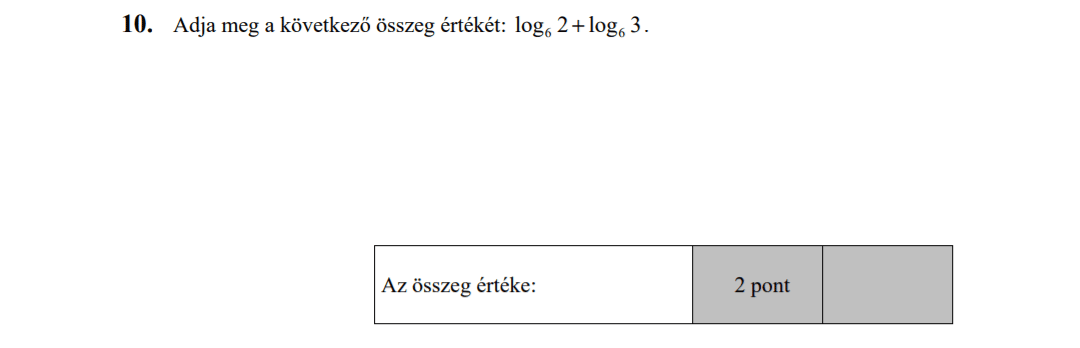

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






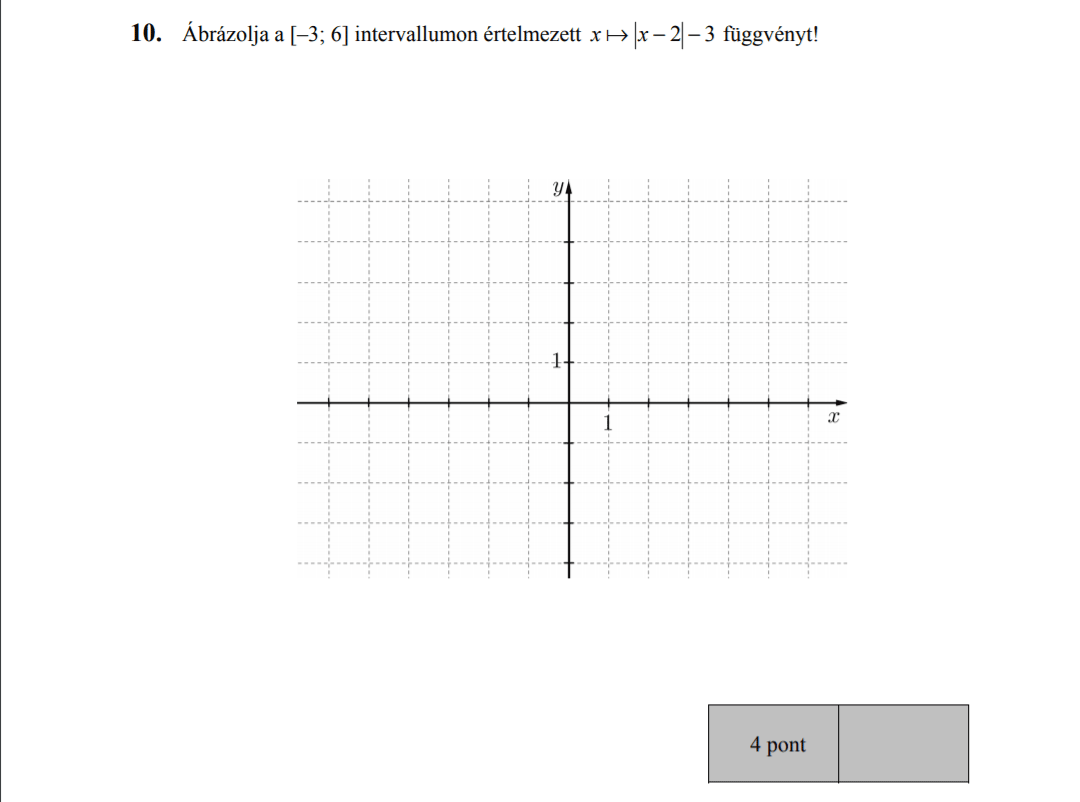

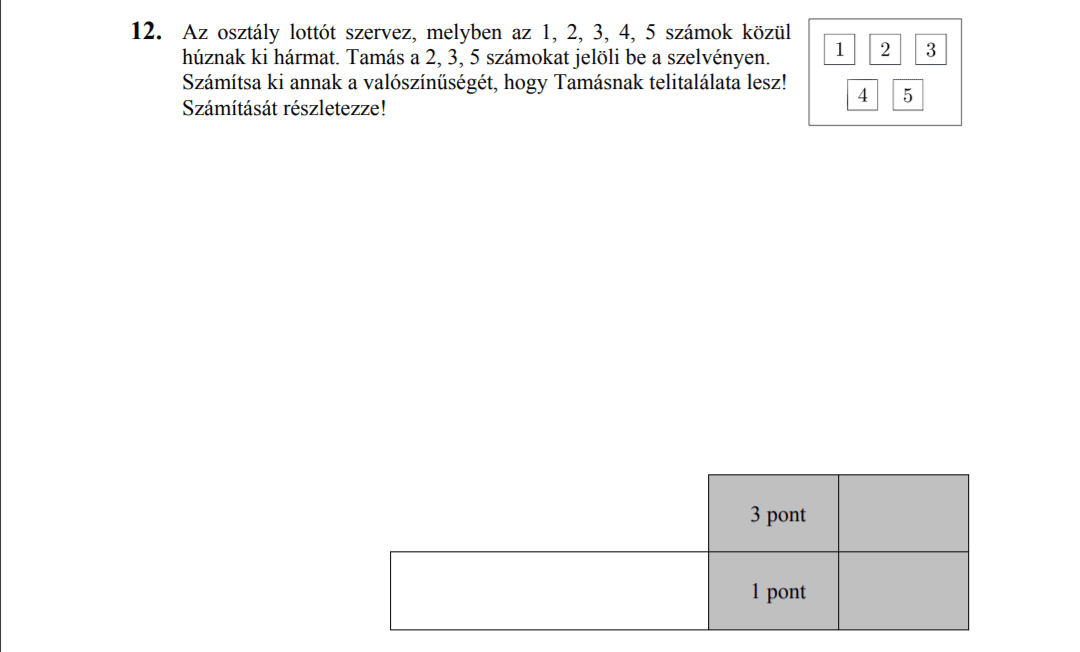
MÁSODIK RÉSZ

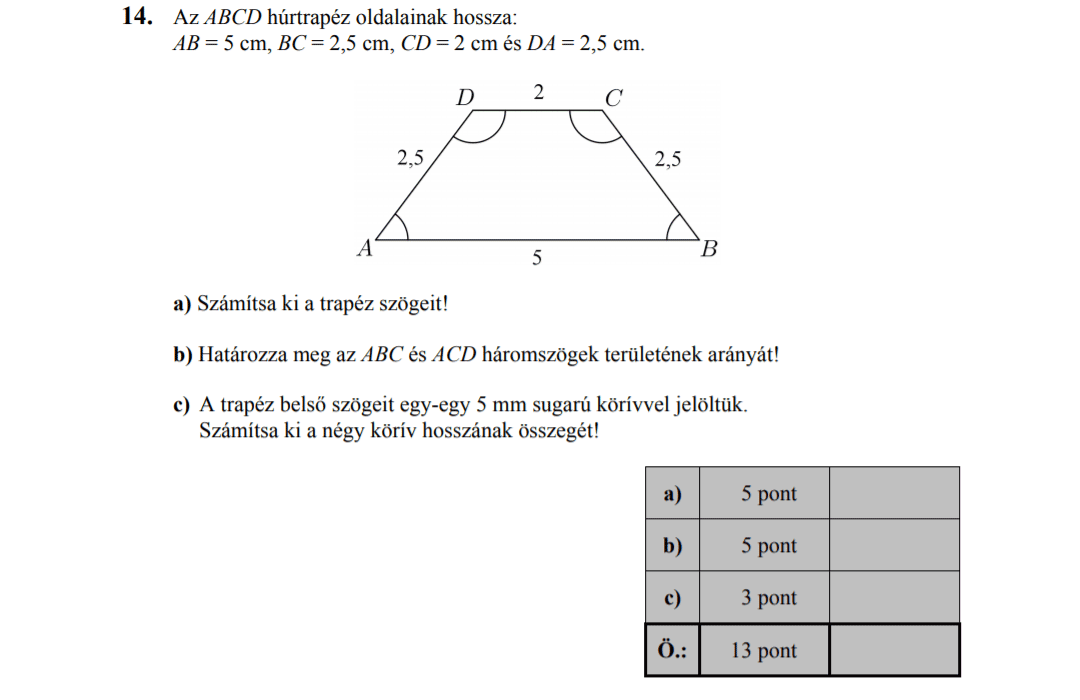

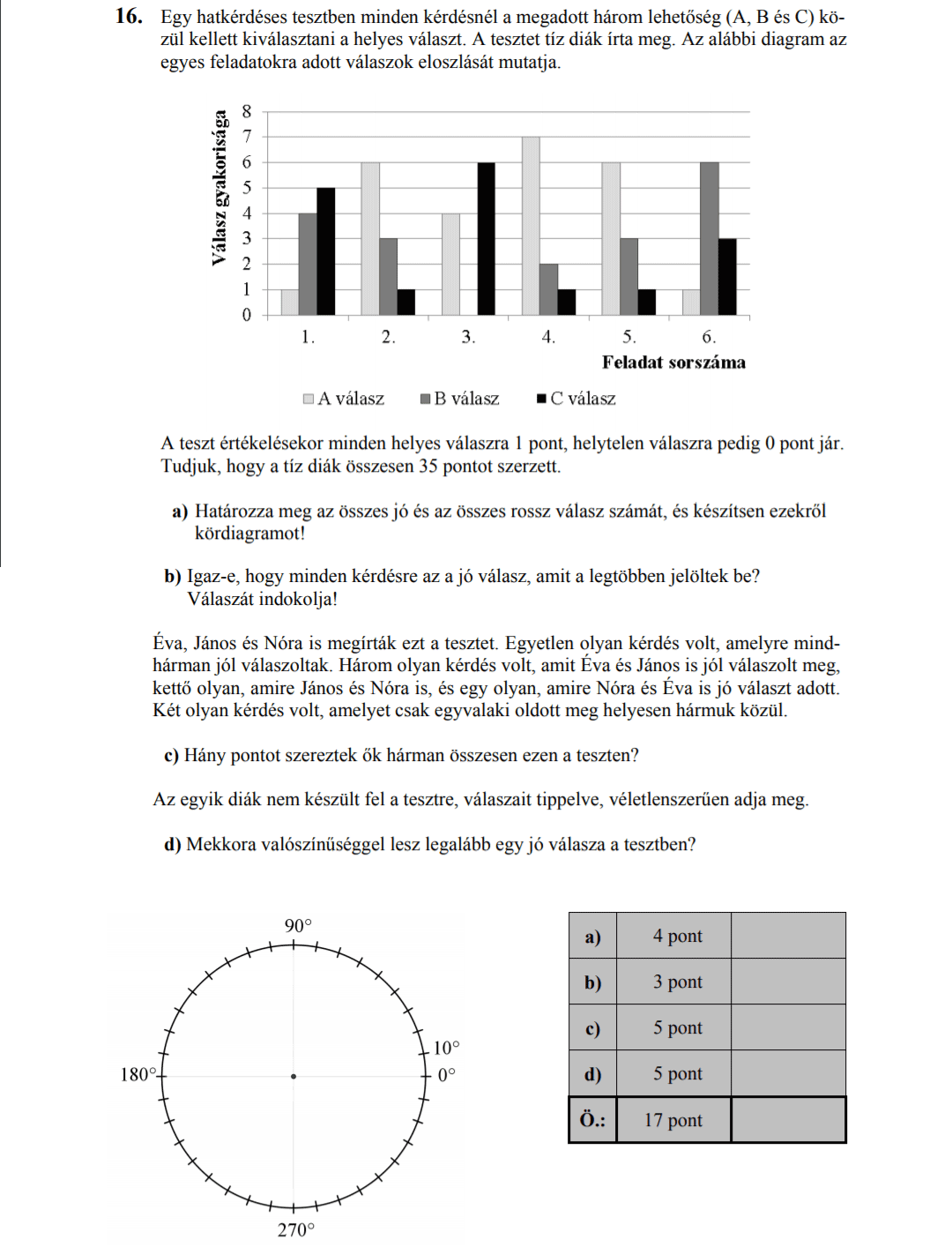


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

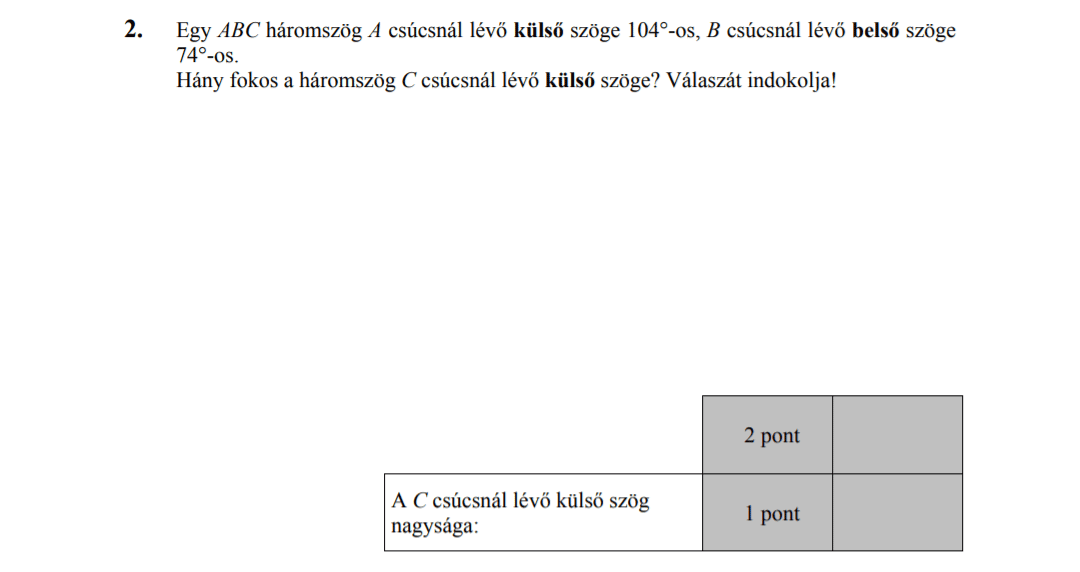





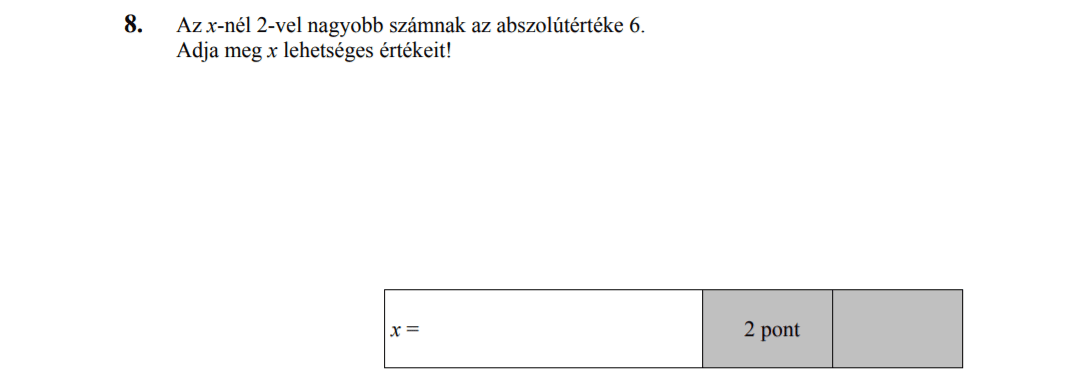

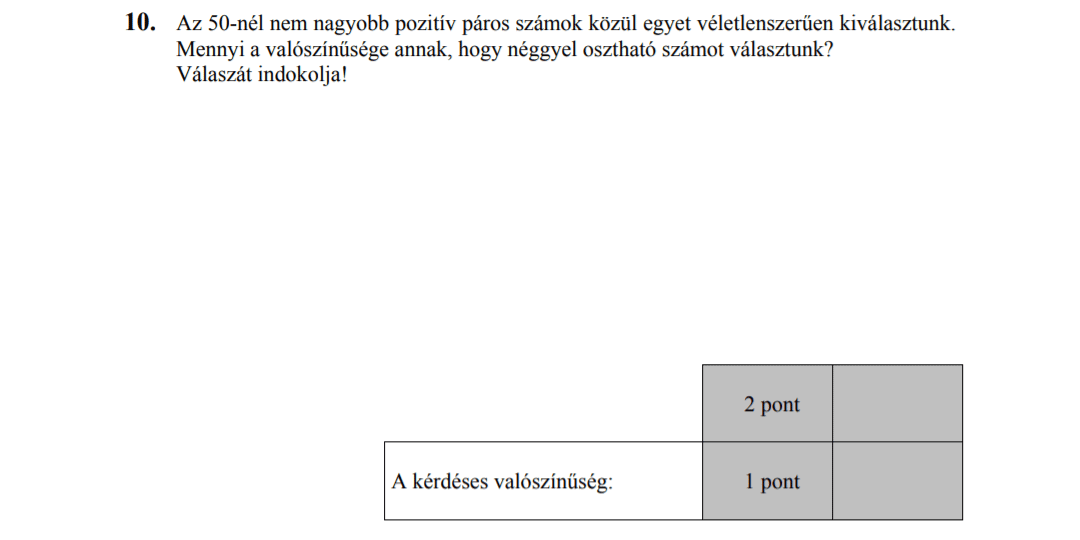


MÁSODIK RÉSZ

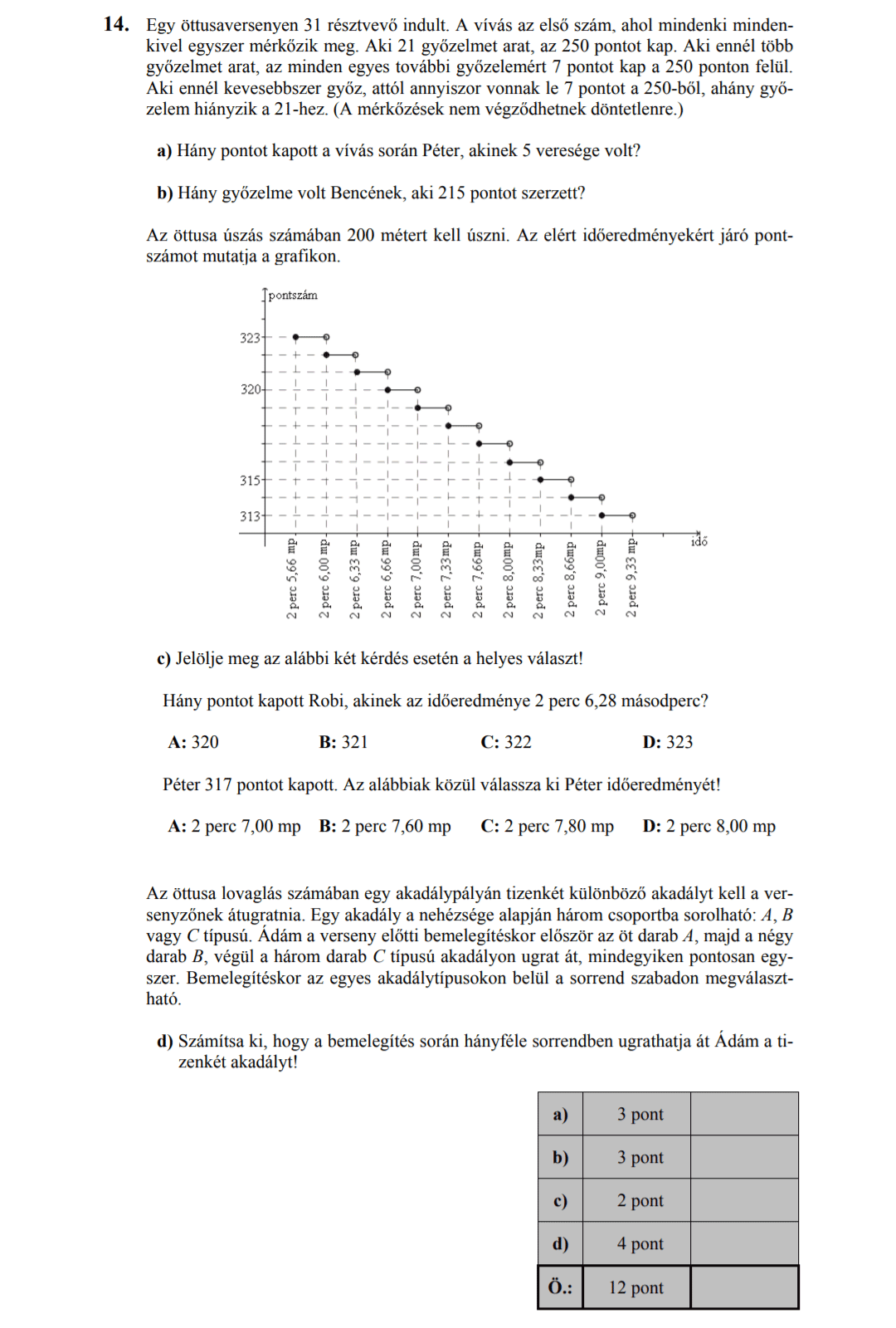
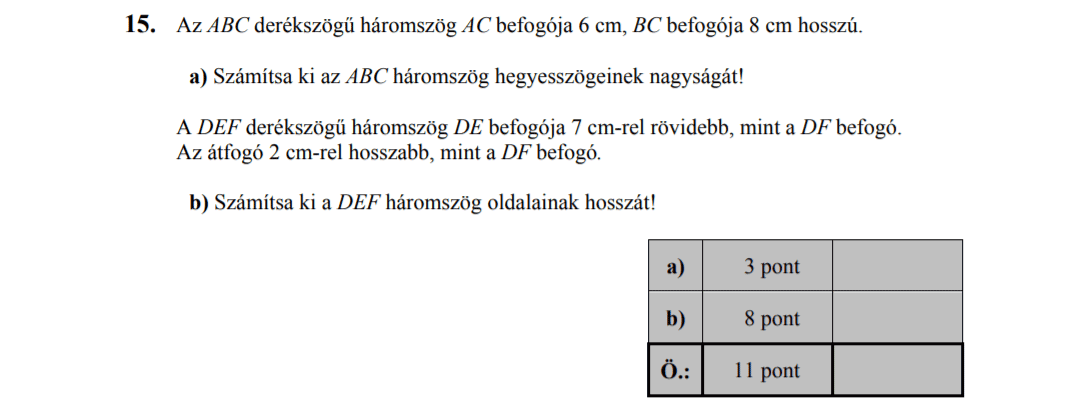



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

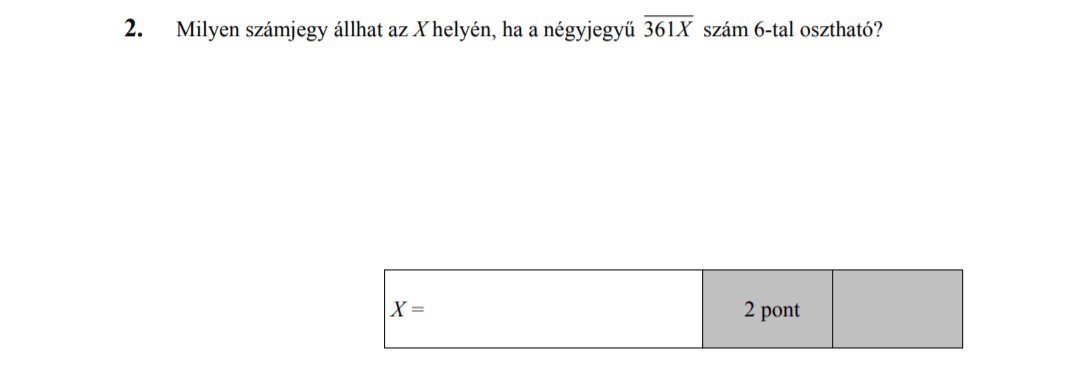



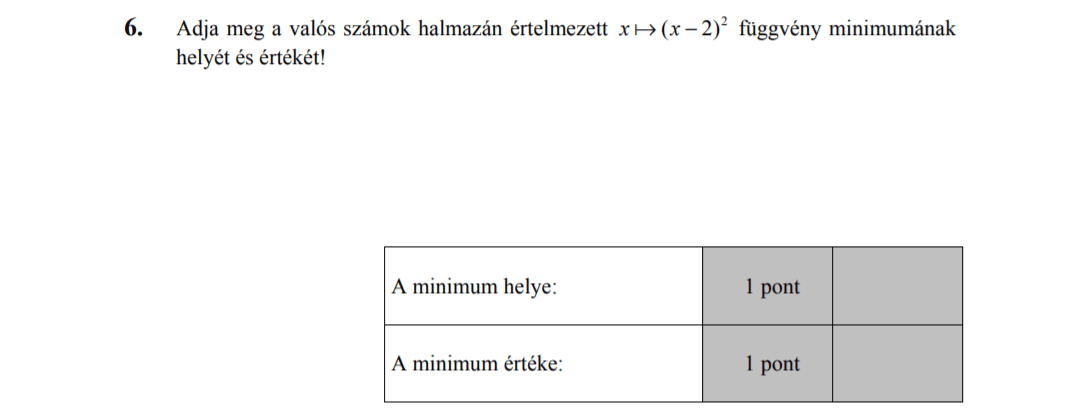

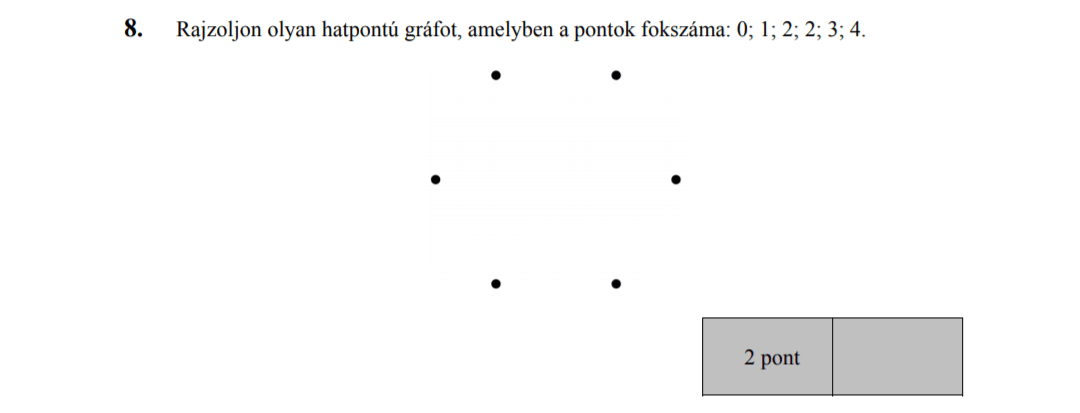


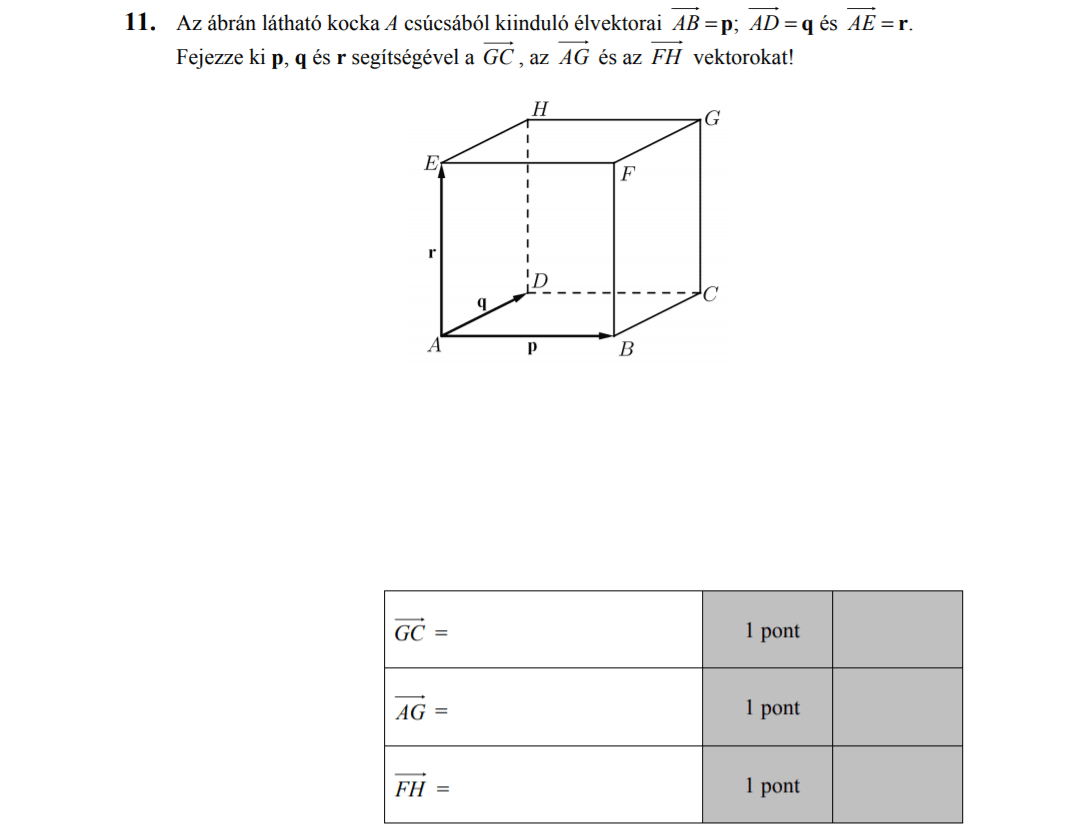
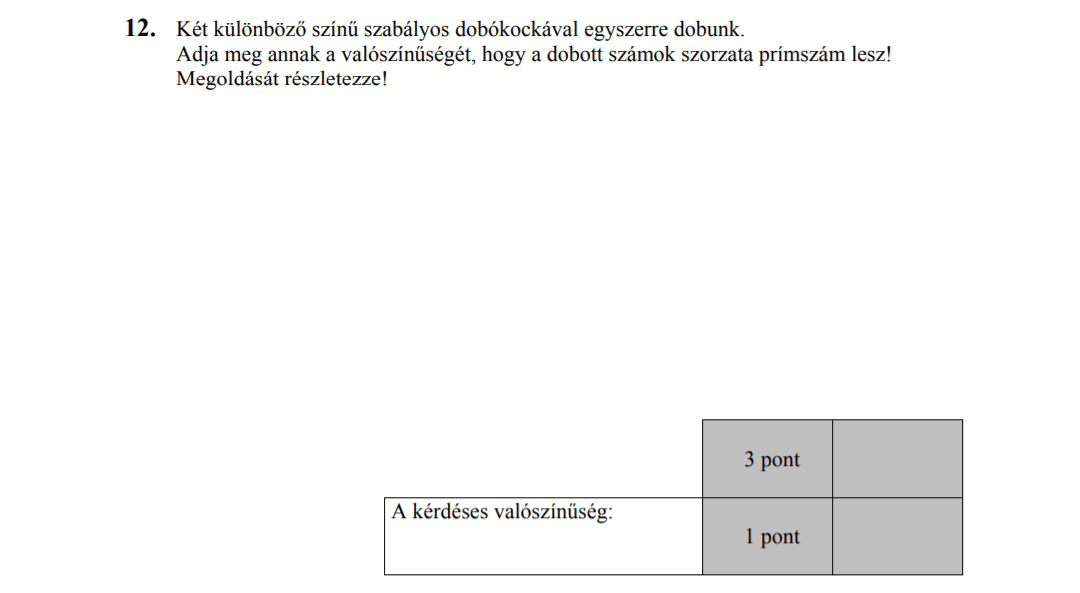
MÁSODIK RÉSZ
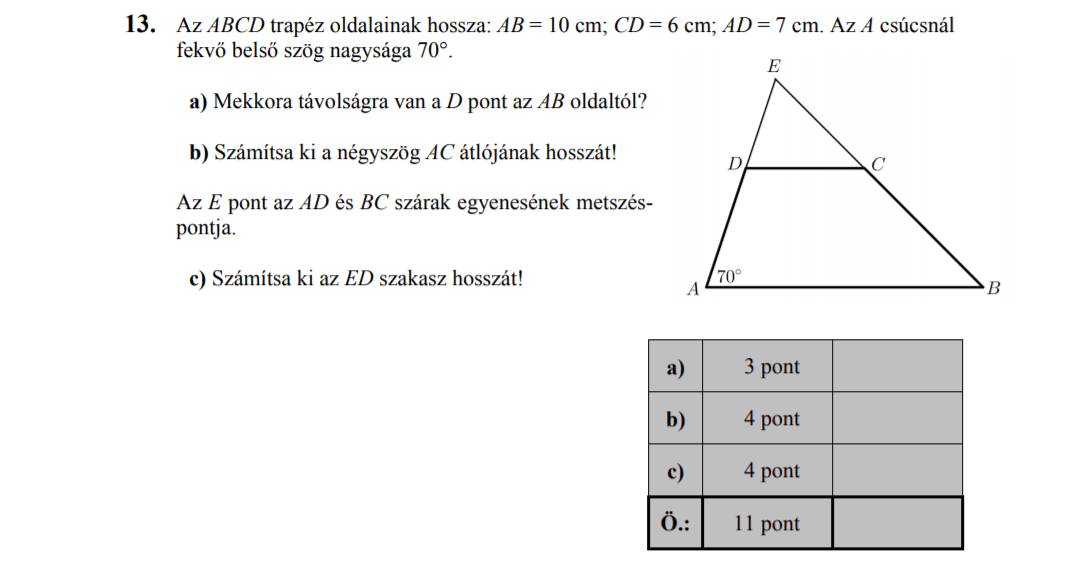





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


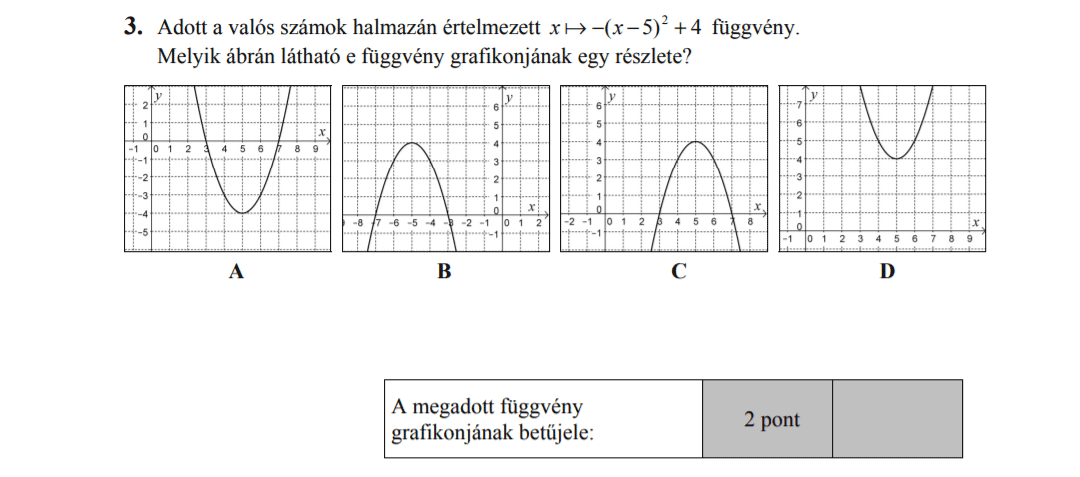








MÁSODIK RÉSZ




- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




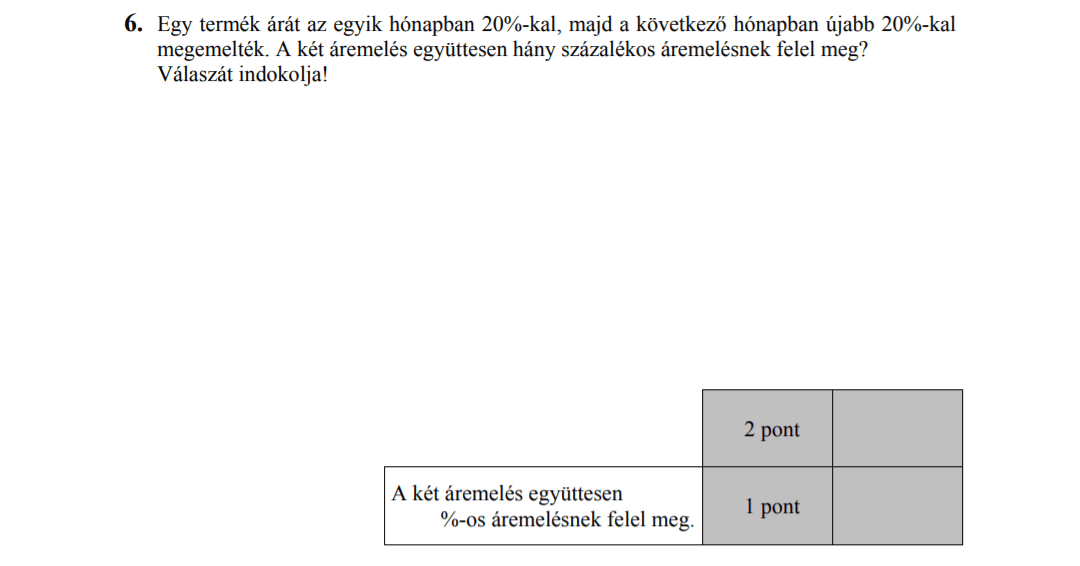
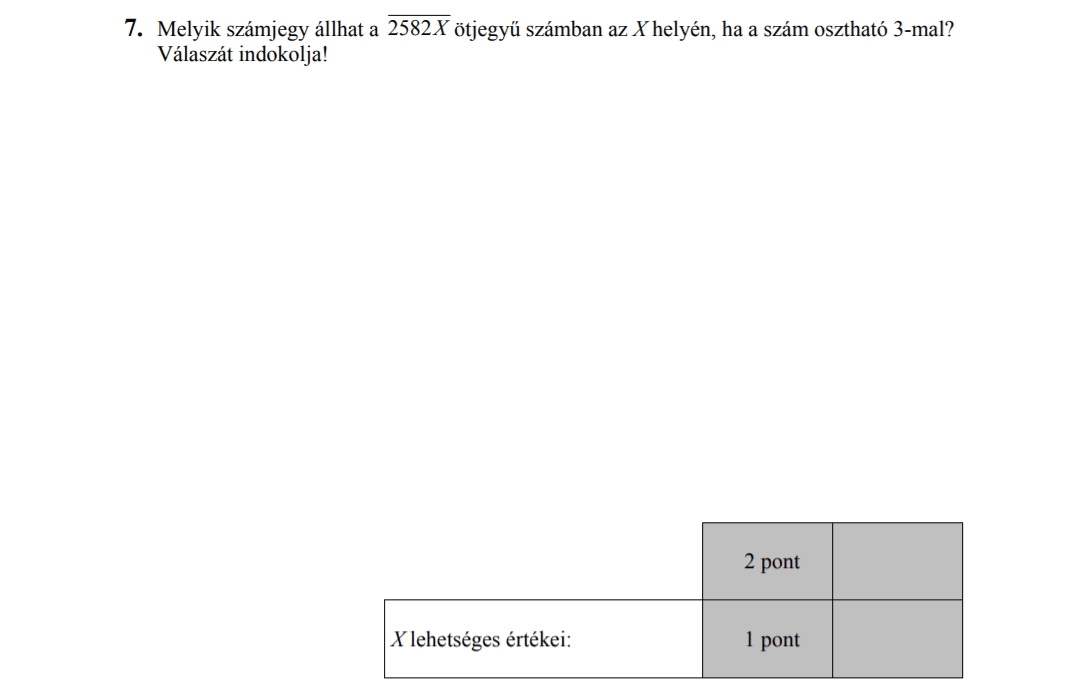
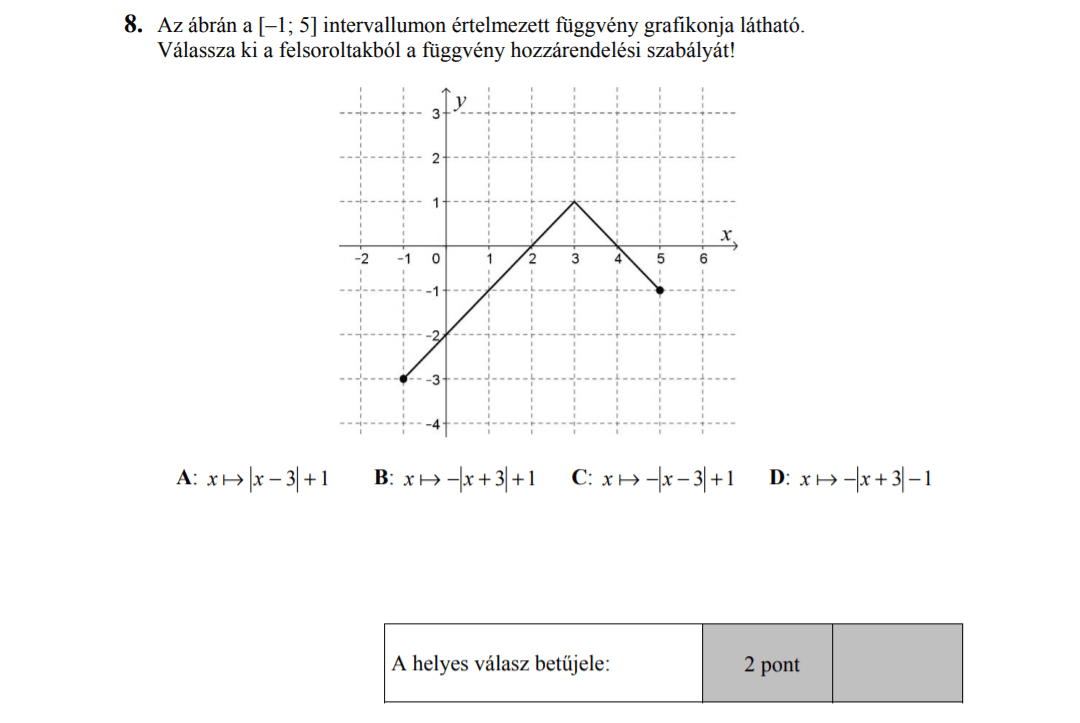


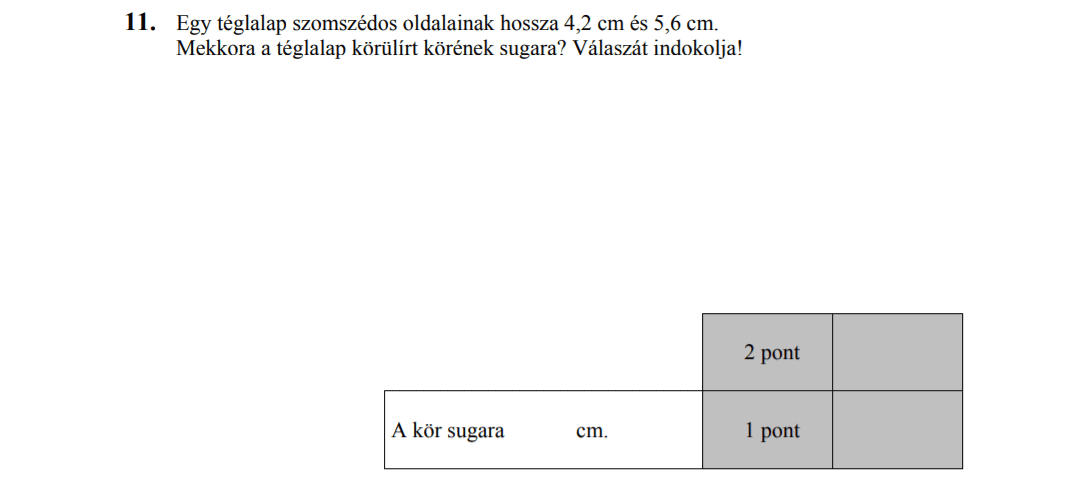

MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


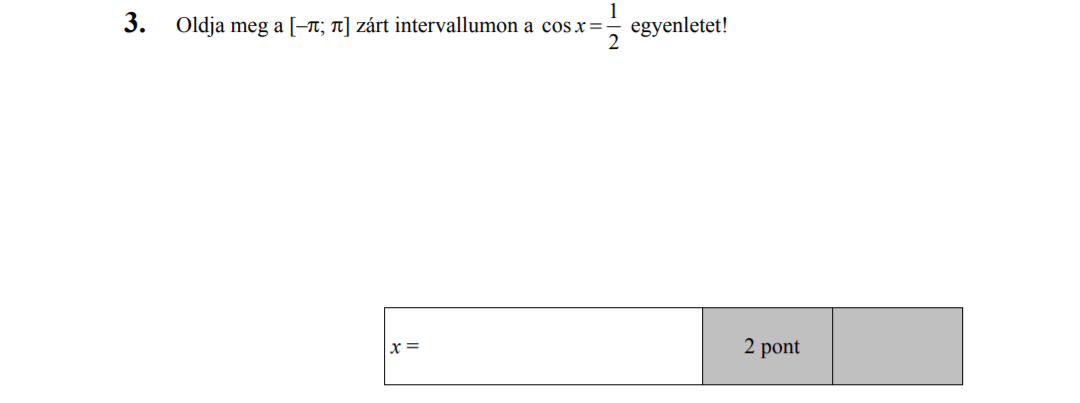


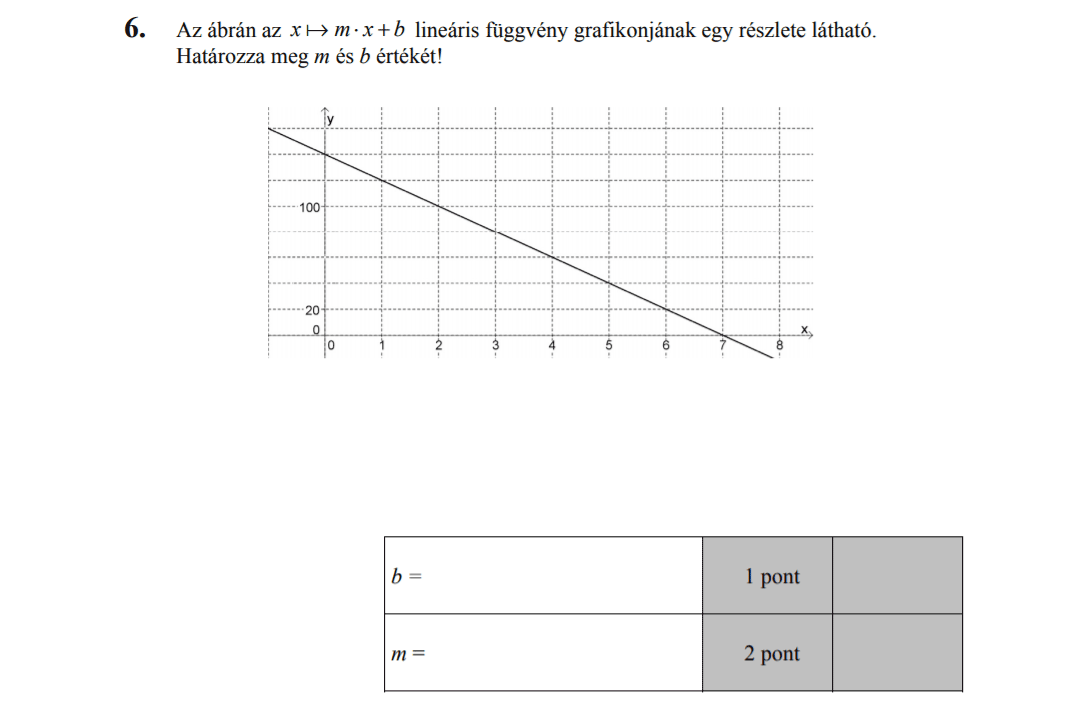



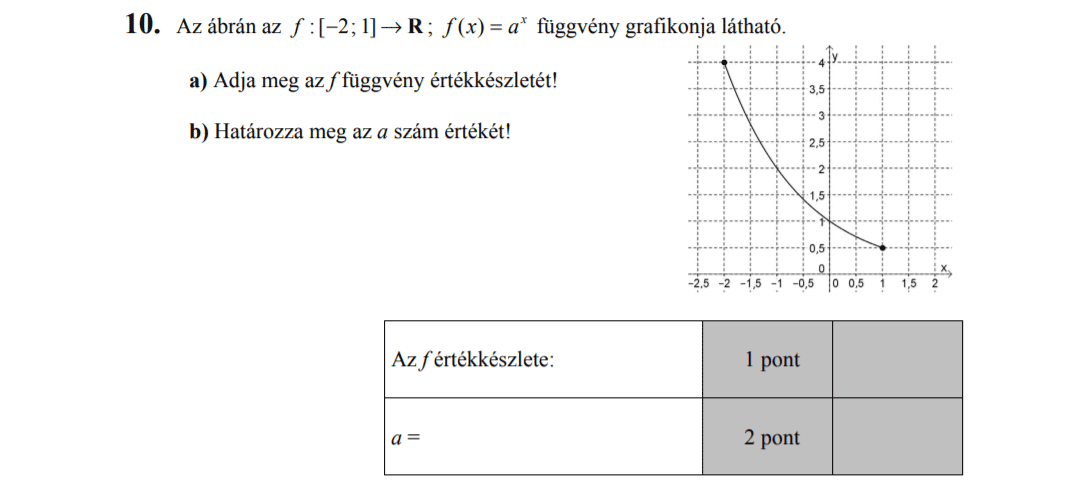

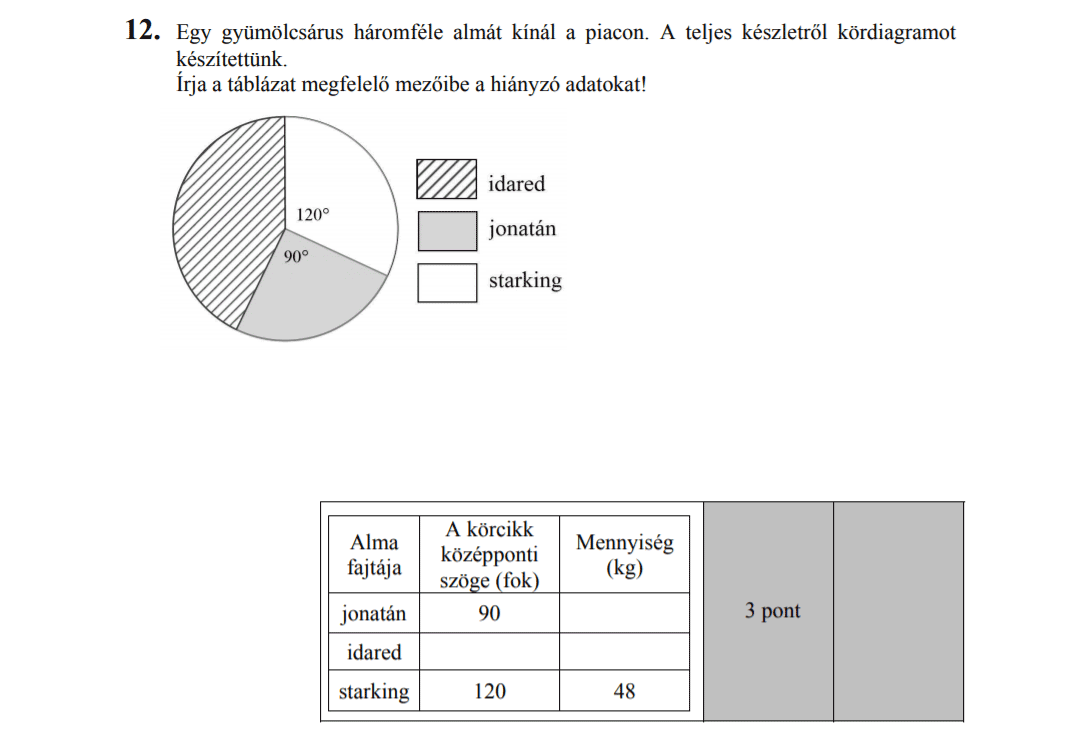
MÁSODIK RÉSZ

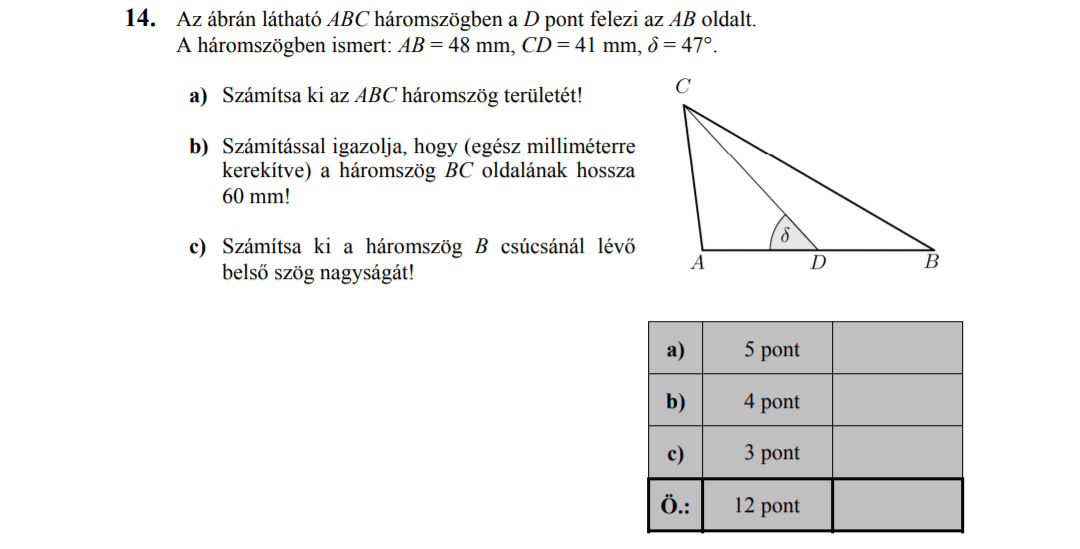




- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


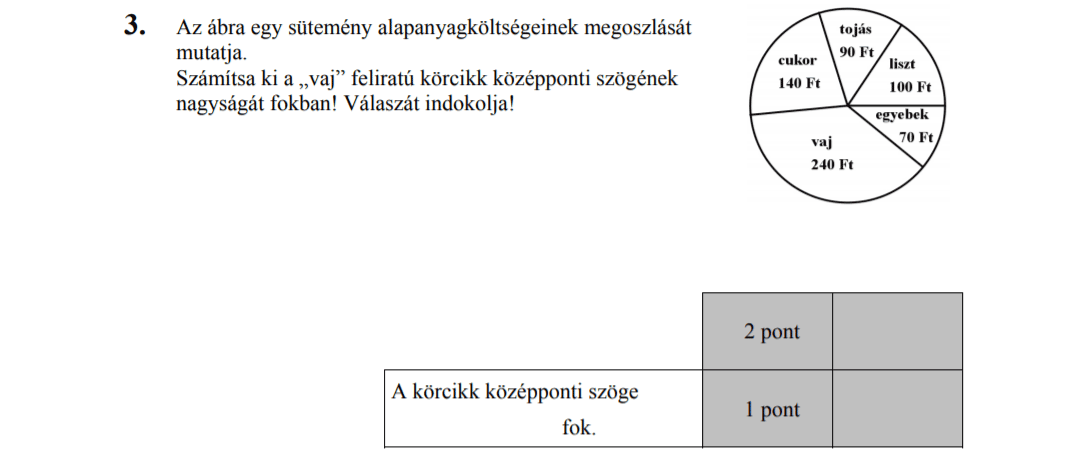
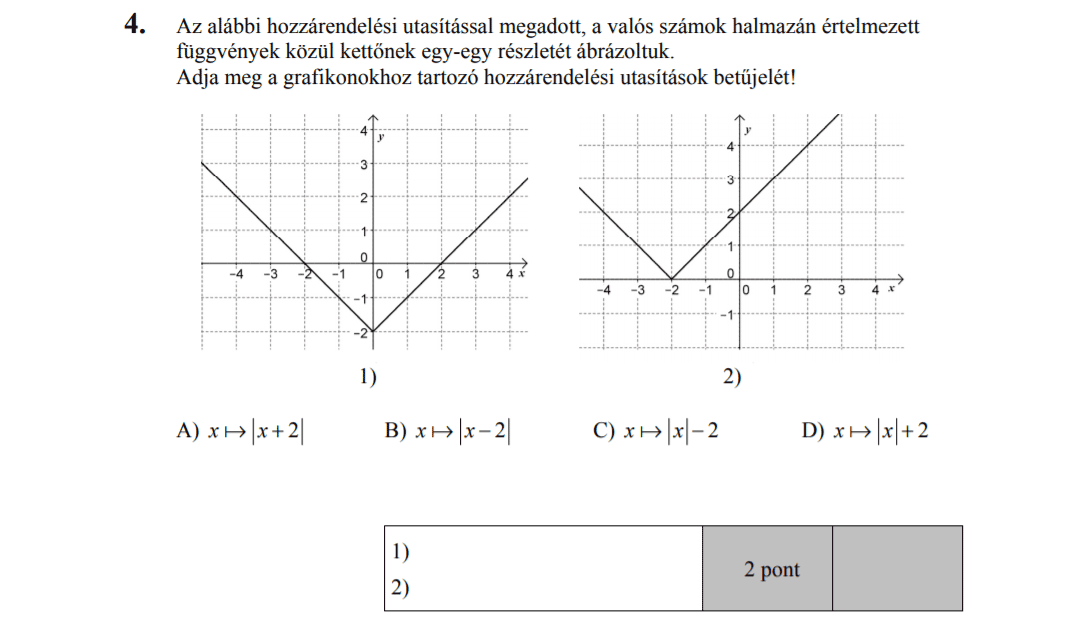
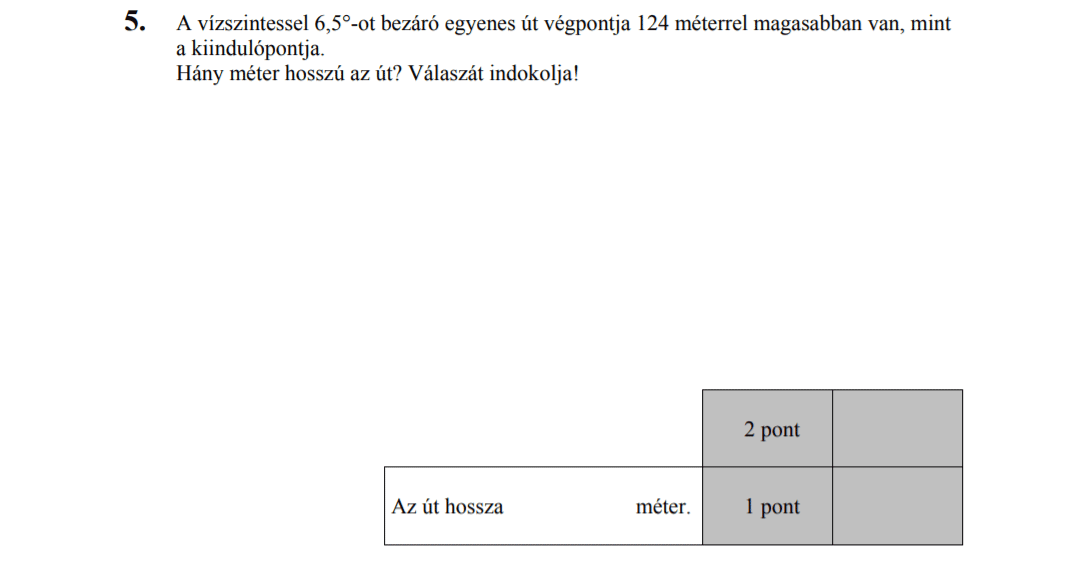

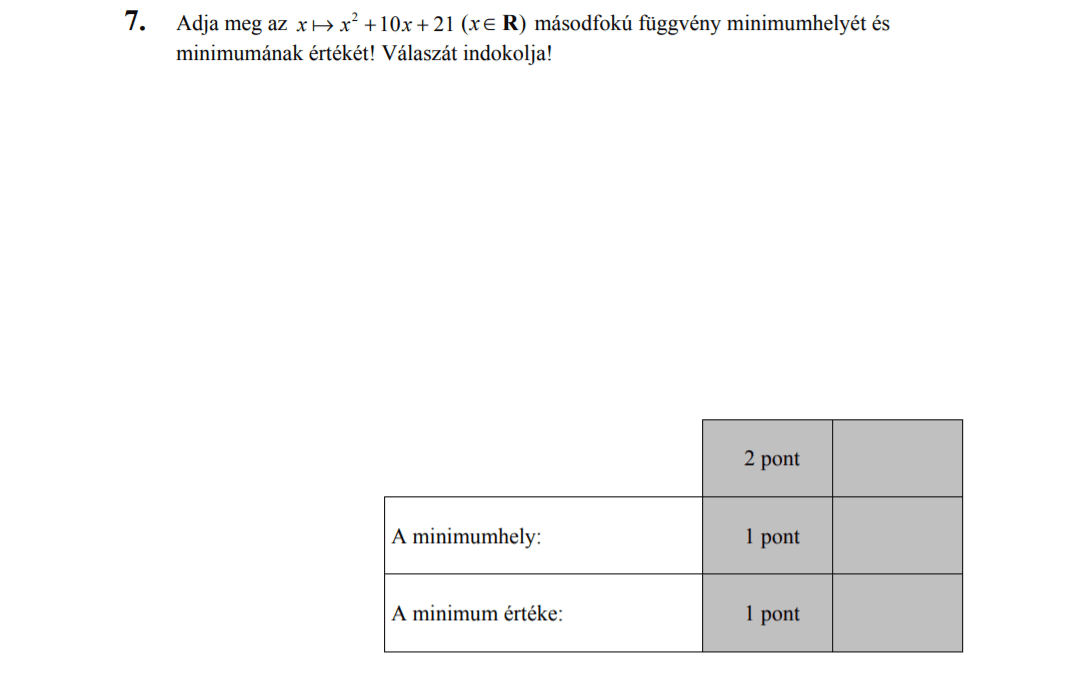



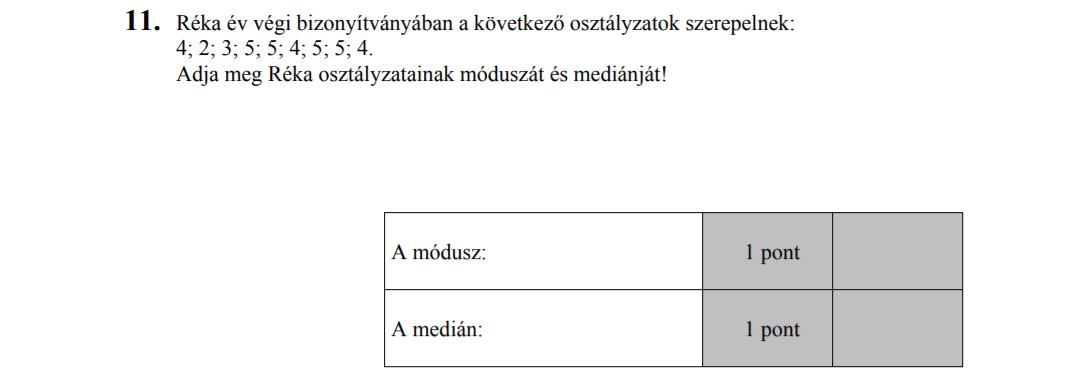

MÁSODIK RÉSZ





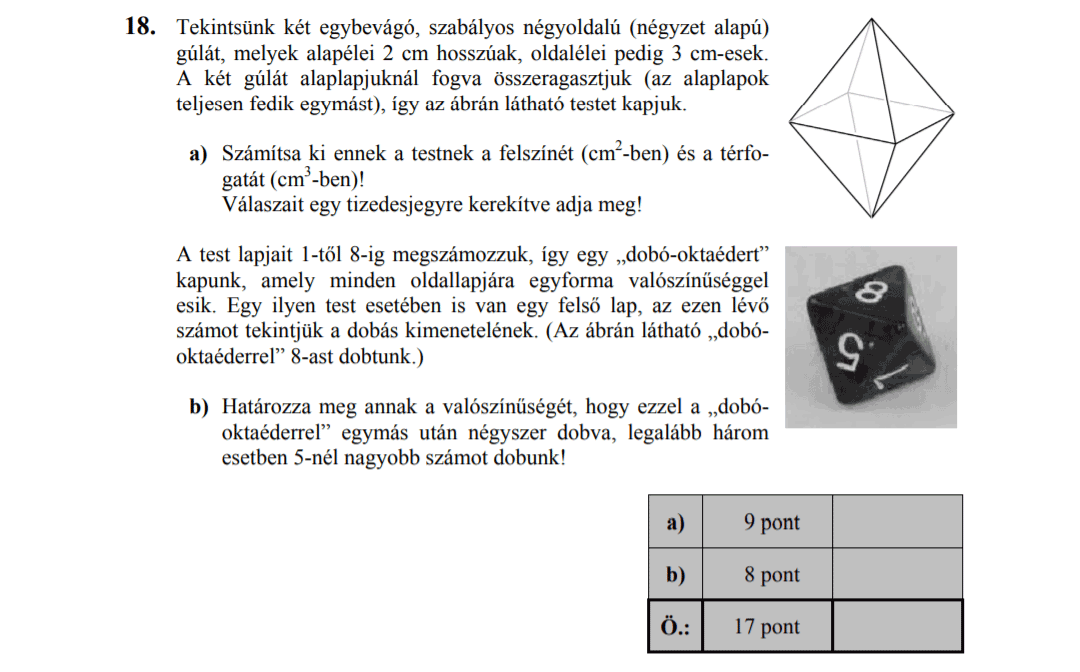
- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



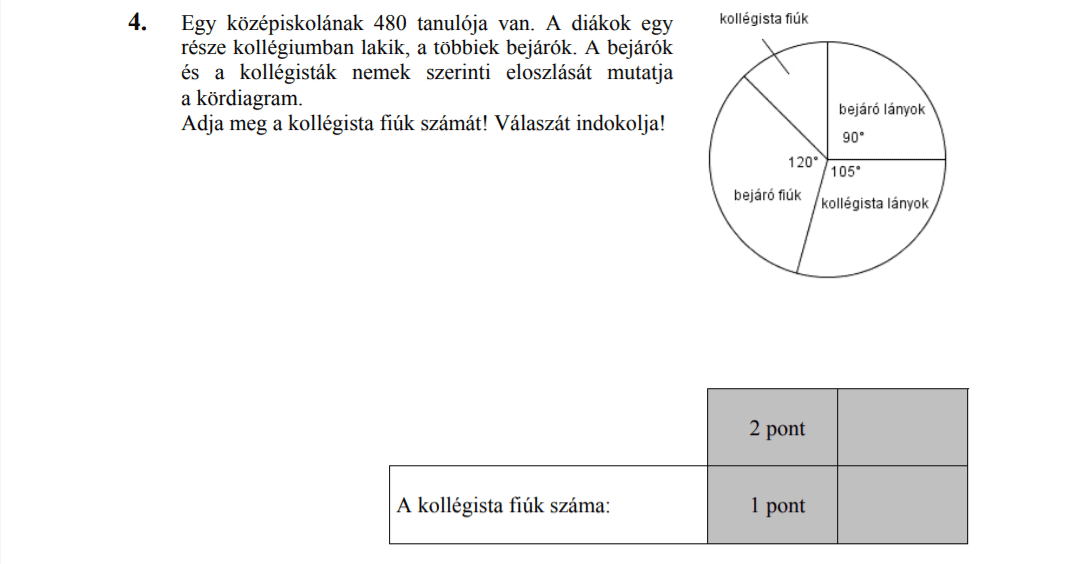





MÁSODIK RÉSZ






Binomiális eloszlás
Ezt a képletet hívjuk binomiális eloszlásnak:
\( P = \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k} \)
ahol $n$ a kísérletek száma,
$k$ a sikeres kísérletek száma,
$p$ pedig a sikeres kísérlet valószínűsége.
Visszatevéses mintavétel
Visszatevéses mintavételről beszélünk, ha egy $p$ valószínűségű elem többszöri kihúzásának esélyét vizsgáljuk úgy, hogy ha kihúzunk egy ilyen elemet, akkor ezt követően azt visszarakjuk.
Például ha azt vizsgáljuk, hogy egy kosárban van 8 piros és 5 kék golyó, és mennyi a valószínűsége, hogy háromszor húzva két piros és egy kék golyót húznánk úgy, hogy a kihúzott golyókat mindig visszatesszük, akkor az egy visszatevéses mintavétel.
A visszatevées mintavételhez kapcsolódó eloszlás a binomiális eloszlás.
Visszatevés nélküli mintavétel
A visszatevés nélküli mintavétel tipikus példája, hogy van egy doboz, benne $N$ darab elem. Közülük $K$ darab valamilyen tulajdonságú, az egyszerűség kedvéért hívjuk selejtesnek. Mondjuk sárga vagy szép vagy ronda. Kihúzunk $n$ darab elemet, és ez a képlet meg fogja nekünk mondani, hogy mekkora az esélye, hogy közülük $k$ darab a vizsgált tulajdonságú:
\( P(X=k)=\frac{\binom{K}{k} \cdot \binom{N-K}{n-k}}{\binom{N}{n}} \)
De vannak olyan esetek, amikor a visszatevés nélküli mintavételnél másik képletet kell használnunk. Ezt a másik képletet binomiális eloszlásnak nevezzük, és olyankor használjuk, amikor a selejtek száma helyett csak a selejtek arányát ismerjük.
Ez a binomiális eloszlás képlete:
\( P = \binom{n}{k} \cdot p^k \cdot (1-p)^{n-k} \)
ahol $n$ a kísérletek száma,
$k$ a sikeres kísérletek száma,
$p$ pedig a sikeres kísérlet valószínűsége.
És, hogy mi alapján döntjük el, hogy a két képlet közül melyiket kell használni? A dolog nagyon logikus, nézd meg a kapcsolódó epizódot és minden világos lesz.
Hipergeometriai eloszlás
A hipergeometriai eloszlás a visszatevés nélküli mintavételhez kapcsolódó eloszlás, képlete pedig:
\( P(X=k)=\frac{\binom{K}{k} \cdot \binom{N-K}{n-k}}{\binom{N}{n}} \)
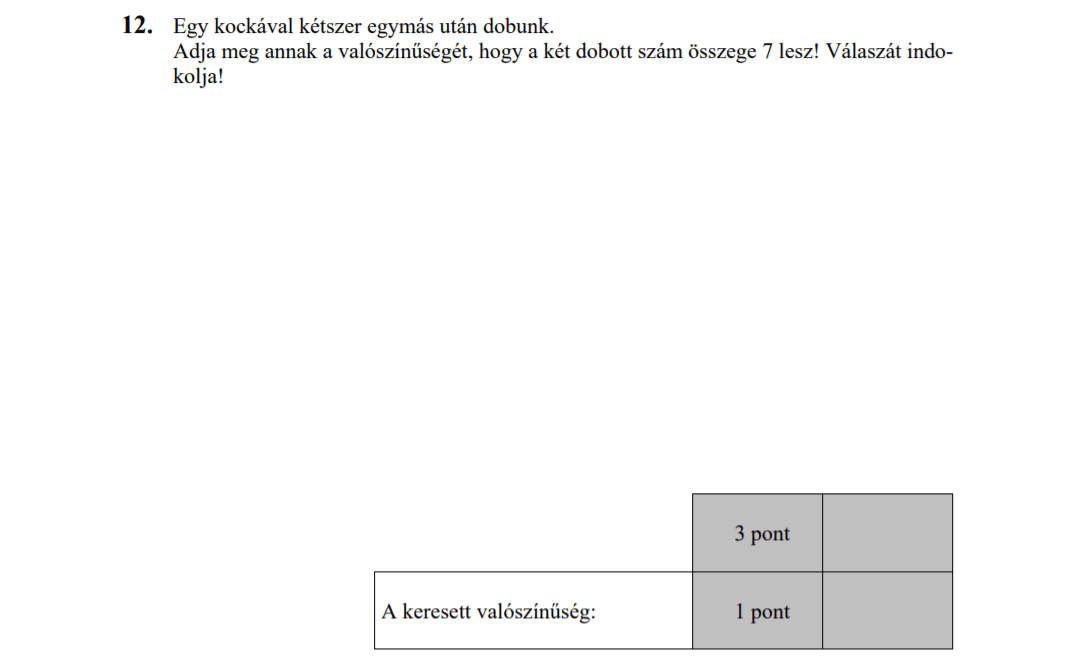
Van két dobókocka. Mennyi a valószínűsége, hogy...
a) mindkét dobókockával 1-est dobunk?
b) mindkét dobás egyforma?
c) különböző számokat dobunk?
d) a dobott pontok szorzata páros?
a) Egy 52 lapos francia kártyából kihúzunk 5 lapot. Mi a valószínűsége, hogy az első és a harmadik lap ász lesz?
b) Egy 52 lapos francia kártyából kihúzunk 5 lapot. Mi a valószínűsége, hogy csak az első és a harmadik lap ász?
c) Egy 52 lapos francia kártyából kihúzunk 5 lapot. Mi a valószínűsége, hogy a lapok közt két ász lesz?
d) Egy kosárlabdacsapat 9 játékosból áll, közülük öten vannak egyszerre a pályán. Mekkora a valószínűsége, hogy a két legjobb játékos egyszerre van a pályán?
e) Egy kosárlabdacsapat 9 játékosból áll, közülük öten vannak egyszerre a pályán. Mia valószínűsége, hogy a két legjobb játékos közül csak az egyik van a pályán?
a) Van egy dobókocka, aminek 3 oldala kék, 2 oldala sárga és 1 pedig piros. Nézzük meg, mekkora a sansza, hogy 4 dobásból 2 sárga.
b) Van egy dobókocka, aminek 3 oldala kék, 2 oldala sárga és 1 pedig piros. Mennyi annak a valószínűsége, hogy 4 dobásból 1 piros.
c) Egy dobozban van 3 kék, 2 sárga és 1 piros labda. Kiveszünk a dobozból 4 labdát. Mi a valószínűsége, hogy 1 sárga?
d) Egy dobókocka 3 oldala kék, 2 oldala sárga és 1 oldala piros. Egymás után 4-szer dobunk a kockával. Mi a valószínűsége, hogy 1 sárga?
e) Egy bárban 100-an vannak, közülük 60-an lányok. A vendégek közül kiválasztunk 10 embert. Mi a valószínűsége, hogy 7 lány?
f) Egy bárban a vendégek 60%-a lány. A vendégek közül kiválasztunk 10 embert. Mi a valószínűsége, hogy 7 lány?
Két dobókockával egyszerre dobunk. Mi a valószínűsége, hogy
a) mindkét dobás páros?
b) legfeljebb az egyik dobás páros?
c) a dobott pontok szorzata páros?
d) a dobott pontok összege páros?
e) a dobott pontok összege legalább 10?
f) a dobott pontok szorzata 6?
a) Öt kockával egyszerre dobunk. Mekkora valószínűséggel lesz mind az öt dobás 1-es?
b) Öt kockával egyszerre dobunk. Mekkora valószínűséggel nem lesz egyik dobás sem 1-es?
c) Öt kockával egyszerre dobunk. Mekkora valószínűséggel lesz legalább egy dobás 1-es?
d) Egy városban 0,2 a valószínűsége annak, hogy egyik nap esik az eső. Mekkora a valószínűsége, hogy egy héten minden nap esik?
e) Egy vizsga 100 vizsgázóból átlag 26-nak nem sikerül. Egyik nap 12-en vizsgáznak. Mi a valószínűsége, hogy legalább egy vizsgázónak nem sikerül a vizsga?
a) Egy telefon biztonsági kódja 6 számjegyből áll és minden számjegy 0-9 bármi lehet. Mi a valószínűsége, hogy ha nem ismerjük a kódot, akkor elsőre kitaláljuk? A kódok hány százalékában szerepel az 1,2,3,4,5,6 számjegyek közül mindegyik?
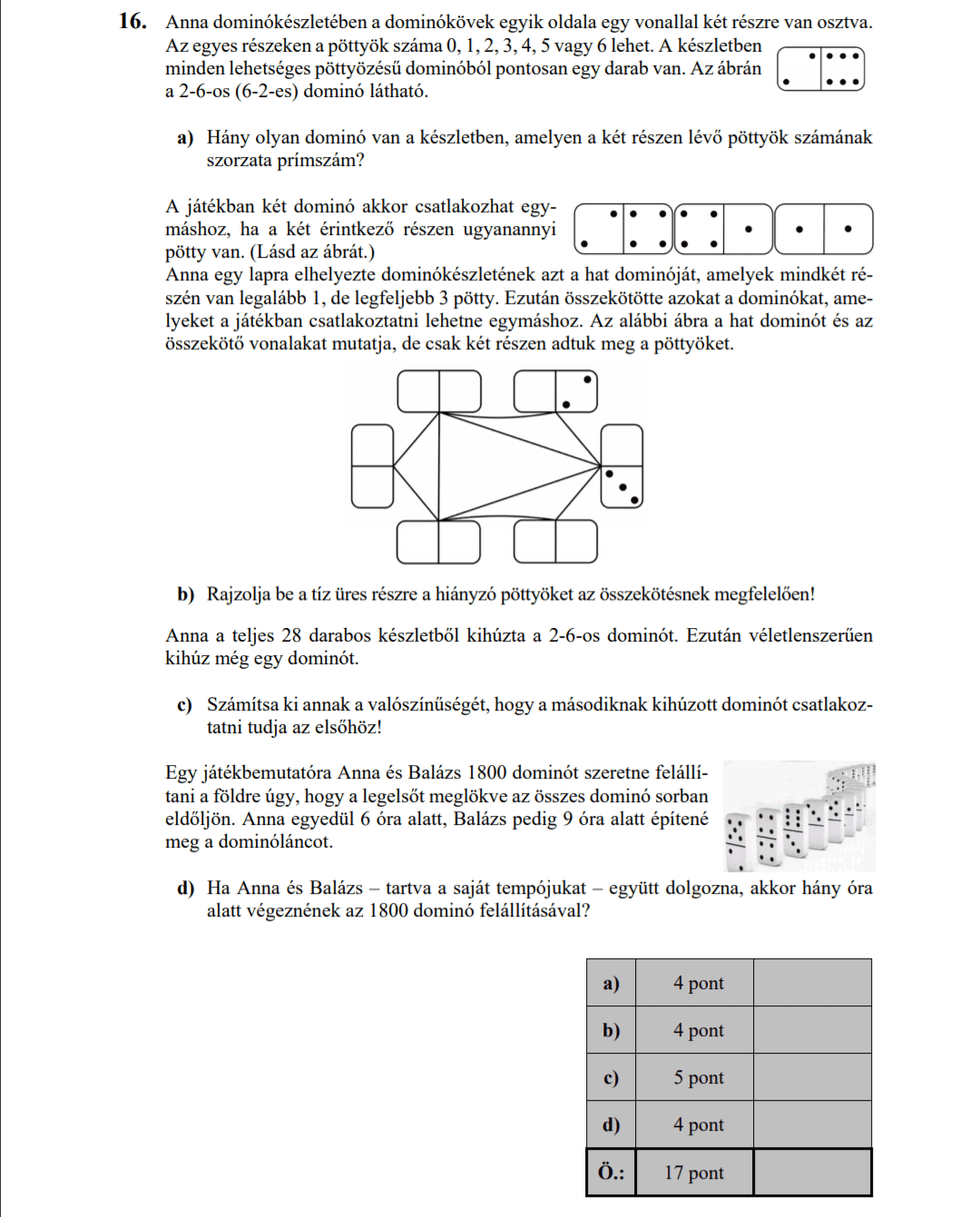
b) Egy dominókészlet azonos méretű dominókból áll. Minden dominó egyik oldala egy vonallal két részre van osztva. Az egyes részeken elhelyezett pöttyök száma 0-tól 6-ig bármi lehet. Minden lehetséges párosításnak léteznie kell, de két egyforma nem lehet egy készletben. Hány darabból áll egy dominókészlet?
Az ötöslottón 90 darab golyóból húznak ki 5 darabot. A golyók 1-től 90-ig vannak számozva. Mi a valószínűsége, hogy
a) a legkisebb kihúzott szám a 64?
b) öt egymás utáni számot húznak ki?
c) csak páratlan számokat húznak ki?
d) a kihúzott számok szorzata kettőhatvány?
Egy dobókockával hatszor dobunk egymás után. Mi a valószínűsége, hogy
a) egyik dobás sem 1-es?
b) csak páros számokat dobunk?
c) mindegyik dobás különböző?
Egy 20 fős osztályba 8 fiú és 12 lány jár. Kiosztanak közöttük 10 mozijegyet. Mi a valószínűsége, hogy
a) ugyanannyi fiú kap mozijegyet, mint ahány lány?
b) csak lányok kapnak mozijegyet?
c) csak fiúk kapnak mozijegyet?
Egy síterepen az egyik felvonó végállomásától három sípálya indul. 20 napból a fekete pálya átlagosan 3 nap van zárva lavinaveszély miatt, a kék átlagosan 2 nap, míg a piros átlagosan 4 nap egymástól függetlenül. Mekkora a valószínűsége, hogy
a) mindhárom pálya nyitva van?
b) csak a kék pálya van zárva?
c) a piros pálya nyitva van?
d) legalább egy pálya nyitva van?
Egy üzlet a következő 20 napból 3 nap zárva tart. Kiválasztunk 5 napot, mi a valószínűsége, hogy 3 nap lesz nyitva?
Egy bizonyos hónap 30 napjából átlag 12 nap szokott esni. Mi a valószínűsége, hogy egy héten három nap esik?
Egy vizsgán a hallgatóknak általában 60%-a megbukik. Egy nap 10-en vizsgáznak, mi a valószínűsége, hogy
a) legfeljebb 2-en mennek át?
b) legalább 2-en mennek át?
A H halmaz az első 90 pozitív egész szám halmaza. H-ból véletlenszerűen kiválasztunk két különböző számot. Mi a valószínűsége, hogy a két kiválasztott szám egy derékszögű háromszög fokban mért valamelyik két szöge?
A fák egy részében megtelepedett a szú. Bármelyik fát kiválasztva 4% annak a valószínűsége, hogy van benne szú. Egy vásárló 50 fát vett. Mennyi a valószínűsége, hogy legfeljebb egy szúrágta fa kerül a rakományba?
Egy dobozban több ezer érme van, amelyek 3%-a hibás. Az érmék közül véletlenszerűen kiválasztunk 80-at. (A kiválasztás visszatevéses mintavétellel is modellezhető.) Mennyi a valószínűsége annak, hogy legfeljebb 2 hibás érme lesz a kiválasztott érmék között?
Itt az ideje, hogy készítsünk egy rövid kombinatorikai összefoglalót. A középiskolai matek felelevenítésével kezdjük, ahol elvileg mindenki tanult valószínűségszámítást és kombinatorikát. De csak elvileg, éppen ezért teljesen az alapoktól kezdünk és nem építünk a középiskolai matematika tanulmányokra. Kezdjük tehát a középiskolai matematika tananyag összefoglalását és átismétlését.
Van n darab elem
mindet kiválasztjuk
kiválasztunk közülük k darabot
a sorrend számít
a sorrend nem számít
PERMUTÁCIÓ
n darab különböző elem permutációinak száma n faktoriális:
mese:
Hányféleképpen ülhet le öt ember egymás mellé egy padon?
VARIÁCIÓ
n darab különböző elemből kiválasztott k darab elem permutációinak száma.
Hányféleképpen ülhet le öt ember közül három egymás mellé egy padon?
KOMBINÁCIÓ
n darab különböző elem közül kiválasztott k darab elem kombinációinak száma.
Hányféleképpen választhatunk ki öt ember közül hármat?
Ez mind nagyon szép. Most pedig lássunk néhány kombinatorika feladatot megoldással. Mindegyik feladat egyszerű középiskolai matek feladat, egyik sem nehezebb, mint amilyennel a matek érettségin találkozhatunk. Nekünk azért fontosak ezek a kombinatorika feladatok, mert sok izgalmas dolog épül majd az alap kombinatorikára és az alap középiskolai matek tudásra. Lássuk.
Egy 52 lapos francia kártyából kihúzunk 5 lapot.
Mi a valószínűsége, hogy az első és a harmadik lap ász?
kedvező eset
összes eset
Kezdjük az összes esettel.
Az 52 lap közül választunk ki 5 darabot. A kérdés az, hogy számít-e a sorrend
vagy nem.
Mivel a szövegben ilyenek vannak, hogy első lap, meg harmadik lap, a jelek szerint számít a sorrend.
Most lássuk a kedvező eseteket.
Az első lap ász, ez négyféle lehet.
A következő lap elvileg bármi lehet a maradék 51 lapból.
Aztán a harmadik lapnak megint ásznak kell lennie.
Lássuk csak hány ász van még.
Fogalmunk sincs. Ha ugyanis a második helyre is ászt raktunk, akkor már csak kettő.
De ha a második helyre nem, akkor három.
Ez bizony probléma.
A kedvező eset számolásánál mindig a kívánsággal kell kezdeni.
Most tehát azzal, hogy az első lap ász és a harmadik lap is ász.
Utána jöhetnek a többi lapok.
Van még 50 darab lap a második helyre.
Aztán még 49 és 48.
Mi a valószínűsége, hogy csak az első és a harmadik lap ász?
Most is számít a sorrend.
Az összes eset ugyanannyi,mint az előbb.
Lássuk mi van a kedvezőkkel.
Megint a kívánsággal kezdünk.
De most csak ez a két ász van, tehát a második lap nem lehet ász.
Így csak 48 féle lehet.
Aztán 47 és 46.
Mi a valószínűsége, hogy a lapok közt két ász lesz?
Itt nem számít a sorrend ezért kombinációt használunk.
A 4 ászból ki kell húznunk kettőt.
Aztán pedig kell még 3 lap ami már nem ász.
Hát ez remek. Végül nézzünk meg még egy feladatot.
Egy kosárlabdacsapat 9 játékosból áll, közülük öten vannak egyszerre a pályán.
Mekkora a valószínűsége, hogy a két legjobb játékos egyszerre van a pályán?
A kiválasztás sorrendje nem számít, csak az, hogy kiket választunk a pályára.
Így aztán kombinációra lesz szükség.
Nézzük mennyi eset van összesen.
A 9 játékosból kell kiválasztanunk ötöt.
A kedvező amikor a két legjobb a pályán van, vagyis őket mindenképp kiválasztjuk,
és még hármat.
Mi a valószínűsége, hogy a két legjobb játékos közül csak az egyik van a pályán?
Az összes eset itt is ugyanannyi.
A kedvező pedig amikor a két legjobb játékosból választunk egyet
és a többi tehetségtelen amatőr közül még négyet.
Két dobókockával egyszerre dobunk. Mi a valószínűsége, hogy
mindkét dobás páros?
legfeljebb az egyik dobás páros?
a dobott pontok szorzata páros?
a dobott pontok összege páros?
a dobott pontok összege legalább 10?
a dobott pontok szorzata 6?
Ha két kockával dobunk, akkor az egyik kockával is hatfélét tudunk dobni…
meg a másikkal is.
Az összes eset tehát 36.
Összes eset:
Most pedig lássuk a valószínűségeket.
egyik kocka: páros
másik kocka: páros
egyik kocka: páros
másik kocka: nem páros
vagy fordítva
vagy
mindkét dobás páratlan
A dobott pontok szorzata akkor lesz páros, ha mindkét dobás páros…
vagy pedig az egyik páros, a másik páratlan.
Végülis mindig páros lesz a szorzat, kivéve olyankor, amikor mindkét dobás páratlan.
Itt jön erre egy másik megoldás is.
Végülis mindig páros lesz a szorzat, kivéve olyankor, amikor mindkét dobás páratlan.
mindkettő
páratlan
Két szám összege akkor páros, ha mindkettő páros…
vagy mindkettő páratlan.
Lássuk, hogyan is lesz a pontok összege 10.
A kérdés úgy szól, hogy legalább 10, tehát az is jó, ha az összeg 11.
És az is jó, ha 12.
Ez hat darab lehetőség.
Nézzük, mikor lesz a szorzat 6.
Van itt ez a két doboz. Az egyikben 4 darab kártya van, a másikban pedig 5.
Véletlenszerűen húzunk mindkét dobozból egy-egy kártyát.
Mi a valószínűsége, hogy a kihúzott kártyákon lévő számok szorzata negatív?
Akkor lesz a szorzat negatív, ha az egyik kártyán pozitív szám van…
és a másikon negatív.
Vagy fordítva.
Az összes eset pedig…
Mi a valószínűsége, hogy a kihúzott kártyákon lévő számok összege páratlan?
Akkor lesz az összeg páratlan, ha az egyik kártyán páros szám van…
a másikon pedig páratlan.
Vagy fordítva.
Öt kockával egyszerre dobunk. Mekkora valószínűséggel lesz mind az öt dobás 1-es?
Annak a valószínűsége, hogy egy dobás 1-es:
Ha van még egy 1-es, akkor ennek az esélye szintén
A két 1-es egyszerre pedig:
A dobások egymástól függetlenek és ilyenkor a valószínűségeket össze kell szorozni.
Aztán, ha dobunk még egy 1-est…
Annak a sansza, hogy mind az öt dobás 1-es:
Most nézzük, mi a valószínűsége annak, hogy öt kockával dobva egyik dobás sem 1-es.
Ez annak a valószínűsége, hogy egy dobás nem 1-es.
Aztán a következő dobás sem 1-es…
és egyik sem.
Végül számoljuk ki annak a valószínűségét, hogy öt kockával dobva legalább egy dobás 1-es.
Ez azt jelenti, hogy vagy egy darab 1-es van…
vagy két darab…
vagy három, vagy négy, vagy öt.
Ezt így külön-külön kiszámolni eléggé sok szenvedéssel járna.
Aki nem annyira szeret szenvedni, jegyezze meg, hogy
Hát, ennyit a kockákról.
Egy városban 0,2 a valószínűsége annak, hogy egy nap esik az eső. Mekkora a valószínűsége, hogy egy héten mindennap esik?
Mekkora a valószínűsége, hogy egy héten egyik nap sem esik?
Mekkora a valószínűsége, hogy egy héten legalább egy nap esik?
Egy vizsga 100 vizsgázóból átlag 26-nak nem sikerül. Egyik nap 12-en vizsgáznak. Mi a valószínűsége, hogy legalább egy vizsgázónak nem sikerül a vizsga?
Itt van például Bob.
Nézzük, mekkora a valószínűsége, hogy nem sikerül a vizsgája.
Annak a sansza pedig, hogy sikerül…
Most pedig jön a szokásos trükk:
