- ÚJ! Kvartilisek és dobozdiagram = sodrófadiagram = box plot
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
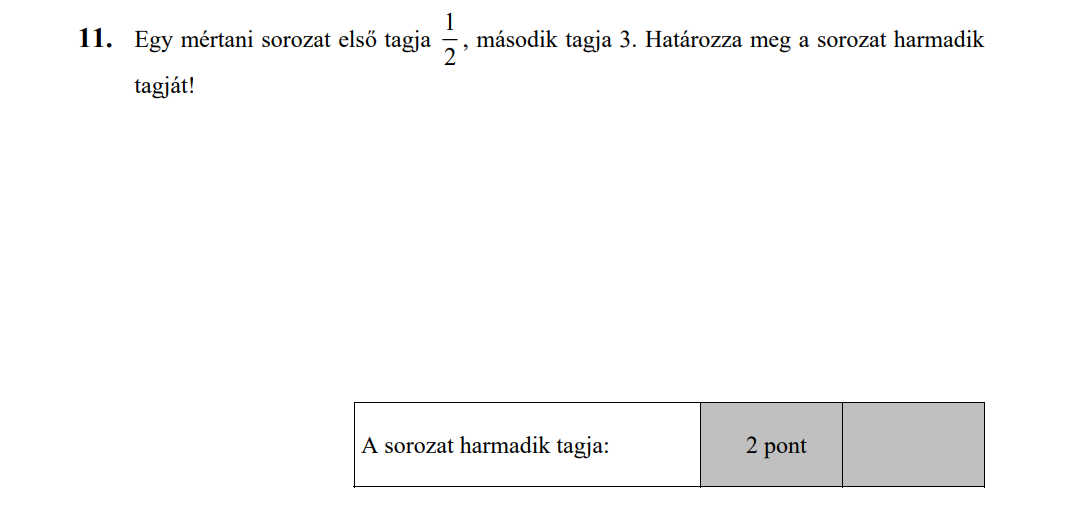
- Számtani és mértani sorozatok (15,3 pont)
- Függvényekkel kapcsolatos feladatok (10,3 pont)
- Térgeometria (10,3 pont)
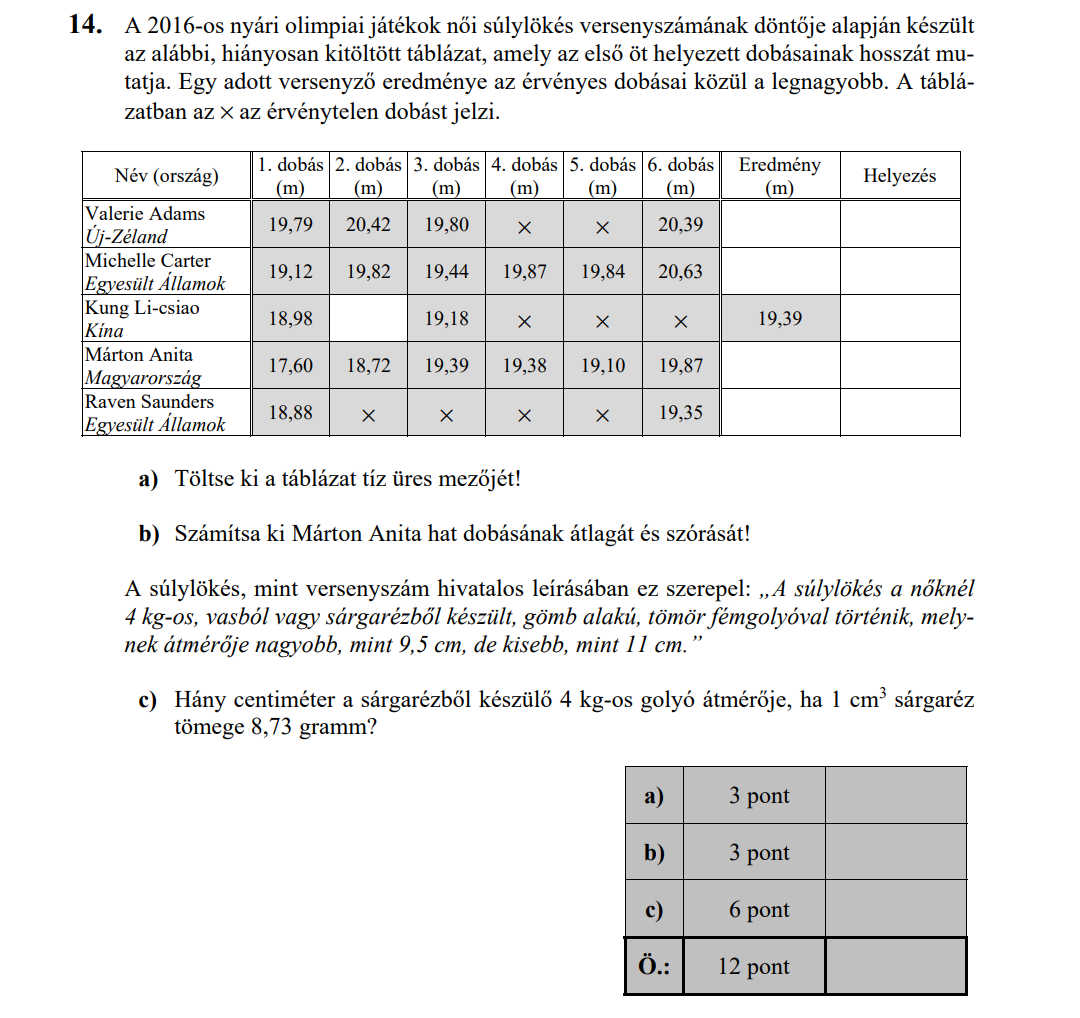
- Statisztika (10,2 pont)
- Valószínűségszámítás (10,2 pont)
- Trigonometria, szinusztétel, koszinusztétel (8,8 pont)
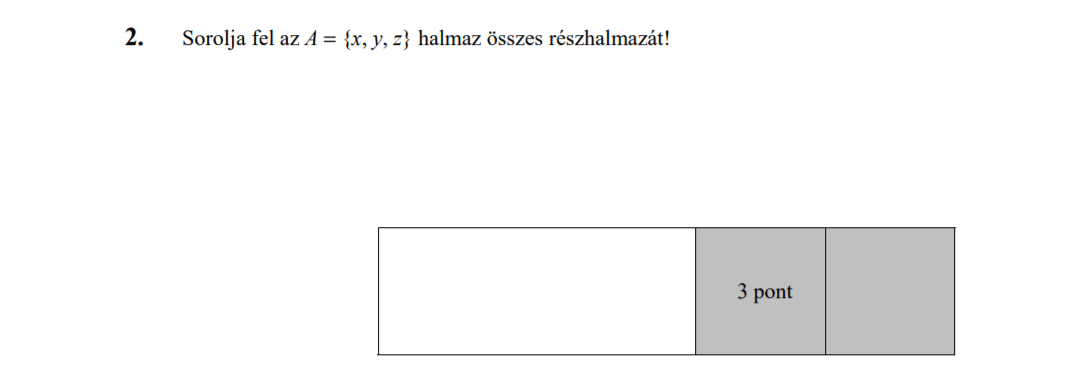
- Halmazok (7 pont)
- Kombinatorika (6,9 pont)
- Síkgeometria (6,5 pont)
- Koordinátageometria (6,2 pont)
- Szöveges feladatok (6 pont)
- Egyenes és fordított arányosság, arányos osztás, szöveges feladatok (3,8 pont)
- Százalékszámítás (2,9 pont)
- Gráfok (2,7 pont)
- Másodfokú egyenletek (2,5 pont)
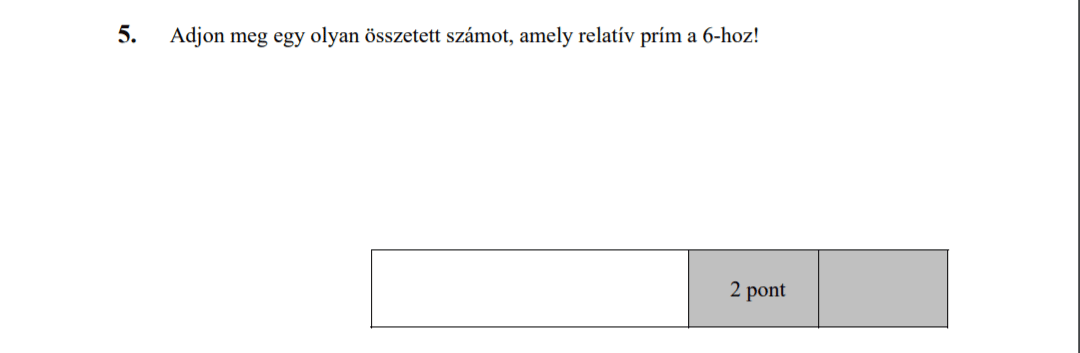
- Számelmélet (2,5 pont)
- Elsőfokú egyenletek (1,3 pont)
- Hatványozás, exponenciális egyenletek (1 pont)
- Egyenlőtlenségek (0,4 pont)
- Algebra, nevezetes azonosságok
- Bizonyítási módszerek, matematikai logika
- Egyenletrendszerek
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Egybevágósági transzformációk
Egyenletrendszerek
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


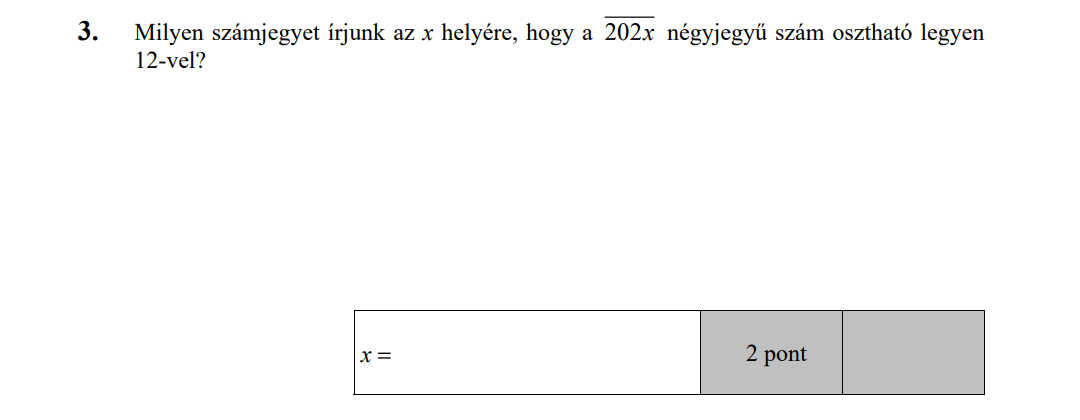
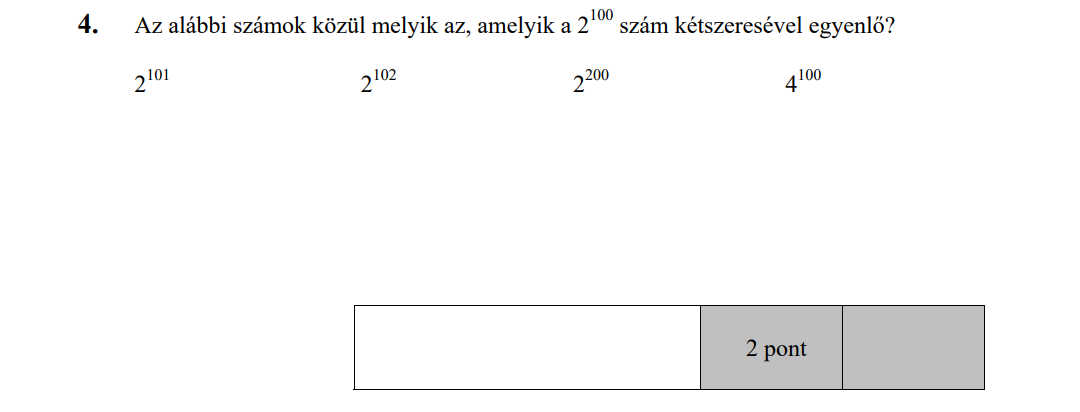



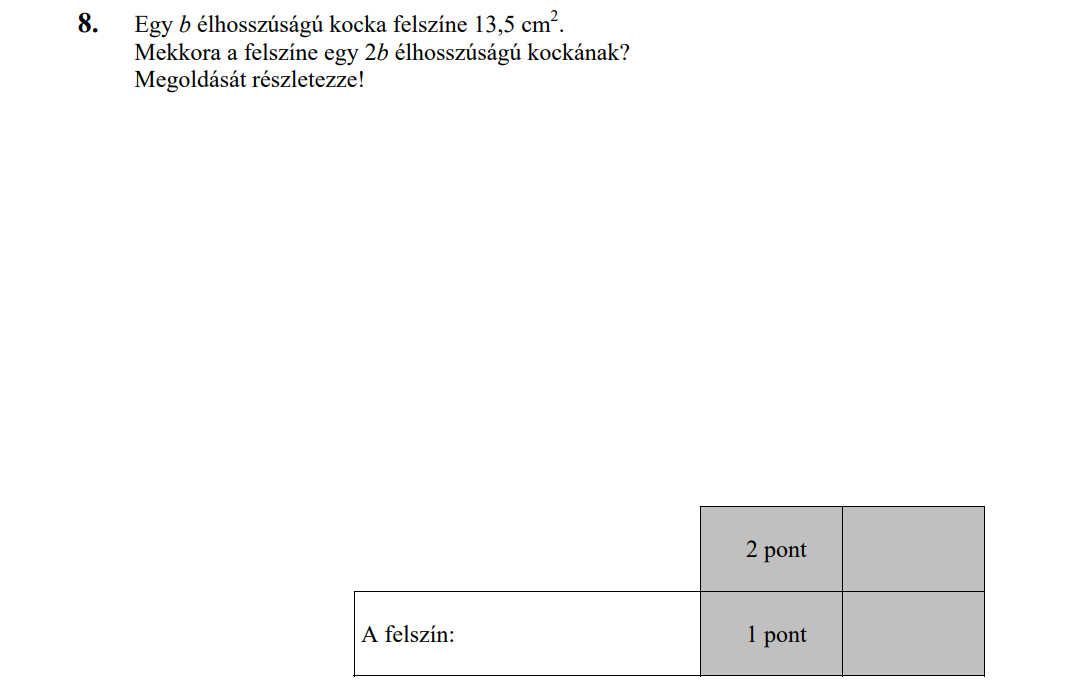




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
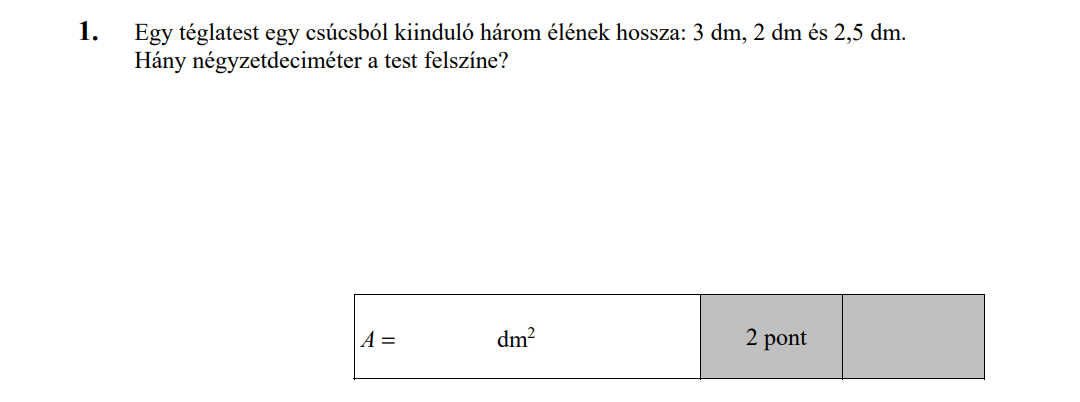
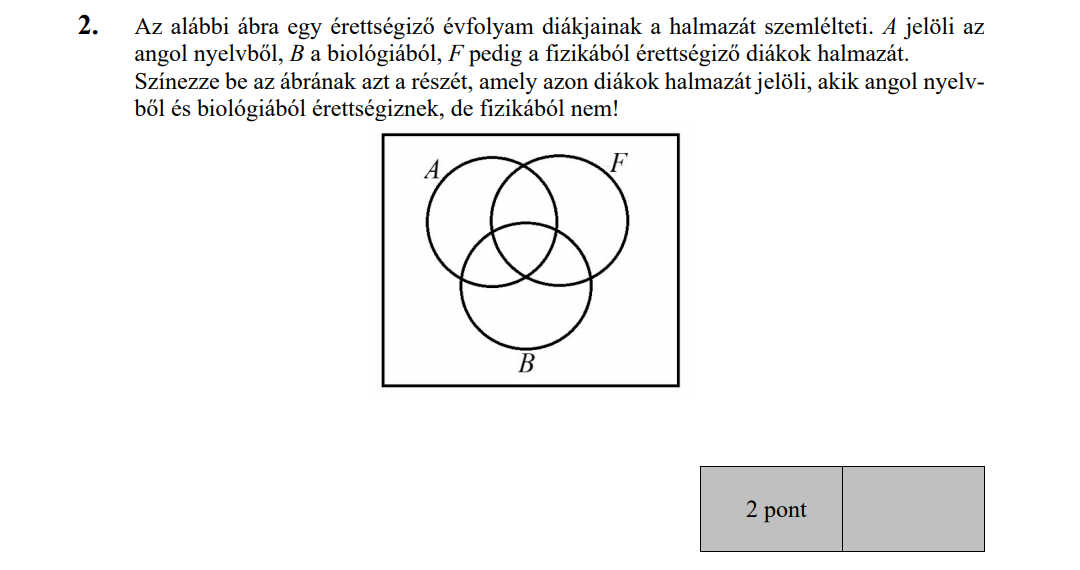

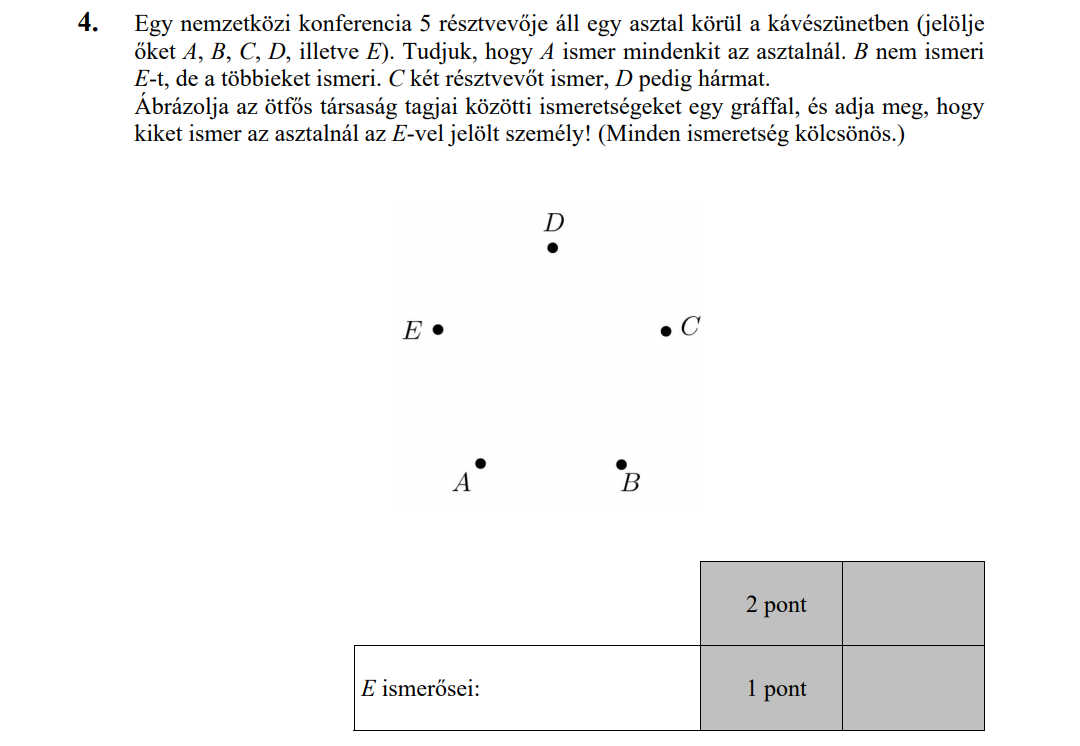

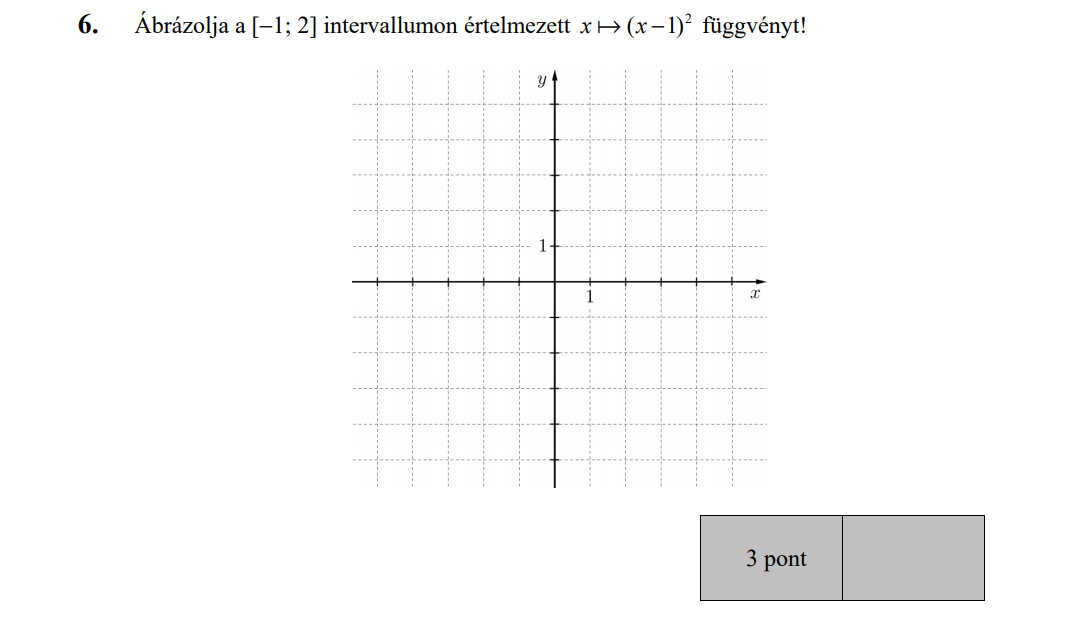



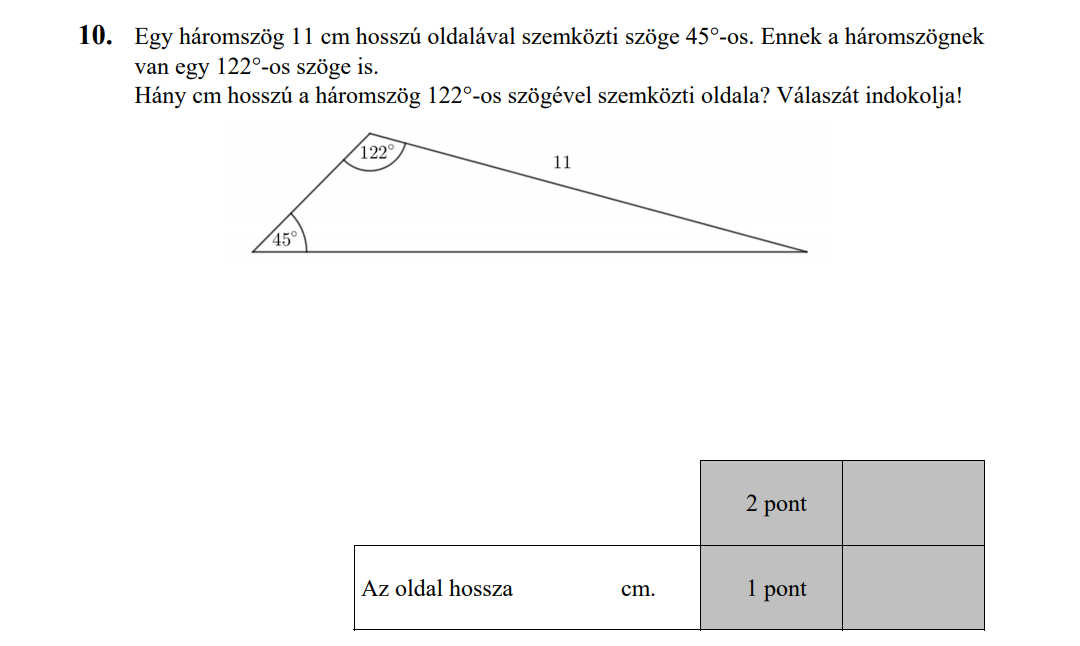

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



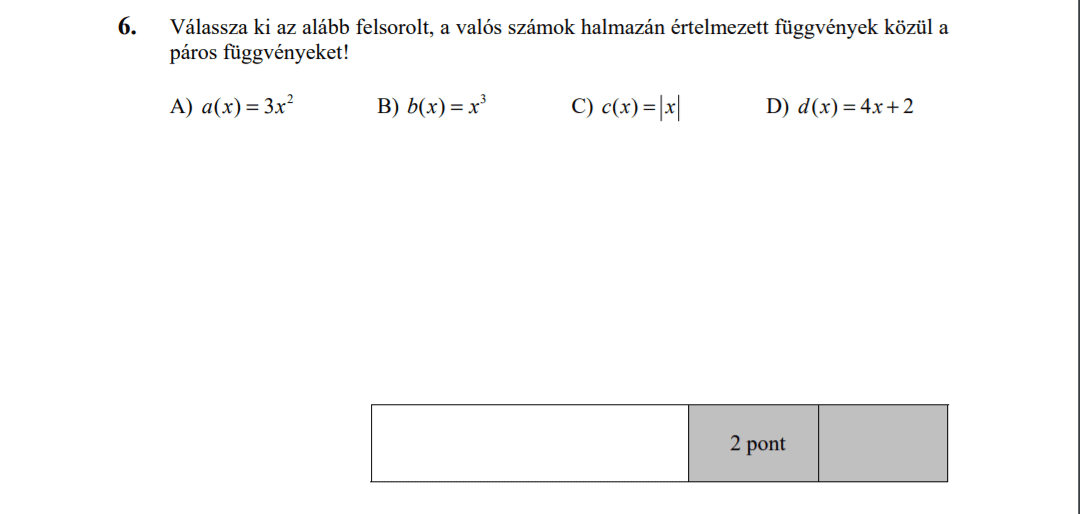
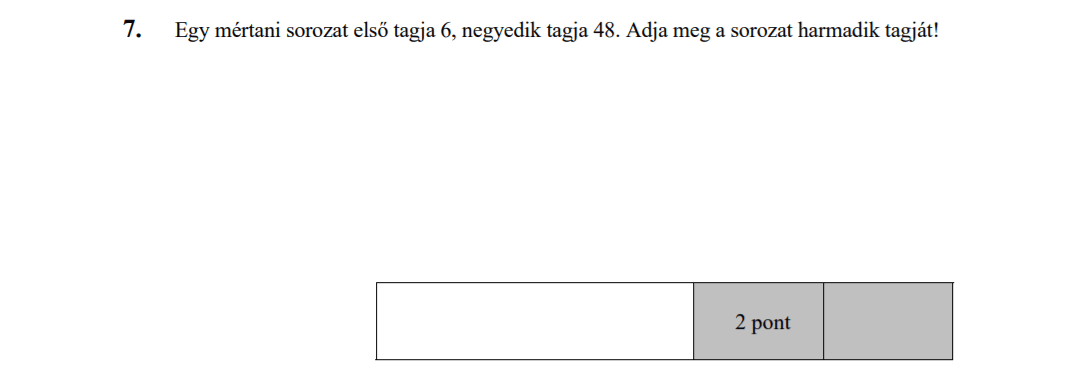



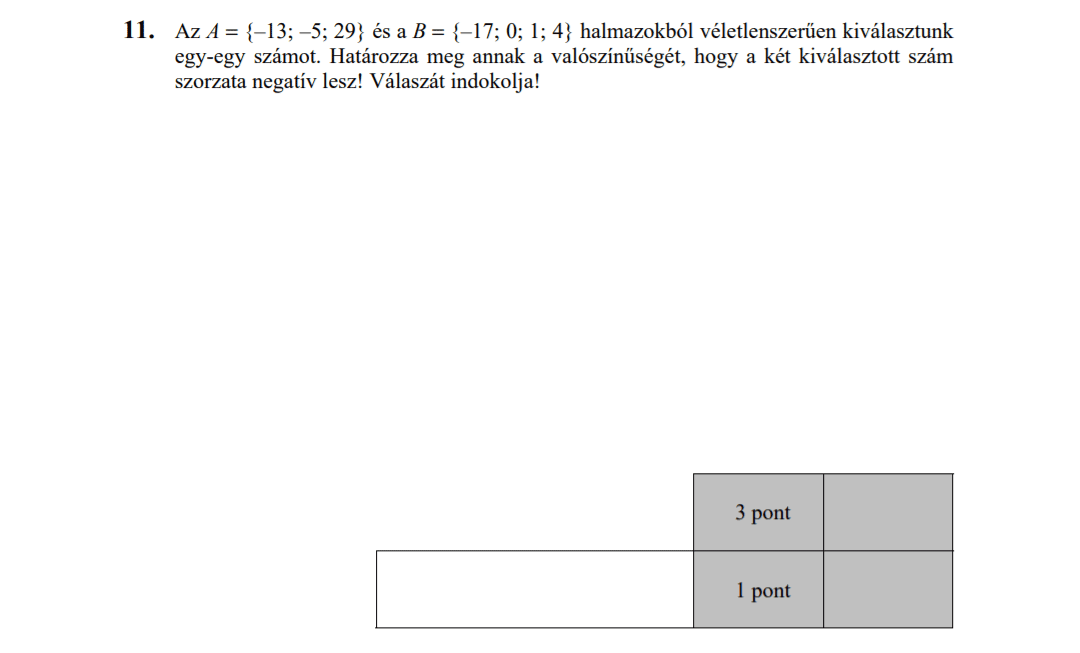

MÁSODIK RÉSZ


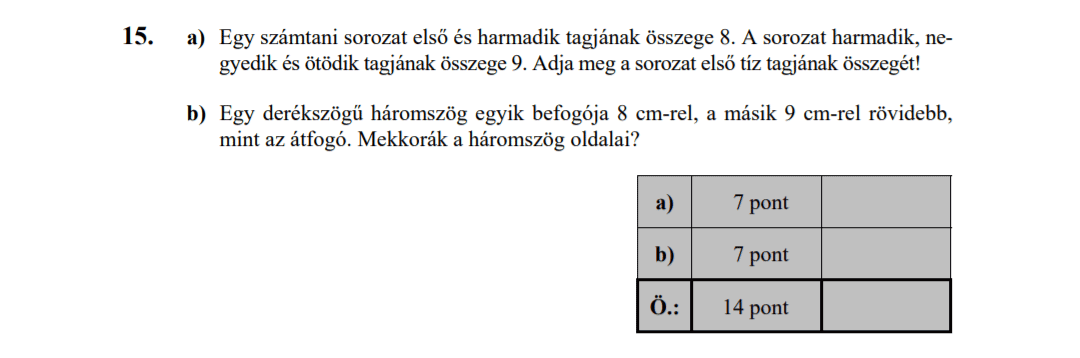



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






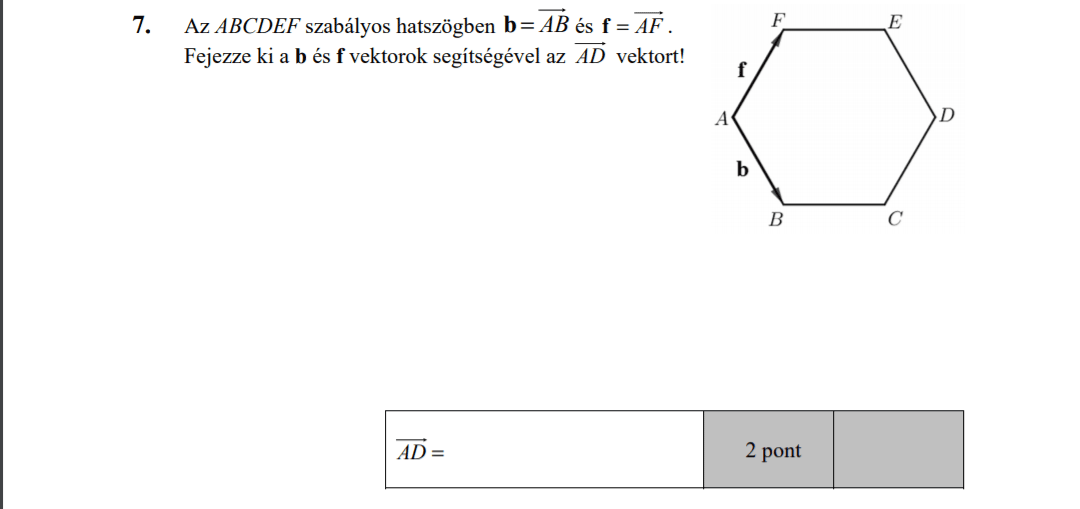



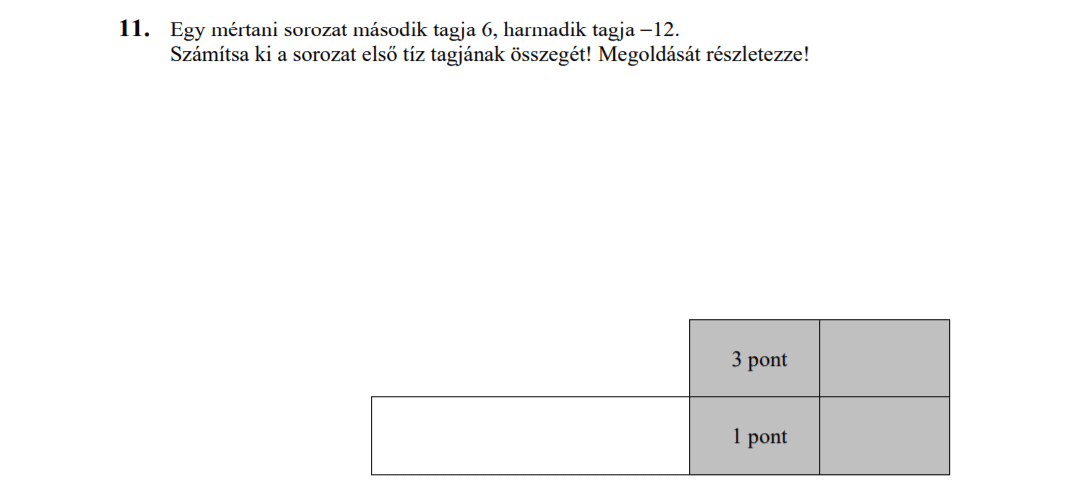

MÁSODIK RÉSZ

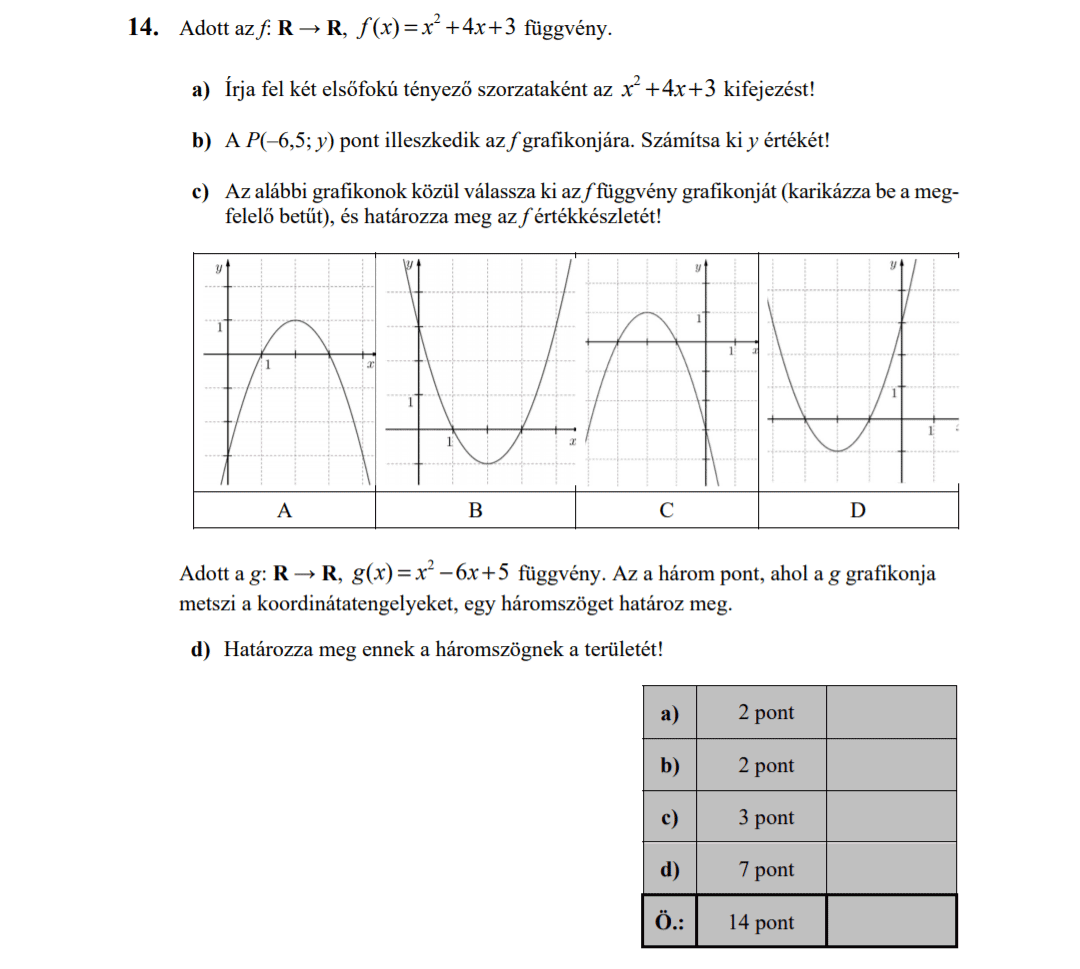




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



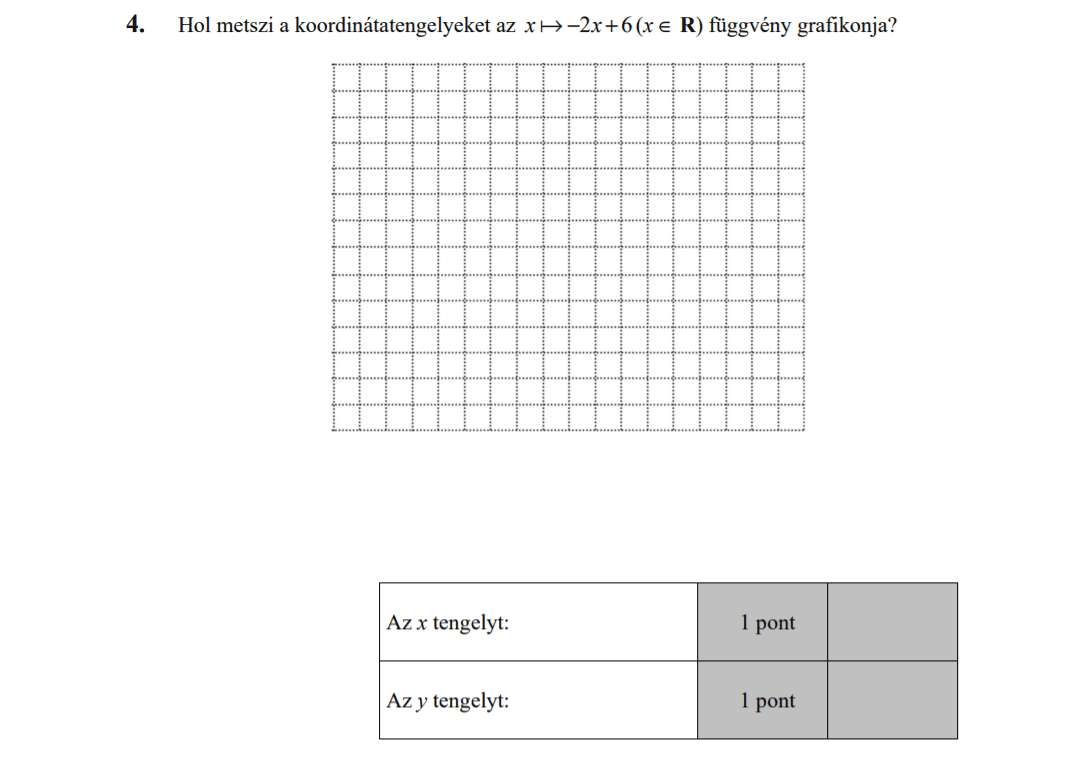

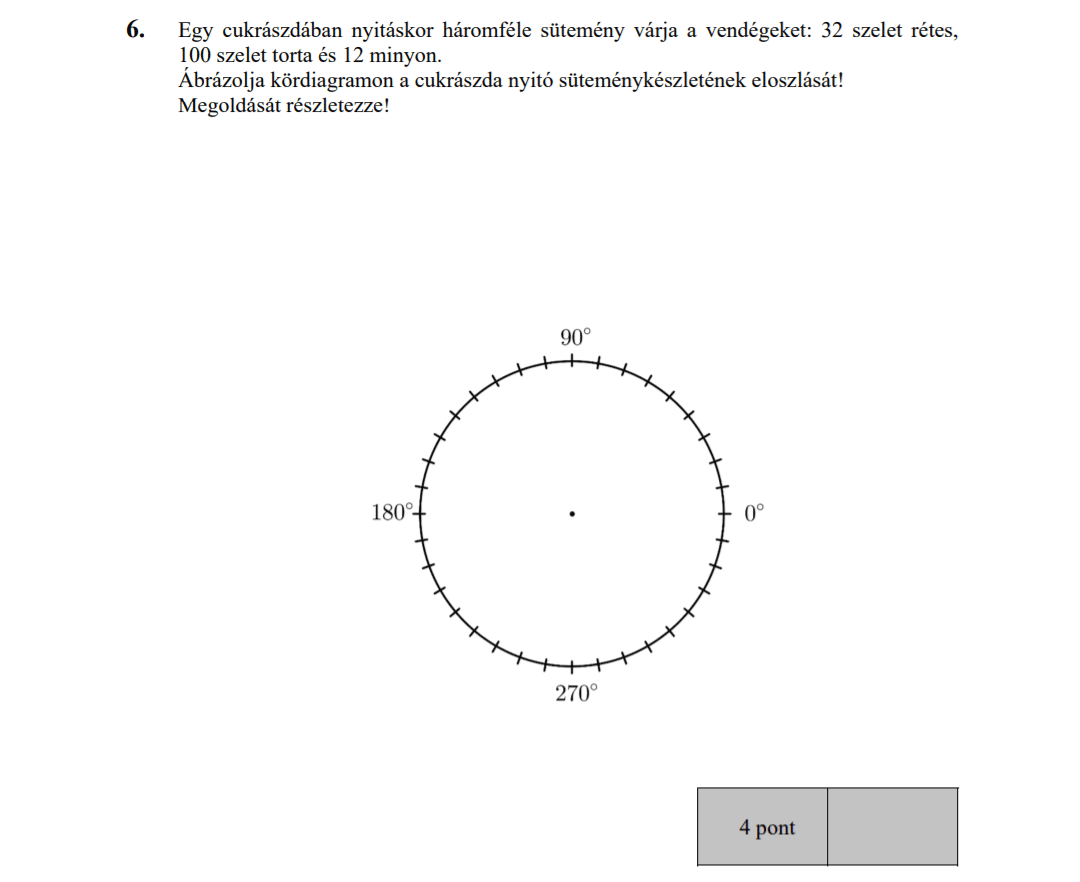






MÁSODIK RÉSZ

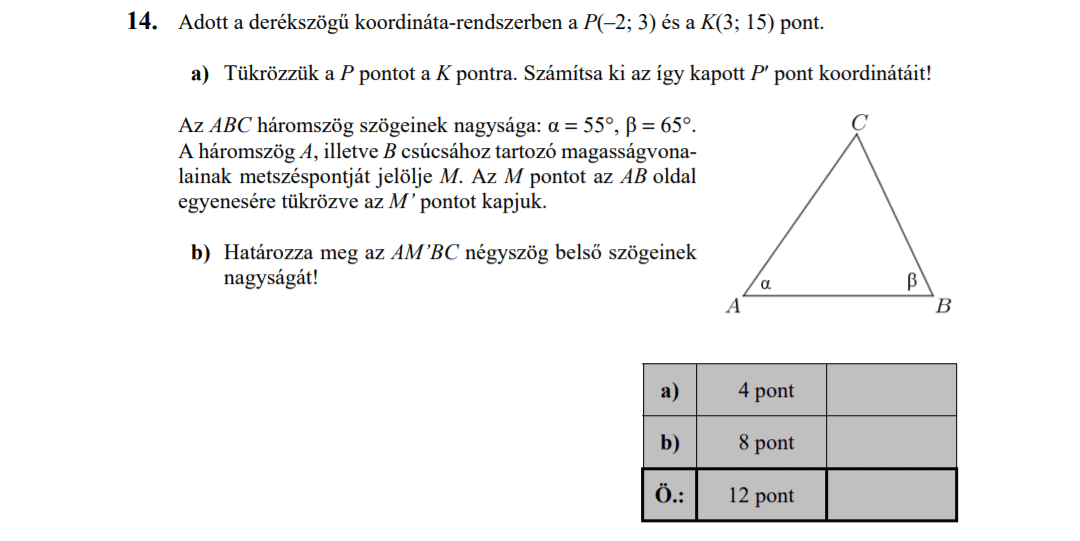




- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
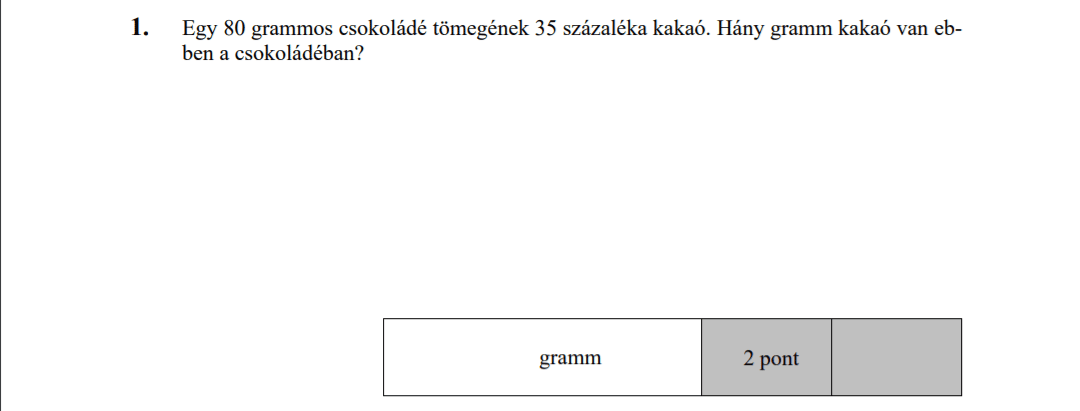

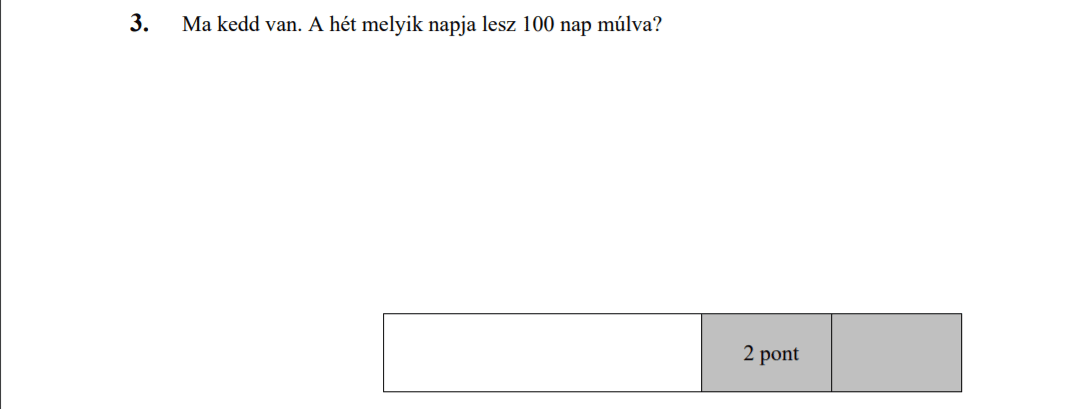
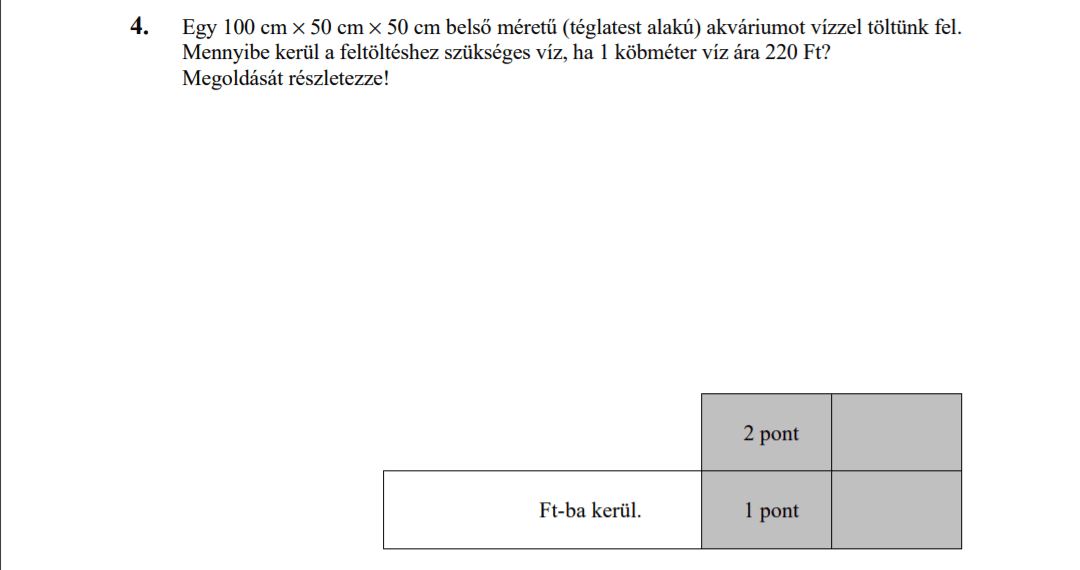
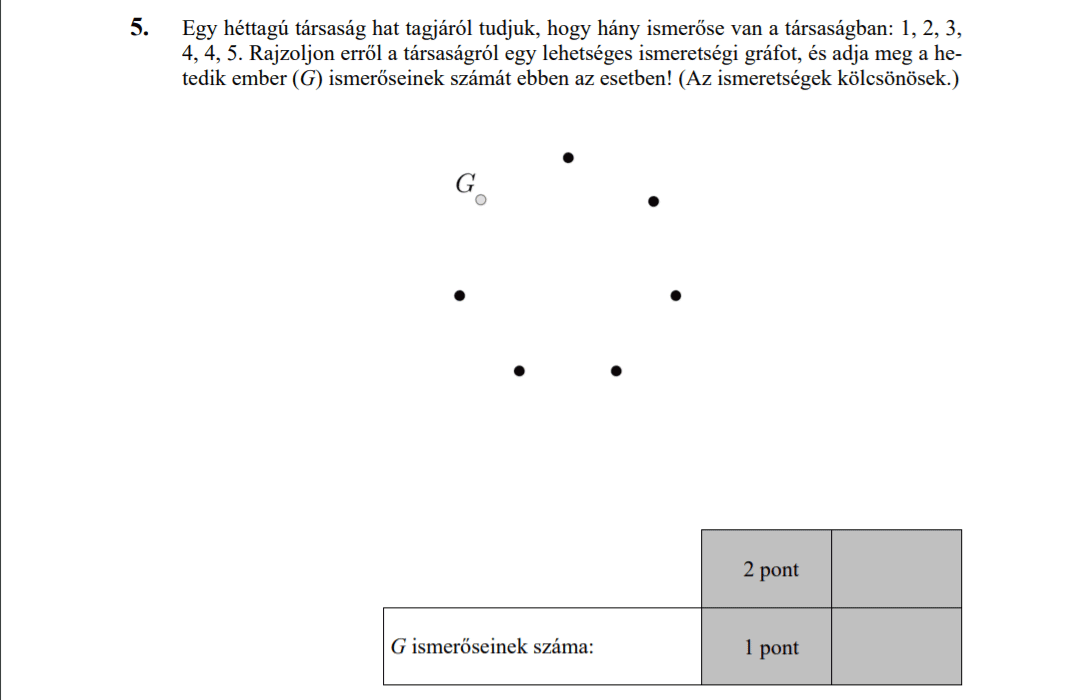







MÁSODIK RÉSZ
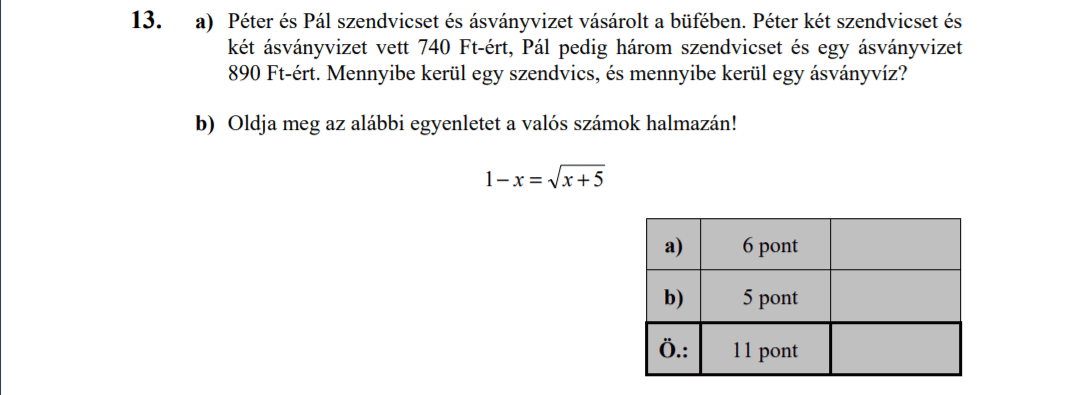
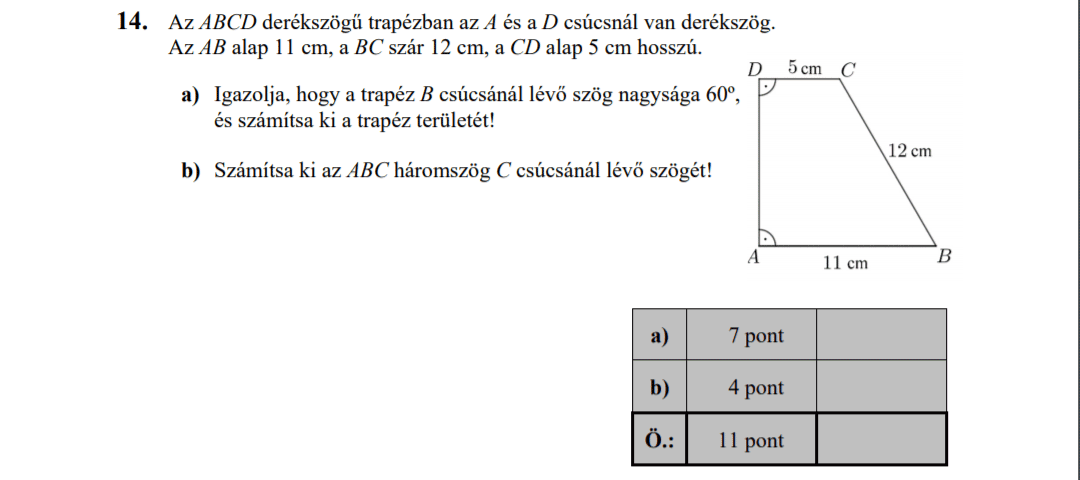

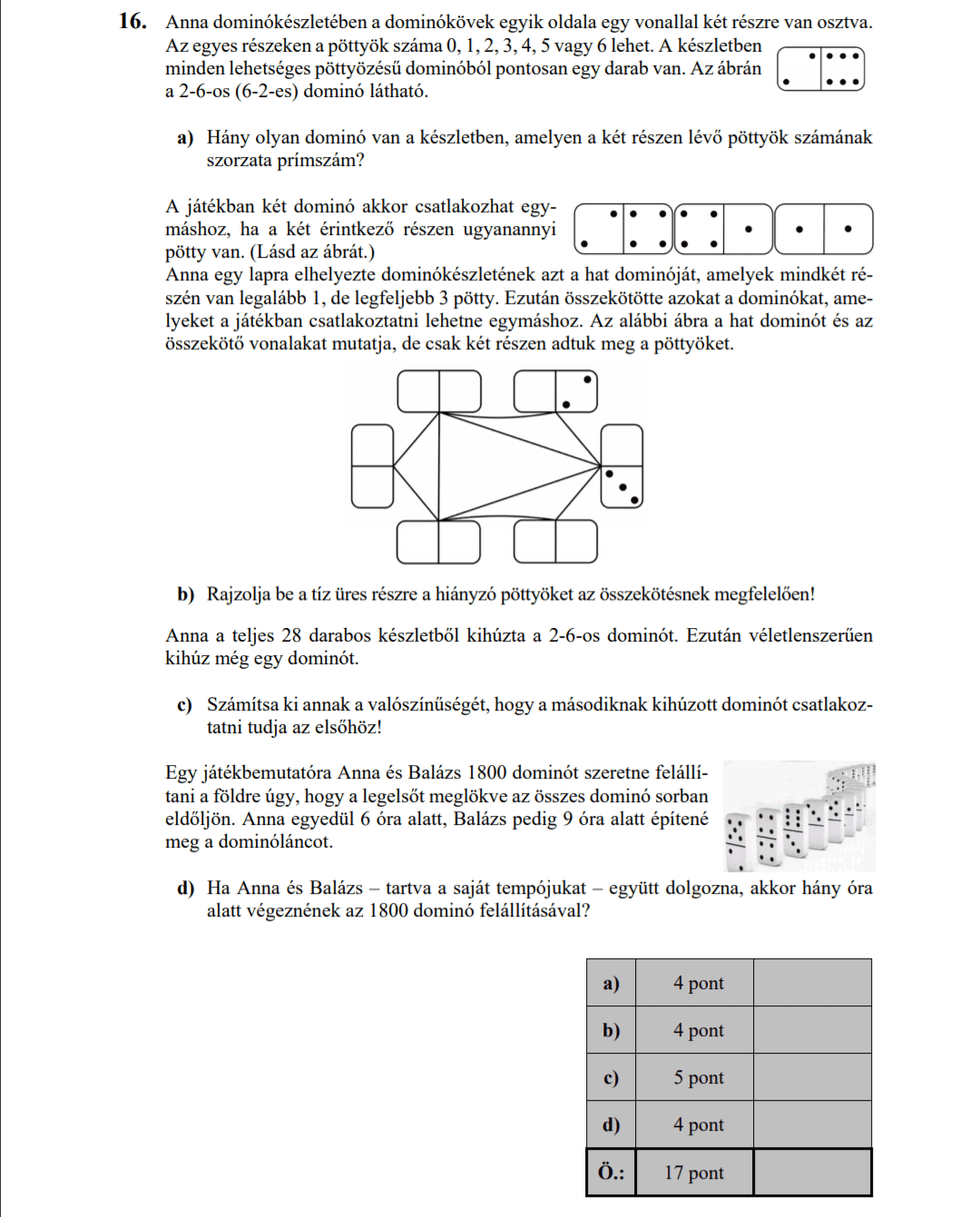


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




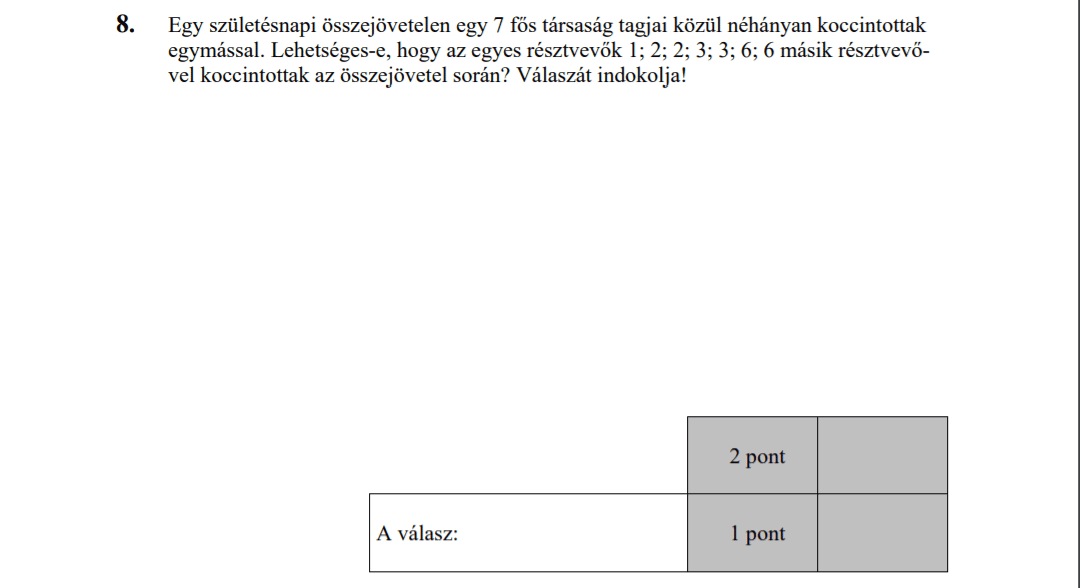



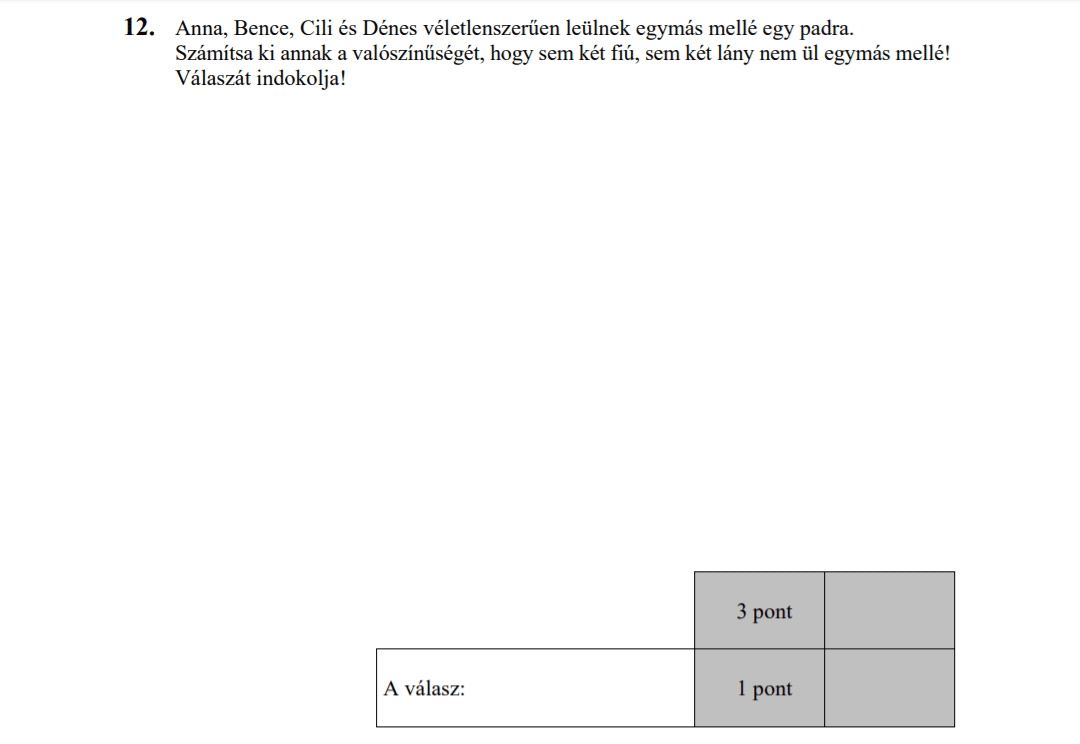
MÁSODIK RÉSZ

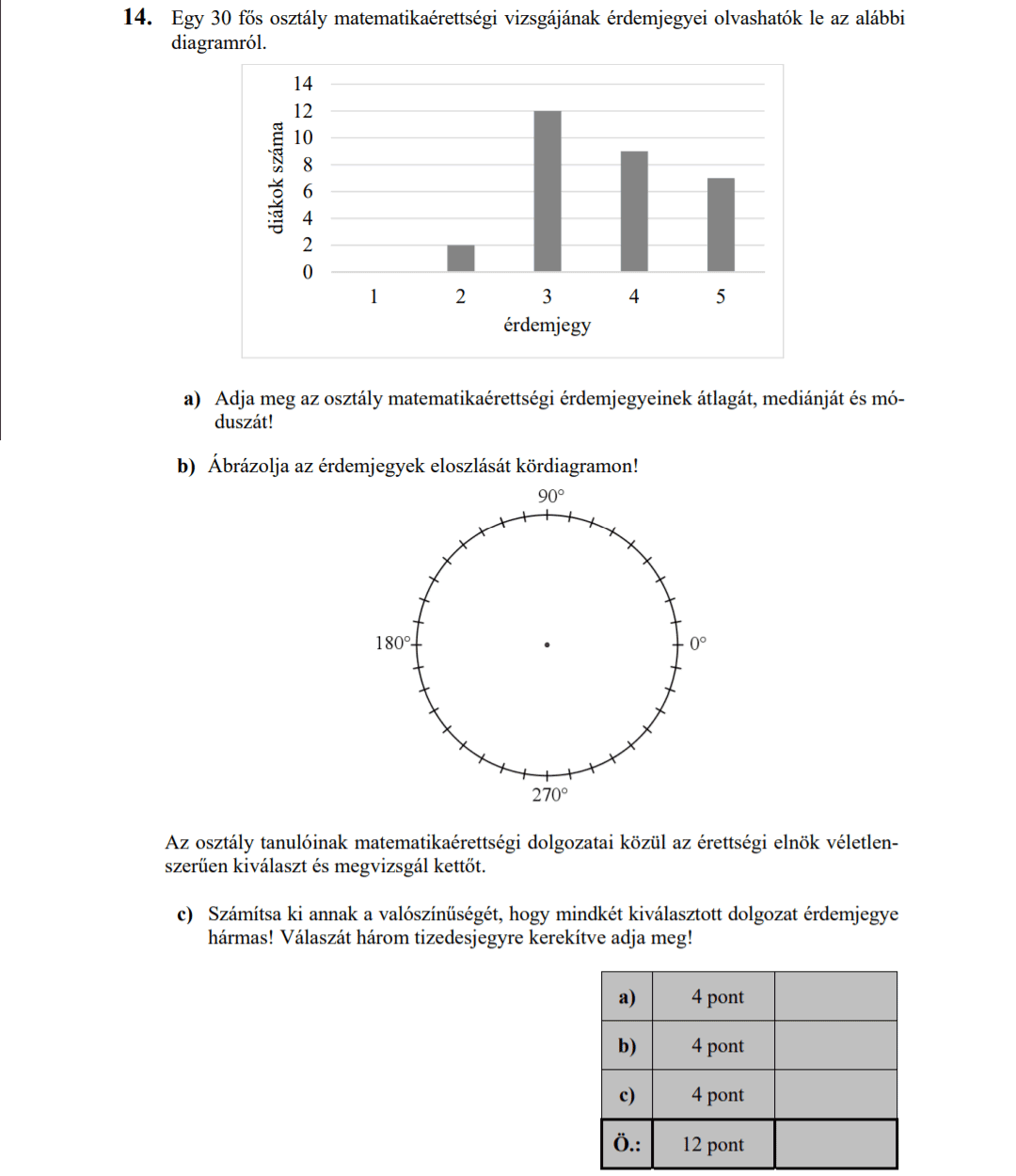
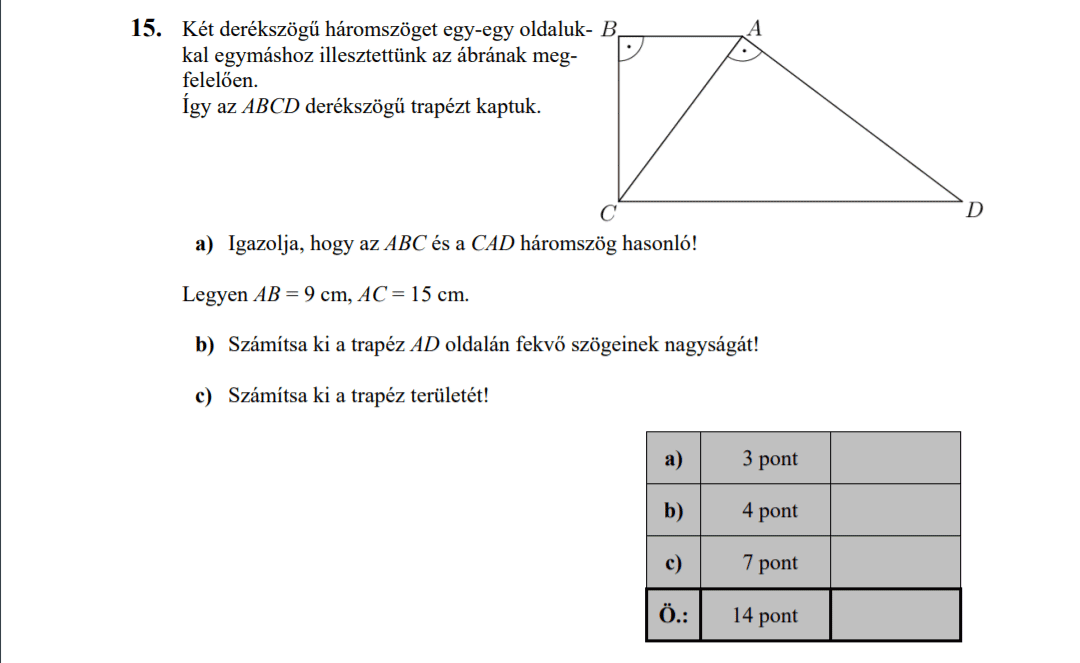



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


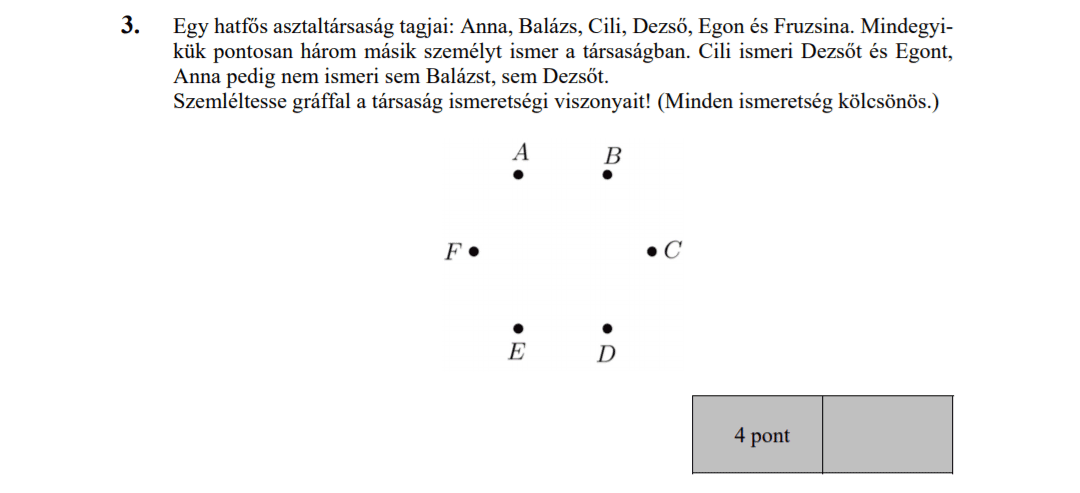


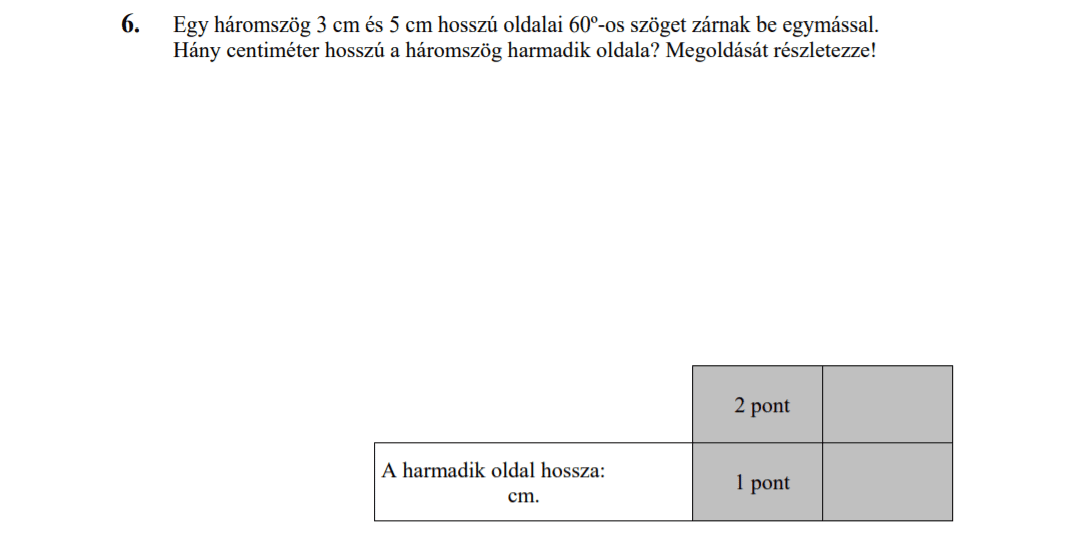

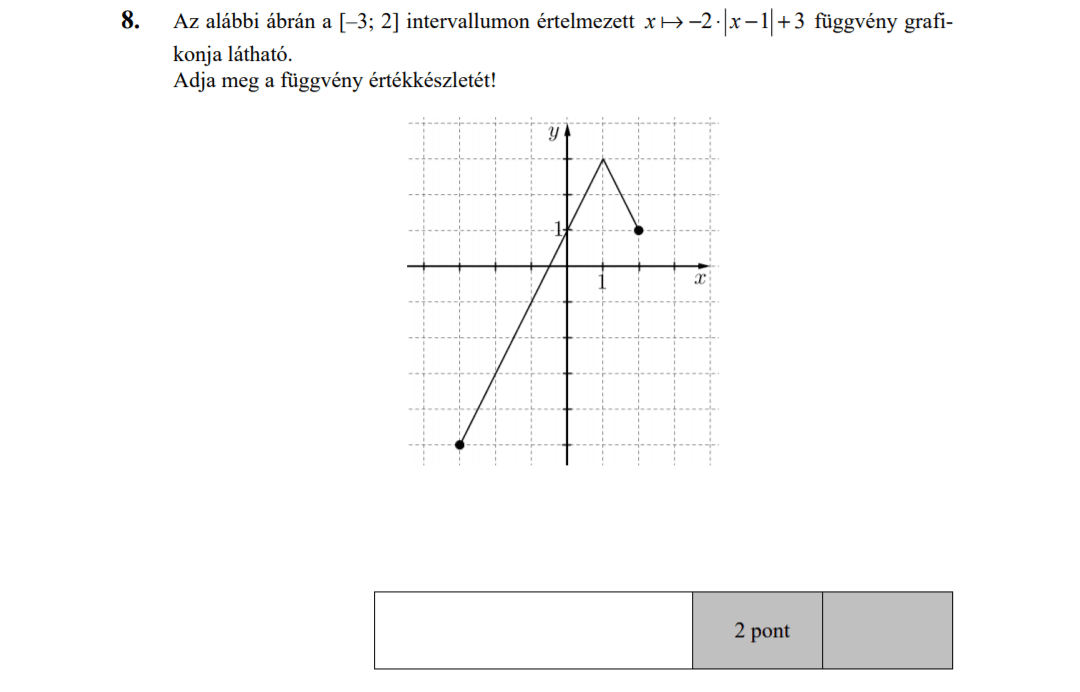

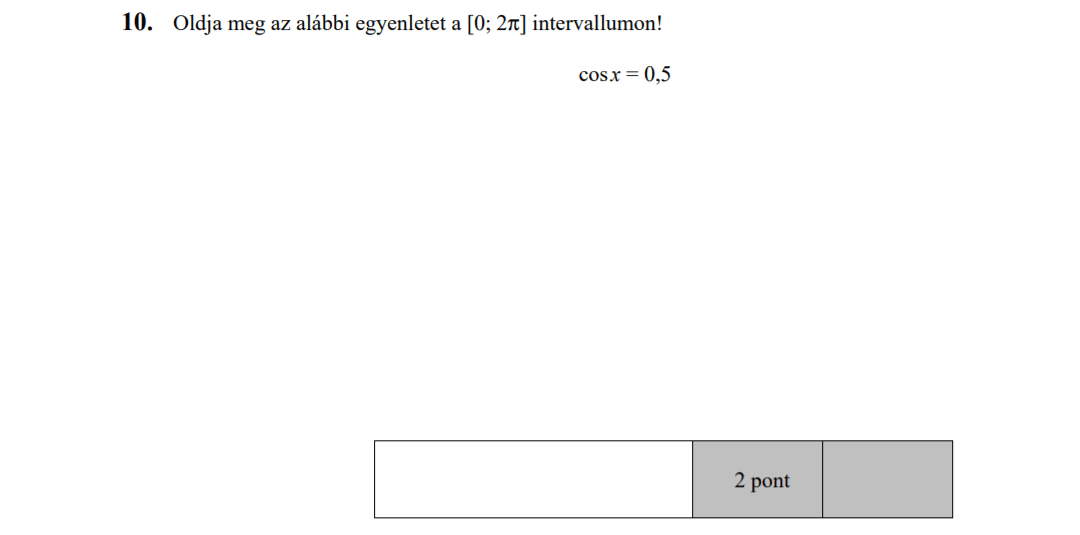

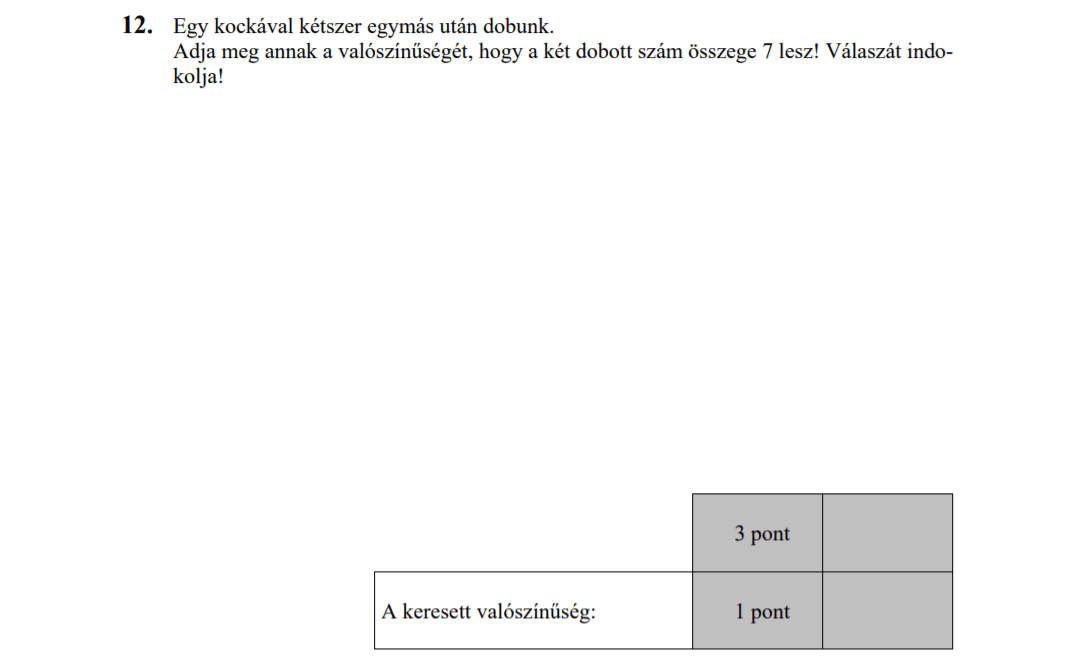
MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
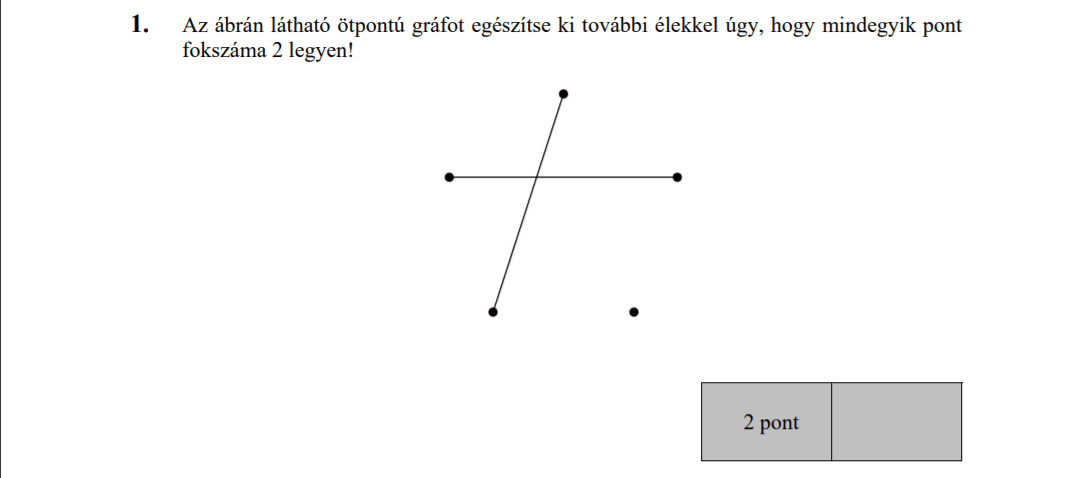
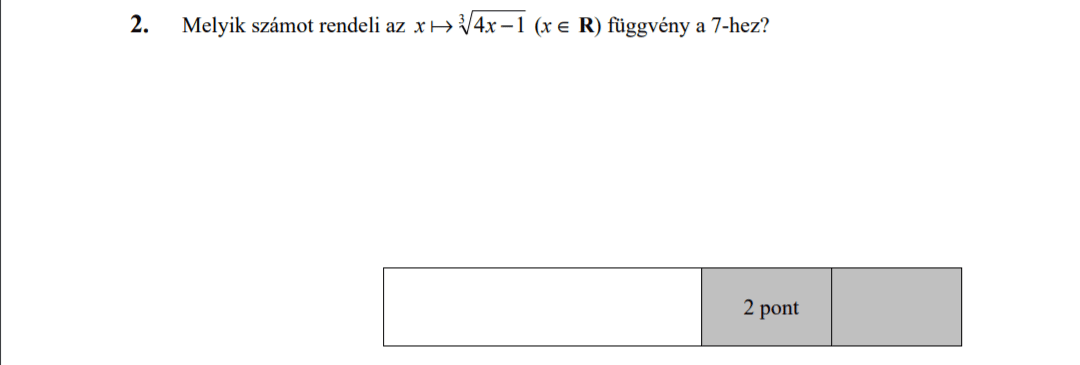
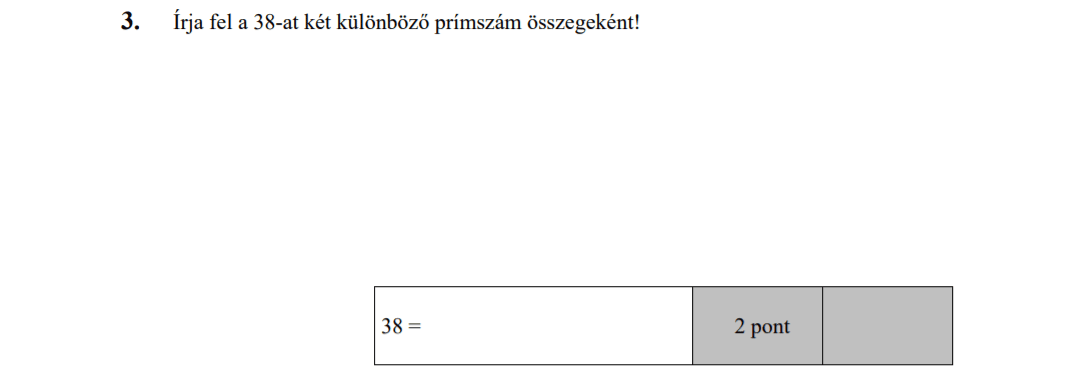


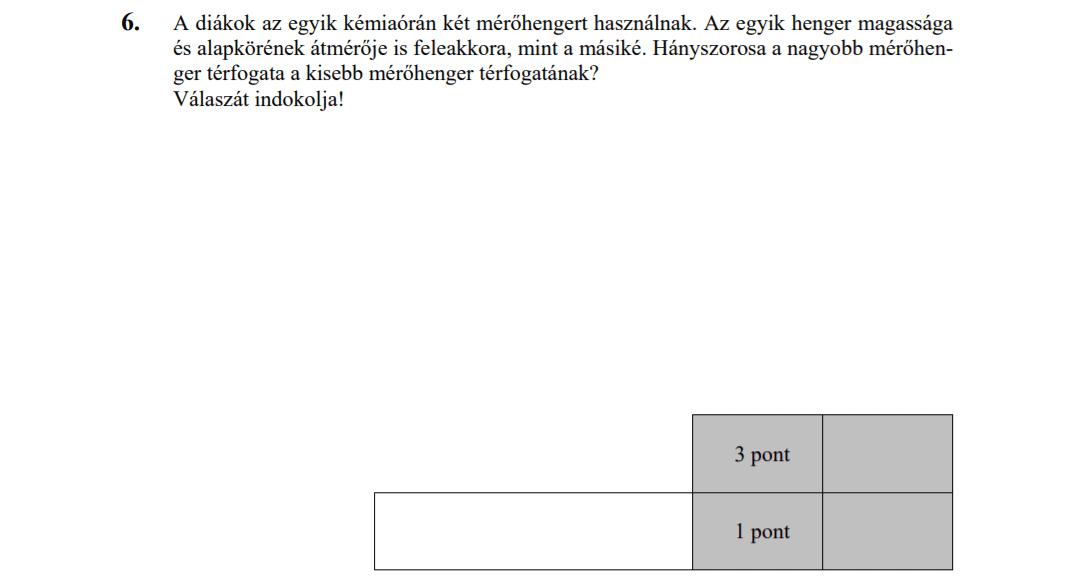
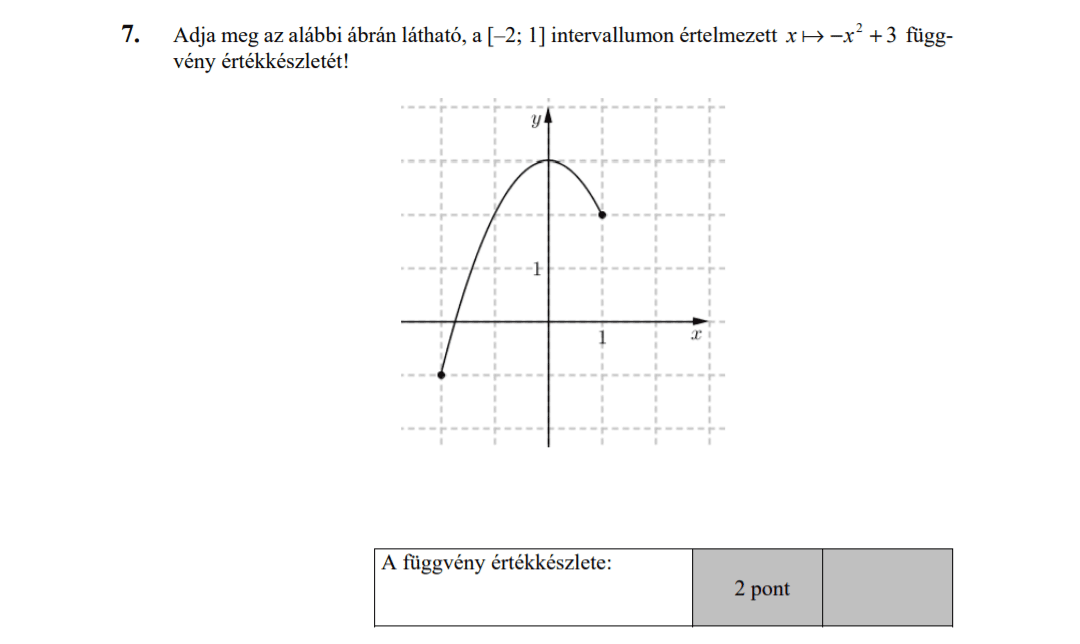

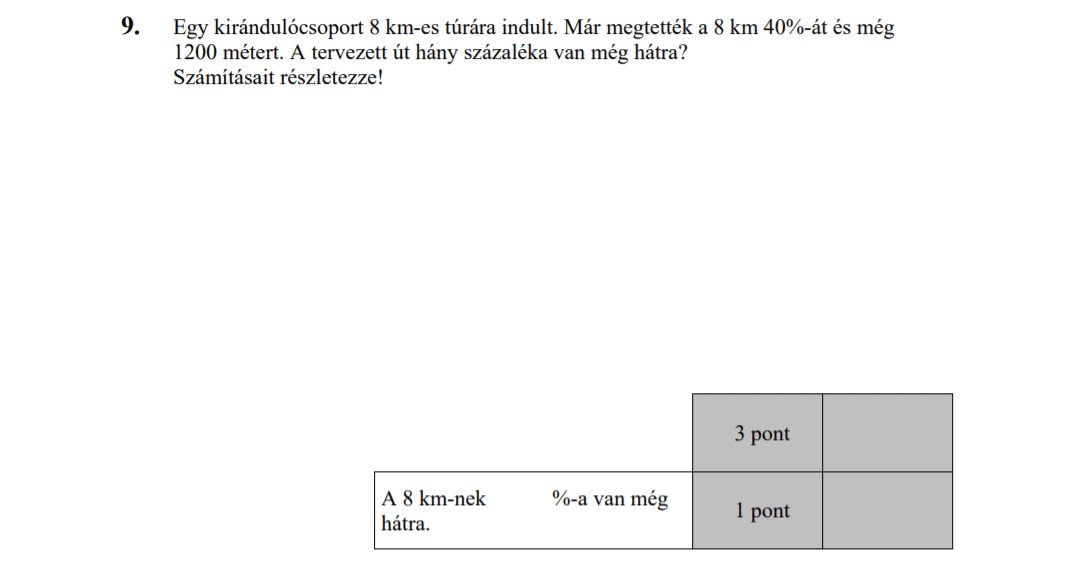
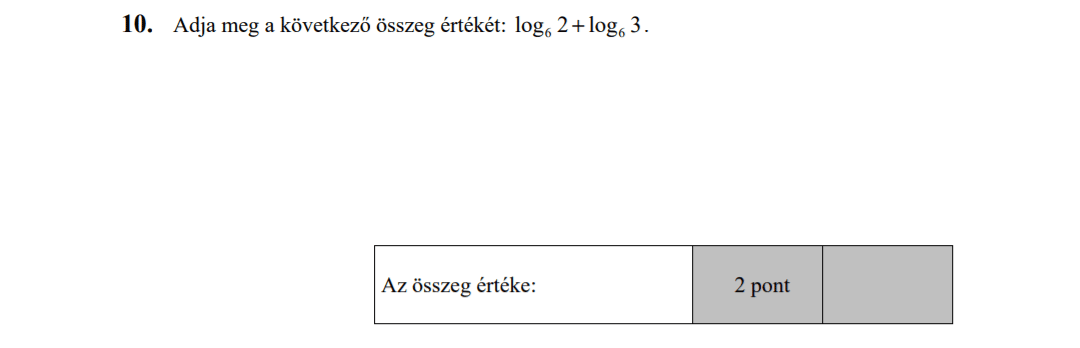
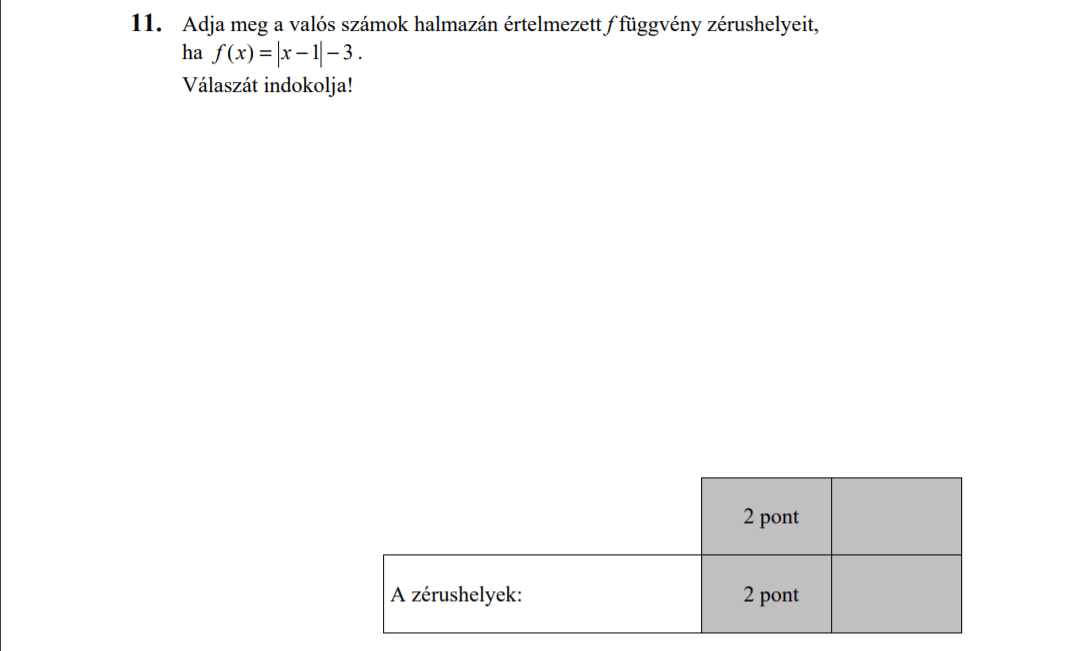

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
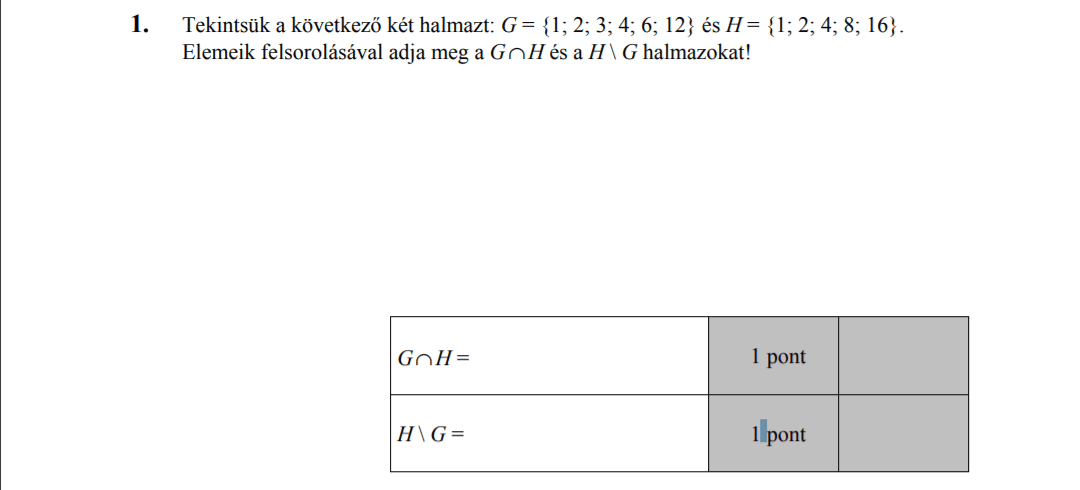



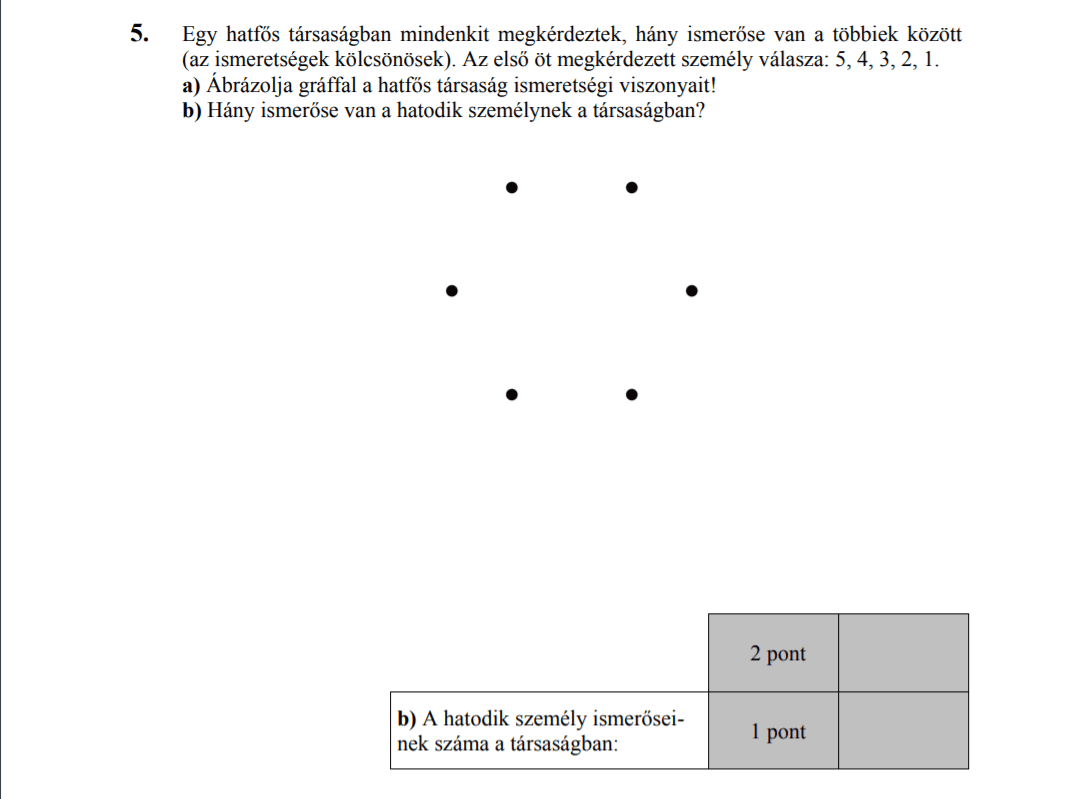


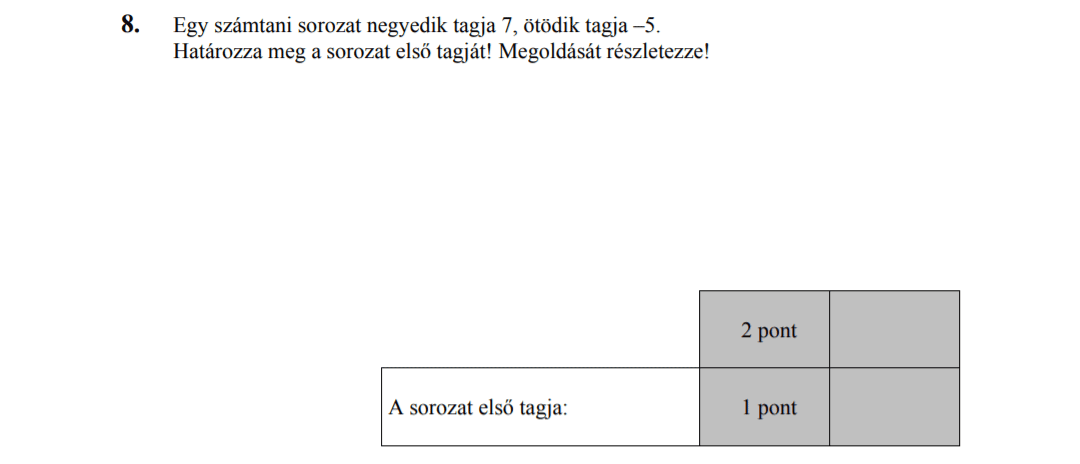

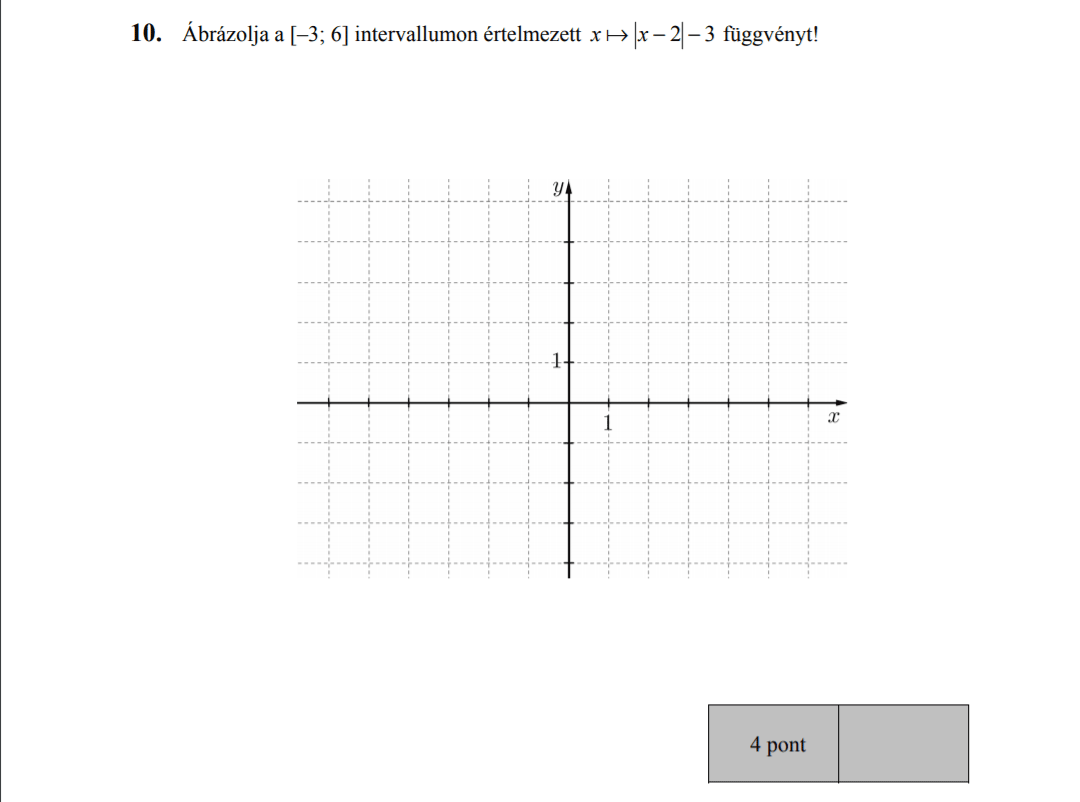

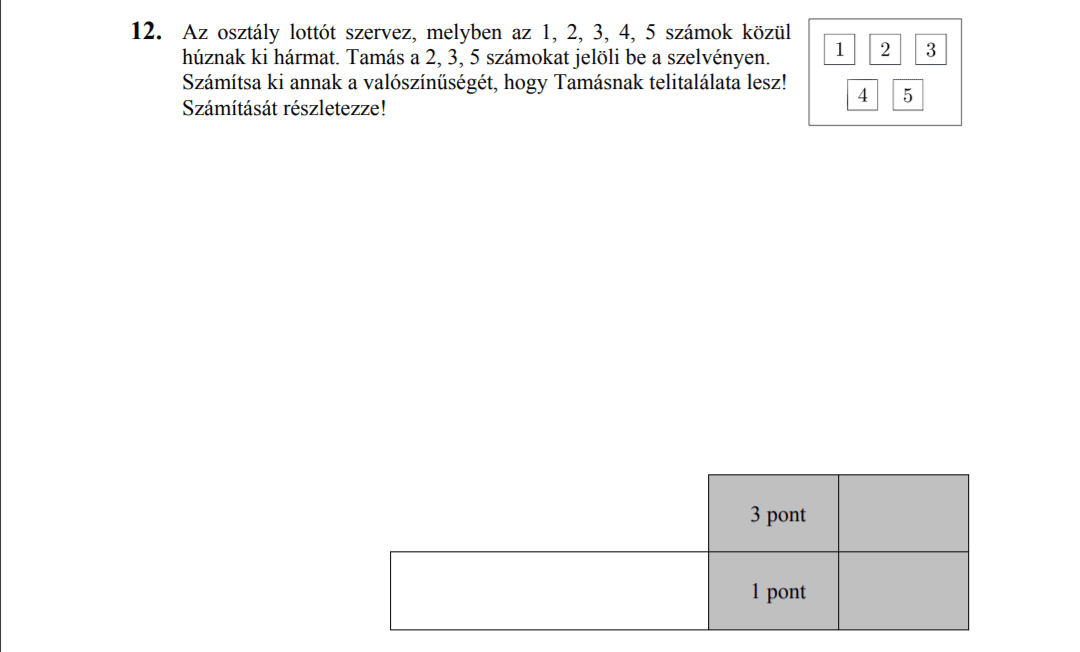
MÁSODIK RÉSZ

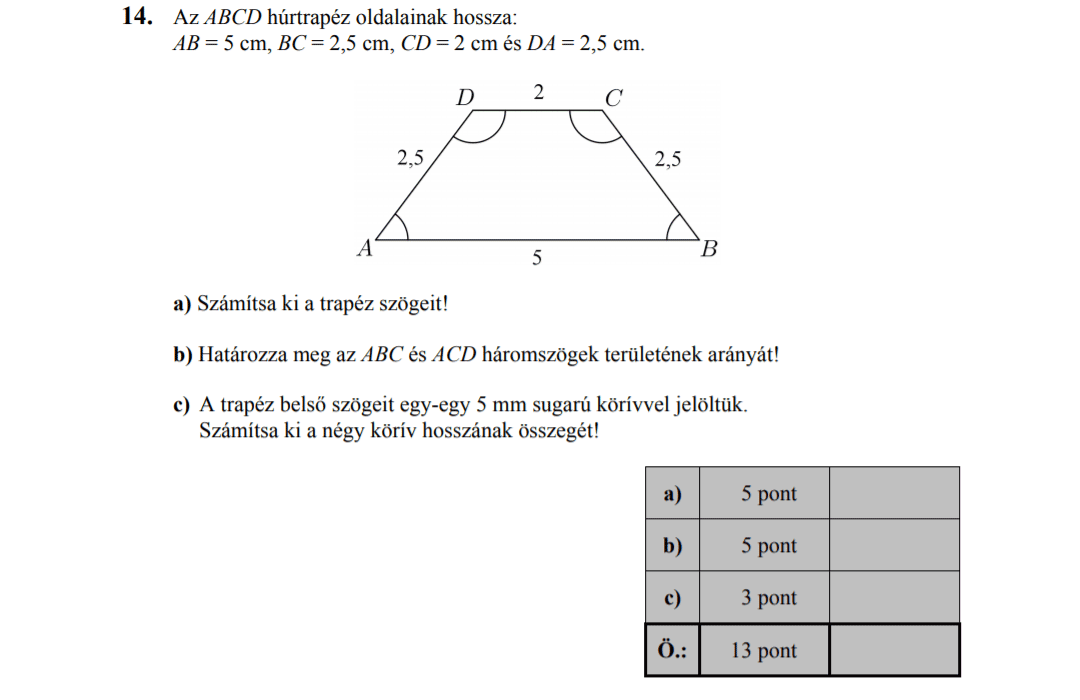

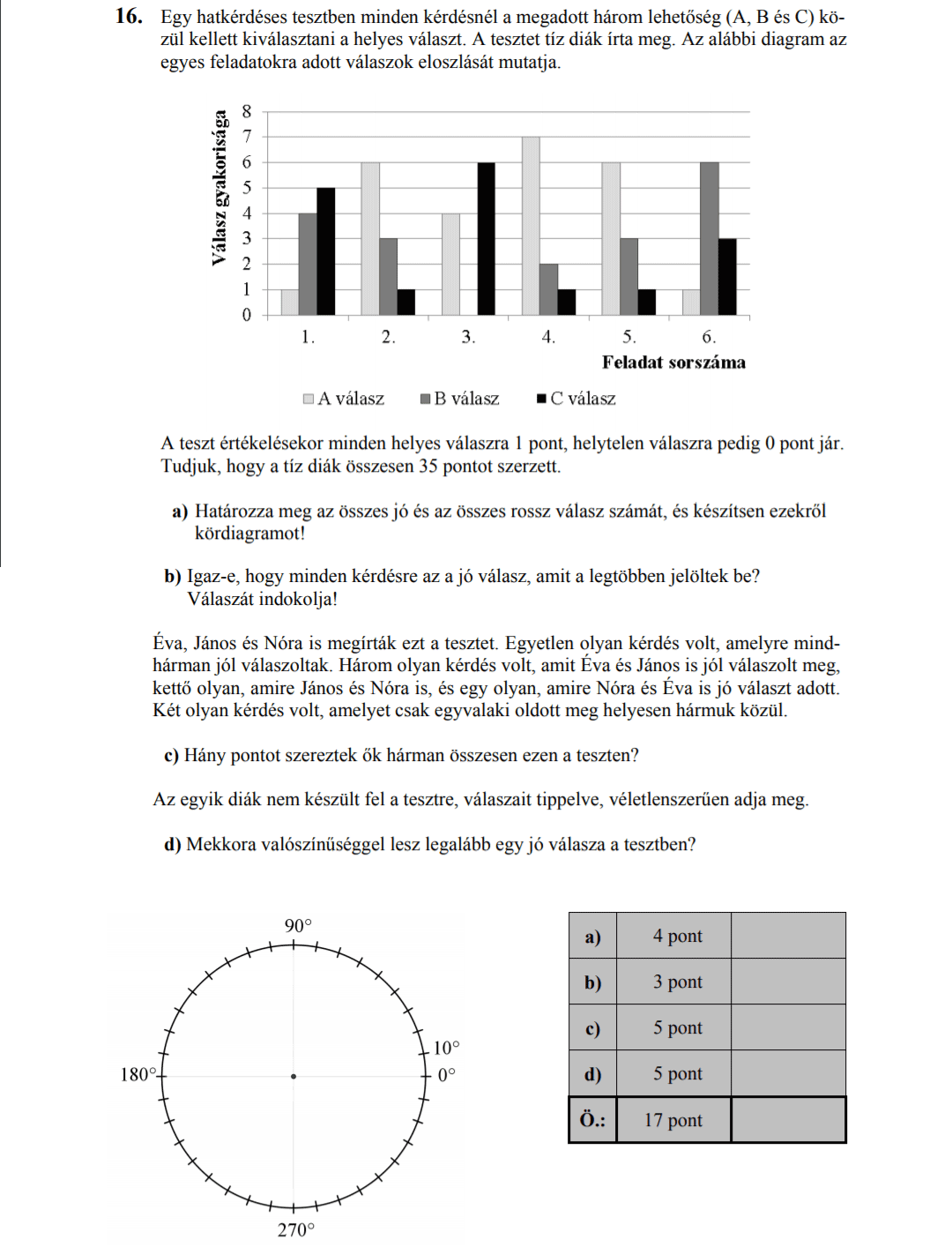


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

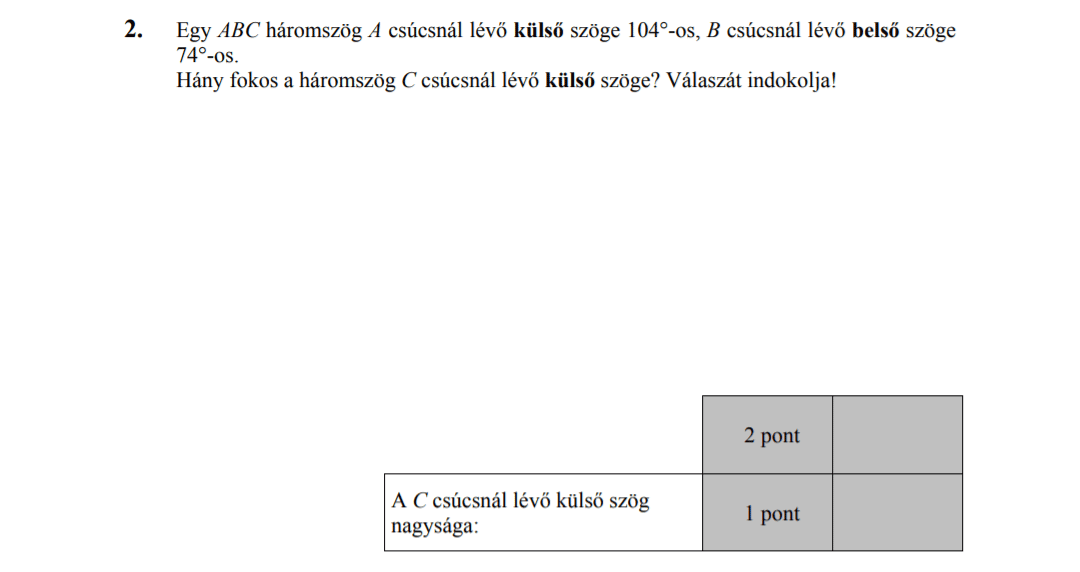





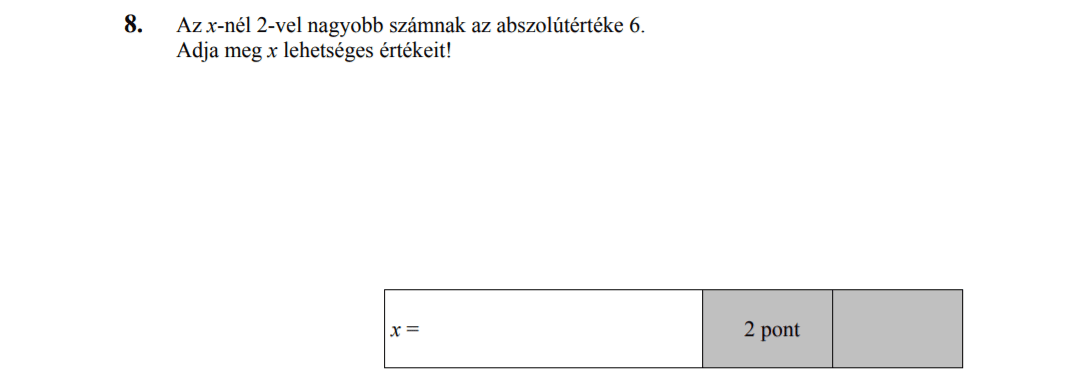

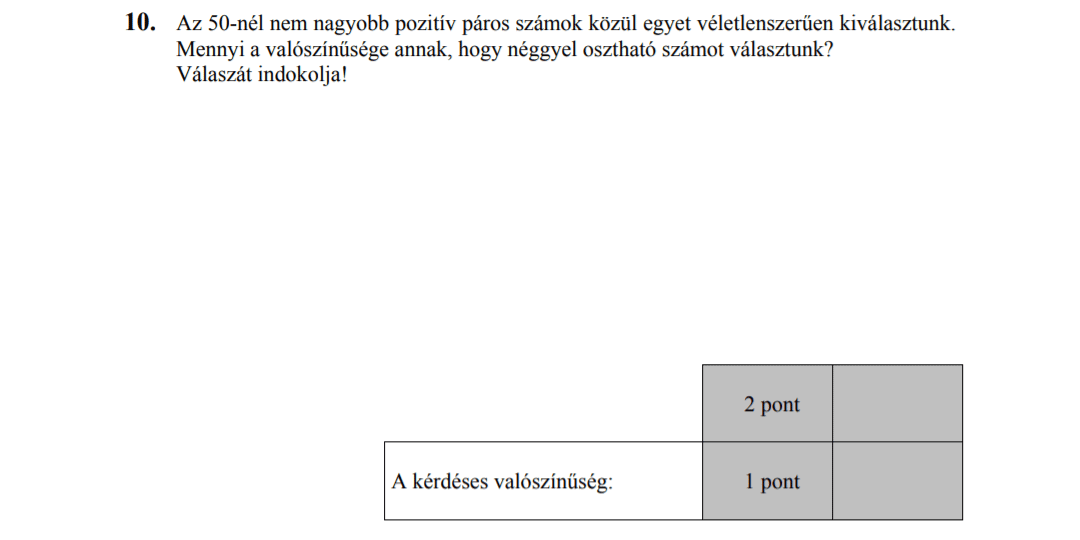


MÁSODIK RÉSZ

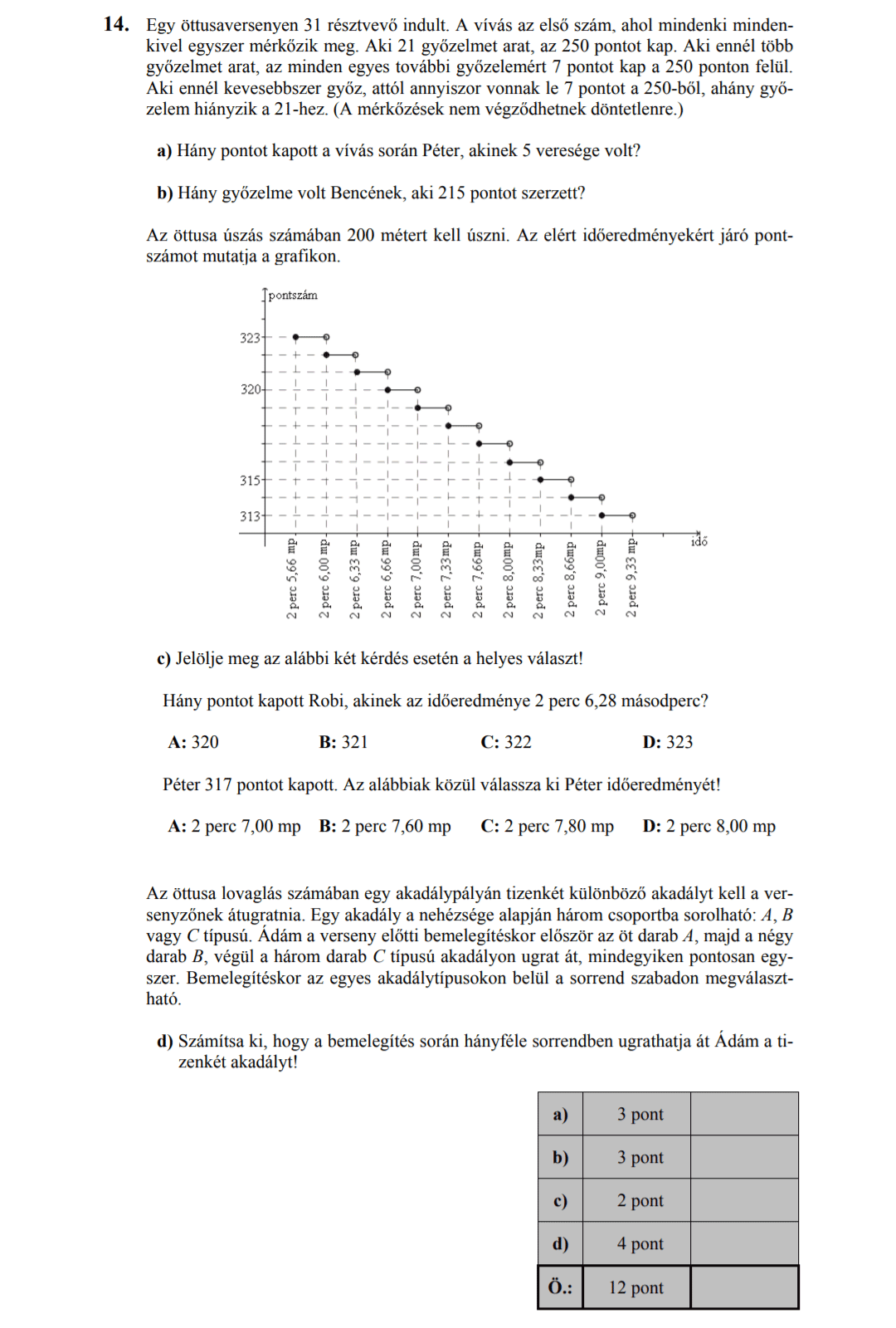
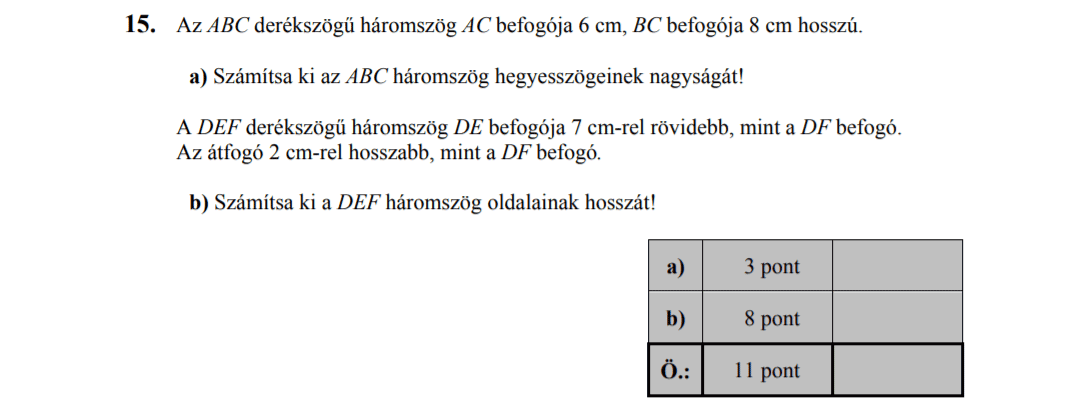



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

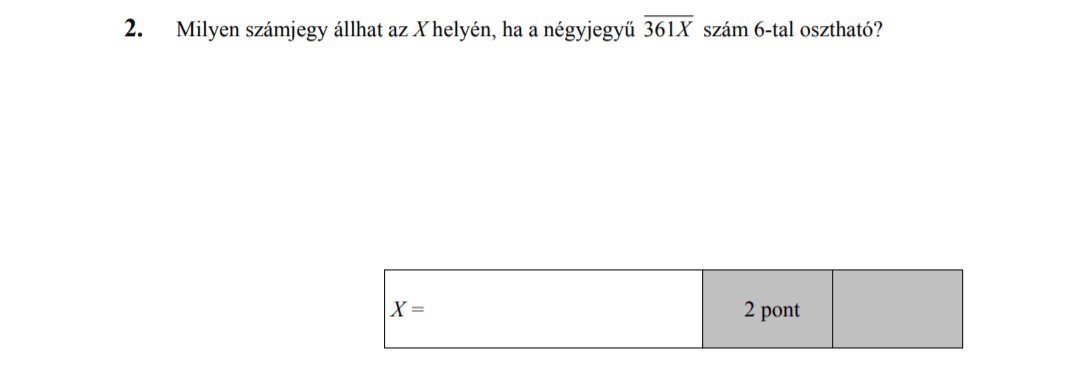



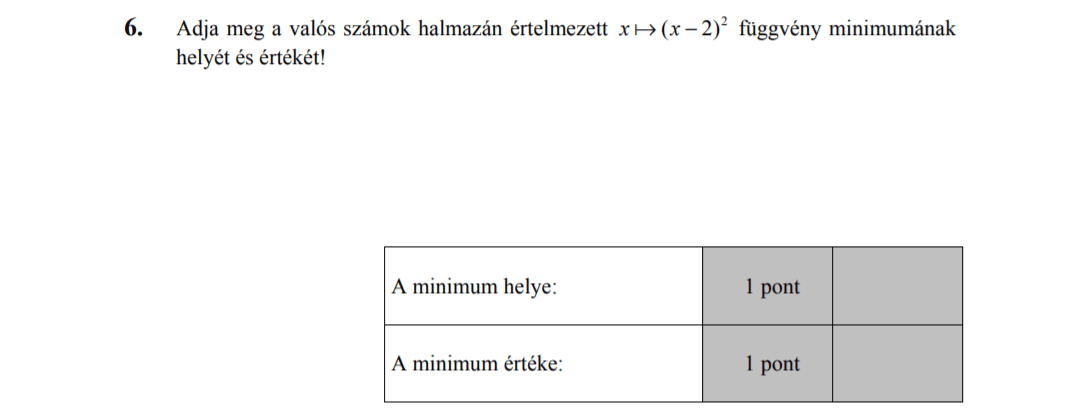

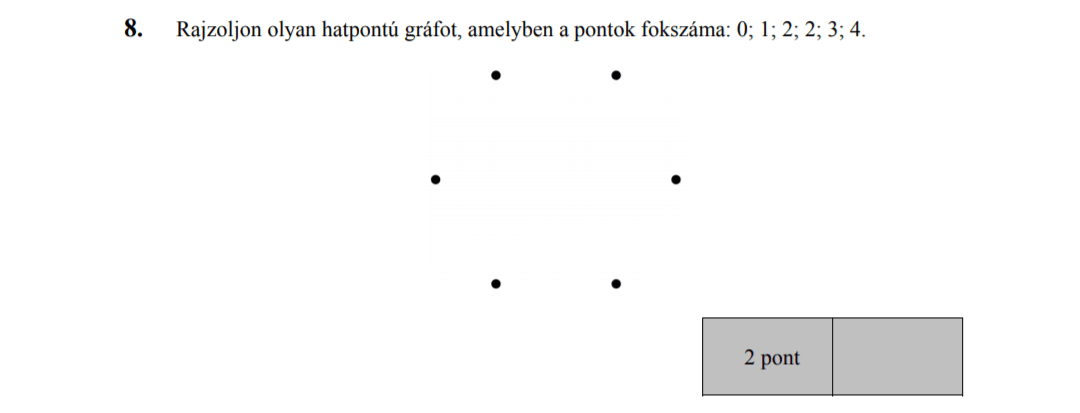


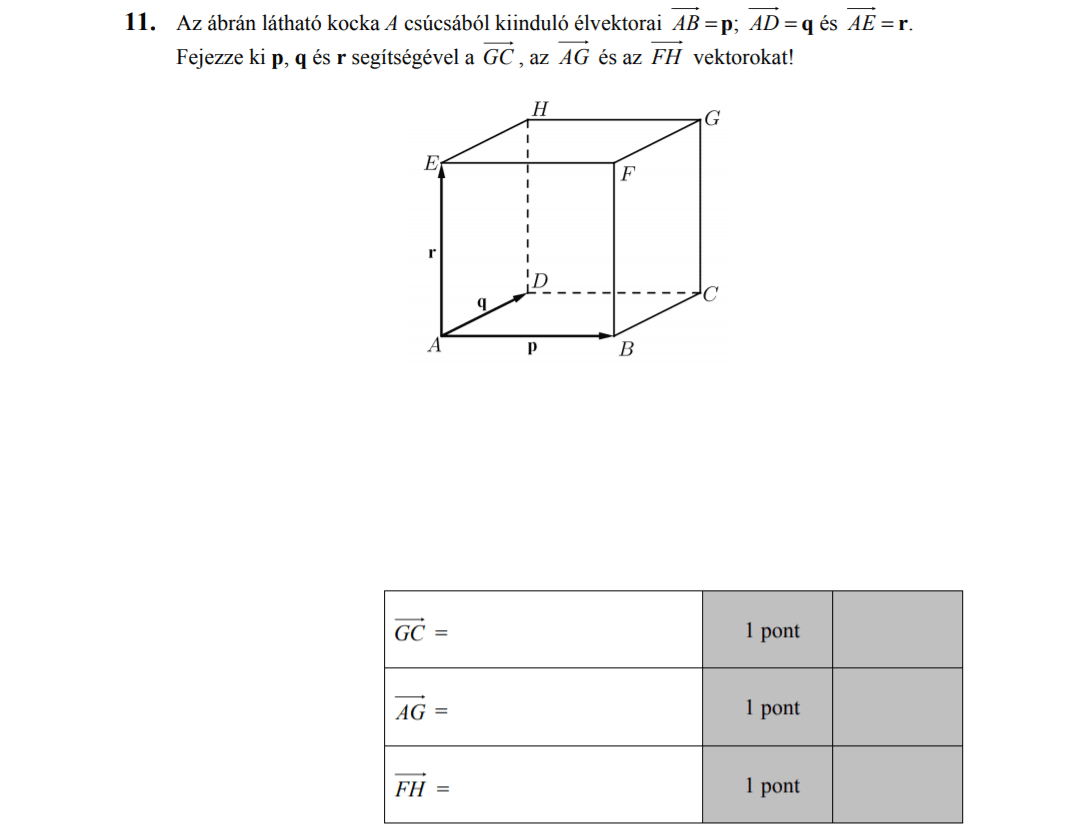
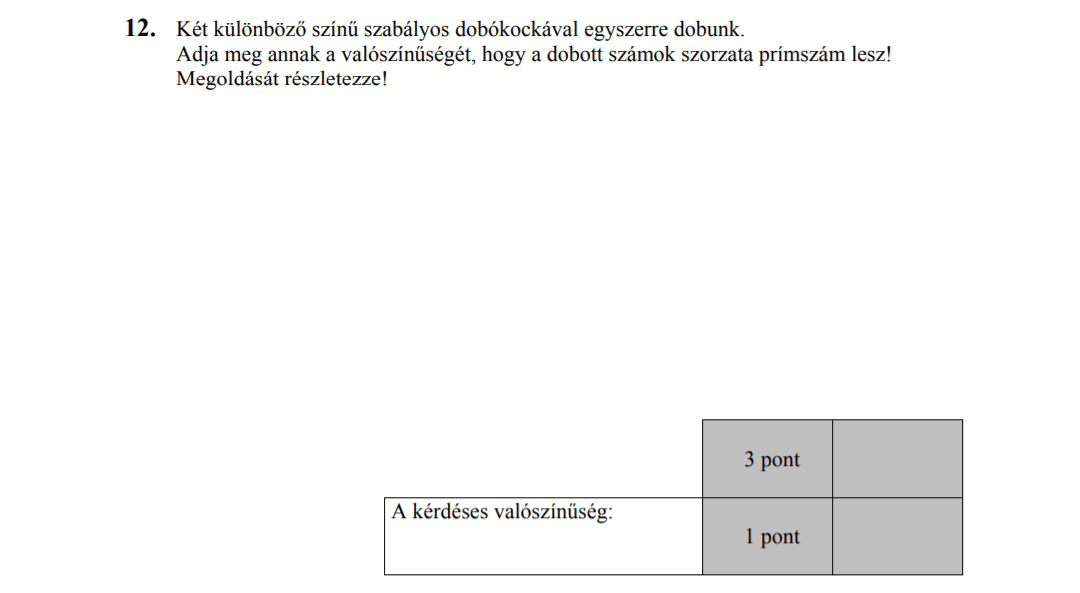
MÁSODIK RÉSZ
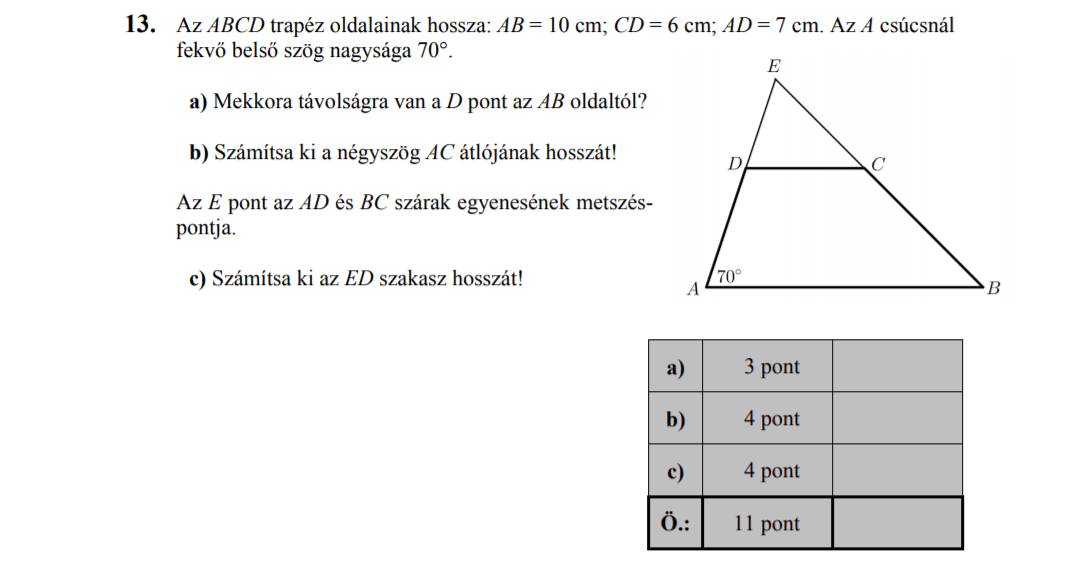





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


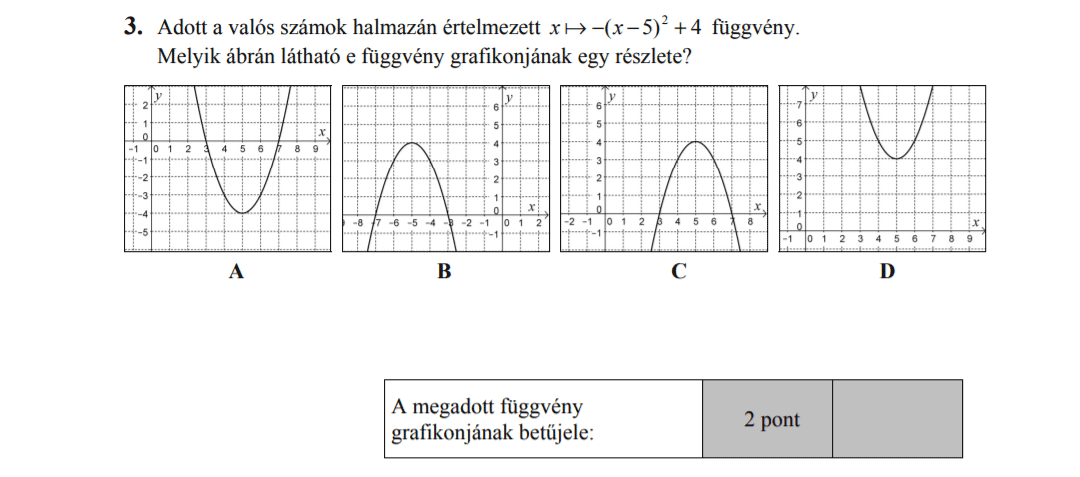






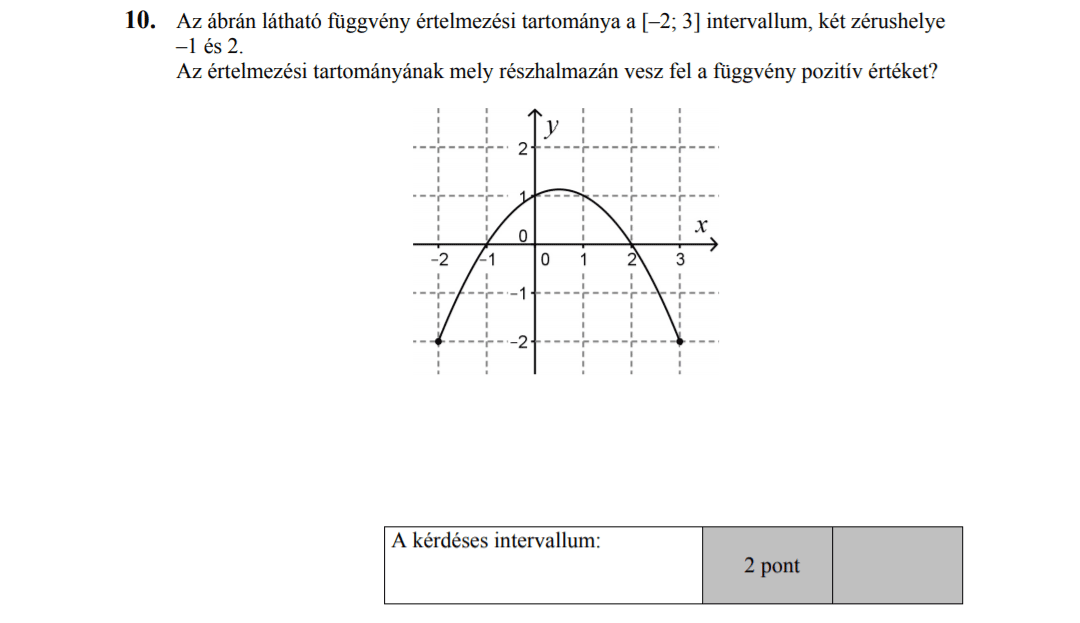


MÁSODIK RÉSZ


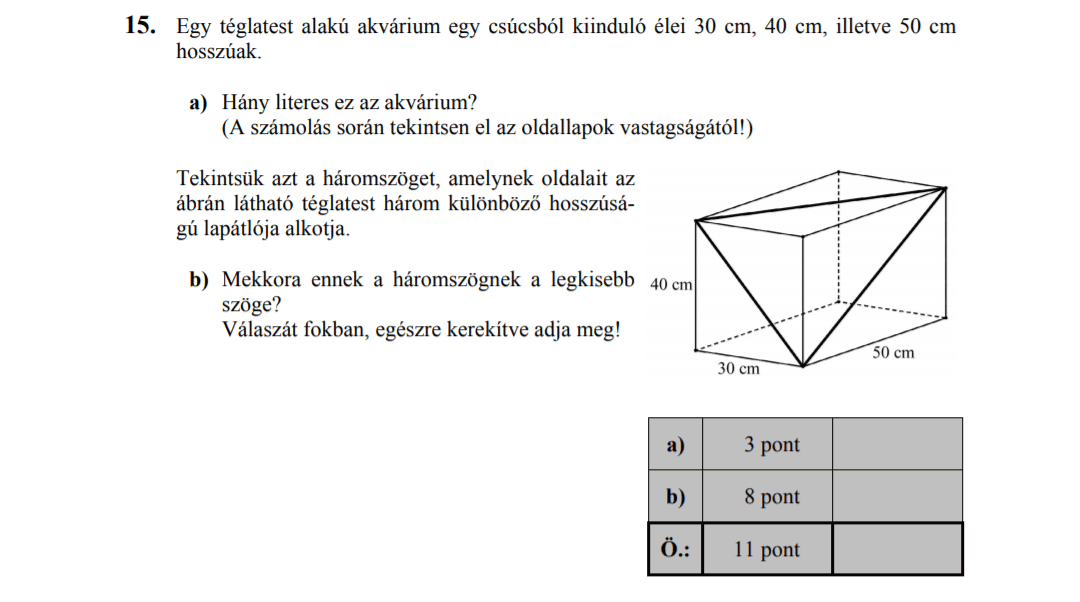

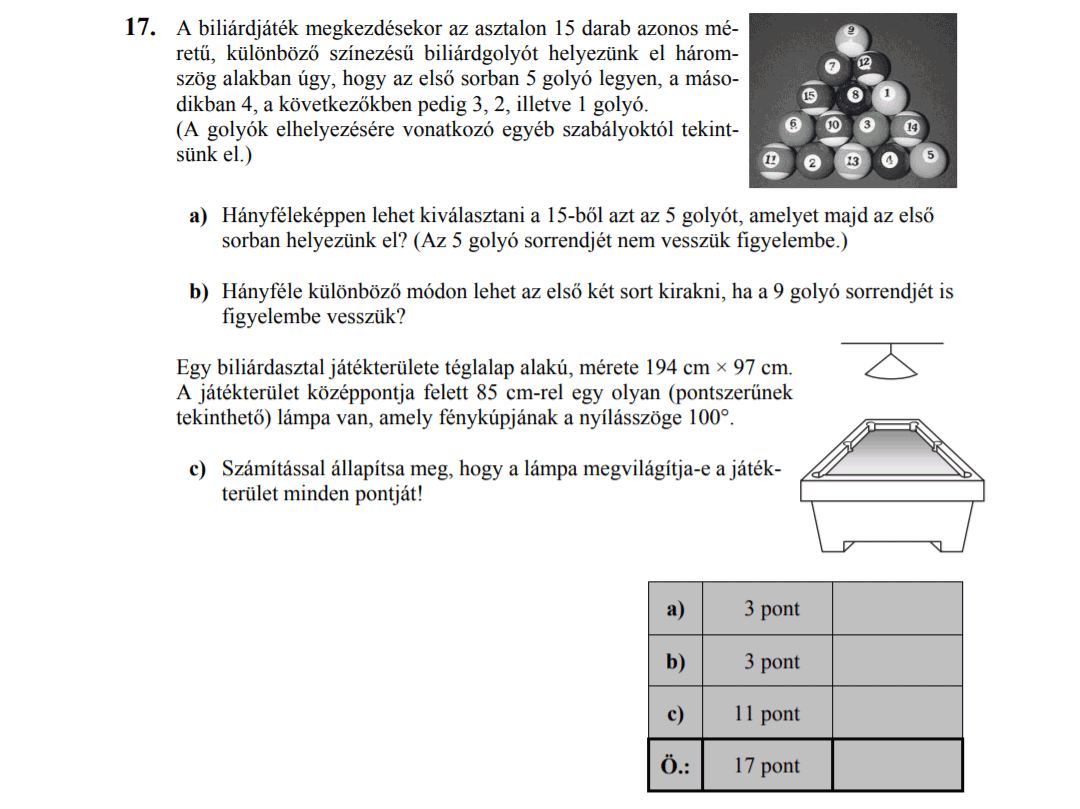

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


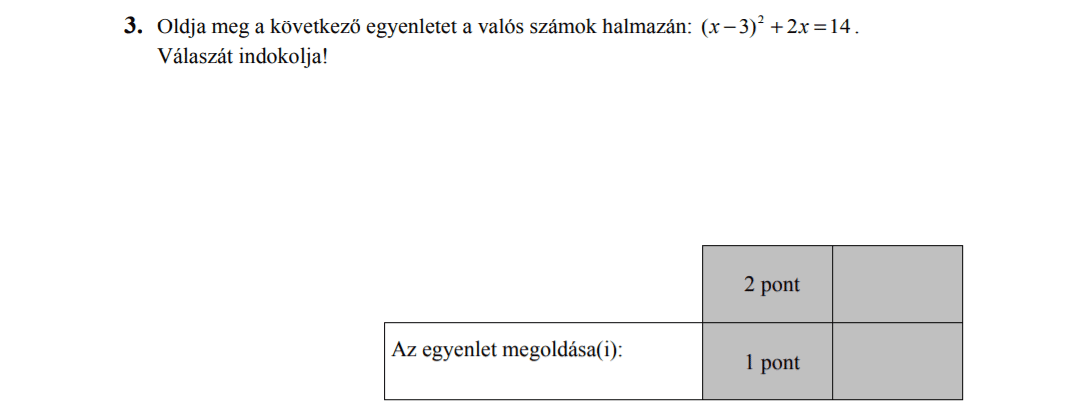


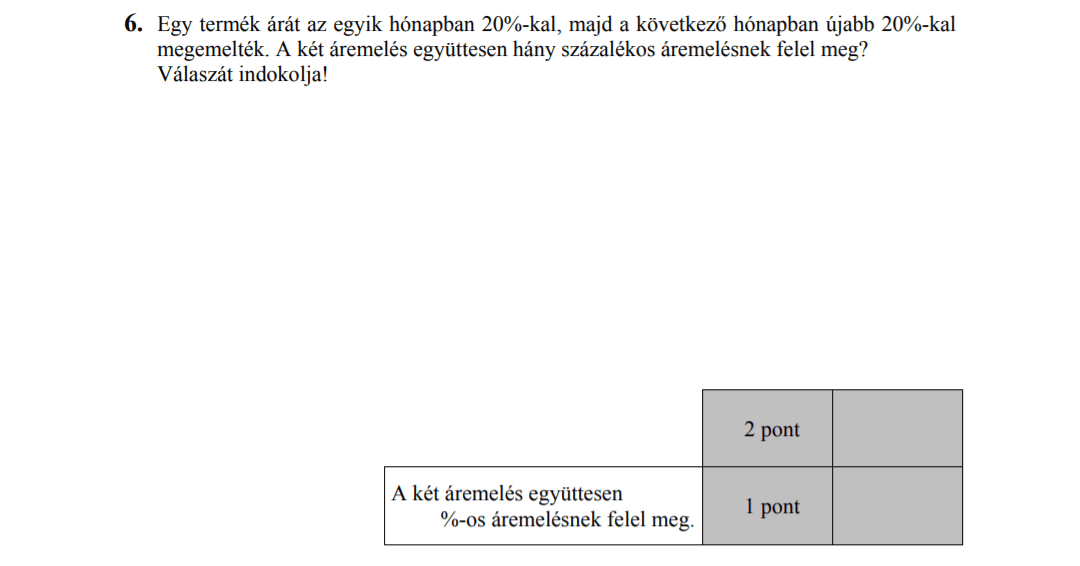
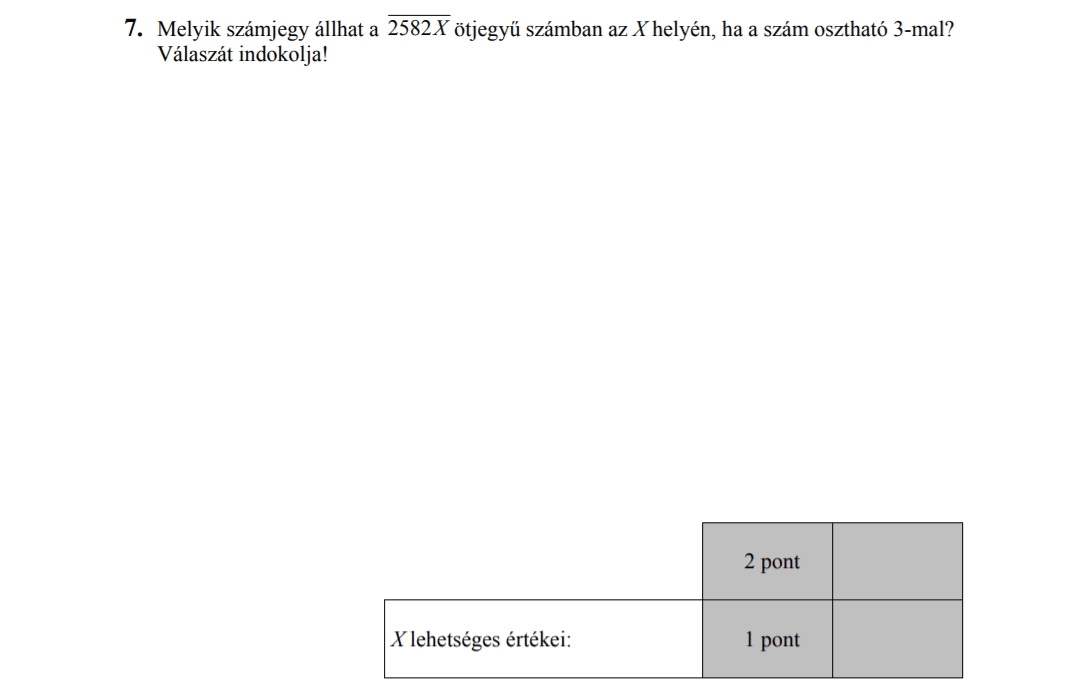
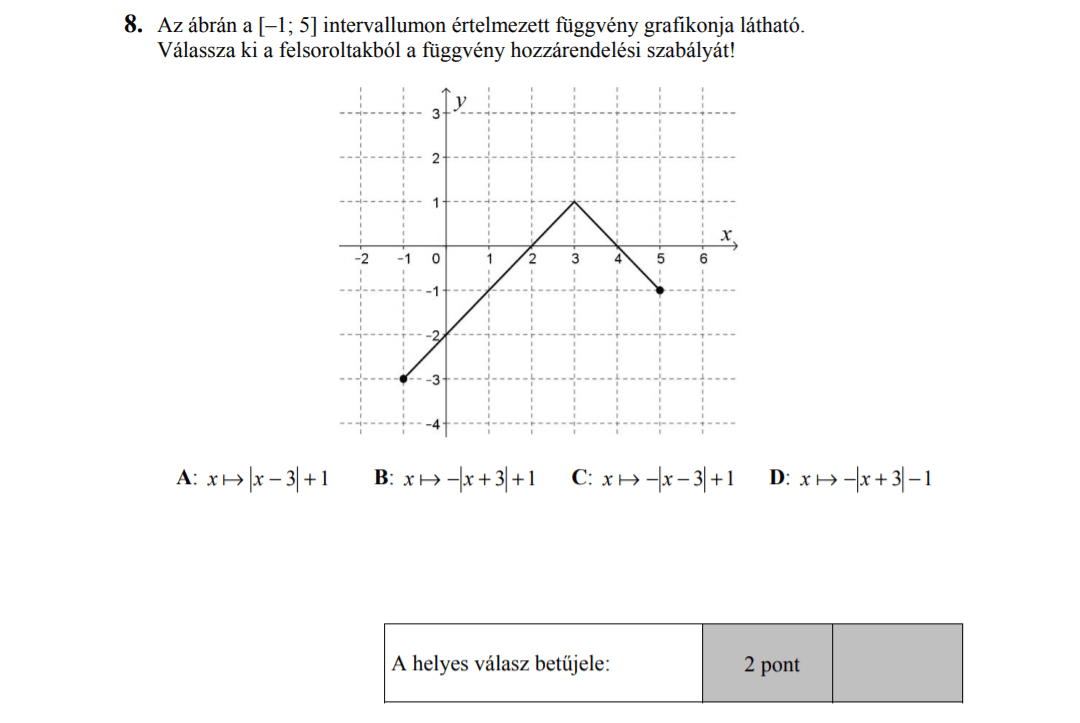


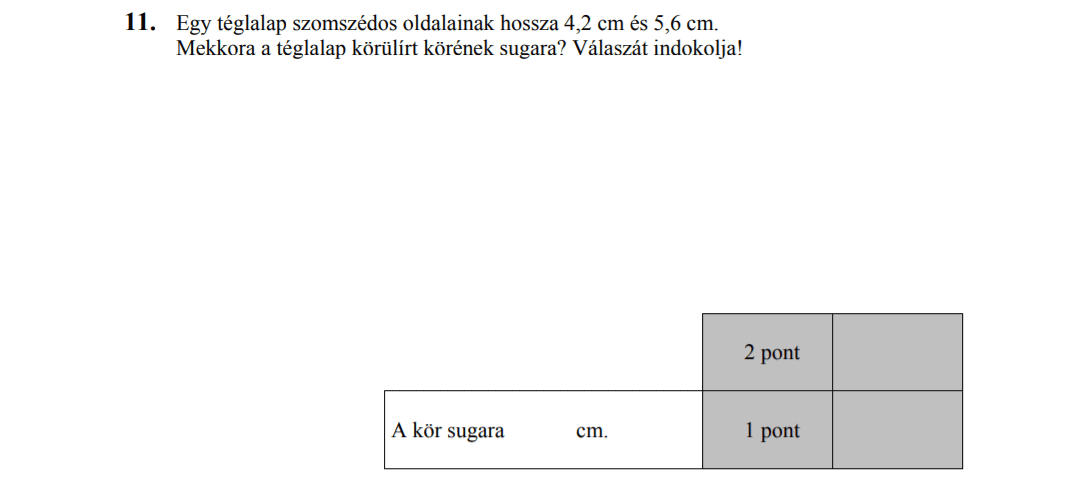

MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


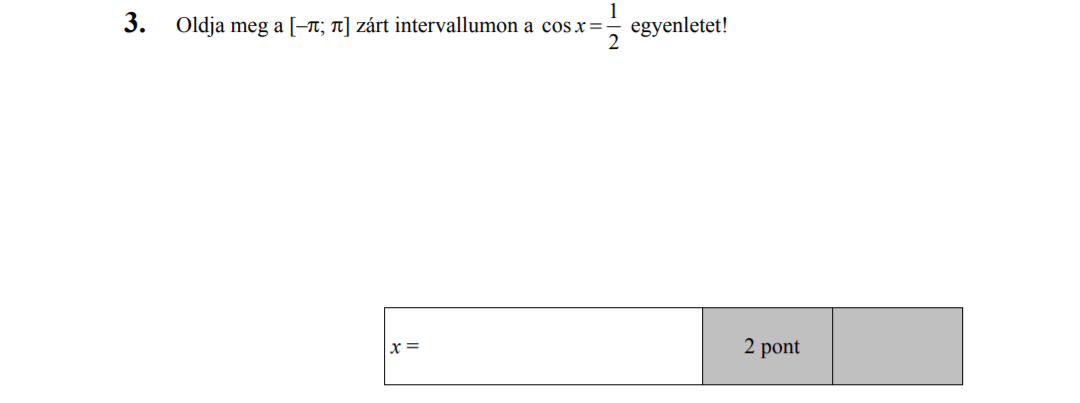


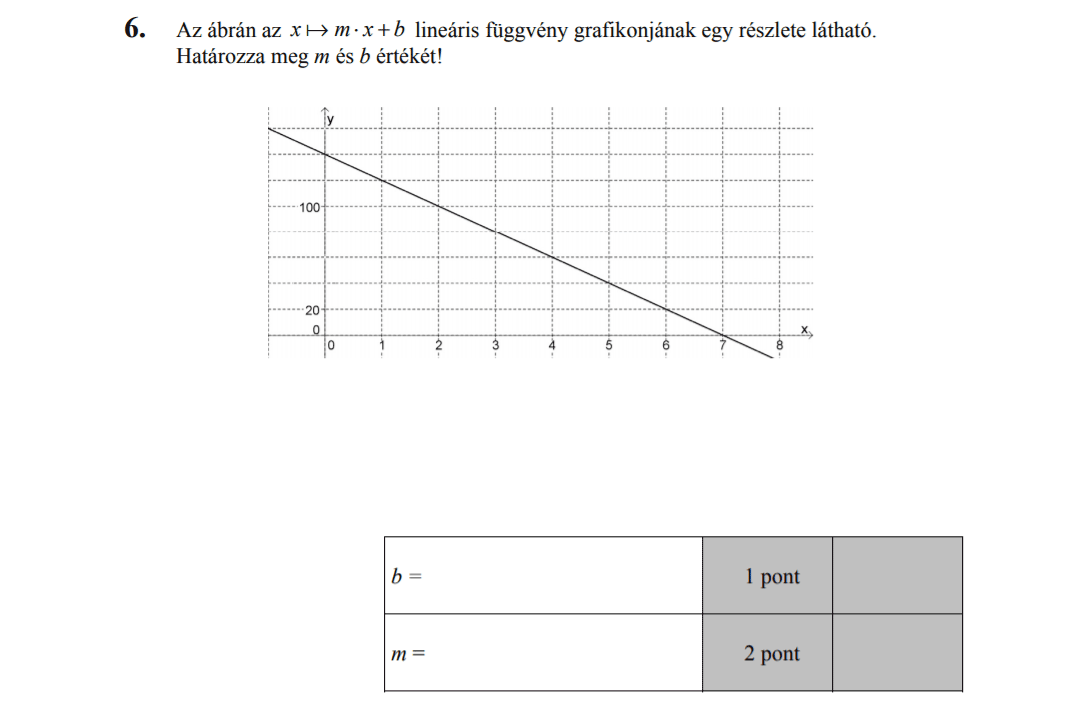



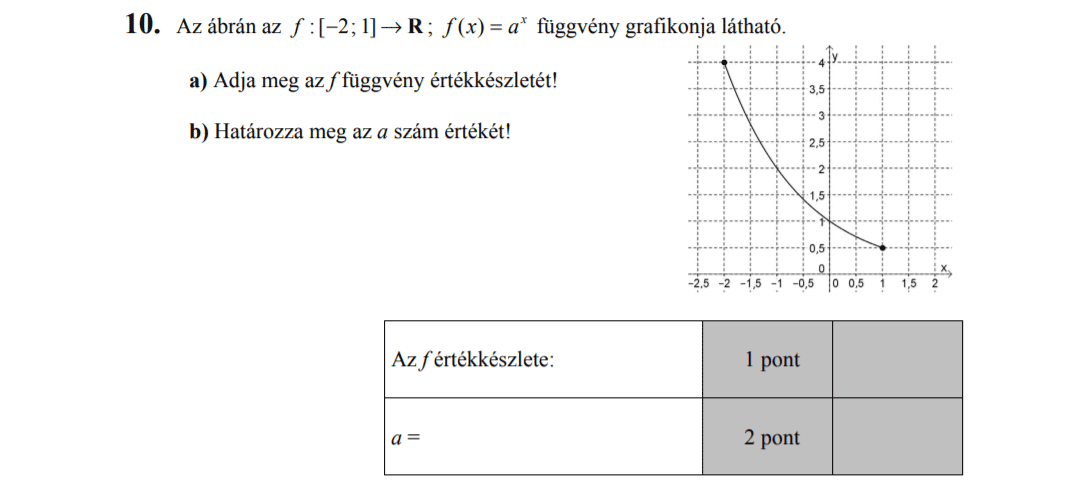

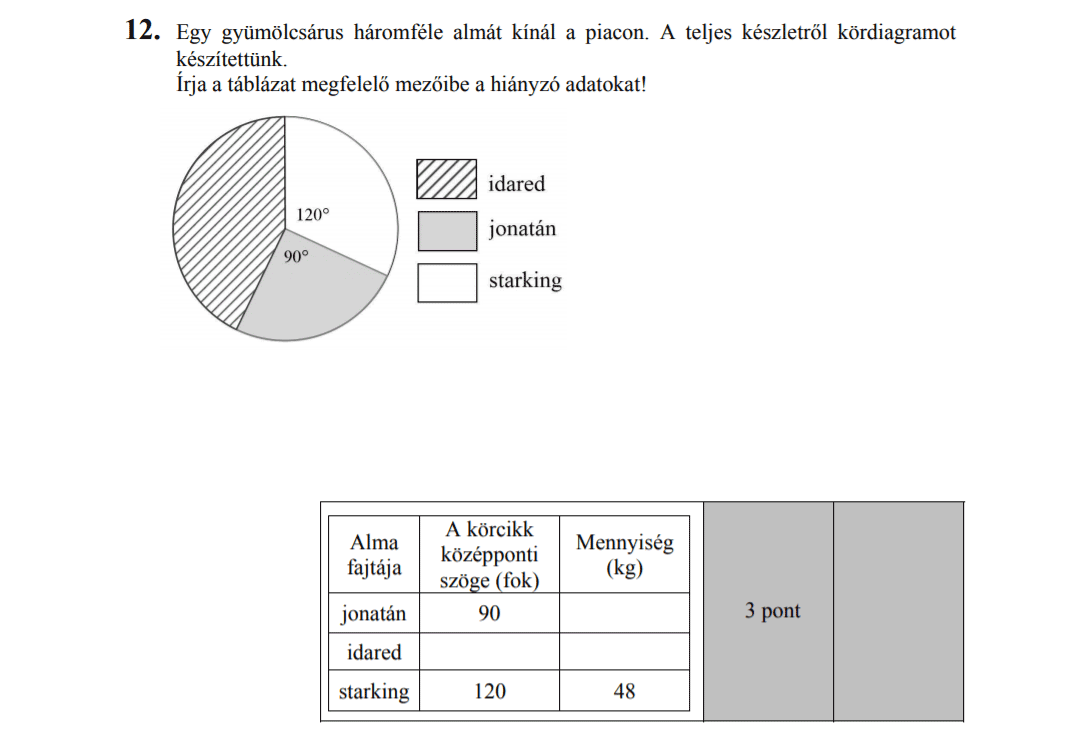
MÁSODIK RÉSZ

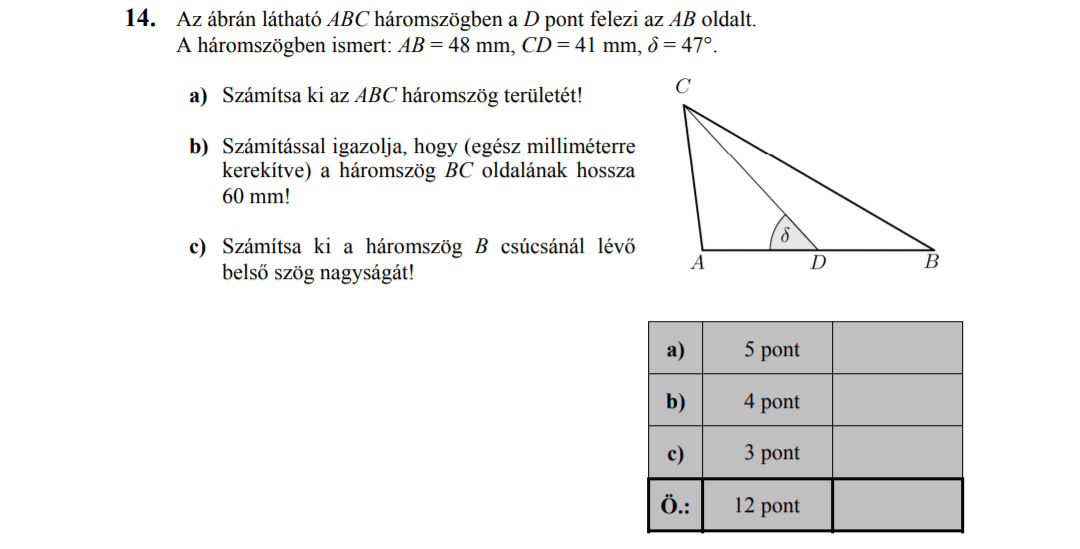




- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


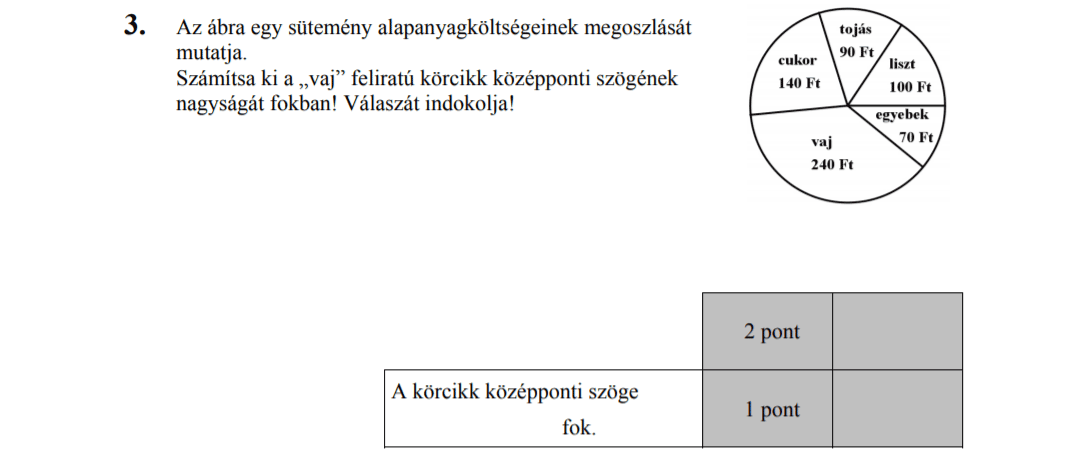
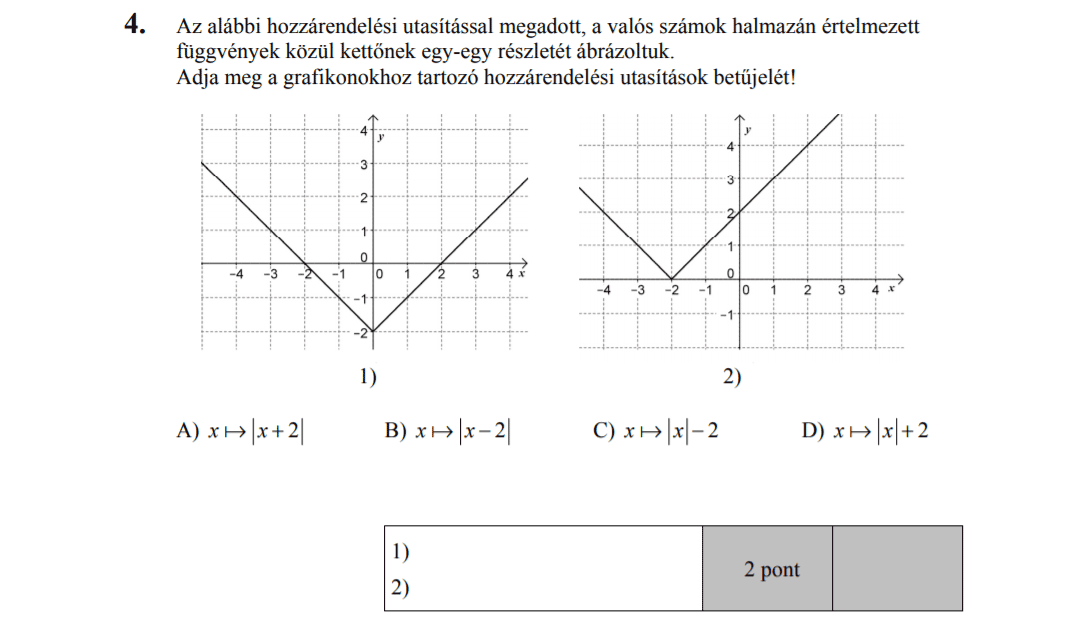
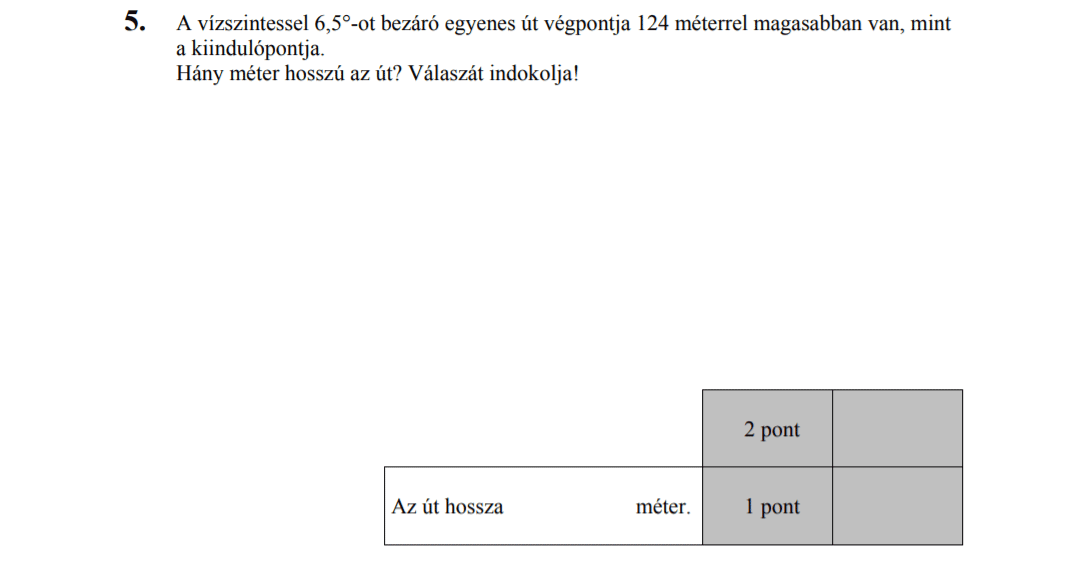

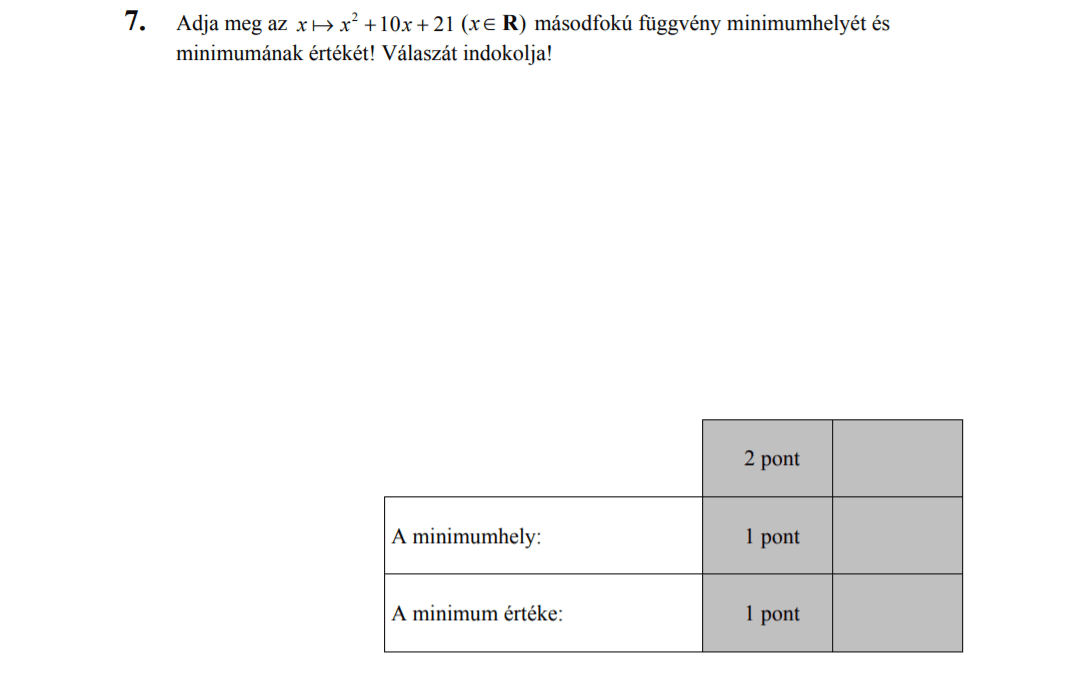



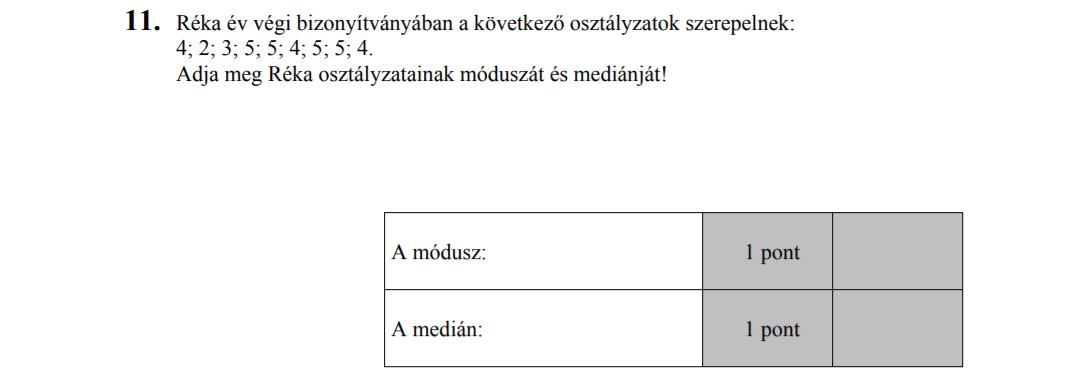

MÁSODIK RÉSZ





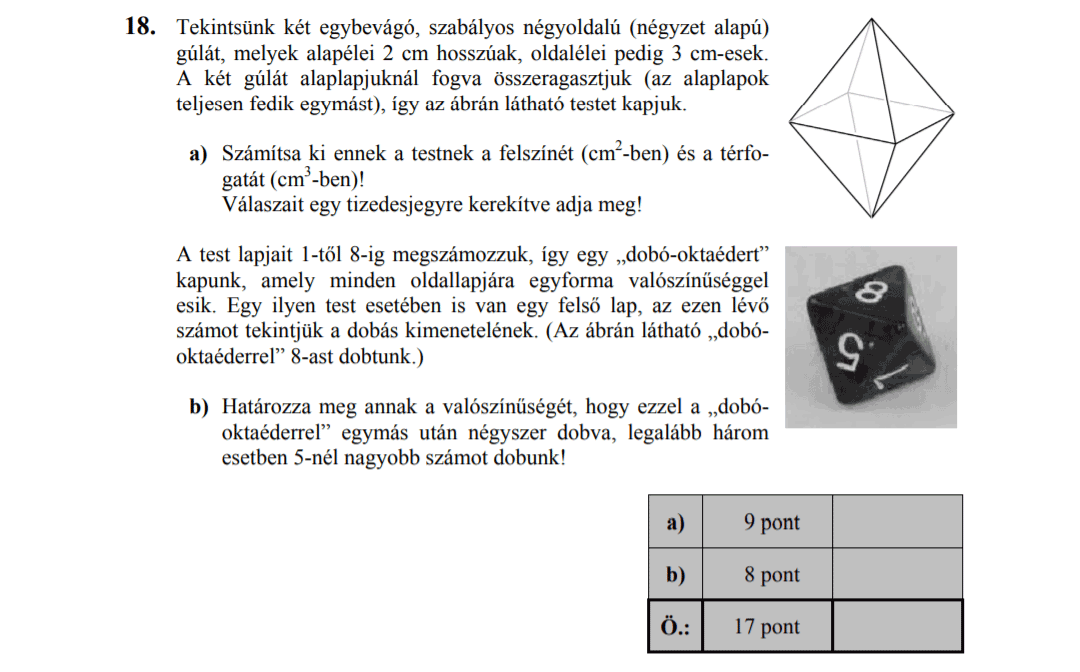
- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



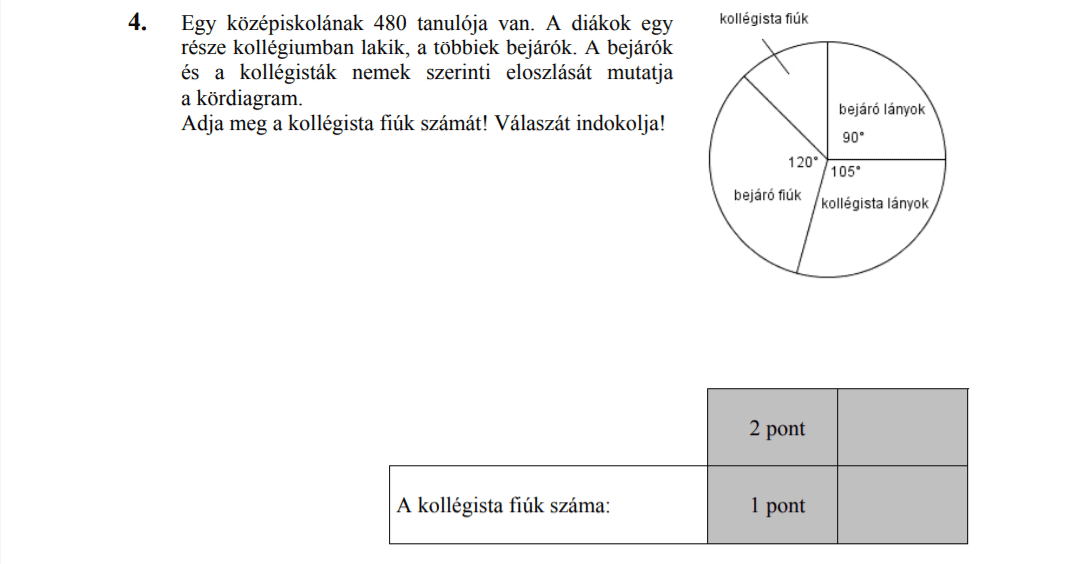



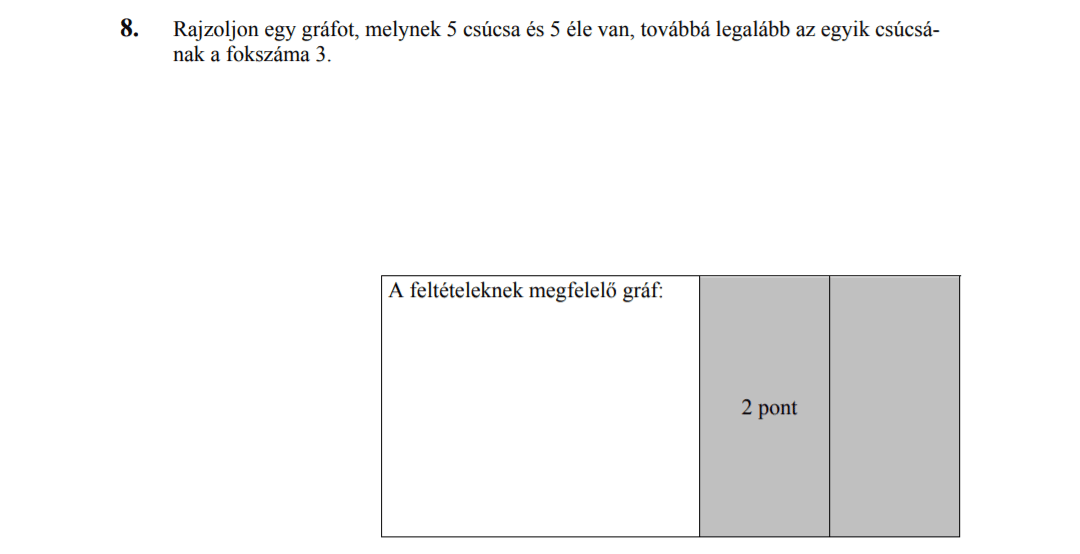
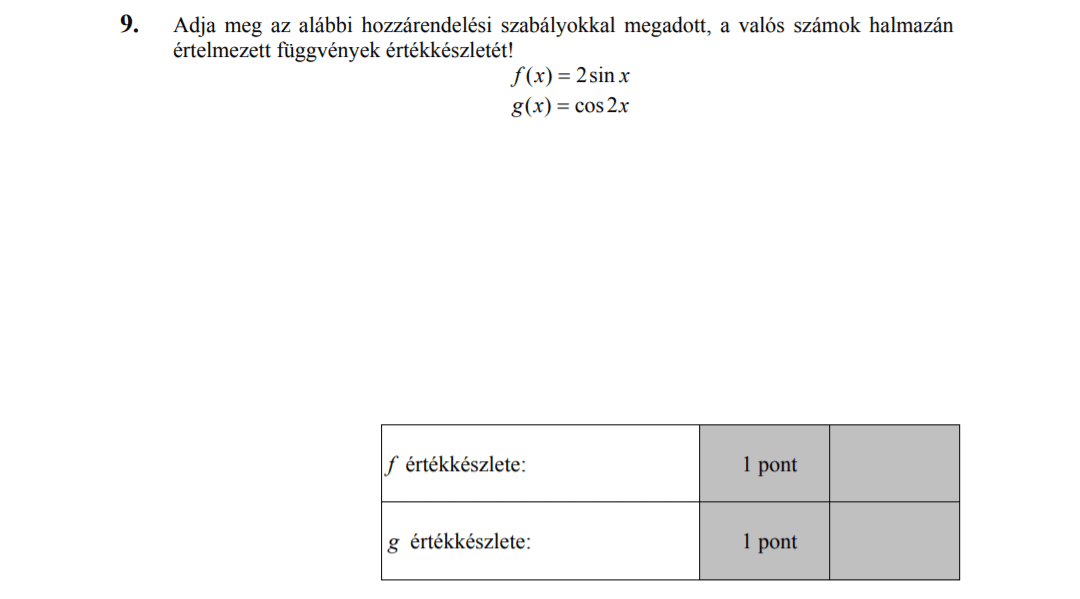

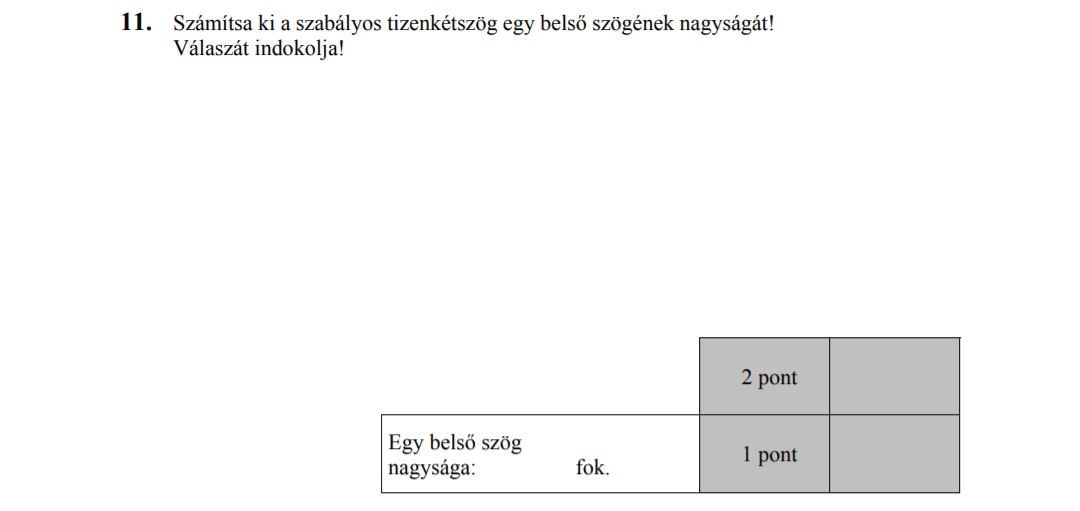

MÁSODIK RÉSZ






Ennek a témakörnek a képletei
Letöltöm az egész kurzus összes képletét:
LetöltömLetöltöm ennek a témakörnek a képleteit:
LetöltömVálogass kedvedre a témakör képletei között:
Behelyettesítő módszer
A behelyettesítő módszer az egyenletrendszerek megoldásának egyik technikája.
Lényege, hogy kiválasztjuk az egyik egyenletet, ahonnét az egyik változót kifejezzük a másikkal. Ilyenkor célszerű a számunkra szimpatikusabb, egyszerűbb egyenletet választani.
Ezt követően az így kapott kifejezést behelyettesítjük a másik, fel nem használt egyenletbe, így egy egyismeretlenes egyenletet kapunk, amit már meg tudunk oldani.
Egyenlő együtthatók módszere
Az egyenlő együtthatók módszere egy megoldási technika az egyenletrendszerekhez.
Lényege, hogy ha a két egyenletben vagy az $x$ vagy az $y$ együtthatói megegyeznek, akkor a két egyenletet egymásból kivonva azok kiesnek, és egy egyismeretlenes egyenletet kapunk, amit már meg tudunk oldani.
Ha az együtthatók egymás ellentettjei lennének, akkor pedig össze kell adni a két egyenletet.
A módszer akkor is működik, ha nem volnának egyenlő együtthatók, ilyenkor bátran szorozhatjuk az egyenleteket addig, amíg nem lesznek egyenlő együtthatók.
Ennek a témakörnek a feladatai
Letöltöm az egész kurzus összes feladatát:
LetöltömLetöltöm ennek a témakörnek a feladatait:
LetöltömVálogass kedvedre a témakör feladatai között:
Oldd meg az alábbi egyenletrendszereket.
a)
\( \frac{3}{x+y} - \frac{2}{x-y}=3 \)
\( \frac{12}{x+y} - \frac{5}{x-y}=9 \)
b)
\( \frac{4x}{x+y}+\frac{6}{x-y}=6 \)
\( \frac{12x}{x+y} - \frac{4}{x-y}=7 \)
Oldd meg az alábbi egyenletrendszert.
\( 5x-3y=131 \)
\( -4x-7y=-48 \)
