- ÚJ! Kvartilisek és dobozdiagram = sodrófadiagram = box plot
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
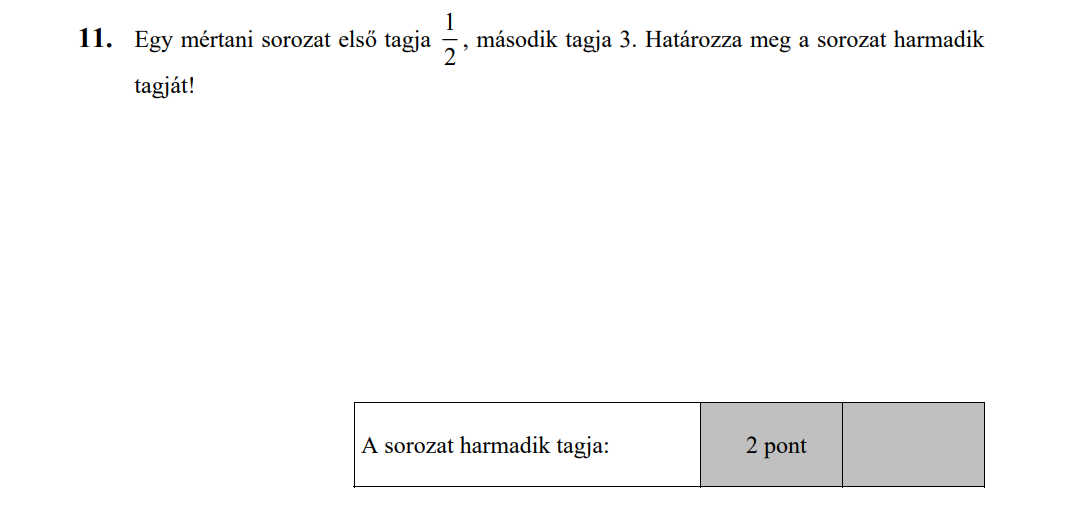
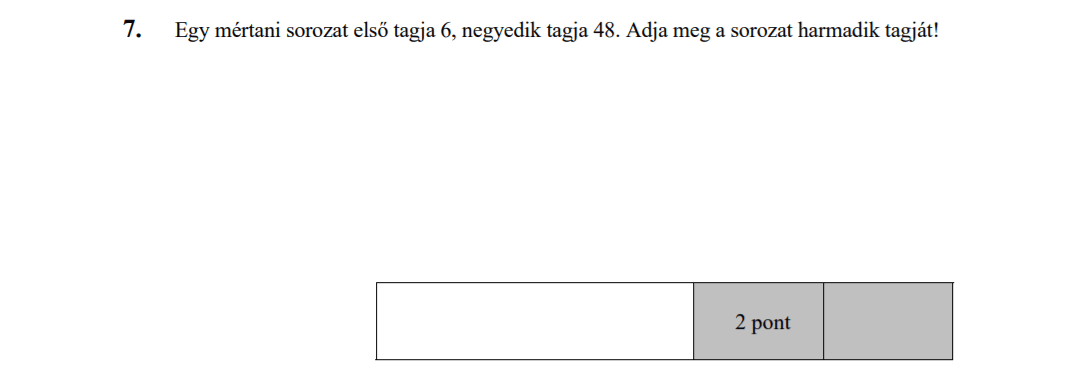
- Számtani és mértani sorozatok (15,3 pont)
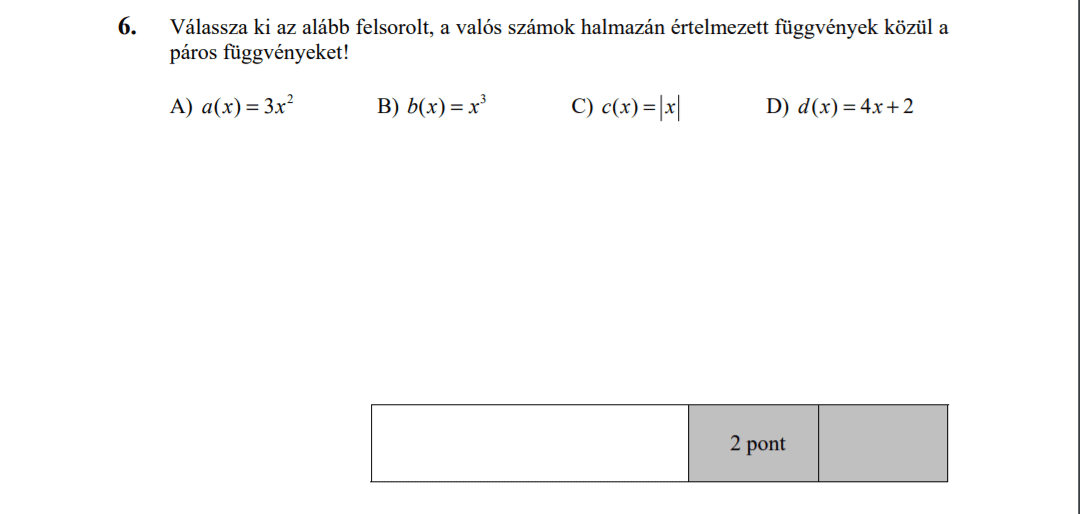
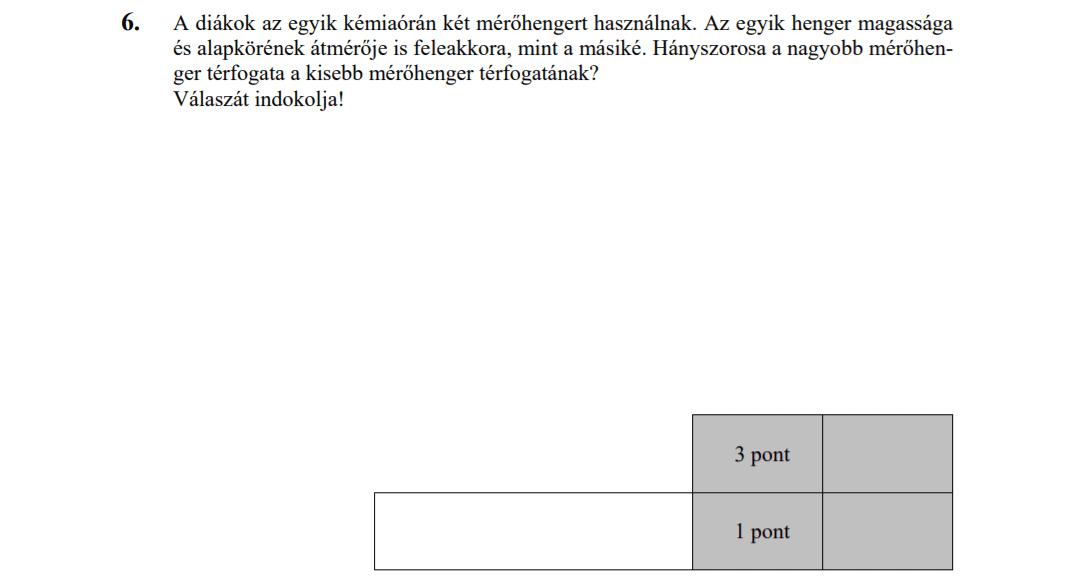
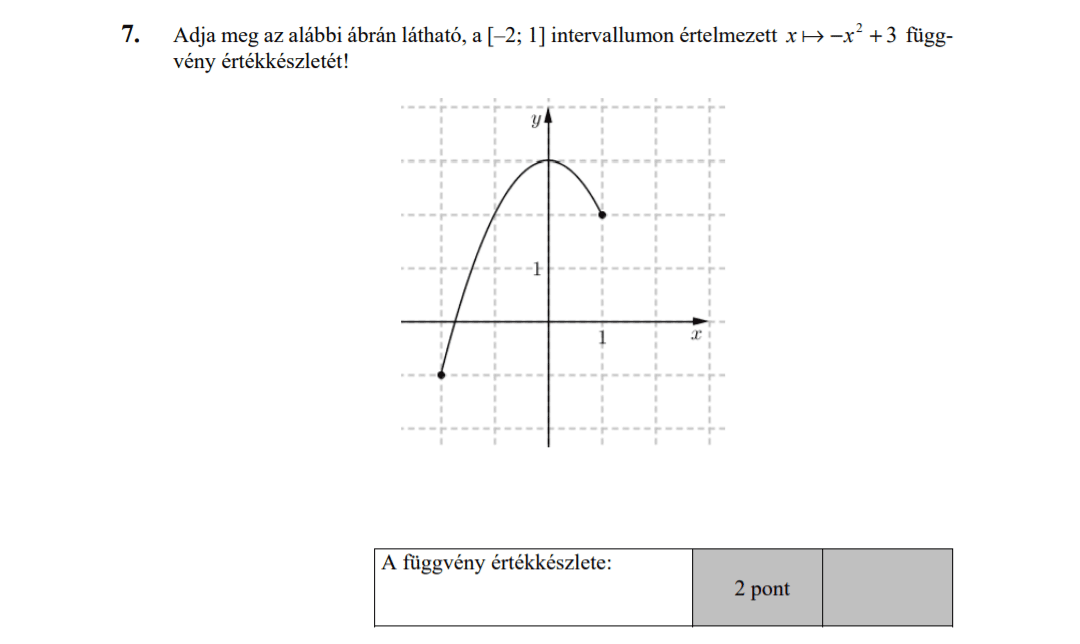
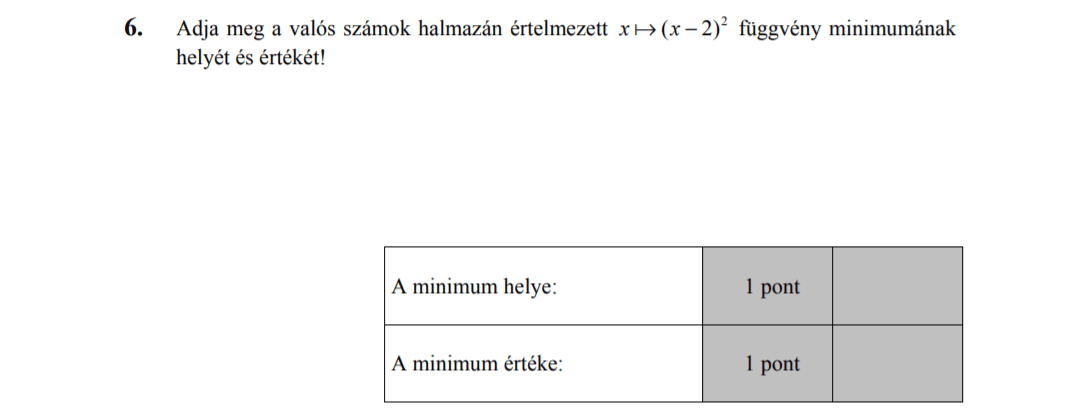
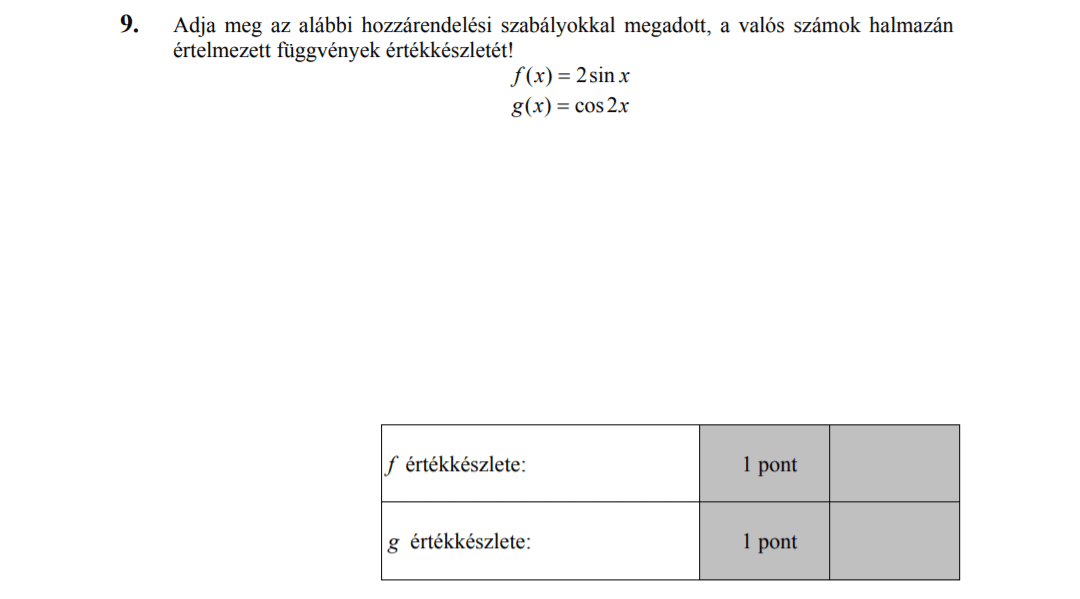
- Függvényekkel kapcsolatos feladatok (10,3 pont)
- Térgeometria (10,3 pont)
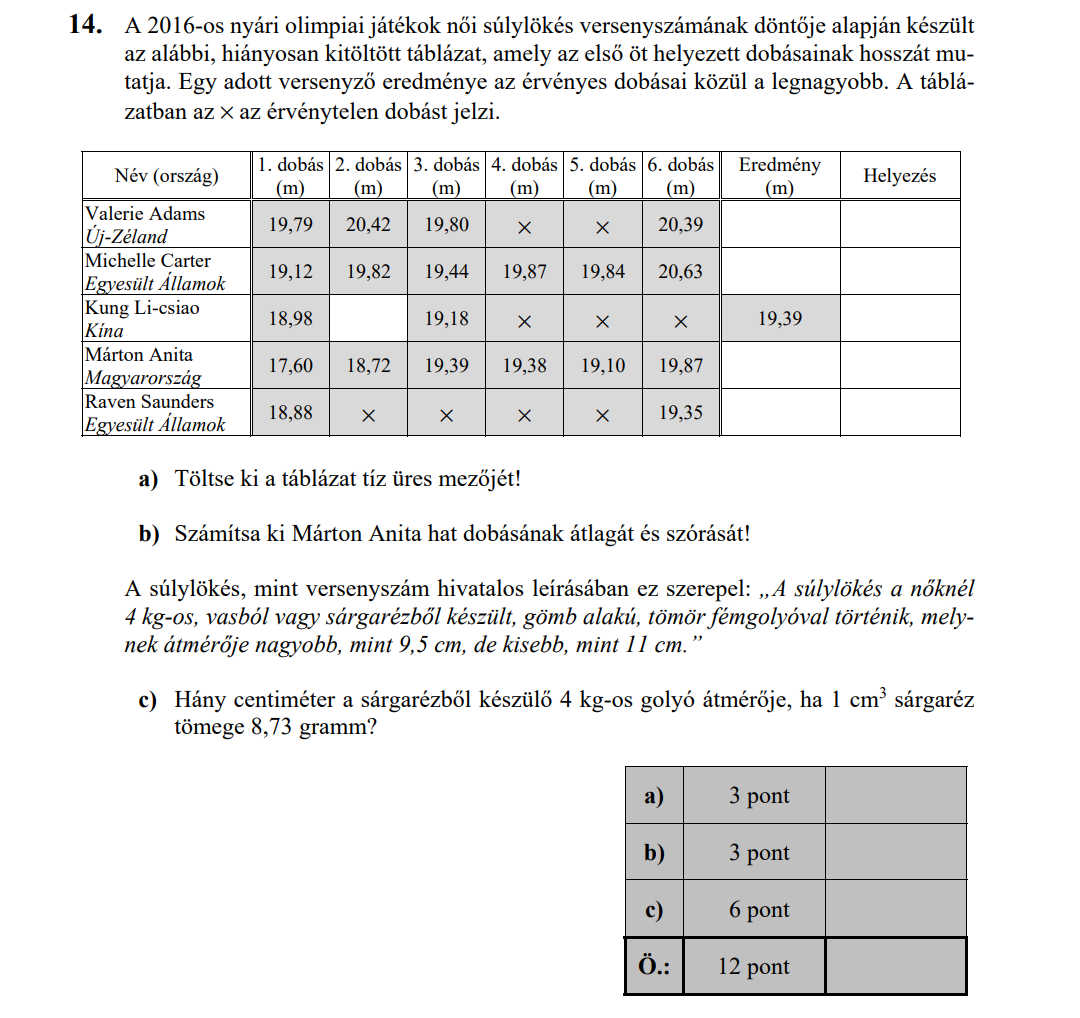
- Statisztika (10,2 pont)
- Valószínűségszámítás (10,2 pont)
- Trigonometria, szinusztétel, koszinusztétel (8,8 pont)
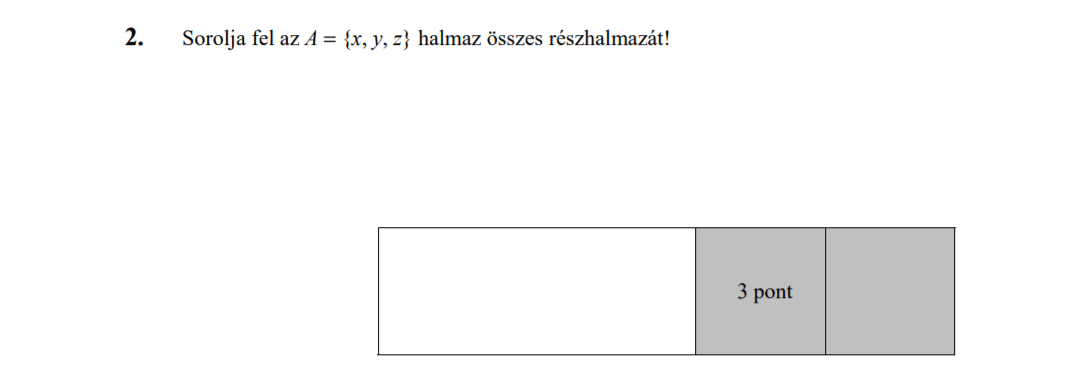
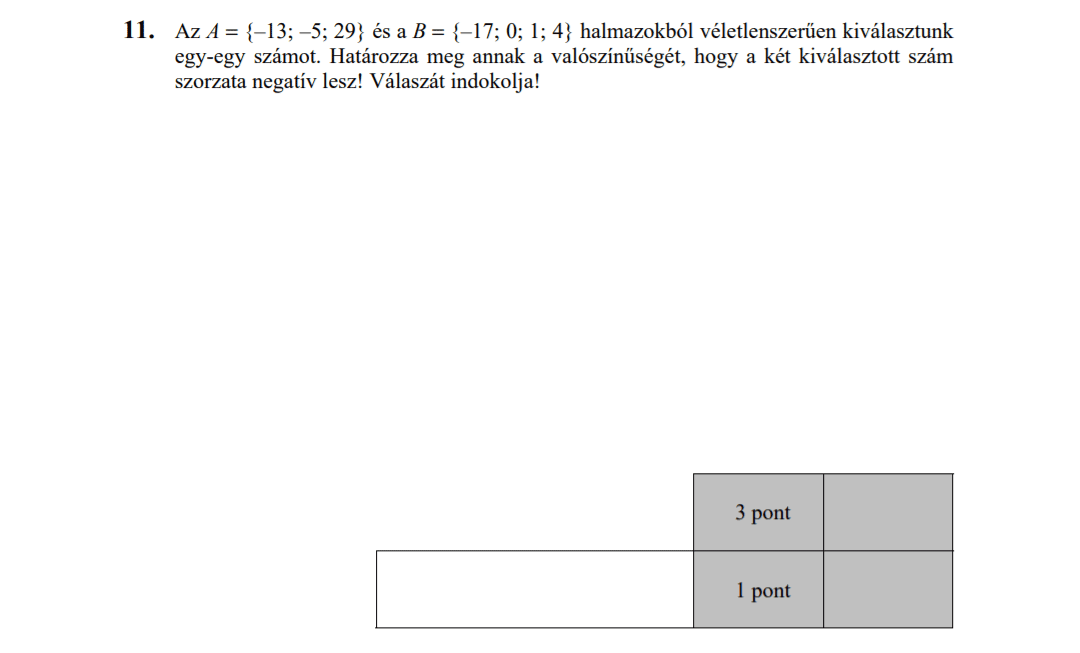
- Halmazok (7 pont)
- Kombinatorika (6,9 pont)
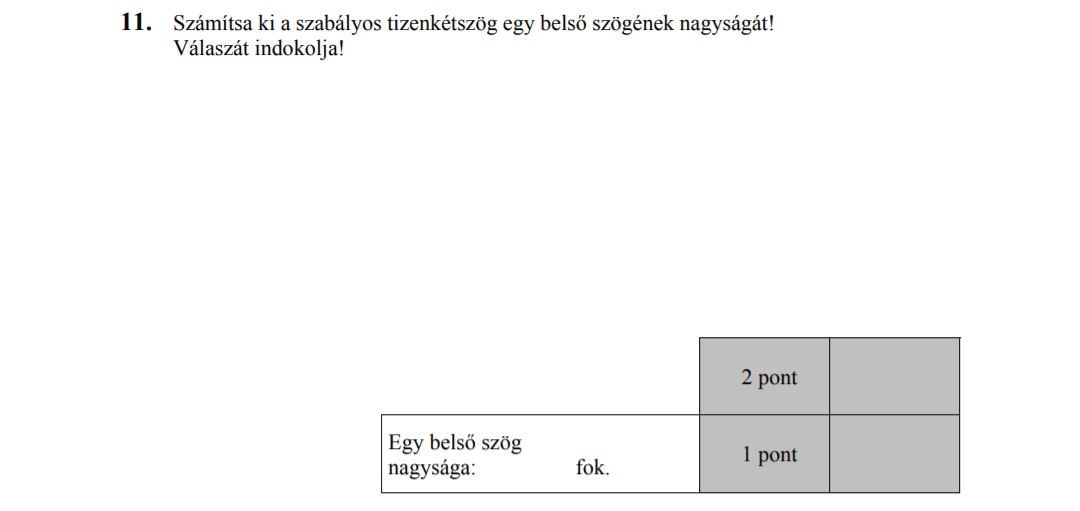
- Síkgeometria (6,5 pont)
- Koordinátageometria (6,2 pont)
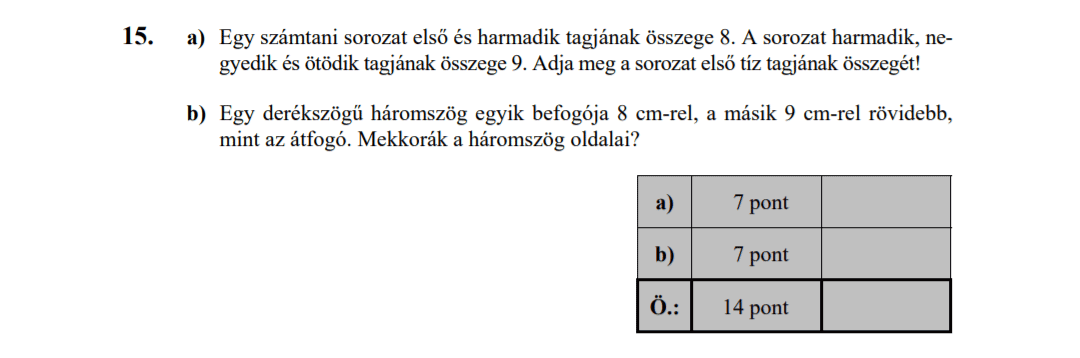
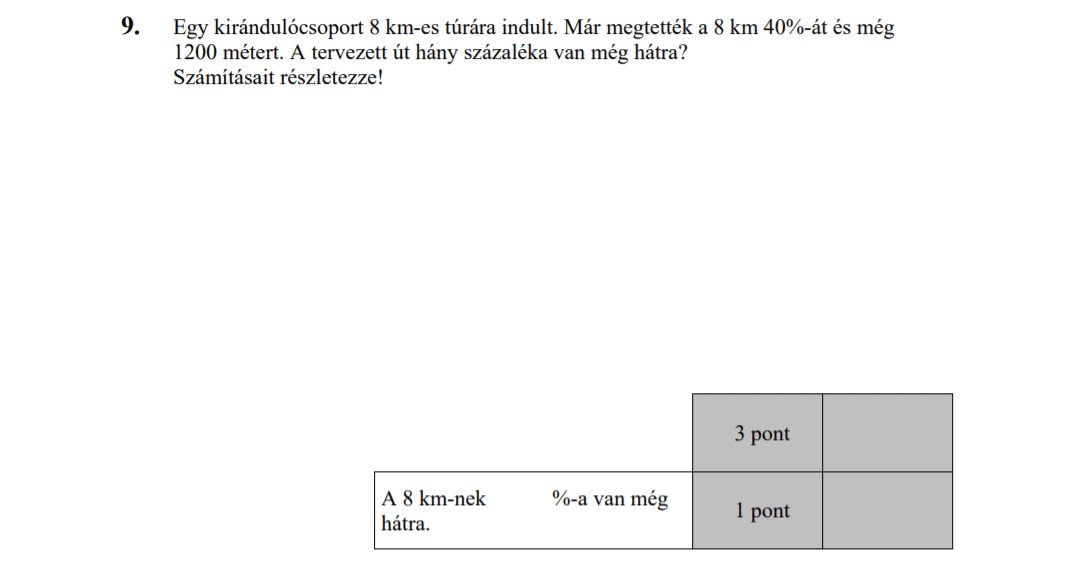
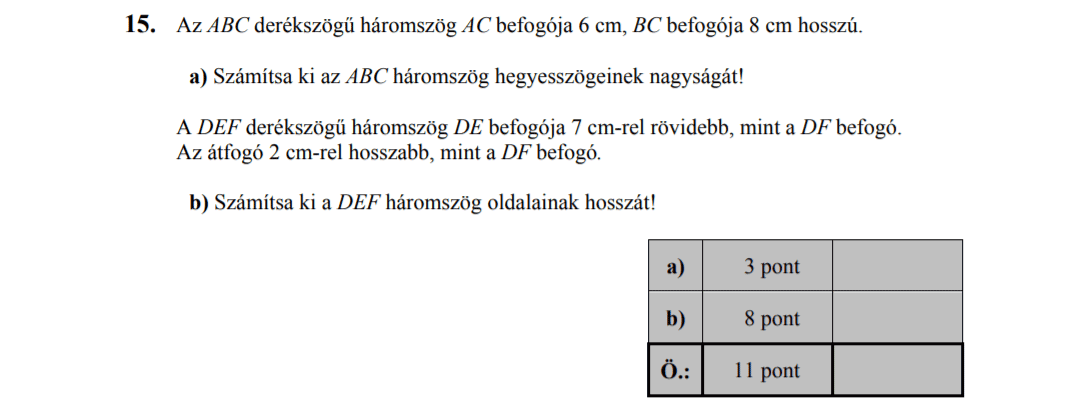
- Szöveges feladatok (6 pont)
- Egyenes és fordított arányosság, arányos osztás, szöveges feladatok (3,8 pont)
- Százalékszámítás (2,9 pont)
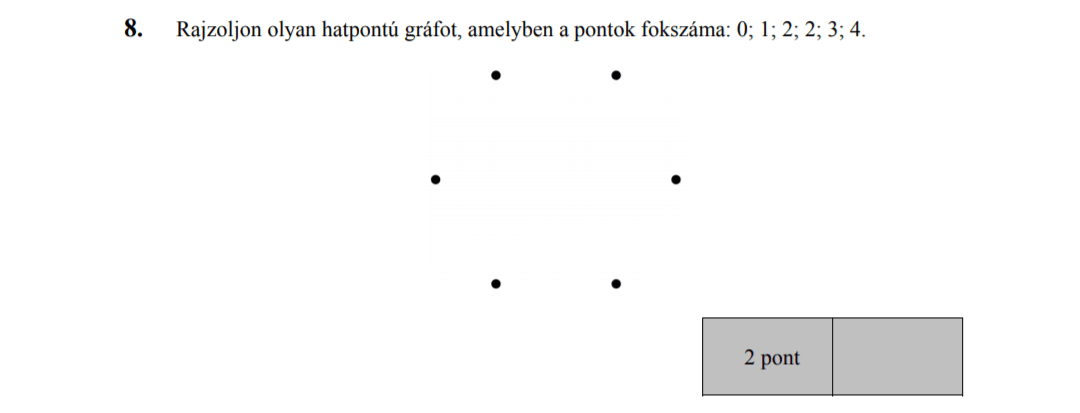
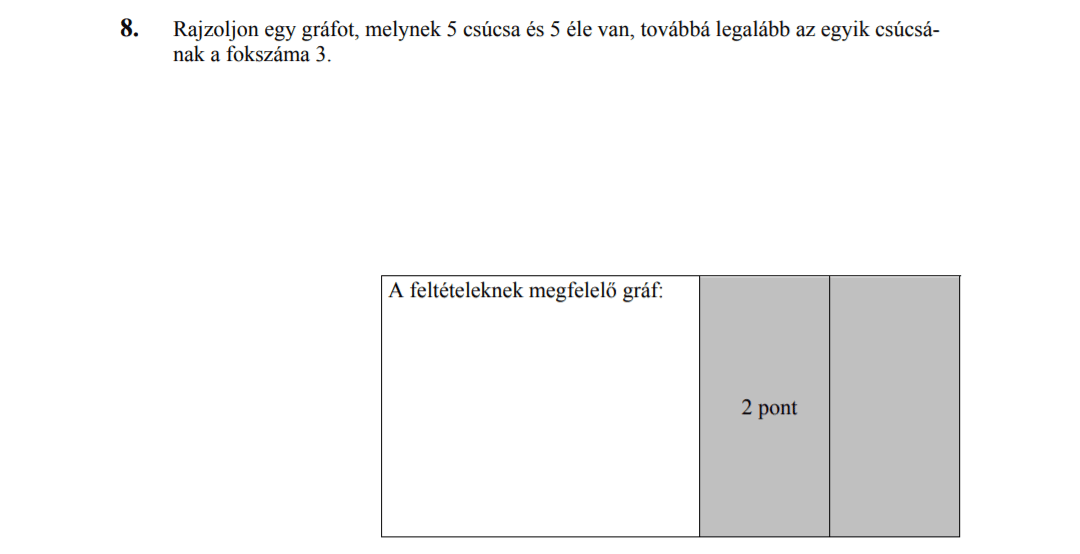
- Gráfok (2,7 pont)
- Másodfokú egyenletek (2,5 pont)
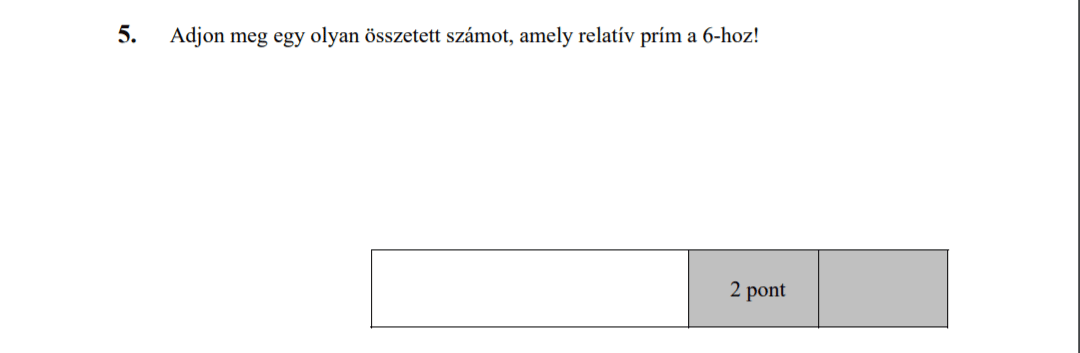
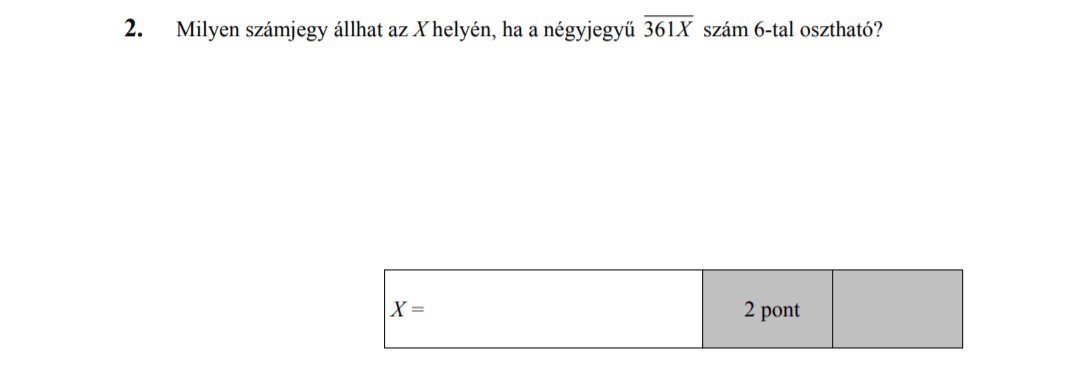
- Számelmélet (2,5 pont)
- Elsőfokú egyenletek (1,3 pont)
- Hatványozás, exponenciális egyenletek (1 pont)
- Egyenlőtlenségek (0,4 pont)
- Algebra, nevezetes azonosságok
- Bizonyítási módszerek, matematikai logika
- Egyenletrendszerek
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
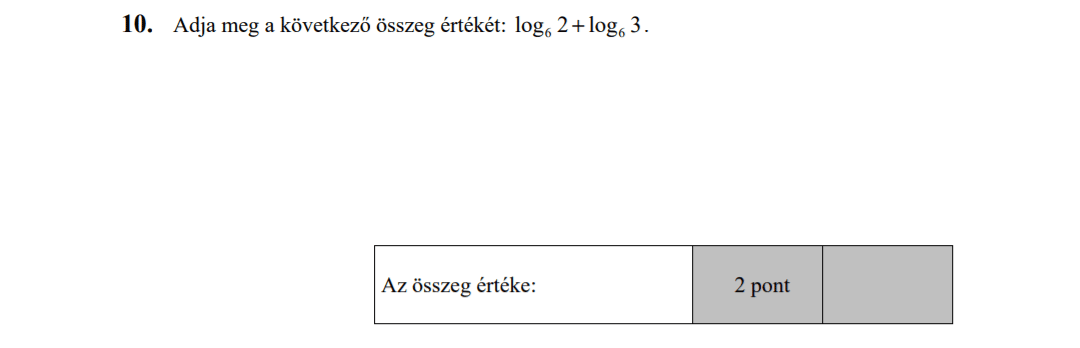
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Egybevágósági transzformációk
Síkgeometria (6,5 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ









MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
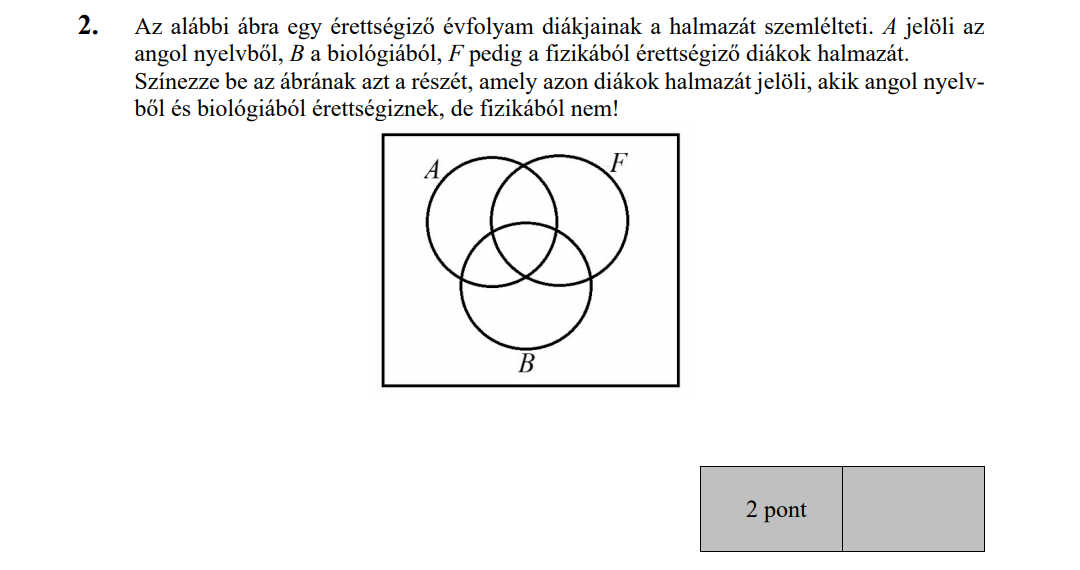

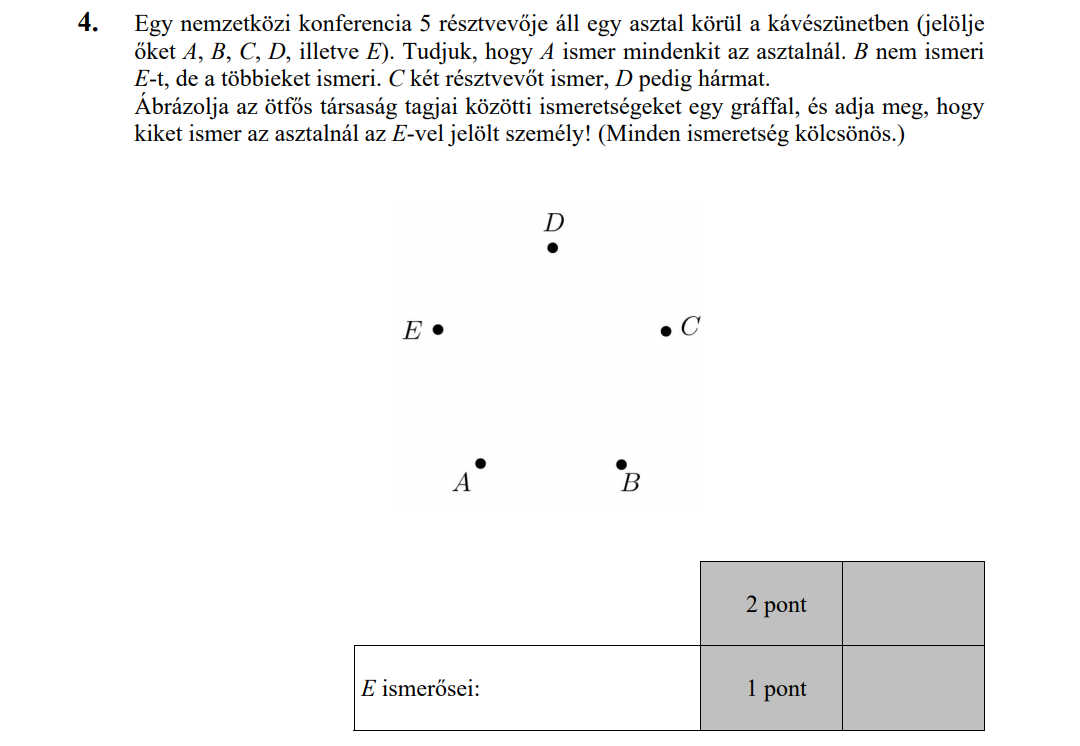

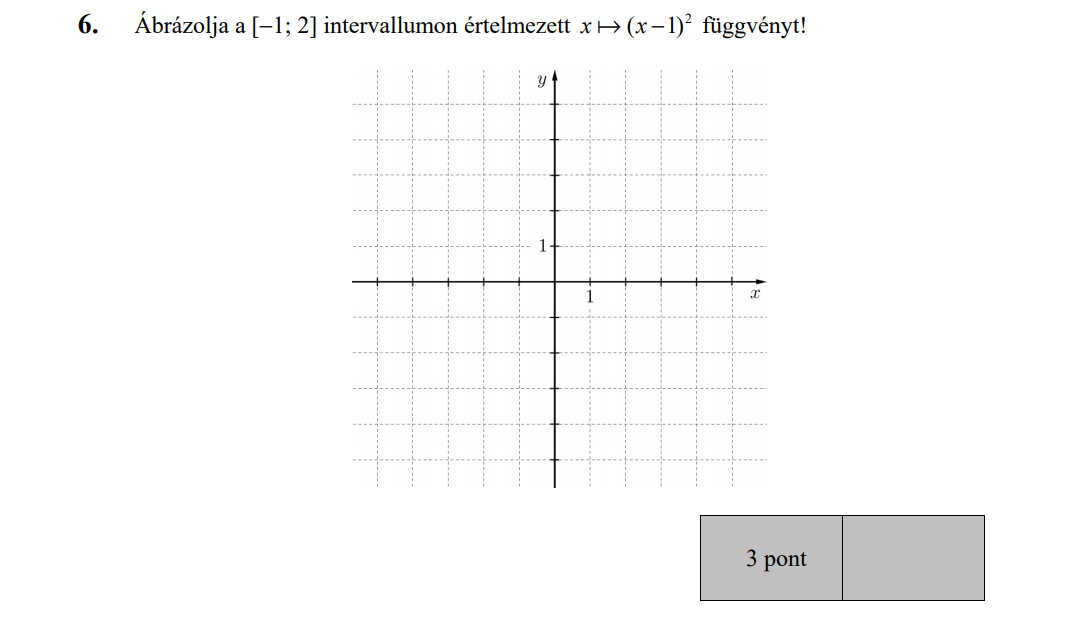



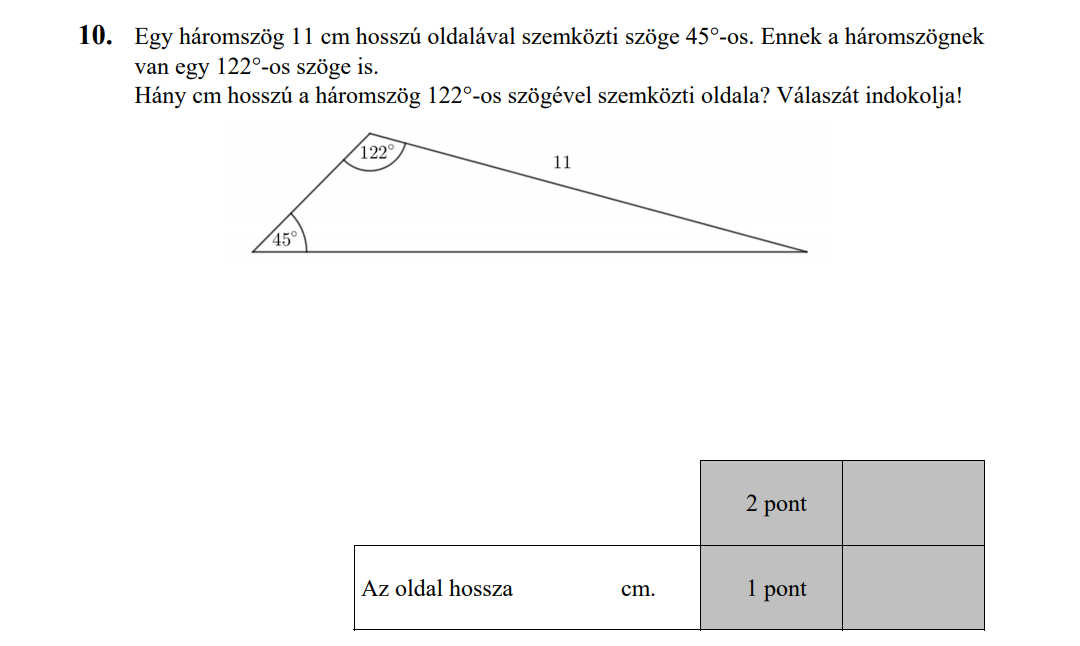

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ





- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




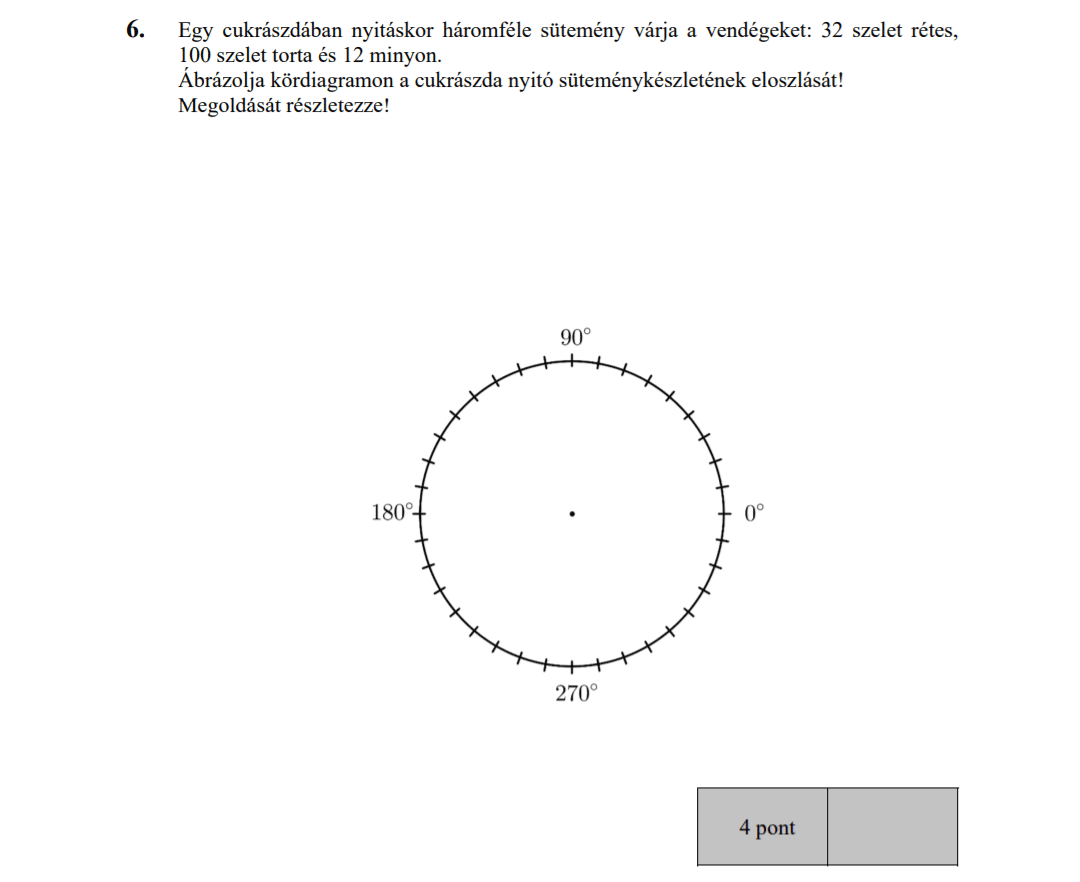






MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








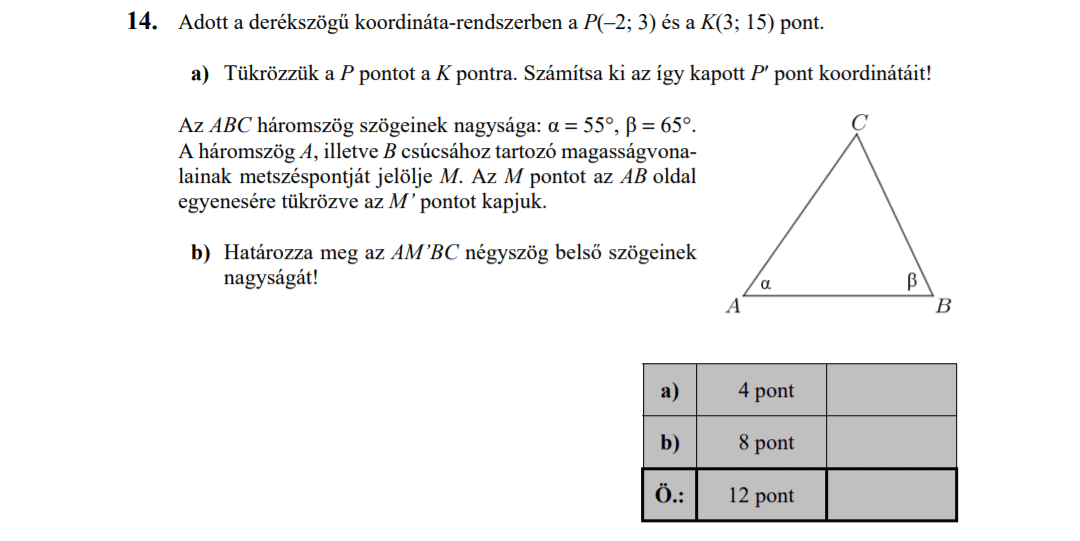
MÁSODIK RÉSZ

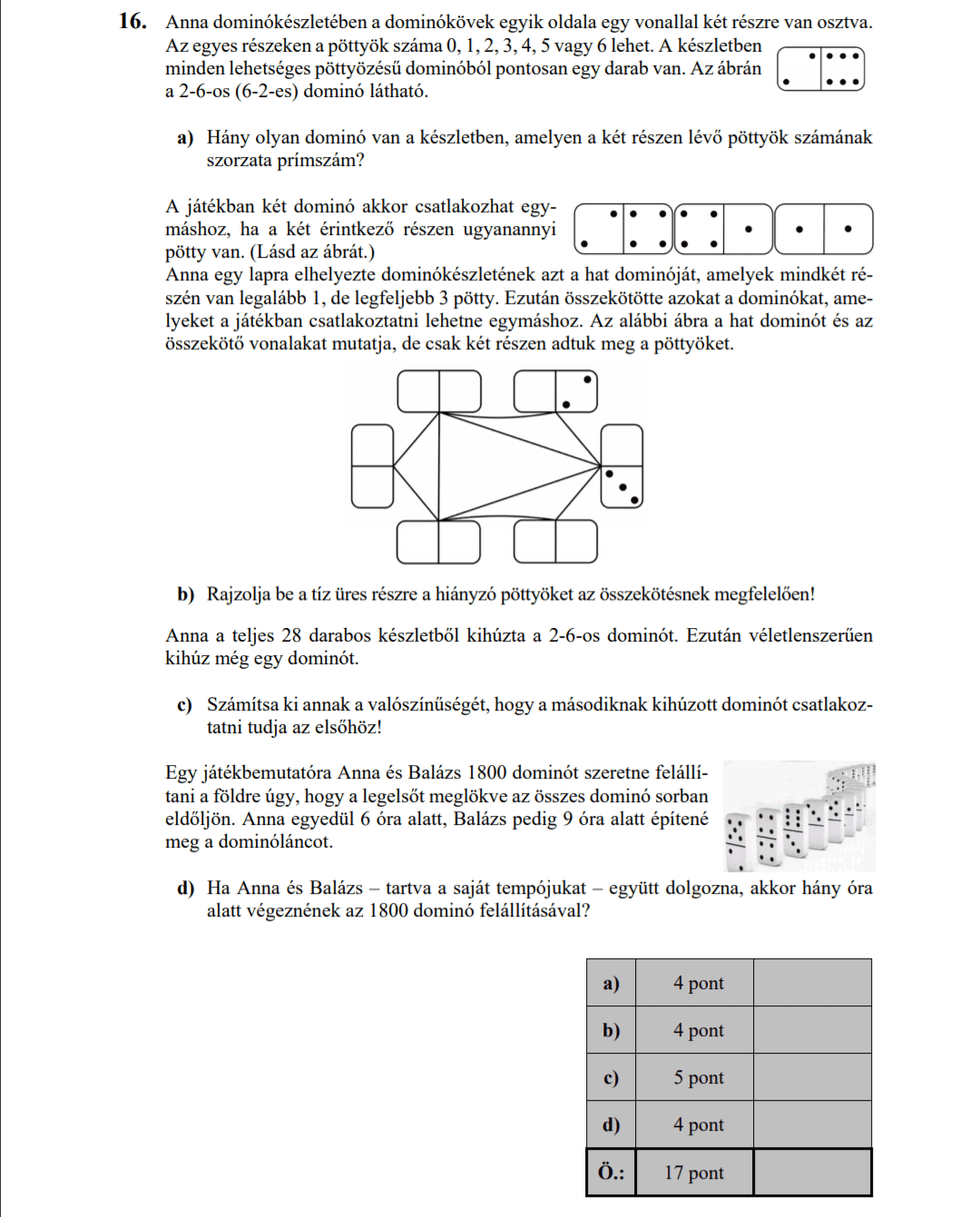


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ




- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


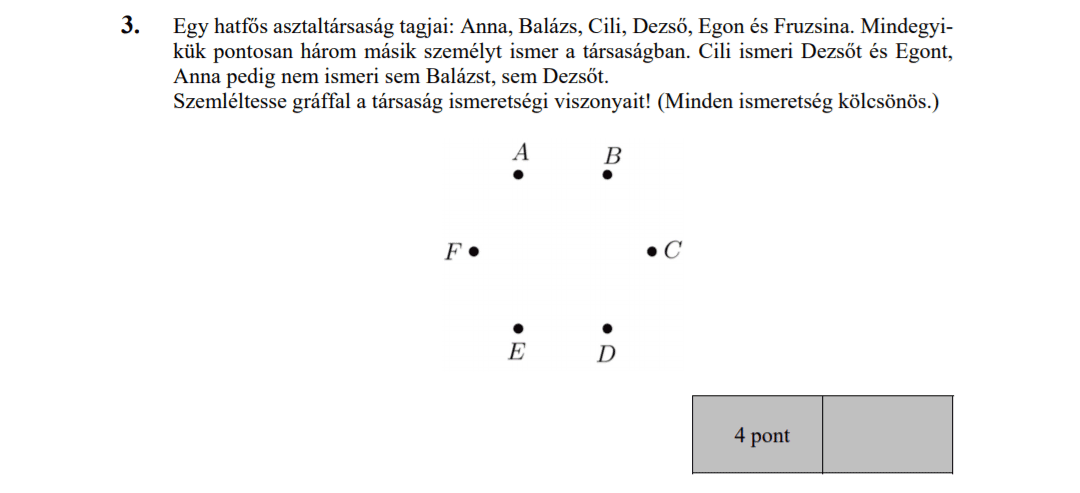





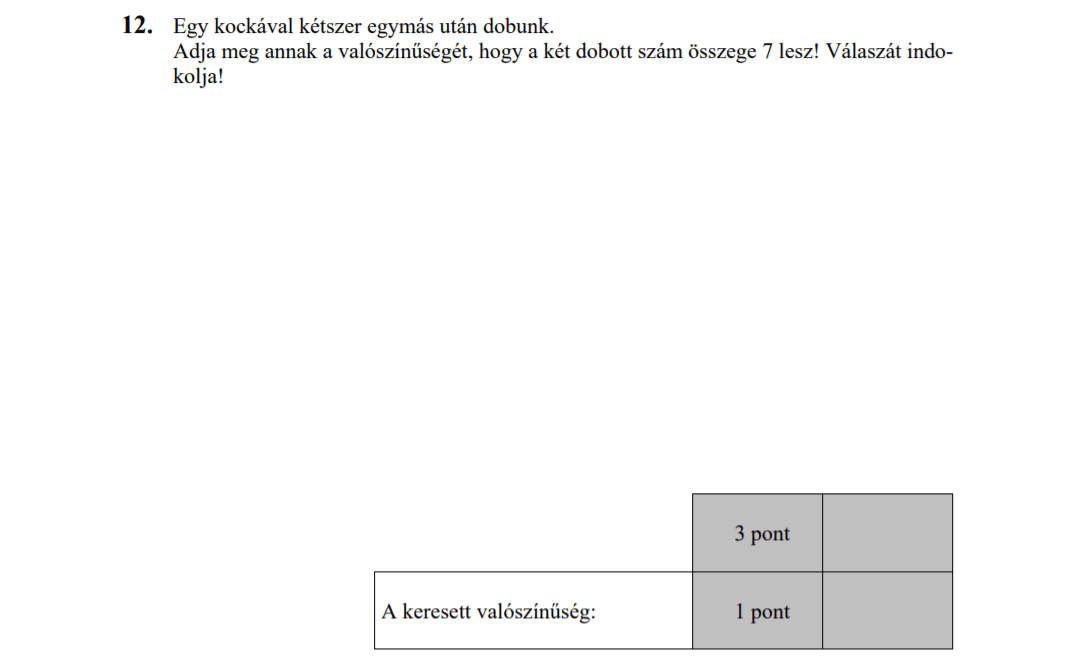
MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
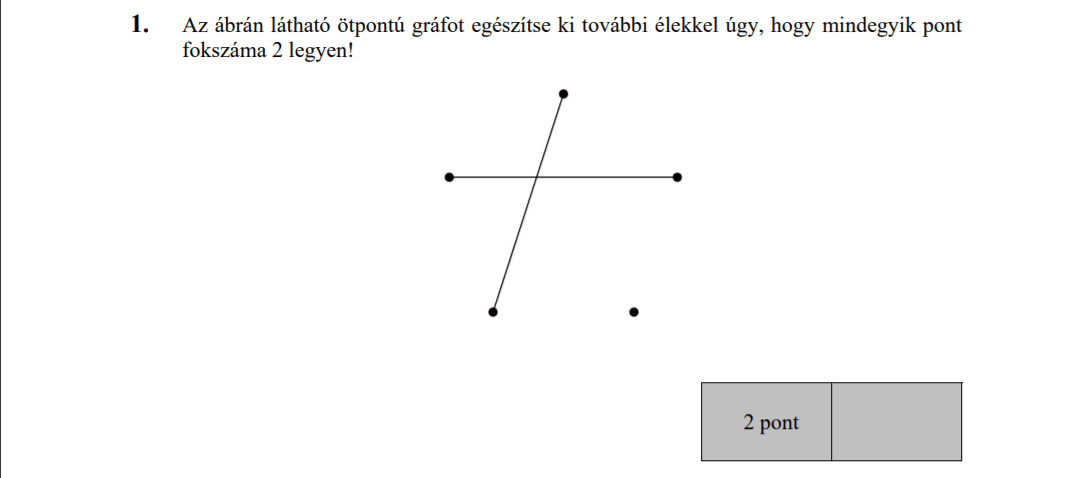
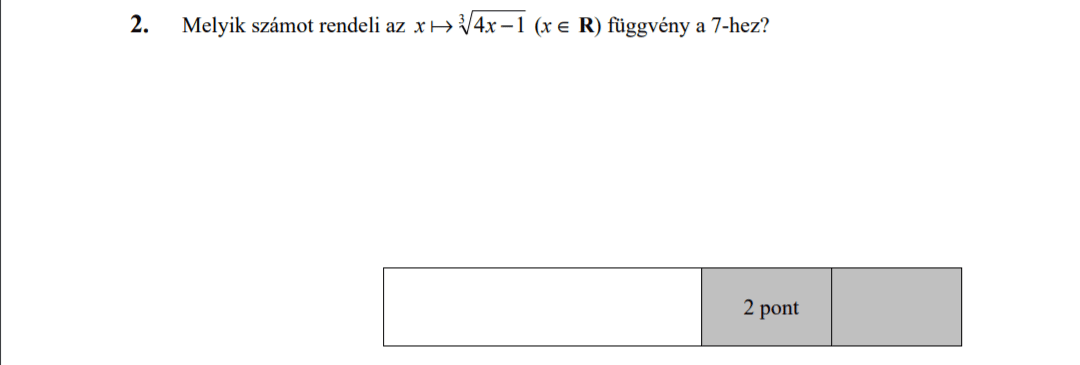
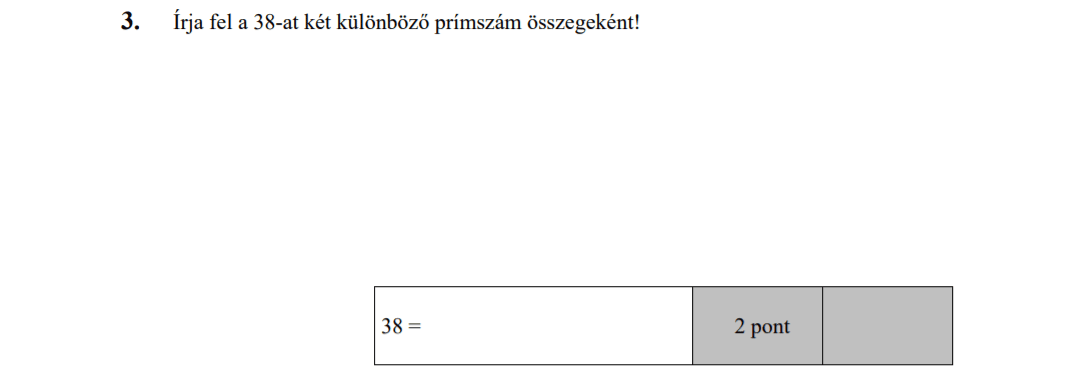




MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ




- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ









MÁSODIK RÉSZ




- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







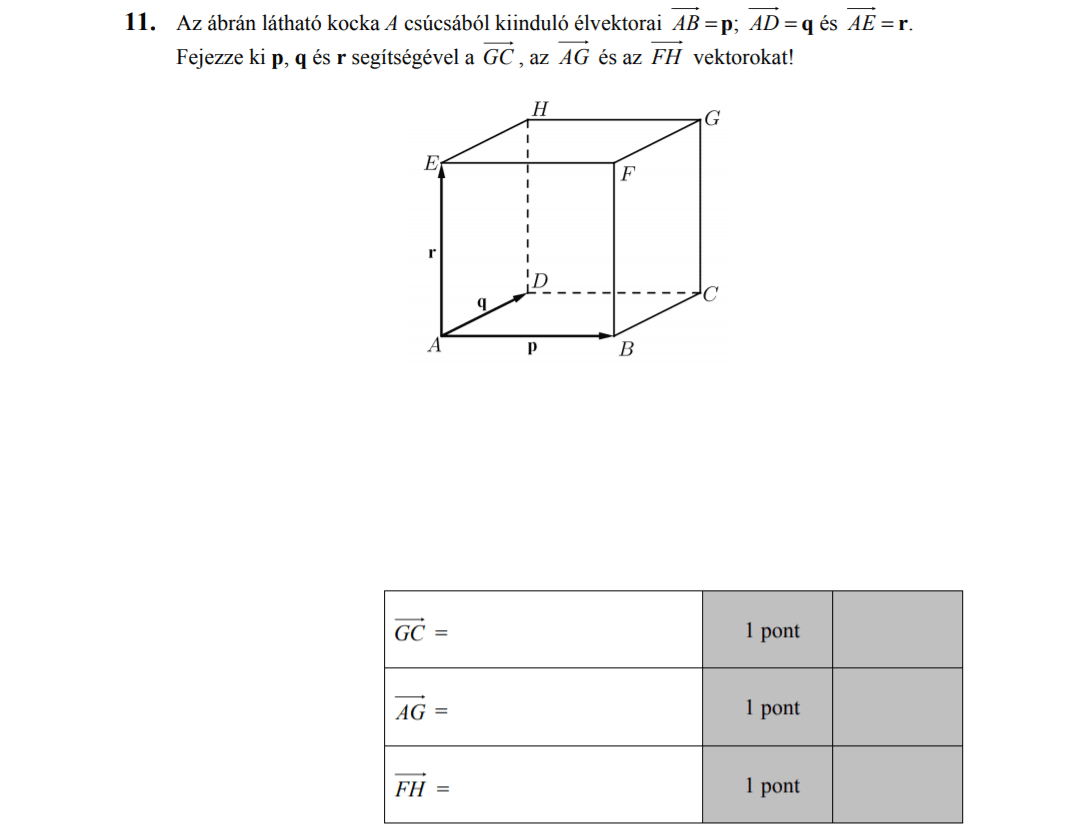
MÁSODIK RÉSZ
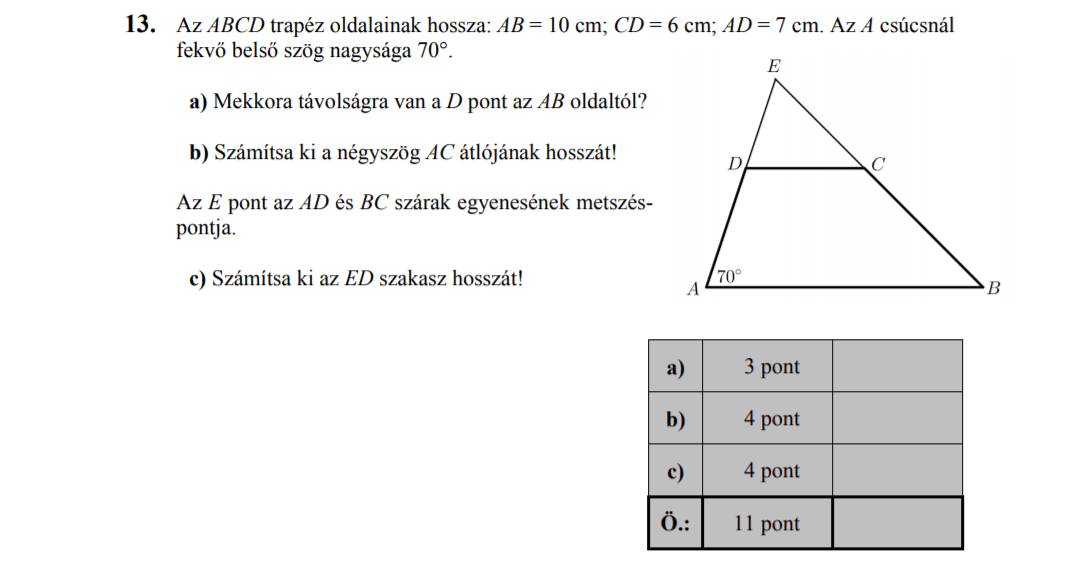





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


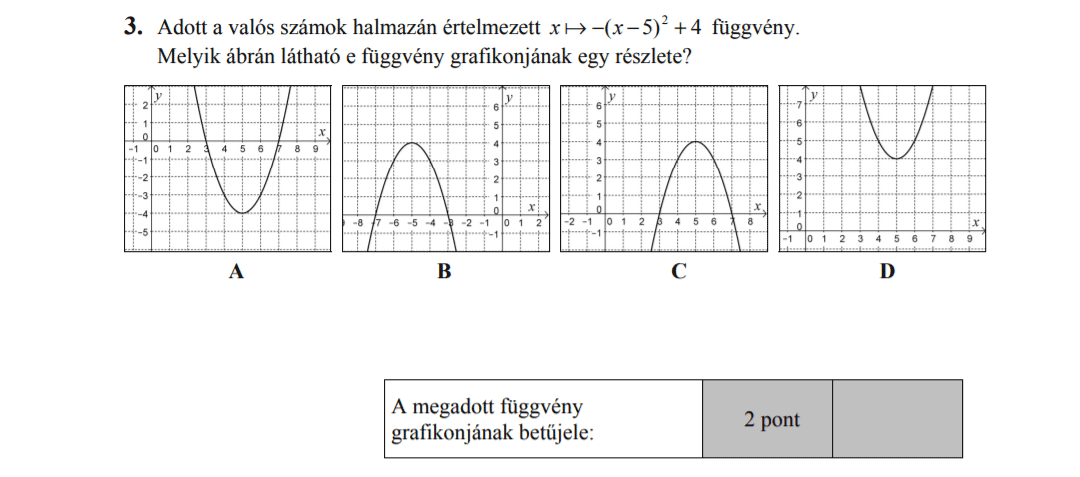








MÁSODIK RÉSZ




- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


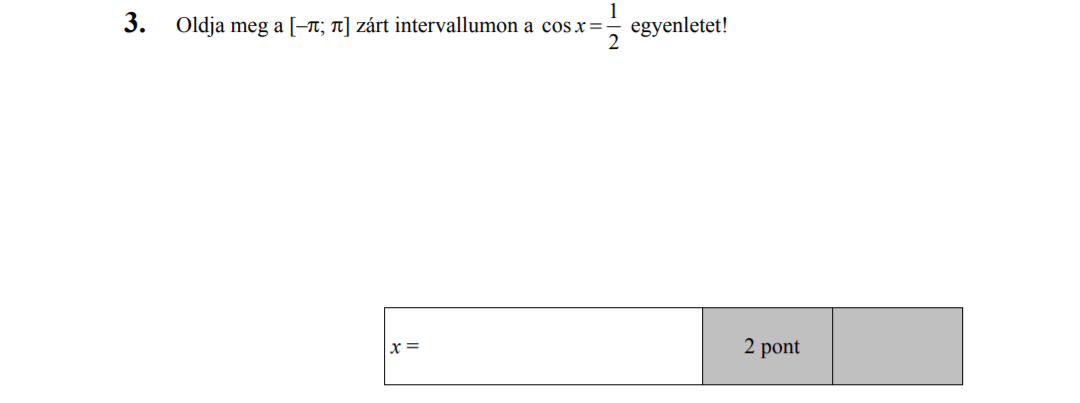


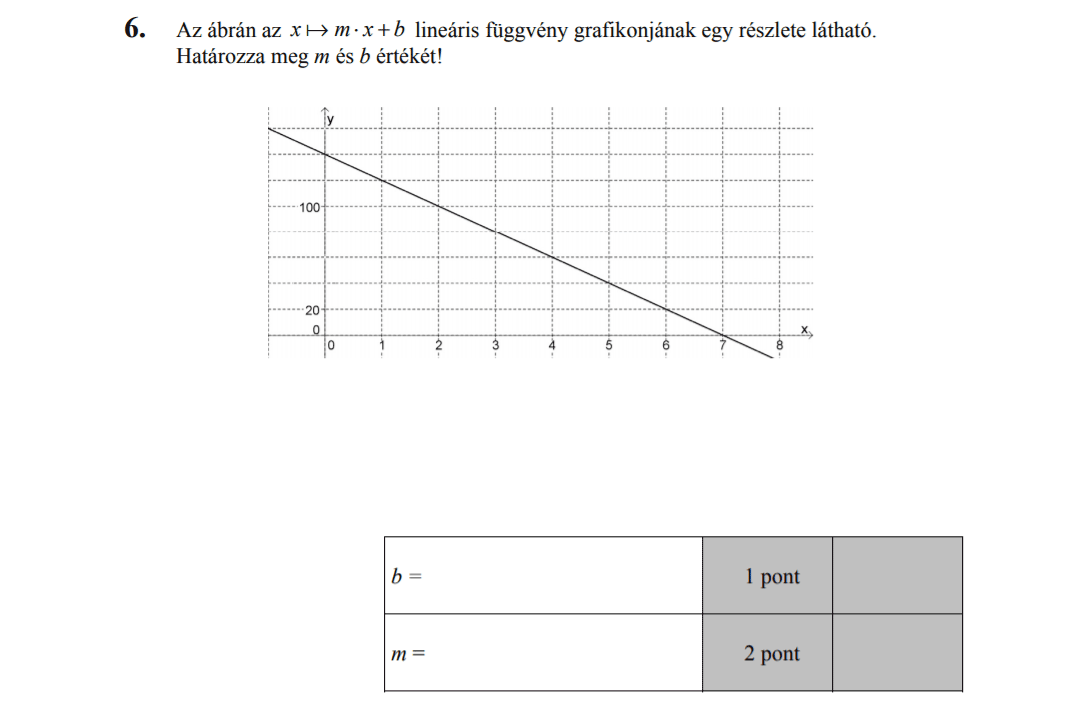



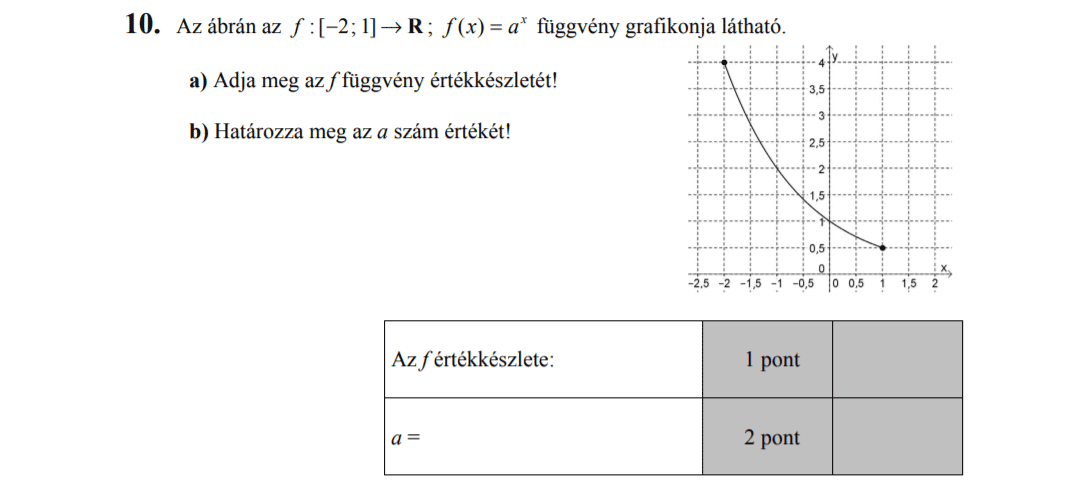

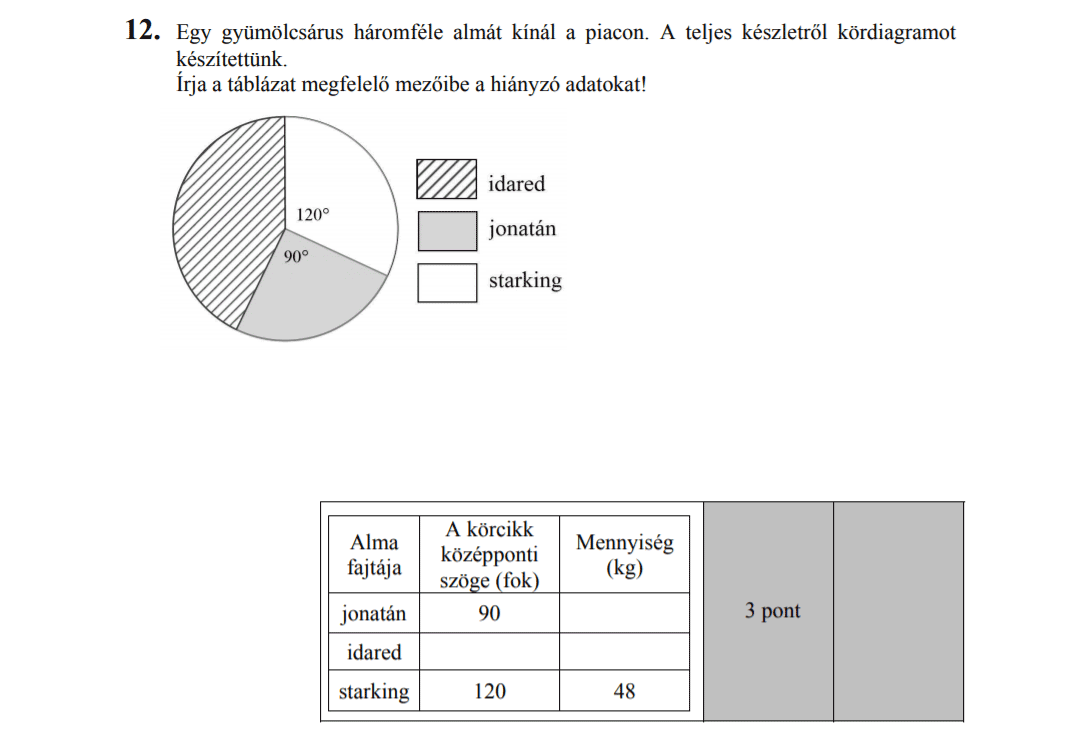
MÁSODIK RÉSZ





- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Síkidom
Síkidomnak nevezzük a sík zárt vonalakkal körülhatárolt részét.
A zárt vonal azt jelenti, hogy fogjuk a ceruzát, elindulunk valahonnan... és hopp, visszaérünk ugyanoda, ahonnan indultunk. Síkodom például egy háromszög, vagy egy négyzet, de síkidom egy kör is, vagy éppen a kölönböző emojik. Egy síkidomot több különböző zárt vonal is atárolhat. Olyankor, amikor csak egy zárt vonal határolja, egyszerű síkidomnak nevezzük. Mindez sokkal könnyebben elképzelhető, ha megnézed az ehhez kapcsolódó epizódot.
Sokszög
Sokszögnek nevezzük azokat a síkidomokat, melyeket véges sok, egymáshoz csatlakozó egyenes szakaszból álló zárt görbe ( töröttvonal ) határol. Vagyis azok a síkidomok sokszögek, amelyek határoló vonalai csak egyenes szakaszokból állnak.
Konkáv síkidom
A konkáv síkidom az, amelyikben ki tudunk választani két olyan pontot, hogy az ezeket összekötő szakasznak egy része a síkidomon kívül halad. Egy kör vagy egy téglalap például nem konkáv, mert bárhogyan választunk benne két pontot, a pontokat összekötő szakasz is a síkidomban halad. De például egy szívecske már konkáv, mert ha a két kidudorodó részét összekötjük, akkor az összekötő vonal kívül halad. Mindez sokkal egyszerűbb, ha megnézed az ehhez a témához kapcsolódó epizódot.
Konvex síkidom
A konvex síkidom az, amelyikben akárhogy veszünk két belső pontot, az őket összekötő szakasz minden pontja a síkidom belsejében lesz.
Egy kör vagy egy téglalap például konvex, mert bárhogyan választunk benne két pontot, a pontokat összekötő szakasz is a síkidomban halad. De például egy szívecske már nem konvex, mert ha a két kidudorodó részét összekötjük, akkor az összekötő vonal kívül halad. Mindez sokkal egyszerűbb, ha megnézed az ehhez a témához kapcsolódó epizódot.
Szabályos sokszög
Egy sokszöget szabályosnak nevezünk, ha minden oldala és minden belső szöge egyforma.
SOKSZÖG OLDALA
Sokszögnek nevezzük azokat a síkidomokat, melyeket véges sok, egymáshoz csatlakozó egyenes szakaszból álló zárt görbe ( töröttvonal ) határol. Ezeket az egyenes szakaszokat nevezzük a sokszög oldalainak.
SOKSZÖG CSÚCSA
Sokszögnek nevezzük azokat a síkidomokat, melyeket véges sok, egymáshoz csatlakozó egyenes szakasz alkotta zárt görbe határol. Ezeket a szakaszokat oldalaknak, vagy másként oldaléleknek nevezzük, és azokat a pontokat, ahol az oldalélek találkoznak, a sokszög csúcsainak hívjuk.
SOKSZÖG ÁTLÓI
A sokszögek nem szomszédos csúcsait összekötő szakaszokat a sokszög átlójának nevezzük.
Egyenlő szárú háromszög
Az egyenlő szárú háromszögben van két egyforma hosszú oldal, amiket szárnak nevezünk. És hát van ugye a harmadik oldal, ez az alap.
Annyit érdemes megjegyezni róla, hogy az alaphoz tartozó súlyvonal, magasságvonal, oldalfelező merőleges és szögfelező mind egybeesik. És ez egyúttal a háromszög szimmetriatengelye is.
És azt is jó tudni róla, hogy az alapon fekvő szögek egyformák.
Szabályos háromszög
Szabályos háromszögnek minden oldala és minden szöge egyenlő (tehát a szögek 60°-osak).
Szabályos háromszögben a körülírt kör középpontja, a magasságpont és a súlypont is egybeesnek.
Derékszögű háromszög
Derékszögű háromszögnek van $90°$-os szöge.
A derékszöggel szemközti oldalt átfogónak nevezzük, a másik kettőt pedig befogónak.
Hegyesszögű háromszög
A hegyesszögű háromszögek minden szöge hegyesszög, azaz $0°$-nál nagyobbak, de $90°$-nál kisebbek.
Tompaszögű háromszögek
A tompaszögű háromszögek azok, amelyeknek van egy tompaszöge, azaz egy olyan szöge, ami $90°$-nál nagyobb, de $180°$-nál kisebb.
Háromszög egyenlőtlenség
A háromszög egyenlőtlenség szerint minden háromszög bármelyik oldalának rövidebbnek kell lennie, mint a másik két oldal összege.
$a+b>c \qquad a+c>b \qquad b+c>a$
Háromszög magasságvonala és a magasságpont
A háromszög magasságvonala a csúcsból a szemközti oldal egyenesére bocsátott merőleges.
Ezek mindig egy pontban metszik egymást, és ezt a pontot magasságpontnak nevezzük.
Ha a háromszög tompaszögű, akkor a magasságpont a háromszögön kívülre esik.
Háromszög súlyvonala és a súlypont
A háromszög súlyvonala a csúcsot a szemközti oldal felezőpontjával összekötő szakasz.
Ezek mindig egy pontban metszik egymást, ezt a pontot hívjuk a háromszög súlypontjának.
További izgalom, hogy a súlypont mindegyik súlyvonalat 2:1 arányban osztja.
Továbbá a súlyvonal felezi a háromszög területét.
Háromszög köré írható kör
A háromszög oldalfelezőmerőlegesei mindig egy pontban metszik egymást. Ez a pont minden csúcstól egyenlő távolságra van és emiatt a háromszög köré írható kör középpontja.
Háromszögbe írható kör
A háromszög belső szögfelezői mindig egy pontban metszik egymást. Ez a háromszögbe írható kör középpontja.
Háromszög középvonala
Ha egy háromszög oldalfelezőpontjait összekötjük, akkor a háromszög középvonalait kapjuk.
A középvonalak párhuzamosak a háromszög oldalaival és éppen fele olyan hosszúak.
Képletek háromszög területére
A jól ismert képlet háromszögek területére:
\( T = \frac{ a \cdot m_a}{2} = \frac{ b \cdot m_b}{2} = \frac{ c \cdot m_c}{2} \)
És it jön egy kevésbé ismert háromszög-területképlet:
\( T = \frac{abc}{4R} \)
Itt $R$ a háromszög köré írható körének sugara.
Ez pedig egy még kevésbé ismert képlet háromszögek területére:
\( T=r\cdot s \)
Itt $r$ a beírható kör sugara, $s$ pedig a kerület fele.
Hérón-képlet
A Hérón-képlet a háromszögek területképletei közül egy kevésbé ismert, de elég jól használható képlet. Akkor érdemes használni, ha ismert a háromszög mindhárom oldala.
$s=\frac{a+b+c}{2} \qquad T=\sqrt{s \cdot (s-a) \cdot (s-b) \cdot (s-c)} $
Négyzet
A legszabályosabb négyszög a négyzet. A négyzet oldalai egyenlő hosszúak és minden szöge derékszög. Egy sokszöget akkor nevezünk szabályos sokszögnek, ha minden oldala és minden szöge egyforma. Így tehát az egyetlen szabályos négyszög a négyzet. Ezen kívül a négyzetek mége egy fontos dolgot tudnak: az átlóik is merőlegesek egymásra.
A négyzet területe:
\( T = a^2 \)
A négyzet kerülete:
\( K = 4a \)
Téglalap
Téglalap olyan négyszög, aminek minden szöge derékszög. Vagyis az oldalak nem feltétlen egyenlő hosszúak. Olyankor, amikor az oldalai is egyenlő hosszúak, egy négyzetet kapunk. A téglalapok egyik fontos tulajdosága, hogy a szemközti oldalai egyforma hosszúak, vagyis két darab a hosszúságú és két darab b hosszúságú oldala van. A téglalapoknak egy másik fontos tulajdonsága pedig, hogy a szemközti oldalai párhuzamosak egymással. Ez pedig azt jelenti, hogy a téglalapok mindig paralelogrammák is egyben (ugyanis a paralelogrammák azok a négyszögek, amelyeknek van két párhuamos oldalpárjuk).
Területe:
\( T = a \cdot b \)
Kerülete:
\( K = 2a + 2b \)
Rombusz
Rombusz egy olyan négyszög, amelynek minden oldala egyforma hosszú. Vagyis egy rombusznál az oldalak egyenlő hosszúságúak, de a szögeknek nem kell derékszögnek lenniük. Amikor a rombusz szögei derékszögek, egy négyzetet kapunk. Vagyis a négyzet is rombusz. A rombuszok másik fontos tulajdonsága, hogy a szemközti oldalaik mindig párhuzamosak egymással, vagyis a rombuszok paralelogrammák. is. Ez elvezet minket a rombusz egy másik definíciójához: a rombusz egyenlő oldalú paralelogramma.
A rombusz magasságát m-mel jelöljük, az átlóit pedig e-nek és f-nek szokás nevezni. Ezeknek a segítségével tudjuk kiszámolni egy rombusz területét.
Területe:
\( T = a \cdot m = \frac{ e \cdot f }{2} \)
Kerülete:
\( K = 4a \)
Paralelogramma
A paralelogramma olyan négyszög, aminek van két párhuzamos oldalpárja. Nagyon sok ilyen tulajdonságú négyszög van. Ilyenek a négyzetek, a téglalapok és a rombuszok. Vagyis minden négyzet, minden téglalap és minden qrombusz egyben paralelogramma is. A paralelogramma magasságát m-mel szokás jelölni.
Területe:
\( T = a \cdot m_a = b \cdot m_b \)
Kerülete:
\( K = 2a + 2b \)
Trapéz
A trapéz olyan négyszög, aminek van legalább egy párhuzamos oldalpárja. Ezeket az oldalakat a trapéz alapjainak nevezzük és a-val meg c-vel jelöljük. Általában a nagyobbik alapot szokás a-val jelölni és a kisebbik alapot pedig c-vel. Olyankor, amikor a trapéz alapjai egyforma hosszúak, paralelogrammát kapunk. Vagyis minden paralelogramma egyben trapéz is. Sőt, ha meggondoljuk, akkor a trapéz definíciója nagyon sok négyszögre ráillik. Egy darab párhuzamos oldalpárja ugyanis van a négyzetnek, a téglalapnak, a rombusznak és a paralelogrammáknak is. Vagyis minden négyzet, minden téglalap, minden rombusz és minden paralelogramma egyben trapéz is.
Mivel azonban ezeknek van külön neve, amikor egy feladatban trapézról van szó, általában olyan trapézra gondoljunk, aminek két különböző hosszúságú párhuzamos oldala van, az egyik "alul" a másik "felül" és ezek a trapéz a-val és c-vel jelölt alapjai.
Területe:
\( T = \frac{a+c}{2} \cdot m \)
Szimmetrikus trapéz
Ha a trapéz alapján fekvő két szög ugyanakkora, olyankor a trapéz szimmetrikus.
A szimmetrikus trapézt még szokás egyenlő szárú trapéznak is hívni, ugyanis a két szára mindig egyforma hosszú.
Ezen kívül van egy fantasztikus tulajdonsága is, hogy van köré írható köre.
Innen ered a harmadik elnevezés: húrtrapéz.
Deltoid
Azokat a négyszögeket nevezzük deltoidnak, amik papírsárkány alakúak és az átlóik merőlegesek egymásra.
Egy kicsit precízebben: deltoid az a négyszög, amelynek átlói merőlegesek egymásra és legalább az egyik átló szimmetriatengely.
A deltoidok közül kétféle speciális deltoidot érdemes megjegyezni, az egyik a rombusz, a másik a négyzet. Vagyis minden négyzet és minden rombusz deltoid. A deltoidok átlóit e-vel és f-fel jelöljük, és ezek csak akkor egyforma hosszúak, ha négyzetről van szó. A deltoidok területét általában az átlóik segítségével érdemes kiszámolni.
Területe:
\( T = \frac{ e \cdot f }{2} \)
Pitagorasz-tétel
A derékszögű háromszögben a befogók négyzetének összege egyenlő az átfogó négyzetével, vagyis ha az átfogót $c$-vel jelöltük:
\( a^2 + b^2 = c^2 \)
Pitagorasz-tétel megfordítása
Ha egy háromszög oldalaira teljesül, hogy
$a^2 + b^2 = c^2$
Akkor a háromszög derékszögű.
Pitagoraszi számhármasok
A Pitagoraszi számhármasok olyan számok, amelyekre teljesül a Pitagorasz-tétel.
Pl.: $3$, $4$ és $5$ együtt Pitagoraszi számhármasok, ugyanis $3^2+4^2=5^2$ igaz.
Kör sugara
Egy kör sugara a kör középpontját a körvonal bármely pontjával összekötő szakasz hossza. A kör sugarát r betűvel jelöljük ami a radius szó kezdőbetűje.

Kör középpontja
A kör azon pontok mértani helye a síkban, amelyek egy adott ponttól egyenlő távolságra vannak. Ezt az adott pontot hívjuk a kör középpontjának. A kör középpontját általában O-val vagy K-val szokás jelölni.

Körvonal
A körvonal azon pontok mértani helye a síkban, amelyek egy adott ponttól ( a kör középpontjától ) egyenlő távolságra vannak. A körvonalat szokás egyszerűen körként is emlegetni.

Körlap vagy körlemez
A körlap vagy körlemez a körvonal és a körvonalon belüli rész együttes elnevezése. Ezt így egyben szokás egyszerűen csak simán körnek is nevezni. Matematikailag precíz definíciója: azon pontok mértani helye a síkban, amelyek egy adott ponttól (a kör középpontjától) legfeljebb egy adott r távolságra (r a kör sugara) vannak.

Kör érintője
Ha egy egyenes éppen olyan távol halad egy kör középpontjától, mint a kör sugara, akkor ez az egyenes érinti a kört. Az érintőnek csak egy közös pontja van a körrel, amit érintési pontnak nevezünk. Az érintési pontba vezető sugár mindig merőleges az érintőre.

szelő a körben
Azokat az egyeneseket, amik metszik a kört úgy hívjuk, hogy szelő. A szelők két pontban metszik a kört és a két pont közötti szakasz a húr. Olyankor, amikor a szelő éppen átmegy a kör középpontján, a szelő a kör területét felezi, és ilyenkor a metszéspontok közötti húrt átmérőnek nevezzük. Az átmérő mindig a kör sugarának a kétszerese.

húr
Egy körben a körvonal két különböző pontját összekötő szakaszt húrnak nevezzük. Olyankor, amikor a húr éppen átmegy a kör középpontján, a húrt átmérőnek nevezzük. Az átmérő mindig a kör sugarának a kétszerese.

Átmérő
A kör középpontját áthaladó húrt átmérőnek nevezzük. Az átmérő a kör maximális szélessége, és az átmérő mindig a kör sugarának a kétszerese. Jele d a diameter szó kezdőbetűje alapján.

Kör és a kör részei
Egy adott ponttól állandó távolságra lévő pontok halmazát körvonalnak nevezzük. És ezt az állandó távolságot hívjuk a kör sugarának. A sugár jele r. A kör középpontját általában K-val jelöljük.
És most nézzük a kör részeit:
Középpont: A kör azon pontok mértani helye a síkban, amelyek egy adott ponttól egyenlő távolságra vannak. Ezt az adott pontot hívjuk a kör középpontjának. A kör középpontját általában O-val vagy K-val szokás jelölni.
Körvonal: A körvonal azon pontok mértani helye a síkban, amelyek egy adott ponttól ( a kör középpontjától ) egyenlő távolságra vannak. A körvonalat szokás egyszerűen körként is emlegetni.
Sugár: Egy kör sugara a kör középpontját a körvonal bármely pontjával összekötő szakasz hossza. A kör sugarát r betűvel jelöljük ami a radius szó kezdőbetűje.
Körlap vagy körlemez: A körlap vagy körlemez a körvonal és a körvonalon belüli rész együttes elnevezése. Ezt így egyben szokás egyszerűen csak simán körnek is nevezni. Matematikailag precíz definíciója: azon pontok mértani helye a síkban, amelyek egy adott ponttól (a kör középpontjától) legfeljebb egy adott r távolságra (r a kör sugara) vannak.
Húr: Egy körben a körvonal két különböző pontját összekötő szakaszt húrnak nevezzük. Olyankor, amikor a húr éppen átmegy a kör középpontján, a húrt átmérőnek nevezzük. Az átmérő mindig a kör sugarának a kétszerese.
Átmérő: A kör középpontját áthaladó húrt átmérőnek nevezzük. Az átmérő a kör maximális szélessége, és az átmérő mindig a kör sugarának a kétszerese. Jele d a diameter szó kezdőbetűje alapján.

Kör és egyenes kölcsönös helyzete
A kör és egyenes kölcsönös helyzete a síkban háromféle lehet. Az egyenes vagy metszi a kört vagy érinti, vagy kitérő.
Szelő: Azokat az egyeneseket, amik metszik a kört úgy hívjuk, hogy szelő. A szelők két pontban metszik a kört és a két pont közötti szakasz a húr. Olyankor, amikor a szelő éppen átmegy a kör középpontján, a szelő a kör területét felezi, és ilyenkor a metszéspontok közötti húrt átmérőnek nevezzük. Az átmérő mindig a kör sugarának a kétszerese.
Érintő: Ha az egyenes éppen olyan távol halad a kör középpontjától, mint a kör sugara, akkor érintőt kapunk. Az érintőnek csak egy közös pontja van a körrel, amit érintési pontnak nevezünk. Az érintési pontba vezető sugár mindig merőleges az érintőre.
Kitérő egyenes: Végül az is lehet, hogy a körnek egyetlen közös pontja sincs a körrel, ilyenkor kitérő egyenesnek nevezzük.

Két kör kölcsönös helyzete
Két kör kölcsönös helyzete a síkban már eléggé sokféle lehet. Két fő esetet lehet megkölönböztetni egymástól. Az egyik eset, amikor a két kör sugara nem ugyanakkora, a másik eset pedig az, amikor a két kör sugara ugyanakkora.
Két kör kölcsönös helyzete, ha a körök sugara nem ugyanakkora:
Elkerülő körök: Ha a két kör középpontjának távolsága nagyobb, mint a körök sugarainak összege, akkor a köröknek nincs közös pontjuk.
Kívülről érintő körök: Ha a középpontok távolsága éppen a sugarak összege, akkor egy közös pontjuk van és ilyenkor a két kör kívülről érinti egymást.
Metsző körök: Ha a körök középpontjainak távolsága kisebb, mint a sugarak összege, de nagyobb, mint a sugarak különbsége, akkor a körök metszik egymást. Ilyenkor a körvonalaiknak két közös pontja van.
Belülről érintő körök: Ha a középpontok távolsága a két kör sugarának a különbsége, akkor az egyik kör belülről érinti a másikat.
Tartalmazó körök: Ha a két középpont távolsága még ennél is kisebb, de pozitív, akkor az egyik kör tartalmazza a másik kört.
Koncentrikus körök: Végül, ha a két kör középpontjának a távolsága nulla, vagyis a középpontok egybeesnek, akkor azt mondjuk, hogy a körök koncentrikus körök.

Két kör kölcsönös helyzete, ha a körök sugara ugyanakkora:
Elkerülő körök: Ha a két kör középpontjának távolsága nagyobb, mint a körök sugarainak összege, akkor a köröknek nincs közös pontjuk.
Kívülről érintő körök: Ha a középpontok távolsága éppen a sugarak összege, akkor egy közös pontjuk van és ilyenkor a két kör kívülről érinti egymást.
Metsző körök: Ha a körök középpontjainak távolsága kisebb, mint a sugarak összege, de nagyobb, mint nulla, akkor a körök metszik egymást. Ilyenkor a körvonalaiknak két közös pontja van.
Egybeeső körök: Ha a középpontok távolsága nulla, vagyis a középpontok egybeesnek, akkor azt mondjuk, hogy a körök koncentrikus körök.
Kör kerülete és területe
Az $r$ sugarú kör kerülete:
\( K = 2r \cdot \pi \)
Területe:
\( T = r^2 \cdot \pi \)
Körcikk ívhossza és területe
A körcikk ívhossza és területe úgy aránylik a kör kerületéhez és területéhez, mint a körcikkhez tartozó középponti szög a 360°-hoz:
\( I_{\alpha} = \frac{ \alpha}{360°} \cdot 2r \cdot \pi \)
\( T_{\alpha} = \frac{ \alpha}{360°} \cdot r^2 \cdot \pi \)
Thalész-tétel
A Thalész-tétel azt mondja, hogy ha az $AB$ szakasz egy kör átmérője, és $C$ a kör tetszőleges harmadik pontja, akkor az $ACB$-szög mindig derékszög.
Ezt úgy is szokás mondani, hogy az $AB$ szakasz a körív bármely harmadik $C$ pontjából derékszögben látszik.
Párhuzamos szelők tétele
Ha egy szög szárait párhuzamos egyenesekkel metsszük, akkor az egyik szögszáron keletkező szakaszok aránya megegyezik a másik szögszáron keletkező megfelelő szakaszok arányával.
Középpontos hasonlóság
A középpontos hasonlósági transzformációhoz adott egy $O$ pont, ez a középpont, és egy $\lambda$ nem nulla valós szám, ez a hasonlóság aránya.
A tér minden $P$ pontjához egy $P'$ pontot rendel a következőképp:
1. ha $P=O$, akkor $P'=P$.
2. ha $P \neq O$, akkor $P'$ az $OP$ egyenes azon pontja, amelyre $OP' = \mid \lambda \mid \cdot OP$ és ha $\lambda >0$, akkor $P'$ az $OP$ félegyenesen van, ha $\lambda <0$, akkor pedig $O$ elválasztja egymástól $P$-t és $P'$-t.
Háromszögek hasonlósága
Két háromszög egymáshoz hasonló, ha...
1.) két szögük egyenlő.
2.) két oldal aránya és a nem kisebbel szemközti szögük egyenlő.
3.) két oldal aránya és az általuk bezárt szögeik egyenlők.
4.) három oldal aránya páronként egyenlő.
Területek és térfogatok aránya
Egy alakzat területe négyzetesen aránylik a méreteihez. Ha a méreteit $\lambda$-szeresére változtatjuk, akkor a területe $\lambda^2$-szeresére változik.
Egy alakzat térfogata köbösen aránylik a méreteihez. Ha a méreteit $\lambda$-szeresére változtatjuk, akkor a térfogata $\lambda^3$-szeresére változik.
a) Mit nevezünk a háromszög magasságvonalának, súlyvonalának?
b) Milyen arányban osztja a súlypont a súlyvonalakat?
c) Mit nevezünk a háromszög középvonalának?
d) Mi a háromszög köré és a háromszögbe írható kör középpontja?
Osztályozzuk a négyszögeket, készítsünk egy halmazábrát a különböző tulajdonságaik szerint.
a) Egy trapéz alapon fekvő szögei közül az egyik 80 fokos, a másik 40 fokos. Mekkora a másik két szög?
b) Egy trapéz egyik szárán fekvő két szögéről tudjuk, hogy az egyik 40 fokkal nagyobb a másiknál. A másik száron fekvő szögekről pedig azt tudjuk, hogy az egyik kétszerese a másiknak. Mekkorák a trapéz szögei?
c) Itt van aztán ez a paralelogramma, aminek az egyik szöge 42°-os. Mekkora a többi szöge?
d) Végül itt jön még egy trapéz, amiben annyit tudunk, hogy a szögeinek aránya 3:4:5:6. Mekkorák a szögei?
a) Egy paralelogramma $a$ oldala 16 cm, a hozzá tartozó magasság pedig 9 cm. Mekkora a területe?
b) Egy paralelogramma oldalainak hossza 7 cm és 9 cm, a rövidebbik oldalhoz tartozó magasság 5 cm. Mekkora a területe és a hosszabbik oldalhoz tartozó magasság?
c) Egy paralelogramma területe $60\; cm^2$, és az oldalaihoz tartozó magasságok 6 cm és 4 cm. Mekkora a kerülete?
d) Egy templom függőleges homlokzata felül háromszögalakban végződik. A homlokzat nem szimmetrikus, az egyik oldalon 23 méter magasan indul a ferde rész, a másik oldalon pedig 14 méter magasan. A homlokzat legmagasabb pontja, ami a háromszögszerű rész csúcsa 36 méter magasan van. Ha ezt a csúcsot merőlegesen összekötjük a talajjal, akkor ez a vonal a homlokzatot egy 10 méter széles és egy 15 méter széles részre osztja ketté. Mekkora a homlokzat területe?
a) Bob őrülten rajong a papírsárkányokért. Egy 12 cm hosszú és egy 32 cm hosszú vékony bambusz rudat felhasználva épít magának egy deltoid alakú sárkányt, ahol a bambusz rudak a deltoid átlói. Mekkora a sárkány teljes felülete?
b) Bob egy még nagyobb papírsárkányt szeretne készíteni, amihez egy 112 centiméter hosszú bambusz rudat használ. A rudat 4:3 arányban kettévágja, és ezek lesznek a deltoid alakú sárkány merevítői, vagyis a deltoid átlói. Hány négyzetcentiméternyi papírból áll a sárkány?
c) Egy deltoid rövidebbik oldala 12 centiméter hosszú, és 90 fokos szöget zár be a deltoid hosszabbik, 16 centiméteres oldalával. A deltoid hosszabbik átlója 20 centiméter. Mekkora a rövidebbik átló?
a) Egy rombusz átlói 16 és 12 cm hosszúak, a rombusz magassága pedig 9,6 cm. Mekkora a rombusz kerülete?
b) Egy paralelogramma átlói merőlegesek egymásra. Az átlók hossza 10 cm és 24 cm. Mekkora a paralelogramma területe?
c) Egy másik paralelogramma rövidebbik átlója 78 cm és 60 fokos szöget zár be a paralelogramma oldalaival. A hosszabbik átló 135,1 cm. Mekkora a paralelogramma kerülete és területe?
d) Egy paralelogramma átlói merőlegesek egymásra. A hosszabbik átló 8 centiméteres. A paralelogramma egyik oldala 5 cm hosszú és az ehhez tartozó magasság 1,2 cm-rel rövidebb a rövidebbik átlónál. Mekkora a paralelogramma területe?
a) Mekkora egy szabályos hétszög belső szögeinek összege?
b) Mekkora egy szabályos 100-szög egy belső szöge?
a) Hány átlója van egy szabályos nyolcszögnek?
b) Hány átlója van egy szabályos 100-szögnek?
a) Egy derékszögű háromszögben a két befogó: $a=6 \; cm$, $b=8 \; cm$. Mekkora az átfogó?
b) Egy derékszögű háromszög befogói $p$ és $q$, az átfogója pedig $r$. Tudjuk, hogy $p=9 \; cm$ és $r=15 \; cm$. Mekkora a $q$ oldal?
c) Egy derékszögű háromszög befogói $w$ és $t$, az átfogója pedig $f$. Tudjuk, hogy $t=24 \; cm$ és $f=41\; cm$. Mekkora a $w$ oldal?
a) Az egyiptomi piramisok közül a Nagy-piramis 147 méter magas, és az alapja egy 232 méter oldalhosszúságú négyzet. Amikor a piramis alapját kezdték építeni, kijelölték a négyzet középpontját, ami fölött majd a piramis csúcsa fog elhelyezkedni. Milyen távol van ez a pont a piramis négy sarkától? Milyen hosszú a piramis egyik oldaléle?
b) Egy téglalapnak az egyik oldala 4 centiméter, az egyik átlója pedig 6 centiméter. Mekkora a téglalap területe?
c) Egy négyzet átlója 5 cm. Mekkora az oldala?
d) Számítsuk ki ennek a deltoidnak a területét.

a) Egy egyenlőszárú háromszögben a szárak $13\; cm$ hosszúak, az alap pedig $10\; cm$. Mekkora a háromszög területe?
b) Egy egyenlőszárú háromszög terülte $120 \; cm^2$, az alapja pedig $30 \; cm$. Mekkorák a szárai?
c) Egy szabályos háromszög oldalai $16 \; cm$ hosszúak. Mekkora a háromszög területe?
d) Mekkora az $a$ oldalú szabályos háromszög területe?
e) Mekkora az $a$ oldalú négyzet átlója?
a) Egy szimmetrikus trapéz szárai 13 cm hosszúak, a kisebbik alapja 6 cm a nagyobbik pedig 16 cm. Mekkora a trapéz területe?
b) Itt jön egy másik trapéz, aminek a szárai 13 és 15 cm hosszúak, a rövidebbik alap 10 cm, a trapéz magassága pedig 12 cm. Mekkora a trapéz területe?
c) És van ez a harmadik trapéz, aminek a területe 108 $cm^2$, az alapjai 24 cm és 3 cm, az egyik szára pedig 10 cm. Mekkora a másik szár?
a) Mekkora egy 32 cm-es pizza sugara?
b) Mi a kör szelője, érintője, átmérője, sugara?
a) Egy kör középpontja a K(6,5)pont és a kör sugara 3 egység. Rajzoljuk fel a kört és jelöljük be azokat a pontokat, amik a K ponttól legfeljebb 3 egység távolságra vannak.
b) Rajzoljuk be azokat a pontokat, amik a K(3,4)ponttól legalább 2 egység távolságra és legfeljebb 5 egység távolságra vannak.
c) Végül rajzoljuk be azokat a pontokat is, amik a K(5,3)ponttól legalább 3 egységre és az M(5,5)ponttól legfeljebb 5 egységre vannak.
Egy 32 cm átmérőjű pizza szélén, egy 4 cm-es sávon általában már nincs semmi. Mekkora ennek az "üres" résznek a területe?
a) Van egy 32 centiméter átmérőjű pizza, meg két darab 22 centiméteres. Melyiknek nagyobb a területe, az egy darab 32 centiméteresnek, vagy a két darab 22 centiméteresnek együtt?
b) Egy templomtorony órája 6 méter átmérőjű körlap. A számok a körlap szélén 1 méter szélességű gyűrűn helyezkednek el. Mekkora ennek a gyűrűnek a területe?
Egy sportpálya belső része 62 méter hosszú és 44 méter széles téglalap alakú füves terület. Körülötte 10 méter széles sávban egy futópálya található. A futópálya párhuzamos a belső téglalap 62 méteres oldalaival, a 44 méteres oldalaknál pedig egy-egy félkörívben halad. Mekkora a futópálya területe?

Bob úgy dönt hogy leugrik a sportpályára futni egy kört. Hány méterrel fut többet, ha a futópálya külső szélén fut, mint akkor, ha a belsőn?
Bob a téglalap alakú füves rész 62 méteres oldalára rajzol két egyforma félkörívet úgy, hogy az átmérőik összege éppen 62 méter legyen. Aztán a másik 62 méter hosszú oldalra is rajzol két félkörívet, de azok nem egyformák, az átmérőik összege viszont szintén 62 méter. Bizonyítsuk be, hogy a pálya egyik oldalára rajzolt görbe vonal hossza ugyanakkora, mint a másik oldalára rajzolt görbe vonal hossza.

a) Van egy 32 cm átmérőjű pizza. Vágjuk 6 egyenlő részre, aztán vegyünk ki egy szeletet. Mekkora ennek a pizzaszeletnek a területe?
b) Egy templomtorony órája 6 méter átmérőjű körlap. Az óra mutatói délután 4 órakor egy körcikket határoznak meg. Mekkora ennek a körcikknek a területe?
a) Egy óriáskerék 16 darab kabinja egyenletesen helyezkedik el a 60 méter átmérőjű keréken. Mekkora a két szomszédos kabin közötti körcikk területe?
b) Egy torony óráján a nagymutató csúcsa éppen az óra kör alakú számlapjának széléig ér. Ahogy a mutató körbefordul, a mutató csúcsa 5 perc alatt 1,6 métert tesz meg. Mekkora az óra számlapjának a területe?
c) Mekkora középponti szög tartozik ahhoz a 10 méter átmérőjű körben lévő körcikkhez, aminek a területe 4 m2?
Bob nem túl jó matekból, viszont szeret rajzolni, így hát elhatározta, hogy ábrázolja a matekjegyeit egy 20 cm átmérőjű kördiagramon.

a) Mekkora középponti szög tartozik a kettesekhez?
b) Milyen hosszú körív tartozik a hármasokhoz?
c) Mekkora a sárga körcikk területe a négyeseknél?
a) Egy 4 egység sugarú körben lévő húr két végpontja A(2,5) és B(6,1). Adjuk meg a kör középpontját.
b) Adott három pont, A(2,5) B(4,3) és C(8,3). Keressük annak a körnek a középpontját, amelyik mindhárom ponton átmegy.
c) Az A(2,4) és B(8,4) pont egy kör átmérőjének két végpontja. Mekkora a kör sugara és hol van a kör középpontja?
a) Egy derékszögű háromszög oldalai 12 cm, 16 cm és 20 cm hosszúak. Mekkora a háromszög köré írható kör sugara?
b) Egy deltoidnak van két 90 fokos szöge, valamint egy 120 fokos meg egy 60 fokos szöge. A deltoid átlói pedig 15 cm és 13 cm hosszúak. Mekkorák a deltoid oldalai?
Számoljuk ki annak a körszeletnek a területét, amelyet egy 13 cm sugarú körből vágunk le a kör középpontjától 5 cm távolságban haladó szelővel.
a) Az \( ABC \) háromszögben \( AB=8 \) cm és \( AC=12 \) cm és a \( B \) csúcsából induló egyenes az \( AC \) oldalt \( D \)-ben metszi. Mekkora \( AD \) és \( DC \), ha \( ABD\angle = ACB\angle \) ?
b) Egy szimmetrikus trapéz hosszabbik alapja 24 cm. Az átlók 3:1 arányban osztják egymást. Ha a trapéz szárait meghosszabbítjuk, akkor egy olyan egyenlő szárú háromszöget kapunk, amelynek a szárai 15 cm hosszúak. Mekkorák a trapéz oldalai?
a) Egy háromszög oldalai a=12 cm, b=14 cm, c=16 cm. Egy ehhez hasonló háromszög kerülete 28 cm. Mekkora a hasonlóság aránya, mekkora a háromszög legrövidebb oldala?
b) Egy derékszögű háromszög befogói a=12 cm, b=9 cm. Egy ehhez hasonló háromszög területe \( 6 cm^2 \). Mekkora a hasonlóság aránya, mekkora a háromszög legrövidebb oldala?
a) Mekkora a háromszög területe, ha az egyik oldala $16\; cm$ és a hozzá tartozó magassága $9\; cm$?
b) Egy háromszög területe $56 \; cm^2$ és a $b$ oldalhoz tartozó magasság $7\; cm$. Mekkora a $b$ oldal?
c) Egy háromszög területe $64 \; cm^2$ és a $c$ oldal $16\; cm$. Mekkora a hozzá tartozó magasság?
d) Egy háromszög $b$ oldala $12\; cm$, a hozzá tartozó magasság $10\; cm$. A $c$ oldalhoz tartozó magasság $15\; cm$. Mekkora a $c$ oldal?
Jelölje a 4 egység oldalú ABC szabályos háromszög BC oldalának B-hez közelebbi negyedelőpontját P, a CA oldal C-hez közelebbi negyedelőpontját Q, az AB oldal A-hoz közelebbi negyedelőpontját pedig R. Jelölje továbbá AP és BQ szakaszok metszéspontját X, BQ és CR szakaszok metszéspontját Y, végül CR és AP szakaszok metszéspontját Z. Mekkora az XYZ háromszög területe?
a) Egy paralelogramma $a$ oldala 16 cm, a hozzá tartozó magasság pedig 9 cm. Mekkora a területe?
b) Egy paralelogramma oldalainak hossza 7 cm és 9 cm, a rövidebbik oldalhoz tartozó magasság 5 cm. Mekkora a területe és a hosszabbik oldalhoz tartozó magasság?
c) Egy paralelogramma területe $60 \; cm^2$, és az oldalaihoz tartozó magasságok 6 cm és 4 cm. Mekkorák az oldalai?
d) Egy paralelogramma $a$ oldala 8 cm és a hozzá tartozó magasság 6 cm. A $b$ oldalhoz tartozó magasság 4,8 cm. Mekkora a paralelogramma kerülete?
a) Egy paralelogramma oldalai 6 cm és 8 cm. A hosszabbik oldalhoz tartozó magasság 1 cm-rel rövidebb, mint a rövidebbik oldalhoz tartozó. Mekkora a paralelogramma területe?
b) Egy paralelogramma oldalainak hossza 8 cm és 10 cm, a rövidebbik oldalhoz tartozó magasság 6 cm. Mekkora a területe és a hosszabbik oldalhoz tartozó magasság?
c) Egy paralelogramma $a$ oldala 8 cm és a hozzá tartozó magasság 6,75 cm. A $b$ oldalhoz tartozó magasság 6 cm. Mekkora a paralelogramma kerülete?
d) Egy paralelogramma oldalai 12 cm és 8 cm. A rövidebbik oldalhoz tartozó magasság 2 cm-rel hosszabb, mint a hosszabb oldalhoz tartozó. Mekkora a paralelogramma területe?
a) Egy paralelogramma hosszabbik oldalhoz tartozó magassága 4 cm-rel rövidebb, mint a rövidebbik oldalhoz tartozó magassága. A hosszabbik oldal éppen kétszerese a rövidebbik oldalnak. Mekkora a paralelogramma kerülete, ha a területe $56 \; cm^2$?
b) Egy másik paralelogramma hosszabbik oldalhoz tartozó magassága 5 cm-rel rövidebb, mint a rövidebbik oldalhoz tartozó magasság. A hosszabbik oldal éppen kétszerese a rövidebbik oldalnak. Mekkora a paralelogramma kerülete, ha a területe $60 \; cm^2$?
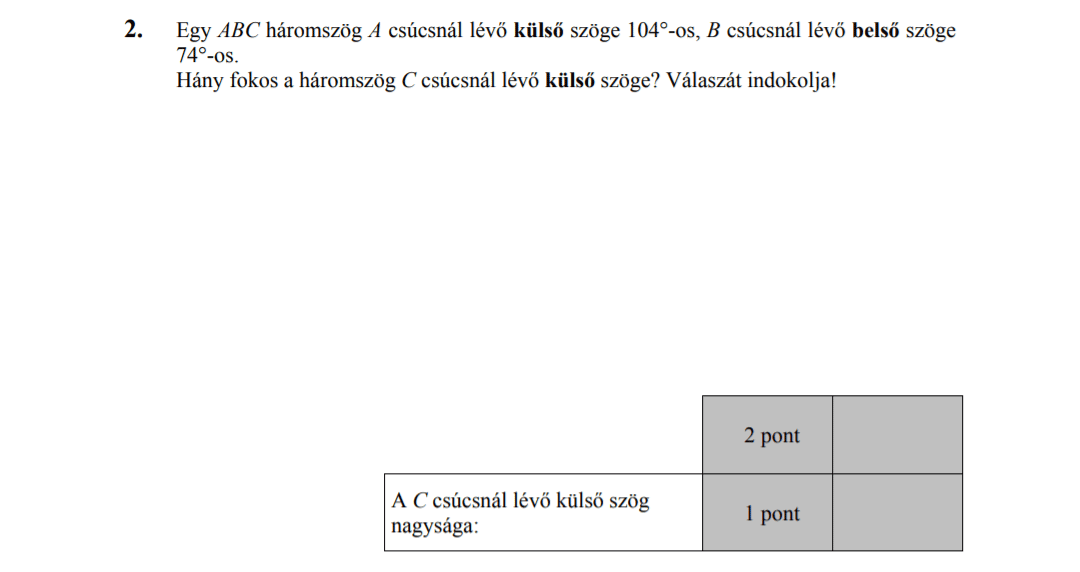
a) Egy háromszög két szöge 65° és 54°. Mekkora a hiányzó harmadik szöge? Mekkorák a külső szögei?
b) Egy háromszög két szöge 62° és 56°. Mekkora a hiányzó harmadik szöge? Mekkorák a külső szögei?
c) Egy egyenlő szárú háromszög alapon fekvő szögei 65°-osak. Mekkora a szárak által közbezárt szög?
d) Egy másik egyenlő szárú háromszögben a szárak által bezárt szög 48°. Mekkorák az alapon fekvő szögei?
e) Egy egyenlőszárú háromszögben a szárszög 15°-kal kisebb, mint az alapon fekvő szögek. Mekkorák a szögei?
f) Egy másik egyenlő szárú háromszögben az alapon fekvő szögek kétszer akkorák, mint a szárszög. Mekkorák a szögei?
g) Egy egyenlőszárú háromszög egyik szöge 48°. Mekkora lehet a másik két szöge?
a) Egy szimmetrikus trapéz hosszabbik alapja 20 cm, szárai 10 cm hosszúak. A trapézt háromszöggé kiegészítő háromszögének szárai 8 cm-esek. Mekkora a trapéz területe?
b) Egy háromszögről azt tudjuk, hogy két szöge 45 és 56 fokos. Egy másik háromszögnek van egy 79 és egy 56 fokos szöge. Hasonló-e a két háromszög?
c) Egy szimmetrikus trapéz két alapja 12 és 6 cm, az átlója pedig 9 cm hosszú. Milyen hosszú szakaszokra osztja ezt az átlót az átlók metszéspontja?
a) A trapéz kiegészítő háromszöge a szárak egyenese és a rövidebb alap által határolt háromszög. Mekkorák a kiegészítő háromszög oldalai, ha az alapok hossza 12 cm és 4 cm, a száraké 8 cm és 3 cm?
b) Egy háromszög oldalai a=12 cm, b=14 cm, c=16 cm. Egy ehhez hasonló háromszög leghosszabb oldala 15 cm. Mekkora a hasonlóság aránya, mekkora a háromszög legrövidebb oldala?
A Pitagorasz után egy másik nagy klasszikus következik, akit Thalésznek hívnak.
Van itt ez a kör és egy rajta átmenő egyenes.
Az egyenesnek a kör belsejében lévő részét húrnak nevezzük.
Ha az egyenes éppen átmegy a kör középpontján, akkor az így keletkező húr neve átmérő.
És a hossza éppen a kör sugarának a kétszerese.
Erről az átmérőről szól a Thalész-tétel.
Válasszunk ki a köríven egy tetszőleges harmadik pontot.
Mondjuk ezt a C pontot itt.
Keletkezik két egyenlő szárú háromszög.
Ez az egyik…
és ez pedig a másik.
Az első háromszögben az alapon fekvő szögeket jelöljük –val.
A másikban pedig –val.
A háromszög belső szögeinek összege 180 fok.
Így van ez az ABC háromszögben is.
Ez a C pont lehet bárhol a köríven…
A C-ben lévő szög mindig derékszög lesz.
Erről szól a Thalész-tétel.
Thalész-tétel:
Ha az AB szakasz egy kör átmérője, és C a kör tetszőleges harmadik pontja, akkor az ACB-szög mindig derékszög.
Ezt úgy is szokás mondani, hogy az AB szakasz a körív bármely harmadik C pontjából derékszögben látszik.
És most nézzük, hogy mi történik akkor, ha az AB szakasz nem átmérő…
Van itt ez az r sugarú kör.
A kör kerületének a kiszámolására már több ezer éve ez a kis képlet van forgalomban:
A kör területe pedig:
Hogyha például a kör sugara 16 cm…
Most nézzük, mi a helyzet a körcikkek területével.
A körcikk területe úgy aránylik a kör területéhez…
mint a körcikkhez tartozó középponti szög a 360o-hoz.
Próbáljuk is ki:
KÖRCIKK TERÜLETE:
Számoljuk ki, hogy egy 10 cm sugarú körben milyen hosszú körív és mekkora területű körcikk tartozik az 50o-os középponti szöghöz.
Itt jön aztán egy másik ügy.
Egy körben 10 cm hosszú körív tartozik a 30 fokos középponti szöghöz. Mekkora a 30 fokos középponti szöghöz tartozó körcikk területe?
Ha van olyan matematikai tétel, amit a világon szinte minden ember ismer, akkor az a Pitagorasz-tétel.
Ismertsége talán annak is köszönhető, hogy nem túl bonyolult dolgot állít:
Vagyis egy derékszögű háromszögben a befogók négyzetének összege egyenlő az átfogó négyzetével.
A Pitagorasz-tétel bizonyítása nagyon egyszerű.
A tétel megfordítása is igaz…
Ja, mondjuk nem ez a megfordítás…
A megfordítás azt jelenti, hogyha egy háromszög oldalaira teljesül, hogy
akkor a háromszög derékszögű.
Derékszögű háromszögben a befogók négyzetének összege egyenlő az átfogó négyzetével.
A Pitagorasz-tételt és a megfordítását az emberiség évezredek óta használja derékszög szerkesztésére.
Egy piramis alapjának az építésénél például elég fontos volt eltalálni a 90 fokot.
Ha csak 1 fokot tévednek, már akkor is olyan ferde lesz a piramis, hogy nem lehet rendesen megépíteni.
Egy nagyon ravasz módszert használtak a derékszög szerkesztésére.
12 darab csomót kötöttek egymástól egyforma távolságra egy kötélre.
Aztán a kötelet háromszög alakban kifeszítették.
Mégpedig így, hogy az oldalak hossza 3 csomó, 4 csomó és 5 csomó legyen.
Ez ugyanis éppen egy pitagoraszi számhármas.
Ami garantálja, hogy itt hajszálpontosan derékszög van.
ennek köszönhetően itt garantáltan derékszög van.
A pitagoraszi számhármasokat már több ezer évvel ezelőtt ismerték, és Több ezer évvel ezelőtt
Pitagoraszi számhármas.
A pitagoraszi számhármasokat a Föld szinte minden jelentősebb civilizációja ismerte, sőt azt is tudták, hogy ez a derékszög szerkesztés egyik legbiztosabb módszere.
A legrégebbi agyagtábla, amin a pitagoraszi számhármasok felbukkannak 3800 éves.
Püthagorasz, akiről a tételt elnevezték úgy durván 2500 éve élt, vagyis biztosan nem ő találta ki, csak neki volt a legjobb a marketingje.
á négyzet meg bé négyzet egyenlő cé négyzet
tezgyén éc őlnegye tezgyén éb gem tezgyén á
A leghíresebb pitagoraszi számhármas a 3,4 és 5, de szintén használták az 5, 12 és 13 számhármast is.
És van még néhány…
Püthagorasz, akiről a tételt elnevezték úgy durván 2500 éve élt, így a tételt nem ő találta ki, csak neki volt a legjobb a marketingje.
A Pitagorasz-tétel használata nagyon egyszerű…
Itt van például ez csinos derékszögű háromszög, amiben ismerjük a két befogót, és a kérdés, hogy mekkora az átfogó.
Már jön is a Pitagorasz-tétel…
És kész is van.
A Pitagorasz-tétel feladatról feladatra megoldja az élet problémáit…
Legalábbis azokat, amik derékszögű háromszögekkel kapcsolatosak.
Itt is jön egy újabb...
Egy derékszögű háromszög befogói p és q, az átfogója pedig r. Tudjuk, hogy p=9 és r=15. Mekkora a q oldal?
Hát igen, ez a p, q és r egy ócska kis trükk, hogy megzavarják az életünket…
Gyakran előfordul, hogy egy feladatban direkt nem a-val, b-vel és c-vel jelölik az oldalakat, hátha így könnyebben elszámoljuk…
A szokásos Pitagorasz-tétel most átalakul:
Ezen nem kell fennakadni, simán jelölhetjük az oldalakat akár így is…
És akkor a jó öreg Pitagorasz-tétel:
De most maradjunk inkább a p, q és r-nél…
Ez is megvan.
De vigyázni kell ezekkel a Pitagorasz-tételes feladatokkal.
Nagyobb mennyiségben ugyanis már ártalmasak lehetnek.
Talán egy még nem árthat meg…
Ebben a derékszögű háromszögben a befogók x és y, az átfogója pedig z. Tudjuk, hogy y = 9 és z = 15. Mekkora az x oldal?
Hopp, erre valami nagyon ronda szám jött ki…
Biztos elszámoltuk…
Az ilyen gyanús végeredményeket érdemes újra csekkolni.
De, ha megint ez jön ki, akkor nincs mit tenni.
Ez a megoldás.
Vagyis simán lehetnek pitagoraszos feladatok csúnya számokkal is.
Az egyiptomi piramisok közül a Nagy-piramis 147 méter magas, és az alapja egy 232 méter oldalhosszúságú négyzet.
Amikor a piramis alapját kezdték építeni, kijelölték a négyzet középpontját, ami fölött majd a piramis csúcsa fog elhelyezkedni.
Milyen távol van ez a pont a piramis négy sarkától?
Rajzoljuk le külön ezt a négyzetet…
És ezt a távolságot keressük.
A négyzet átlói merőlegesek egymásra…
Vagyis ez egy derékszögű háromszög.
És a másik befogója is x.
Jöhet a Pitagorasz…
Számoljuk ki azt is, hogy milyen hosszú a piramis egyik oldaléle.
Már megint egy derékszögű háromszög…
Az egyik befogója 164 méter hosszú…
A másik befogó pedig a piramis magassága.
Jöhet megint a Pitagorasz-tétel…
A piramis oldaléle 220,24 méter hosszú.
A Pitagorasz-tétellel lazán ki tudunk számolni néhány dolgot egyenlő szárú háromszögekben is.
Egy szimmetrikus trapéz szárai 13 cm hosszúak, a kisebbik alapja 6 cm a nagyobbik pedig 16 cm. Mekkora a trapéz területe?
Mivel a trapéz szimmetrikus…
ez a szakasz itt…
ugyanolyan hosszú, mint ez a másik.
Itt jön aztán egy kis Pitagorasz-tétel.
A trapéz területe pedig:
Itt jön egy másik trapéz, aminek a szárai 13 és 15 cm hosszúak, a rövidebbik alap 10 cm trapéz magassága pedig 12cm.
Mekkora a trapéz területe?
Az ilyen feladatoknál az első lépés mindig az, hogy ne essünk pánikba.
Hogyha ezzel megvagyunk, akkor innen már könnyű.
A magasságot mindig úgy érdemes berajzolni, hogy derékszögű háromszögek keletkezzenek.
Most pedig jön két Pitagorasz-tétel.
És a trapéz területe:
És van ez a harmadik trapéz, aminek a területe 108 cm2, az alapjai 24 cm és 3 cm, az egyik szára pedig 10 cm. Mekkora a másik szár?
A trapéz területe:
A trapéz egyik szára 10 cm, ami éppen ennek a derékszögű háromszögnek az átfogója.
És a trapéz másik szára is egy derékszögű háromszög átfogója…
Hát, ez is megvan.
és 24 cmszimmetrikus trapéz szárai 13 cm hosszúak, a kisebbik alapja 6 cm a nagyobbik pedig 16 cm. Mekkora a trapéz területe?
A Pitagorasz-tétellel lazán ki tudunk számolni néhány dolgot egyenlő szárú háromszögekben is.
Ebben az egyenlő szárú háromszögben a szárak 13 cm hosszúak, az alap pedig 10 cm. Mekkora a háromszög területe?
A jó öreg területképlet szerint ekkora.
Az a oldalról tudjuk, hogy 10 cm…
De kellene még a háromszög magassága is.
És itt kerül képbe a Pitagorasz-tétel.
Az alaphoz tartozó magasság az alapot felezi…
Ez meg is van.
Nézzünk meg még egyet…
Egy egyenlő szárú háromszög Területe 120 cm2, az alapja pedig 30 cm. Mekkorák a szárai?
Lássuk, mit kezdhetnénk a területtel…
És most jöhet a Pitagorasz-tétel…
Kész is, megvannak a szárak.
Hát, ez nem túl szép…
Nézzük, mekkora lesz a terület…
Végül itt jön egy szabályos háromszög, aminek az oldalai 16 cm hosszúak. Mekkora a háromszög területe?
Ezt akár általánosan is kiszámolhatjuk…
Nézzük meg, hogy mekkora lesz az a oldalú szabályos háromszög területe.
Mindent ugyanúgy csinálunk, mint az előbb…
Itt az ideje rendet tenni egy kicsit…
Síkidomnak nevezzük a sík zárt vonalakkal körülhatárolt részét.
Bob tehát nem tekinthető síkidomnak, mert kiállnak belőle ezek a vonalak.
Az összes többi viszont síkidom.
A síkidomok közül most csak azokkal foglalkozunk, amikben nincsenek belül lukak.
A luk nélküli síkidomokat egyszerű síkidomoknak nevezzük.
Hogyha megszüntetjük itt a lukakat…
Hopp, akkor már ezek is egyszerű síkidomok lesznek.
Mivel csak egyszerű síkidomokkal foglalkozunk, hívjuk őket simán síkidomnak.
A síkidomok között vannak olyanok, ahol a határoló vonalak csak egyenes szakaszokból állnak.
Ezeket hívjuk sokszögeknek.
Vagyis mindegyik sokszög síkidom.
És itt jön még egy dolog…
Ez itt egy vár, felülről nézve.
Ami végülis szintén egy síkidom.
Ráadásul egy sokszög.
A várakat egy nagyon ravasz trükkel építették meg…
Amikor jön az ostromló tömeg…
És odaérnek a várfal tövébe…
A vár védői, a vár belsejéből is rálátnak a várfalra.
És így a várból tudják támadni az ostromlókat.
A dolog lényege ez.
Tudunk találni olyan pontokat, amik a váron belül vannak, de ha összekötjük őket, az összekötő szakasz mégis a váron kívül halad.
Egy háromszögben ez lehetetlen volna.
Ezért nem építenek háromszög alaprajzú várakat.
A vár-típusú sokszögeket konkáv sokszögeknek nevezzük.
A másik pedig a konvex.
Remek, újabb definíciók, ahol lehetetlen megjegyezni, hogy melyik az egyik és melyik a másik…
De csak mostanáig.
Itt jön ugyanis egy trükk.
Mindez nem csak sokszögekre, hanem bármilyen síkidomra is működik.
A konvex és konkáv szemléltetésére van egy unalomig ismert példa.
Várak nélkül…
A konkáv síkidom az, amelyikben el lehet bújni…
A konvex pedig, amiben nem lehet elbújni.
De hát miért akarna bárki is egy síkidomban elbújni?
És azon kívül, hogy ennek az elbújásnak semmi értelme, még simán összekeverhetjük, hogy most akkor a konkáv vagy a konvex az elbújós…
Úgyhogy maradjunk inkább a váraknál.
Most pedig folytassuk a sokszögekkel…
A sokszögeknél tartottunk…
És addig jutottunk, hogy vannak köztük konvexek és konkávok.
Most pedig nézzük meg, hogy mit tudnak még a sokszögek…
Vannak csúcsaik…
Oldalaik…
És szögeik.
Ráadásul mindegyikből ugyanannyi.
Ez itt például egy hatszög.
Vagyis hat darab csúcsa van, hat darab oldala és hat darab szöge.
Egy sokszöget szabályosnak nevezünk, ha minden oldala és minden belső szöge egyforma.
Ez például egy szabályos hatszög.
Mint ahogyan ez is hatszög…
Csak éppen ez a másik hatszög nem szabályos.
Ennek is minden oldala egyforma hosszú…
De a szögei, azok nem ugyanakkorák.
Aztán itt van egy szabályos ötszög.
Ez egy szabályos négyszög…
Amit úgy hívunk, hogy négyzet.
És ez itt egy szabályos háromszög.
Végül nézzük meg, hogy mi történik akkor, ha egy sokszögnek kiválasztjuk két csúcsát…
És összekötjük őket.
Olyankor, amikor szomszédos csúcsokat választunk…
A sokszögnek az egyik oldalát kapjuk.
Amikor viszont a csúcsok nem szomszédosak…
Az így kapott szakaszt a sokszög átlójának nevezzük.
A sokszögek nem szomszédos csúcsait összekötő szakaszokat átlónak nevezzük.
Egy háromszögben minden csúcs szomszédos egymással…
Úgyhogy a háromszögeknek nincsenek átlóik.
A négyszögeknek két darab átlójuk van.
A többi sokszögnek pedig…
Hát, azoknak már jó sok.
És most elérkezett az idő, hogy egy kicsit jobban megismerjük a háromszögeket.
És most nézzük, mit tudnak a háromszögek.
Vannak hegyes-szögű háromszögek…
Ezeknek minden szöge hegyes-szög.
És vannak tompaszögű háromszögek…
Ezeknek minden szöge tompaszög.
Ja, nem.
A tompaszögű háromszögeknek csak az egyik szöge lehet tompaszög.
Hogyha ugyanis két tompaszögük is lenne…
Hát igen, így már nem kapnánk háromszöget…
Van még egy harmadik kategória is…
Ezek a derékszögű háromszögek.
Ezt jó tudni, írjuk is föl magunknak valahova ide.
És így szépen megjelent egymás mellett a háromszög mindhárom belső szöge.
Vannak aztán a háromszögnek külső szögei is.
A B csúcsnál a külső szög…
Hát, az nem ez…
A B csúcsnál a külső szög az ez.
De lehet ez is.
A külső szögek tehát ilyen kiegészítő szögek.
És bármely háromszögben a külső szögek összege 360o.
Ezt is felírhatnánk ide…
De inkább mégse.
A háromszögek belső szögeinek az összege ugyanis mindig 180 fok.
Így hát nem lehet benne két olyan szög, ami 90 foknál nagyobb.
Most pedig essünk túl néhány dögunalmas formaságon.
A háromszögek csúcsait az ABC nagy betűivel jelöljük.
És a szögeket pedig görög betűkkel jelöljük.
Hogyha veszünk most még egy ugyanilyen háromszöget…
És így szépen egymás mellé rakjuk őket…
Akkor ez a szög itt éppen 180o.
Ezek a szögek pedig váltószögek…
Tehát egyforma nagyok.
Vagyis bármely háromszög belső szögeinek összege éppen 180o.
A belső szögek összege mindig 180 fok.
És van itt még valami…
A háromszög bármelyik oldalának rövidebbnek kell lennie, mint a másik két oldal összege.
Csak így tudunk belőlük háromszöget építeni.
Hogyha a c oldal hosszabb lenne, mint az a és b oldal összege…
Bárhogyan is próbálkozunk…
Nem lesz belőle háromszög.
Ezt a nem túl bonyolult dolgot hívjuk háromszög-egyenlőtlenségnek.
HÁROMSZÖGEK
Háromszög-egyenlőtlenség
Minden háromszögben bármelyik két oldal összege nagyobb a harmadik oldalnál.
Ezt háromszög-egyenlőtlenségnek hívják.
A háromszögek egyik speciális típusa az egyenlő szárú háromszögek.
Az egyenlő szárú háromszögek úgy működnek, hogy van két ugyanakkora oldaluk…
Ezeket hívjuk száraknak.
És van még egy harmadik oldal, amit alapnak nevezünk.
.
Az egyenlő szárú háromszögek tengelyesen szimmetrikusak.
Vagyis az alapon fekvő szögek egyformák.
A szárak által bezárt szöget pedig a szimmetriatengely felezi.
Az alapot a-val szoktuk jelölni…
A szárakat pedig b-vel.
Az a oldallal szemben van az A csúcs…
És az A csúcsnál van az a szög.
A szárakat b-vel jelöljük.
És ezek béta szöget zárnak be az alappal.
Hogyha az egyenlő szárú háromszögben az alap is ugyanolyan hosszú, mint a szárak…
Akkor szabályos háromszöget kapunk.
A szabályos háromszögnek minden oldala ugyanakkora.
És minden szöge is ugyanakkora.
Mivel pedig a háromszögek belső szögeinek összege 180 fok…
Végül itt jön még egy speciális háromszögfajta…
A derékszögű háromszög.
A derékszögű háromszögnek azt az oldalát, ami a derékszöggel szemben van, átfogónak hívjuk.
átfogó
A másik két oldal pedig, amik befogják a derékszögű csúcsot…
Azok a befogók.
befogó
És még egy dolog…
A derékszöget lehet jelölni így is…
Meg így is.
A csúcsokat úgy szoktuk a derékszögű háromszögekben elnevezni, hogy mindig a C csúcsnál legyen a derékszög.
És a vele szemben lévő oldalt vagyis az átfogót hívjuk c-nek.
A másik két csúcs A és B…
És velük szemben van az a és b oldal, amik mindketten befogók.
Kezdetnek ennyit a háromszögekről.
Íme, ez egy négyszög.
A csúcsokat az abc nagy betűivel jelöljük, az oldalakat pedig…
Az oldalakat az abc kis betűivel jobb sodrással.
És a négyszögek rendelkeznek valami olyannal, amiről a háromszögek még csak nem is álmodhatnak…
Vannak átlóik.
Most pedig nézzük, hogy milyen típusú négyszögek vannak.
A legszabályosabb négyszög a négyzet.
Az oldalai egyenlő hosszúak, a csúcsaik derékszögek.
És az átlóik is merőlegesek egymásra.
A négyzetet kétféleképpen tudjuk elrontani.
Vagy az oldalait rontjuk el…
vagy a szögeit.
Az egyiket téglalapnak hívjuk, itt csúcsoknál lévő szögek továbbra is derékszögek, csak éppen az oldalaknak nem kell egyforma hosszúnak lennie.
TÉGLALAP
A másiknak a neve rombusz. Itt az oldalak továbbra is mind egyforma hosszúak, csak éppen a csúcsoknál nem kell derékszögnek lenni.
ROMBUSZ
De a téglalap és a rombusz hivatalos definíciója nem ez.
A helyzet egy kicsit izgalmasabb.
Ez itt mind téglalap…
Ez pedig itt mind rombusz.
Tehát a négyzet is téglalap.
Sőt a négyzet rombusz is.
Most már egy kicsit kezd zavarossá válni a helyzet, de aggodalomra semmi ok.
Mindjárt kitisztul.
Csak előbb itt jön még egy dolog.
Amiben a téglalap és a rombusz minden rossz tulajdonságát egyesítjük.
És íme, itt is van.
Ez egy oldalba lökött téglalap.
Vagy hivatalos nevén paralelogramma.
Rossz hír: újabb osztály…
És kiderül, hogy tulajdonképpen itt eddig mindenki paralelogramma.
A paralelogramma olyan négyszög, aminek van két párhuzamos oldalpárja.
Egy darab oldalpár…
és még egy.
A téglalap nem más, mint derékszögű paralelogramma.
A rombusz pedig egyenlő oldalú paralelogramma.
De van ám itt még más is.
Jönnek a trapézok.
A trapéz egy olyan négyszög, aminek van legalább egy párhuzamos oldalpárja.
Persze ettől még lehet neki több is…
Na, csináljunk egy kis helyet a trapézoknak is.
Úgy néz ki, hogy eddig itt mindenki trapéz.
De még mindig van újabb típus…
Ehhez most az átlókat kell nézni.
Mégpedig azt, hogy merőlegesek-e vagy sem.
A merőleges átlójúak közül azokat nevezzük deltoidnak, amik papírsárkány-alakúak.
Ez deltoid…
Ez nem deltoid.
És végül vannak azok a négyszögek, amiknek nincsen semmilyen különösebb ismertetőjele.
Ez tehát a teljes kollekció.
A két nagy csoport a trapézok és a deltoidok csoportja.
Deltoid az a négyszög, amelynek átlói merőlegesek egymásra és legalább az egyik átló szimmetriatengely.
Trapéz pedig az, amelynek van legalább egy párhuzamos oldalpárja.
A trapézok közül azokat, akiknek két párhuzamos oldalpárja is van paralelogrammának nevezzük.
Az egyenlő oldalú paralelogrammák a rombuszok.
A derékszögű paralelogrammák pedig a téglalapok.
Van azonban egy olyan dolog, amely minden négyszögben egyforma.
Hogyha összeadjuk a négyszögek belső szögeit…
akkor mindig 360 fokot kapunk.
És most lássuk, mi a helyzet a négyszögek területével.
A többi négyszög területét általában úgy lehet csak kiszámolni, hogy földaraboljuk őket háromszögekre…
A háromszögek területével pedig már valahogyan el tudunk bánni.
A teljesen általános négyszögekkel nem igazán tudunk mit kezdeni…
Általában ilyenkor azt csináljuk, hogy az egyik átlója mentén kettévágjuk két darab háromszögre.
És a háromszögekre már egy tonna területképletünk meg mindenféle egyéb képletünk van.
Így hát most csak a speciális négyszögekkel fogunk foglalkozni.
A speciális négyszögek két nagy osztályba sorolhatók.
Az egyik csoport a trapézok, a másik pedig a deltoidok.
Most a trapézokkal fogunk foglalkozni.
Jönnek is a trapézok...
Trapézok
A trapéz olyan négyszög, aminek van két párhuzamos oldala.
Ezeket hívjuk a trapéz alapjának.
És most lássuk a trapéz szögeit.
A trapéz szárain fekvő szögek tehát mindig 180 fokra egészítik ki egymást.
Ha a trapéz egyik alapján fekvő két szög ugyanakkora, olyankor a trapéz szimmetrikus.
A szimmetrikus trapézt szokás még egyenlő szárú trapéznak is hívni, ugyanis a két szára mindig egyforma hosszú.
Ezen kívül van egy fantasztikus tulajdonsága is, hogy van köré írható köre.
Egy téglalap területét kiszámolni őrülten egyszerű.
Csak összeszorozzuk a két oldalát, és kész is.
A dolog akkor válik egy kicsit érdekesebbé…
Ha a téglalapot egy kicsit oldalba lökjük.
Ezt úgy hívjuk, hogy paralelogramma.
A paralelogramma területét egy trükk segítségével tudjuk kiszámolni.
Átdaraboljuk téglalappá.
Ezt a vonalat itt a paralelogramma magasságának nevezzük.
Legalábbis az a oldalhoz tartozó magasságnak.
Mert tartozik magasság a b oldalhoz is.
De most maradjunk inkább az a oldalnál.
Hogyha veszünk egy ollót, és a magasságvonalnál szétvágjuk a paralelogrammát…
És aztán a levágott darabot átrakjuk ide…
Hopp, akkor éppen egy téglalapot kapunk.
Aminek az egyik oldala a a másik pedig ma.
És így a területe…
Most nagyon óvatosan visszatesszük ezt a kis háromszöget…
És meg is van a paralelogramma területe.
Ezt gyorsan írjuk is föl magunknak ide.
elrontjuk.
A trapézoknál tartottunk…
