- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
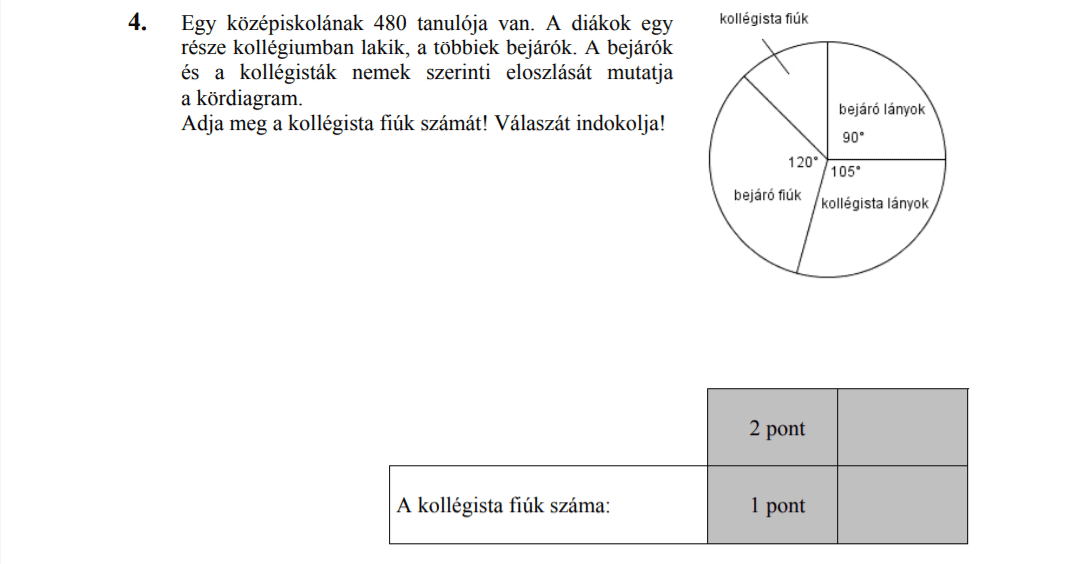
- ÚJ! Számrendszerek
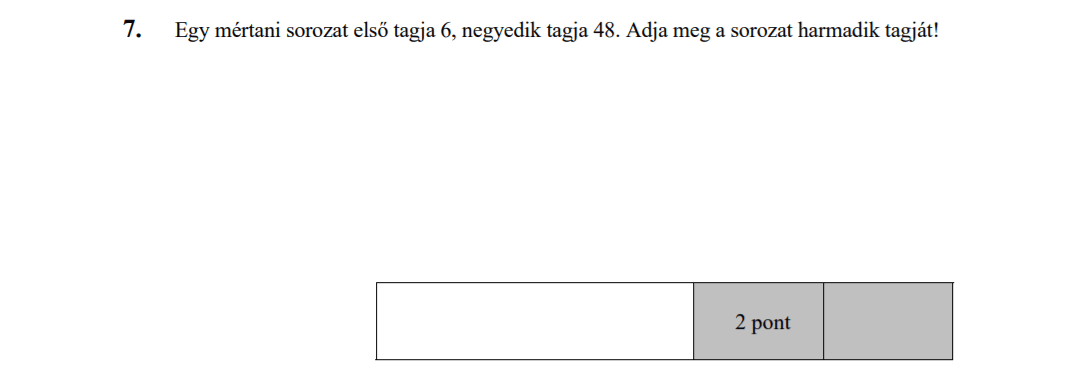
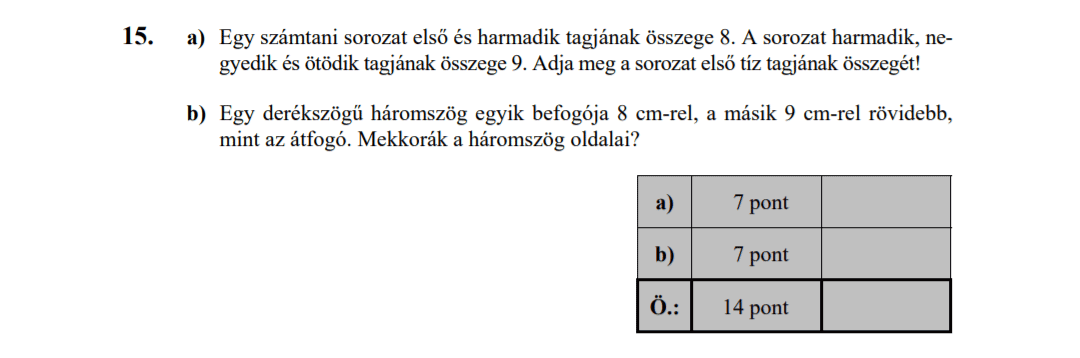
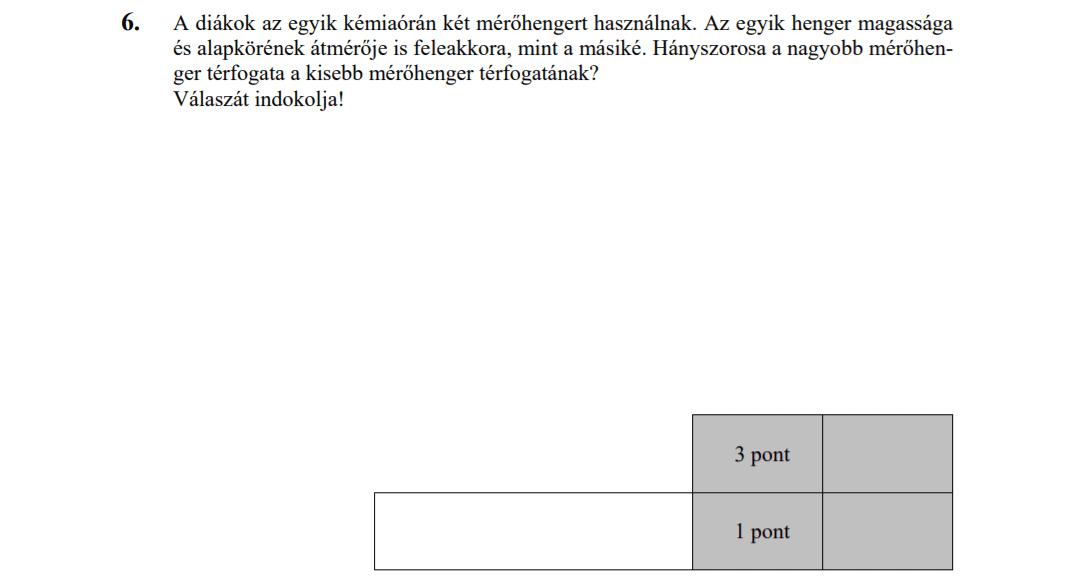
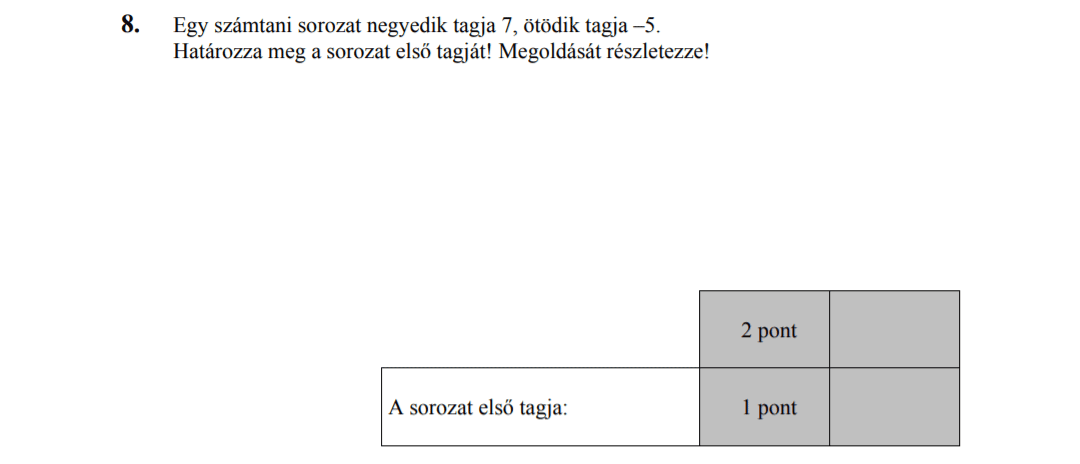
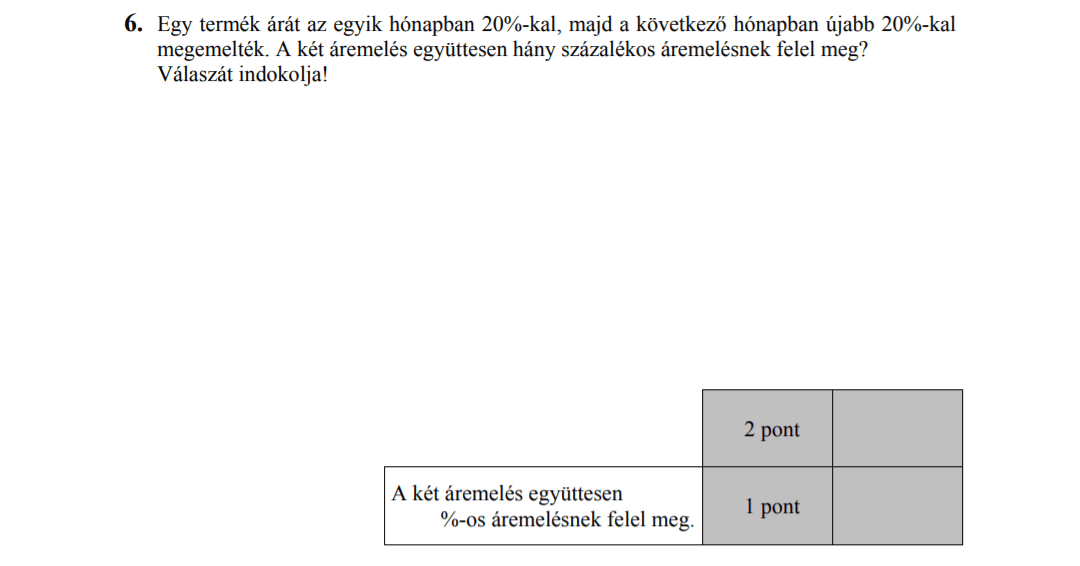
- Számtani és mértani sorozatok (16 pont)
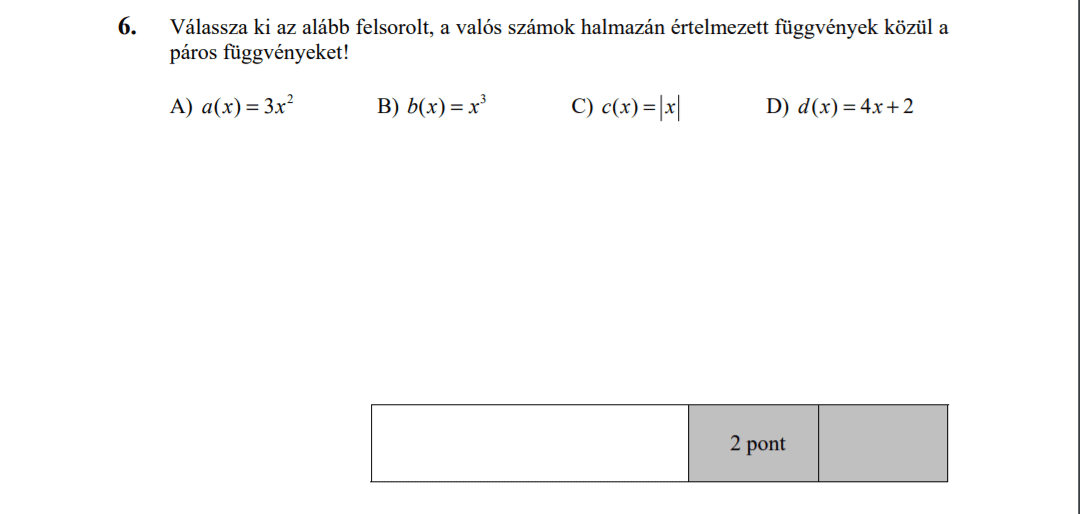
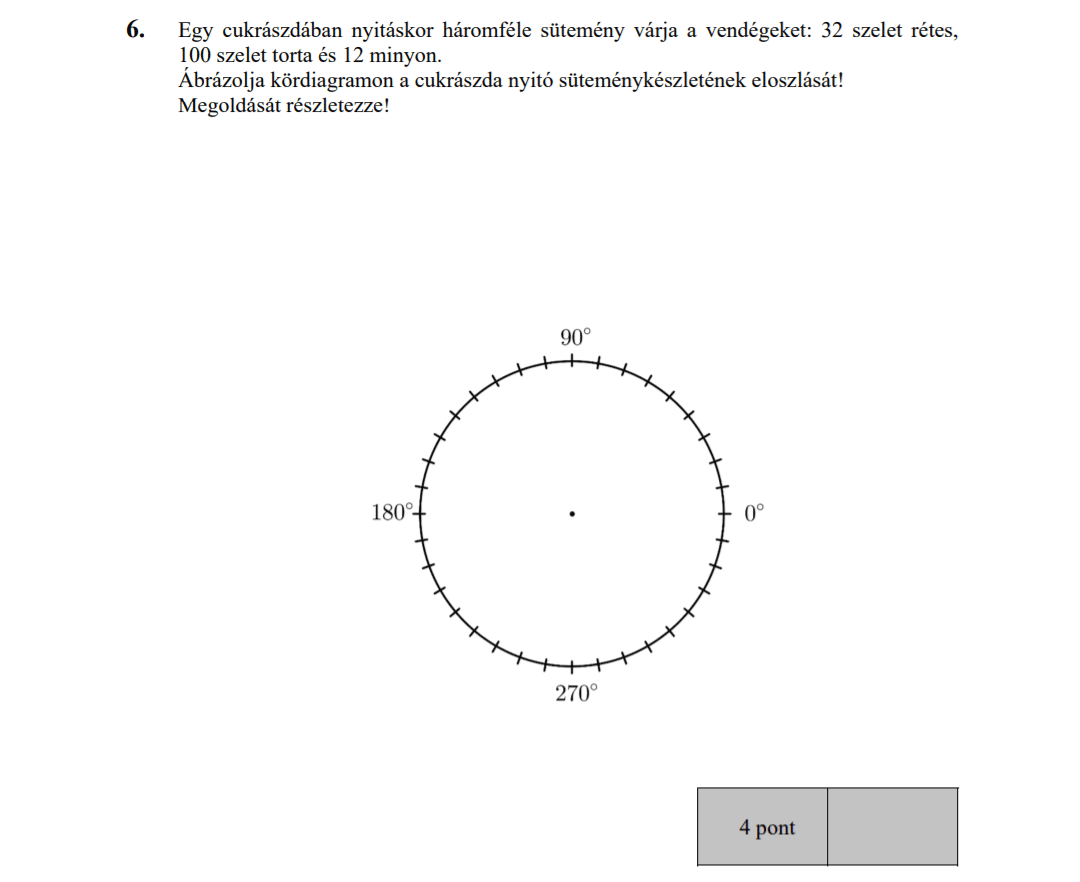
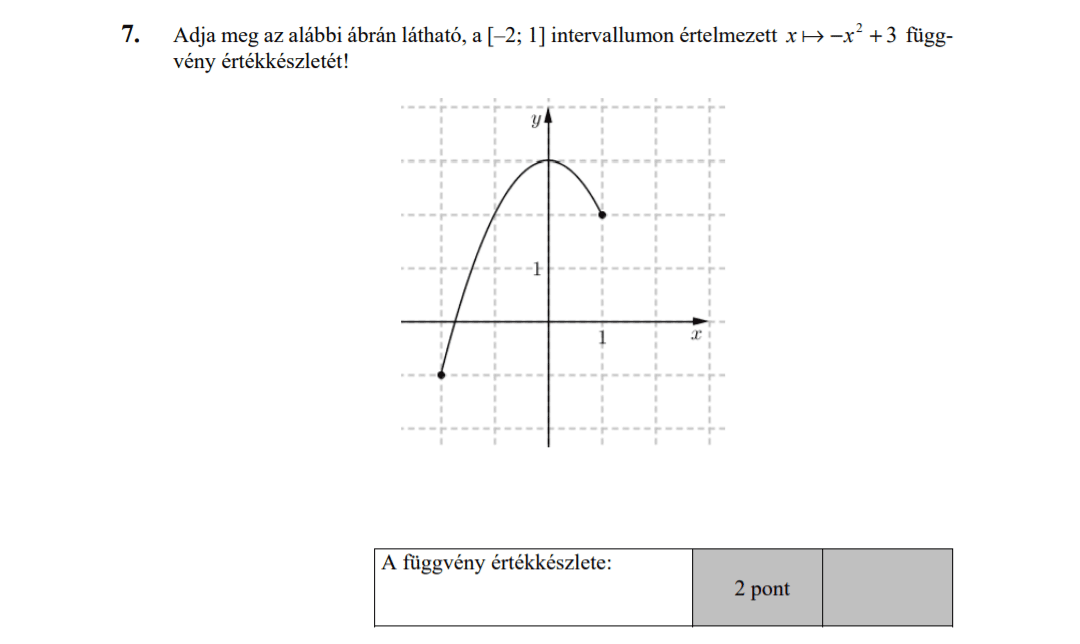
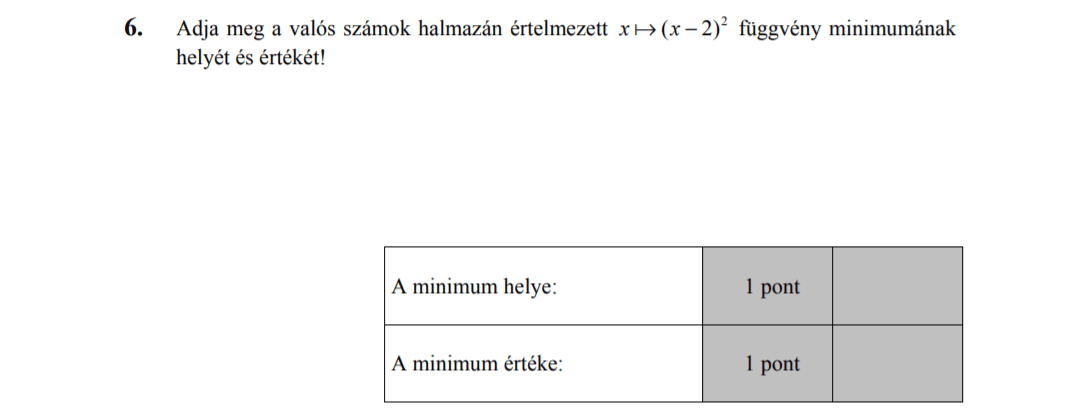
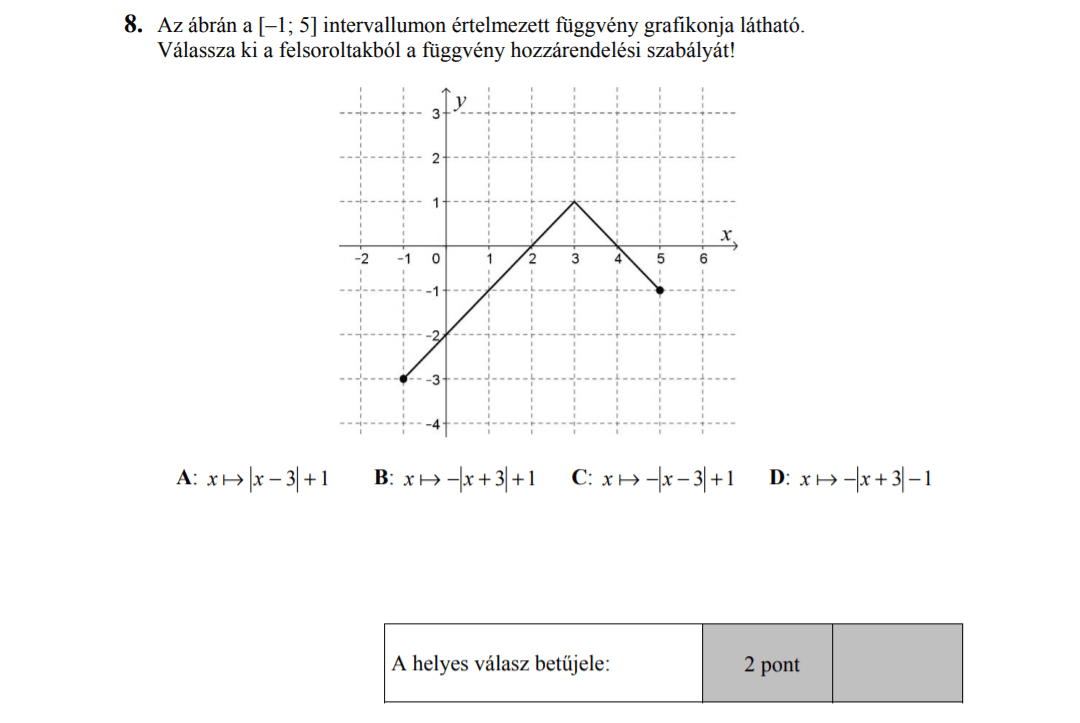
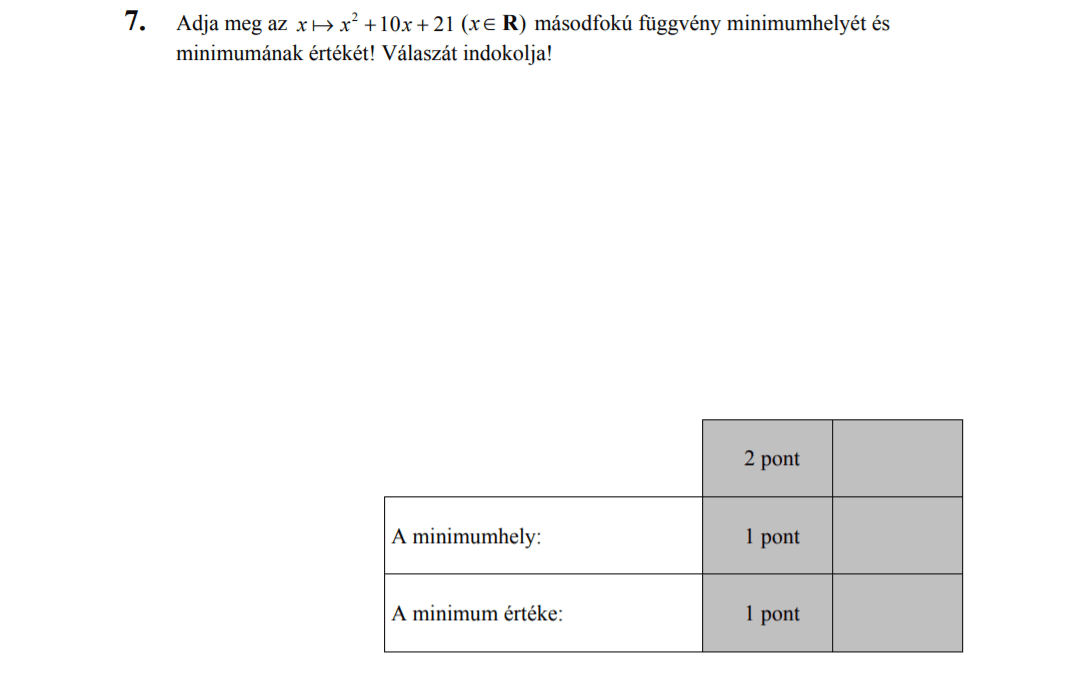
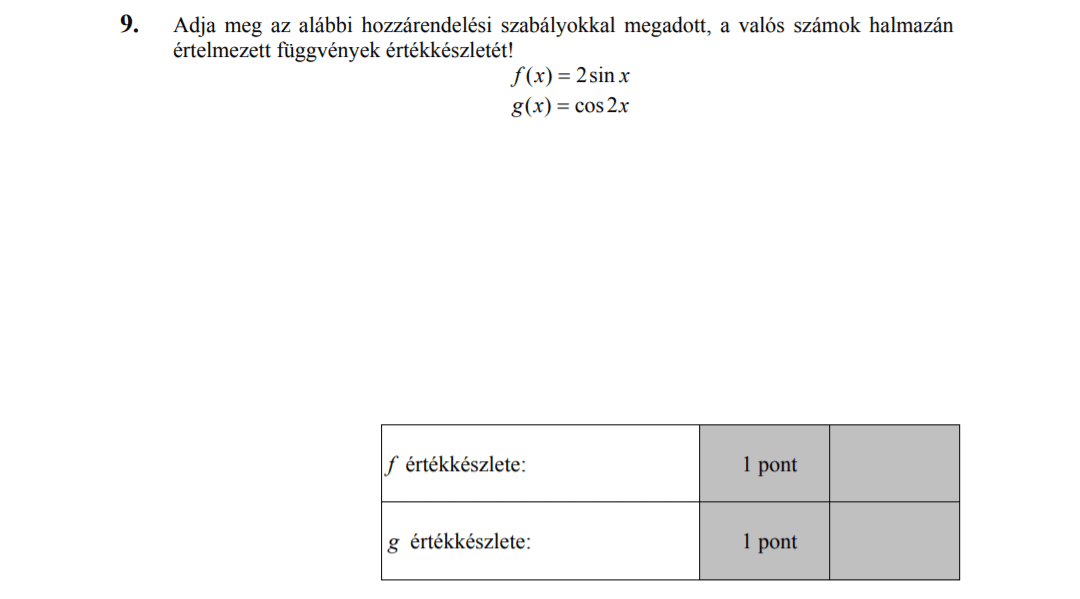
- Függvényekkel kapcsolatos feladatok (9,8 pont)
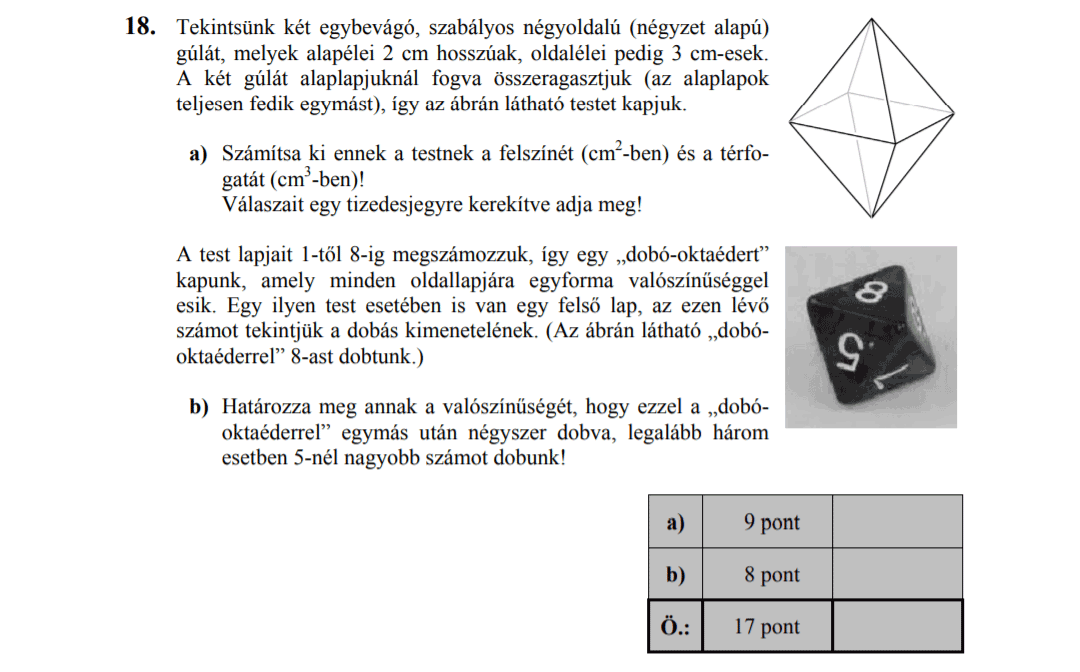
- Térgeometria (9,8 pont)
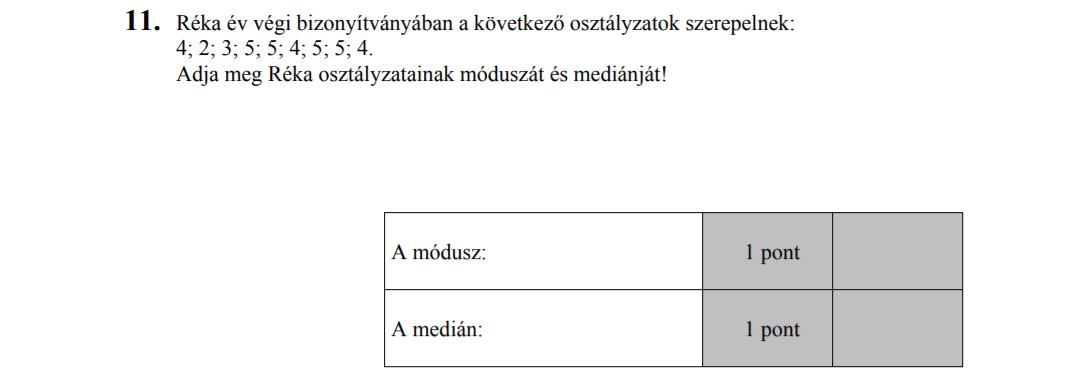
- Statisztika (9,3 pont)
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
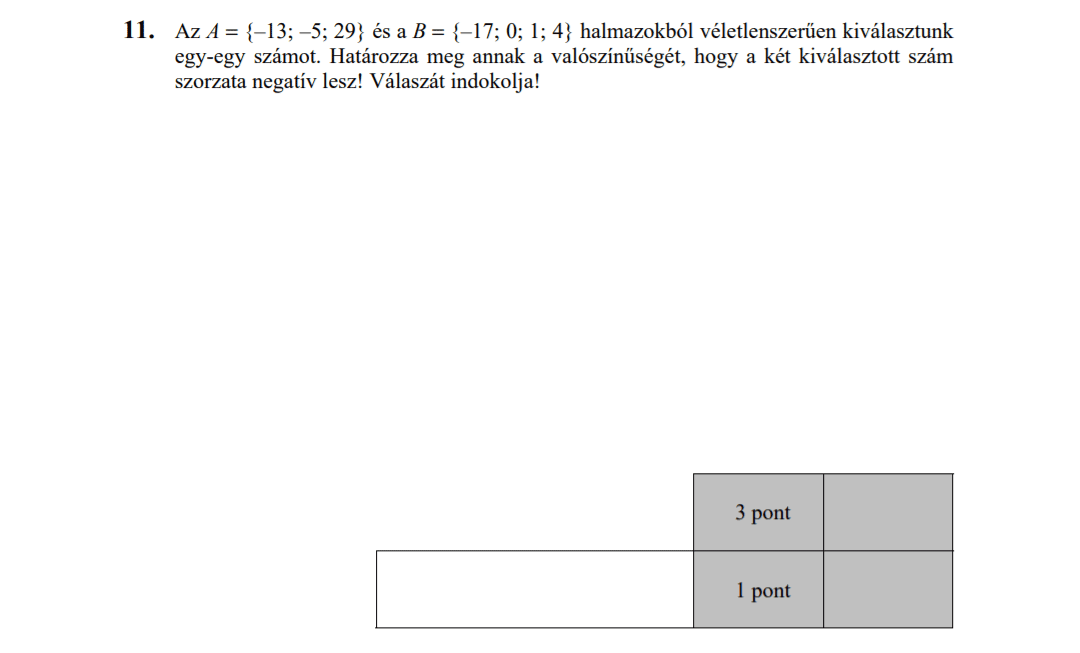
- Valószínűségszámítás (9,1 pont)
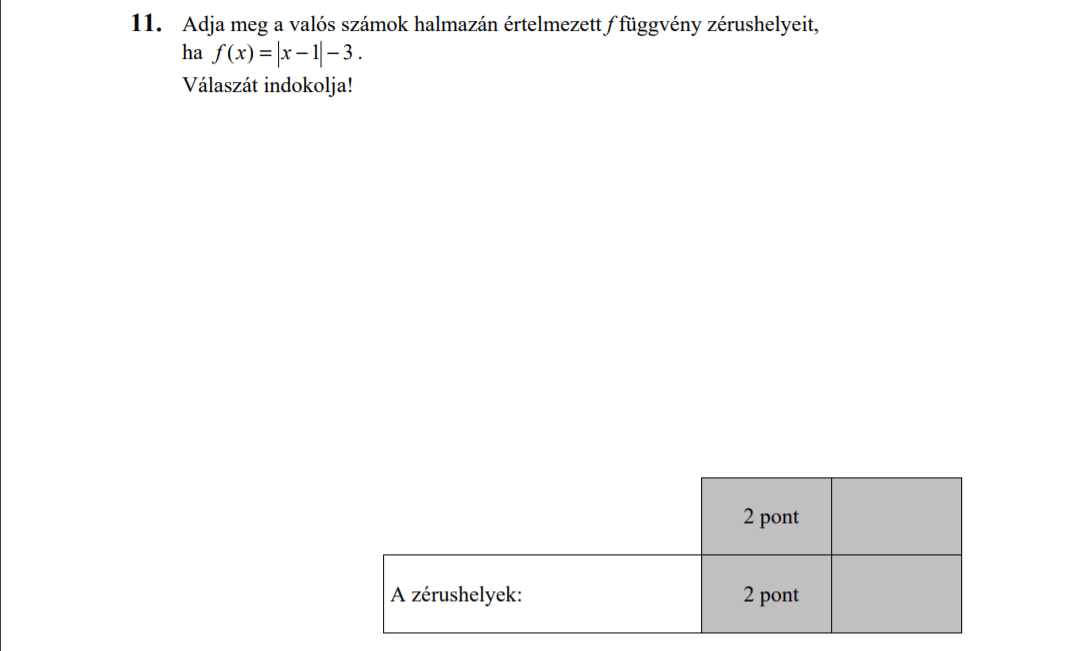
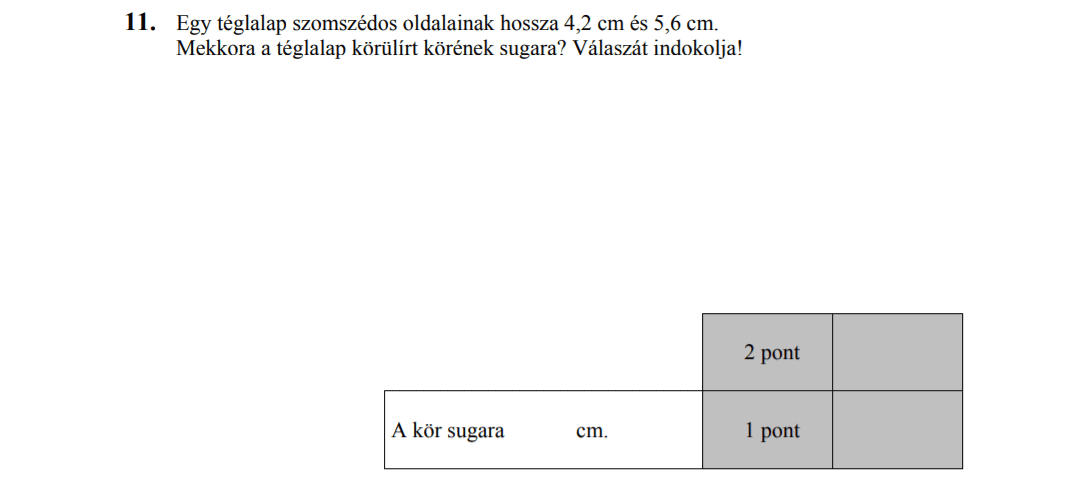
- Szöveges feladatok (7,4 pont)
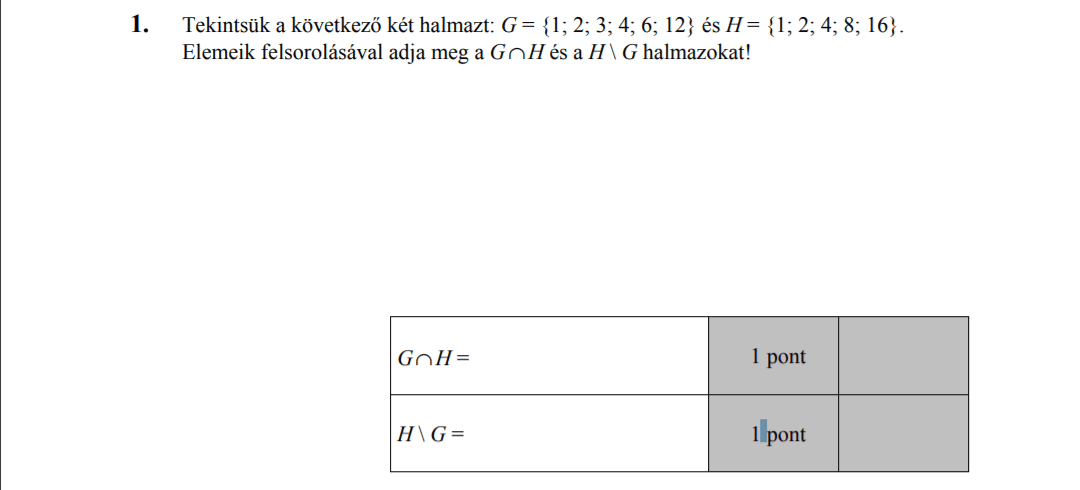
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
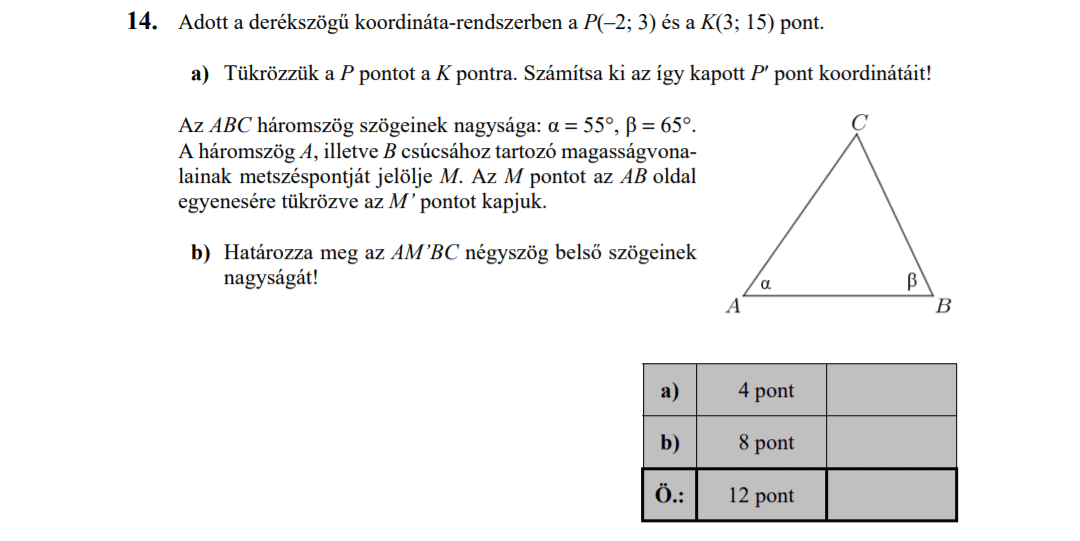
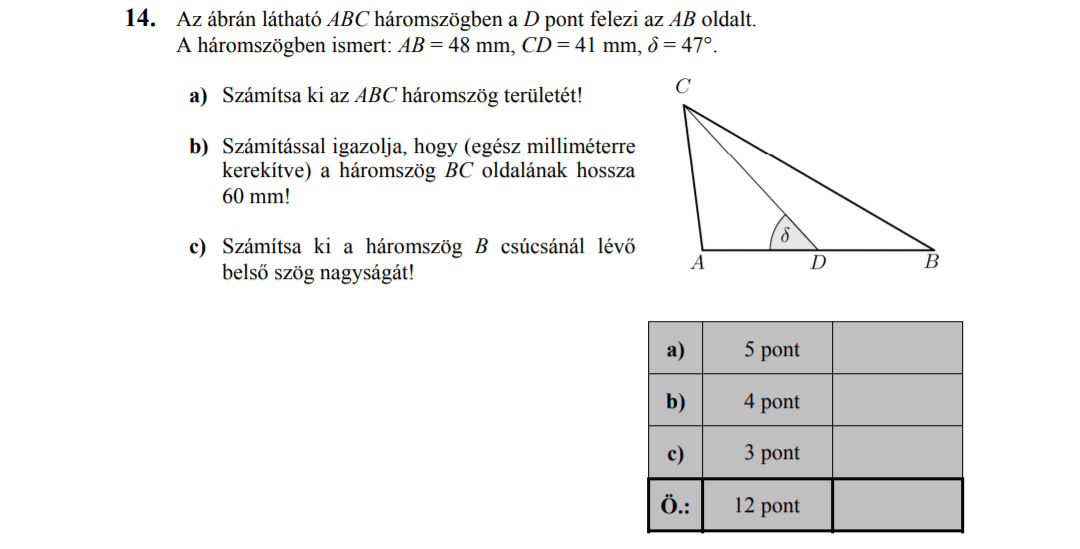
- Síkgeometria (4,5 pont)
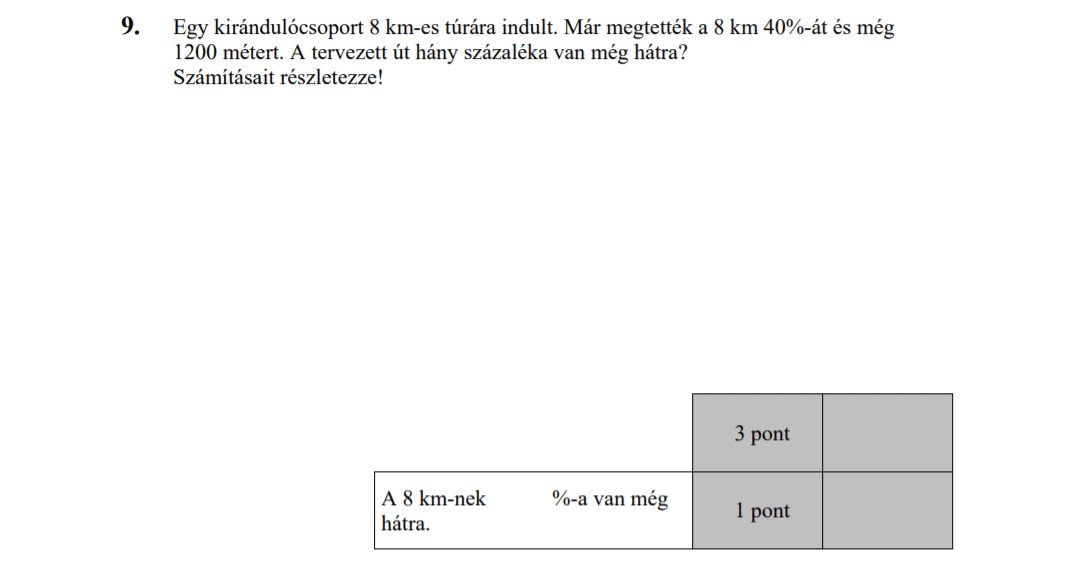
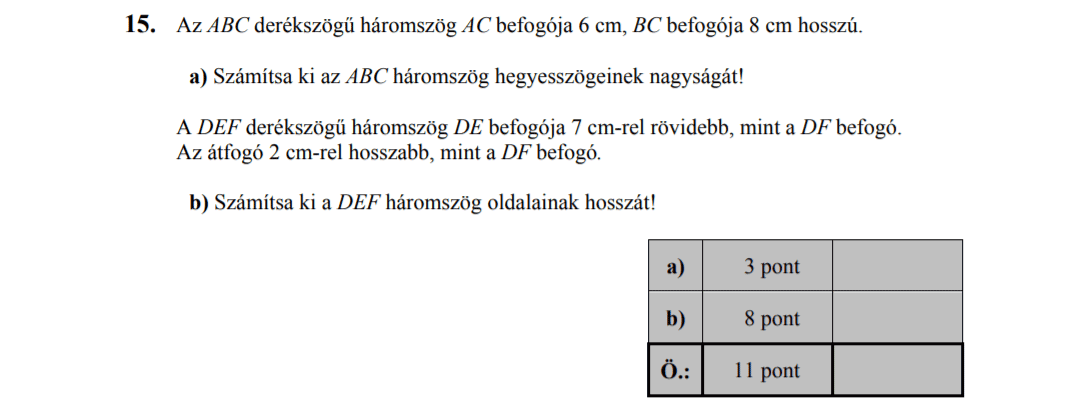
- Százalékszámítás (3,8 pont)
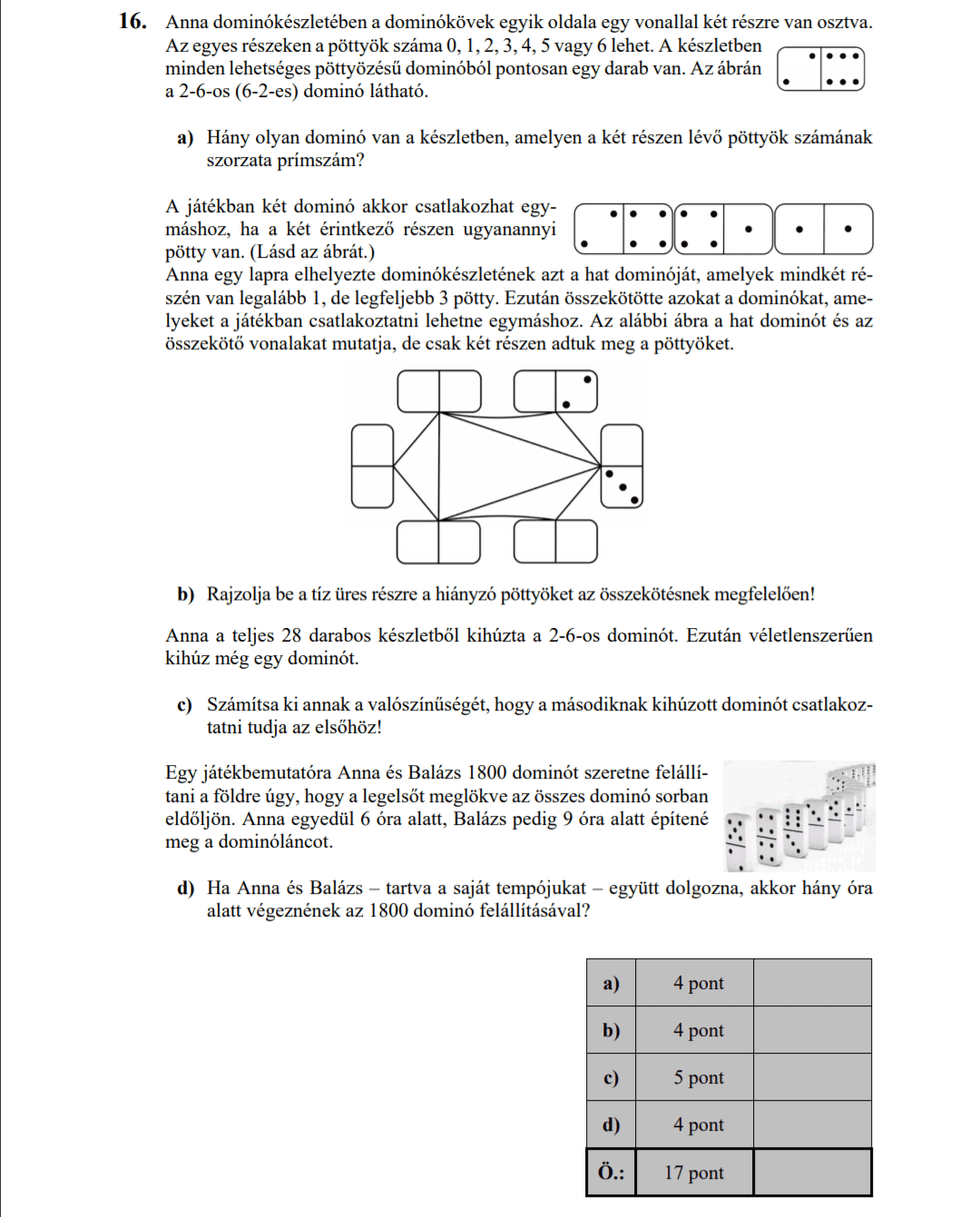
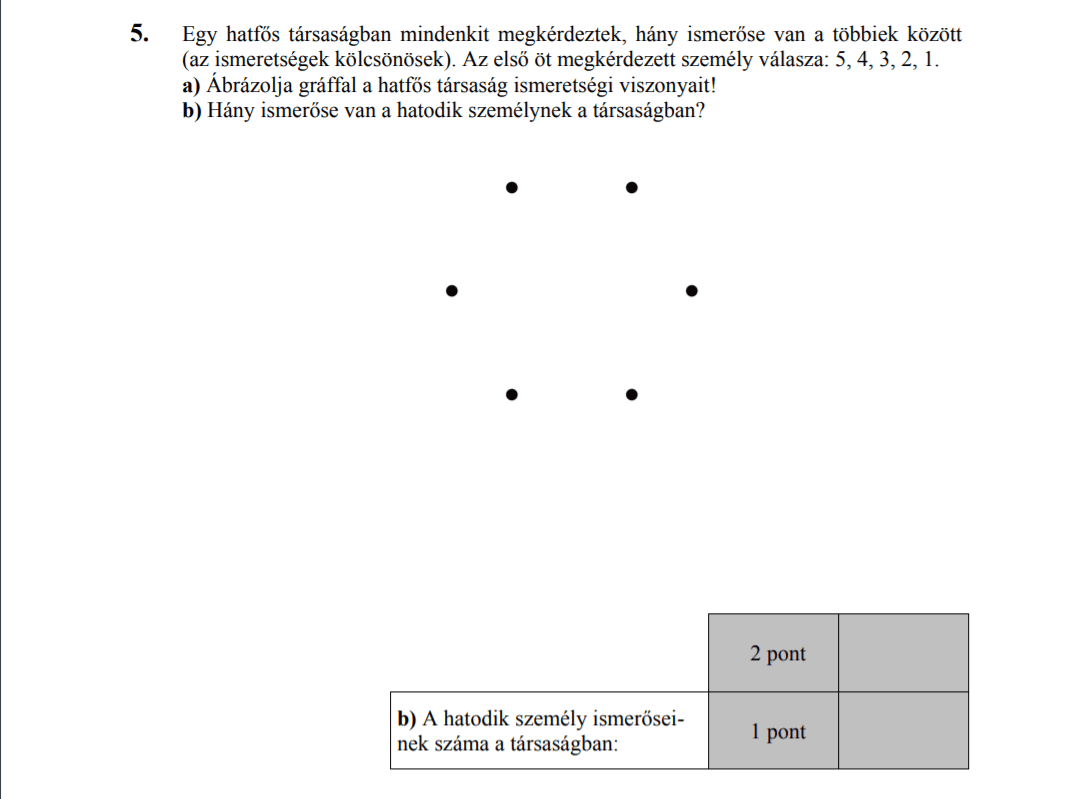
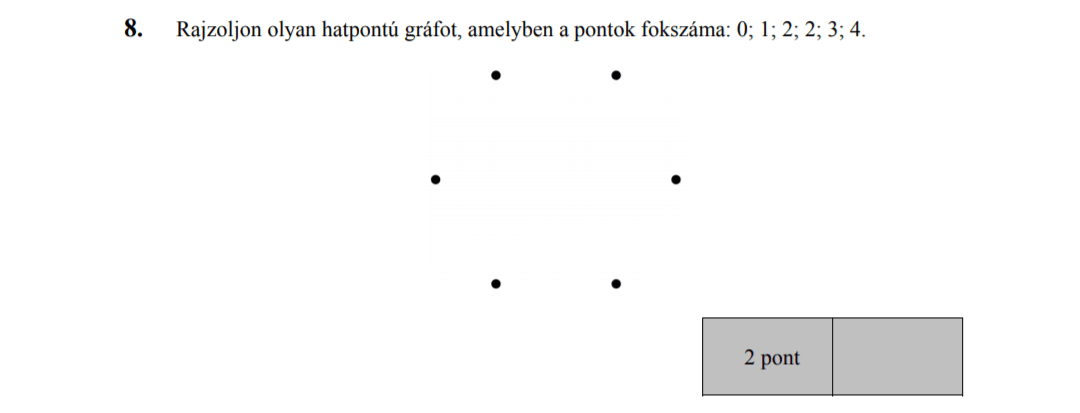
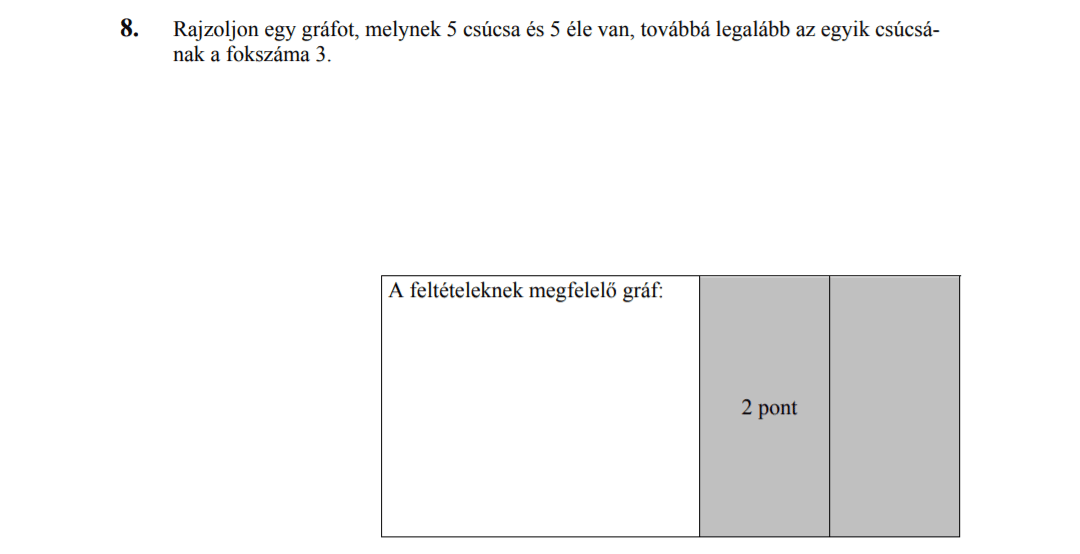
- Gráfok (3 pont)
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
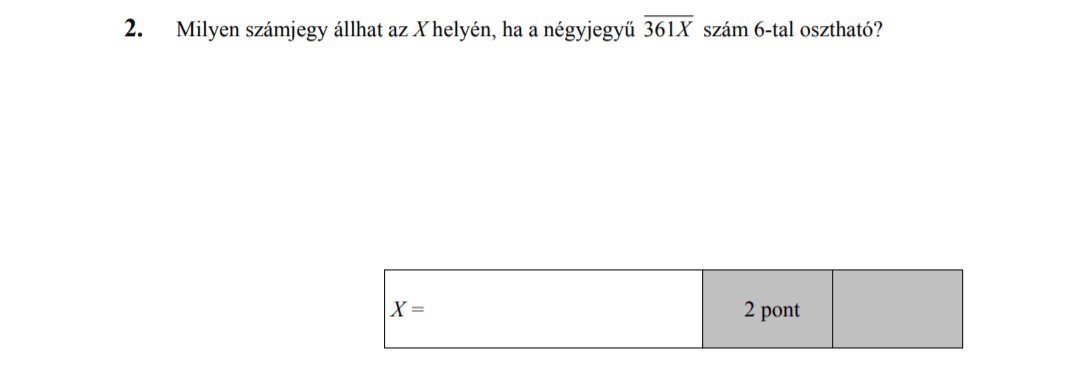
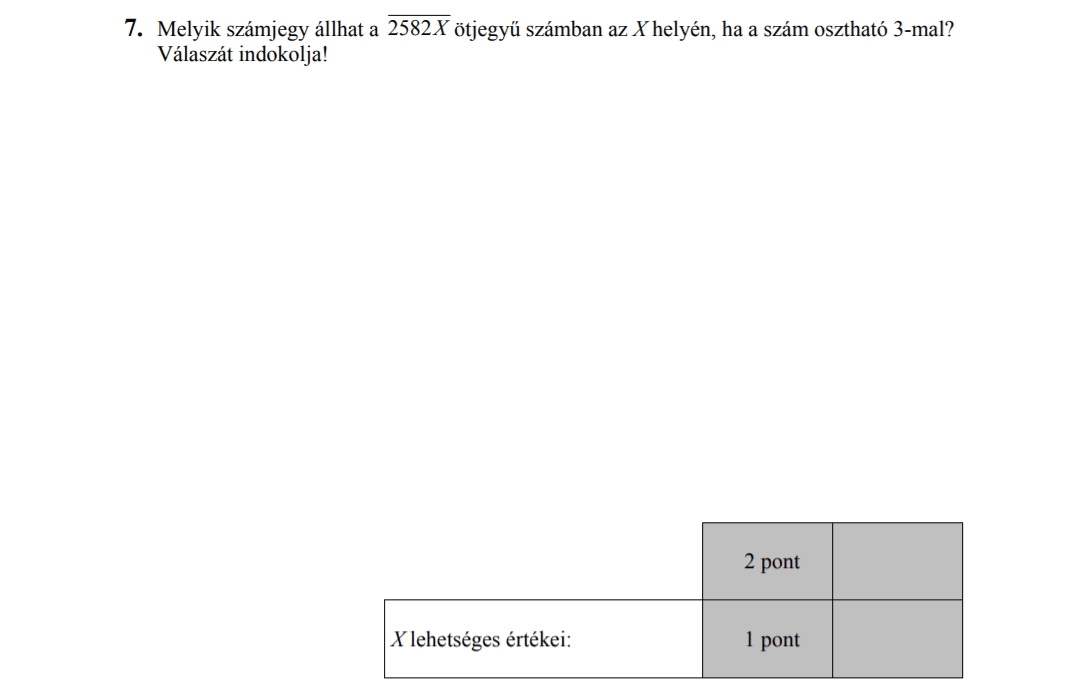
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
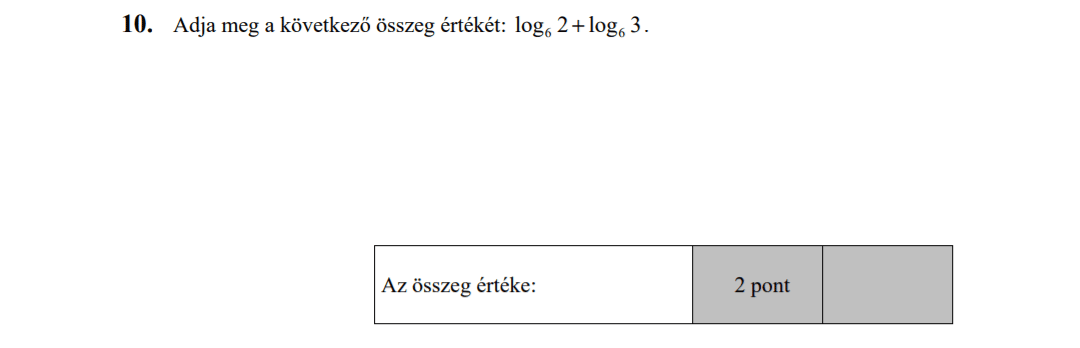
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
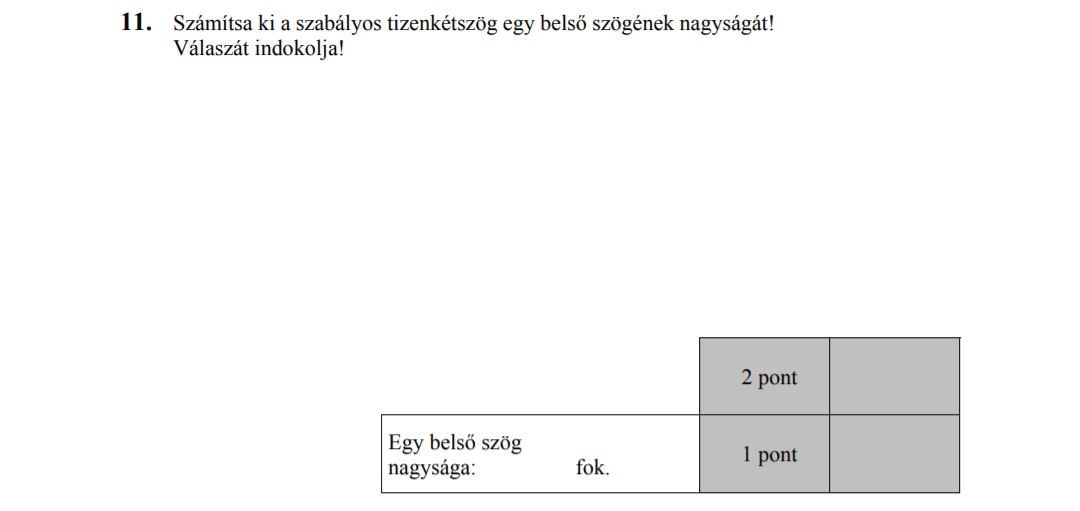
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Gyökös azonosságok és gyökös egyenletek
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


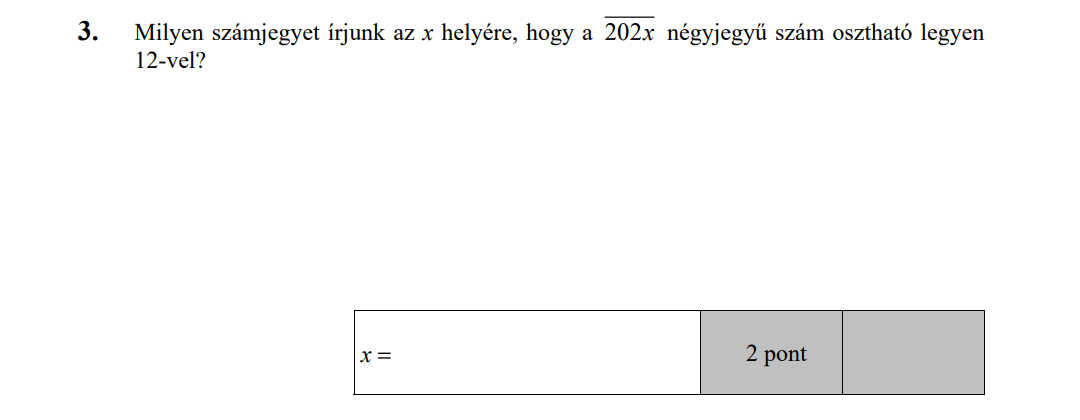
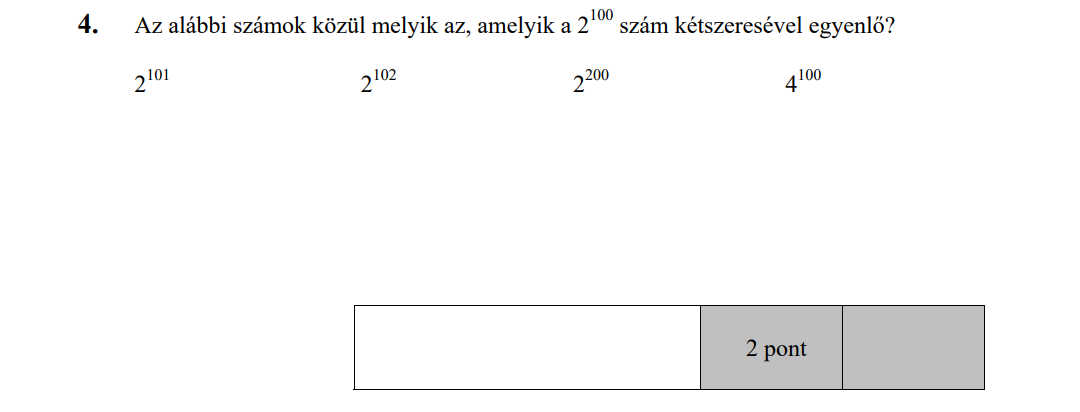



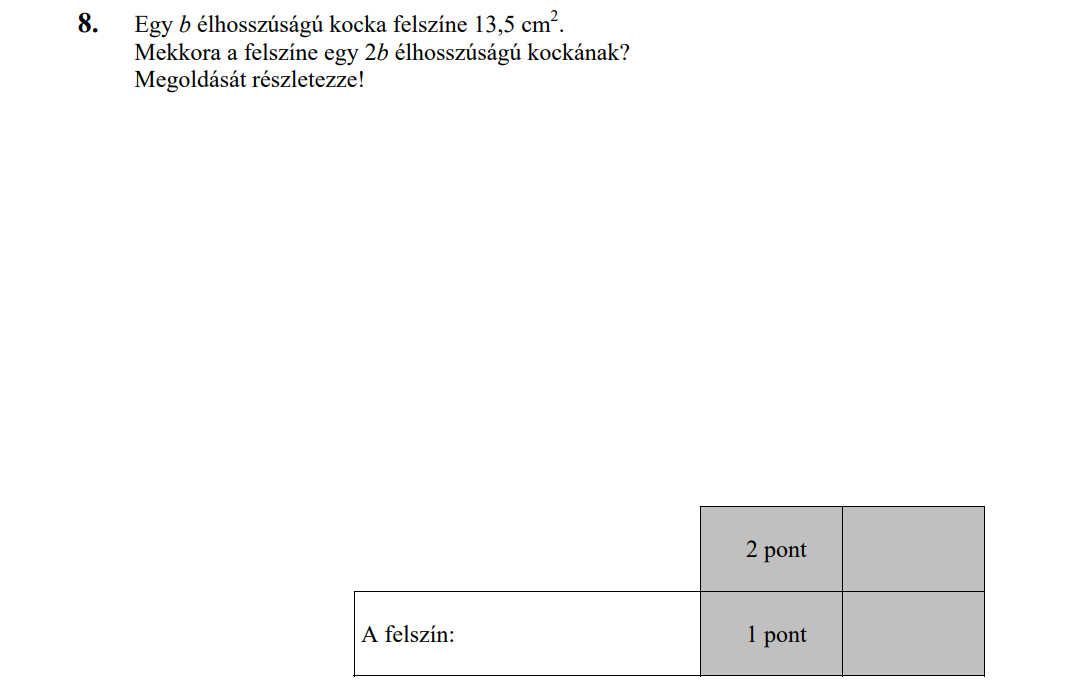




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
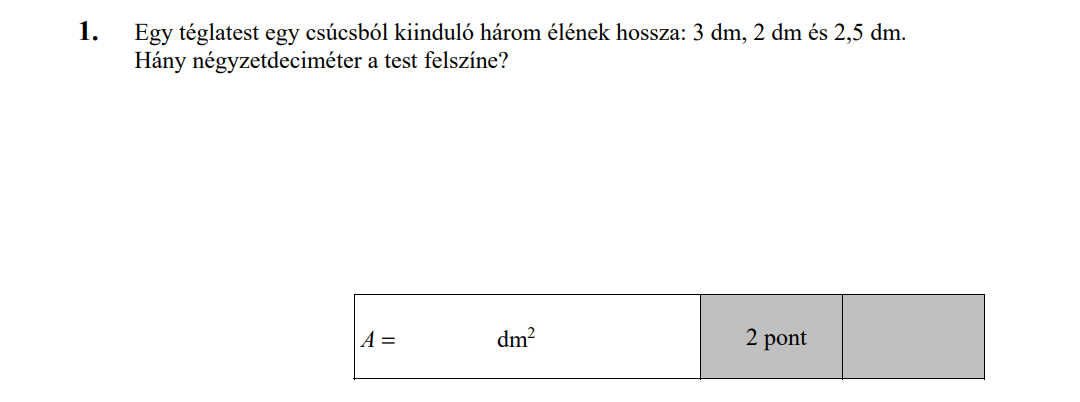
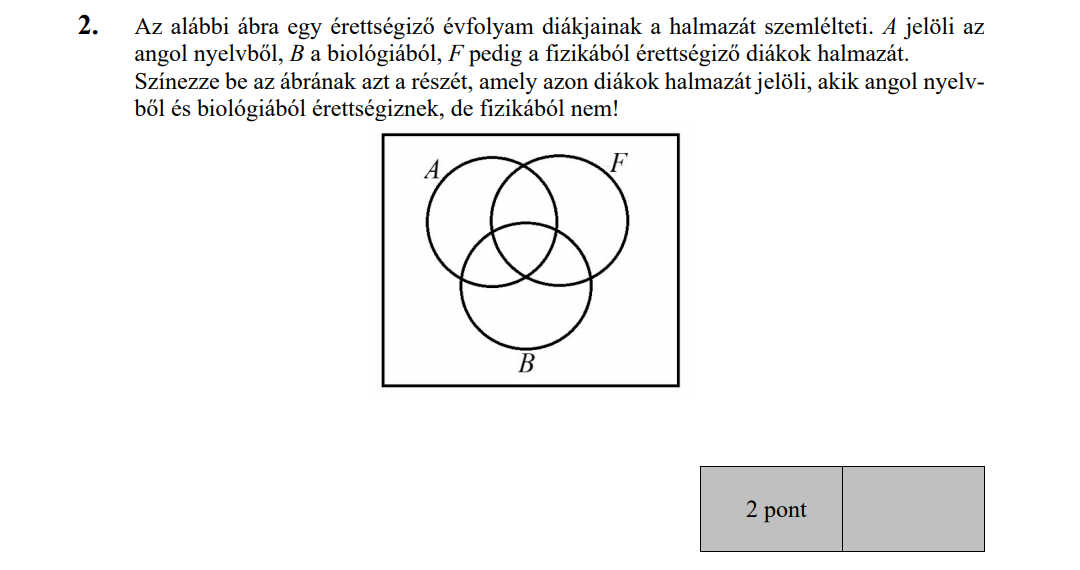

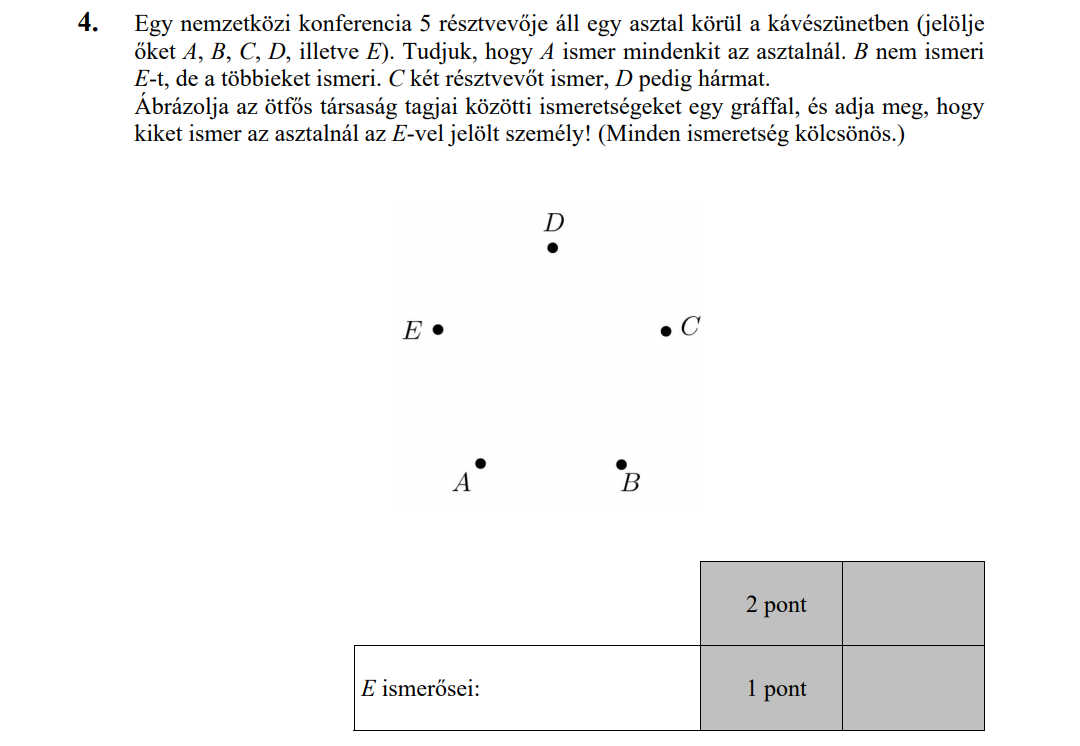

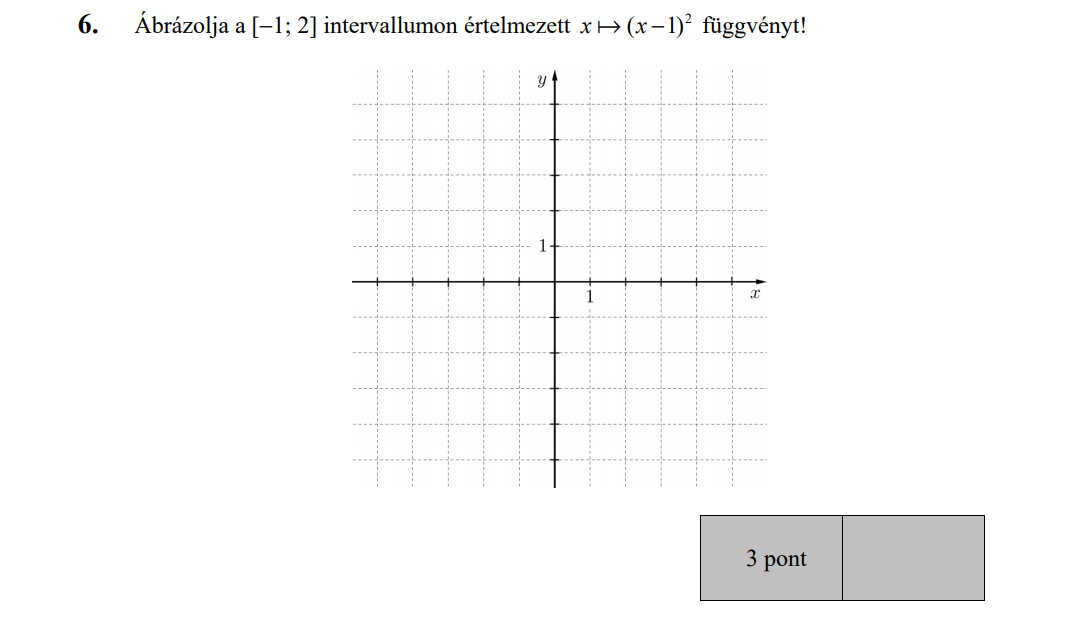



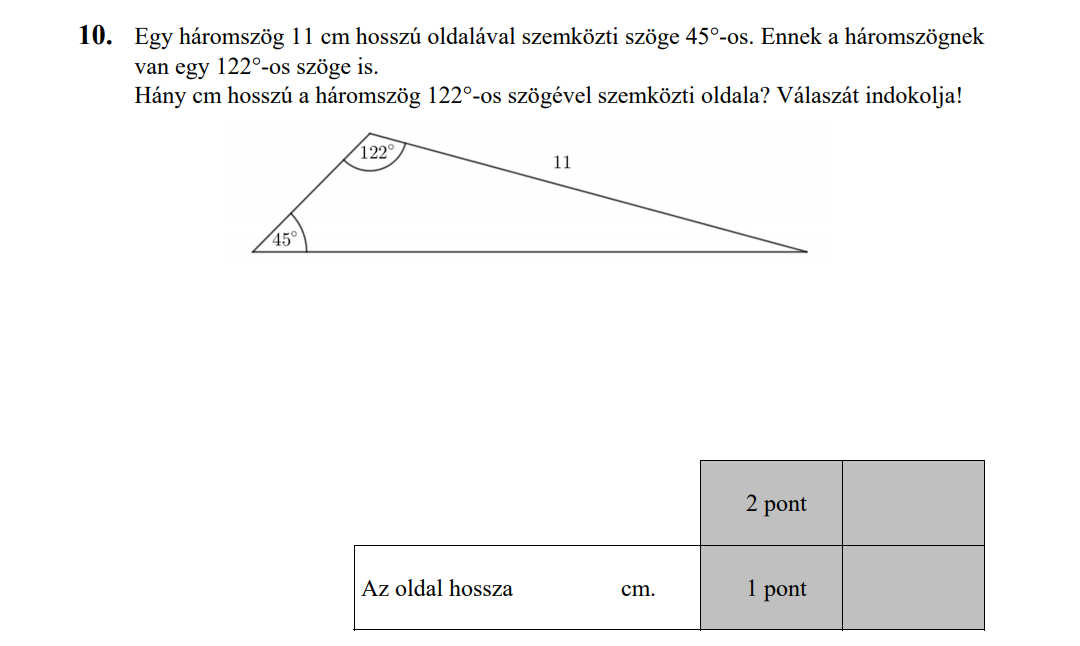
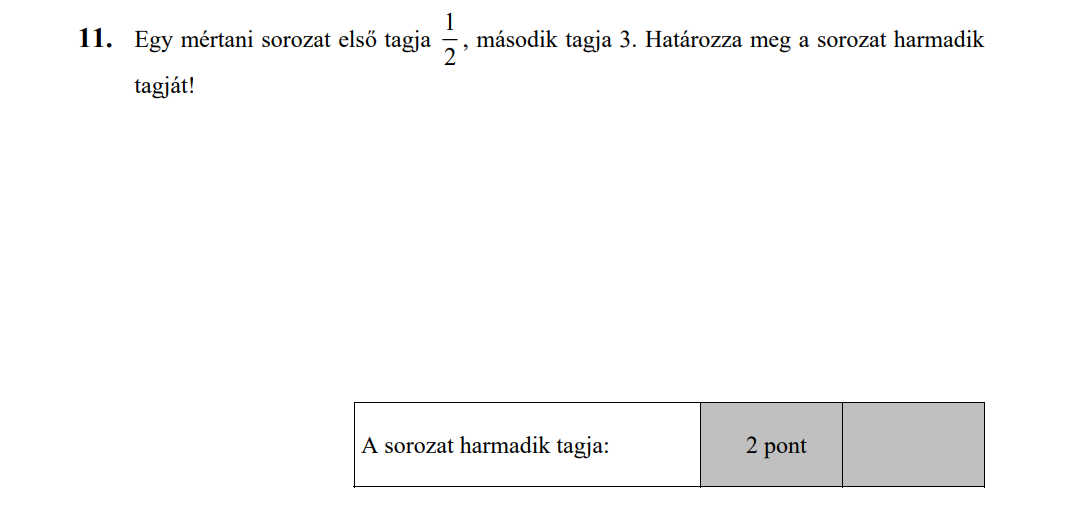

MÁSODIK RÉSZ

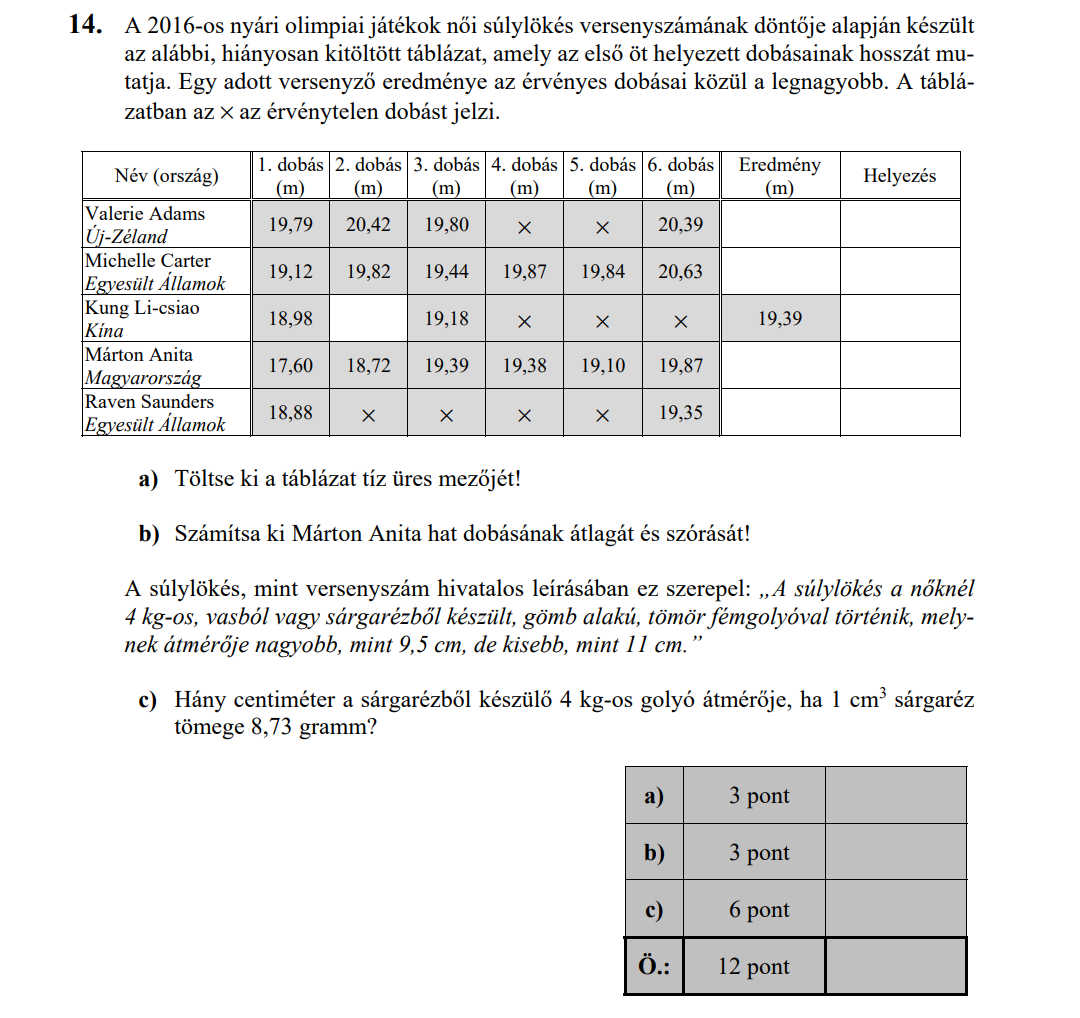




- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

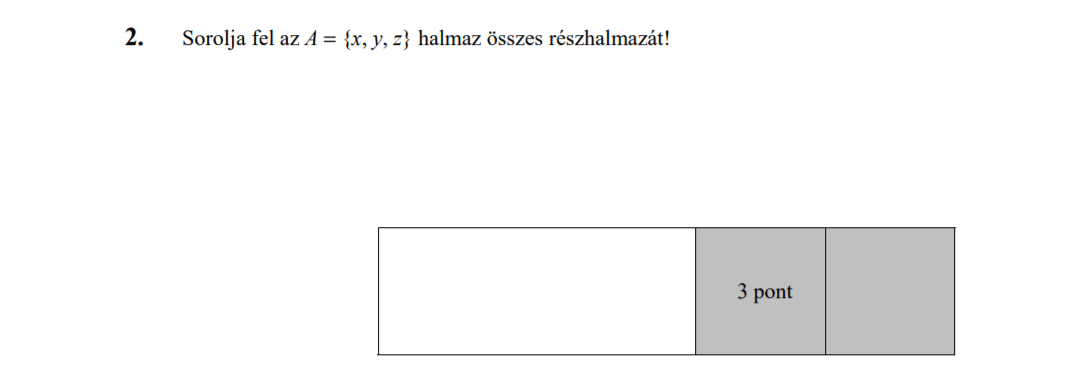


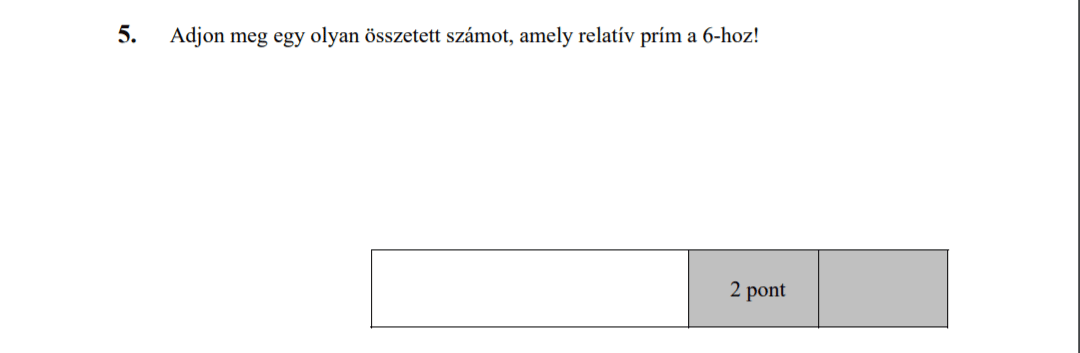




MÁSODIK RÉSZ





- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






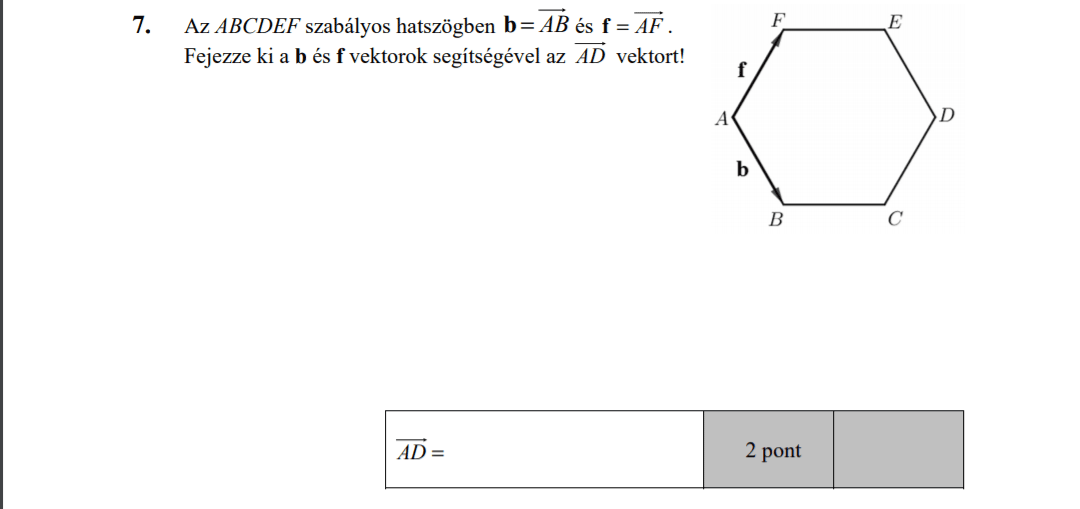




MÁSODIK RÉSZ

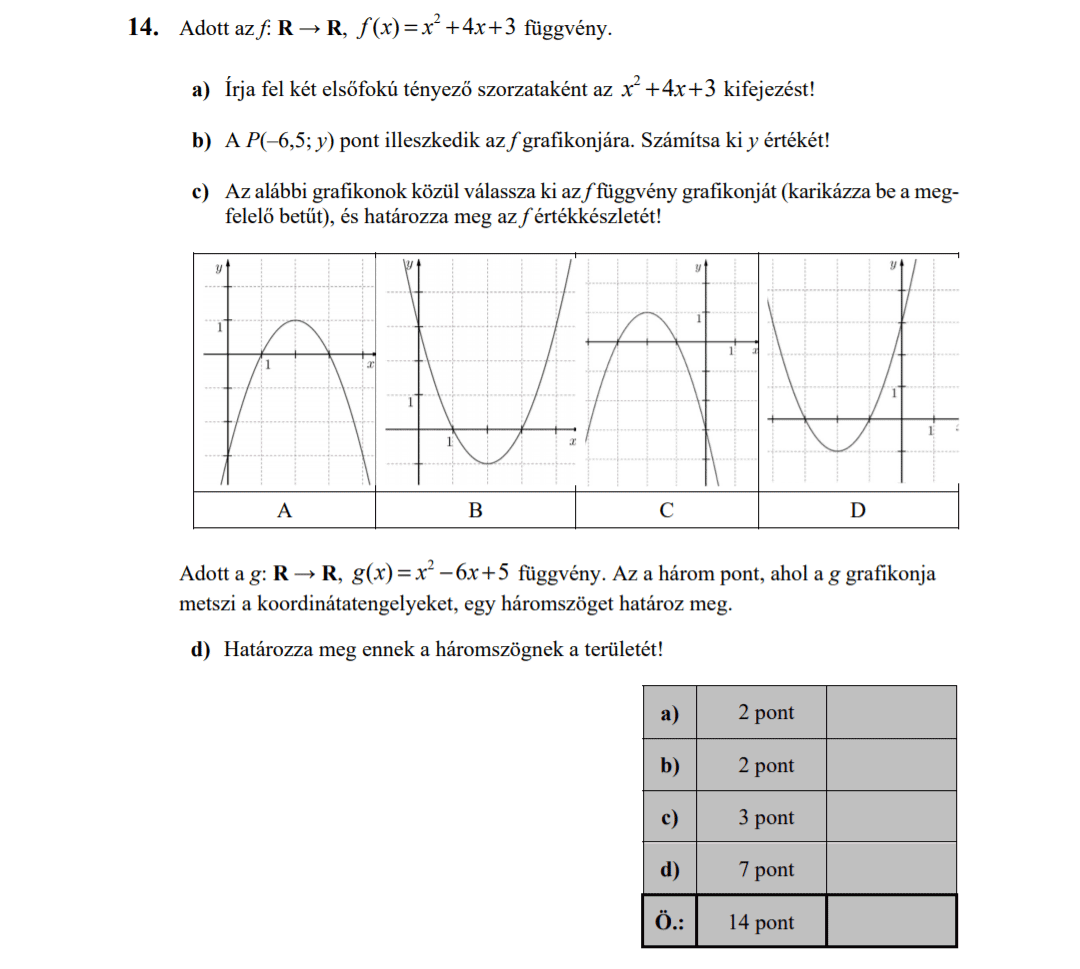




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

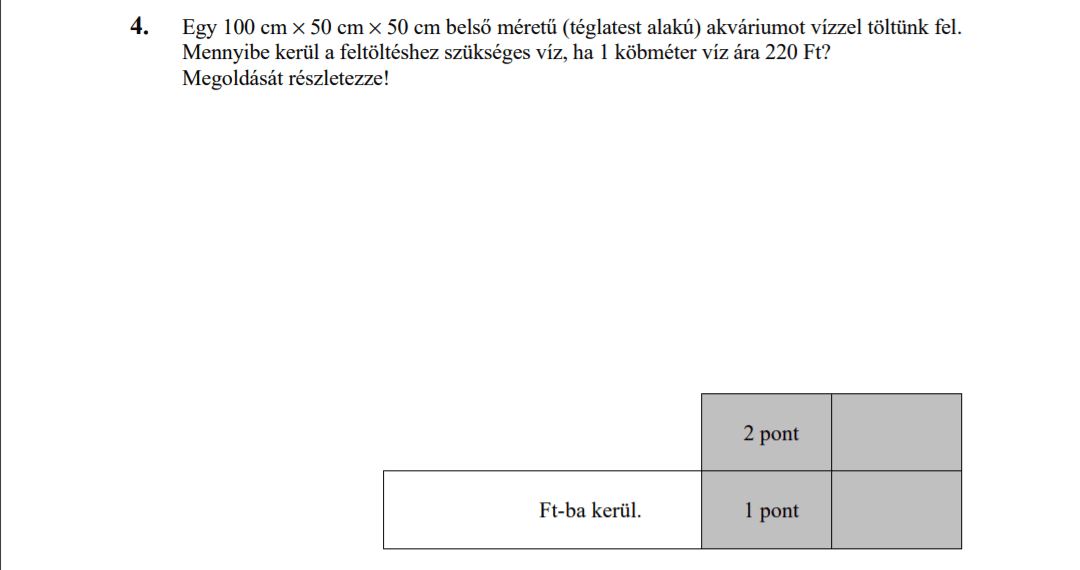
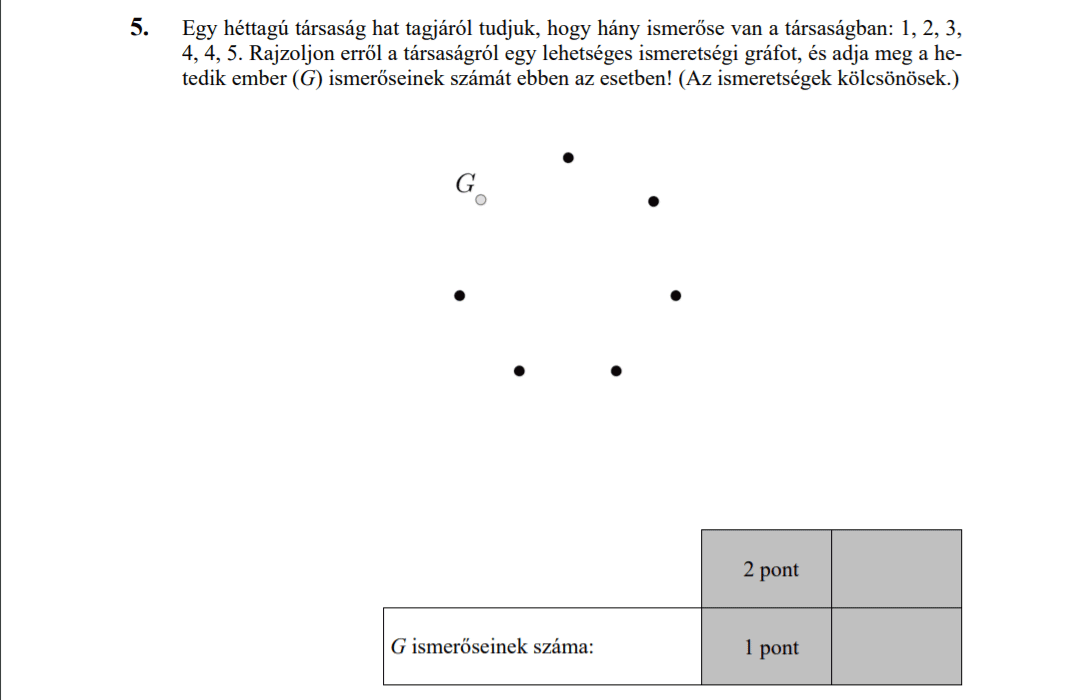







MÁSODIK RÉSZ
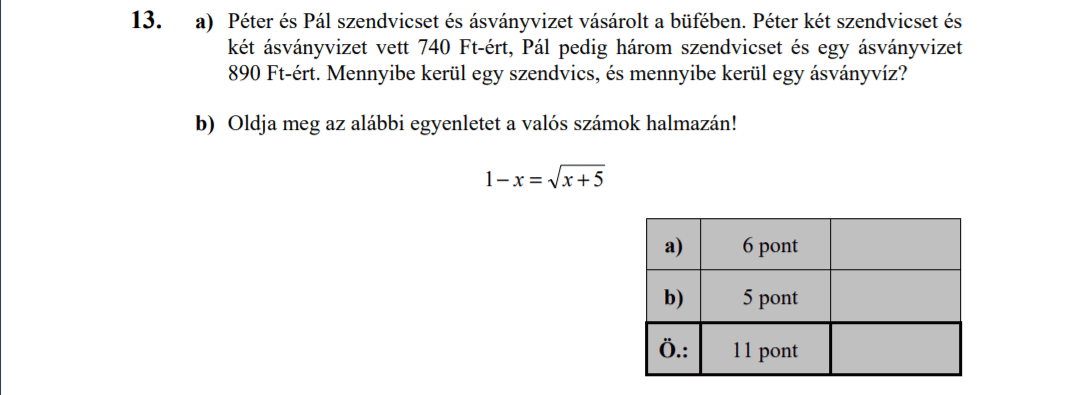
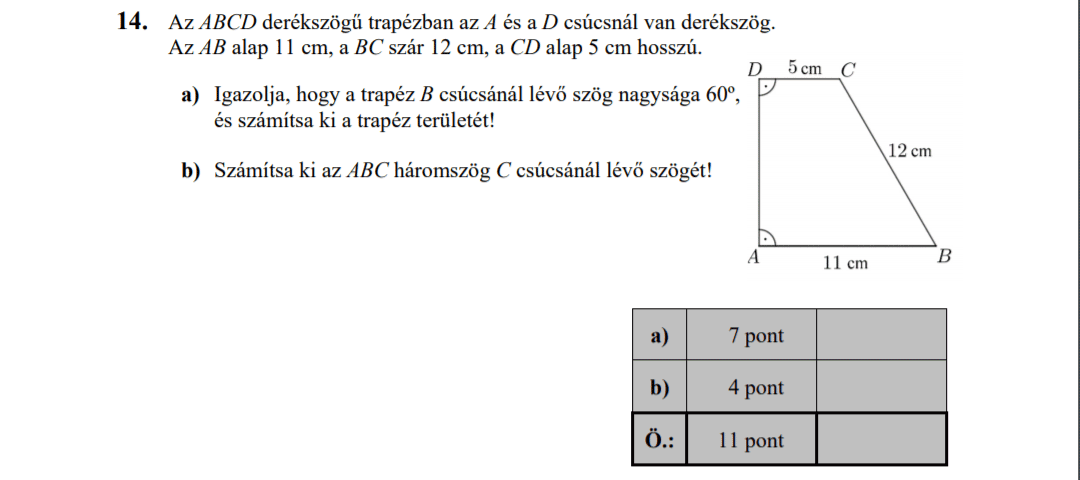



- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
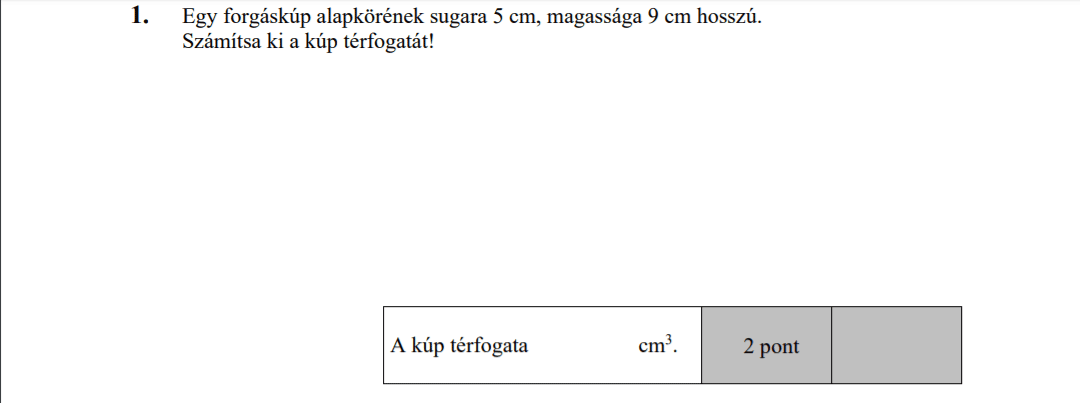


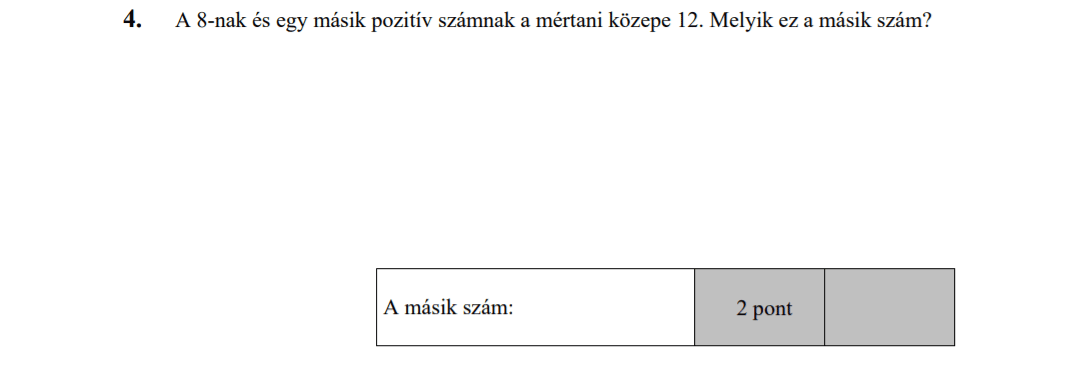
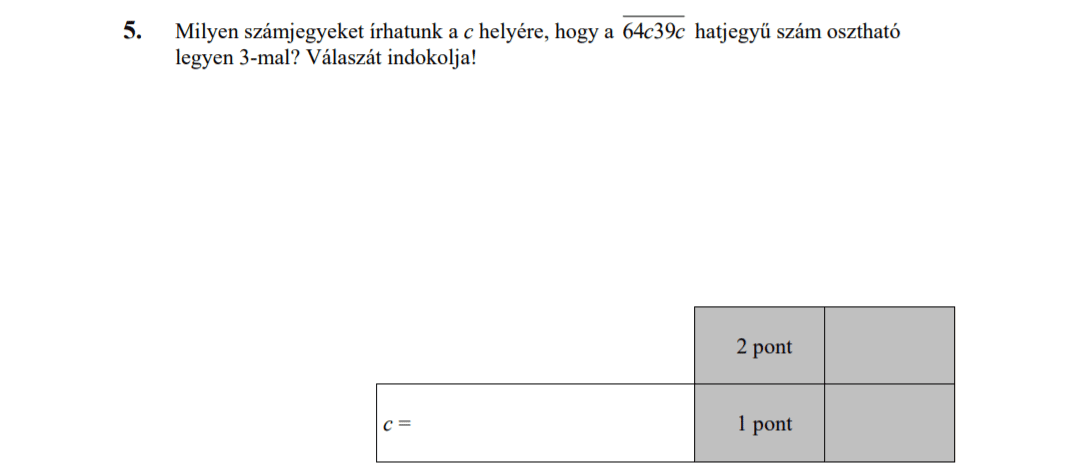


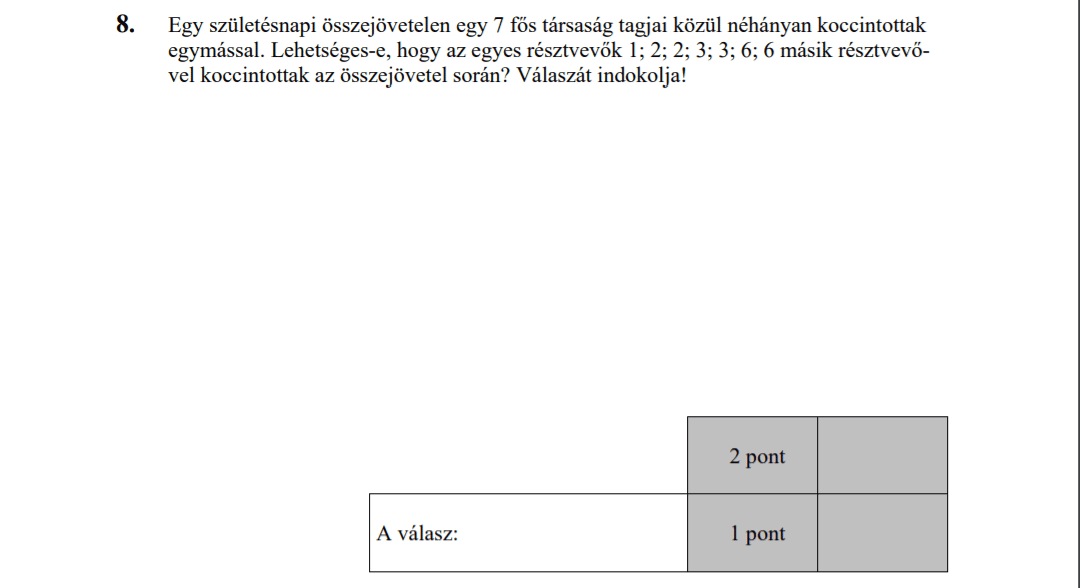



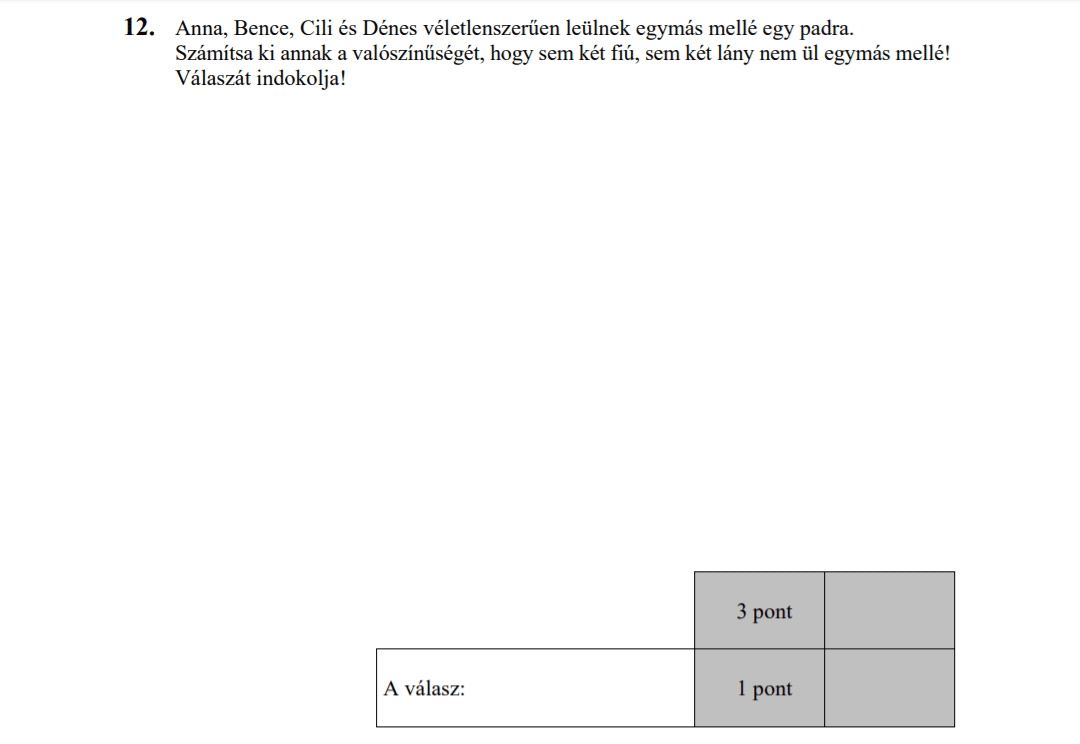
MÁSODIK RÉSZ

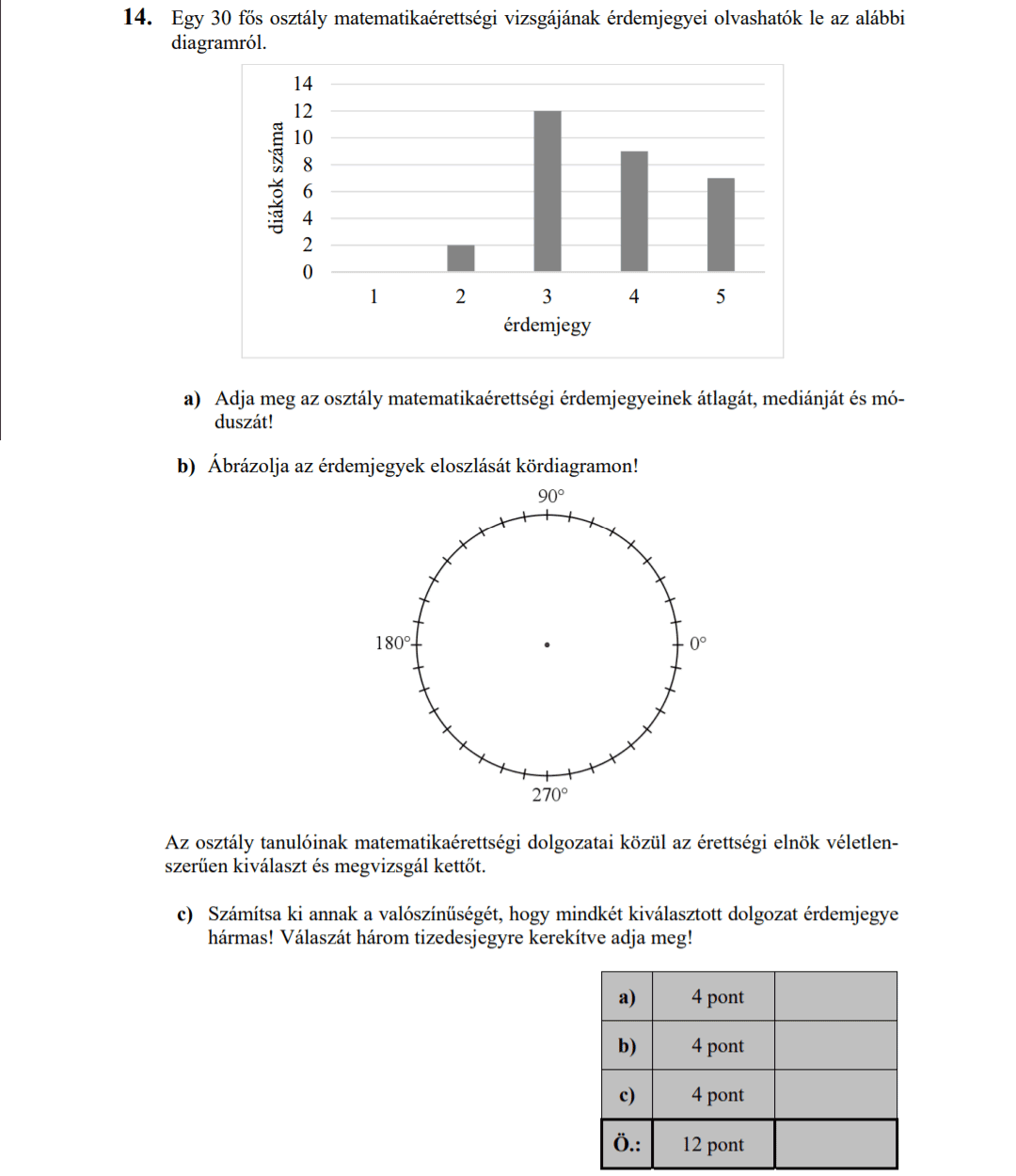
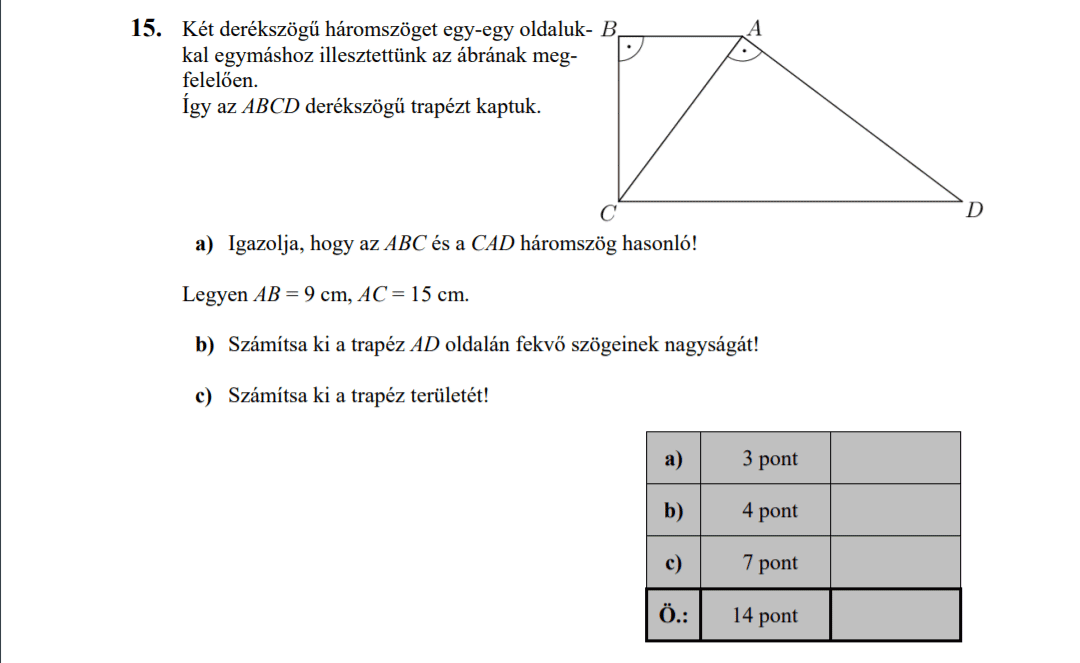



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


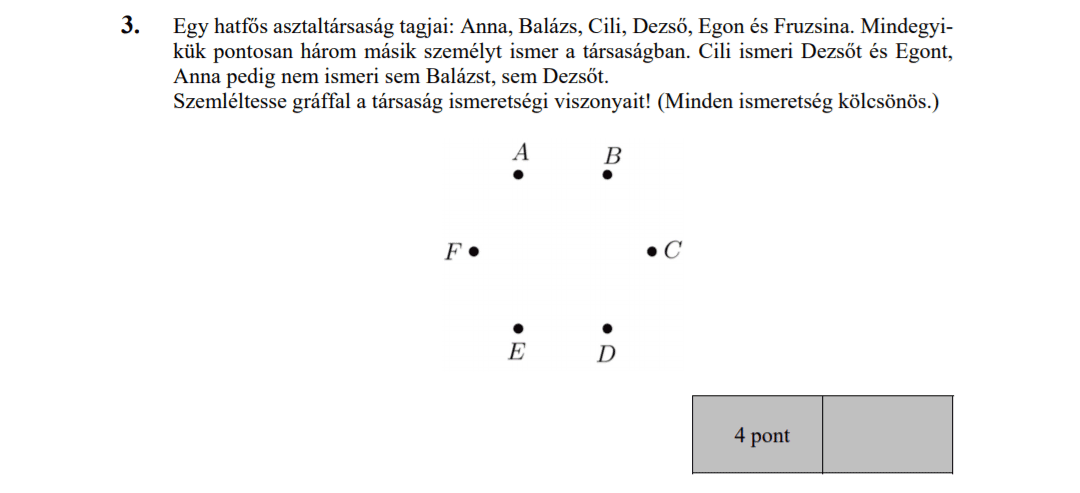


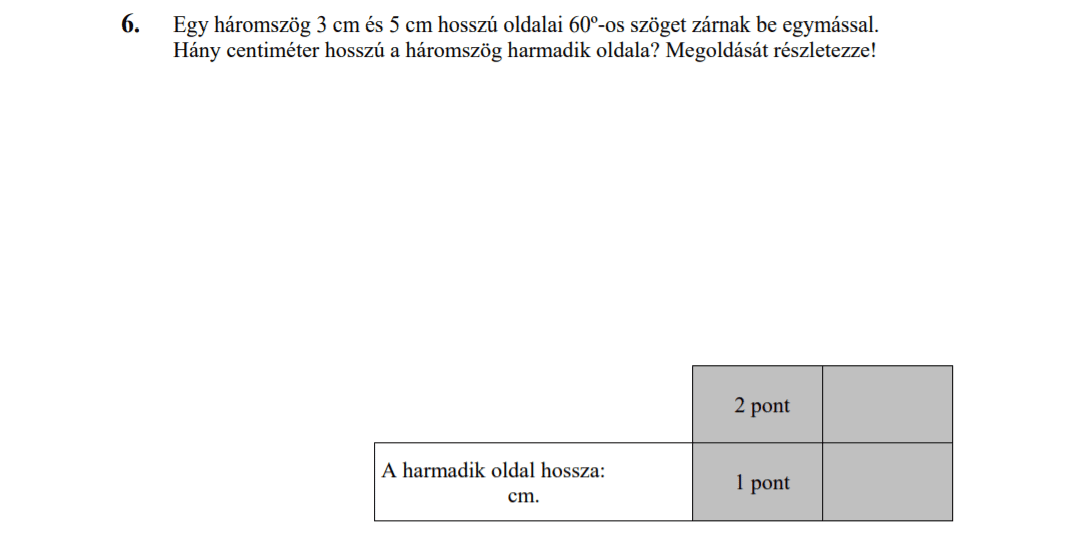

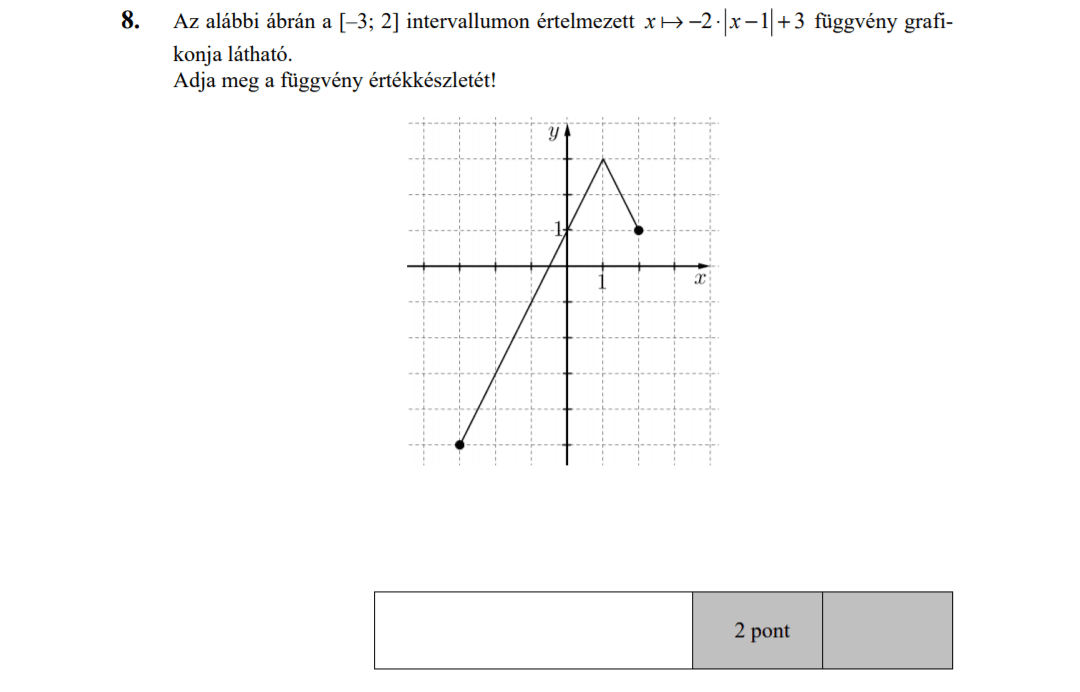

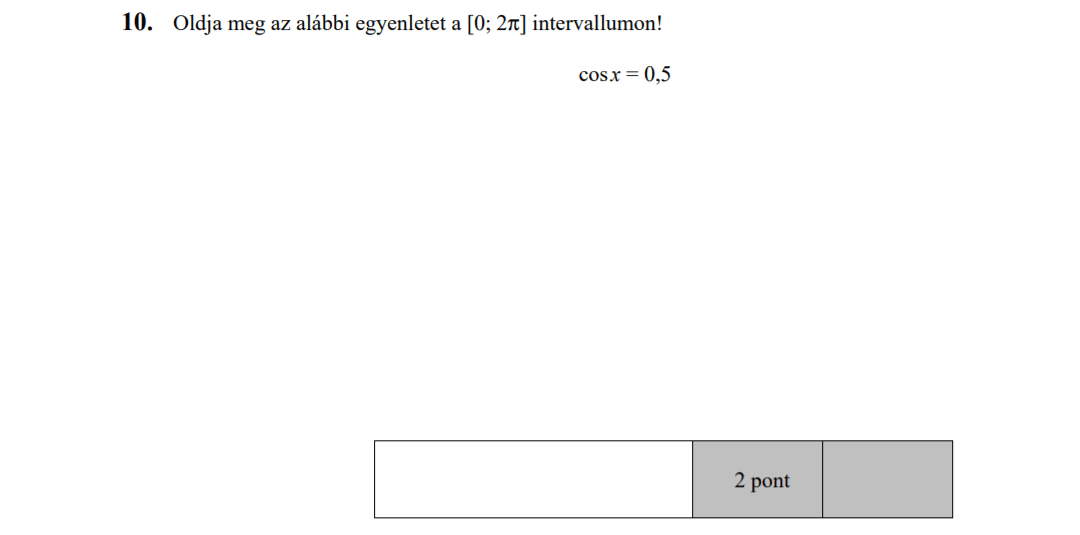

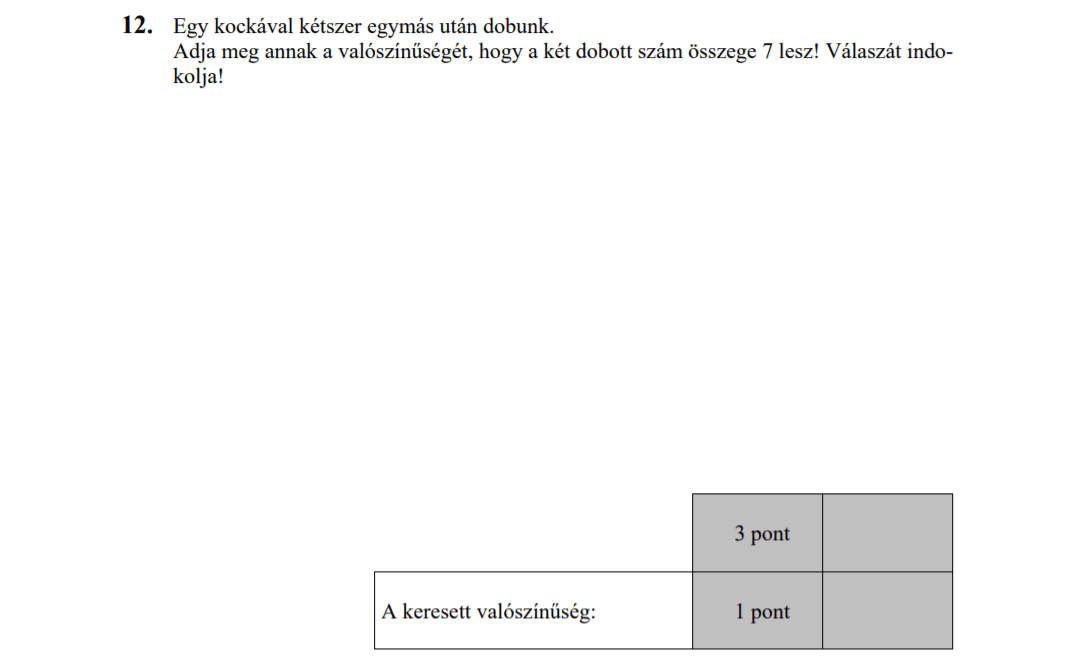
MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
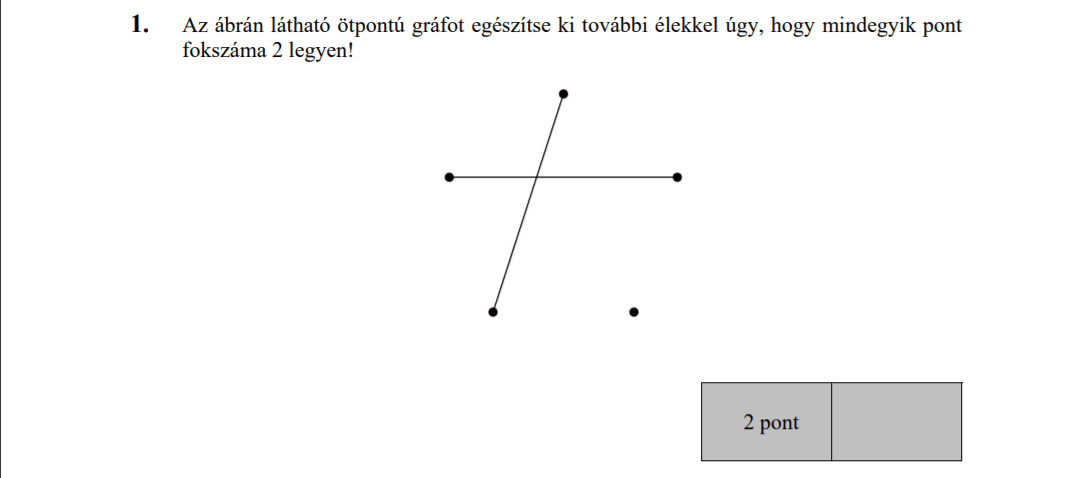
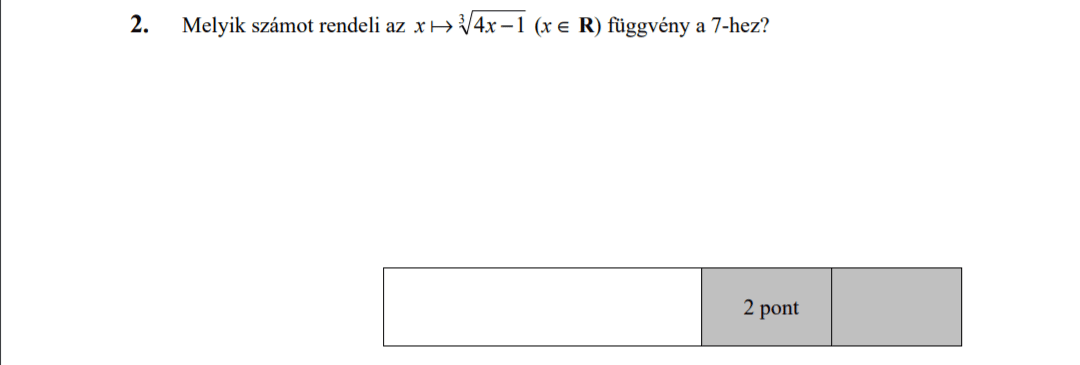
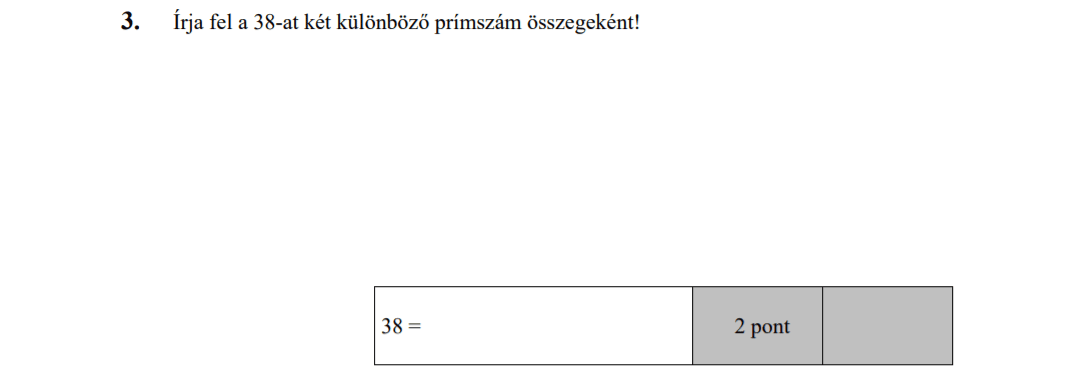




MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ




- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ









MÁSODIK RÉSZ




- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







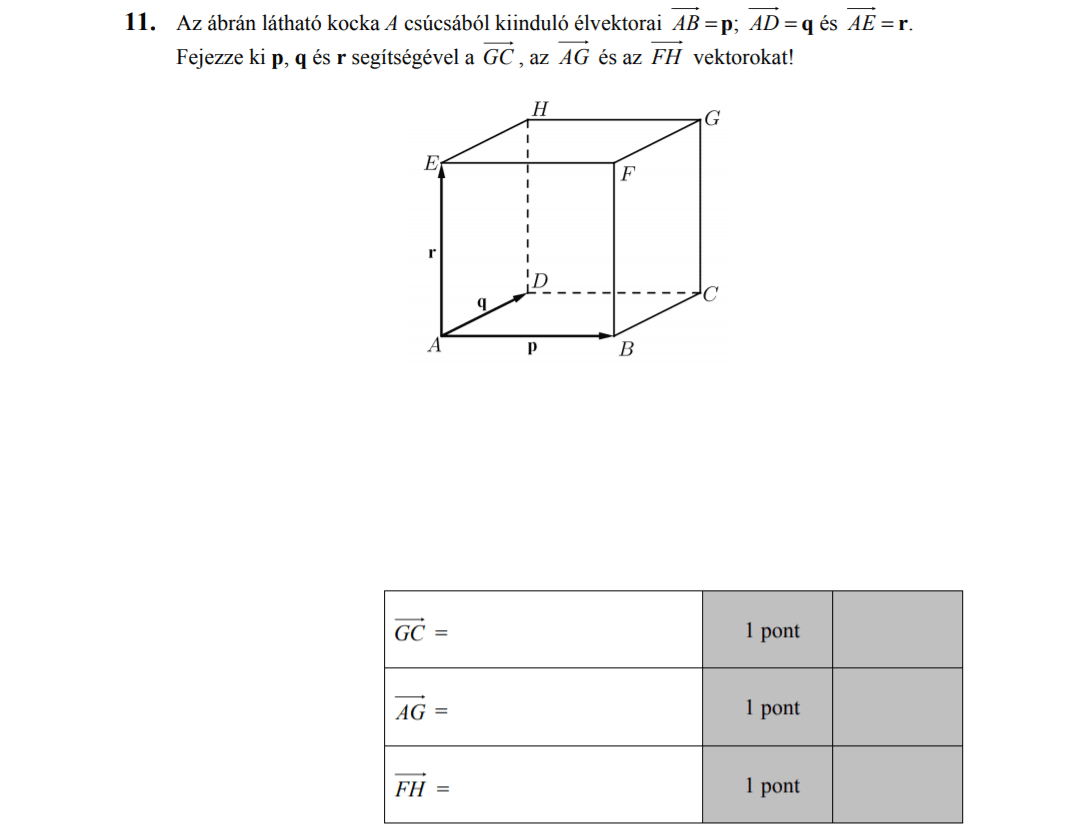
MÁSODIK RÉSZ
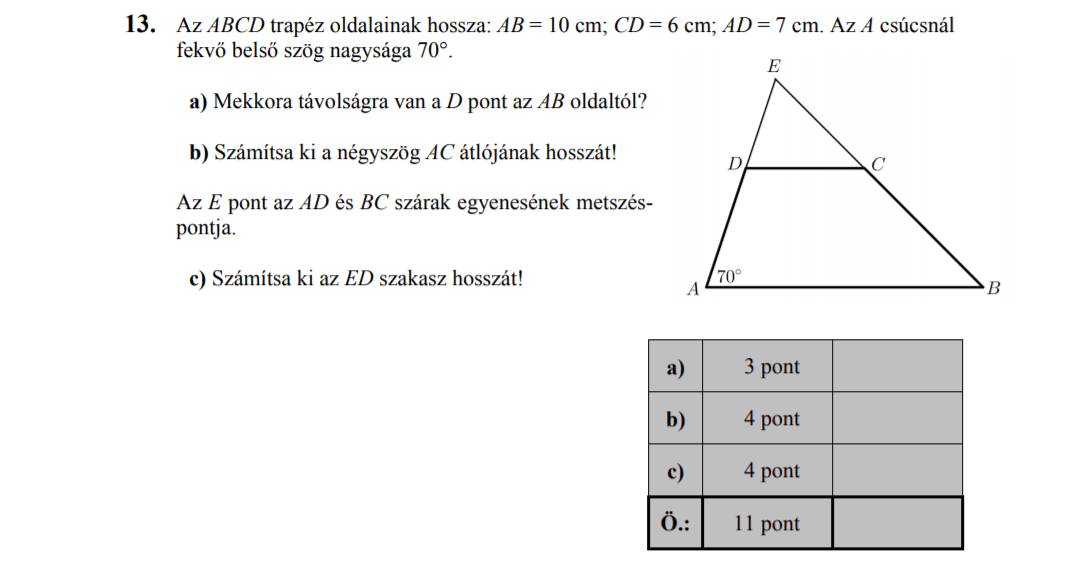





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


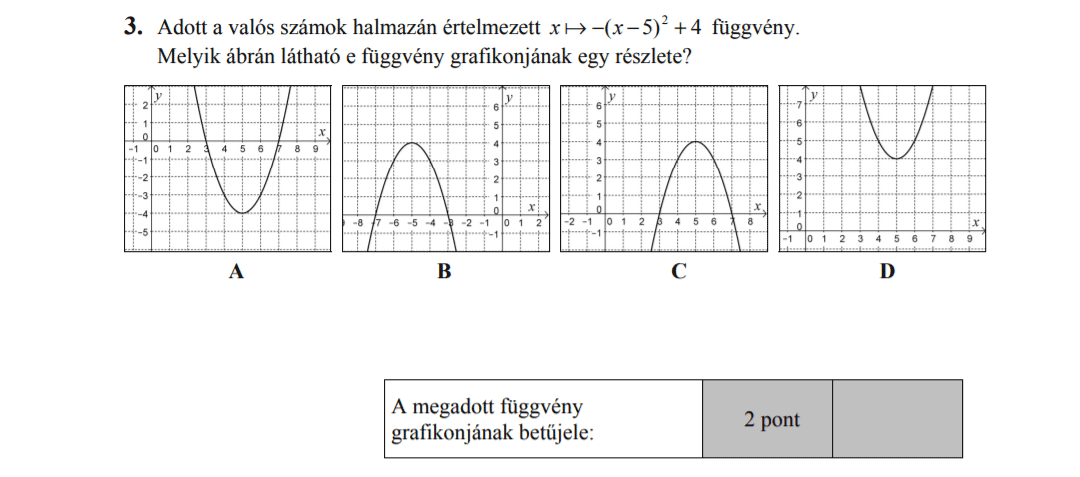






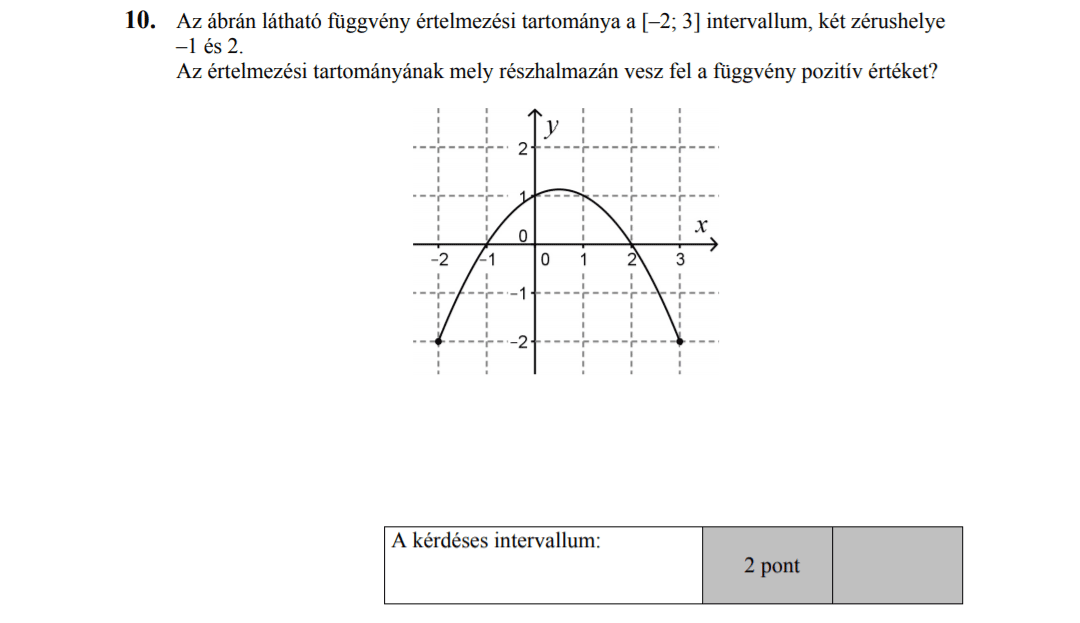


MÁSODIK RÉSZ


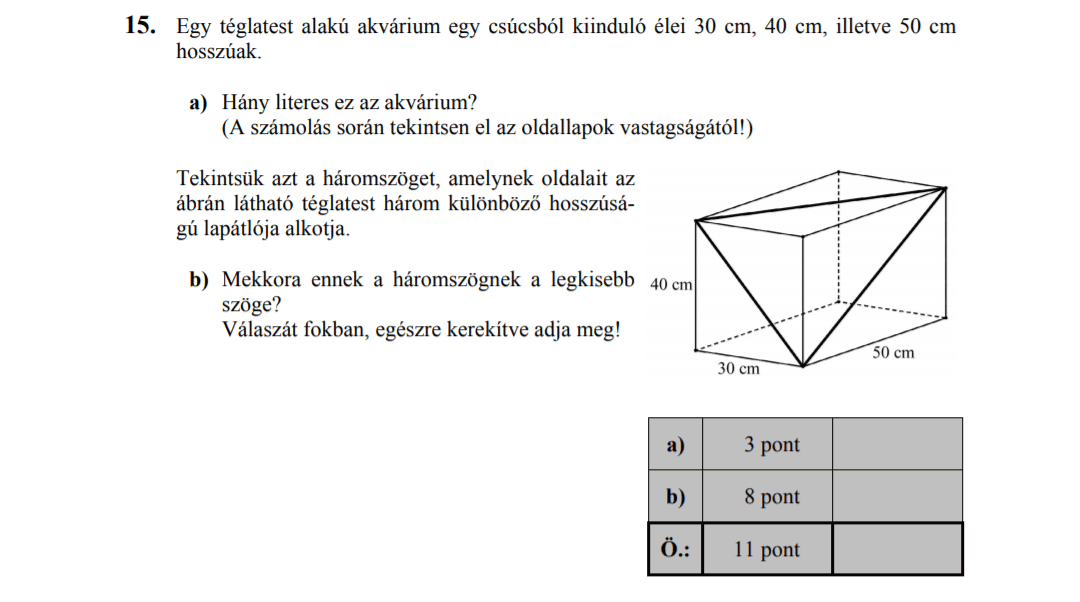

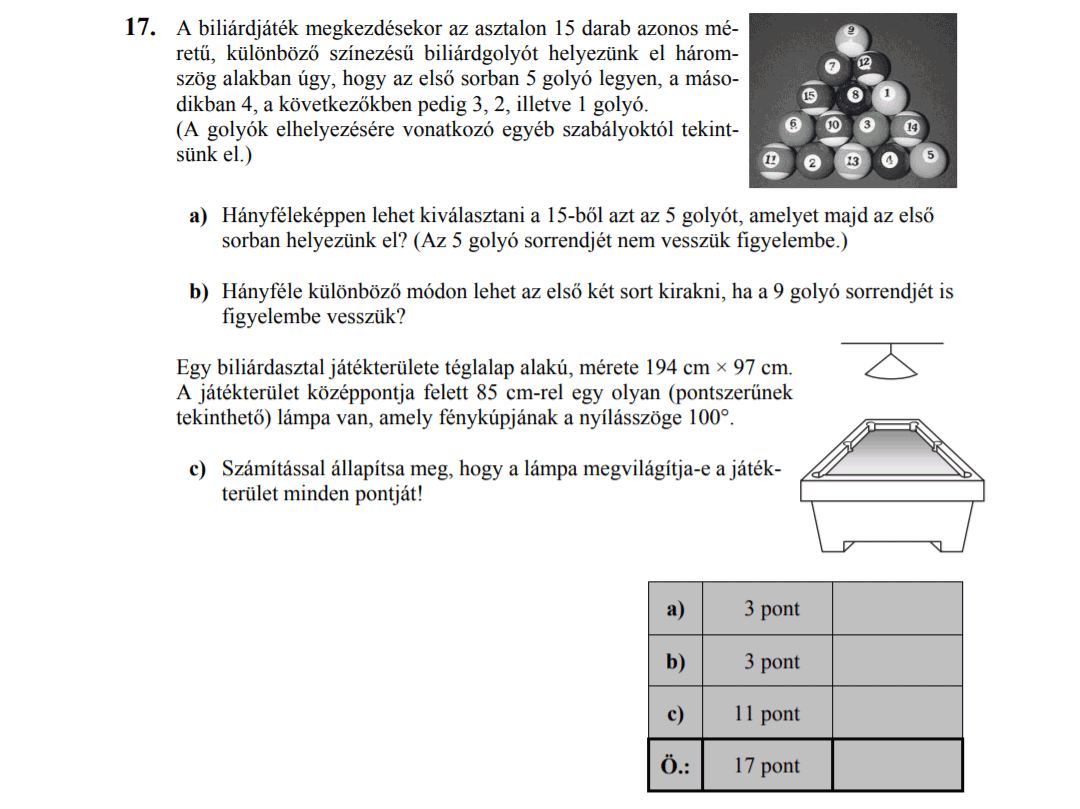

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


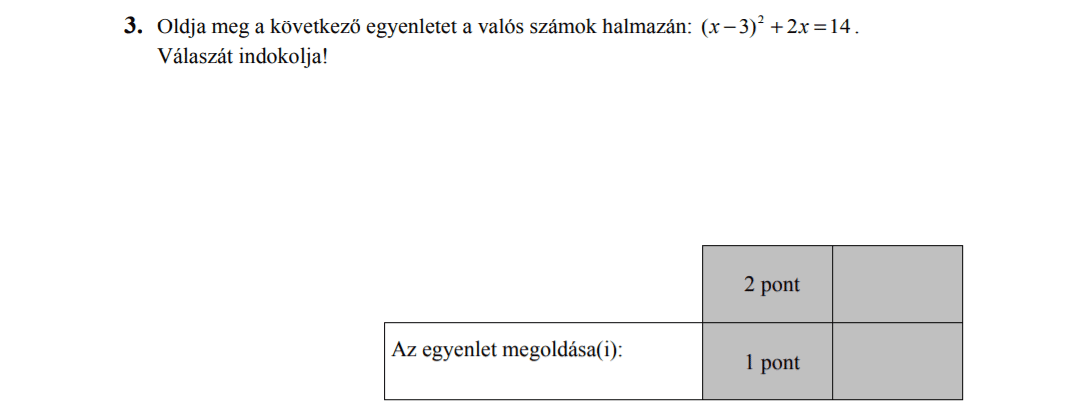





MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


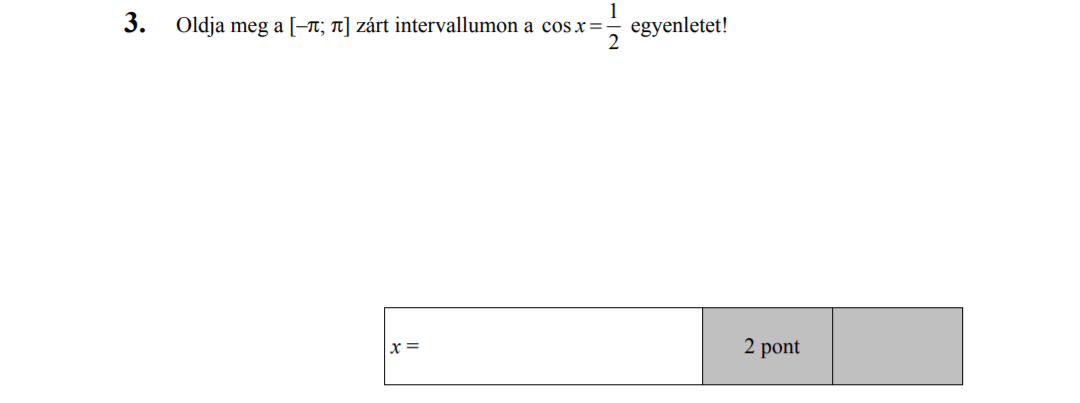


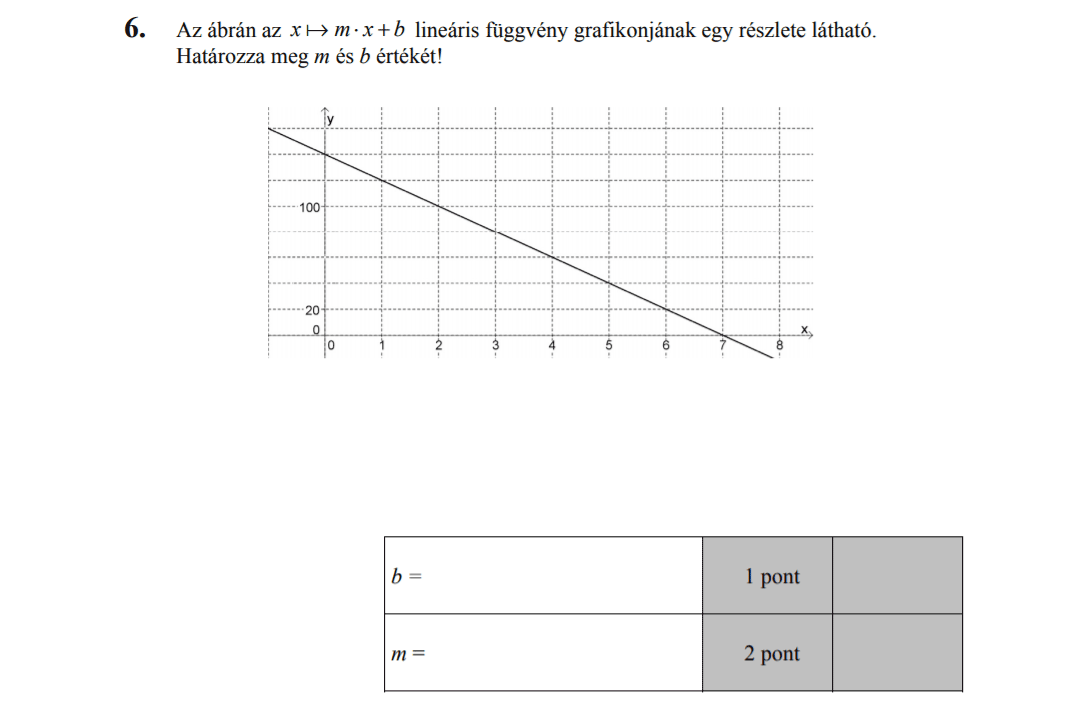



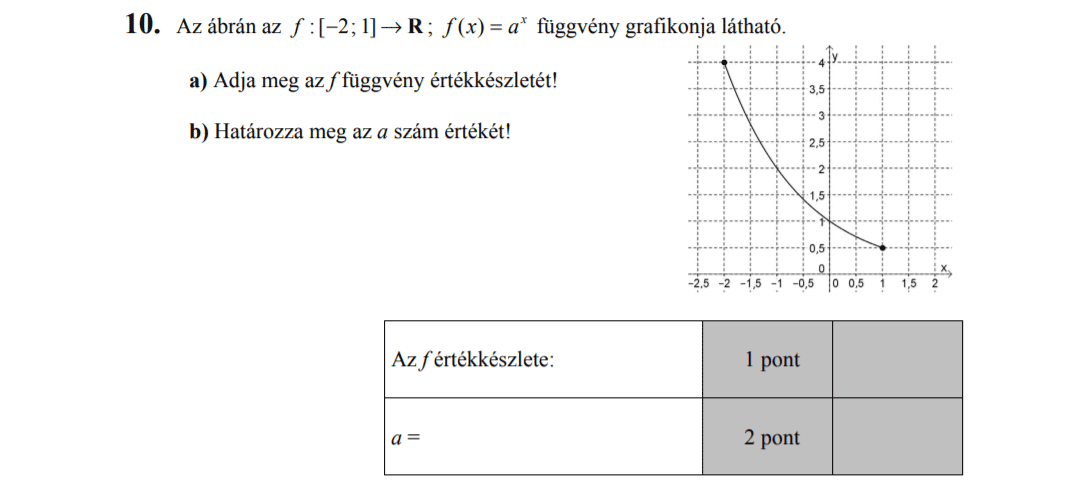

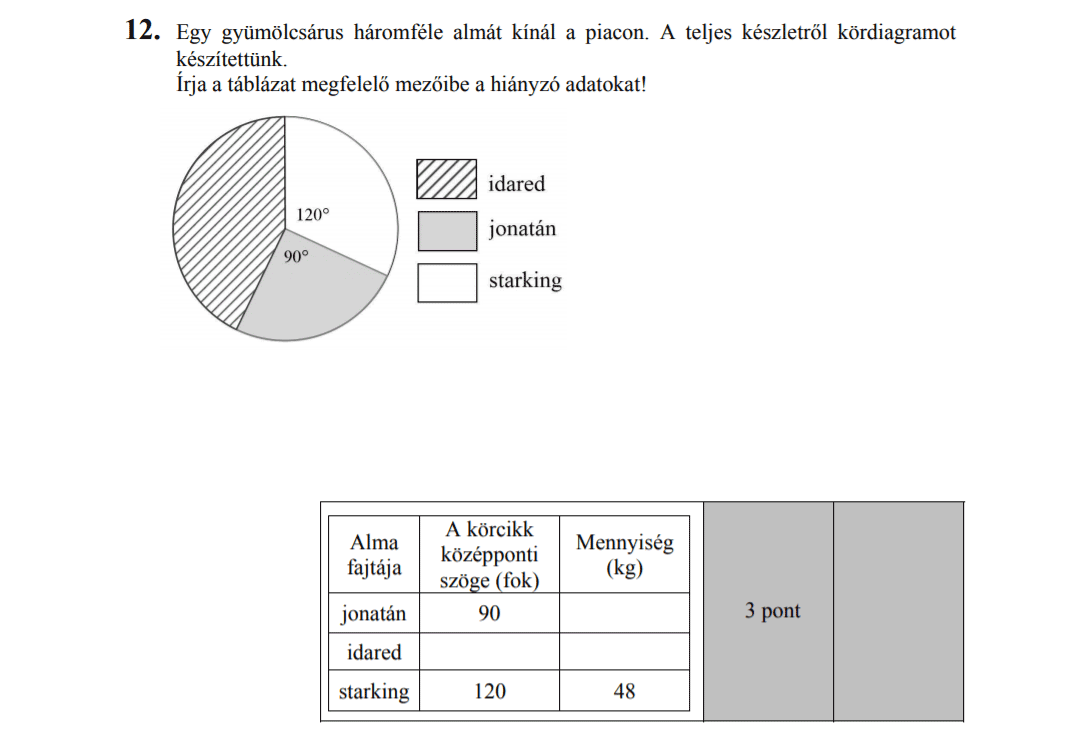
MÁSODIK RÉSZ





- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


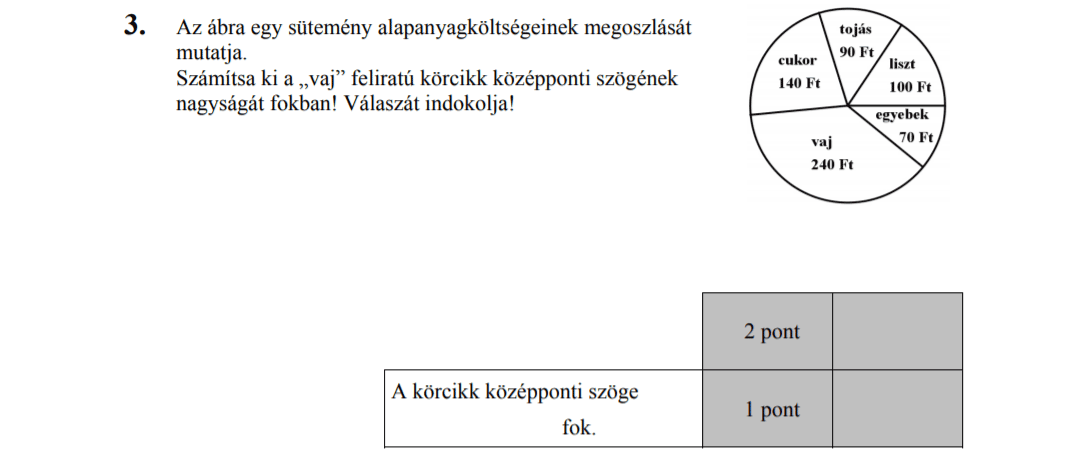
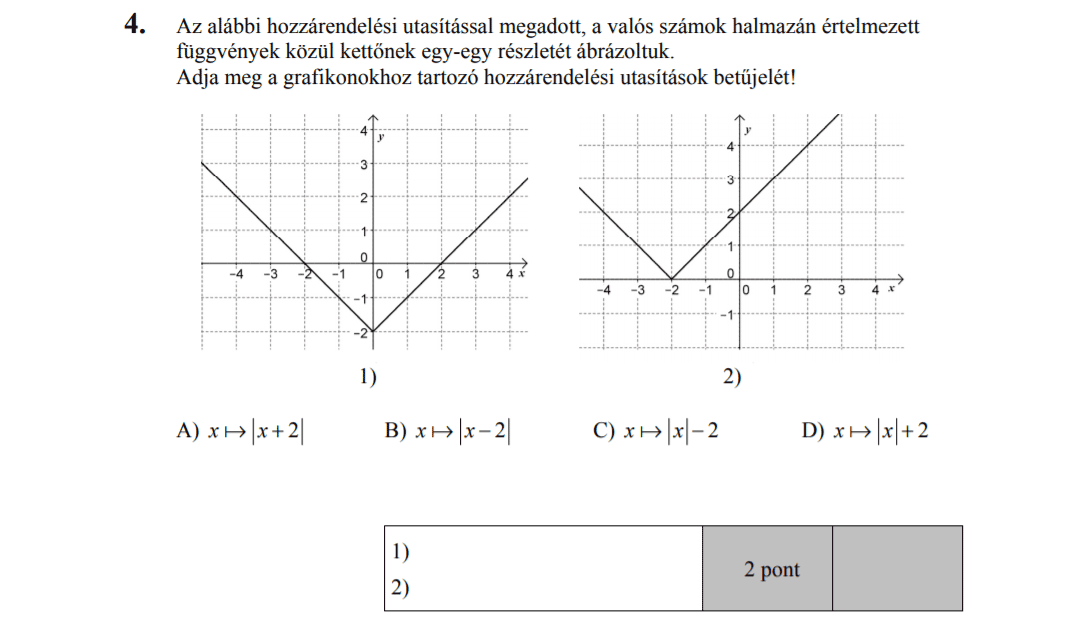





MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Négyzetgyök
Egy $a$ nem negatív szám négyzetgyöke az a nem negatív szám, aminek a négyzete $a$.
\( a \geq 0 \qquad \sqrt{a}\geq 0 \qquad \sqrt{a}^2 = a \)
Gyökös azonosságok
\( \sqrt{ a \cdot b } = \sqrt{a} \cdot \sqrt{ b } \qquad a \geq 0, \; b \geq 0 \)
\( \sqrt{ \frac{a}{b} }= \frac{ \sqrt{a} }{ \sqrt{b} } \qquad a \geq 0, \; b > 0 \)
Köbgyök
Egy $a$ szám köbgyöke az a szám, aminek a köbe $a$.
\( a \in R \qquad \left( \sqrt[3]{a} \right)^3 = a \)
Köbgyökös azonosságok
\( \sqrt[3]{a \cdot b} = \sqrt[3]{a} \cdot \sqrt[3]{b} \qquad a \in R, \; b \in R \)
\( \sqrt[3]{ \frac{a}{b} } = \frac{ \sqrt[3]{a} }{ \sqrt[3]{b} } \qquad a \in R, \; b \in R \)
n-edik gyök
A gyökvonás másképpp viselkedik páros, illetve páratlan gyökkitevő esetén, így kétféle definíciónk lesz.
Egy $a$ nem negatív szám $n=2k$-adik gyöke az a nem negatív szám, amire:
\( \left( \sqrt[2k]{a} \right)^{2k} = a \)
Egy tetszőleges $a$ szám $n=2k+1$-edik gyöke az a szám, amire:
\( \left( \sqrt[2k+1]{a} \right)^{2k+1} = a \)
Gyökös egyenletek megoldása
A gyökös egyenletek megoldását mindig ezzel kell kezdeni:
\( \sqrt{ \text{IZÉ} } \Rightarrow \text{IZÉ} \geq 0 \)
\( \sqrt{ \text{IZÉ} } = \text{VALAMI} \Rightarrow \text{VALAMI} \geq 0 \)
Ezt követően az elsőszámú célunk, hogy megszabaduljunk a gyökjeltől, amit négyzetreemeléssel végezhetünk. Ilyenkor az a lehető legjobb, ha a gyökös izé magányosan álldogál.
Ha megszabadultunk a gyökjeltől, minden úgy megy tovább, ahogy azt már megszokhattuk az egyenleteknél.
A végén viszont fontos, hogy ellenőriznünk kell, a megoldásunk megfelel-e a feladat elején felírt kritériumnak.
a) \( \sqrt{2} \cdot \sqrt{18} = ? \)
b) \( \sqrt{6} \cdot \sqrt{24} = ? \)
c) \( \sqrt{6} \cdot \sqrt{24} = ? \)
d) \( \sqrt{112}-\sqrt{28}+\sqrt{63} = ? \)
e) \( \sqrt{96} - \sqrt{54} + \sqrt{24} = ? \)
f) \( \left( \sqrt{12} + \sqrt{3} \right)^2 = ? \)
Gyöktelenítsük a törteket.
a) \( \frac{1}{\sqrt{3}} \)
b) \( \frac{5}{\sqrt{5}} \)
c) \( \frac{2}{\sqrt{x}} \)
d) \( \frac{3}{\sqrt{3}-1} \)
e) \( \frac{2}{\sqrt{3}-\sqrt{2}} \)
f) \( \frac{6}{\sqrt{x}+3} \)
Oldjuk meg az alábbi egyenleteket.
a) \( \sqrt{x-4}=3 \)
b) \( \sqrt{x-5}=\sqrt{2-6x} \)
c) \( \sqrt{x-4}=6-x \)
d) \( \sqrt{x-1}=x-7 \)
Oldjuk meg az alábbi egyenletet.
\( \sqrt{x+5}=3 \)
\( \sqrt{x+5}=1-x \)
Most pedig lássuk mi az a négyzetgyök.
Ép itt jön rá egy példa:
Ez egy olyan szám, amit ha négyzetre emelünk,
Akkor 9-et kapunk.
Hát ilyen éppen van…
Nézzünk még néhány példát:
Nos, ezzel viszont lesz egy kis gond…
√a-nak ugyanis azt kell tudnia, hogy 〖 √a〗^2 = a
És ez alapján〖 √(-3)〗^2= -3
Csak hát ez sajnos lehetetlen. Nem tudunk olyan számot
mondani, aminek a négyzete negatív.
A pozitív számok négyzete pozitív…
És a negatív számok négyzete is pozitív.
Így aztán nem létezik olyan szám, aminek a négyzete -3.
A gyökjel alatt tehát nem állhat negatív szám.
Ezek alapján a négyzetgyök definíciója valahogy így szól.
Egy a nem negatív szám négyzetgyöke az a
szám, aminek a négyzete a.
De sajnos van itt még egy kis gond.
Próbáljuk meg például megmondani ez alapján a definíció alapján,
hogy mennyi 9-nek a négyzetgyöke
Lássuk, megfelel-e ez a definíciónak:
*******
Nos, úgy néz ki, igen.
Mi ezzel a baj?
Nos, az a baj, hogy √9 nem lehet egyszerre +3 és -3 is.
A kettő közül csak az egyik lehet, annak ellenére, hogy
egyébként mindkét szám négyzete 9.
El kell döntenünk, hogy a kettő közül melyik legyen és ezt a
négyzetgyök definíciójába is bele kell építenünk.
Jegyezzük meg, hogy mindig a pluszosat tekintjük egy szám
négyzetgyökének.
…. nem negatív…
Egy a nem negatív szám négyzetgyöke az a
nem negatív szám, aminek a négyzete a.
És most lássuk, miket tud ez a négyzetgyök.
Na, ezt például nem…
A gyökvonás nem nagyon szereti az összeadást és a kivonást.
Vagyis nem létezik olyan azonosság, hogy mivel egyenlő
Hát ez nagy kár...
A szorzásra és osztásra viszont működik a dolog:
Itt jön aztán a köbgyök.
Ez azt tudja, hogy ha köbre emeljük, akkor a-t kapunk.
Lássunk néhány példát:
*** mert ***
Négyzetgyöknél nem lehetett negatív a gyökjel alatt.
De most igen…
A négyzetgyök alatt tehát csak nem negatív szám állhat,
de köbgyök alatt bármi.
Egy a szám köbgyöke az a szám, aminek a köbe a.
Ez azt tudja, hogy ha köbre emeljük, akkor a-t kapunk.
Egy a szám köbgyöke az a szám, aminek a köbe a.
Lássunk néhány példát:
mert
mert
mert
mert
Négyzetgyöknél nem lehetett negatív a gyökjel alatt.
De most igen…
A négyzetgyök alatt tehát csak nem negatív szám állhat, de köbgyök alatt bármi.
a
És most oszlassunk el egy téveszmét.
Itt jön ez az egyenlet…
és lássuk, mi történik, ha mindkét oldalból gyököt vonunk.
Nos, az történik, hogy
Ha egy egyenletből gyököt vonunk…
akkor az x mindig lesz.
Mert két olyan szám is van, aminek a négyzete 9.
Az egyik a 3 a másik a -3.
Ha viszont itt van ez, hogy
akkor csak egy megoldás van, mégpedig a 2.
A -2 azért nem jó, mert .
Na persze, ha éppen ezt kell megoldani…
Akkor pedig a -2 lesz a megoldás.
Végül nézzük mi a helyzet a negyedik gyökkel, ötödik gyökkel és társaival.
A negyedik gyök, hatodik gyök, sőt bármilyen páros kitevős gyök pontosan úgy viselkedik, mint a négyzetgyök.
Egy a nem negatív szám 2k-adik gyöke az a nem negatív szám, amire:
A páratlan kitevős gyök pedig úgy viselkedik, mint a köbgyök.
Egy tetszőleges a szám 2k+1-edik gyöke az a szám, amire:
