- ÚJ! Kvartilisek és dobozdiagram = sodrófadiagram = box plot
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
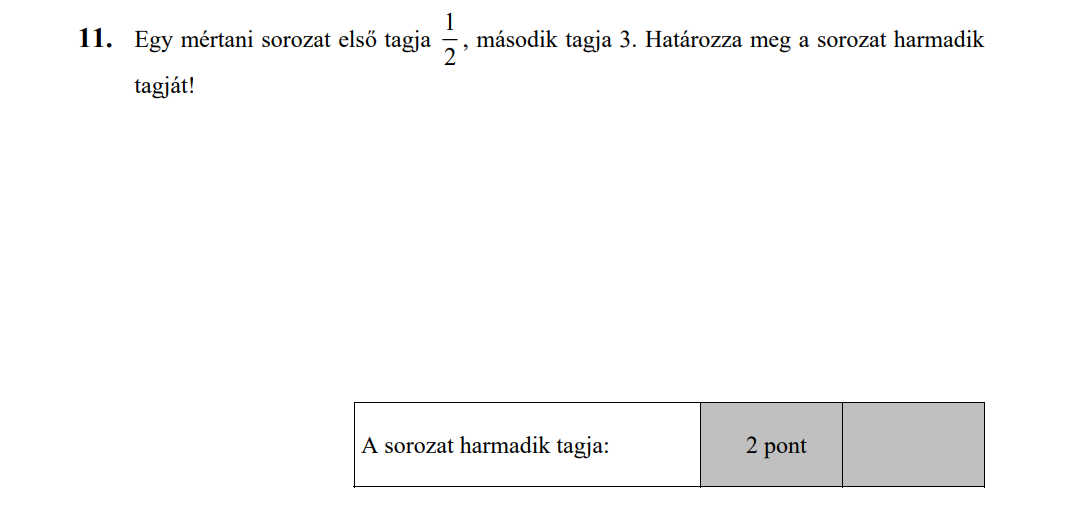
- Számtani és mértani sorozatok (16,7 pont)
- Térgeometria (10,8 pont)
- Statisztika (10,1 pont)
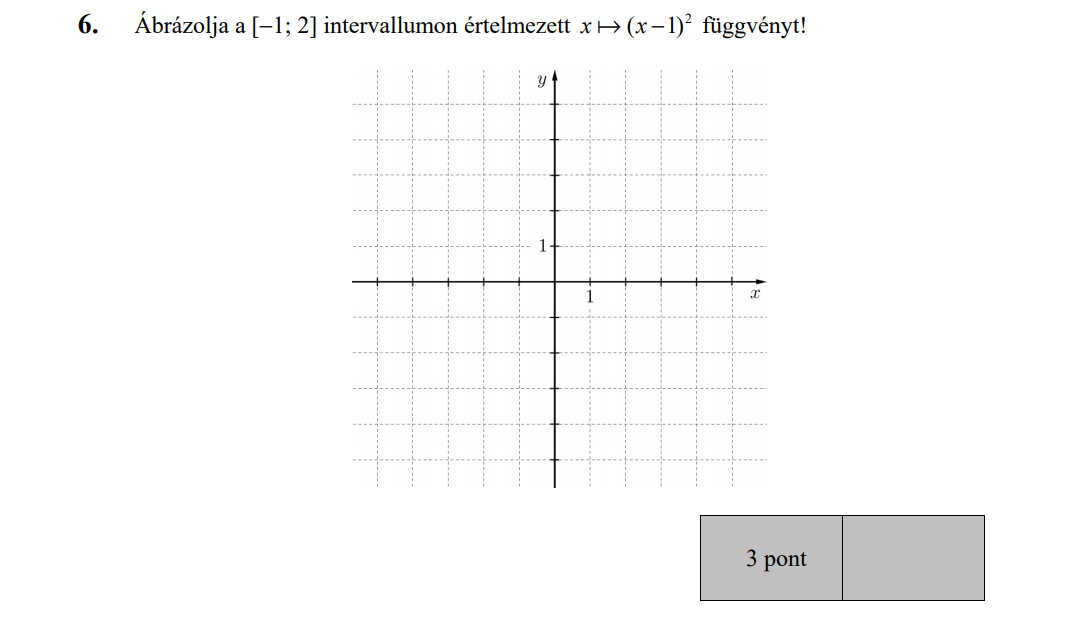
- Függvényekkel kapcsolatos feladatok (9,4 pont)
- Valószínűségszámítás (9,3 pont)
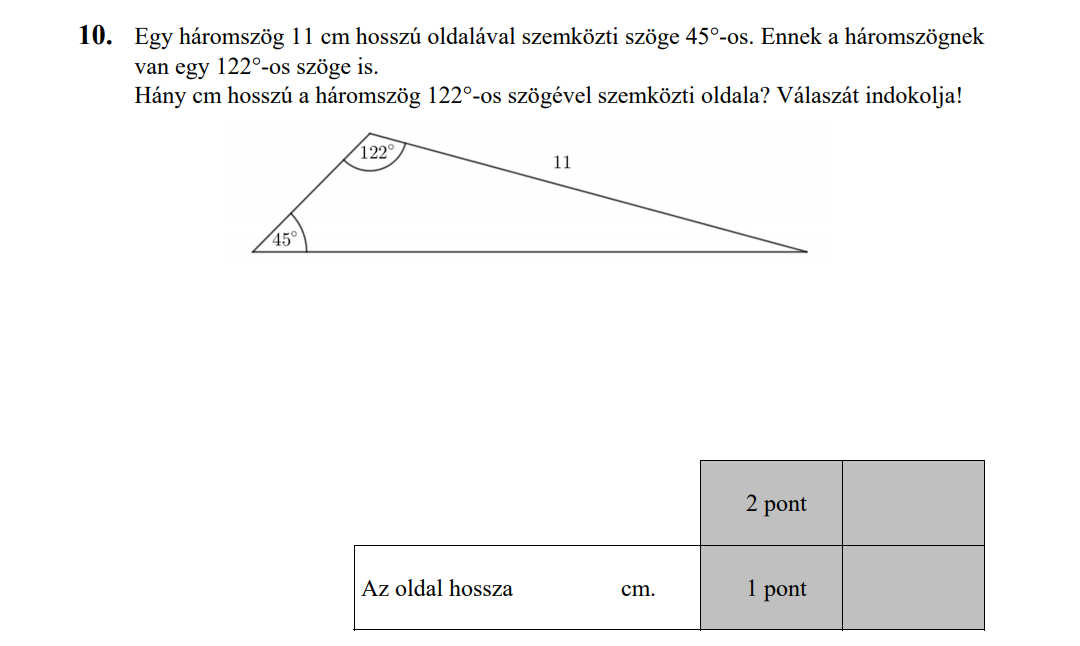
- Trigonometria, szinusztétel, koszinusztétel (8,4 pont)
- Kombinatorika (7,8 pont)
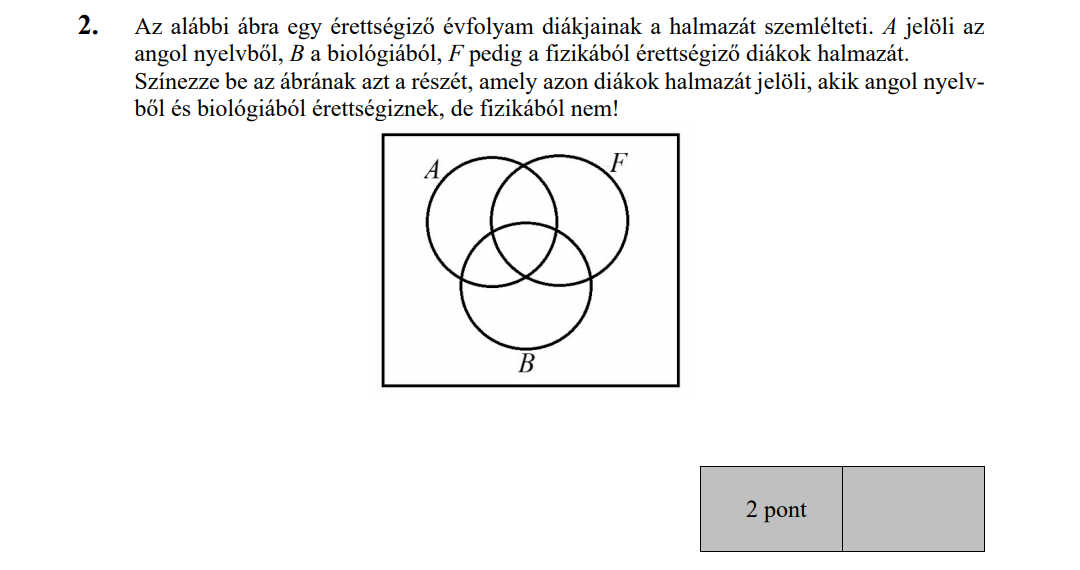
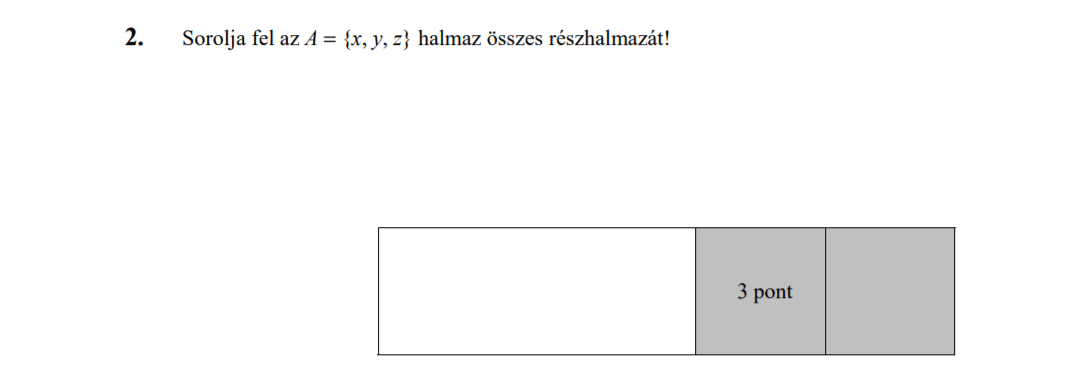
- Halmazok (7,1 pont)
- Szöveges feladatok (5,7 pont)
- Koordinátageometria (5,2 pont)
- Síkgeometria (3,7 pont)
- Százalékszámítás (3,5 pont)
- Egyenes és fordított arányosság, arányos osztás, szöveges feladatok (3,3 pont)
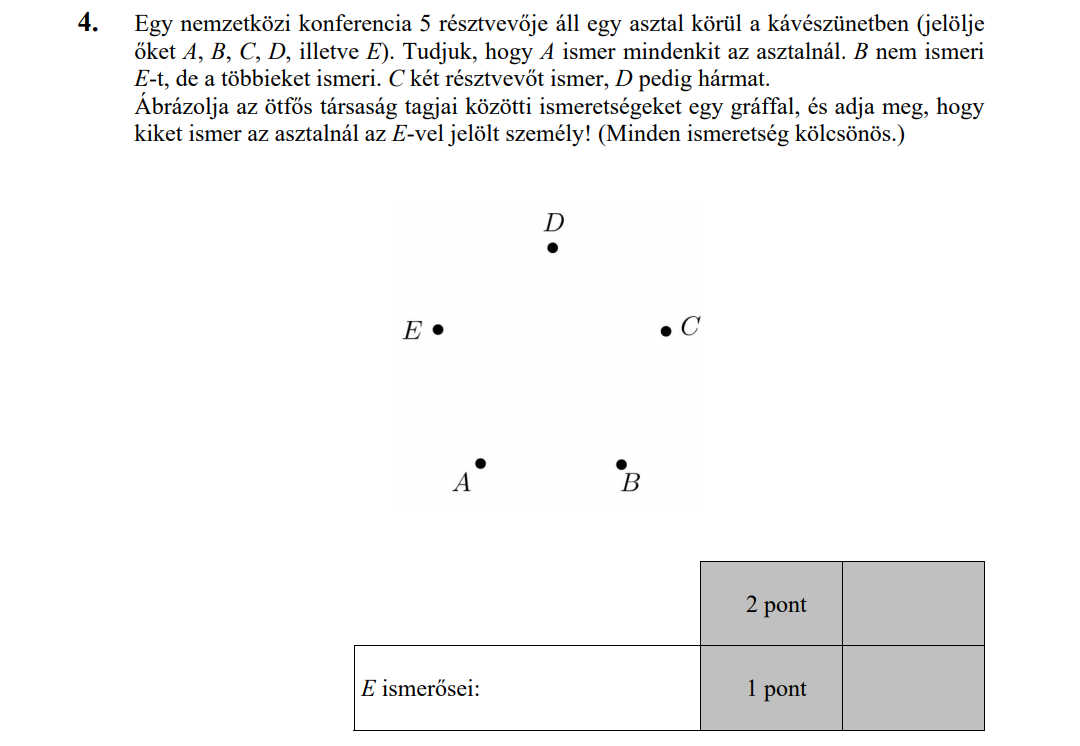
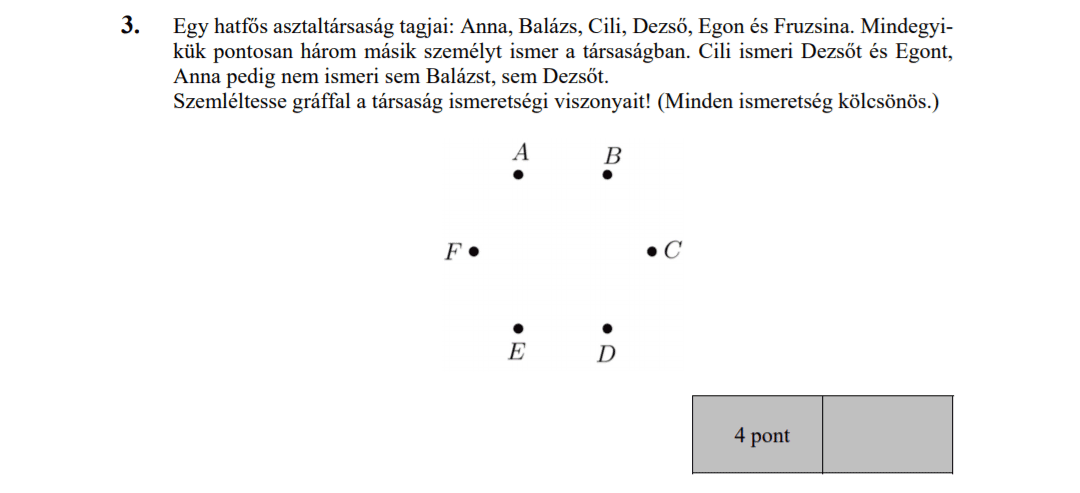
- Gráfok (2,6 pont)
- Másodfokú egyenletek (2,5 pont)
- Elsőfokú egyenletek (2 pont)
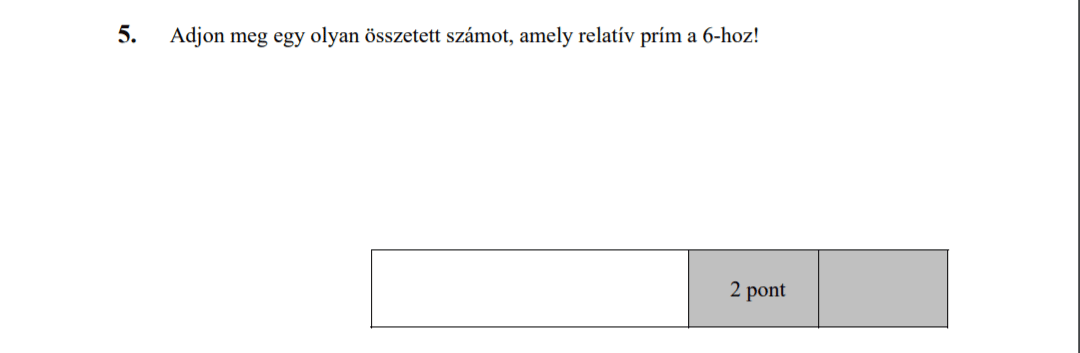
- Számelmélet (1,8 pont)
- Hatványozás, exponenciális egyenletek (0,8 pont)
- Egyenlőtlenségek (0,4 pont)
- Algebra, nevezetes azonosságok
- Bizonyítási módszerek, matematikai logika
- Egyenletrendszerek
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Egybevágósági transzformációk
Trigonometria, szinusztétel, koszinusztétel (8,4 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
2025 OKTÓBERI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2025 MÁJUSI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2024 OKTÓBERI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2024 MÁJUSI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2023 OKTÓBERI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2023 MÁJUSI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2022 OKTÓBERI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2022 MÁJUSI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2021 OKTÓBERI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs2021 MÁJUSI KÖZÉPSZINTŰ
MATEMATIKA ÉRETTSÉGI
Középszintű matek érettségi feladatlap Középszintű matek érettségi megoldókulcs- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


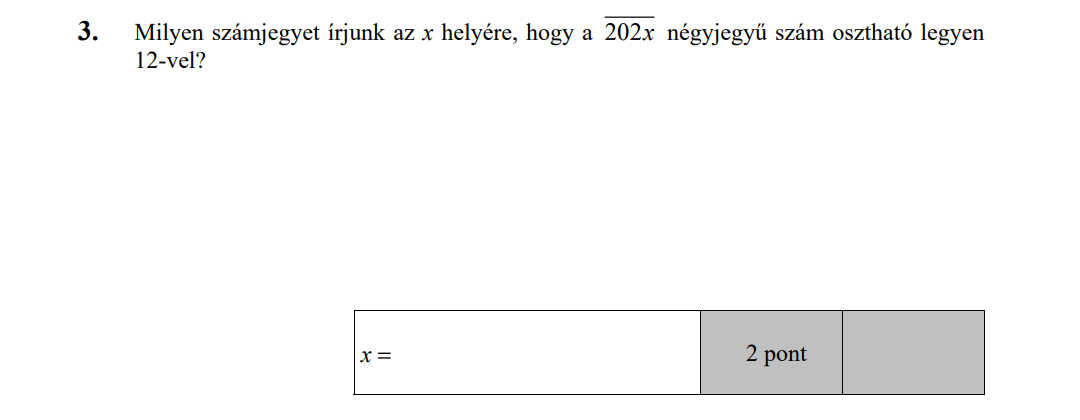
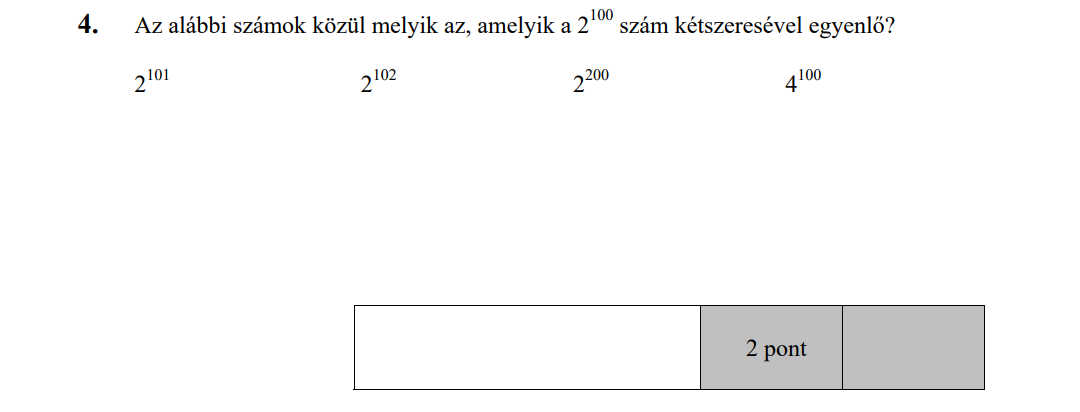



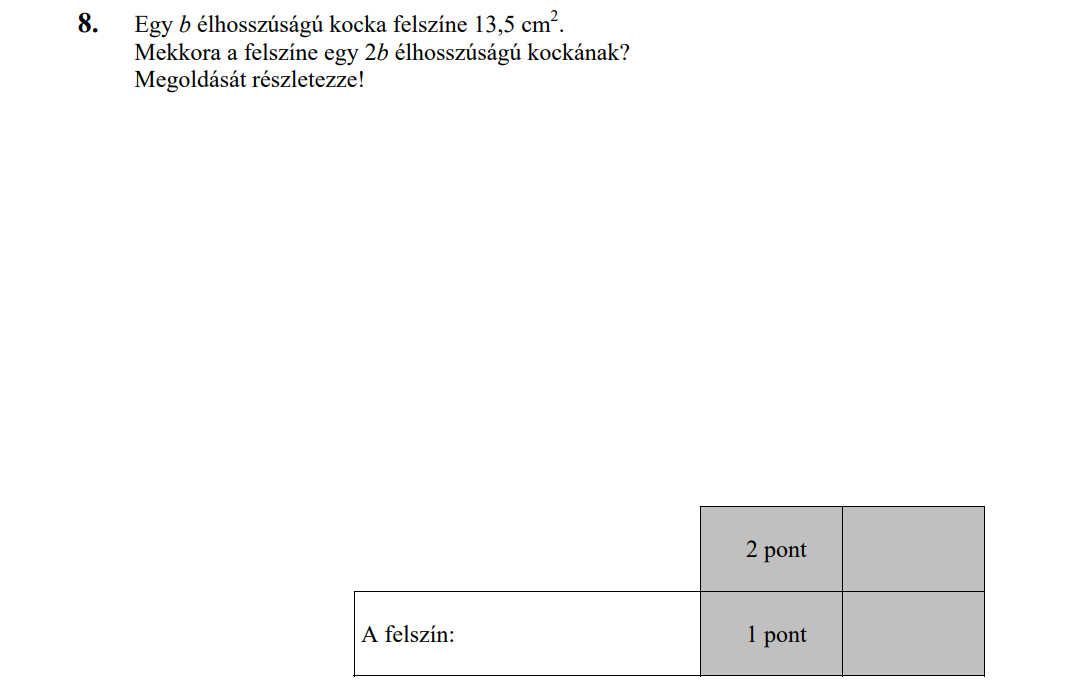




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
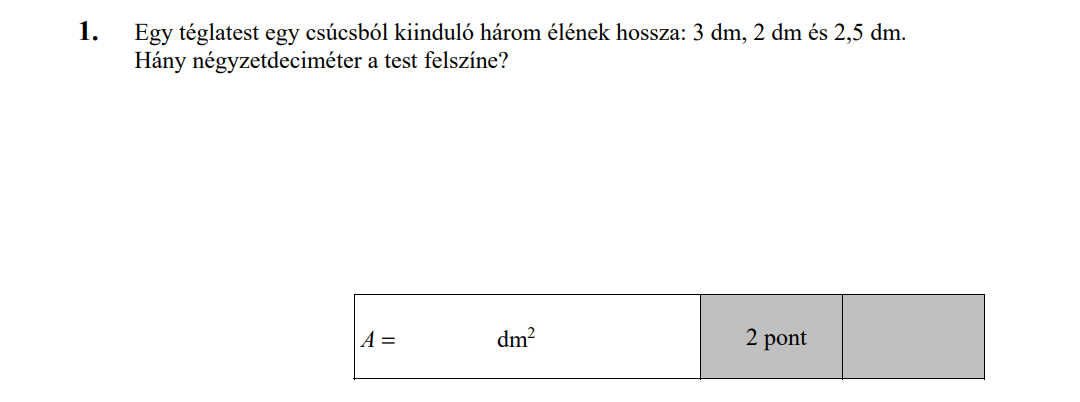






MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



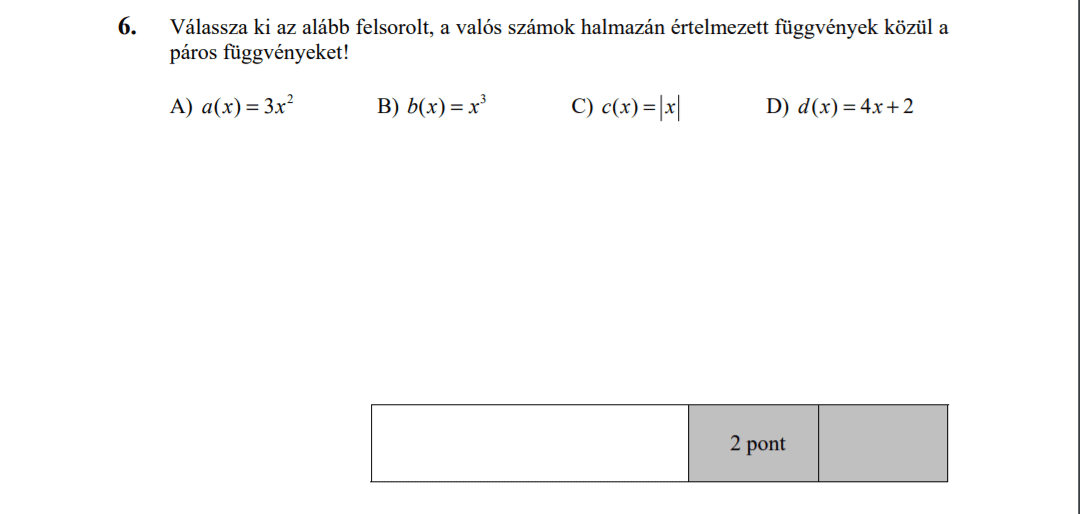
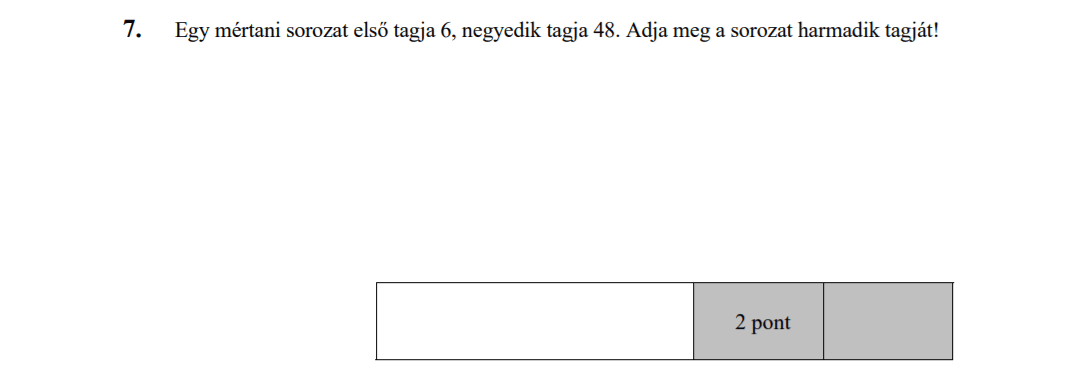



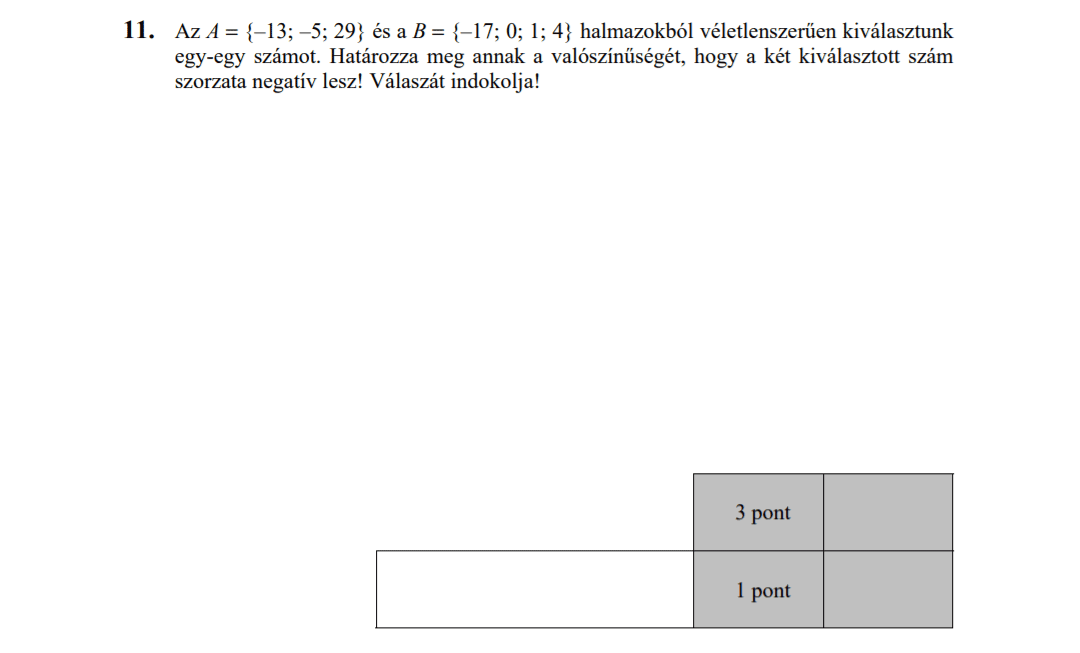

MÁSODIK RÉSZ


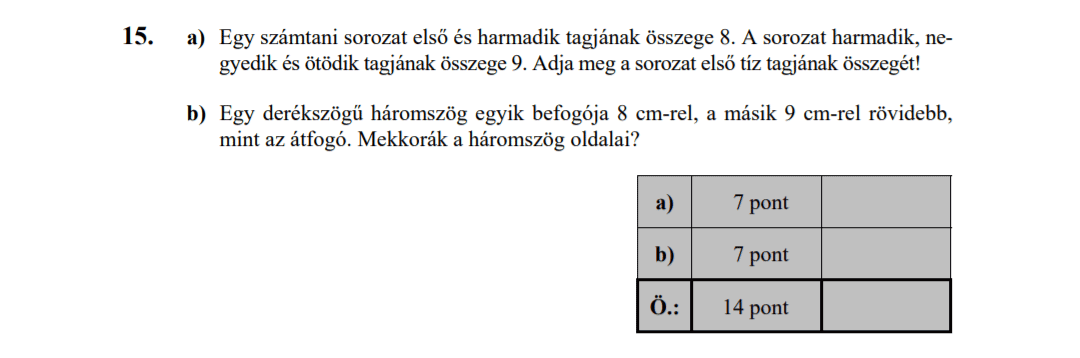



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






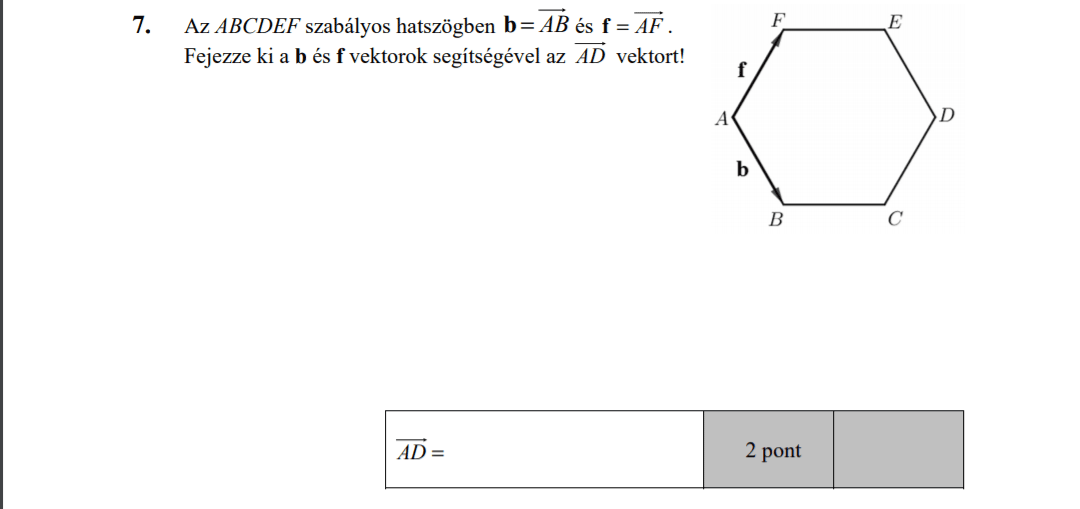



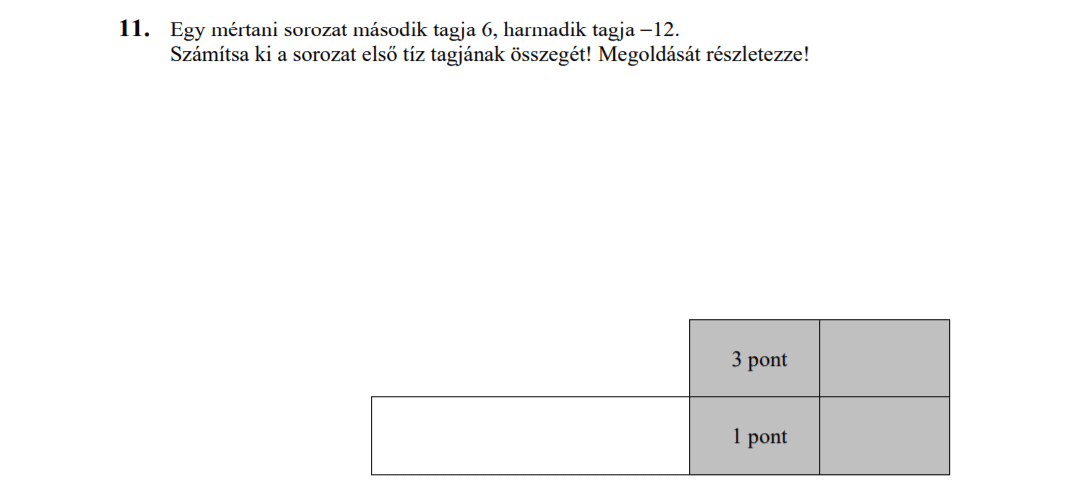

MÁSODIK RÉSZ

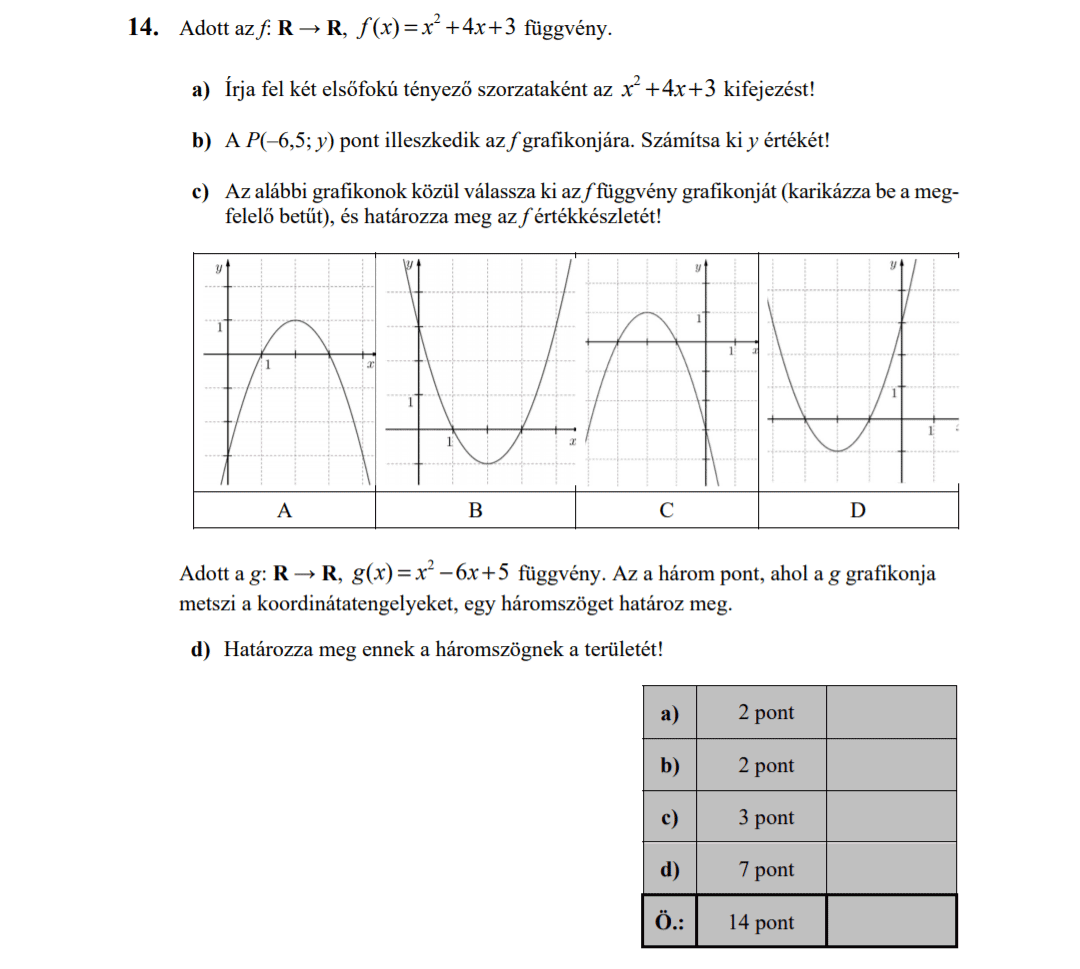




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



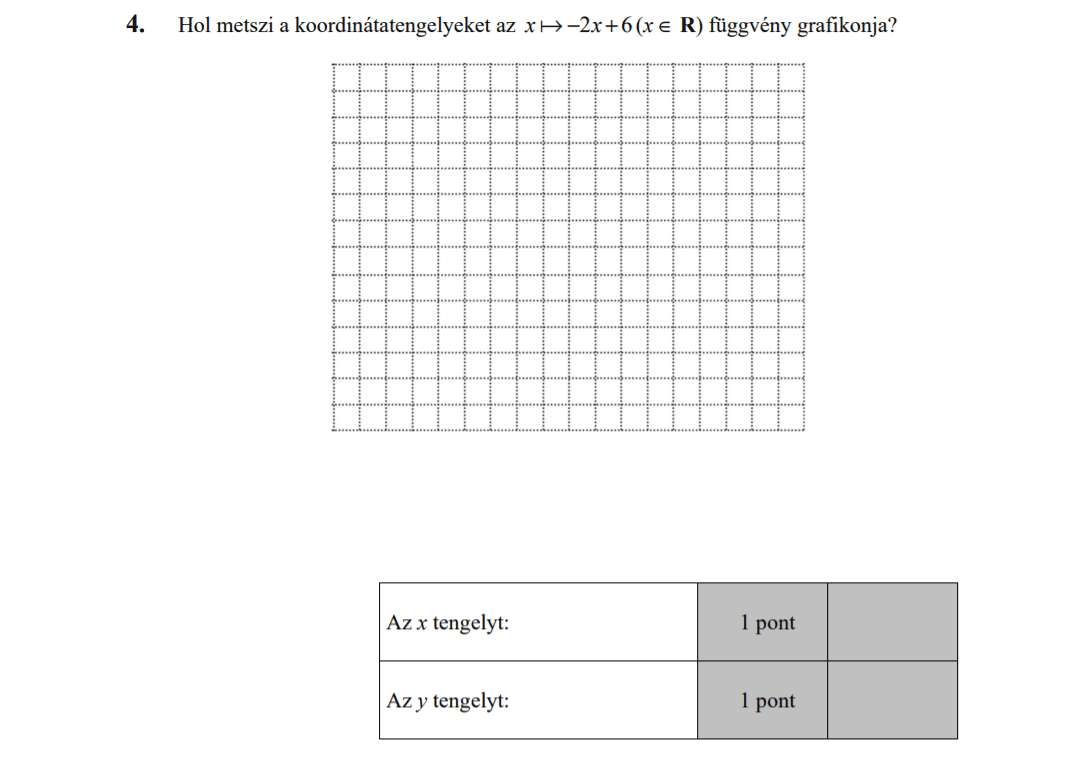

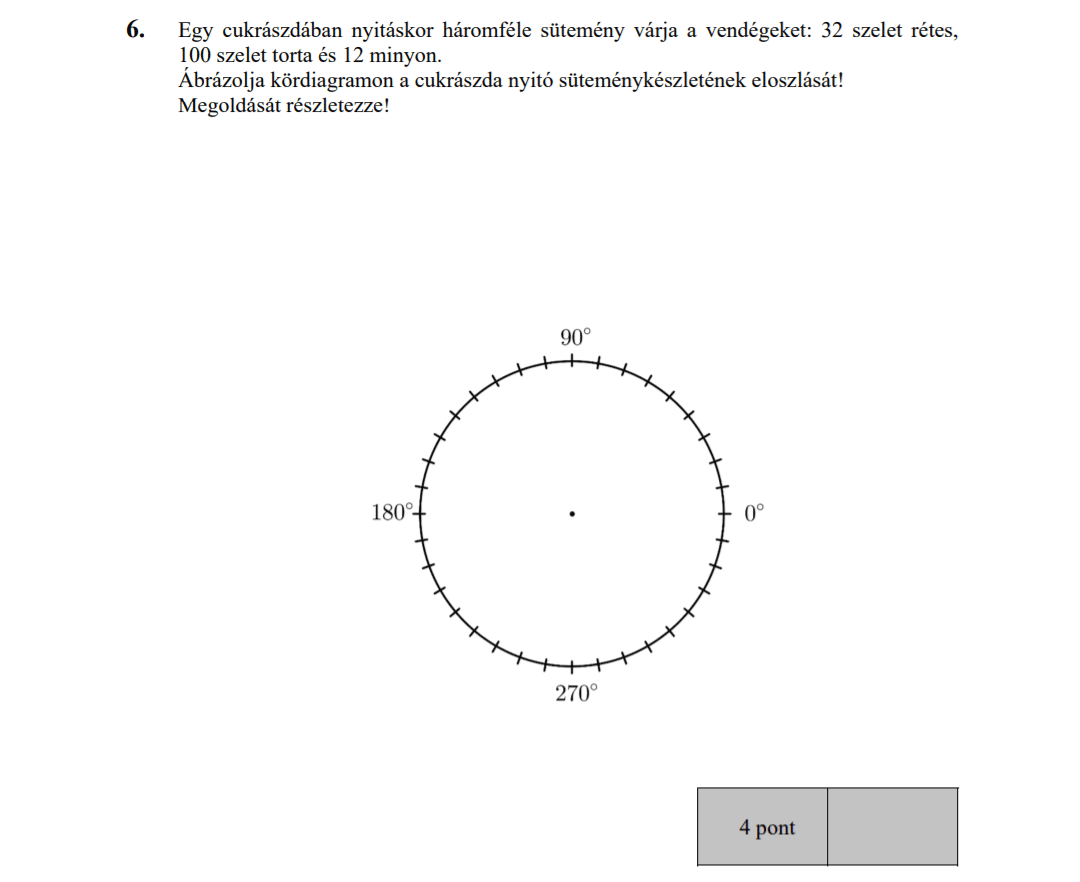






MÁSODIK RÉSZ

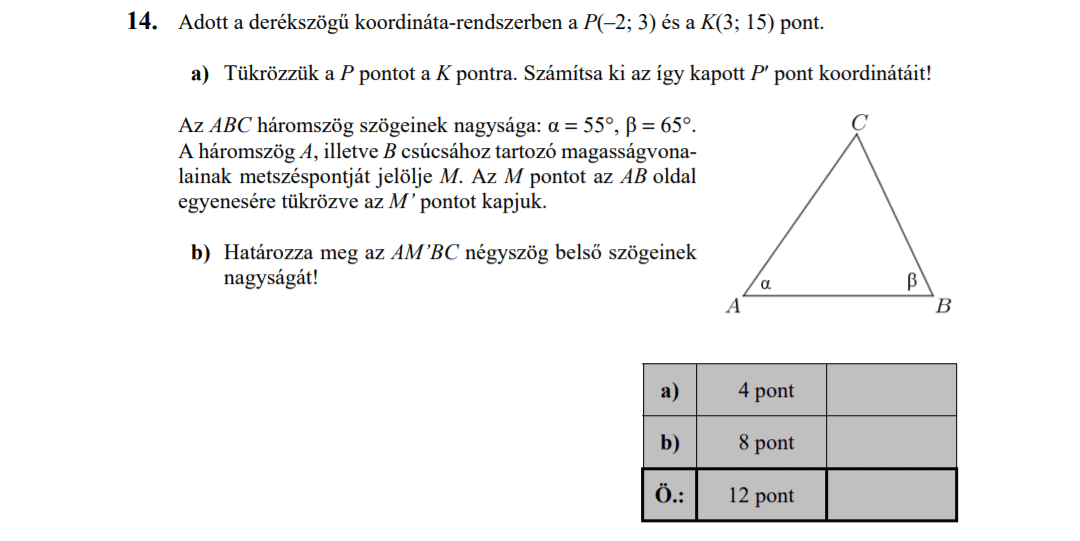




- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
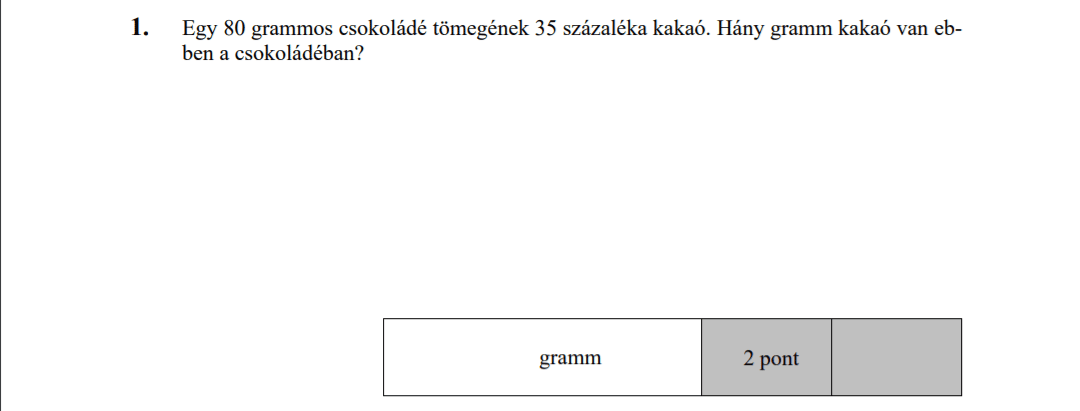

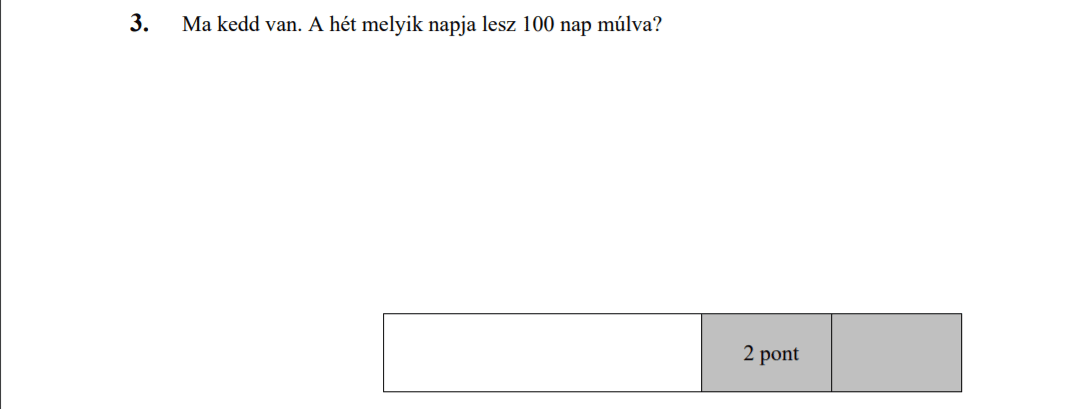
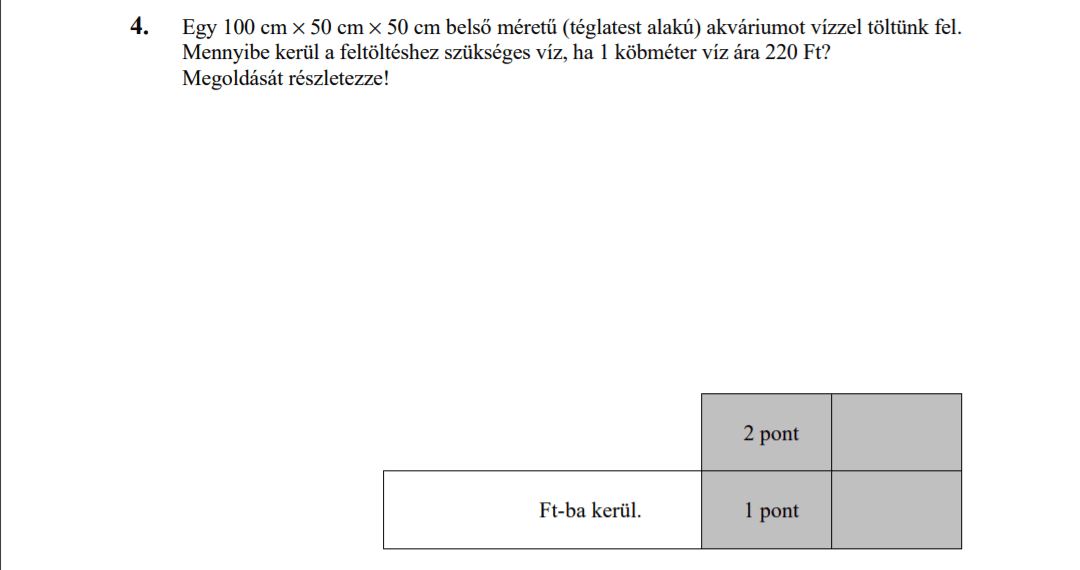
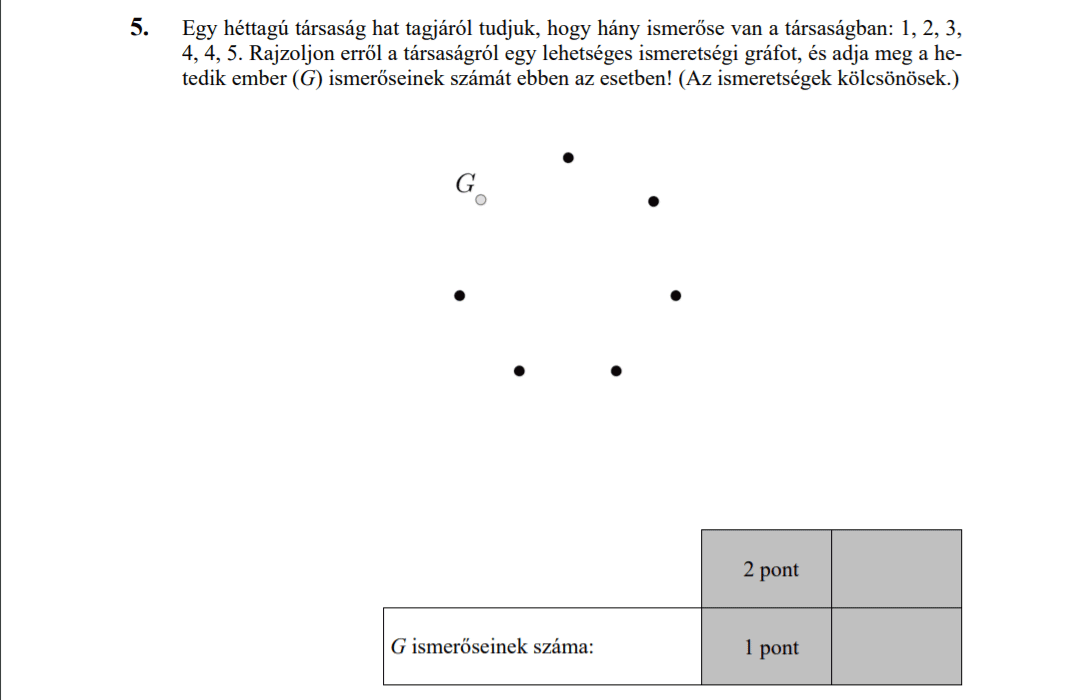







MÁSODIK RÉSZ
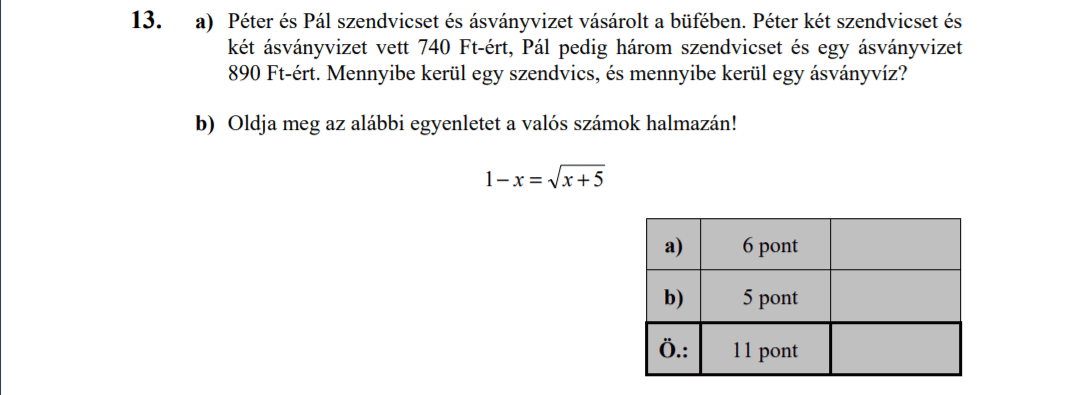
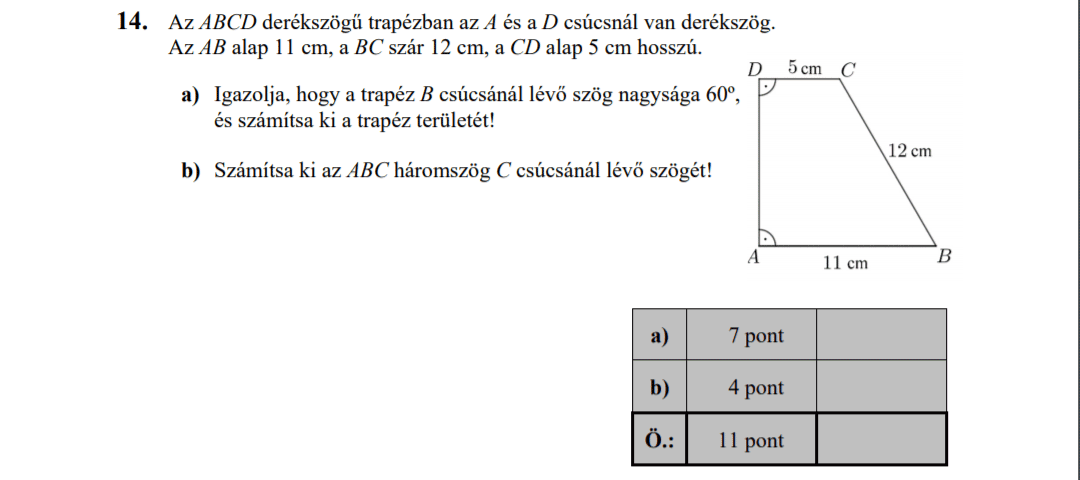

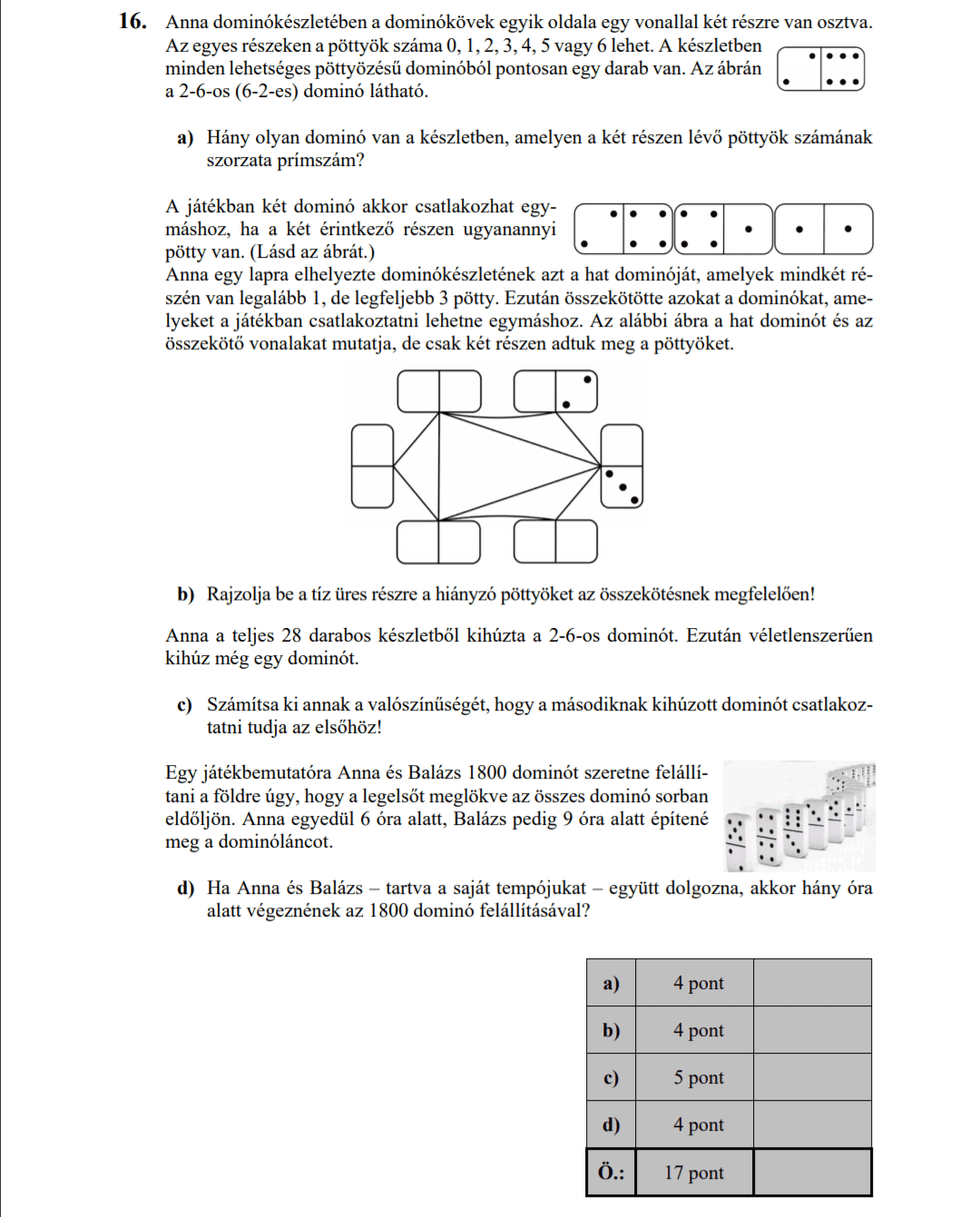


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ




- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







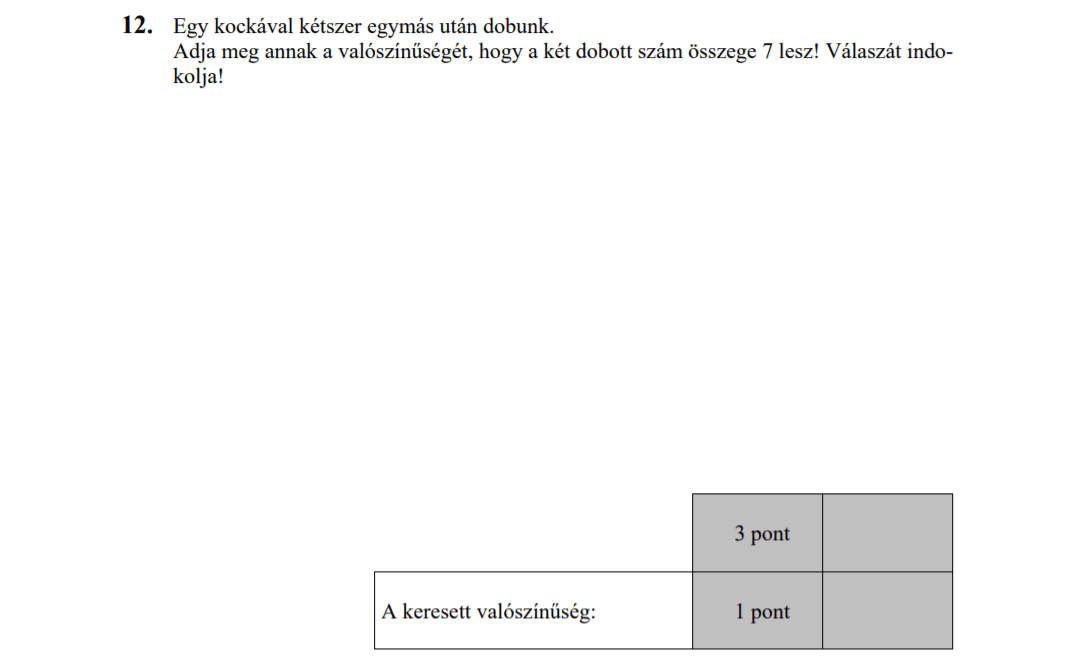
MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
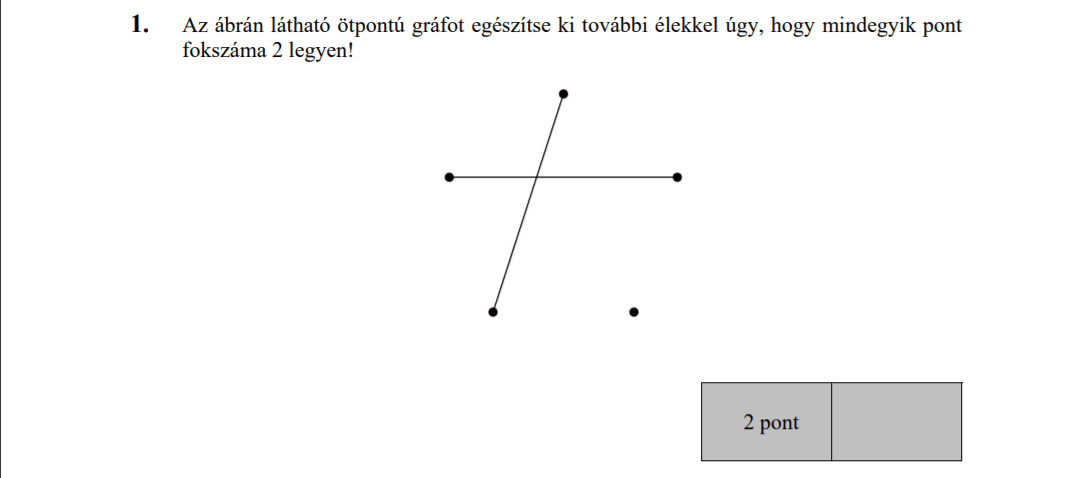
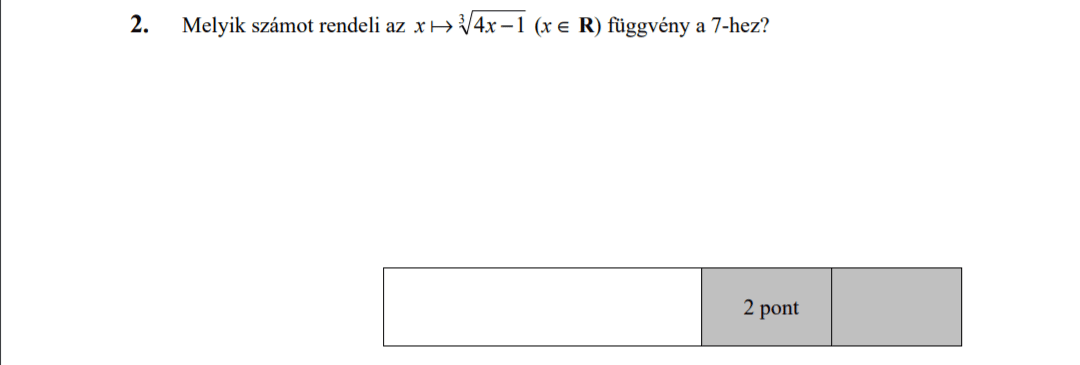
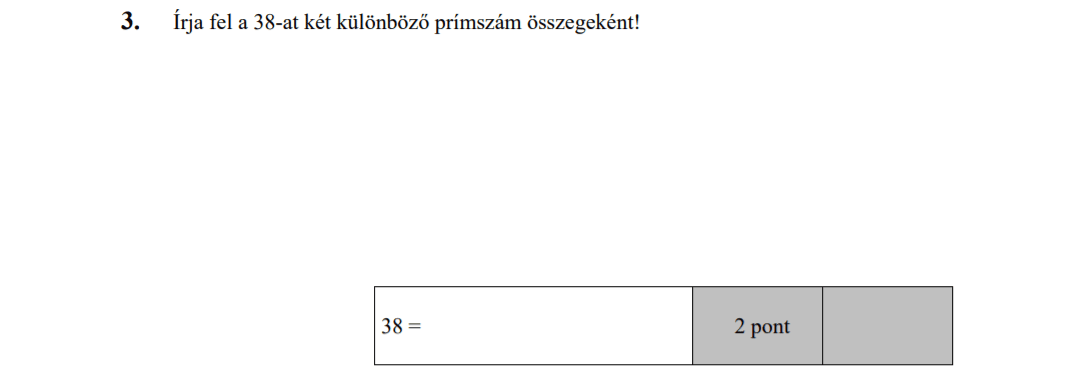




MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ




- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

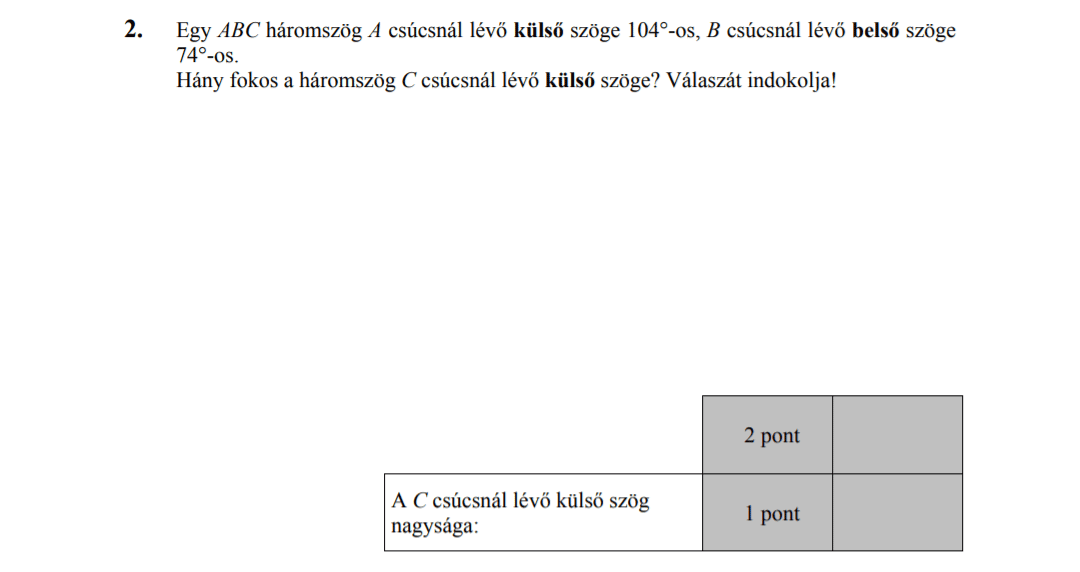





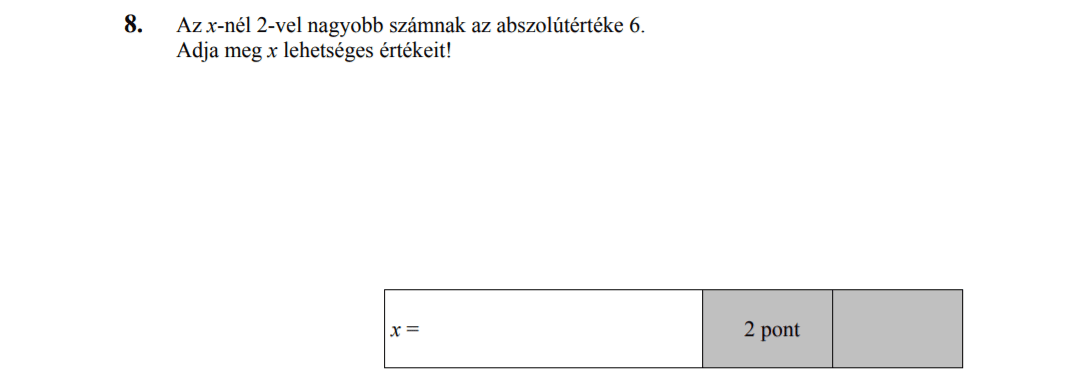

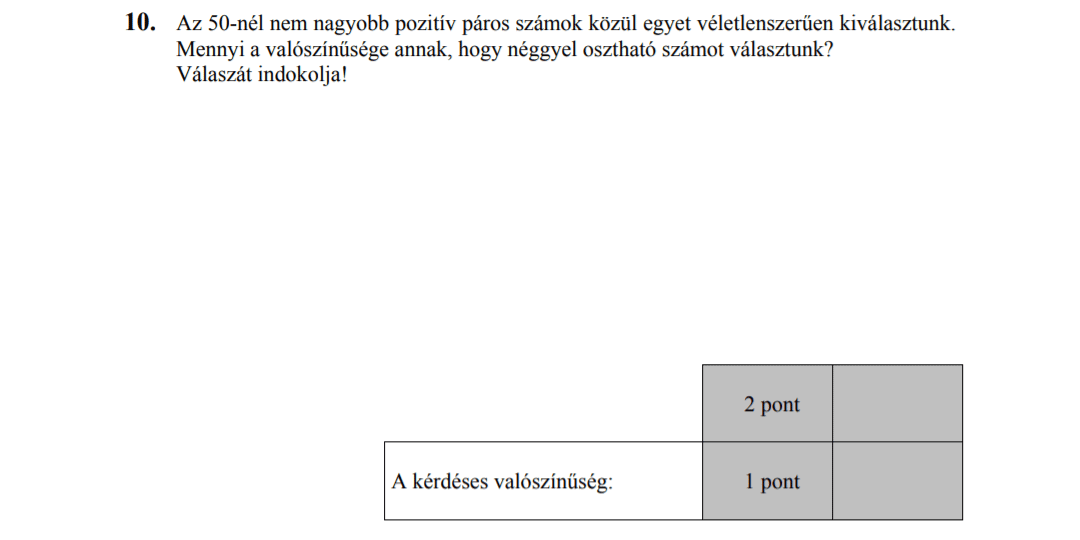


MÁSODIK RÉSZ

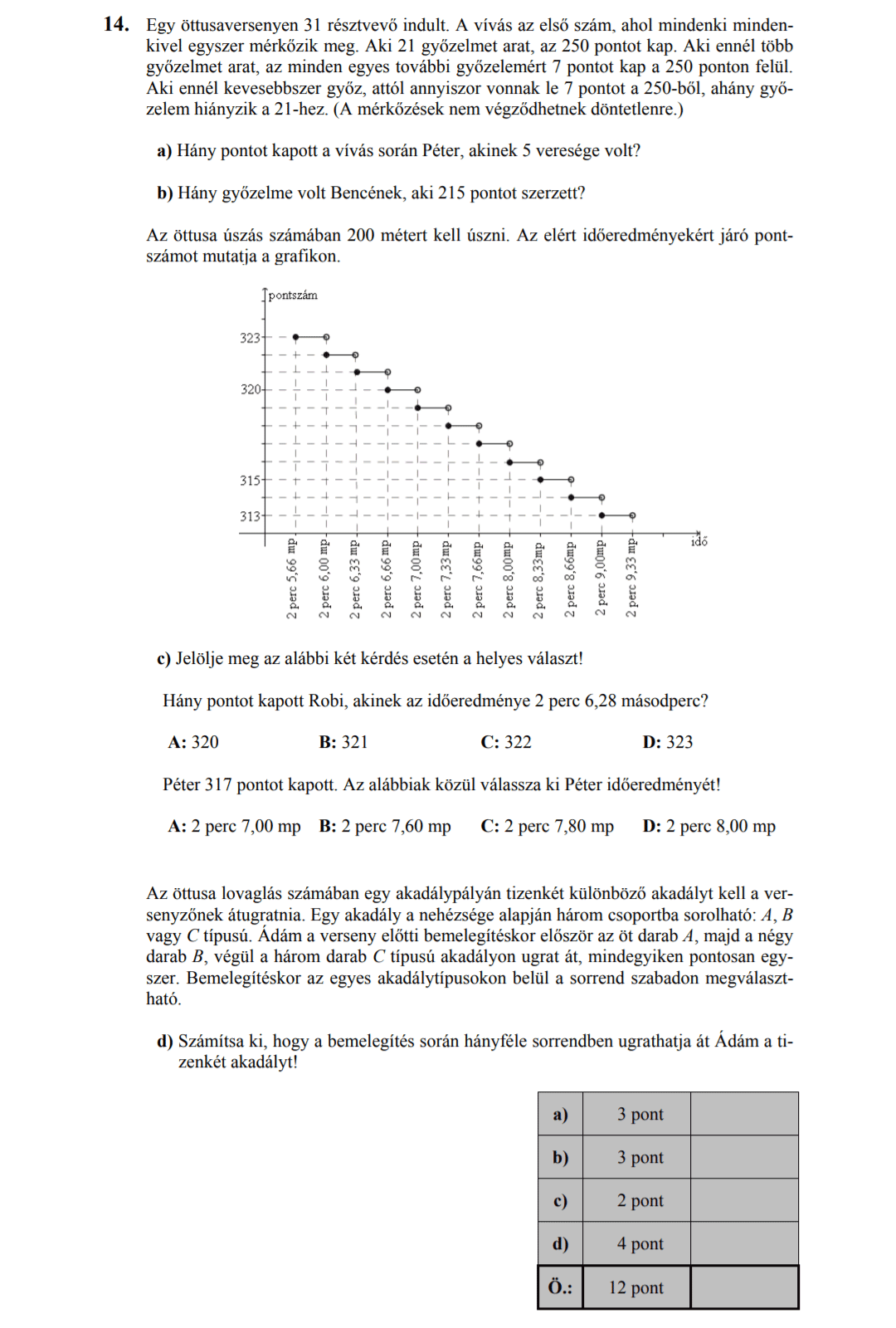



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ




- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ





- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



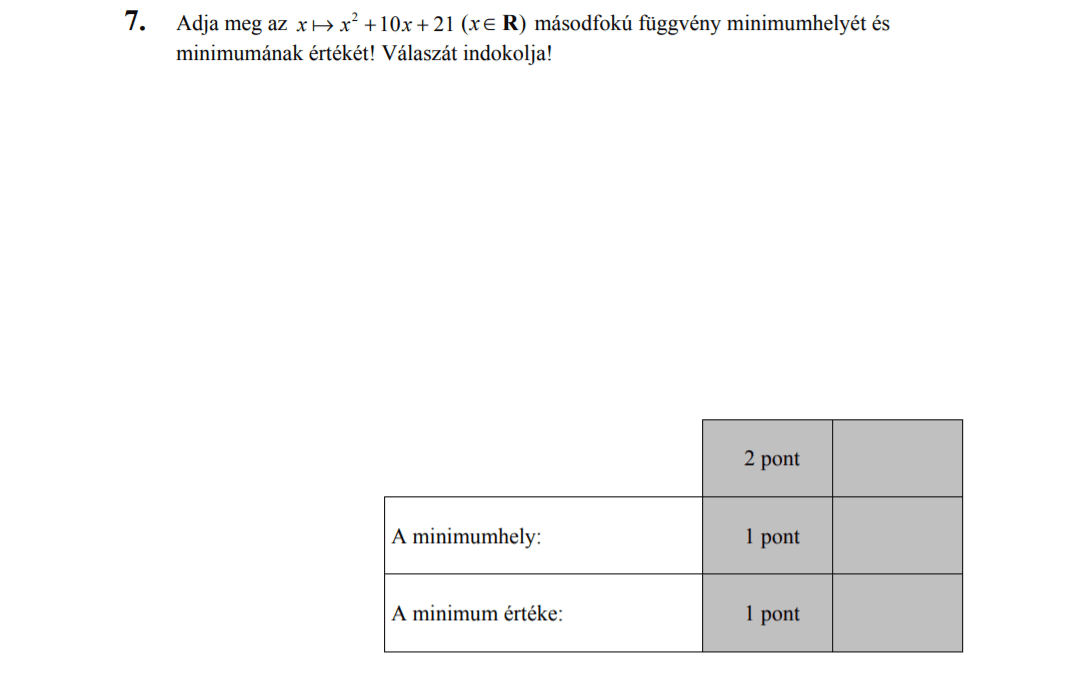



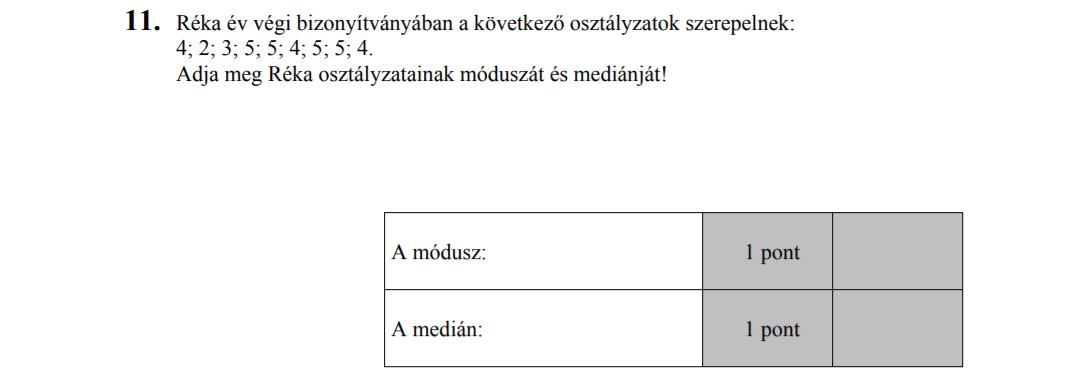

MÁSODIK RÉSZ





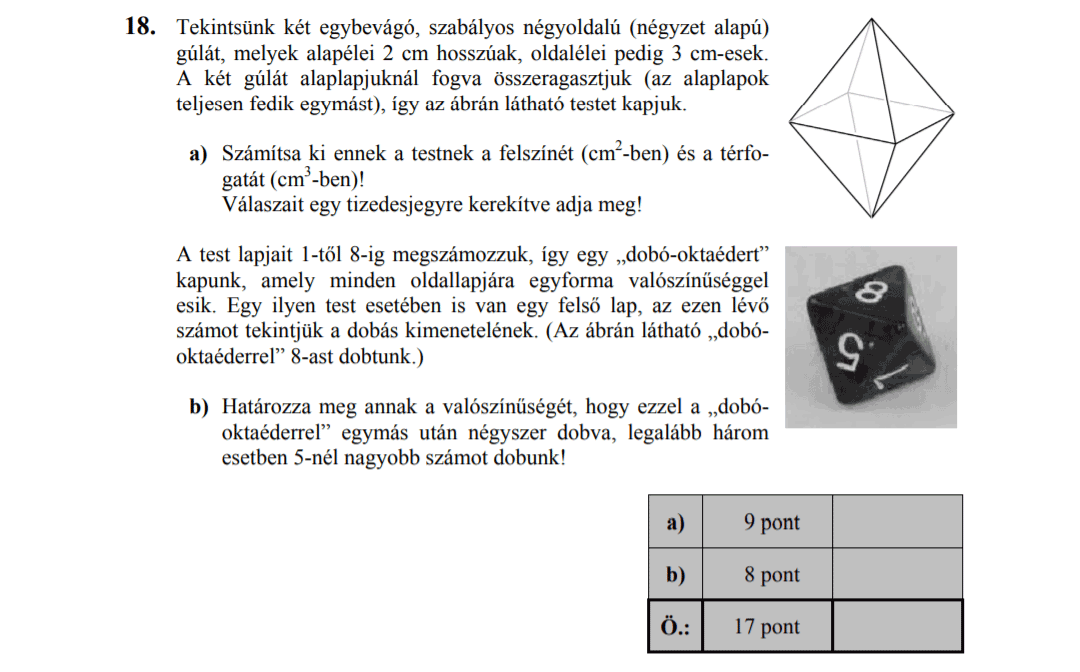
- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



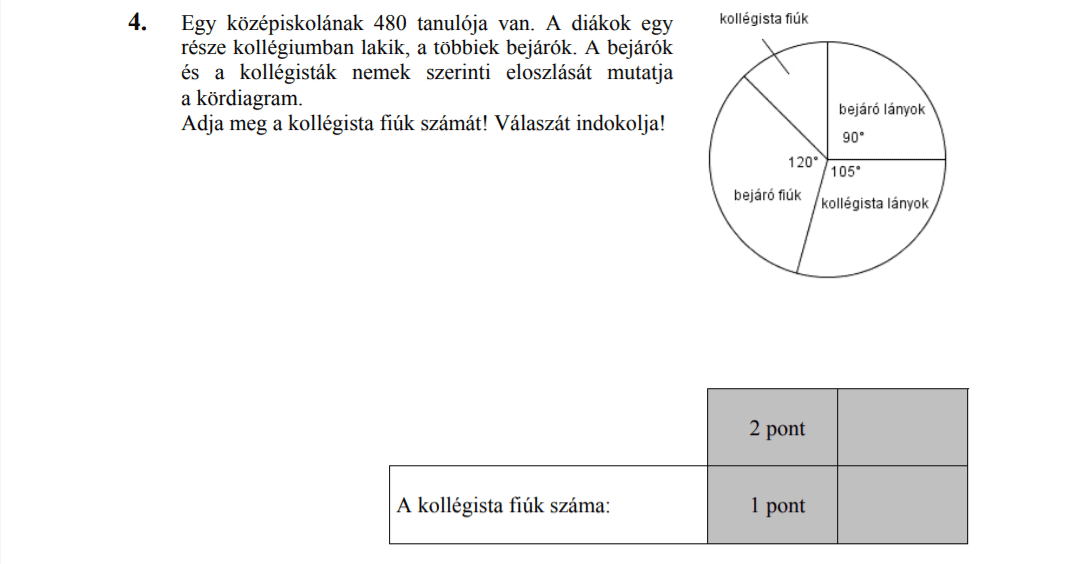



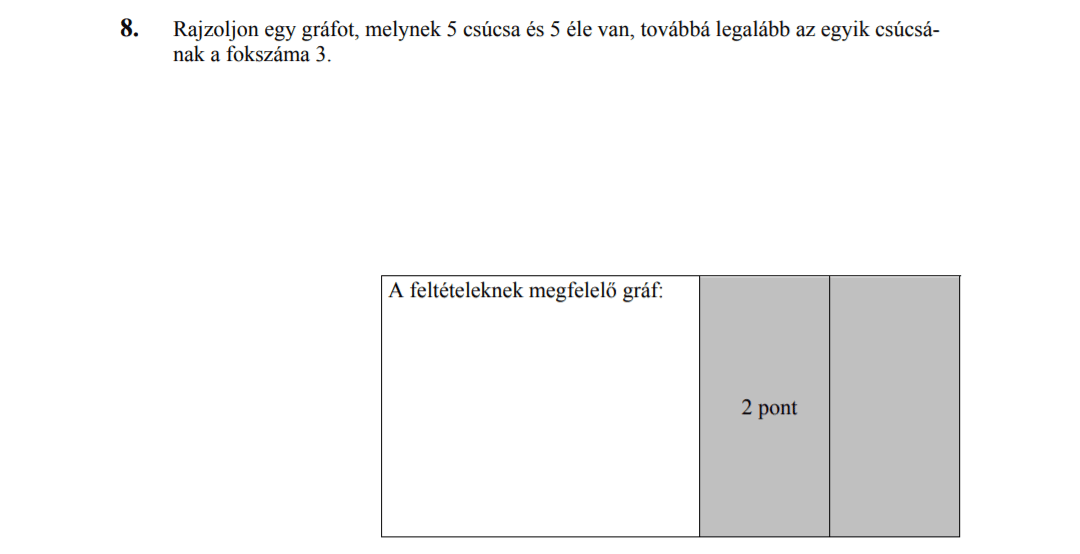
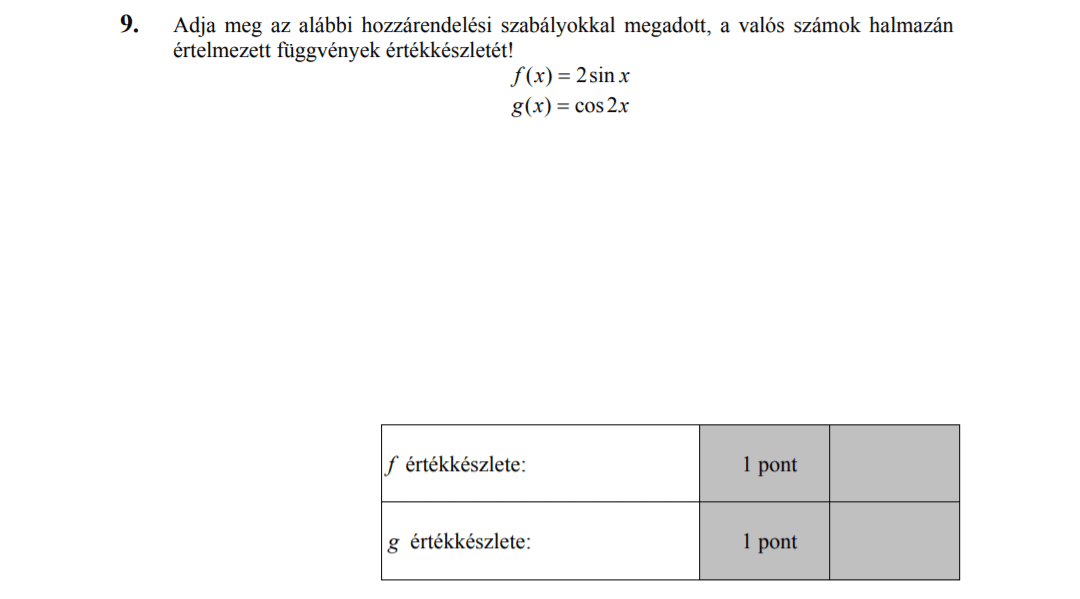

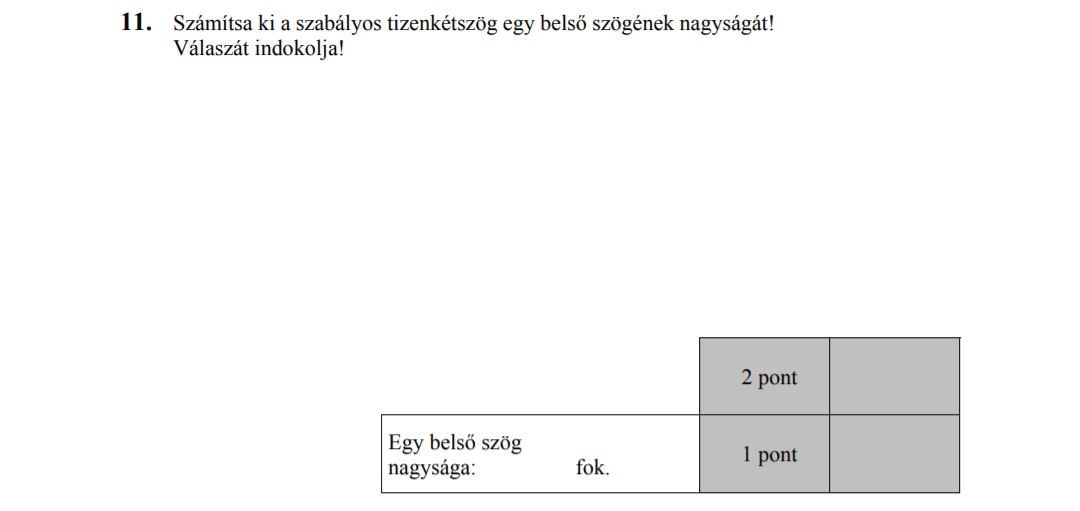

MÁSODIK RÉSZ






Ennek a témakörnek a képletei
Letöltöm az egész kurzus összes képletét:
LetöltömVálogass kedvedre a témakör képletei között:
Szögfüggvények derékszögű háromszögben
\( \sin{\alpha} = \frac{ \text{szöggel szemközti befogó} }{ \text{átfogó} } = \frac{a}{c} \)
\( \cos{\alpha} = \frac{ \text{szög melletti befogó} }{ \text{átfogó} } = \frac{b}{c} \)
\( \tan{\alpha} = \frac{ \text{szöggel szemközti befogó} }{ \text{szög melletti befogó} } = \frac{a}{b} \)
Koszinusz derékszögű háromszögekben
Derékszögű háromszög $\alpha$ hegyesszögének koszinuszát a következőképp értelmezzük:
\( \cos{\alpha} = \frac{ \text{ szög melletti befogó} }{ \text{átfogó} } \)
Szinusz derékszögű háromszögekben
Derékszögű háromszög $\alpha$ hegyesszögének szinuszát a következőképp értelmezzük:
\( \sin{\alpha} = \frac{ \text{ szöggel szemközti befogó} }{ \text{átfogó} } \)
Tangens derékszögű háromszögekben
Derékszögű háromszög $\alpha$ hegyesszögének tangensét a következőképp értelmezzük:
\( \tan{\alpha} = \frac{ \text{ szöggel szemközti befogó } }{ \text{szög melletti befogó} } \)
Háromszög szinusz gammás területképlete
\( T = \frac{a \cdot b \cdot \sin{\gamma} }{2} \)
Körszelet területe
A körszelet területét úgy kapjuk, hogy először kiszámoljuk, hogy mekkora területű a körcikk, aztán pedig kivonjuk belőle az ebbe beleeső egyenlőszárú háromszög területét:
\( T_{\text{sz}} = \frac{ \alpha}{360°} \cdot r^2 \cdot \pi - \frac{ r^2 \cdot \sin{alpha} }{2} \)
Szinusztétel
Bármely háromszögben az oldalak aránya megegyezik a velük szemközti szögek szinuszának arányával. De ne ezt jegyezzük meg. A szinusztétel ennél sokkal többet is tud. Mégpedig ezt, ahol R a háromszög köré írható körének a sugara:
\( 2R = \frac{a}{\sin{\alpha}} = \frac{b}{\sin{\beta}}=\frac{c}{\sin{\gamma}} \)
Koszinusztétel
A Koszinusz tétel minden háromszögben felírható:
\( c^2 = a^2 + b^2 - 2ab \cos{\gamma} \)
Ennek a témakörnek a feladatai
Letöltöm az egész kurzus összes feladatát:
LetöltömVálogass kedvedre a témakör feladatai között:
a) Egy világítótorony teteje 32 fokos emelkedési szögben látszik abból a csónakból, ami a torony lábától 100 méter távolságban van. Milyen magas a torony?
b) Egy 50 méter magas világítótorony tetejéről egy hajó 14°-nyi depresszió szög (vízszinteshez képest lefele mért szög) alatt látszik. A torony alja éppen a tenger szintjében van. Milyen távol van a hajóa torony aljától?
Végezzük el az alábbi feladatokat:
a) Egy egyenlőszárú háromszög szárai 12 cm hosszúak, és az alapon fekvő szöge 70 fokosak. Mekkora az alap és mekkora a háromszög területe?
b) Egy másik egyenlőszárú háromszögben az alap 16 cm, a szárak pedig 12 cm-esek. Mekkorák a háromszög szögei és a terület?
c) Egy egyenlőszárú háromszög szárai 10 cm-esek, a szárak által bezárt szög pedig 50 fokos. Mekkora a háromszög területe és az alapja?
Végezzük el az alábbi feladatokat:
a) Egy trapéz két alapja 20 cm és 10 cm, az egyik szára 12 cm és ez a szár 60°-os szöget zár be a hosszabbik alappal. Mekkora a trapéz területe és negyedik oldala?
b) Egy másik trapézban a hosszabbik alapon fekvő szögek 45 és 60 fokosak, a trapéz magassága 12 cm, a trapéz területe pedig 156 cm2. Mekkorák a trapéz oldalai?
a) Mekkora annak az egyenlő szárú háromszögnek a területe, amelynek szárai 12 cm hosszúak, és a szárak által bezárt szög 30 fok.
b) Egy másik egyenlő szárú háromszögről azt tudjuk, hogy az alapon fekvő szögei 30 fokosak, és a szárak 10 cm hosszúak. Mekkora a háromszög területe?
c) Egy paralelogramma oldalainak hossza 16 cm és 12 cm, az általuk bezárt szög 30°. Mekkora a paralelogramma területe?
d) Egy paralelogramma egyik átlójának hossza 7 cm és ez az átló 40 fokos szöget zár be a paralelogramma 12 cm hosszú oldalával. Mekkora a paralelogramma területe?
e) Egy trapézról tudjuk, hogy a két alapja 16 cm és 10 cm, az egyik szára 8 cm és ez a szár 60 fokos szöget zár be a hosszabbik alappal. Mekkora a trapéz területe?
Számoljuk ki annak a körszeletnek a területét, amelyet egy 13 cm sugarú körből vágunk le a kör középpontjától 5 cm távolságban haladó szelővel.
Végezzük el az alábbi feladatokat:
a) Egy háromszögben \( a=12 \), \( \alpha = 30° \), \( \beta = 40° \). Mekkorák a háromszög oldalai és a körülírt kör sugara?
b) Egy másik háromszögben \( a=12 \), \( b=13 \) és \( \alpha = 50° \). Mekkora a \( c \) oldal?
c) Egy harmadik háromszögben \( a=8 \), \( b=13 \) és \( \beta= 60° \). Mekkora a \( c \) oldal?
d) És végül egy negyedik háromszögben \( a=12 \), \( b=13 \), \( c= 8 \) és \( \gamma = 37° \). Mekkorák a háromszög szögei?
Végezzük el az alábbi feladatokat:
a) Az \( ABC \) háromszögben \( BC=14 \), \( AC=12 \), és az \( ACB \) szög 60°-os. Mekkorák az \( AB \) oldal és a háromszög területe?
b) Egy háromszög egyik oldala 5 cm, a szemben levő szög 60°. A másik két oldal összege 8 cm. Mekkora a másik két oldal és a háromszög területe?
Végezzük el az alábbi feladatokat:
a) Az \( ABC \) háromszögben \( BC=16 \), \( AC=12 \), és az \( ACB \) szög 60°-os. Mekkora az \( AB \) oldal és a háromszög területe?
b) Egy másik háromszögben \( a=16 \), \( \alpha = 30° \), \( \beta = 40° \). Mekkorák a háromszög oldalai és a háromszög területe?
c) És itt jön végül ez a harmadik háromszög, amiben a három oldal \( a=10 \), \( b=12 \) és \( c=16 \). Mekkorák a háromszög szögei és a háromszög területe?
a) Egy szikla tetején álló világítótoronyhoz vezető út a vízszinteshez képest 14°-os szögben emelkedik. Az út a szikla aljától indul és egyenesen halad a torony lábához, a hossza 150 méter. Milyen magas a szikla és hány fokos szögben látszik a vízszinteshez képest az 50 méter magas torony tetejéből az út eleje?
b) Egy másik világítótorony 30 méter magas sziklára épült. A torony teteje 15°-os emelkedési szögben, az alja 10°-os emelkedési szögben látszik egy hajóról. Milyen magas a torony?
c) Egy hegycsúcs tengerszint feletti magasságát szeretnénk megmérni. A hegycsúcs alatt elterülő völgyben 1800 méteres tengerszint feletti magasságban lézeres mérőeszközzel megállapítjuk, hogy a hegy csúcsa éppen 6854,11 méter távolságban van. A lézernyaláb emelkedési szöge 24 fokos. Milyen magas a hegycsúcs?
a) Egy toronyantennához 640 m hosszú egyenes út vezet, melynek emelkedési szöge 10°. Az út elejéről az antenna csúcsa az úthoz képest 20° emelkedési szög alatt látszik. Milyen magas az antenna?
b) Egy hegycsúcs 7 fokos emelkedési szögben látszik egy vele szomszédos 3089 méter magas hegyről. Ha a hegycsúcs irányában elindulunk egy 1 km hosszú 45 fokos lejtőn lefelé, akkor a lejtő aljáról ugyanennek a hegycsúcsnak a teteje 11,2 fokos emelkedési szögben látszik. Milyen magas a hegycsúcs?
a) Egy torony árnyéka a vízszintes talajon kétszer olyan hosszú, mint a torony magassága. Hány fokos szöget zár be ekkor a Nap sugara a vízszintes talajjal?
b) Egy egyenlőszárú háromszög alapja 12 centiméter, a szárai pedig 16 centiméteresek. Mekkorák a háromszög szögei?
a) Egy húrtrapéz két párhuzamos oldalának hossza 20 cm és 8 cm, az alapon fekvő szögei $\alpha=60°$. Mekkorák az oldalak és a trapéz területe?
b) Egy húrtrapéz két párhuzamos oldalának hossza 10 cm és 6 cm, területe $40 cm^2$. Mekkorák a trapéz szögei?
c) Egy egyenlőszárú trapéz szárai 30 fokos szöget zárnak be az egyik alappal. A szárak hossza 8 cm, a trapéz területe $36 cm^2$. Mekkora a trapéz kerülete?
Egy függőleges tartórúdra a talajtól 4 m magasan mozgásérzékelős lámpát szereltek, ami 140°-os nyílásszögű forgáskúpban világít függőlegesen lefelé.
a) Milyen messze van a lámpától a legtávolabbi megvilágított pont?
b) Megvilágítja-e az érzékelő lámpája azt a tárgyat, amelyik a talajon a tartórúd aljától 15 m távolságra van?
Számoljuk ki annak a körszeletnek a területét, amelyet egy 15 cm sugarú körből vágunk le a kör középpontjától 8 cm távolságban haladó szelővel.
a) Egy egyenlőszárú háromszögben az alap 10 cm, a szárak pedig 16 cm-esek. Mekkorák a háromszög szögei?
b) Egy egyenlőszárú háromszögben az alap és a szár összege 11 cm, az alapon fekvő szögek 53° nagyságúak. Mekkorák a háromszög oldalai, csúcsnál fekvő szöge, és területe?
c) Egy egyenlőszárú háromszög területe $108 \; cm^2$, a csúcsánál levő szöge $36°$. Mekkora az alapja és a magassága?
a) Egy derékszögű háromszögben $\tan{\alpha}=\frac{3}{4}$, a háromszög területe pedig $24 \; cm^2$.
Mekkorák a háromszög oldalai?
Mekkora a köré írható kör sugara?
b) Egy hegyre két ösvény vezet, melyek azonos szintről, ellentétes oldalról, egymástól 500 m távolságról indulnak. Az ösvények emelkedési szöge 32° és 42°. Milyen magas a hegy?
Az óceánban fekvő egyik szigeten a földrengést követően kialakuló szökőár egy körszelet alakú részt tarolt le. A körszeletet határoló körív középpontja a rengés középpontja, sugara pedig 18 km. A rengés középpontja a sziget partjától 17 km távolságban volt. Mekkora a szárazföldön elpusztult rész területe egész négyzetkilométerre kerekítve?
Számoljuk ki az adott derékszögű háromszögekben a hiányzó oldalakat és szögeket, ha
a) $a=12, \beta=48° $
b) $b=14, \alpha=34° $
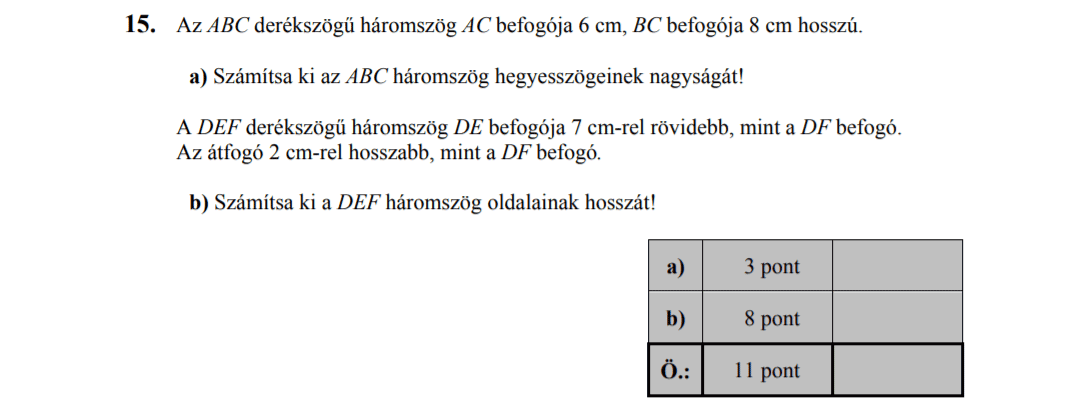
c) $a=6, b=8$
Egy háromszög egyik oldala 6 cm, a másik két oldal különbsége 4 cm, és a 6 cm-es oldallal szemközti szög 75°-os. Mekkorák a háromszög ismeretlen oldalai és szögei?
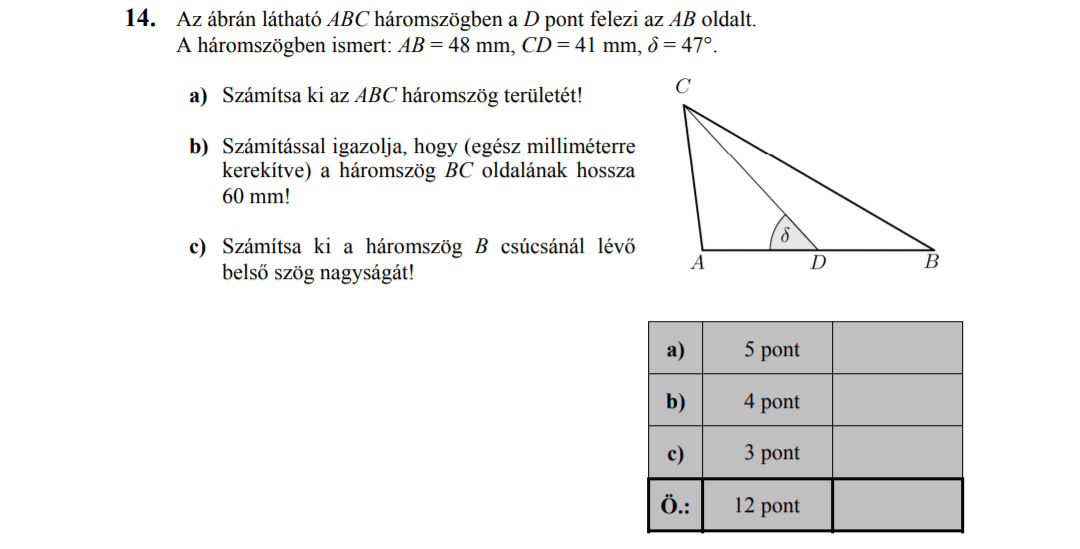
Az \( ABC \) hegyesszögű háromszögben legyen az \( AB \) oldal felezőpontja \( C_1 \). Az \( AB \) oldal hossza 36, a \( CC_1 \) szakaszé 24, továbbá a \( C_1CB \) szög 40°-os
a) Mekkora a háromszög \( B \) csúcsnál lévő belső szög?
b) Mekkora a \( BC \) oldal hossza?
c) Mekkora a háromszög területe?
Egy háromszög egyik oldala 10 cm hosszú. Az ezzel az oldallal szemközti szög 28,96°. A másik két oldal négyzetének összege 625 \( cm^2 \). Mekkorák a háromszög ismeretlen oldalai és szögei?
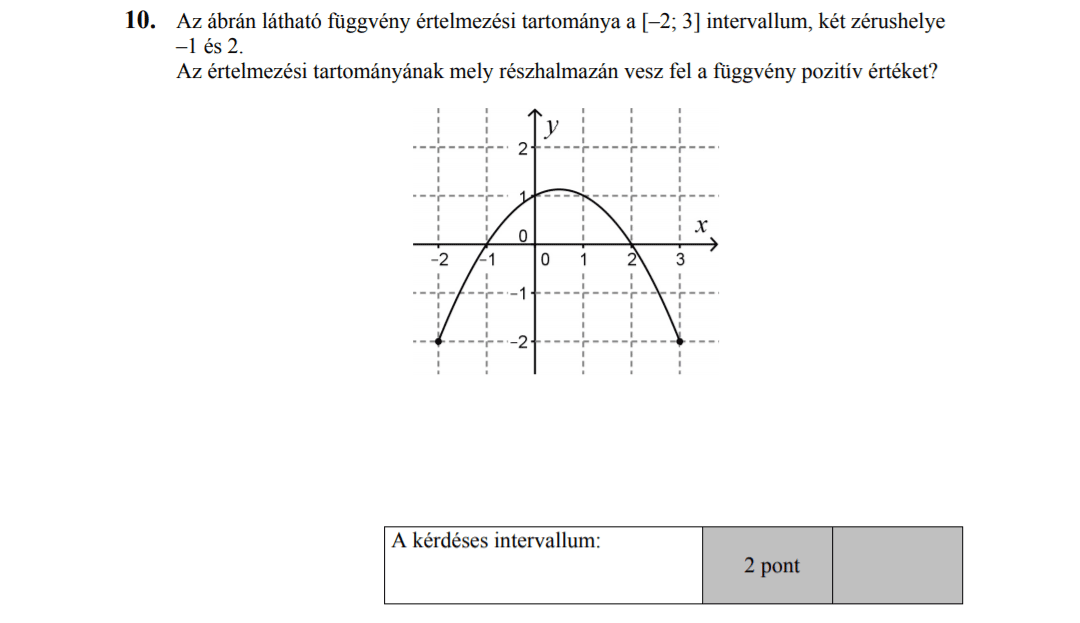
a) Egy háromszög három oldala $a=5$, $b=6$ és $c=10$.
Mekkora a háromszög legnagyobb szöge?
b) Egy háromszög három oldala $a=6$, $b=8$ és $c=12$.
Mekkora a háromszög legnagyobb szöge?
Egy háromszög szögei: ABC szög 50°-os, BCA szög 60°-os, CAB szög 70°-os, és BC=5.
a) Mekkora a háromszög területe?
b) Mekkora a köré írható kör sugara?
Egy toronyantennához 230 m egyenes út vezet, melynek emelkedése 21°. Az út elejéről az út síkjához képest az antenna csúcsa 39° szögben látszik. Milyen magas az antenna?
Egy hegymászó a hegyoldal valamely pontjából a tőle 1657 m távolságban levő hegycsúcsot 23° emelkedési szögben s ugyanennek a hegycsúcsnak a tükörképét az alatta elterülő tó tükrében 49°-os depressziószög alatt látja. Milyen magasan van a hegymászó, s milyen magasan van a hegycsúcs a tenger színe felett, ha a tó felszíne 608 m-nyire van a tenger színe felett?
Az \( ABC \) hegyesszögű háromszögben \( BC=14 \), \( AC=12 \), és a \( BCA \) szög 40°-os. Mekkora az \( AB \) oldal? Legyen az \( AB \) oldal felezőpontja \( C_1 \) és a \( BC \) oldal felezőpontja \( A_1 \). Mekkora az \( AC_1A_1C \) négyszög területe?
Egy derékszögű háromszögben \( \tan{\alpha}=\frac{3}{4} \), a háromszög területe pedig \( 24 cm^2 \).
a) Mekkorák a háromszög oldalai?
b) Mekkora a köré írható kör sugara?
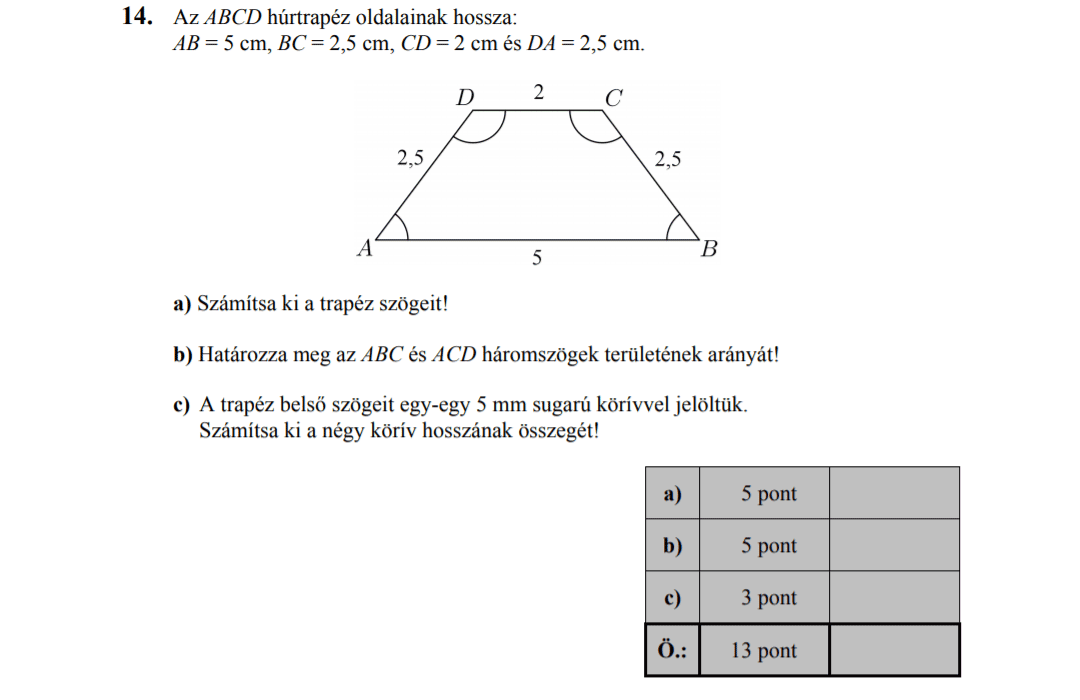
Az \( ABCD \) trapéz oldalainak hossza: \( AB=10 \), \( BC=5 \), \( CD=4 \), \( DA=5 \).
a) Számítsa ki a trapéz szögeit!
b) Határozza meg az \( ABC \) és \( ACD \) háromszögek területének arányát!
c) A trapéz belső szögeit egy-egy 5mm sugarú körívvel jelöljük be. Számítsa ki a négy körív hosszának összegét!
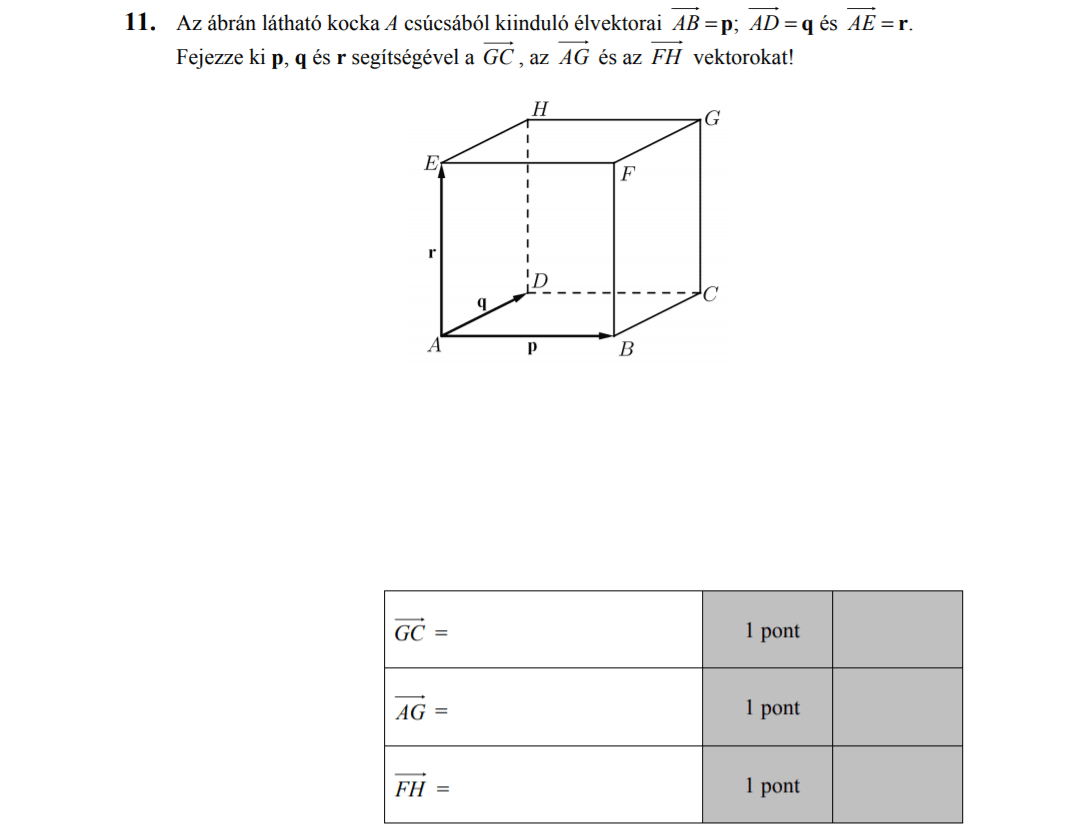
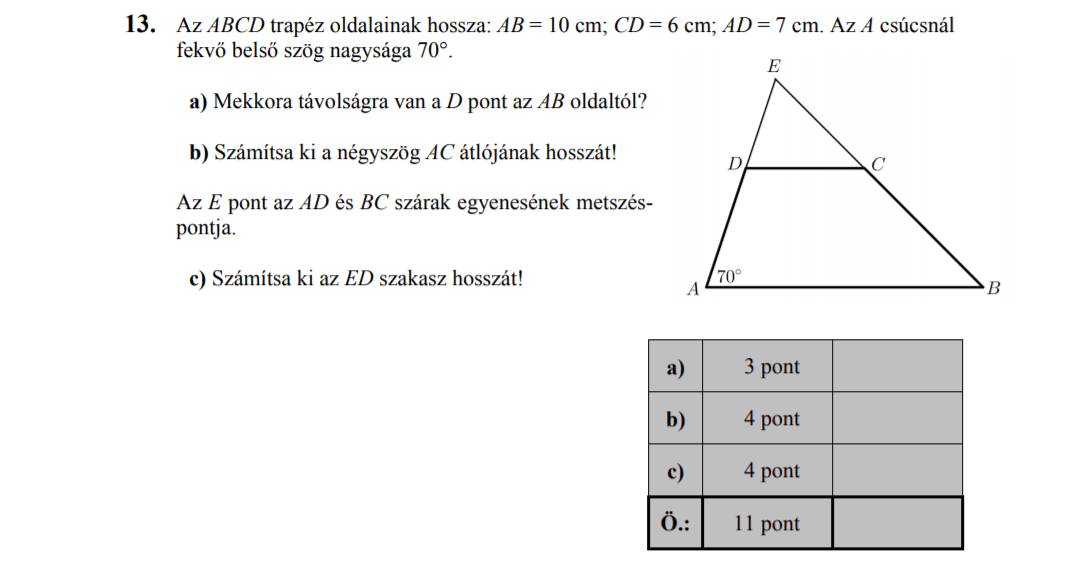
Az \( ABCD \) trapéz oldalainak hossza: \( AB=10 \), \( CD=6 \), \( AD=7 \). Az \( A \) csúcsnál fekvő belső szög 70°-os.
a) Mekkora távolságra van a \( D \) pont az \( AB \) oldaltól?
b) Számítsa ki a négyszög \( AC \) átlójának hosszát!
Az \( E \) pont az \( AD \) és \( BC \) szárak egyenesének metszéspontja.
c) Számítsa ki az \( ED \) szakasz hosszát!
Egy háromszög egyik oldala 5 cm, a másik két oldal összege 8 cm, és az 5 cm-es oldallal szemben lévő szög 60°. Mekkora a másik két szög, és a másik két ismeretlen oldal?
Az $ABCD$ húrnégyszögben $AB=20$, $BC=18$, az $ABC$ szög 70°-os, a $CAD$ szög 50°-os. Milyen hosszú a $CD$ oldal és mekkora a húrnégyszög területe?
Egy háromszög kerülete $598 \; cm$, $a=258 \; cm$, $\alpha = 98°33'$. Mekkorák a háromszög ismeretlen oldalai és szögei?
A hegycsúcsok magasságát egy ügyes kis trükkel lehet megmérni...
Kell hozzá egy lézeres távolságmérő…
Szögmérővel ellátva.
A távolságmérővel becélozzuk a hegycsúcs tetejét…
És lemérjük a távolságot.
Aztán megmérjük ezt a szöget.
És most jön a trükk.
Van itt ez a derékszögű háromszög…
Ebben a háromszögben itt a hegycsúcs magassága.
És mindjárt meg is tudjuk mondani, hogy ez mennyi ez a magasság.
Egy nagyon ravasz képlet segítségével.
Egy derékszögű háromszögben a szöggel szemközti befogó és az átfogó arányát
A hegycsúcs magassága meg is van.
Hogyha pedig tudjuk, hogy mekkora a mérési pont tengerszintfeletti magassága…
Csak hozzáadjuk ehhez az 1926,1 métert…
És meg is van a hegycsúcs tengerszintfeletti magassága.
És most nézzünk meg egy másik érdekes történetet.
Egy világítótorony teteje 32 fokos emelkedési szögben látszik abból a csónakból, ami a torony lábától 100 méter távolságban van. Milyen magas a torony?
A 32 fokos emelkedési szög ezt jelenti…
A vízszinteshez képest 32 fok fölfelé…
És ez itt a 100 méter.
Megint van egy derékszögű háromszög…
Amiben a torony magassága az egyik befogó…
És a 100 méter a másik befogó.
Ez a történet a háromszög két befogójáról szól…
Az ilyen esetekre pedig itt jön most egy újabb képlet.
Sőt, essünk túl mindegyiken…
Az ilyen derékszögű háromszöges problémáknál szinuszt, koszinuszt és tangenst fogunk használni.
A szinusz már megvan.
Itt jön a koszinusz…
És itt van még a tangens…
Most az egyik befogót keressük, és a másik befogót ismerjük…
Vagyis a három közül az fog kelleni, amiben két befogó szerepel.
És most nézzük, mi van ezzel a szinusszal…
És most néhány nagyon izgalmas kérdésre fogunk választ kapni.
Kezdjük azzal, hogy vajon hogyan lehet megmérni azt, hogy egy
csillag milyen távol van a Földtől.
Vannak persze az életben ennél sokkal fontosabb kérdések is,
például az, hogy hogyan szerezzünk több követőt az Instragramon,
de mégis foglalkozzunk most egy picit a csillagokkal.
A csillag távolságának kiszámolásához egy trükköt fogunk
használni. Megmérjük, hogy milyen szögben látszik a csilla a
Földről nézve nyáron… és télen.
Ez alapján pedig ki tudjuk számolni ezt a szöget.
Aminek a fele is egész lesz.
Azt már tudjuk, hogy milyen messze van a Föld a Naptól…
Úgy kb. 150 millió kilométerre.
És ez a két adat éppen elég is.
A csillagászok ugyanis magányos éjszakáikon kifejlesztettek egy függvényt a
derékszögű háromszögekre, amit szinusz névre kereszteltek el.
szöggel szemközti befogó
sin α = _______________________
átfogó
Ha mondjuk α = 1◦ akkor a csillag távolsága:
x = 8823,53 millió km
Van aztán egy ilyen is:
szög melletti befogó
__________________
átfogó
És végül itt van még ez:
szöggel szemközti befogó
______________________
szög melletti befogó
És most lássunk néhány érdekes történetet.
Kezdjük azzal, hogy milyen magasan áll a kecske…
mármint ez a kecske.
Ha tudjuk, hogy a szikla lábától 28 méterre…
éppen 30 fokos szögben látni a szikla tetejét.
x=16,17 méter
Egy másik világítótorony 30m magas sziklára épült. A torony teteje 15◦-os szögben, az alja
10◦-os szögben látszik egy hajóról. Milyen magas a torony?
m = 15,59 méter
Van itt ez a háromszög, amiben a csúcsokat az ABC nagy
betűivel jelöljük…
Az oldalakat pedig kis betűkkel úgy, hogy az A csúccsal
szemben az a oldal van, a B csúccsal szemben a b…
Most pedig megismerkedünk a háromszögek nevezetes
pontjaival és vonalaival.
A háromszög magasságvonala a csúcsból a szemközti oldal
egyenesére bocsátott merőleges.
Ezek mindig egy pontban metszik egymást, és ezt a pontot
magasságpontnak nevezzük.
Vannak tompaszögű háromszögek is…
a magasságpont ilyen esetekben a háromszögön kívül tartózkodik.
A háromszög súlyvonala a csúcsot a szemközti oldal
felezőpontjával összekötő szakasz.
Nos, ezek is mindig egy pontban metszik egymást, ezt a pontot
hívjuk a háromszög súlypontjának.
További izgalom, hogy a súlypont mindegyik súlyvonalat 2:1
arányban osztja.
A háromszög oldalfelező merőleges egyenesei szintén egy pontban
metszik egymást. Ez a pont minden csúcstól egyenlő távolságra van és a
háromszög köré írható kör középpontja.
A háromszög belső szögfelezői szintén egy pontban metszik
egymást. Ez a háromszögbe írható kör középpontja.
Most pedig lássunk néhány képletet a háromszögek
területének kiszámolására.
És itt egy kevésbé ismert képlet is:
Jönnek a trapézok…
A trapéz olyan négyszög, aminek van kép párhuzamos oldala.
Ezeket hívjuk a trapéz alapjának.
És most lássuk a trapéz szögeit.
A trapéz területét általában így szokták kiszámolni:
Ha a trapéz egyik alapján fekvő két szög ugyanakkora,
olyankor a trapéz szimmetrikus.
A szimmetrikus trapézt szokás még egyenlő szárú trapéznak
is hívni, ugyanis a két szára mindig egyforma hosszú.
Ezen kívül van egy fantasztikus tulajdonsága is, hogy van
köré írható köre.
Innen ered a harmadik elnevezés: húrtrapéz.
De nem csak valami random helyre…
Hanem úgy, hogy derékszögű háromszögeket kapjunk.
Egy másik trapézban a hosszabbik alapon fekvő szögek 45 és 60 fokosak, a trapéz magassága 12 cm a trapéz területe pedig 156 cm2. Mekkorák a trapéz oldalai?
A körök területének a kiszámolása nem túl izgalmas elfoglaltság.
Van itt rá ez a kis képlet:
A körök területének a kiszámolása nem túl izgalmas elfoglaltság.
Van itt rá ez a kis képlet:
Hogyha például a kör sugara 16 cm, akkor a területe…
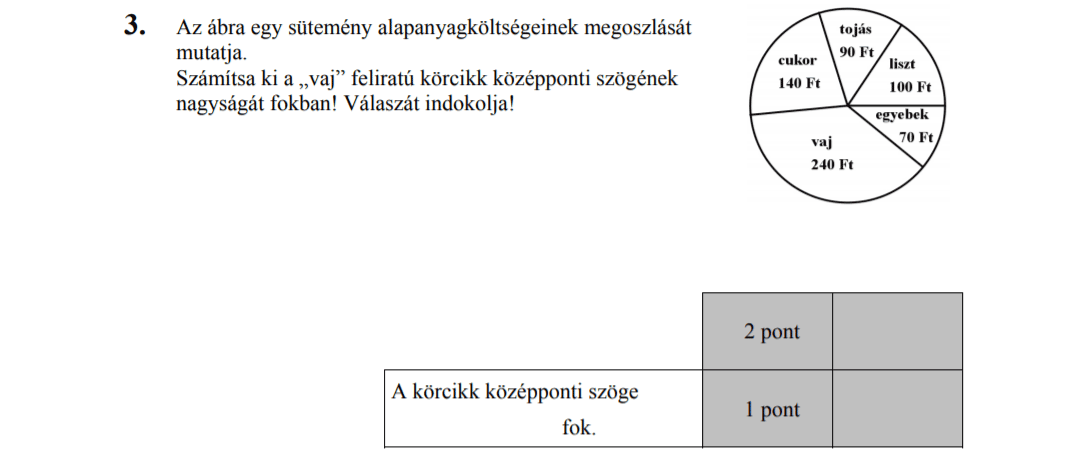
Most nézzük, mi a helyzet a körcikkek területével.
A körcikk területe úgy aránylik a kör területéhez…
mint a körcikkhez tartozó középponti szög a 360o-hoz.
Próbáljuk is ki:
KÖRCIKK TERÜLETE:
És most lássunk valami izgalmasabbat.
Kell hozzá egy védősisak, egy kis benzin, néhány befőttesüveg, védőszemüveg…
Á, mégse, ez már túl izgalmas lenne.
Helyette inkább számoljuk ki ennek a körszeletnek a területét.
A körszelet területét úgy kapjuk meg, hogy először kiszámoljuk, hogy mekkora területű ez a körcikk…
aztán pedig kivonjuk belőle ennek az egyenlőszárú háromszögnek a területét.
Számoljuk ki például annak a körszeletnek a területét, amelyet egy 13 cm sugarú körből vágunk le a kör középpontjától 5 cm távolságban haladó szelővel.
Készítsünk egy rajzot.
Itt van a kör.
Ez a szelő…
Ami a kör középpontjától 5 cm távolságban halad.
És itt volna a körszelet.
A körszelet területéhez szükségünk van a középponti szögre.
Amit ebből a derékszögű háromszögből fogunk kinyerni.
A szög melletti befogó és az átfogó segítségével.
A világ legmeredekebb fogaskerekű vasútja a Pilatusbahn, ami a legdurvább szakaszokon 48%-os emelkedőn megy föl. Azt, hogy egy emelkedő hány százalékos, úgy kapjuk meg, hogy amennyit fölfelé elmozdulunk, elosztjuk azzal amennyit vízszintesen elmozdulunk, és aztán beszorozzuk 100-zal.
a) Egy szakaszon a fogaskerekű 50 métert tett meg, és 23 fokos volt az emelkedő. Mekkora a szintkülönbség ezen a szakaszon? Hány százalékos ez az emelkedő?
b) A fogaskerekű egy szakaszon 60 méret tett meg, és közben 19 métert emelkedett. Hány fokos szögben ment fölfelé? Hány százalékos ez az emelkedő?
c) Hány fokos szögben megy a fogaskerekű, amikor épp a legmeredekebb szakaszon, a 48%-os lejtőn megy fölfelé?
Ez itt az 50 méter…
És ez pedig a 23 fokos szög.
A szintkülönbség ennek a háromszögnek az egyik befogója.
És most nézzük, hány százalékos ez az emelkedő…
Ehhez kell még a másik befogó is…
Számoljuk ki például egy koszinusszal.
A százalékot úgy kapjuk meg, hogy amennyit fölfelé elmozdulunk…
Elosztjuk azzal amennyit vízszintesen elmozdulunk…
És aztán beszorozzuk 100-zal.
Itt jön most egy trükk, amivel sokkal egyszerűbben is ki tudjuk számolni, hogy egy emelkedő hány százalékos.
A százalékot úgy kapjuk, hogy amennyit fölfelé elmozdulunk…
Elosztjuk azzal amennyit vízszintesen elmozdulunk.
És aztán beszorozzuk 100-zal.
És itt jön a trükk.
A százalékot így lehet a legkönnyebben kiszámolni.
Próbáljuk is ki…
A kérdés pedig, hogy mekkora ez a szög…
A történetünk szereplői a szöggel szemközti befogó és az átfogó…
Szemközti, mint szinusz…
És most lássuk, mekkora az szög.
Számoljuk ki először, hogy mekkora ez a szög…
A szöggel szemközti befogót ismerjük, meg az átfogót.
Ebből kéne kideríteni, hogy mekkora az alfa szög.
Ezt is a számológép fogja megmondani…
De most fordítva kell gondolkodnunk.
Eddig mindig úgy volt, hogy a szöget ismertük, és ezt keressük…
Most viszont a szöget keressük.
Az emelkedő 17,5 fokos.
És most nézzük, hány százalékos…
Jön a tangenses trükk:
18,46
A hegycsúcsok magasságát egy ügyes kis trükkel lehet megmérni...
Kell hozzá egy lézeres távolságmérő…
Szögmérővel ellátva.
A távolságmérővel becélozzuk a hegycsúcs tetejét…
És lemérjük a távolságot.
Aztán megmérjük ezt a szöget.
És most jön a trükk.
