- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
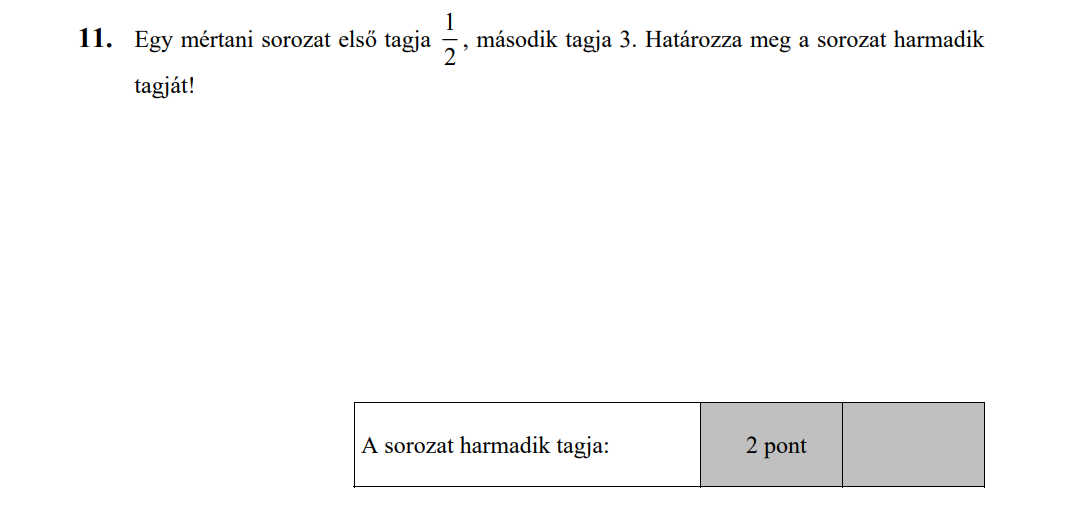
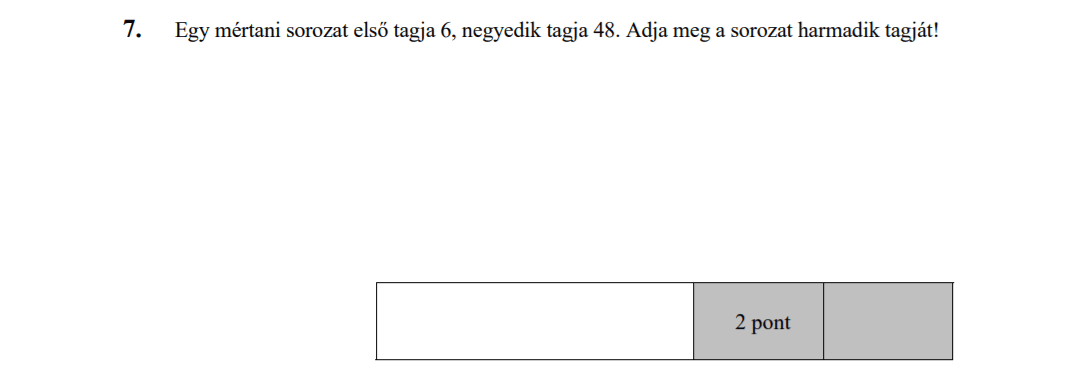
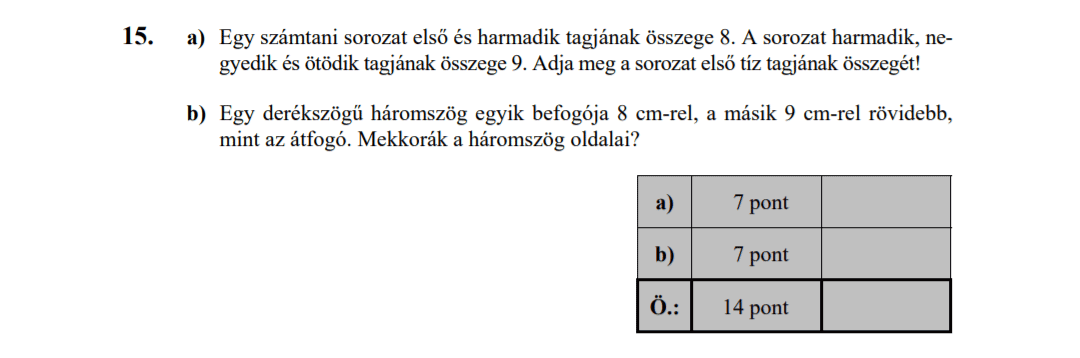
- Számtani és mértani sorozatok (16 pont)
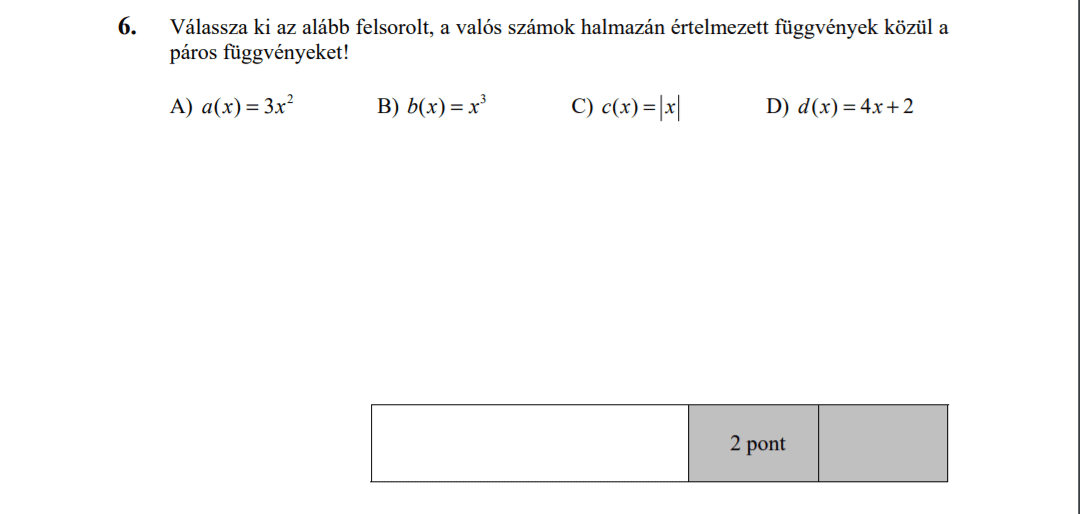
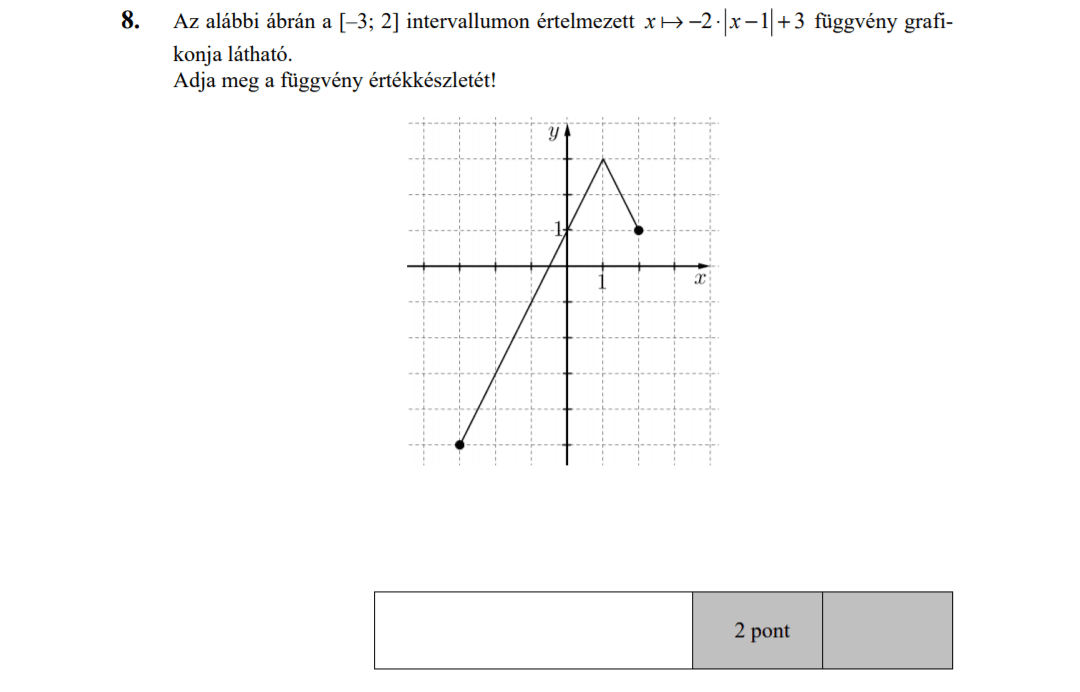
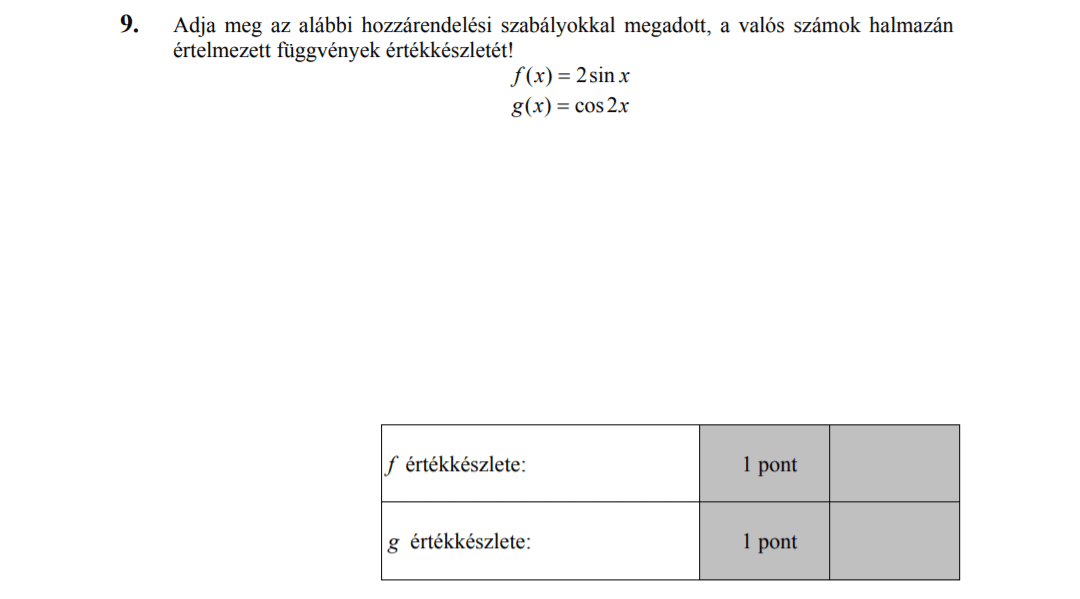
- Függvényekkel kapcsolatos feladatok (9,8 pont)
- Térgeometria (9,8 pont)
- Statisztika (9,3 pont)
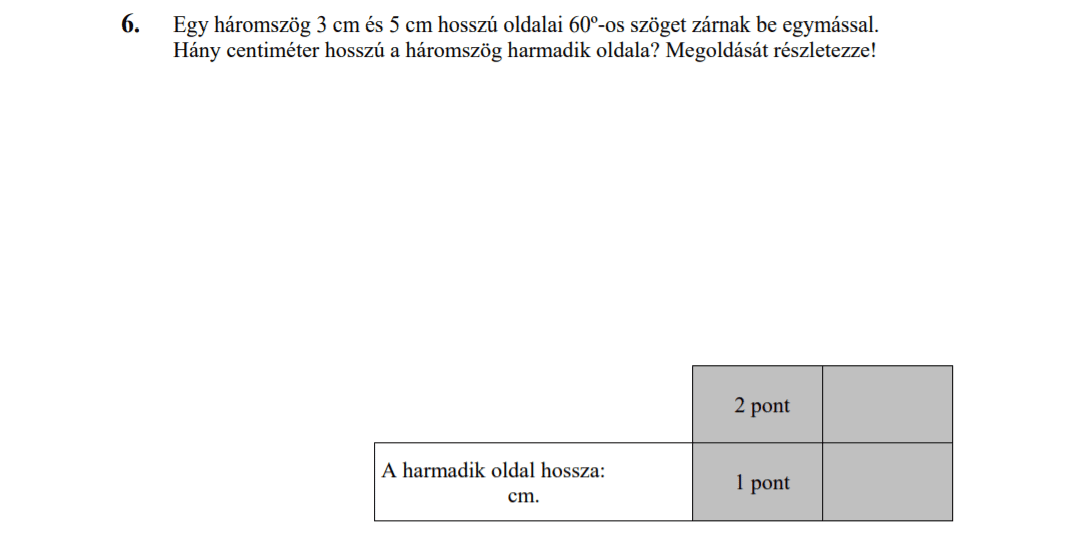
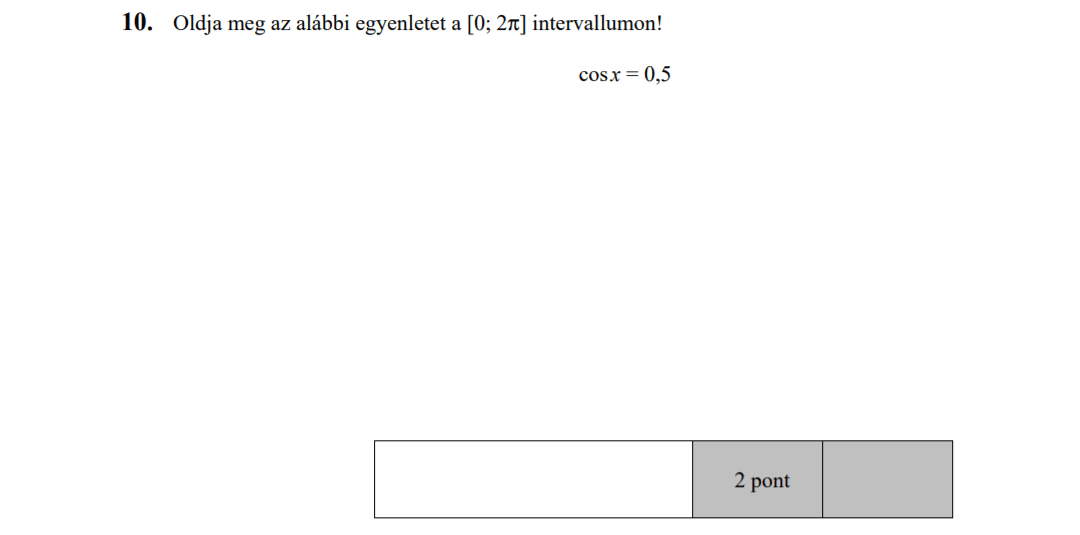
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
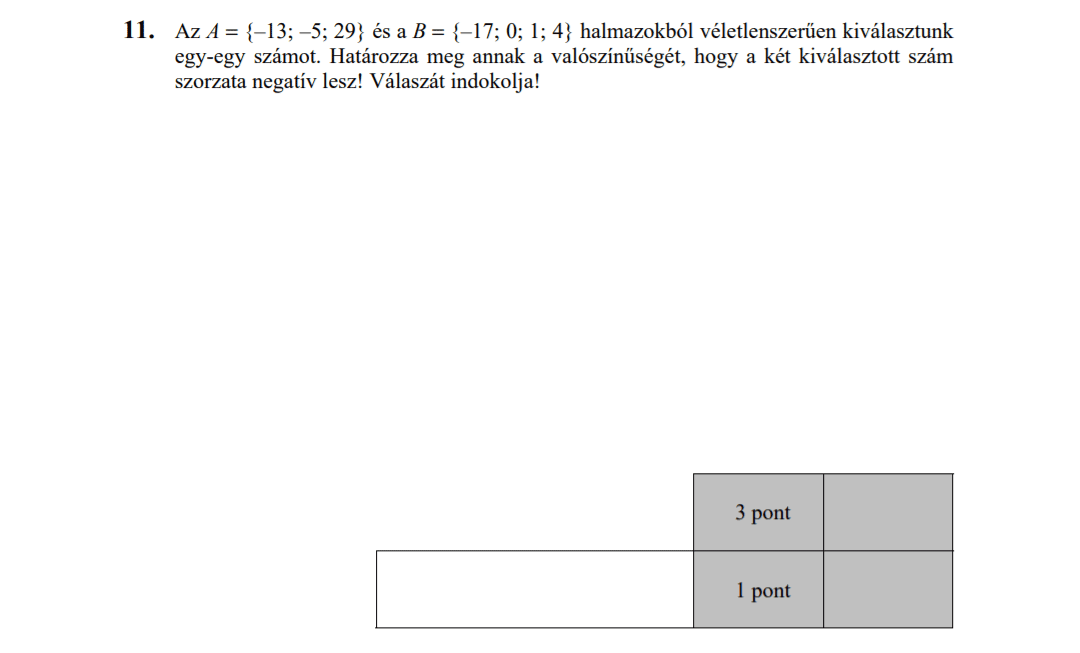
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
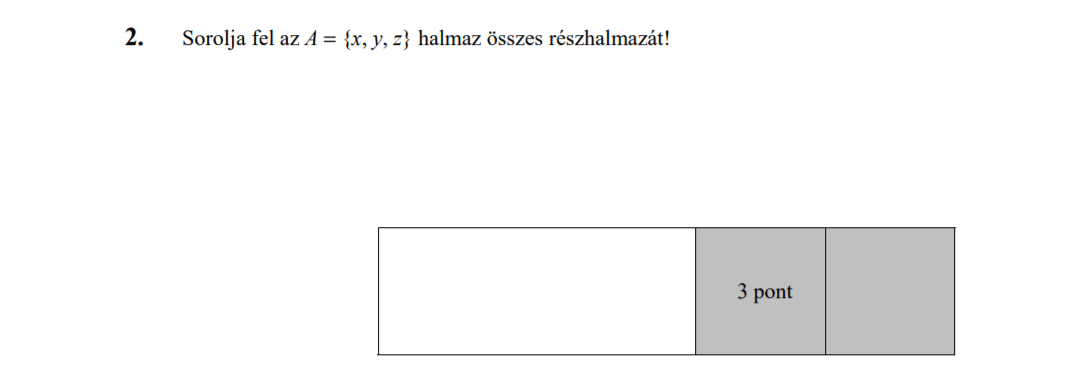
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
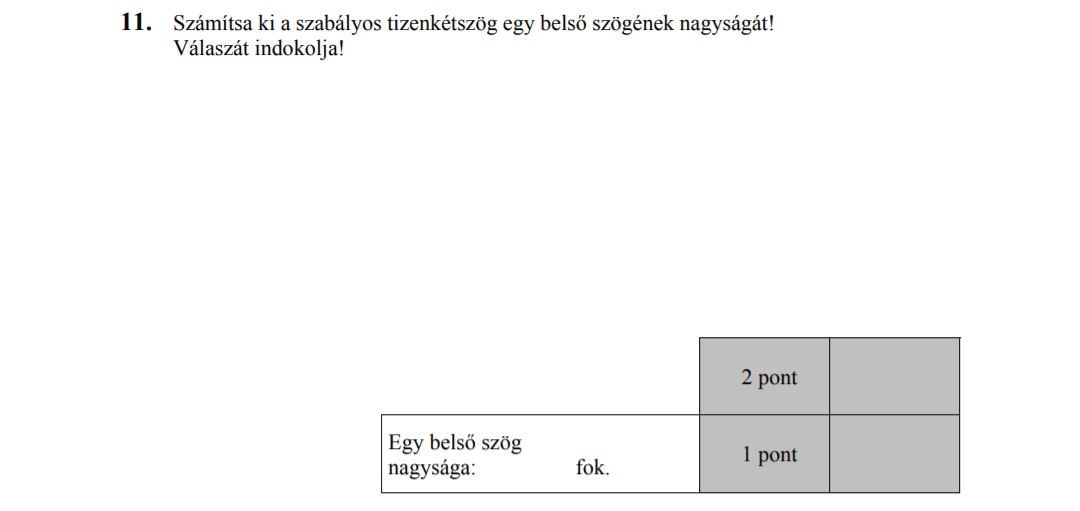
- Síkgeometria (4,5 pont)
- Százalékszámítás (3,8 pont)
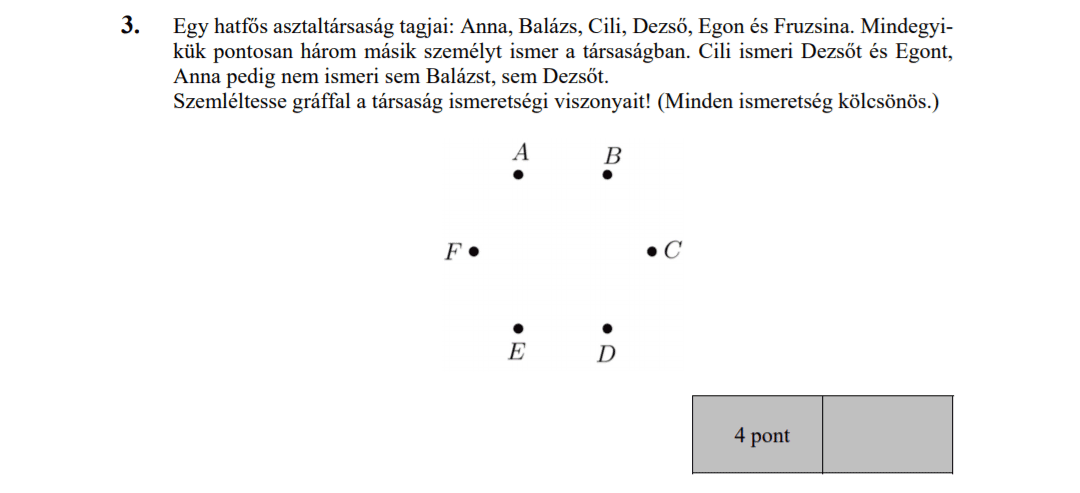
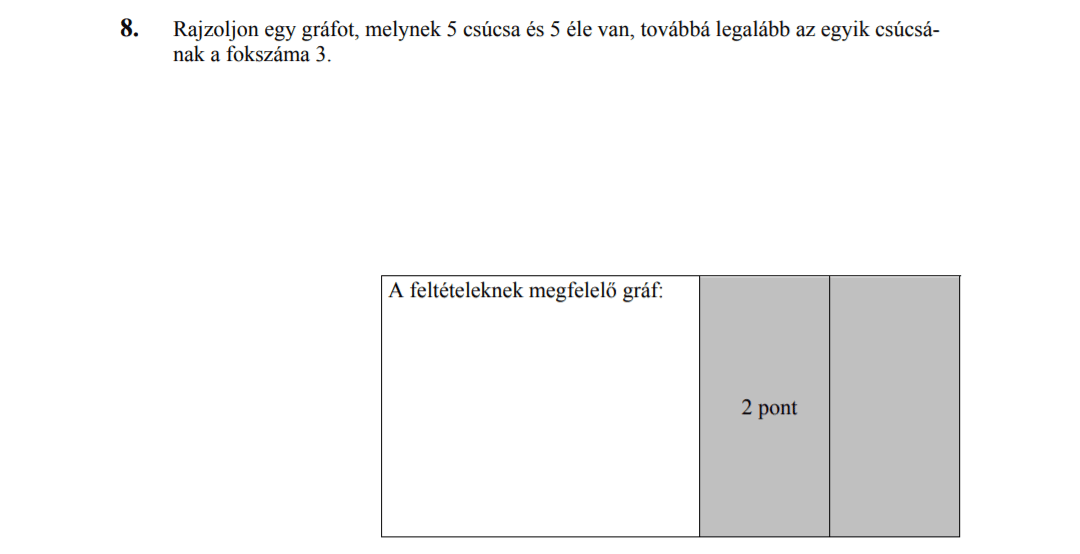
- Gráfok (3 pont)
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
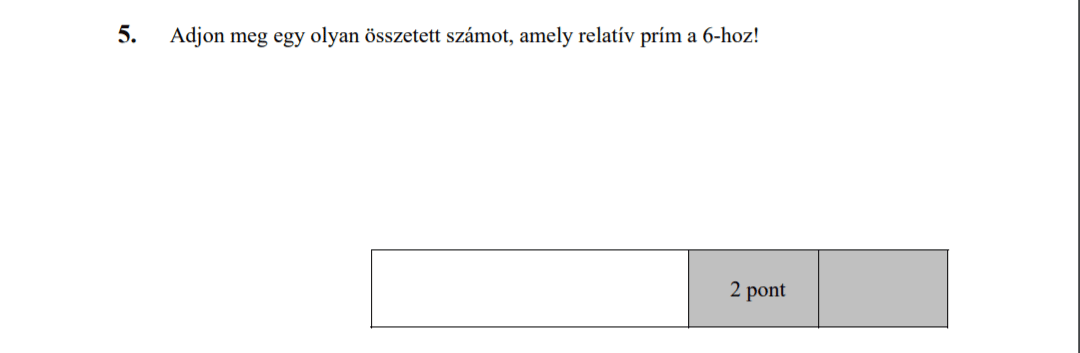
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Halmazok (6 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


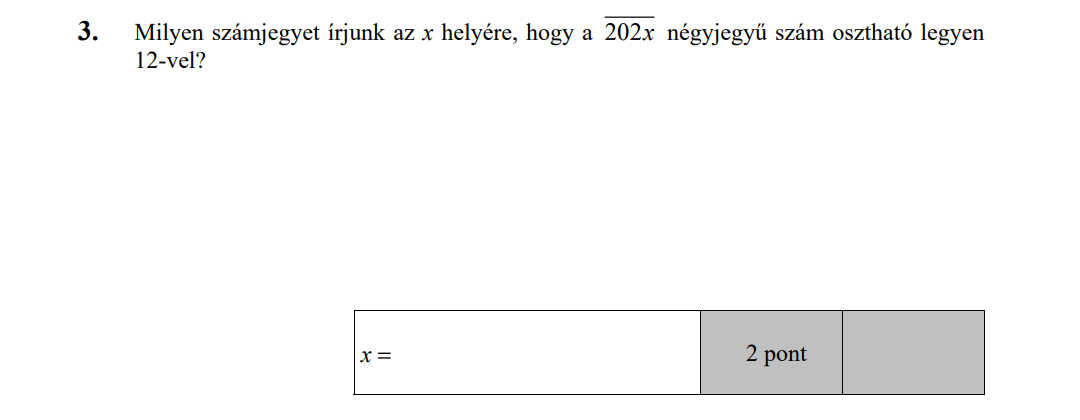
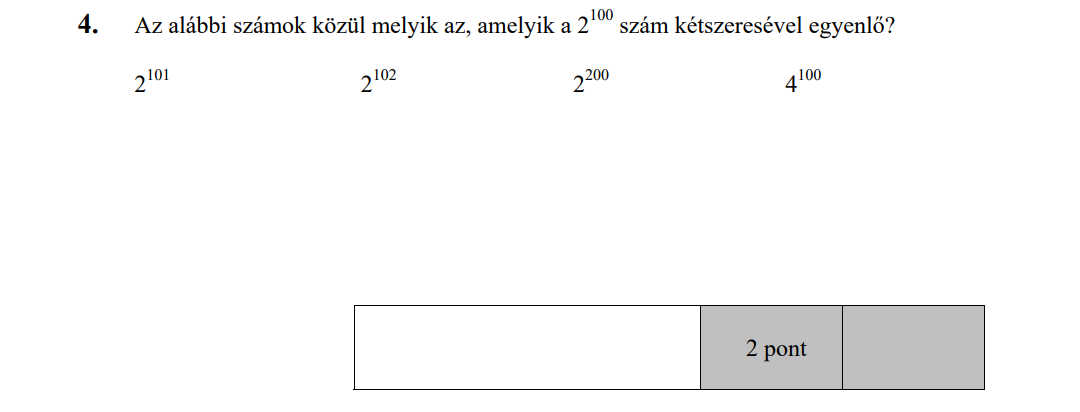



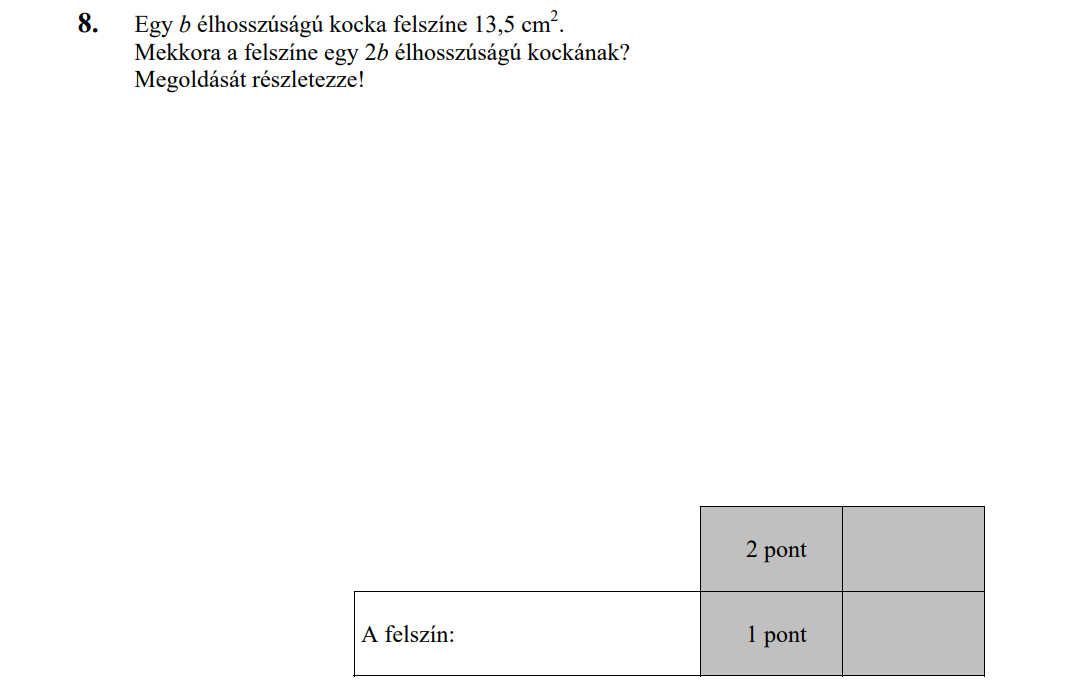




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
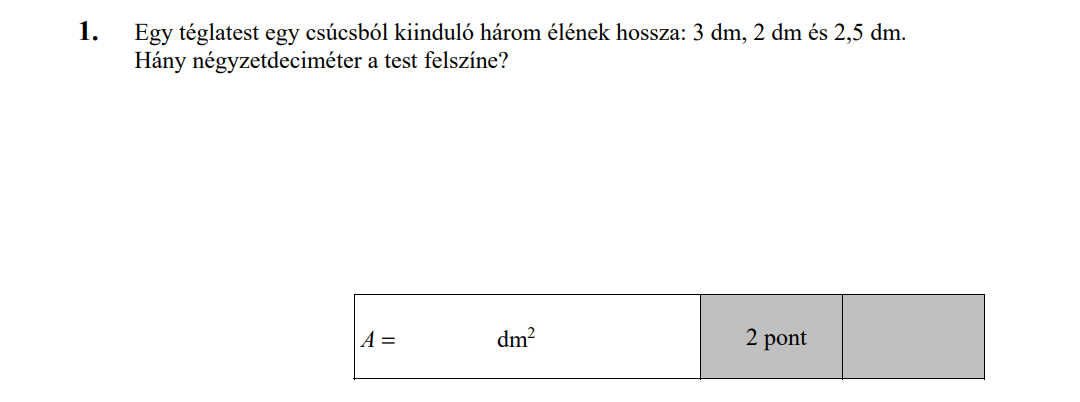
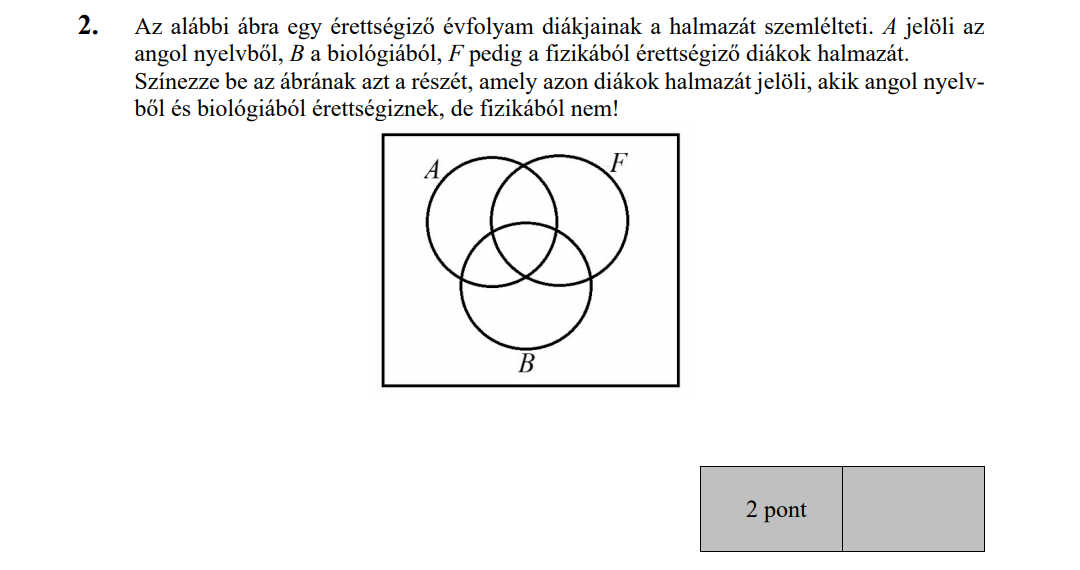

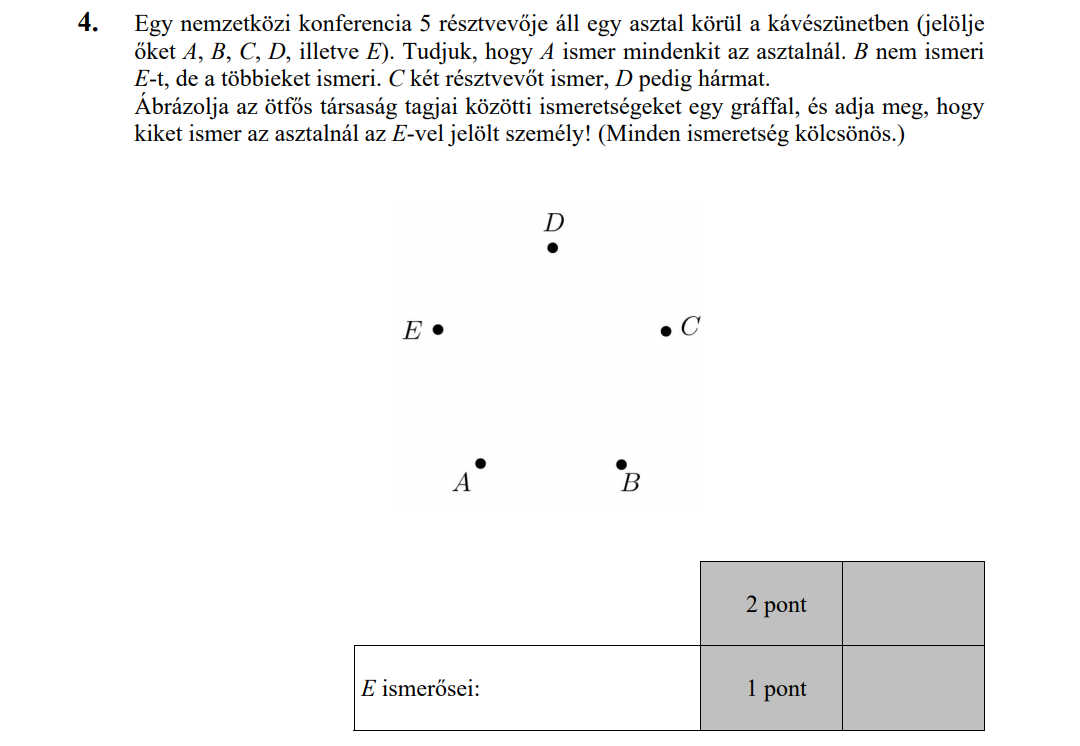

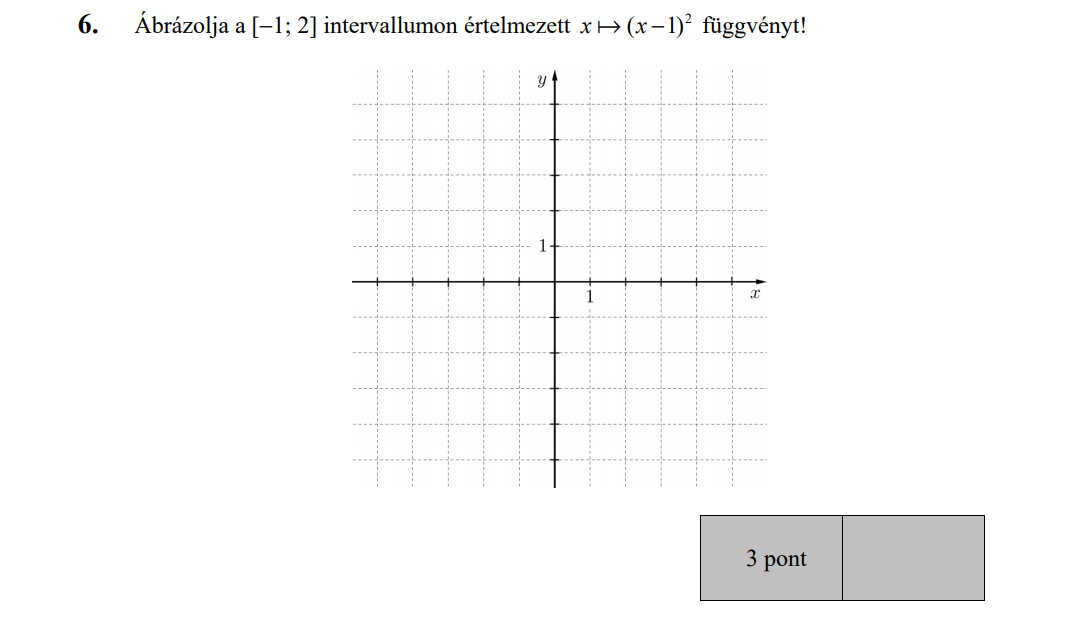



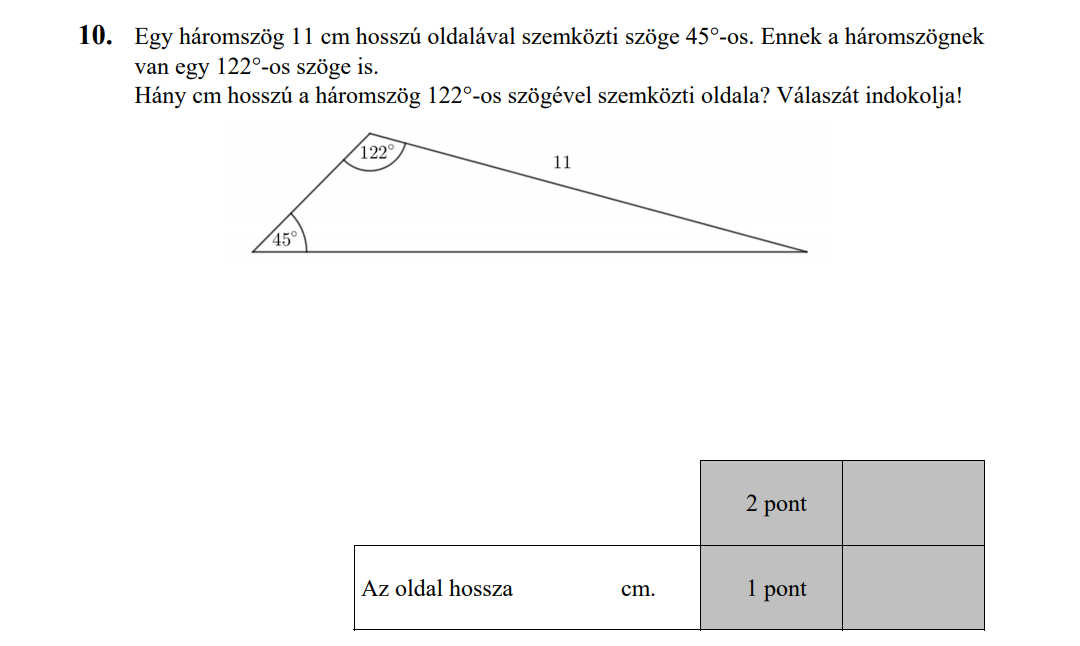

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






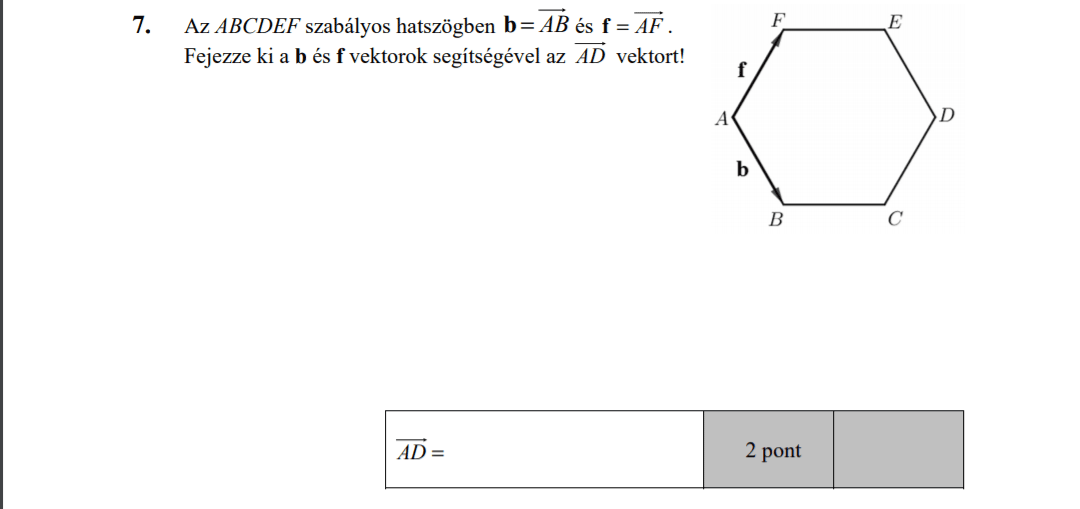



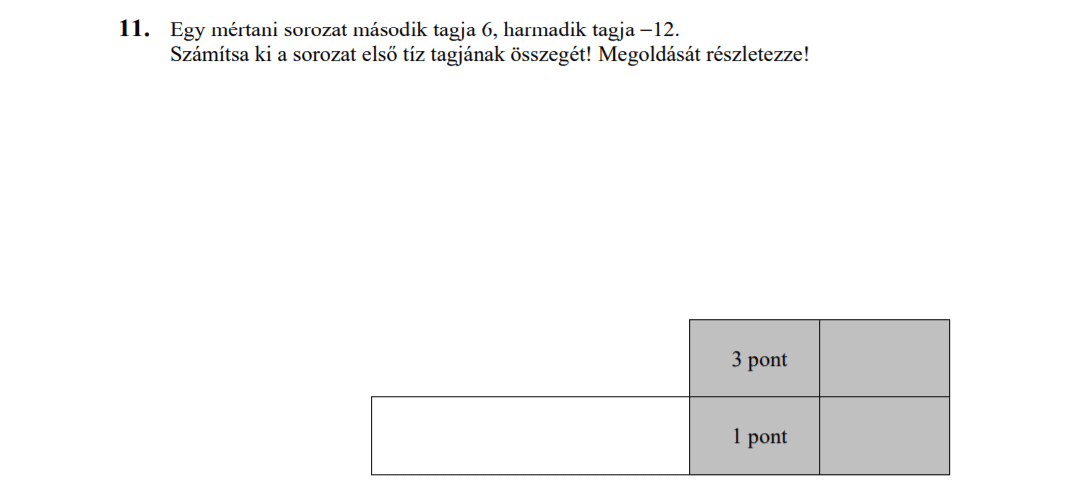

MÁSODIK RÉSZ

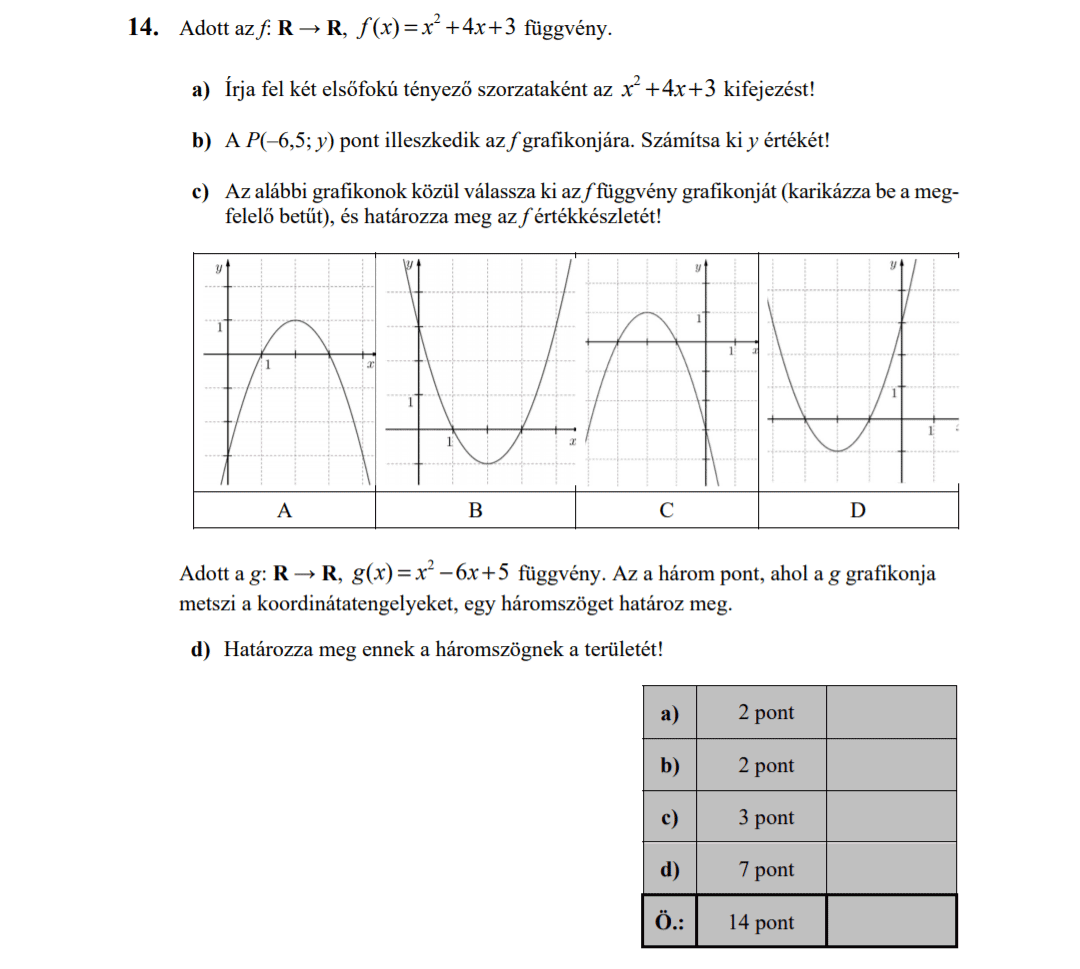




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



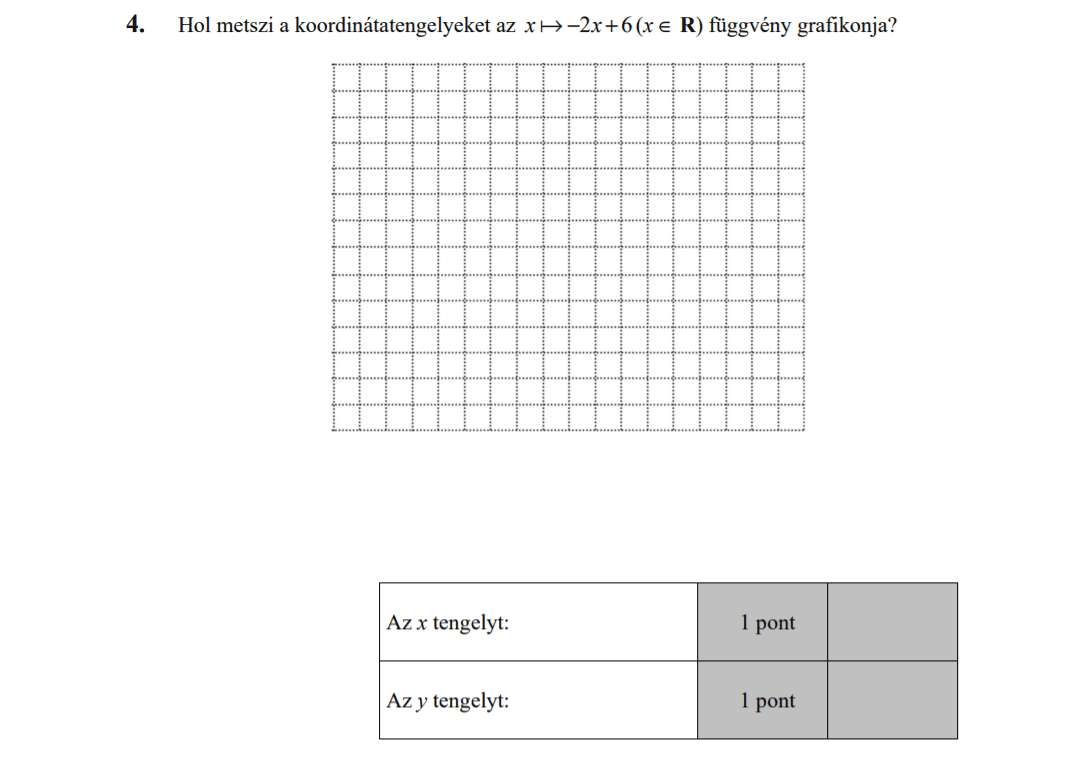







MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

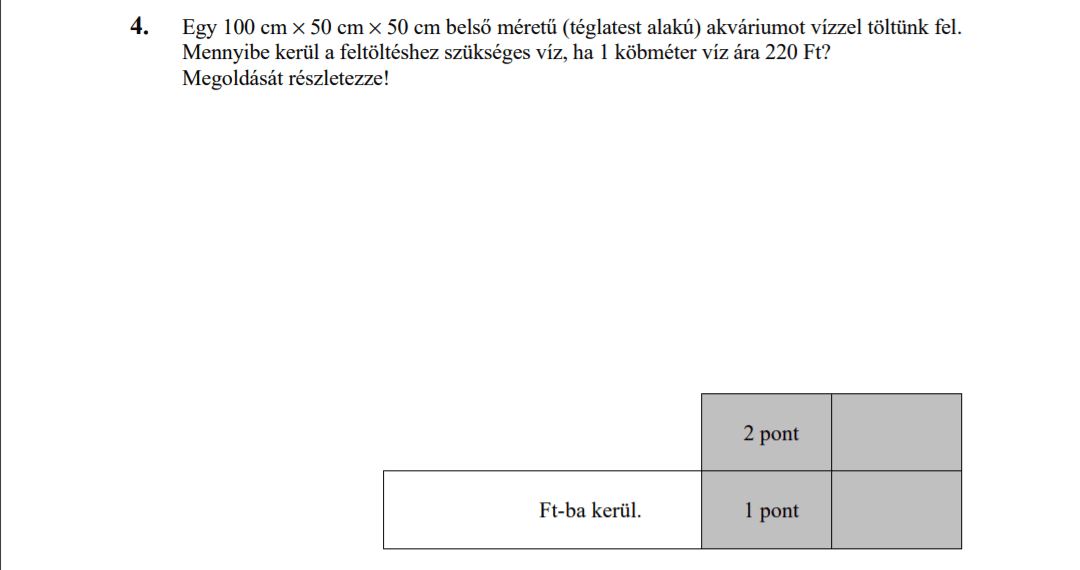
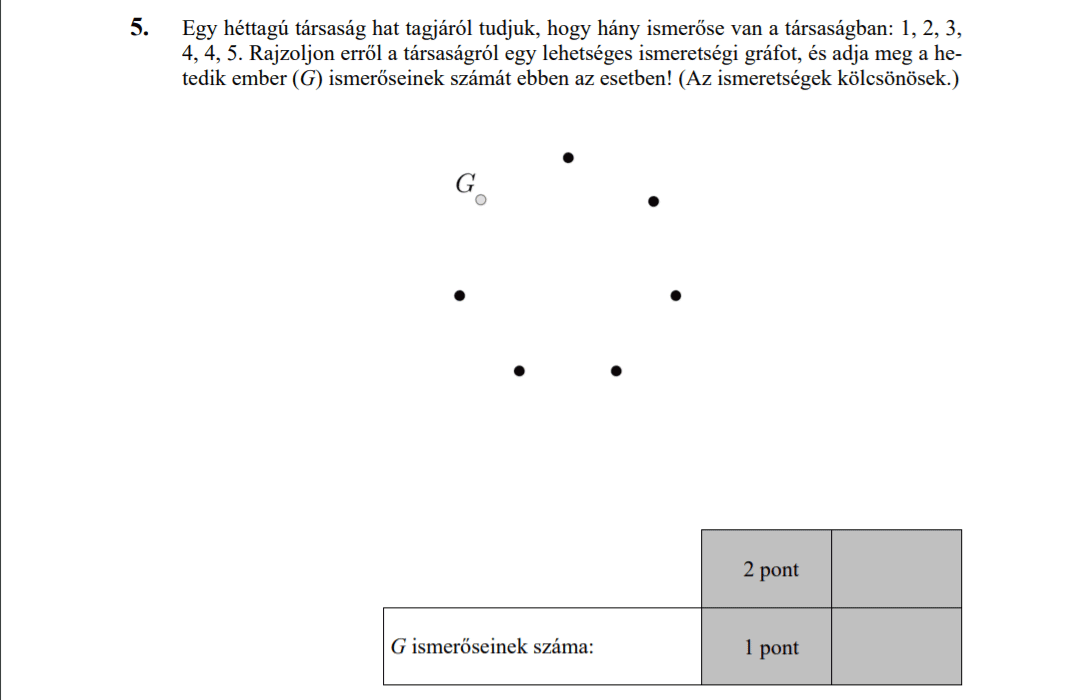







MÁSODIK RÉSZ
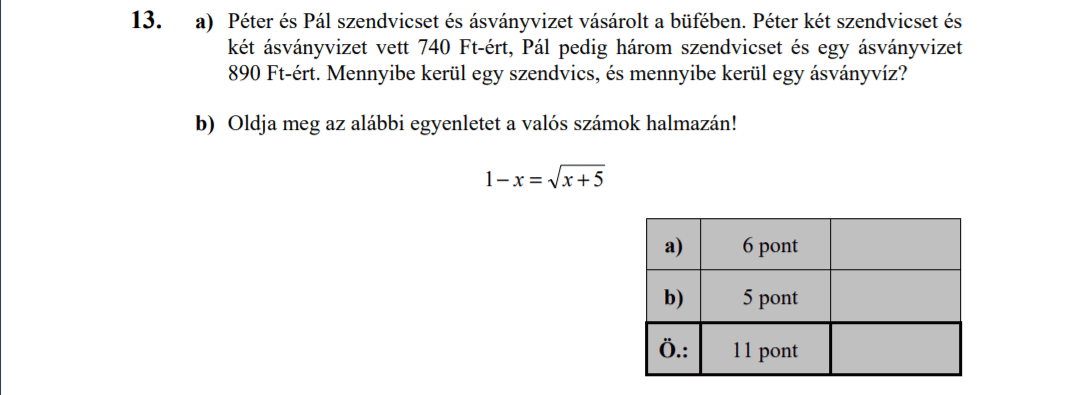
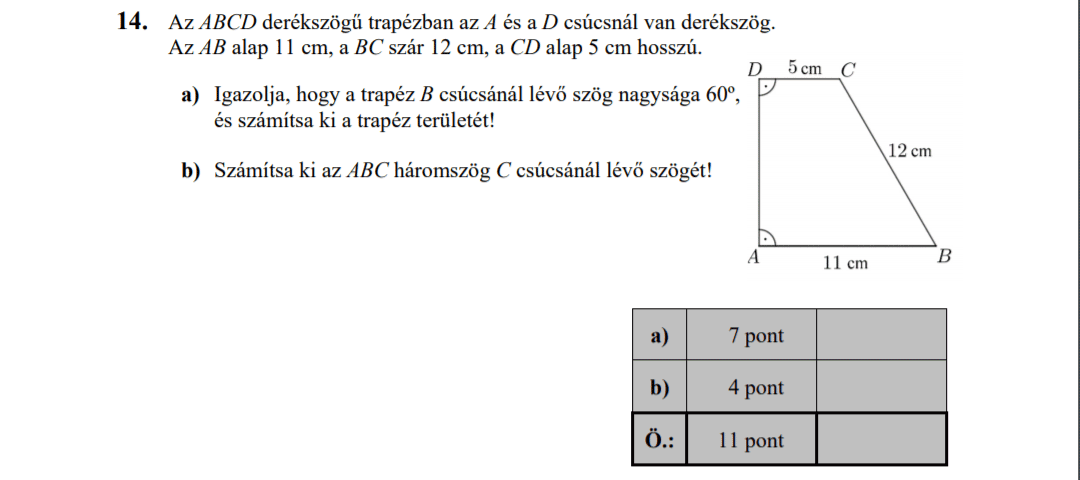

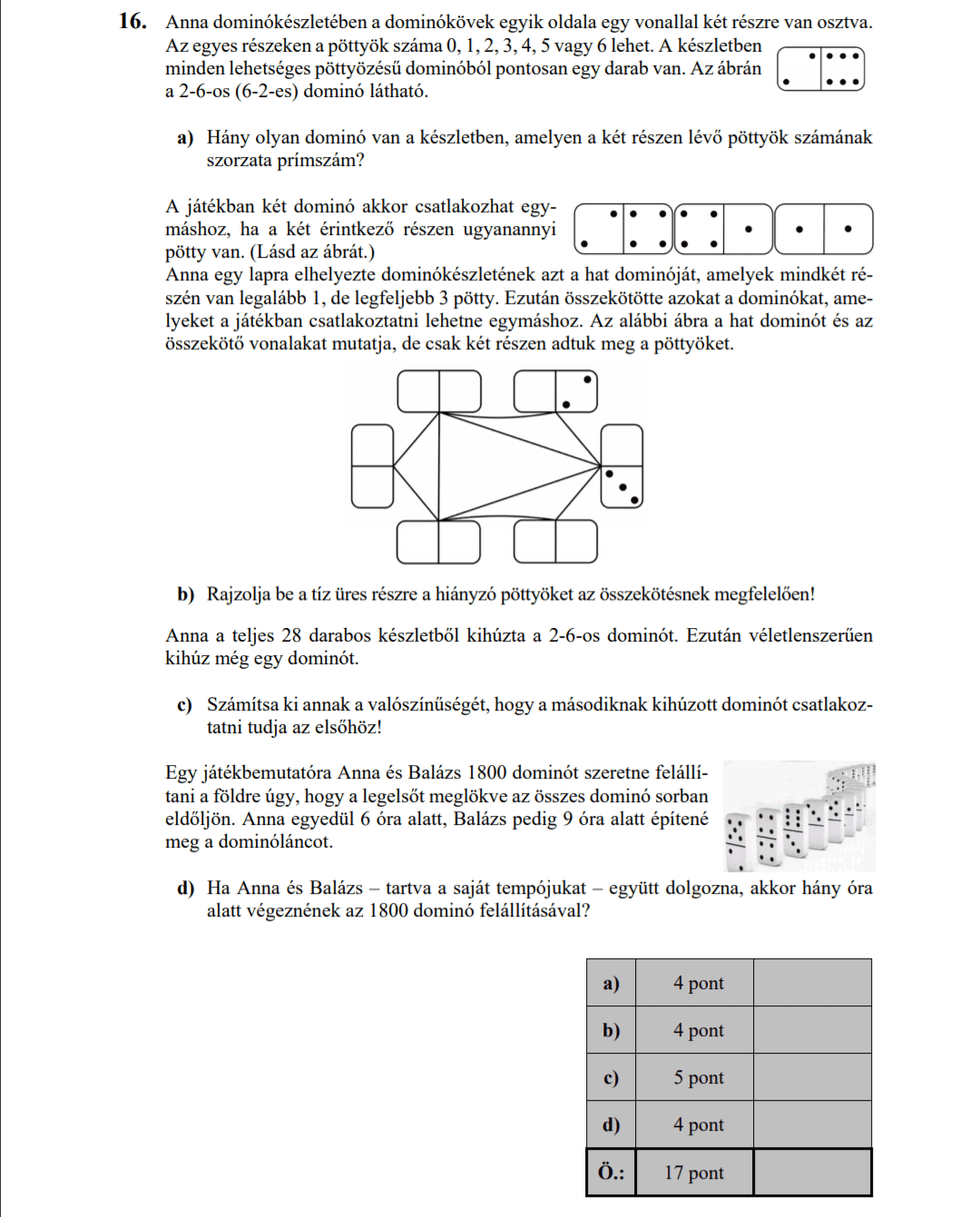


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




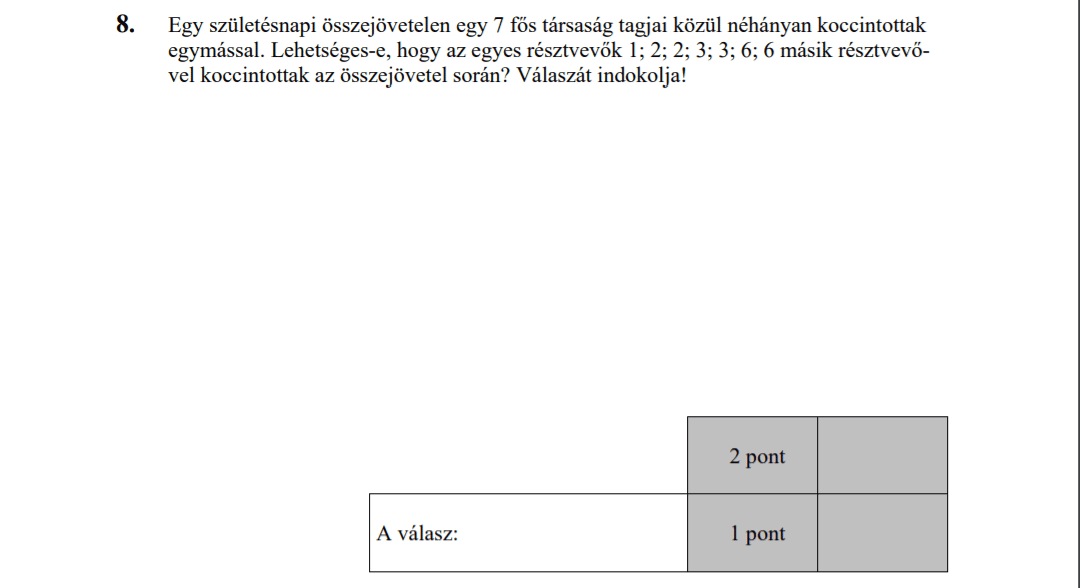



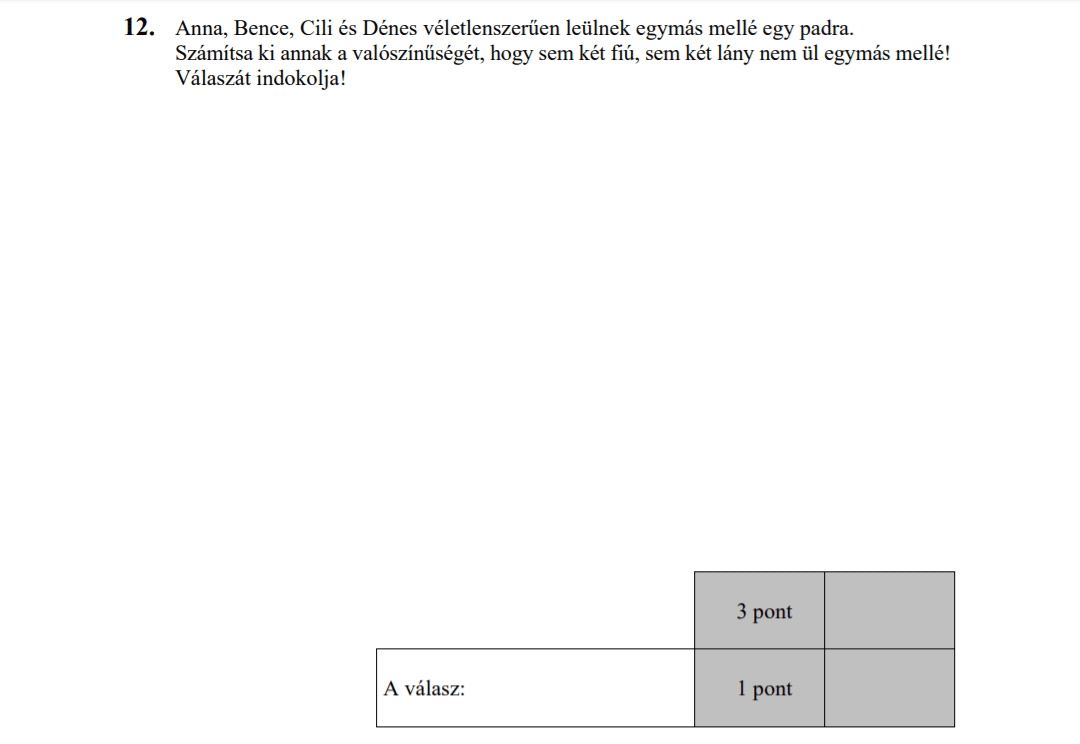
MÁSODIK RÉSZ

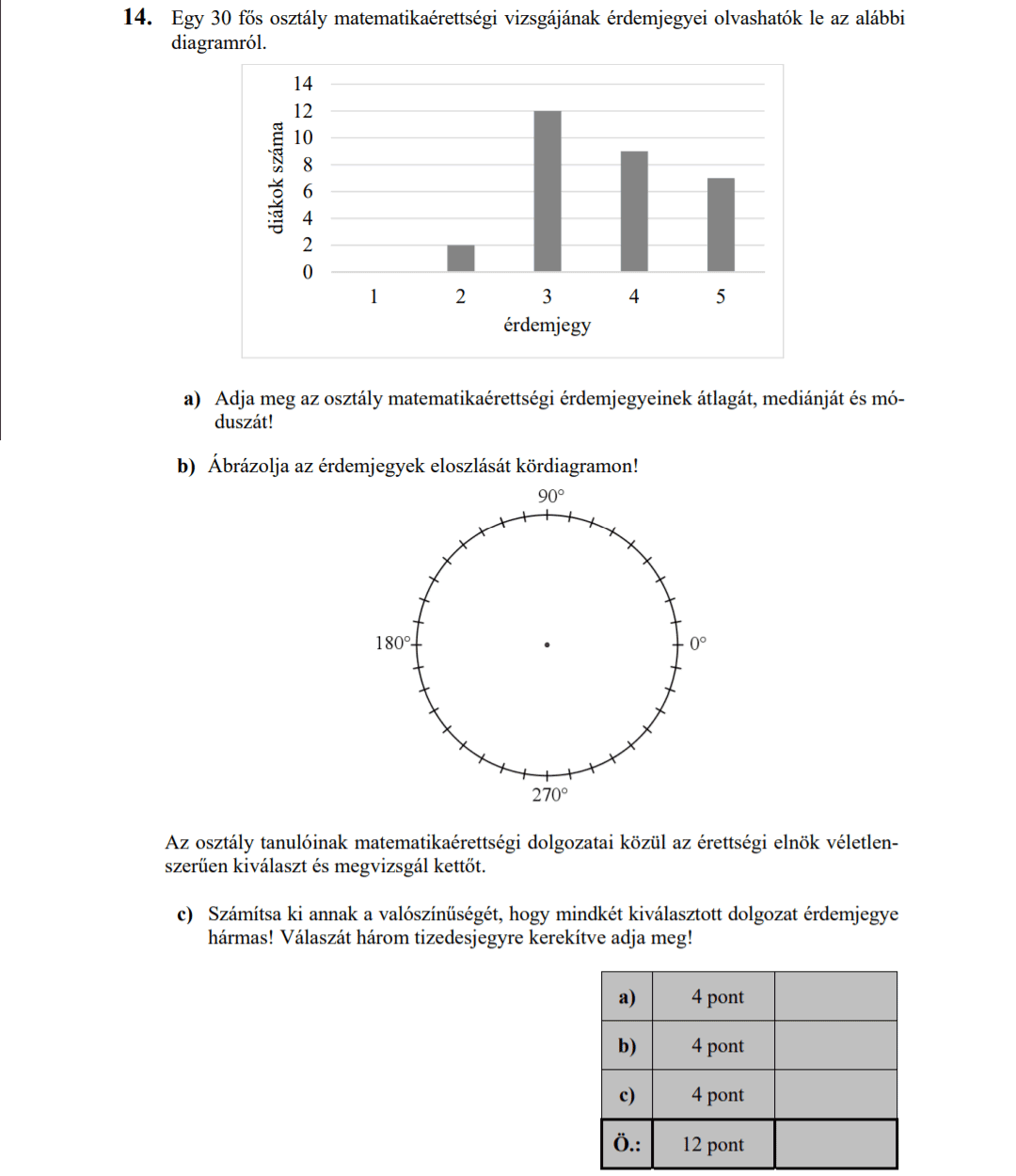
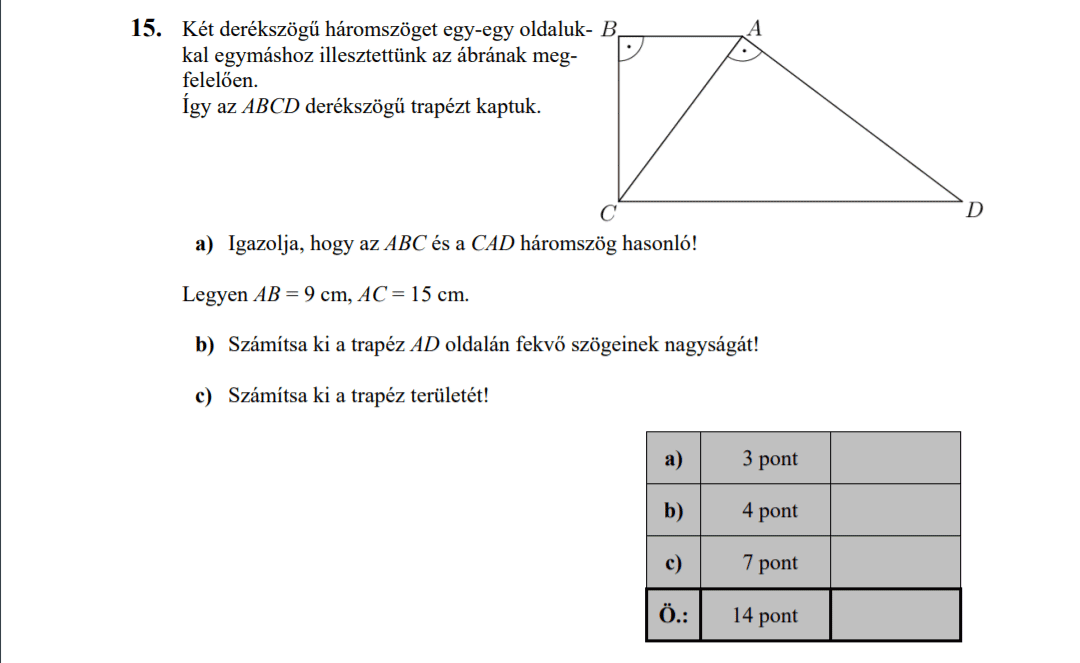



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


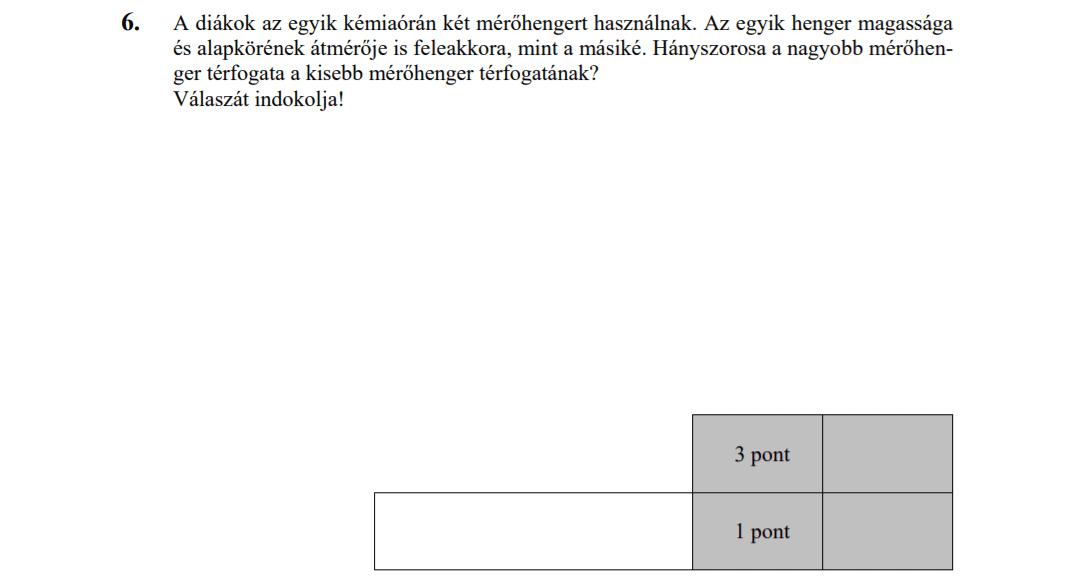
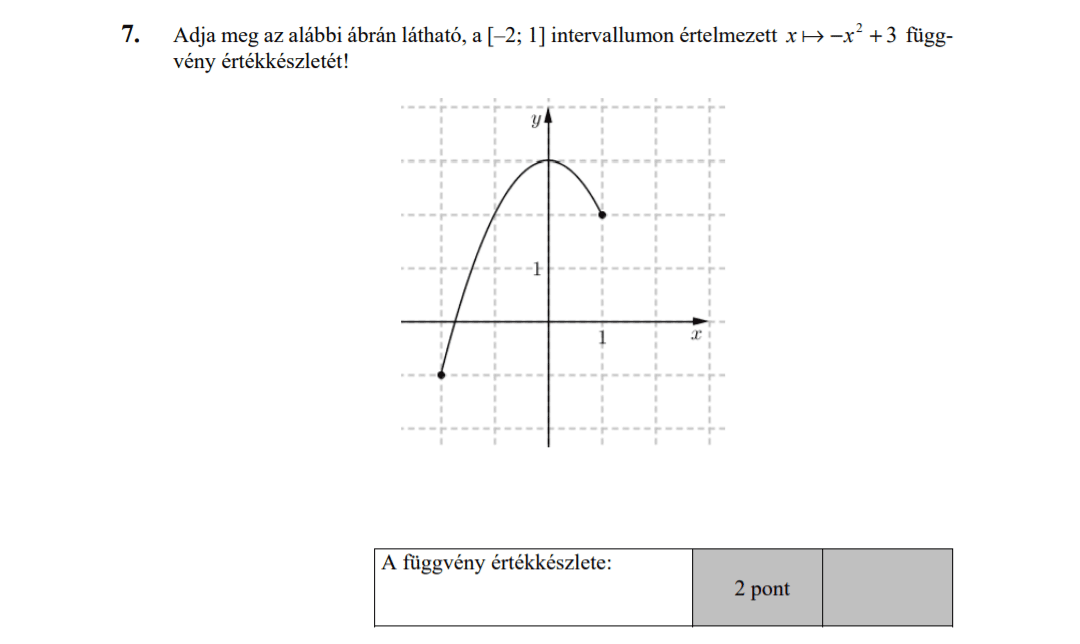

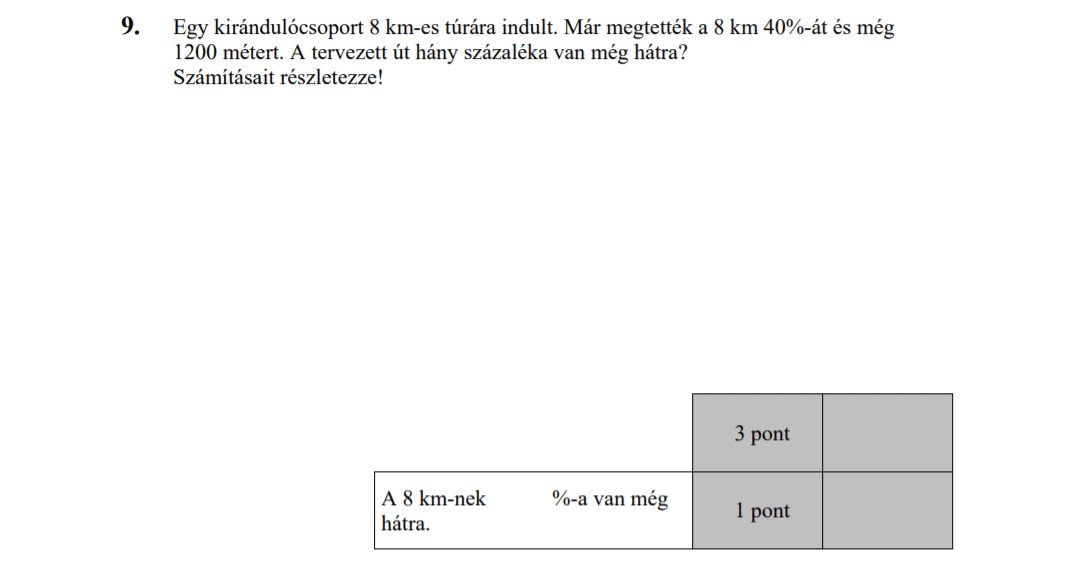
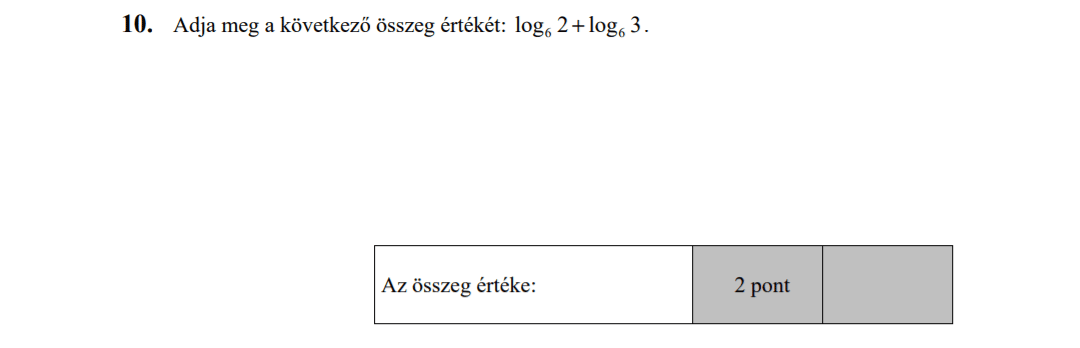

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






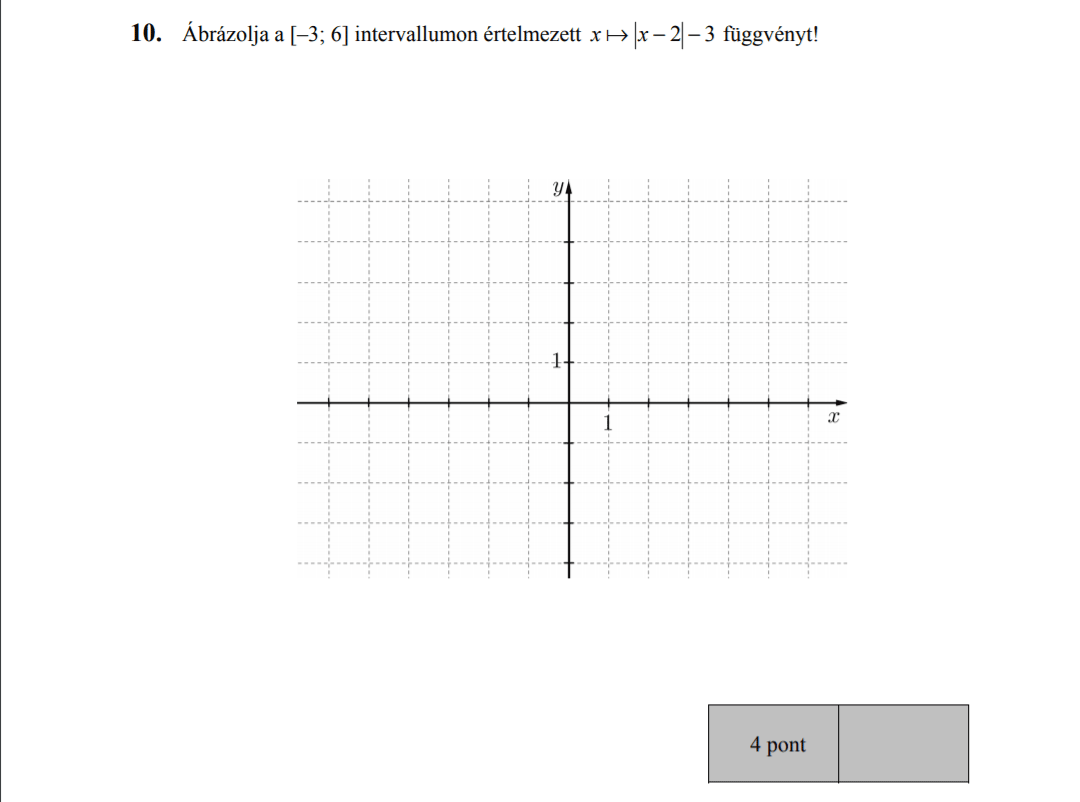

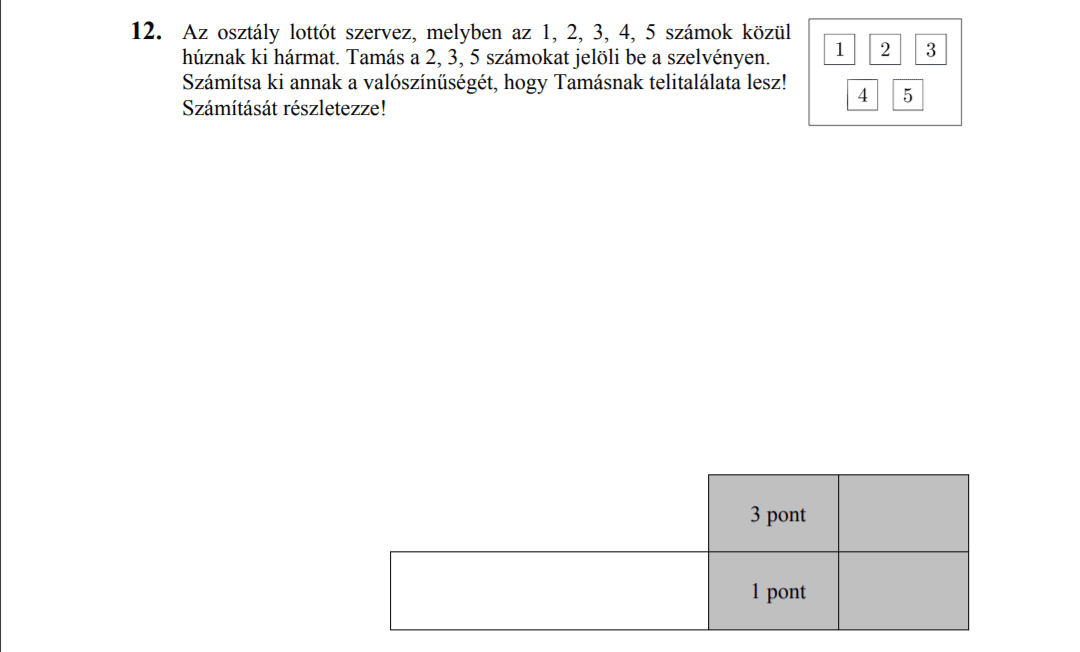
MÁSODIK RÉSZ

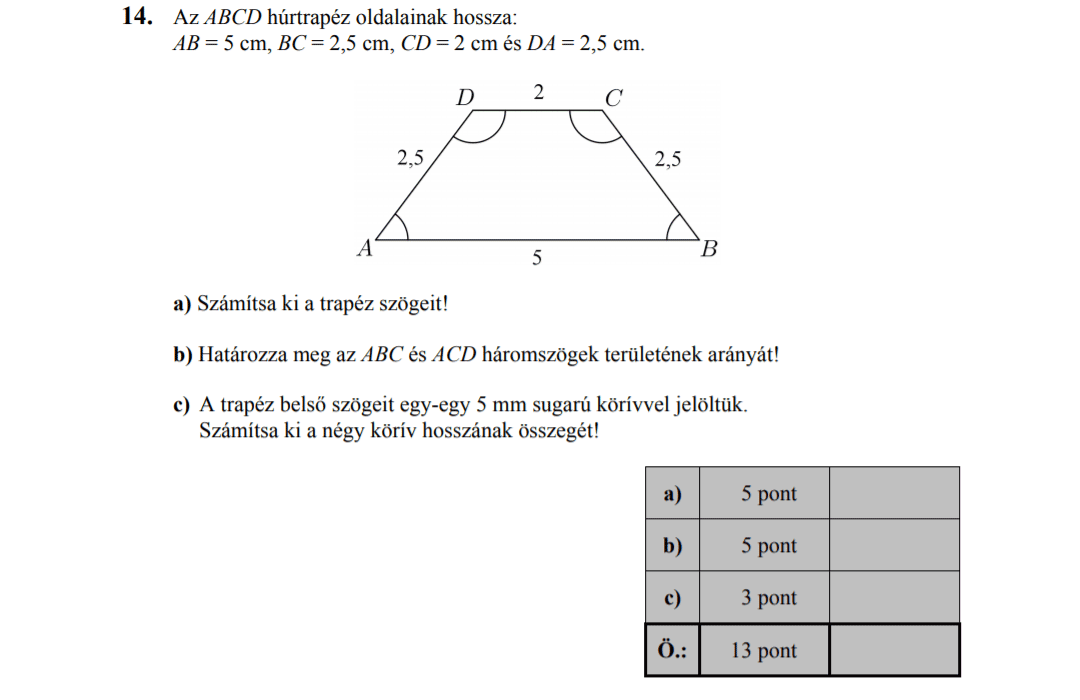

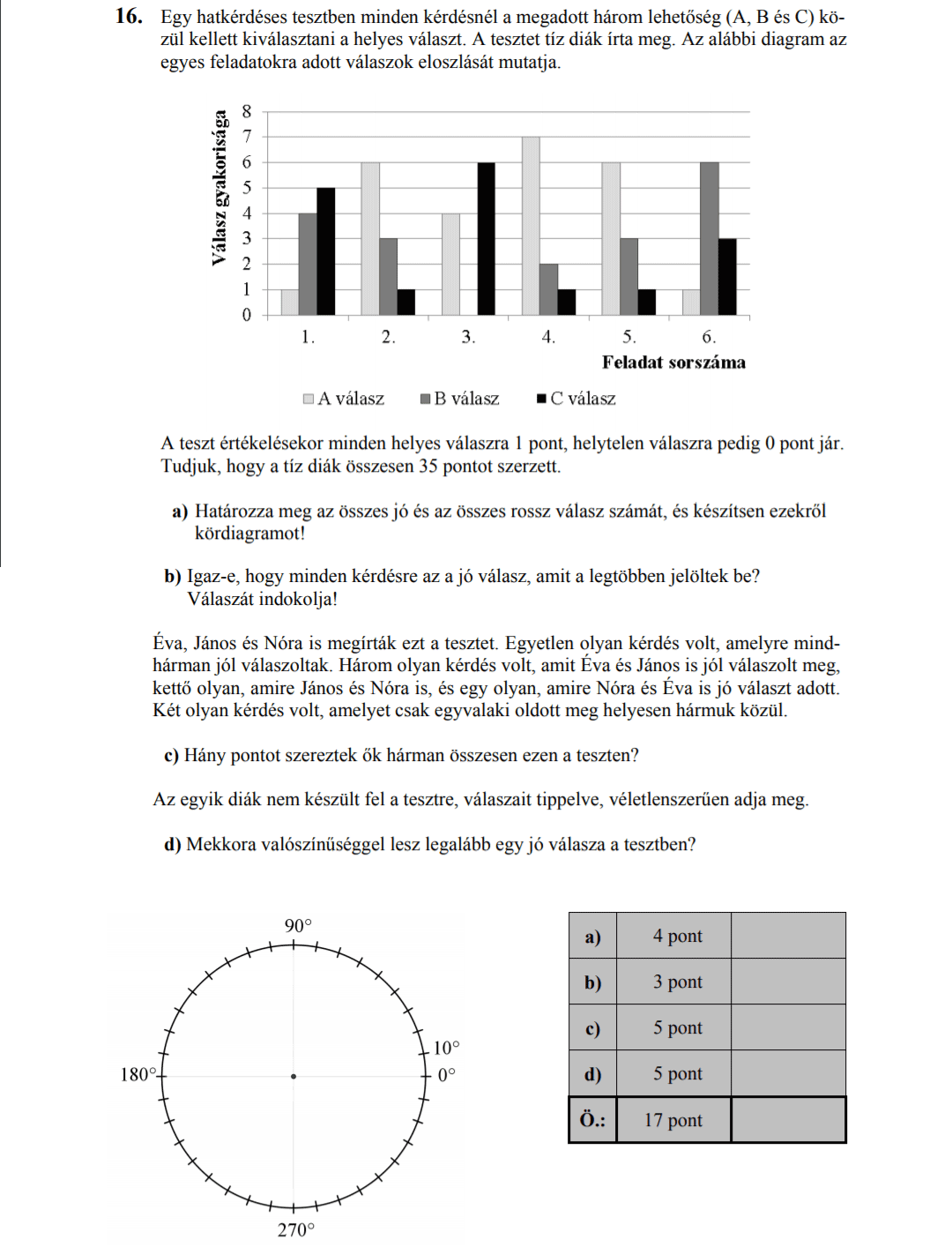


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

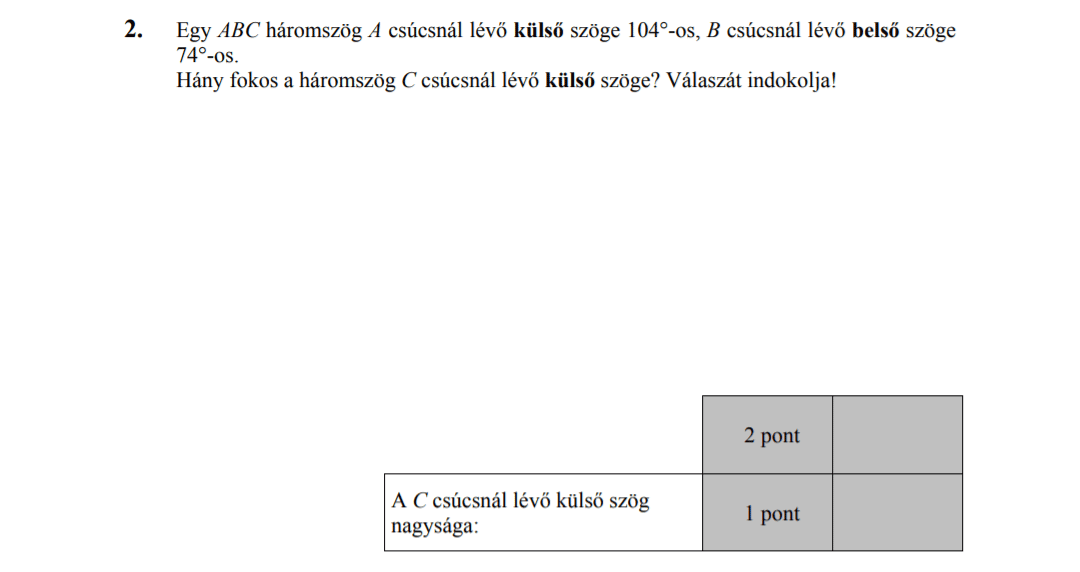





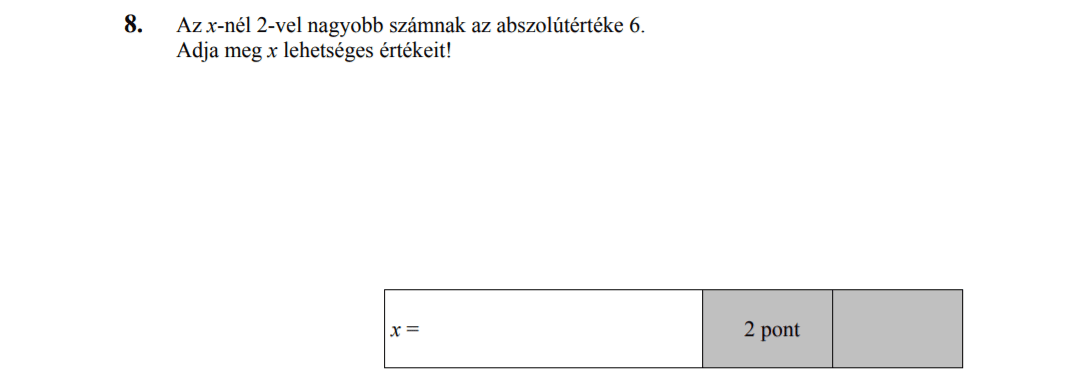

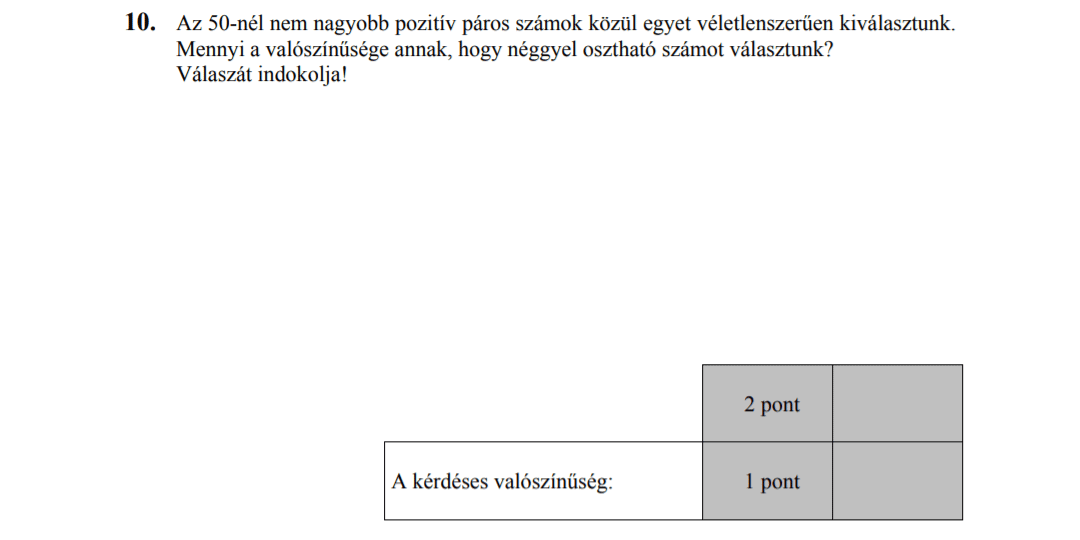


MÁSODIK RÉSZ

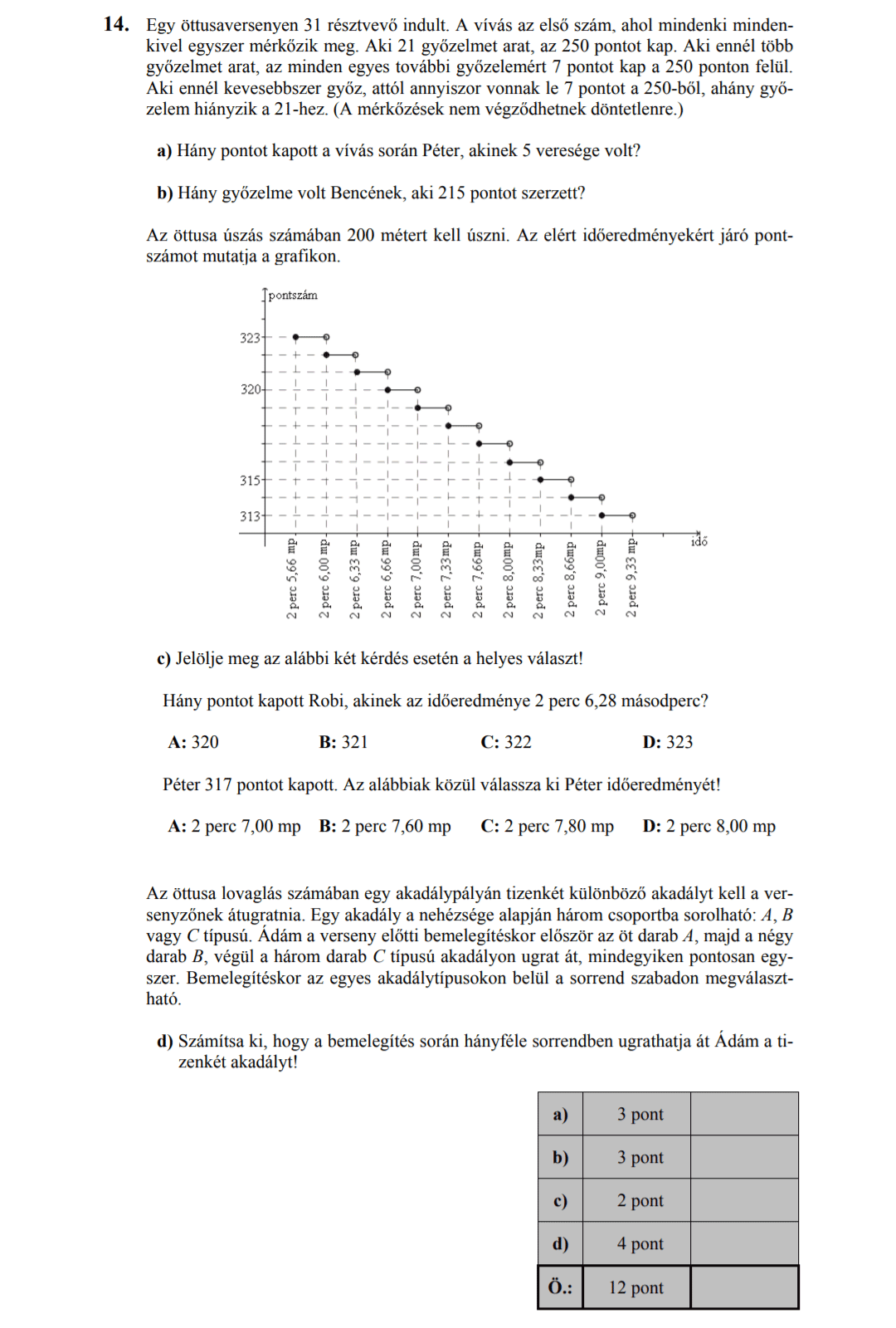
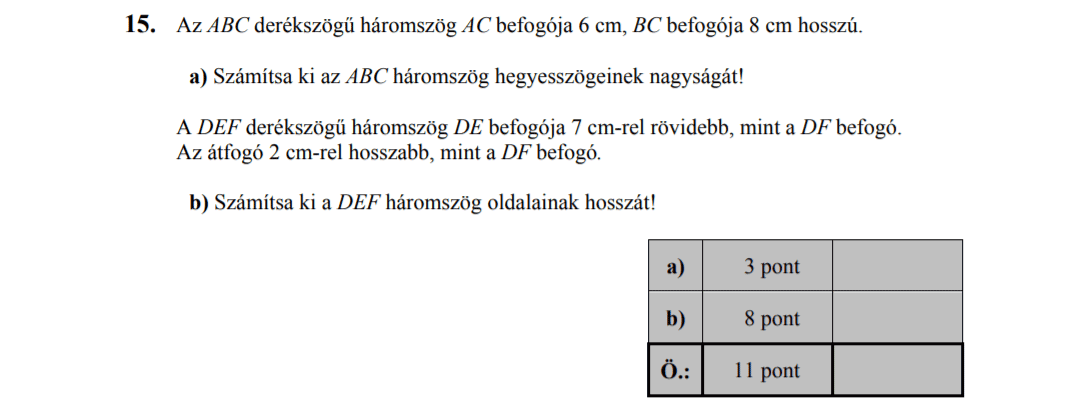



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

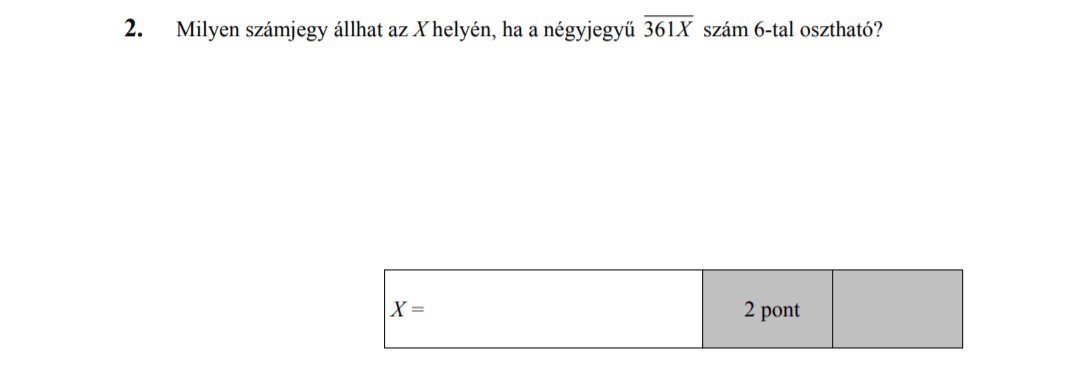



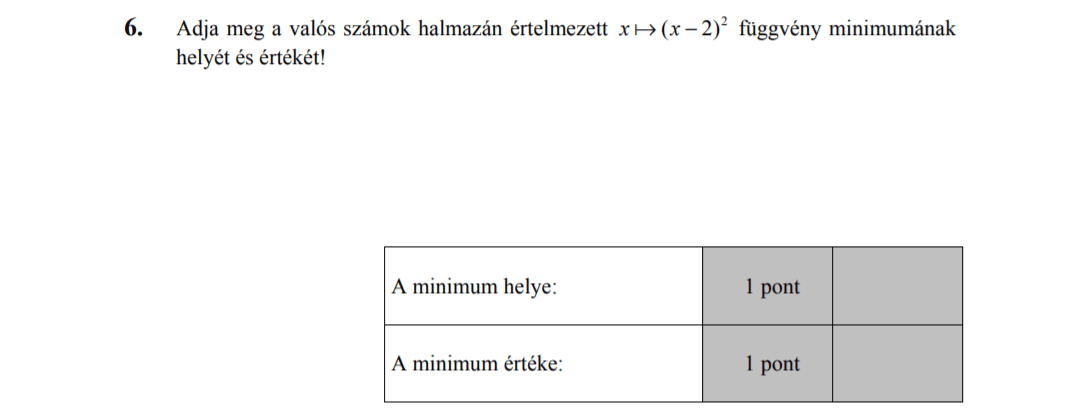

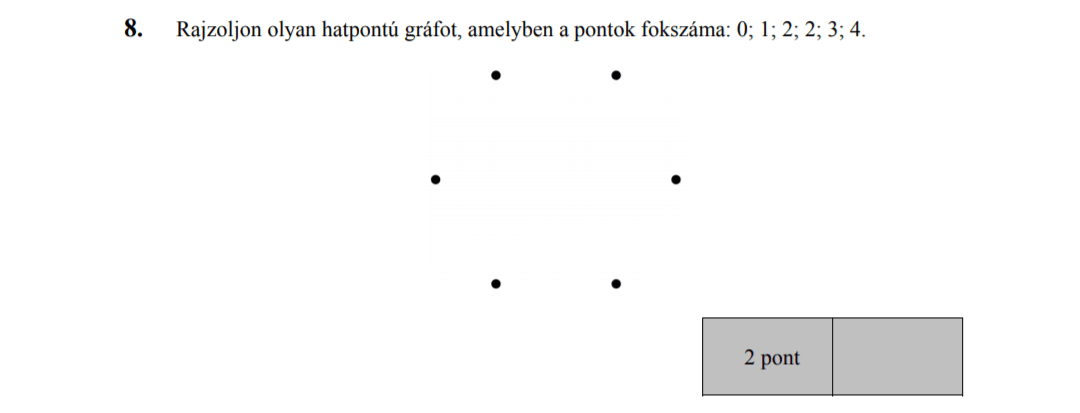


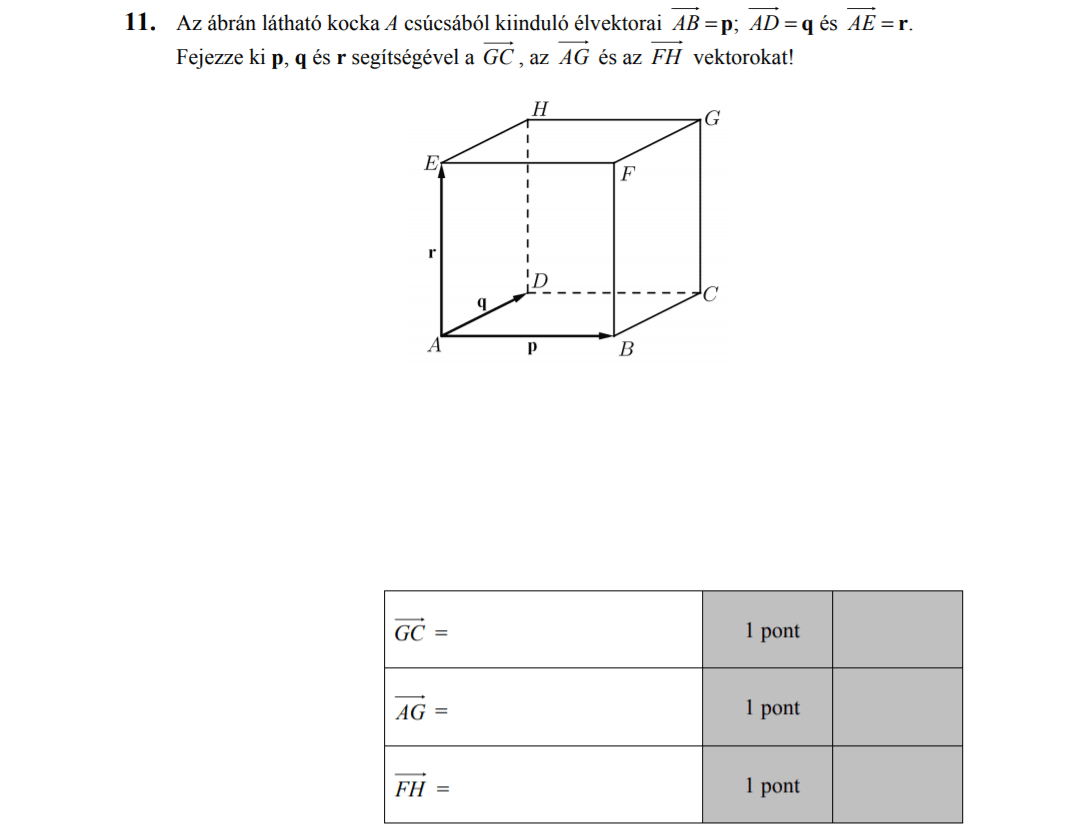
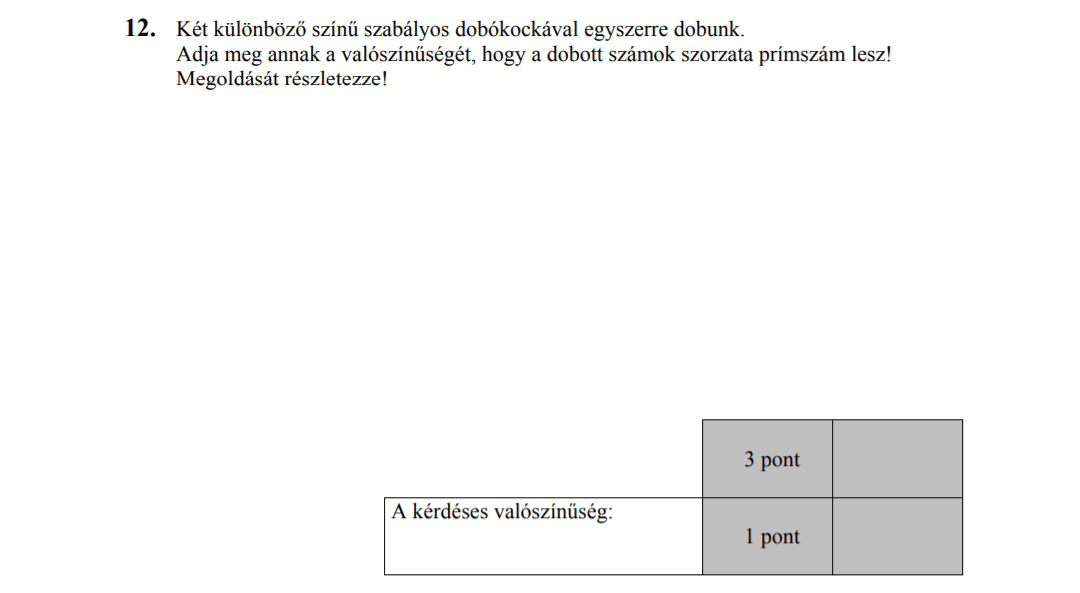
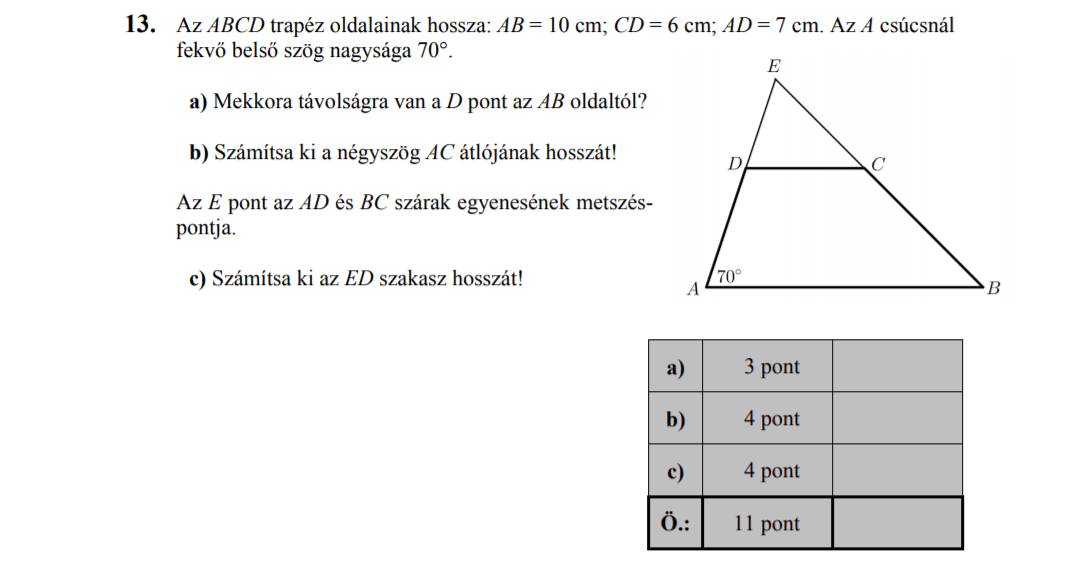
MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


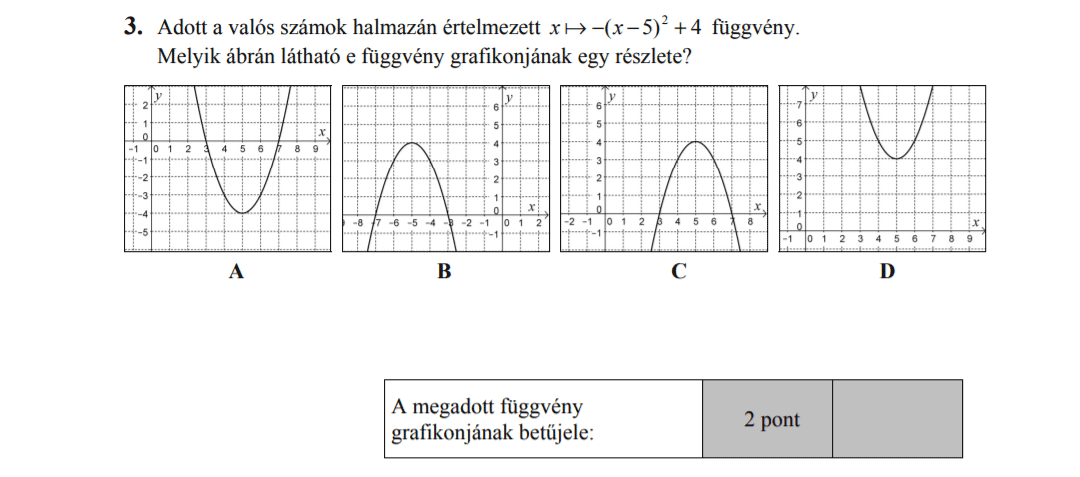






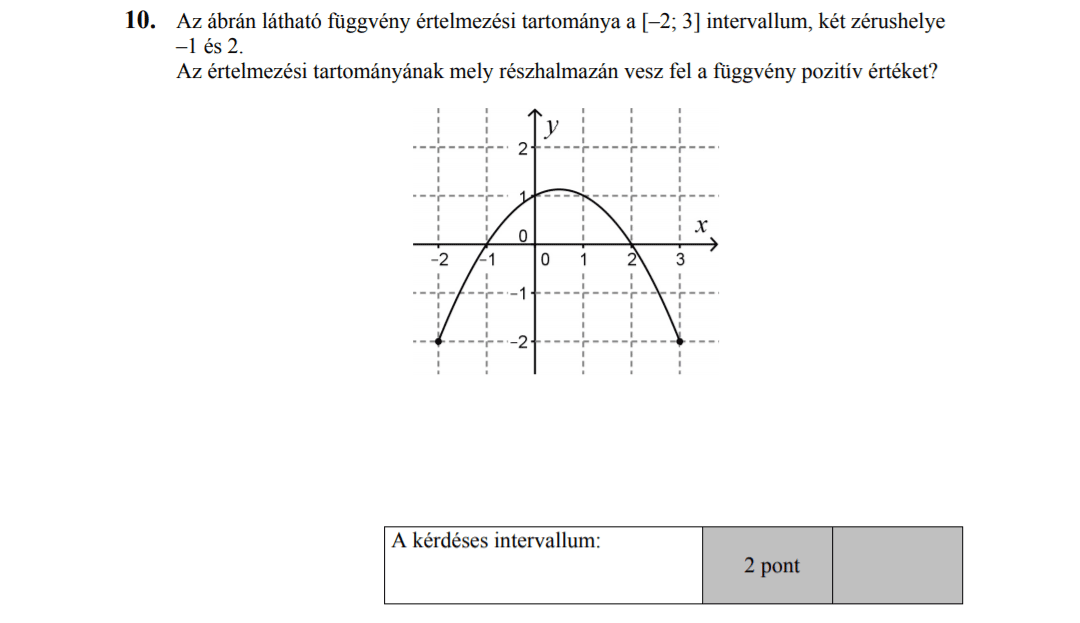


MÁSODIK RÉSZ


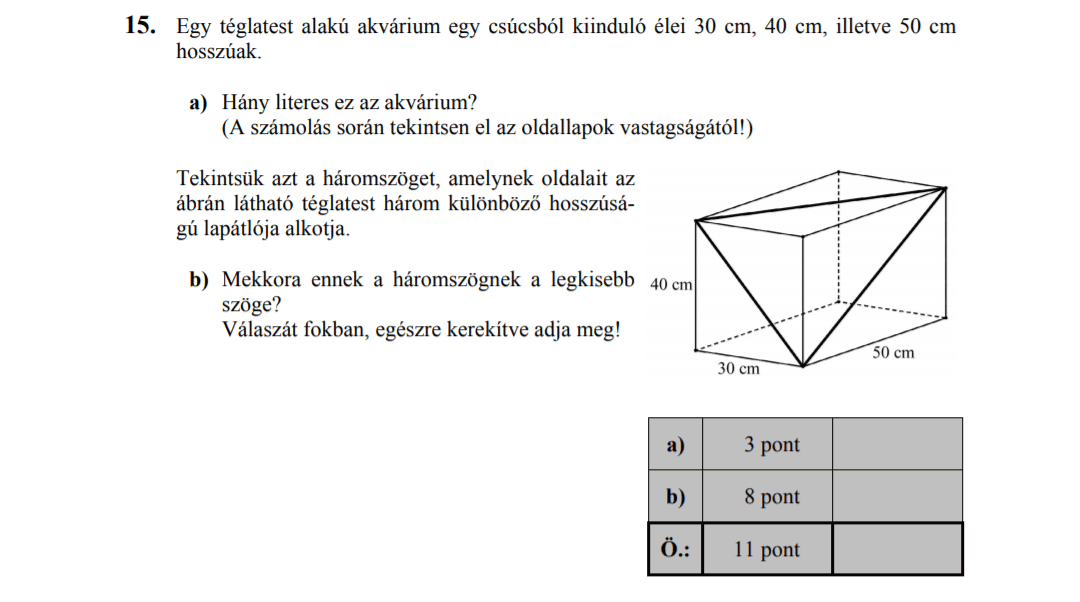

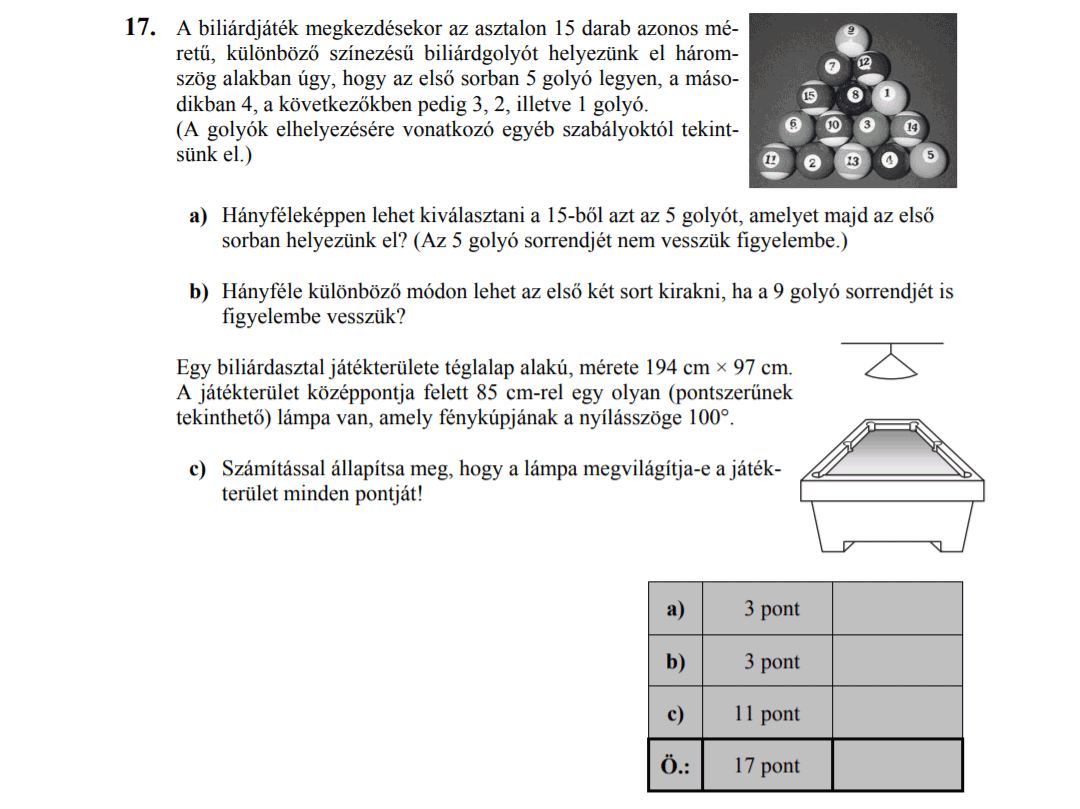

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


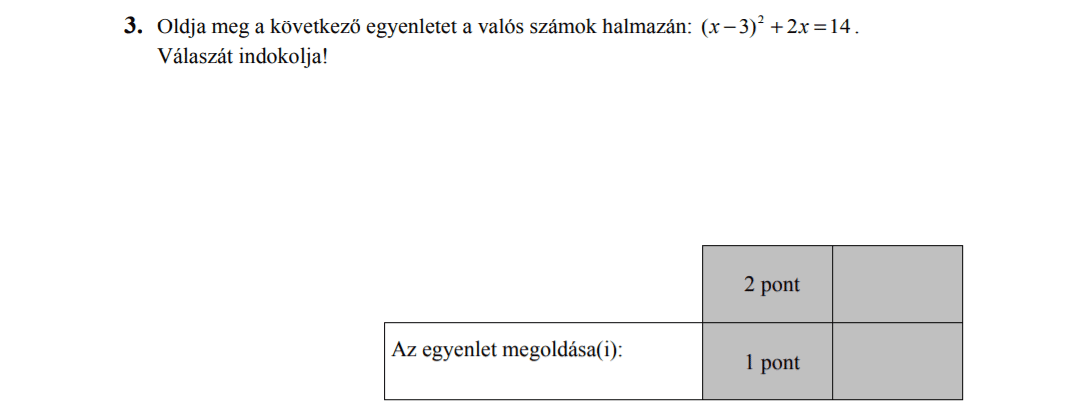


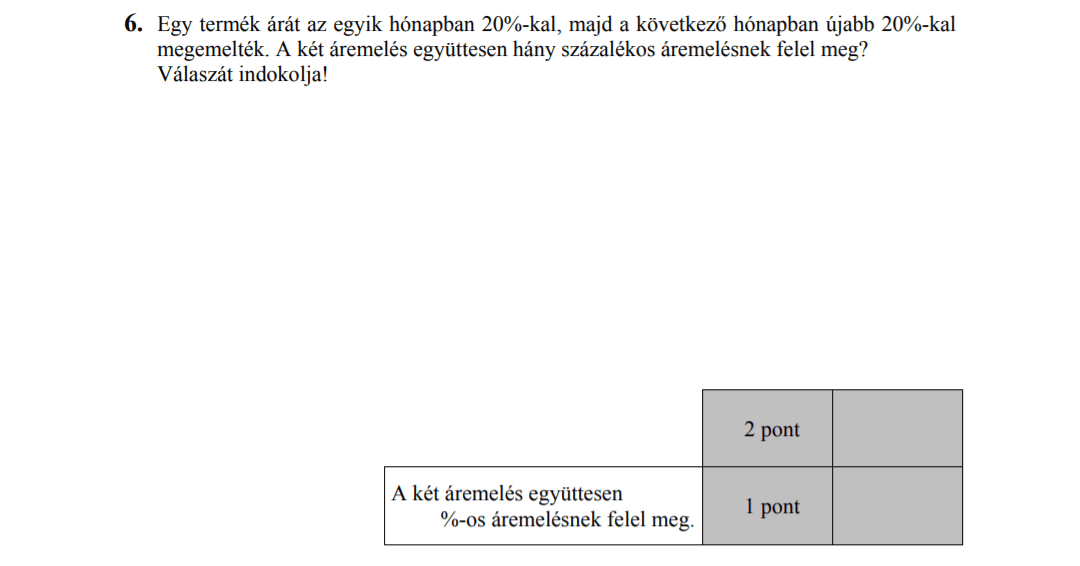
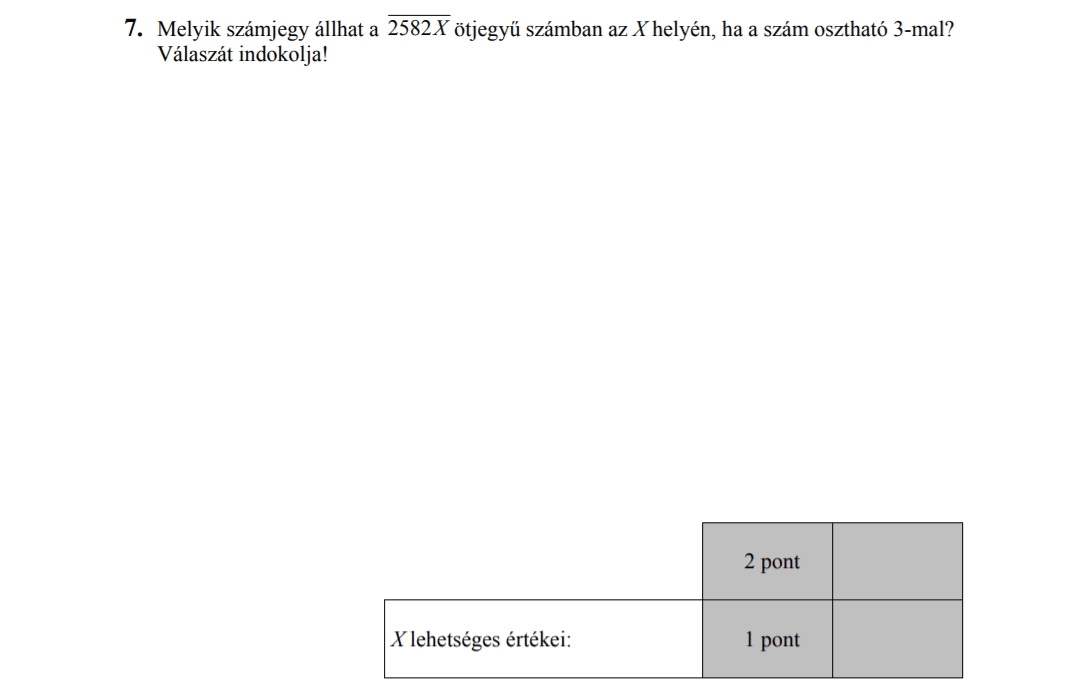
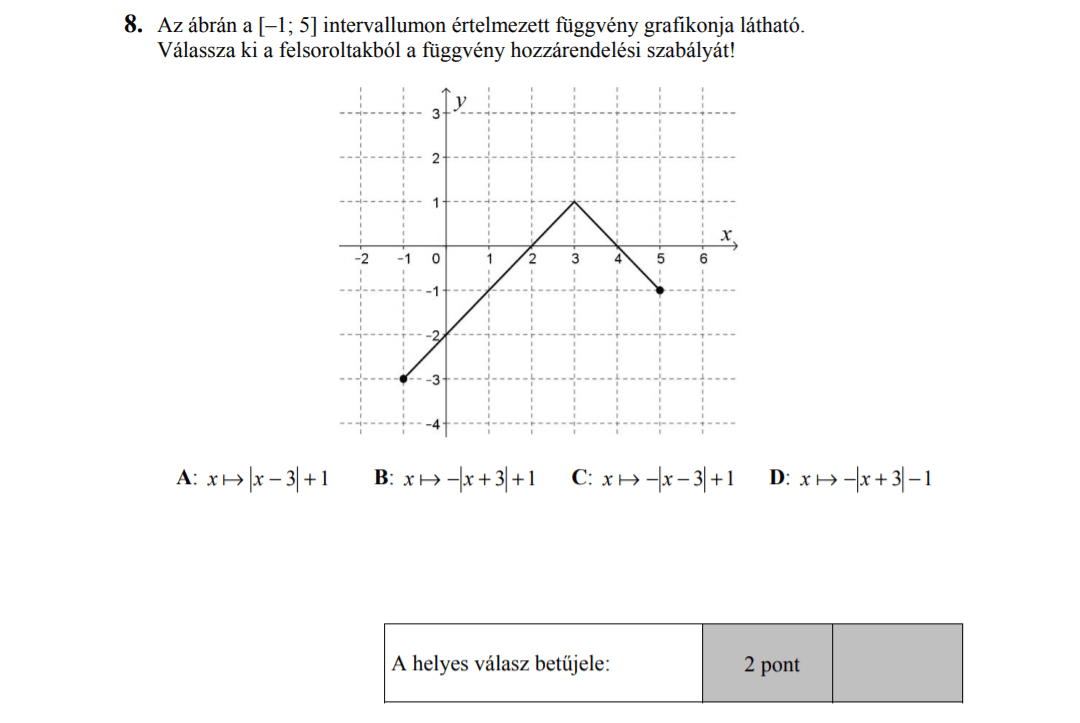


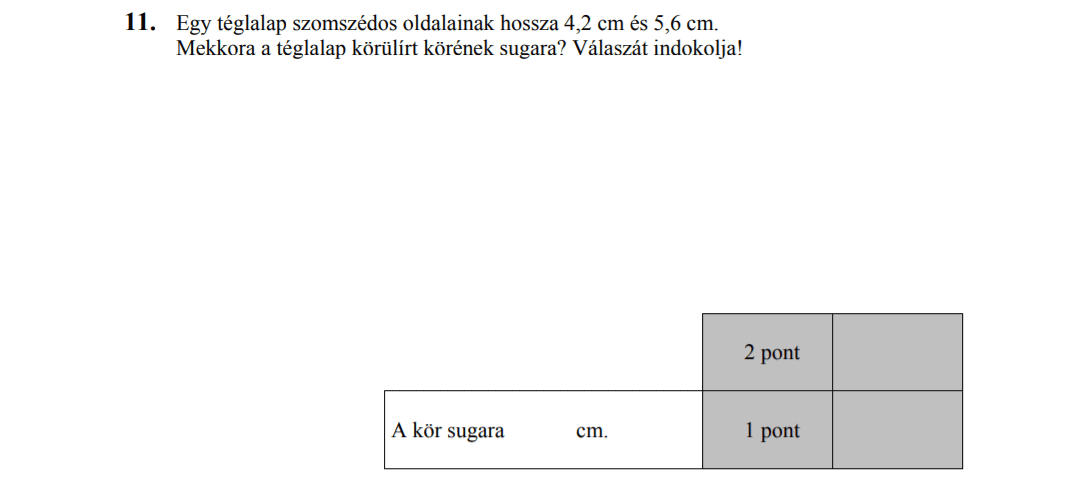

MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ

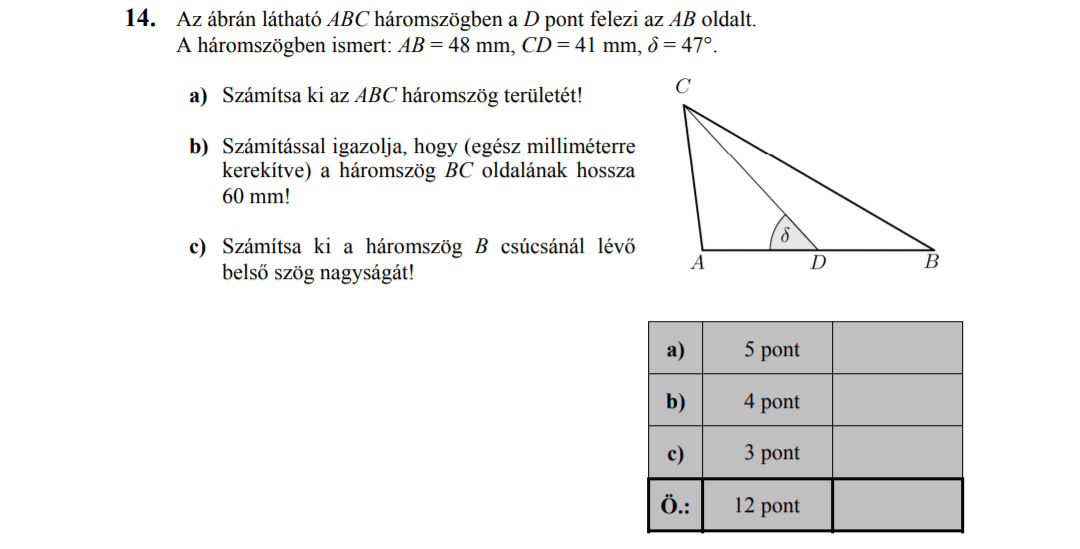




- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


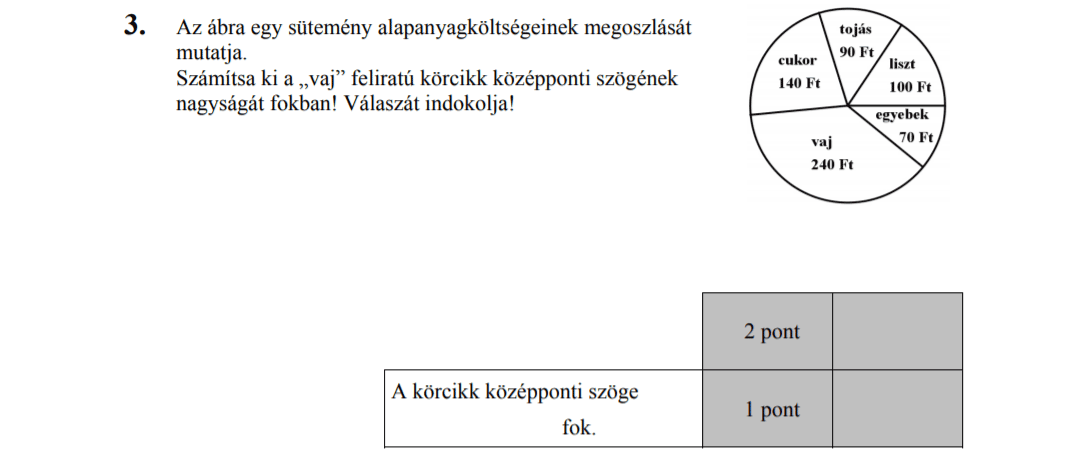
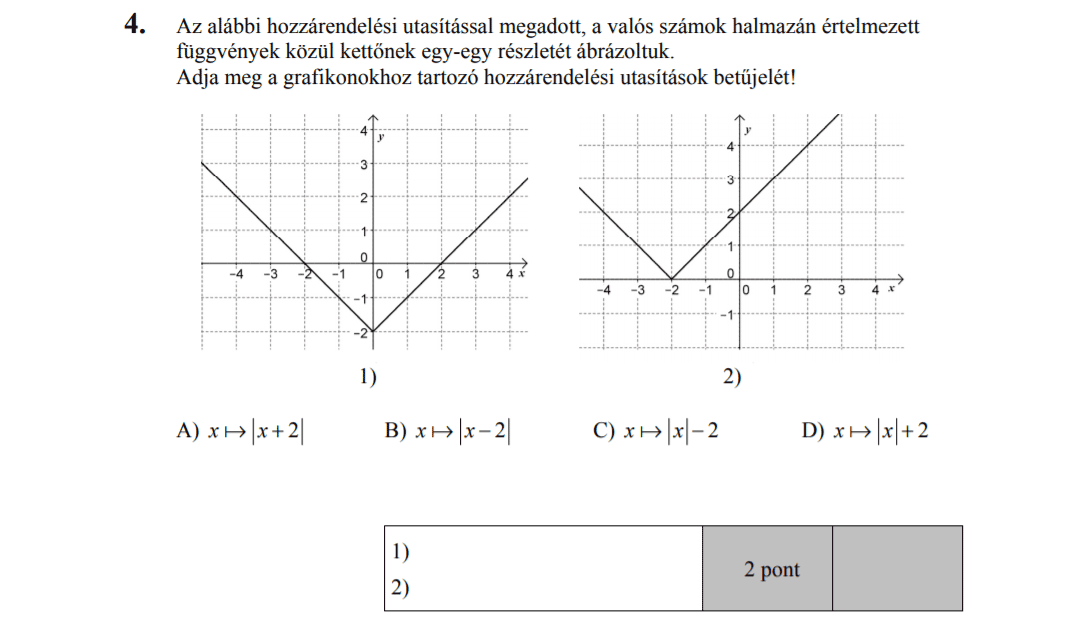





MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Halmazműveletek
Vannak az $A$ és $B$ halmazok.
Az $A$ és $B$ halmazok uniója: Azon elemek halmaza, amelyek legalább az egyik halmazban benne vannak.
Jele: $A \cup B$
Az $A$ és $B$ halmazok metszete: Azon elemek halmaza, amelyek mindkét halmazban benne vannak.
Jele: $A \cap B$
Az $A$ és $B$ halmazok különbsége: Azon elemek halmaza, amelyek az $A$ halmazba benne vannak, de a $B$ halmazba nem.
Jele: $A \setminus B$
Az $A$ halmaz komplementere a $H$ alaphalmazon nézve: Az alaphalmaz azon elemeinek halmza, amelyek nincsenek benne az $A$-ban.
Jele: $ \overline{A}$
Logikai szita formula
A logikai szita formula két halmazra:
\( \mid A \cup B \mid = \mid A \mid + \mid B \mid - \mid A \cap B \mid \)
A logikai szita formula három halmazra:
\( \mid A \cup B \cup C \mid = \mid A \mid + \mid B \mid + \mid C \mid - \mid A \cap B \mid - \mid A \cap C\mid - \mid B \cap C \mid + \mid A \cap B \cap C \mid \)
De Morgan azonosságok halmazokra
Az első De Morgan azonosság azt mondja, hogy a metszet komplementere pont megegyezik a komplementrek uniójával:
\( \overline{ A \cap B} = \overline{A} \cup \overline{B} \)
A második De Morgan azonosság pedig azt mondja, hogy az unió komplementere éppen megegyezik a komplementerek metszetével:
\( \overline{ A \cup B } = \overline{A} \cap \overline{B} \)
Adottak az $A$ és $B$ halmazok:
\( A= \{ 1, 2, 3, 4, 7, 8 \} \quad B= \{ 1,3,4,5,6 \} \)
Határozzuk meg...
a két halmaz metszetét!
a két halmaz unióját!
$ B\setminus A $-t!
Az $A$ halmaz legyen a $[2,6]$ zárt intervallum, a $B$ halmaz pedig az $]1,4[$ nyílt intervallum.
Határozzuk meg ezeket:
\( A \cap B \quad A \cup B \quad A \setminus B \)
a) Egy osztályban 12-en utálják a matekot és 18-an a fizikát. Összesen 20-an vannak, akik a kettő közül legalább az egyiket utálják. Hányan utálják mindkettőt?
b) Egy osztályba 20 tanuló jár. Az osztály összes tanulója közül 9-en szeretik a matekot és közülük 5 lány. Tudjuk még, hogy 5 fiú nem szereti a matekot. Hány lány jár az osztályba?
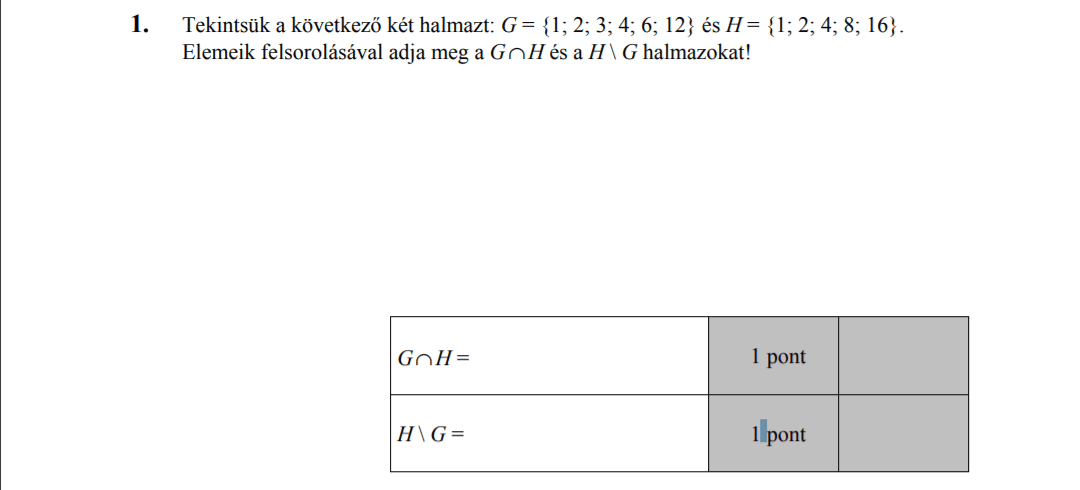
a) Adottak a $G$ és $H$ halmazok:
\( G= \{ 1,2,3,4,6,12 \} \quad H= \{ 1,2,4,8,16 \} \)
Határozzuk meg a $G \cap H$ és $G \setminus H $ halmazokat!
b) Az $A$ halmaz elemei a 28 pozitív osztói, a $B$ halmaz elemei a 49 pozitív osztói. Adjuk meg az $A \cap B$ és $B \setminus A$ halmazokat elemeik felsorolásával!
c) Egy városban 60 étterem, 56 bár és 36 reggeliző hely üzemel. Olyan, ami étterem és bár is egyben 16 darab van, ami reggelizőként és bárként is üzemel, olyanból 20 darab van, és ami reggeliző és étterem is, olyan 11 darab van. 4 olyan hely van, ami reggelizőként, étteremként és bárként egyszerre működik. Hány olyan bár működik a városban, ami nem étterem és nem reggeliző hely?
d) Van három halmaz, $A=\{ 2, 3, 5, 7, 11 \}$, $B=\{x \in Z^+ | 1 \leq x^2 \leq 24 \}$ és $C$ pedig a 15 pozitív osztóinak halmaza. Ábároljuk ezeket a halmazokat és adjuk meg elemeinek felsorolásával az $A\cup B \cap C$ és az $A \cap B \setminus C$ halmazokat.
Egy osztályba 20-an járnak. Közülük 16-an vannak, akik a matekot és a fizikát is utálják. Hányan vannak, akik legalább az egyik tantárgyat szeretik?
a) Írd fel a ${2; 3; 4}$ halmaznak azon részhalmazait, melyeknek a 2 eleme, és a 4 nem eleme!
b) Az $A$ és $B$ halmazokról a következőket tudjuk:
\( A \cap B = \{ 1;2 \} \quad A \cup B = \{ 1;2;3;4;5;6;7 \} \quad A \setminus B = \{ 5;7 \} \)
c) Adottak a következő halmazok:
\( A= \{ 2;3;5;7;11;13;17;19 \} \)
\( B= \{ 1;4;7;10;13;16;19 \} \)
\( C= \{ 1;2;3;5;8;13 \} \)
Elemeik felsorolásával adjuk meg a $ C \setminus A$ és az $(A \cup B ) \cap C$ halmazt!
Egy osztályban a következő háromféle sportkört hírdették meg: kosárlabda, foci és röplabda. Az osztály 30 tanulója közül kosárlabdára 14, focira 19, röplabdára 14 tanuló jelentkezett. Ketten egyik sportra sem jelentkeztek. Három gyerek kosárlabdázik és focizik, de nem röplabdázik, hatan fociznak és röplabdáznak, de nem kosaraznak, ketten pedig kosárlabdáznak és röplabdáznak, de nem fociznak. Négyen mind a három sportot űzik. Készítsünk halmazábrát!
Anett és Berta egy írott szöveget figyelmesen átolvasott. Anett 24 hibát talált benne, Berta 30-at. Ezek között 12 hiba volt csak, amit mindketten észrevettek. Később Réka is átnézte ugyanazt a - javítatlan - szöveget, és ő is 30 hibá talált. Réka az Anett által megtalált hibákból 8-at vett észre, a Berta által észleltekből 11-et. Mindössze 5 olyan hiba volt, amit mind a hárman észrevettek.
a) Együtt összesen a szöveg hány hibáját fedezték fel?
b) A megtalált hibák hány százalékát vették észre legalább ketten?
Egy város 18 étterme közül 11-ben reggelit, 11-ben vegetáriánus menüt lehet kapni, és 10-ben van felszolgálás. Mind a 18 étteremben legalább egy szolgáltatást nyújt az előző három közül. Öt étteremben adnak reggelit, de nincs vegetáriánus menü. Azok közül az éttermek közül, ahol reggelizhetünk, ötben van felszolgálás. Csak egy olyan étterem van, ahol mindhárom szolgáltatás megtalálható.
a) Hány étteremben lehet vegetáriánus menüt kapni, de reggelit nem?
b) Hány olyan étterem van, ahol felszolgálnak vegetáriánus menüt?
a) Egy biztosítóhoz az egyik hónapban 24 autós biztosítási kárigény érkezett, és ezek közül 8-an más kárigényt is benyújtottak. Lakásbiztosításra 7 igény érkezett, és egyéb igény 17. 30 olyan ügyfél volt, aki csak egy igényt nyújtott be, 1-1 olyan ügyfél volt, aki a lakáson kívül még pontosan egy kárigényt nyújtott be és nem volt olyan, aki mindhármat. Készítsünk ábrát, és állapítsuk meg, hogy hányan vannak, akik pontosan két kárigényt nyújtottak be!
b) Egy középiskolába 700 tanuló jár. Közülük 10% sportol rendszeresen a két iskolai egyesület közül legalább az egyikben. Az atlétikai egyesületnek 36 tanuló tagja, és pontosan 22 olyan diák van, aki az atlétika és a kosárlabda egyesületnek is tagja.
1) Ábrázoljuk az egyesületekben sportoló diákok megoszlását halmazokkal.
2) Hányan sportolnak a kosárlabda egyesületben?
Halmazok, metszet, unió, és egyebek
Van itt egy A halmaz
aminek a komplementere ez. Minden ami körülötte van.
A helyzet akkor válik izgalmasabbá, ha kerítünk az A halmaz mellé
egy B halmazt is.
A halmaz komplementere:
Az a rész, ami mindkettőben benne van az A és B halmazok metszete.
A és B halmazok metszete:
Ez pedig az A és B halmazok uniója.
A és B halmazok uniója:
Ha pedig fogunk egy ollót és szépen kivágjuk az A halmazból azt a részt
ami a B-ben is benne van, nos amit így kapunk az a két halmaz különbsége.
A és B halmazok különbsége:
És most lássuk, mi az a részhalmaz.
A-nak egy részhalmaza például a páros számok halmaza:
Vagy éppen részhalmaza a páratlan számok halmaza is:
És részhalmaza mondjuk a 3-mal osztható számok halmaza is:
Adottak az A és B halmazok:
Határozzuk meg…
a két halmaz metszetét!
a két halmaz unióját!
a B\V-t!
Egy biztosítóhoz az egyik hónapban 24 autós biztosítási kárigény érkezett, és ezek közül
8-an más kárigényt is benyújtottak. Lakásbiztosításra 7 igény érkezett, és egyéb igény 17.
30 olyan ügyfél volt, aki csak egy igényt nyújtott be, 1-1 olyan ügyfél volt, aki a lakáson
kívül még pontosan egy kárigéényt nyújtott be és nem volt olyan, aki mindhármat.
Készítsünk ábrát, és állapítsuk meg, hogy hányan vannak, akik pontosan két kárigényt
nyújtottak be!
Akik pontosan két kárigényt nyújtottak be:
Végül itt jön még egy nagyon érdekes mese bárányokról és számhalmazokról…
Beszélgessünk egy kicsit a számokról.
Ez itt például 3.
Ez pedig 4.
És néha sajnos szükség van negatív számokra is.
Így jutunk el az egész számok halmazáig, amit Z-vel jelölünk.
Aztán fölmerülhet az igény olyan számokra is,
amelyek arányokat fejeznek ki.
Ezeket racionális számoknak nevezzük.
Mondjuk ennek az egyenletnek
a megoldása:
A racionális számokat Q-val jelöljük.
Vannak aztán olyan egyenletek, amiknek
a megoldásai nem racionális számok.
Ilyen például ez az egyenlet:
És így megjelennek az irracionális számok,
amik feltöltik a racionális számok közötti
hézagokat a számegyenesen.
A racionális és az irracionális számok
alkotják együttesen a valós számokat.
Hogyha a számegyenest felszeleteljük részekre…
akkor intervallumokat kapunk.
Ez itt például az 1 és 5 közötti intervallum.
Az 1 és az 5 az intervallum végpontjai.
Olyankor, amikor a végpontok nincsenek benne az intervallumban…
az intervallumot nyílt intervallumnak hívjuk.
NYÍLT INTERVALLUM
Ha mindkét végpont benne van, akkor az a neve, hogy zárt intervallum.
ZÁRT INTERVALLUM
Előfordulhat az is, hogy az intervallum egyik vége nyílt, a másik pedig zárt.
BALRÓL NYÍLT, JOBBRÓL ZÁRT INTERVALLUM:
Az A halmaz
Most pedig nézzük, mi történik, hogyha két intervallumnak vesszük a metszetét…
vagy épp az unióját.
Az intervallumok
Az A halmaz legyen a [2,6] zárt intervallum, a B halmaz pedig az ]1,4[ nyílt intervallum.
Határozzuk meg ezeket:
Úgy tűnik, hogy a 4 nincs benne B-ben…
Így aztán amikor a B halmazt kivonjuk az A halmazból…
akkor a 4-et nem vonjuk ki, az benne marad A-ban.
És ezáltal egy mindkét végén zárt intervallumot kapunk.
Hát, ennyit az intervallumokról.
