- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
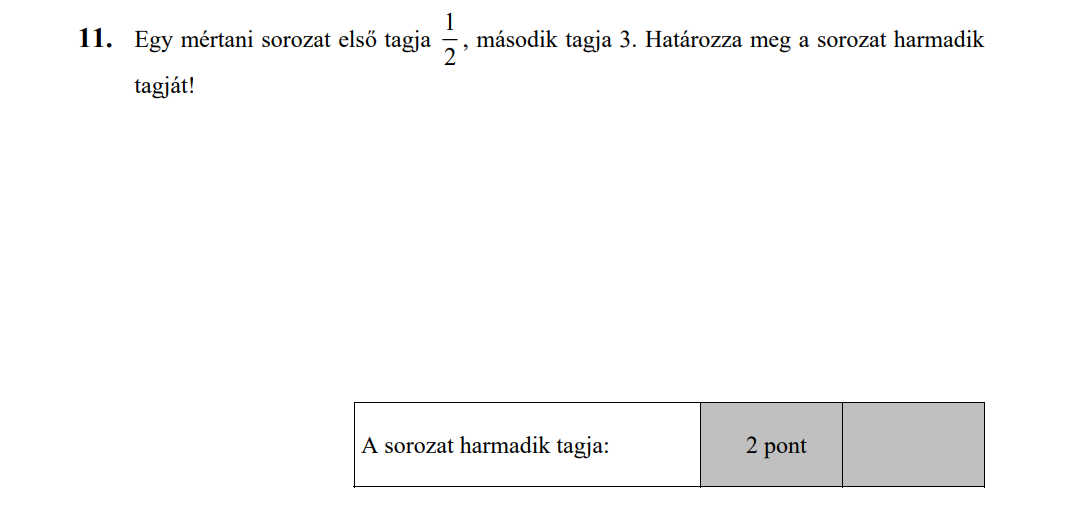
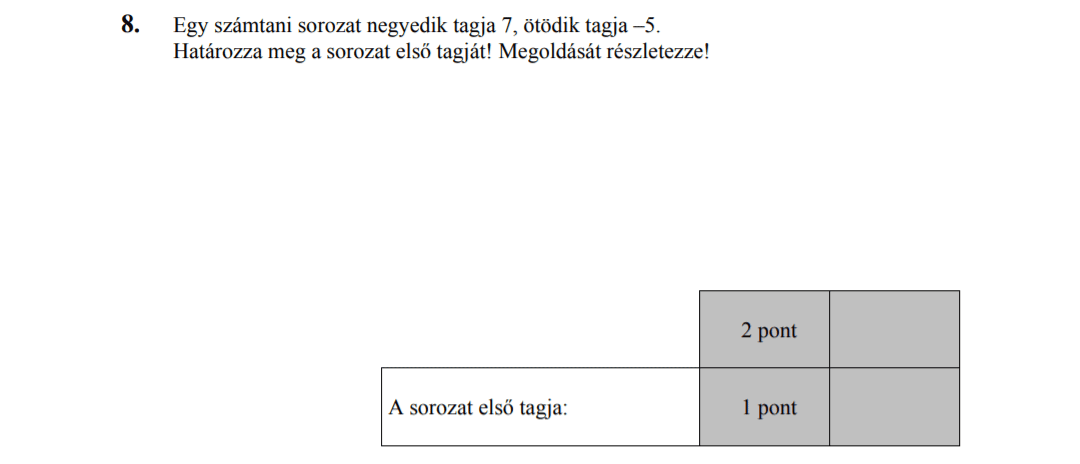
- Számtani és mértani sorozatok (16 pont)
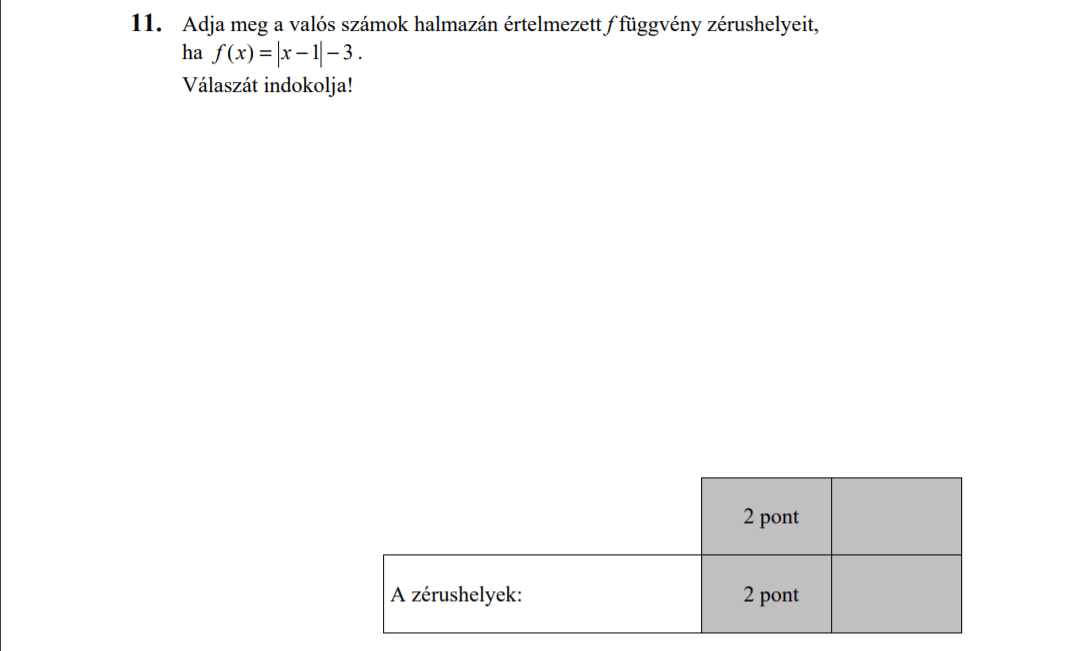
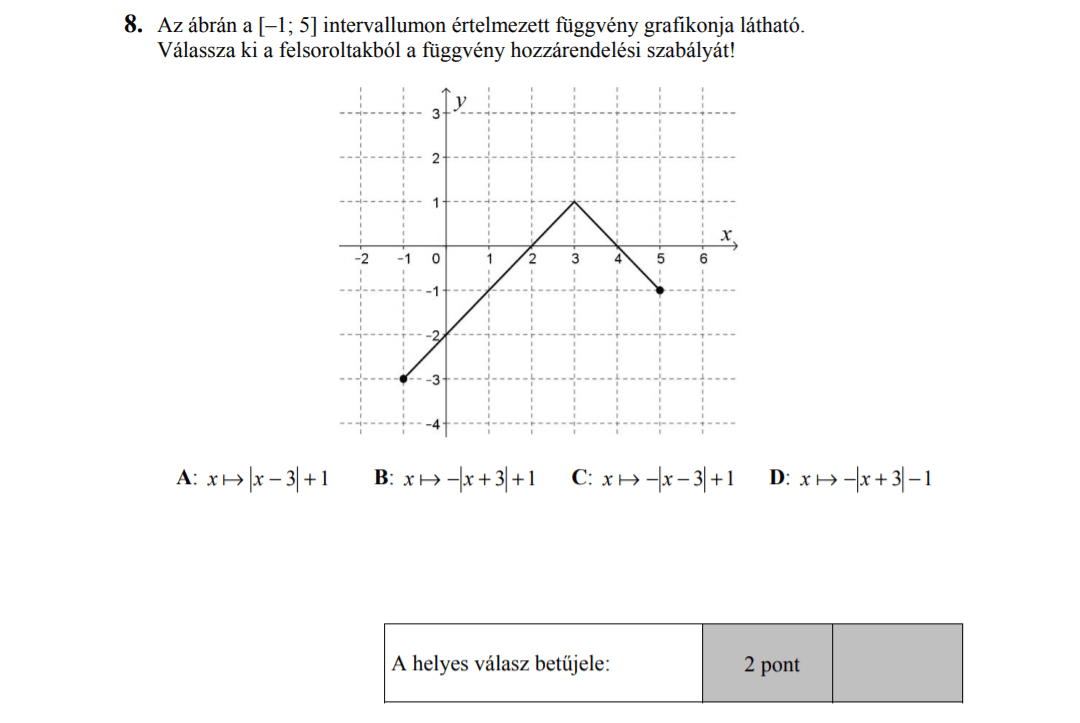
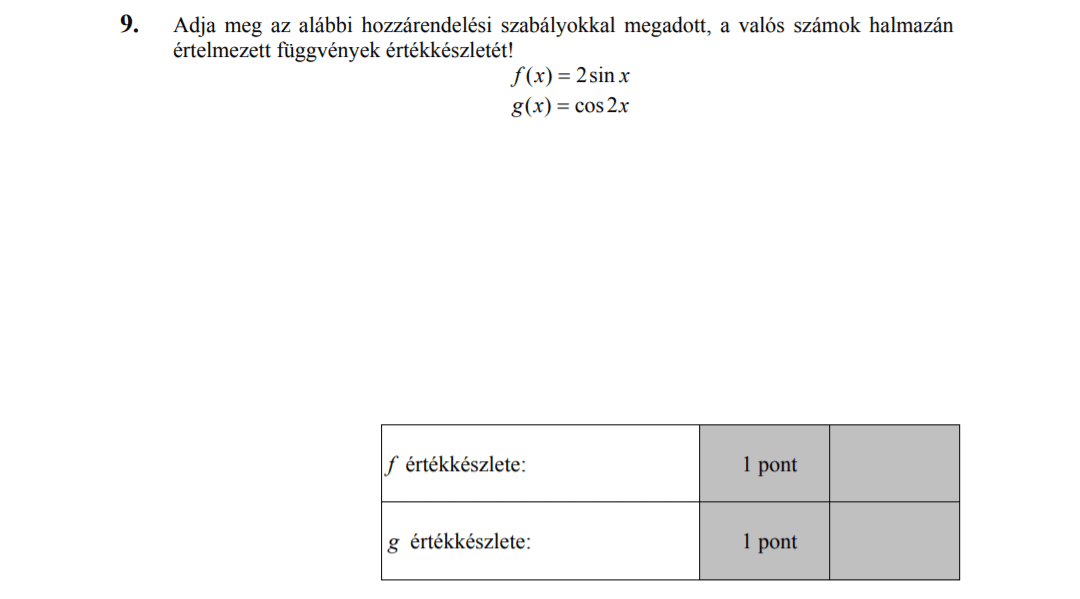
- Függvényekkel kapcsolatos feladatok (9,8 pont)
- Térgeometria (9,8 pont)
- Statisztika (9,3 pont)
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
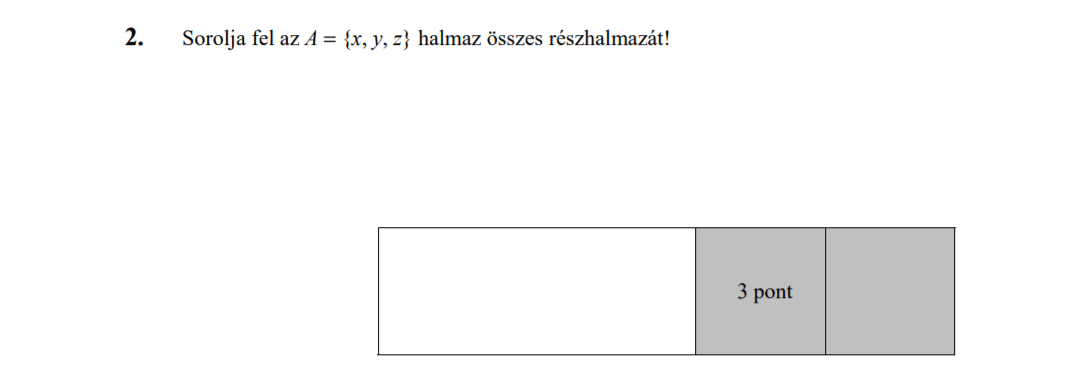
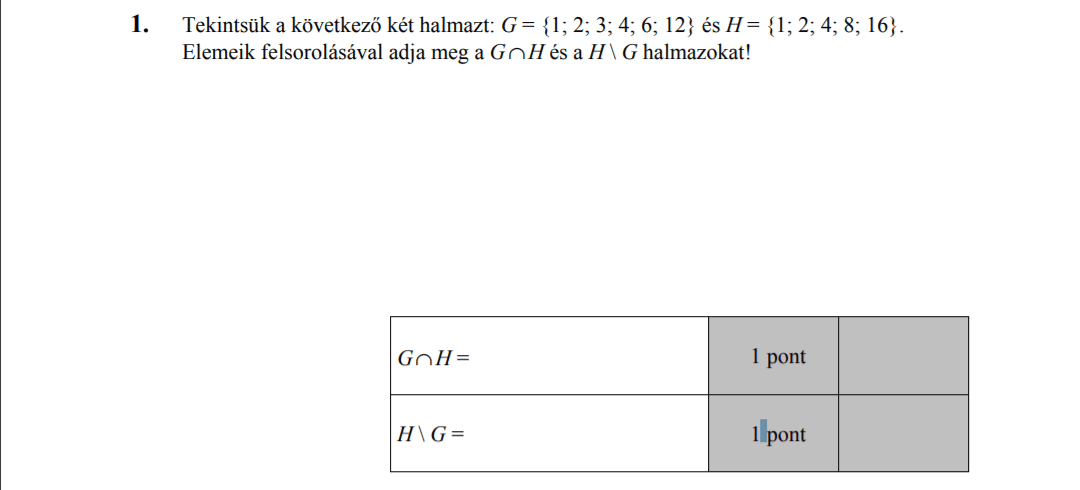
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
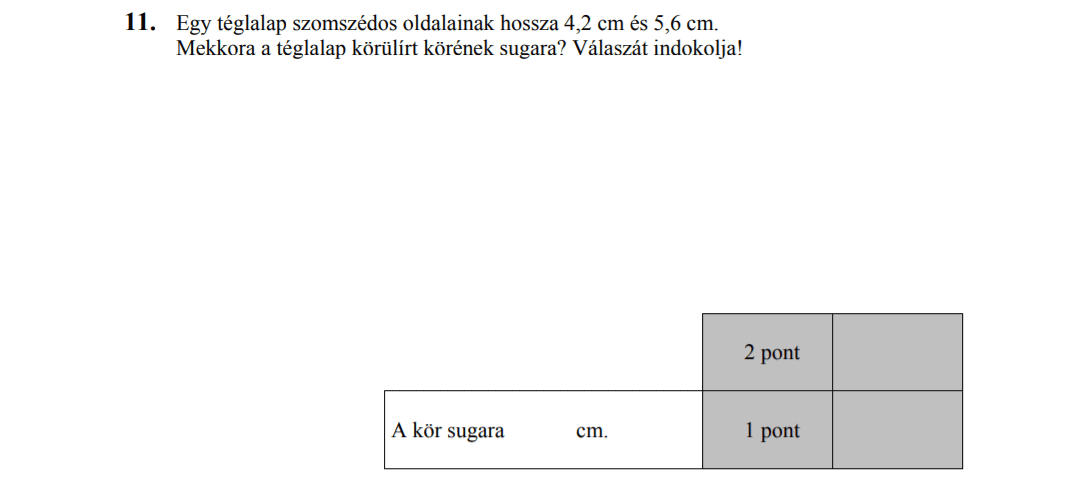
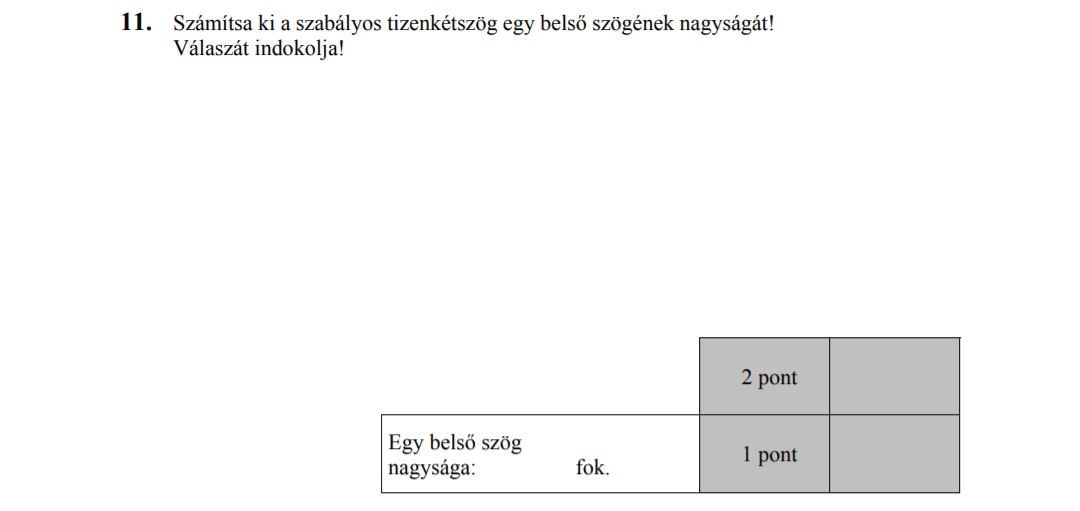
- Síkgeometria (4,5 pont)
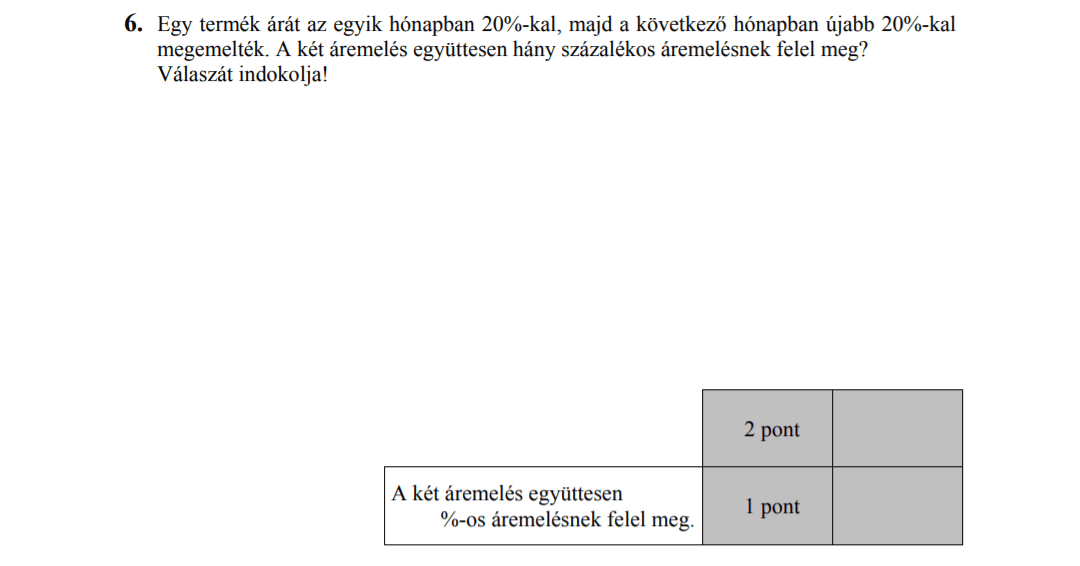
- Százalékszámítás (3,8 pont)
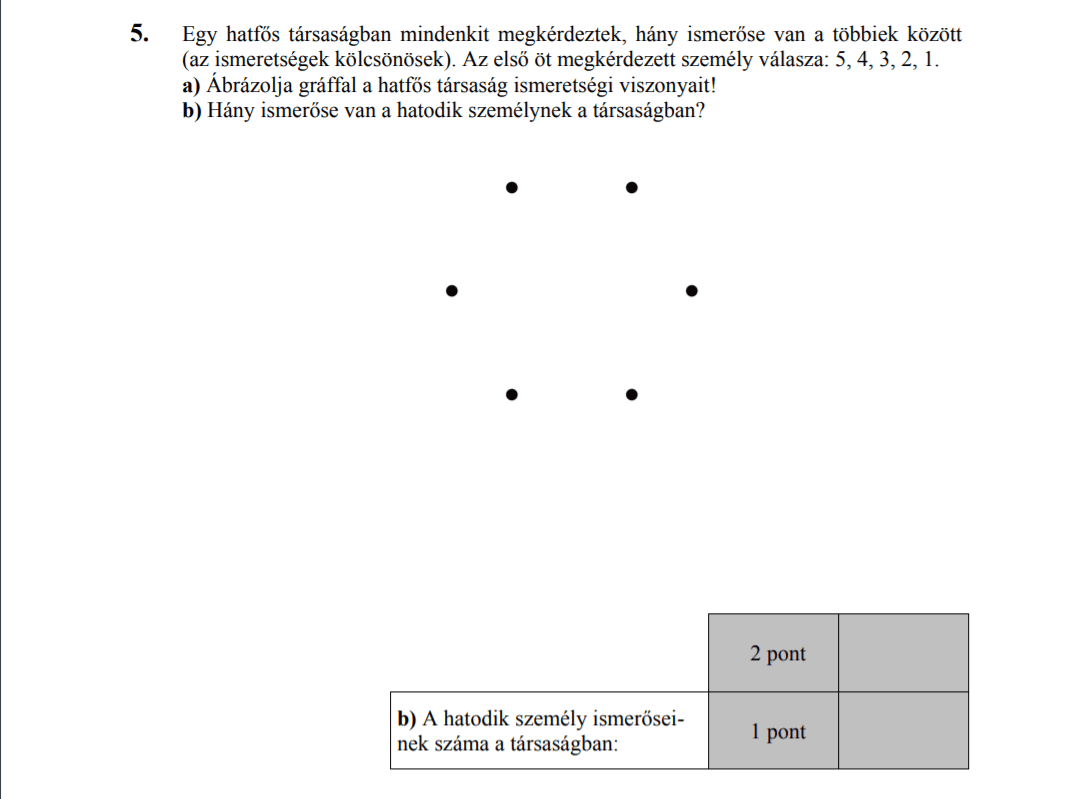
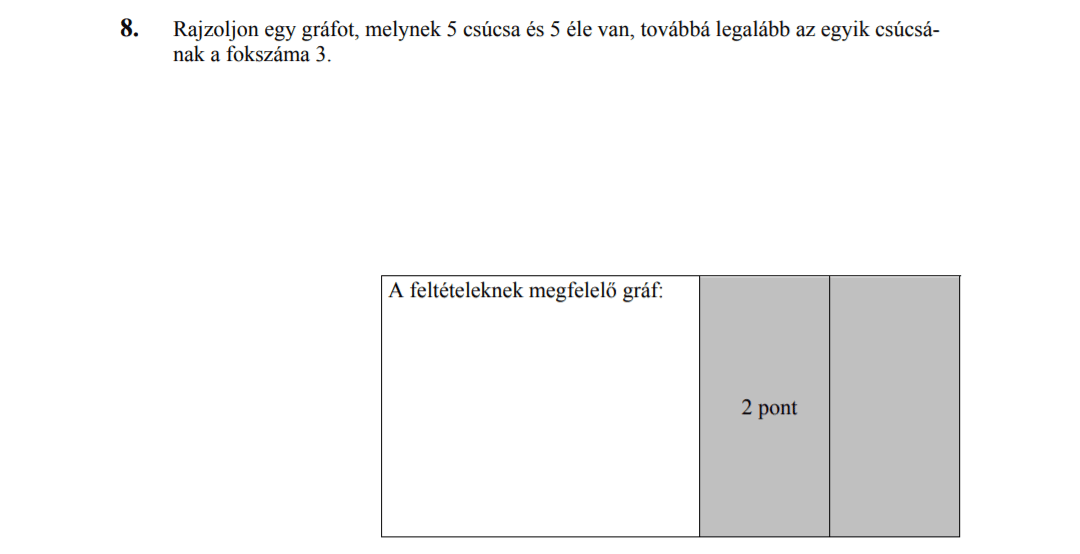
- Gráfok (3 pont)
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
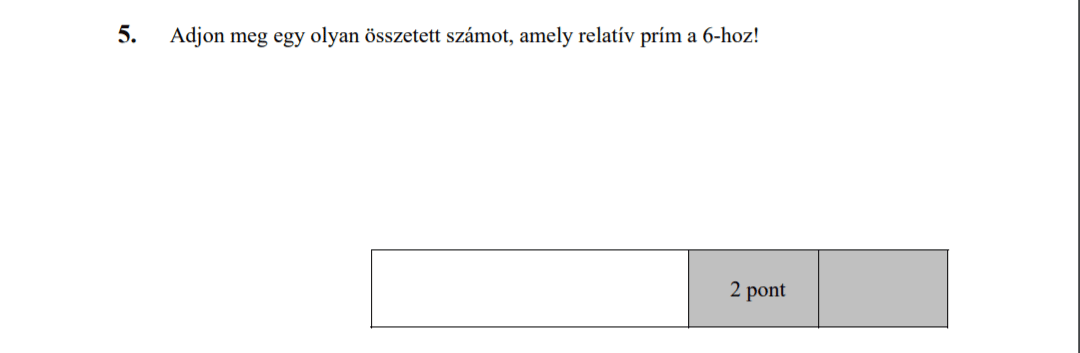
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Számelmélet (2,6 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


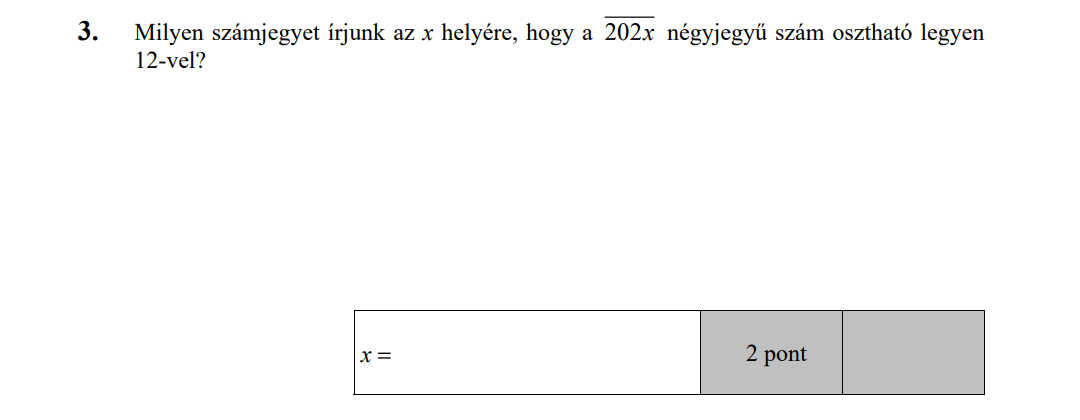
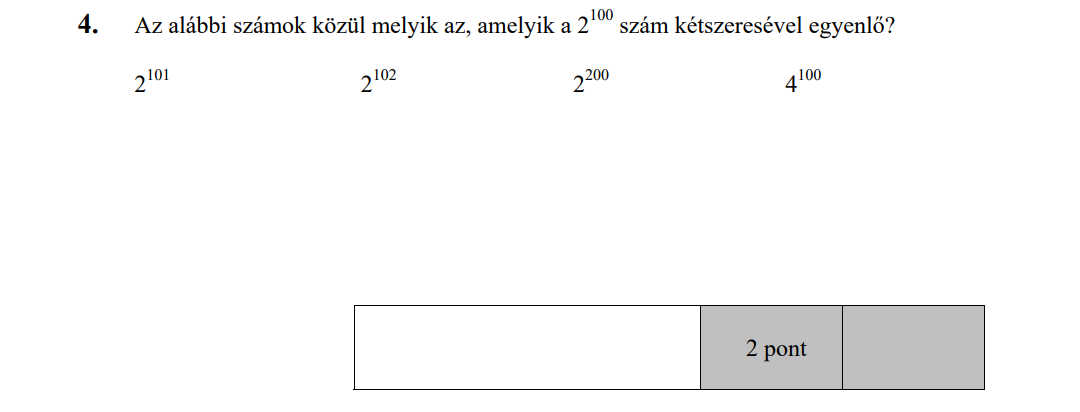



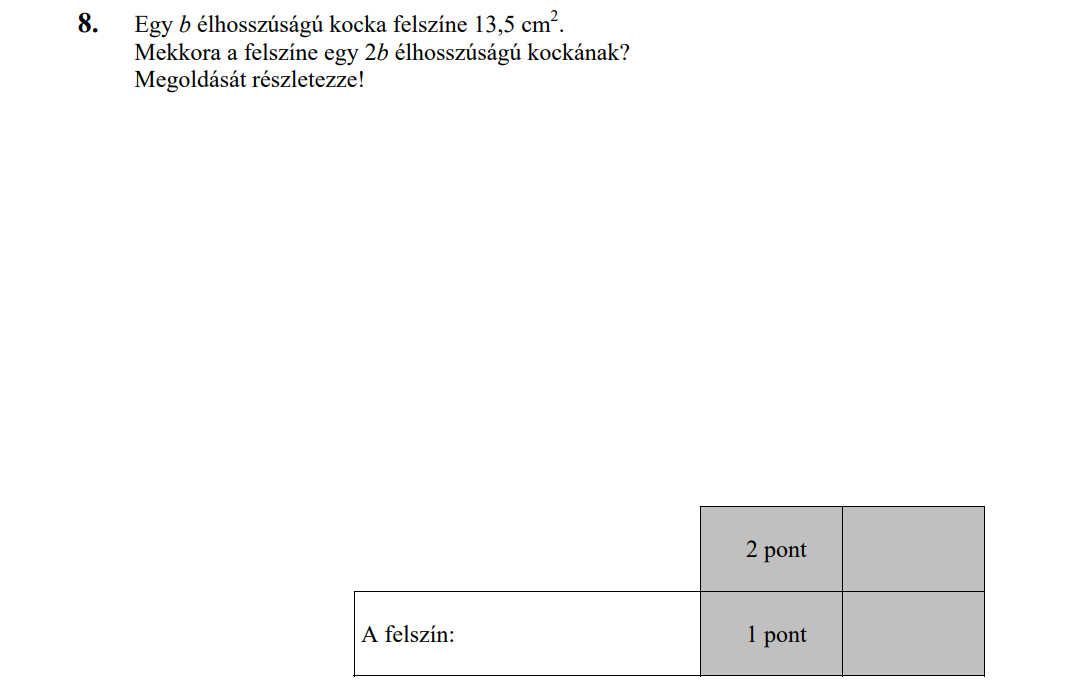




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
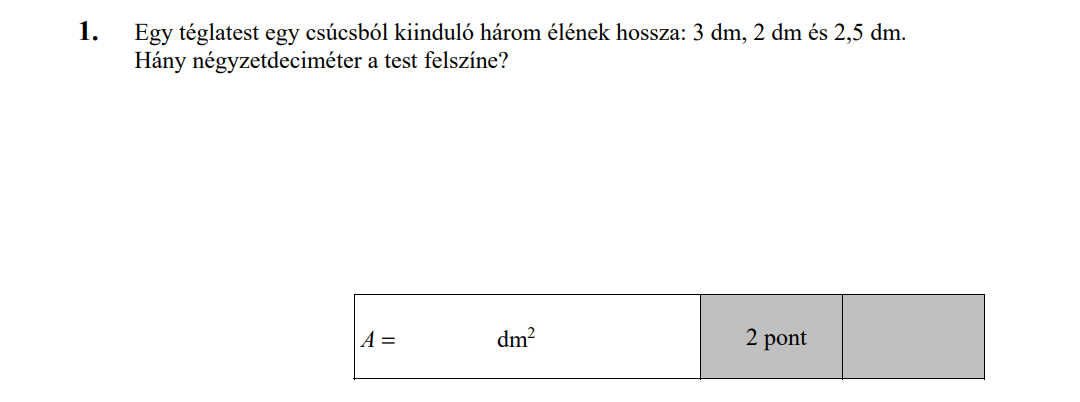
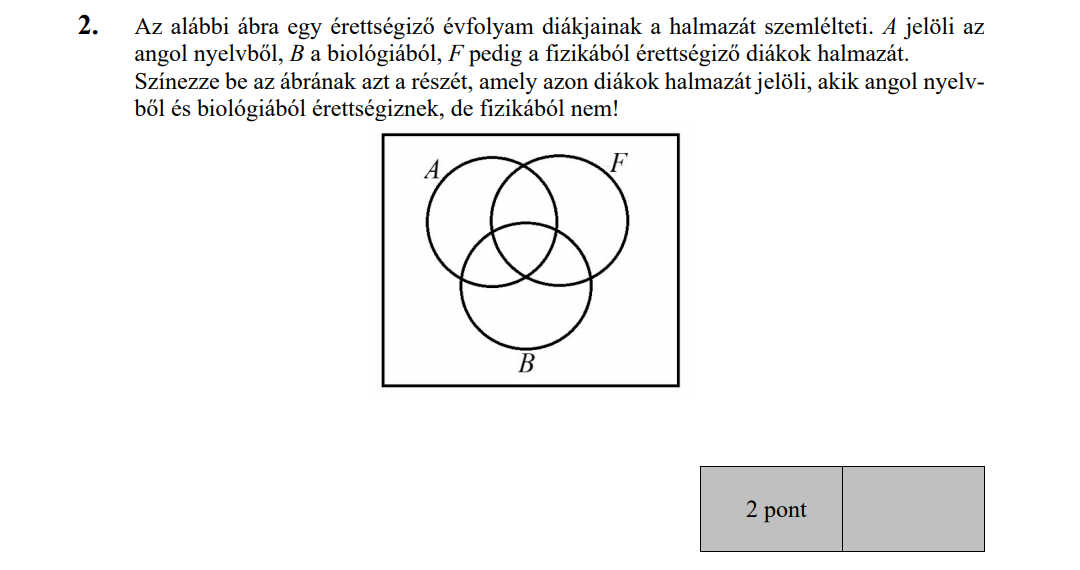

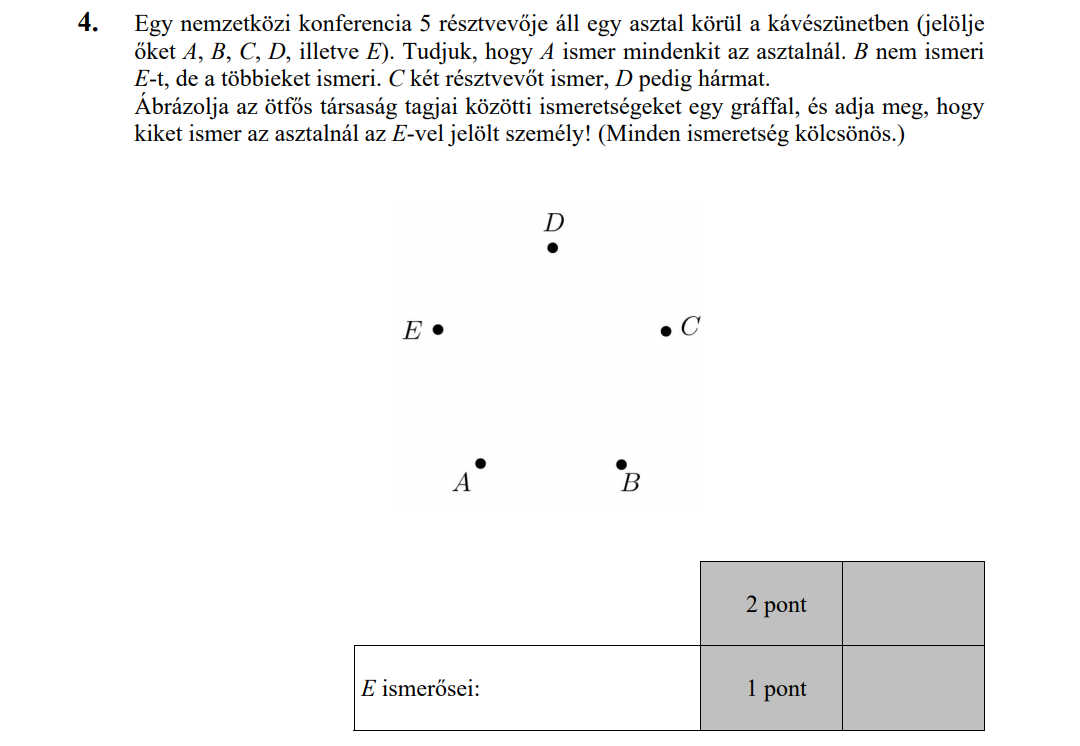

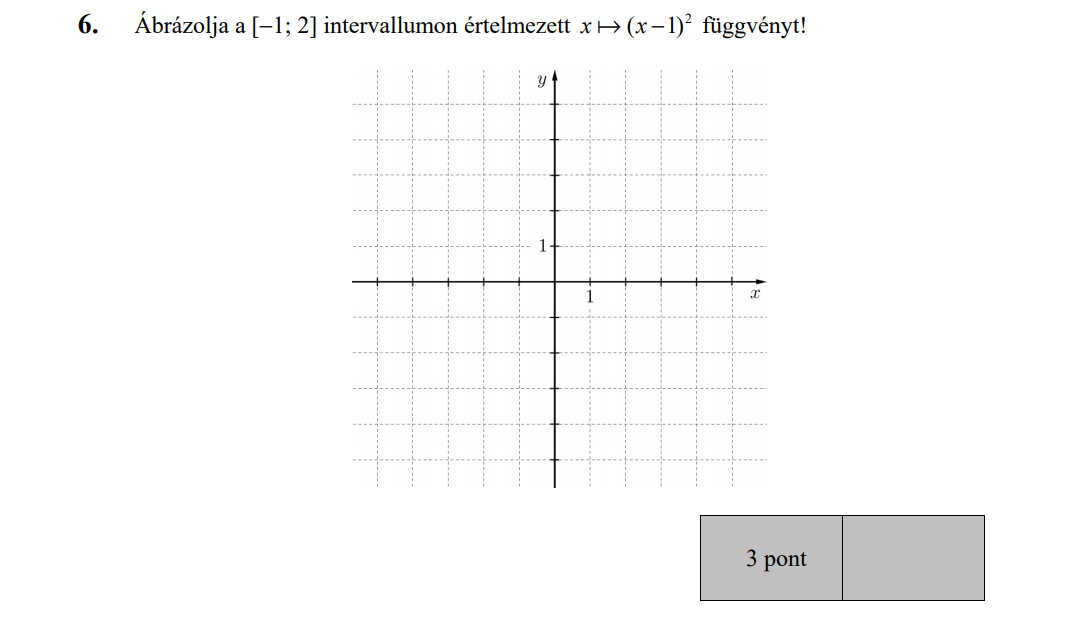



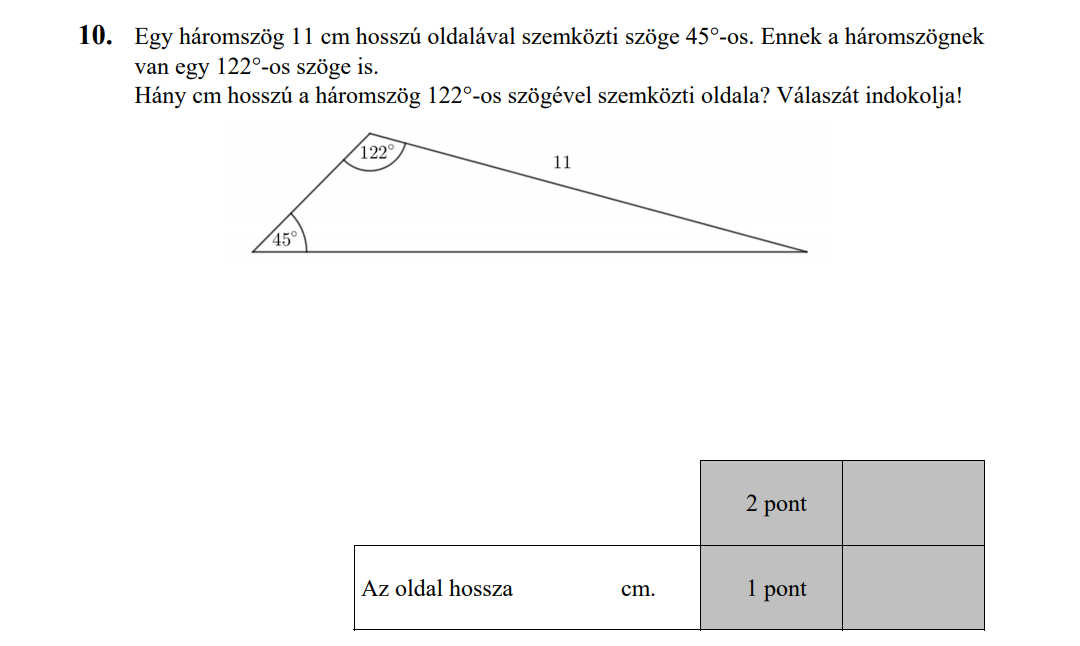

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



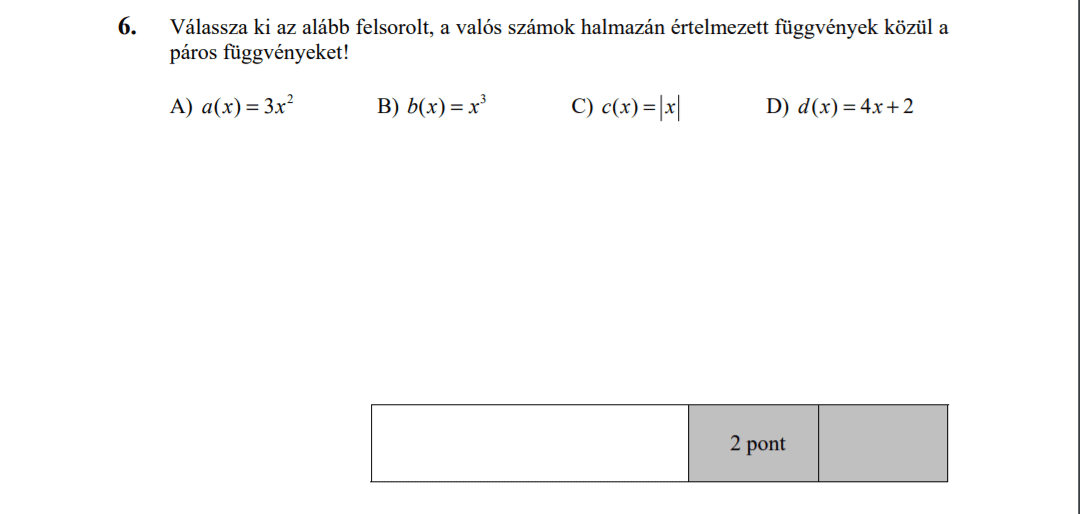
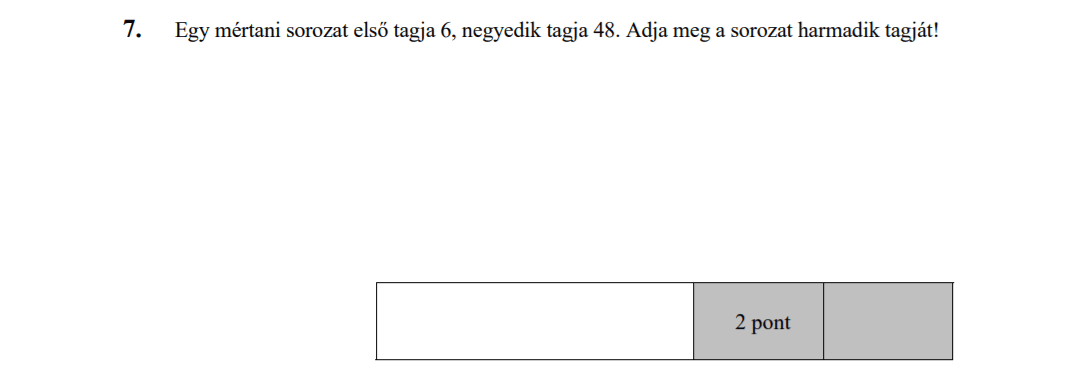



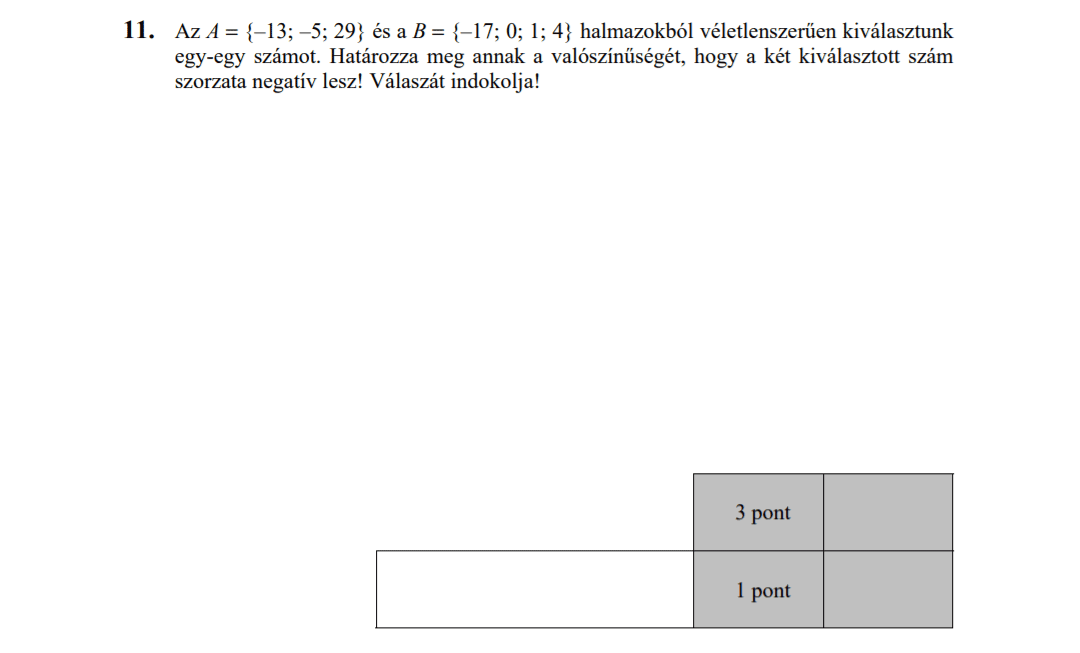

MÁSODIK RÉSZ


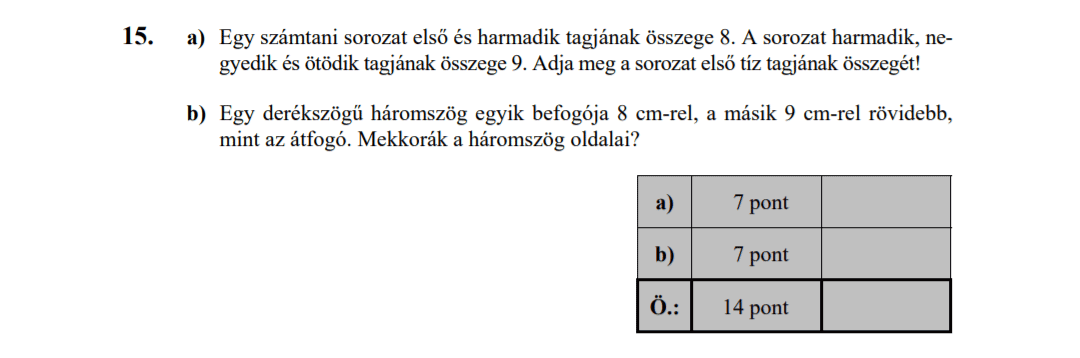



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






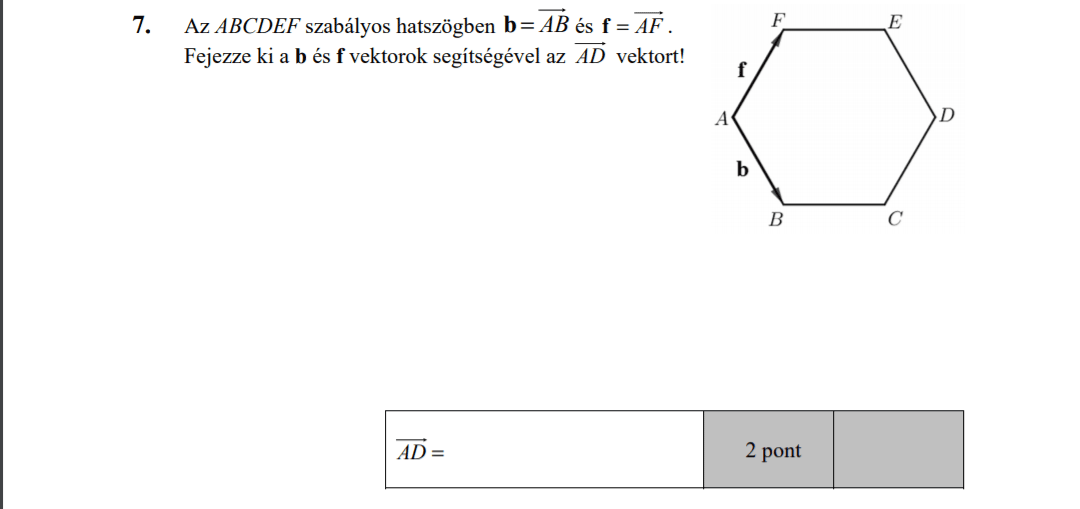



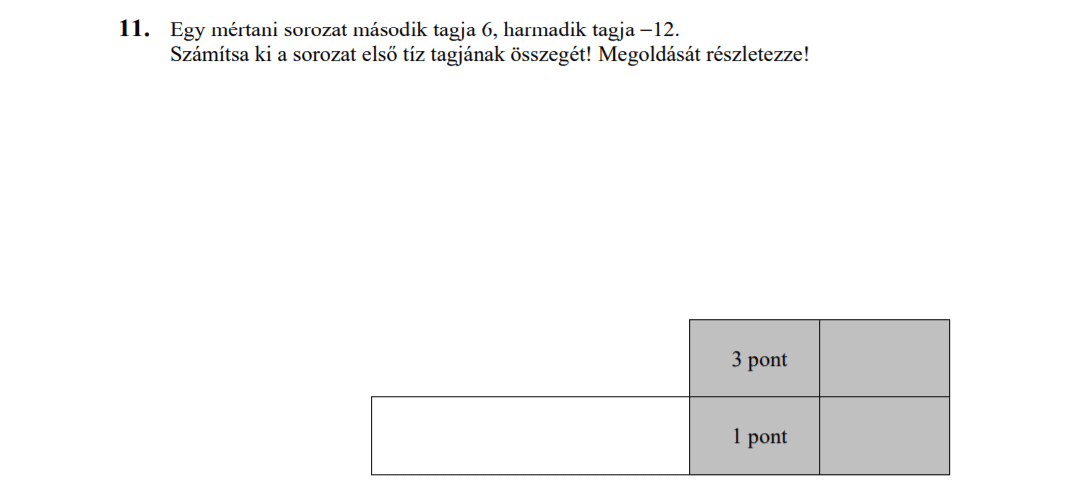

MÁSODIK RÉSZ

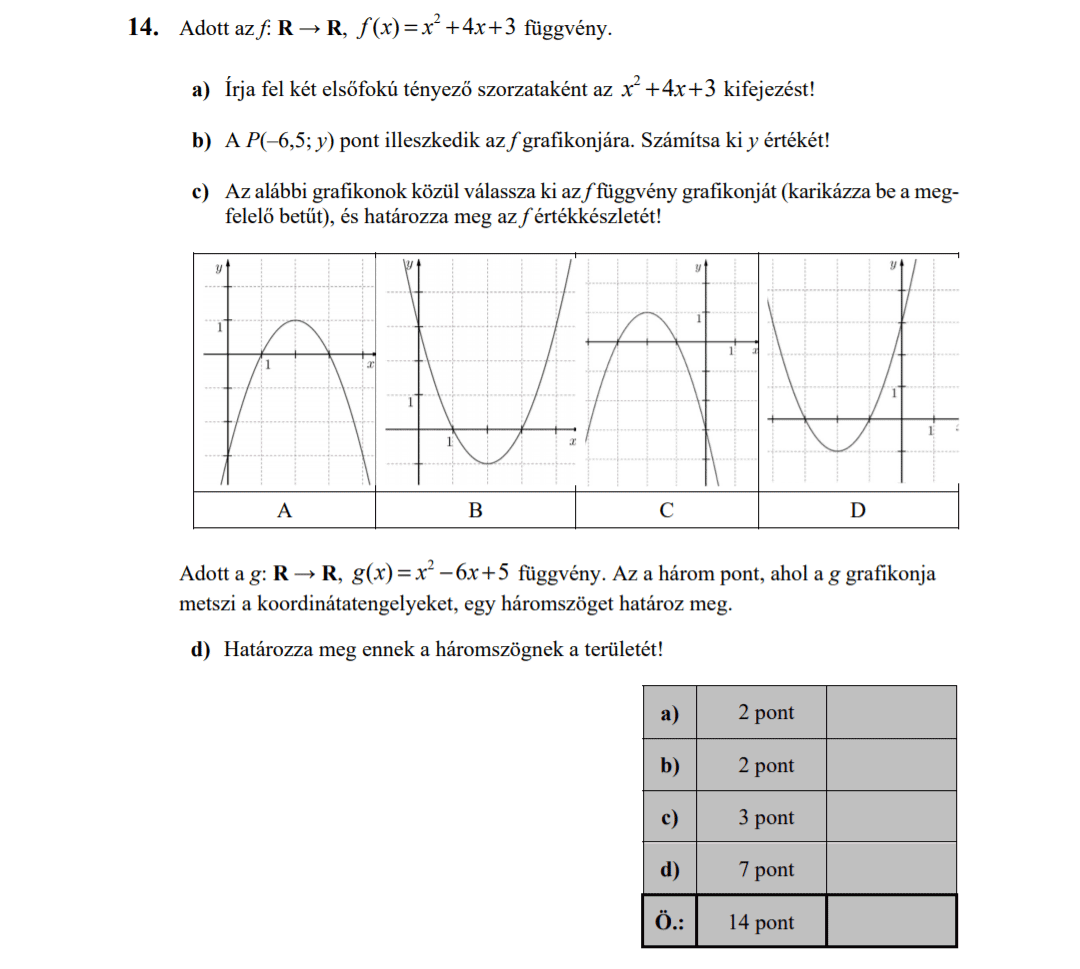




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



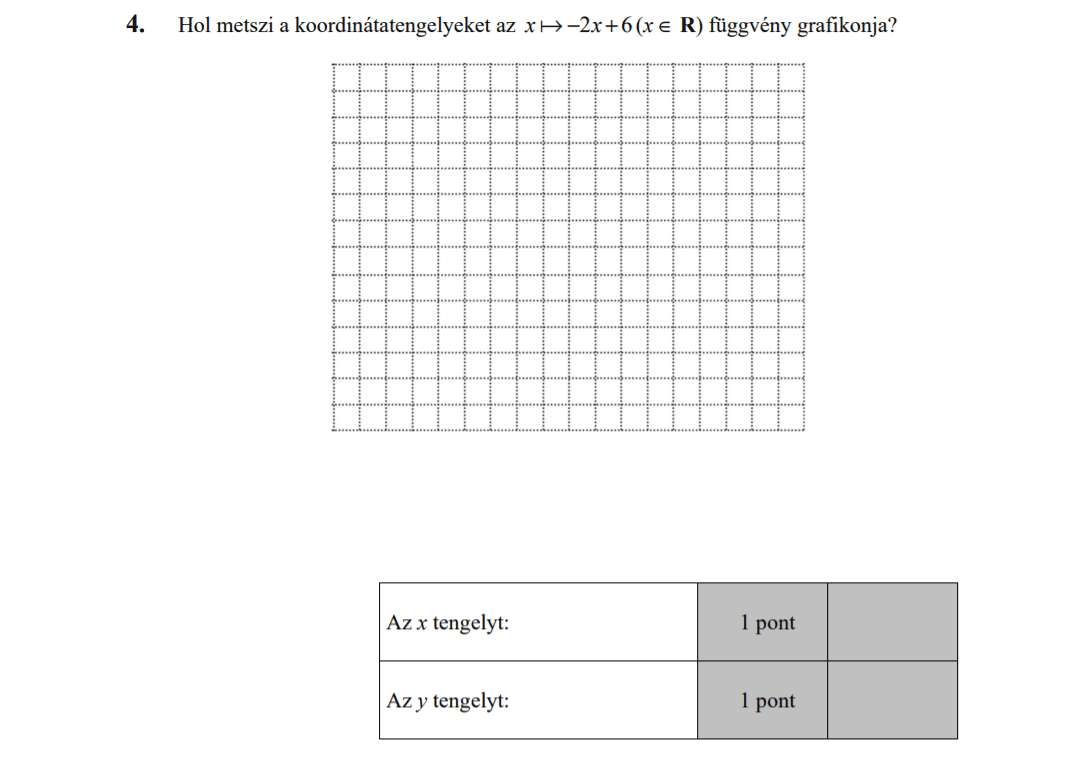







MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ

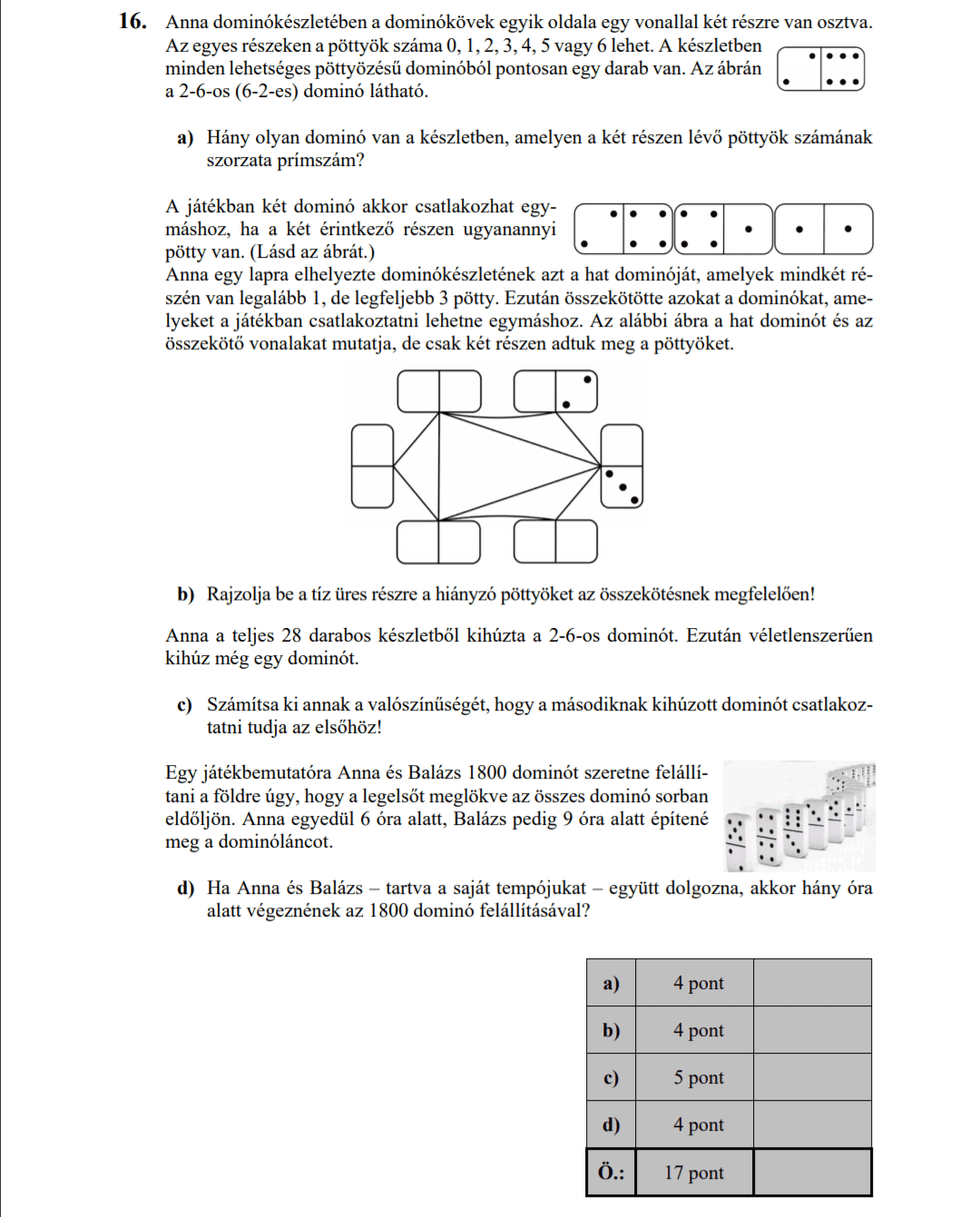


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




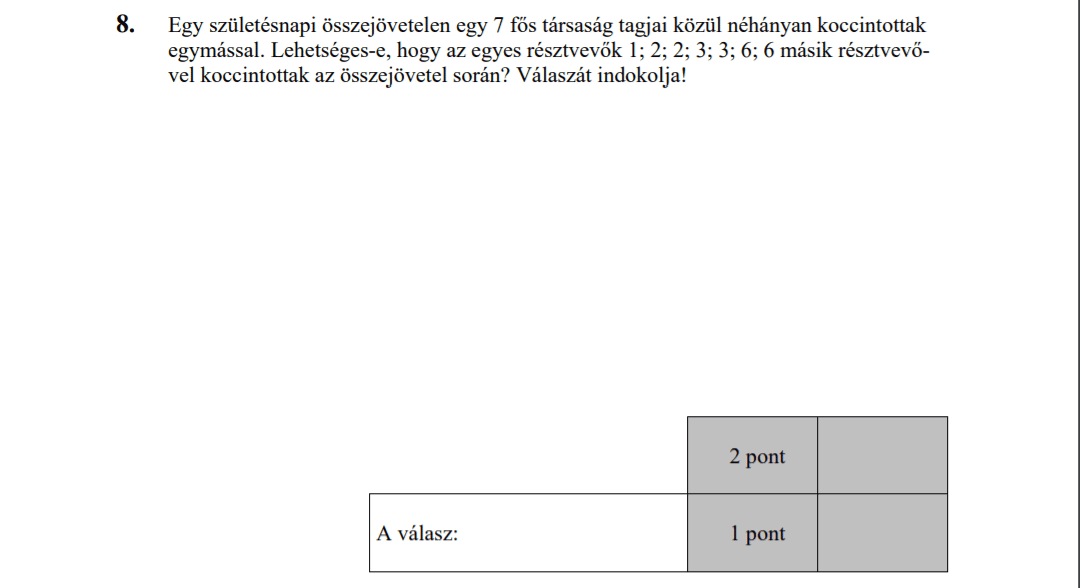



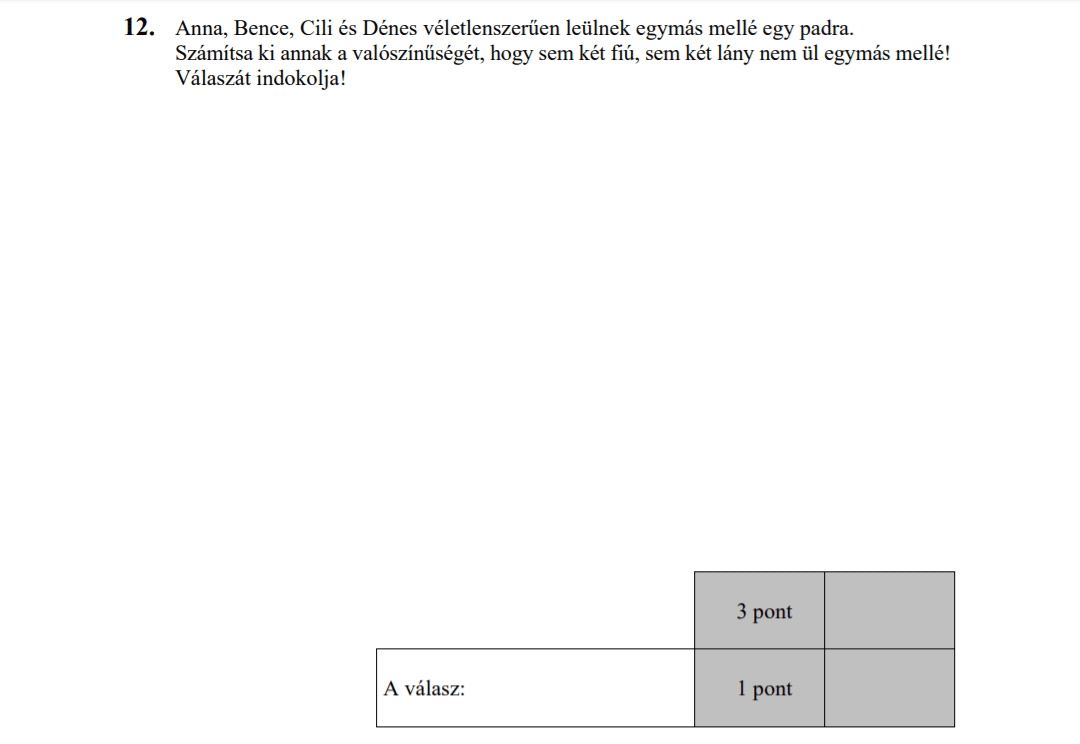
MÁSODIK RÉSZ

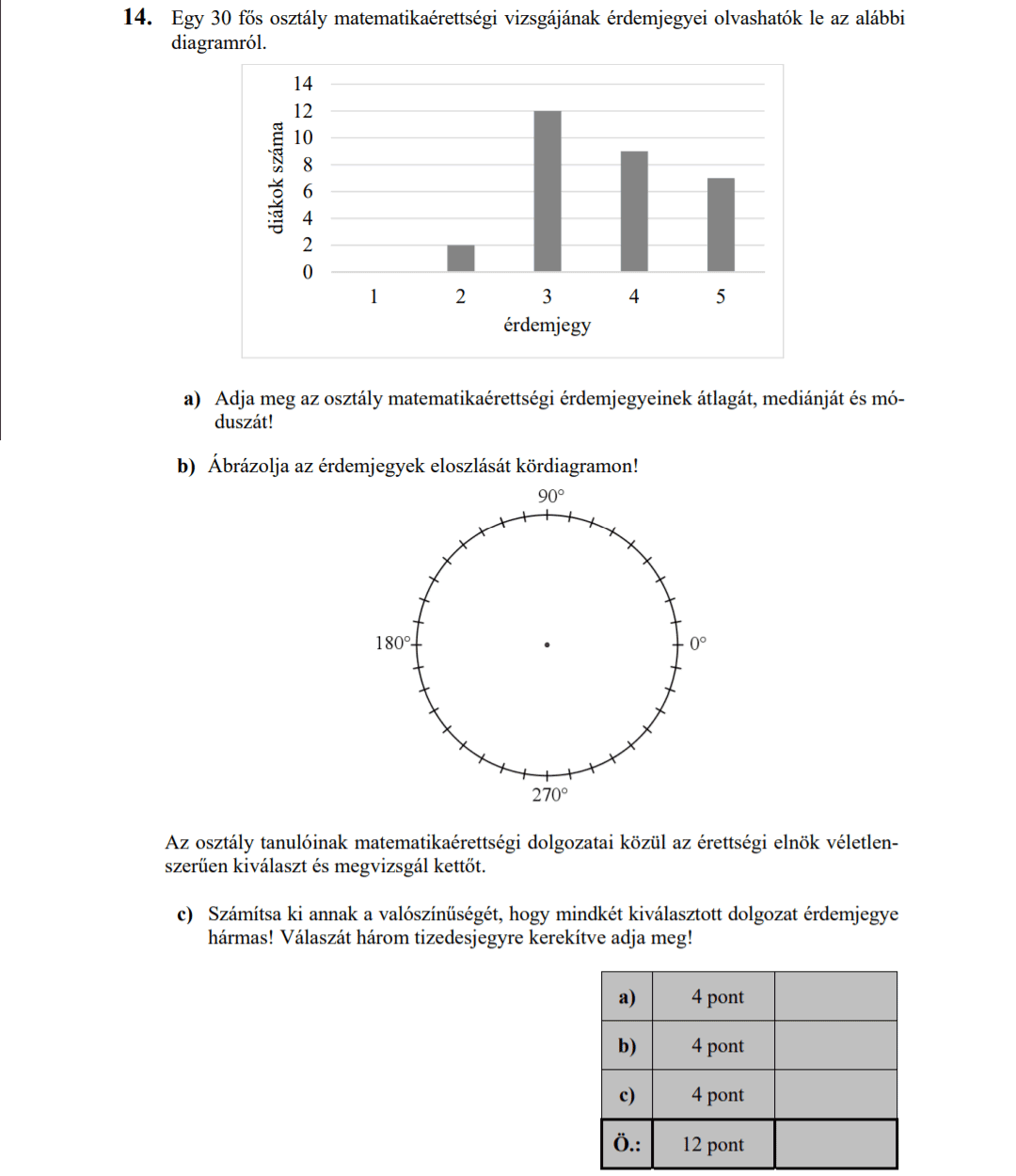
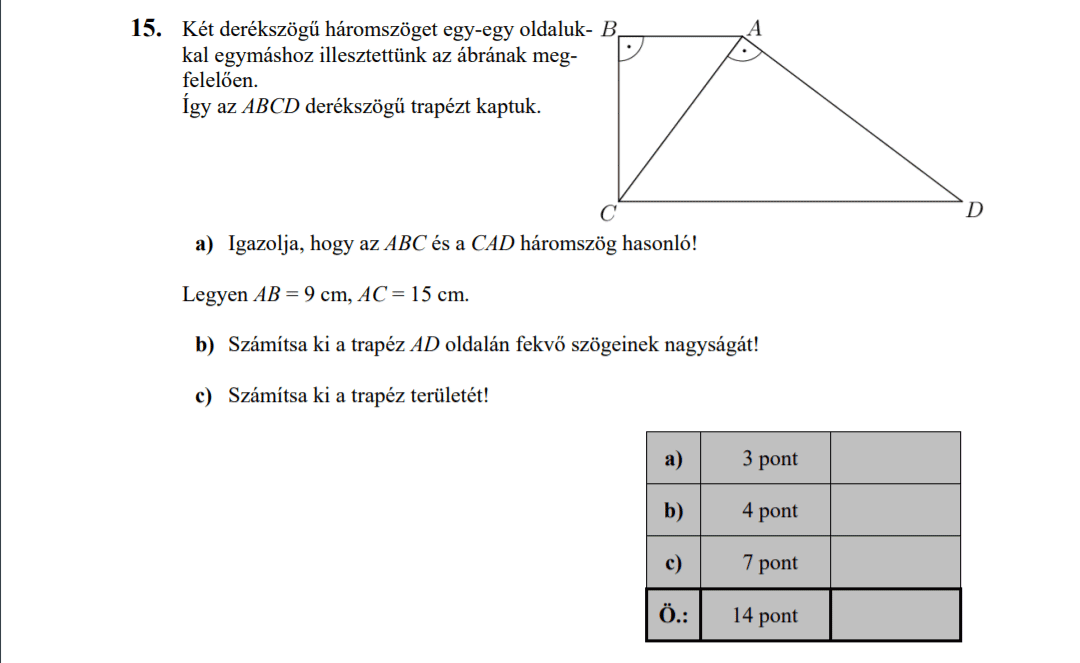



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


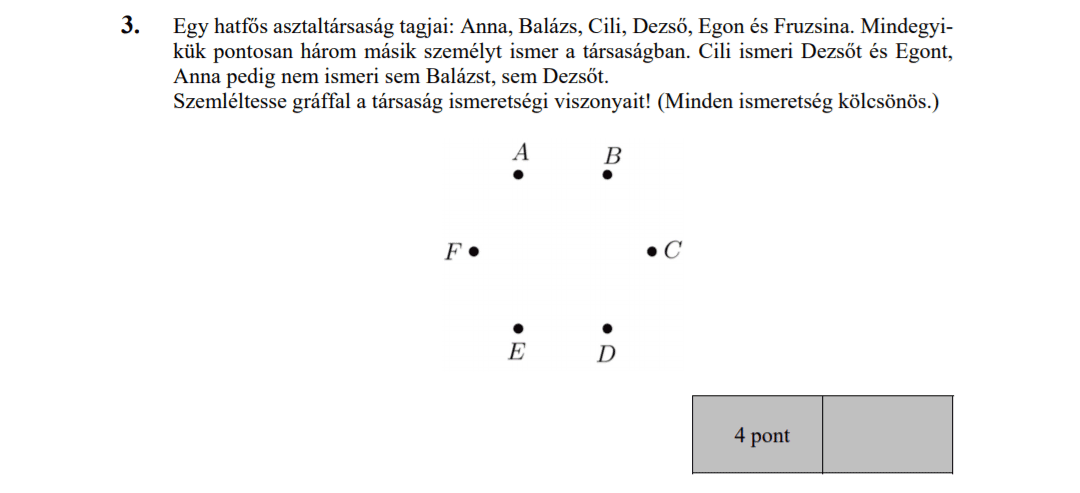


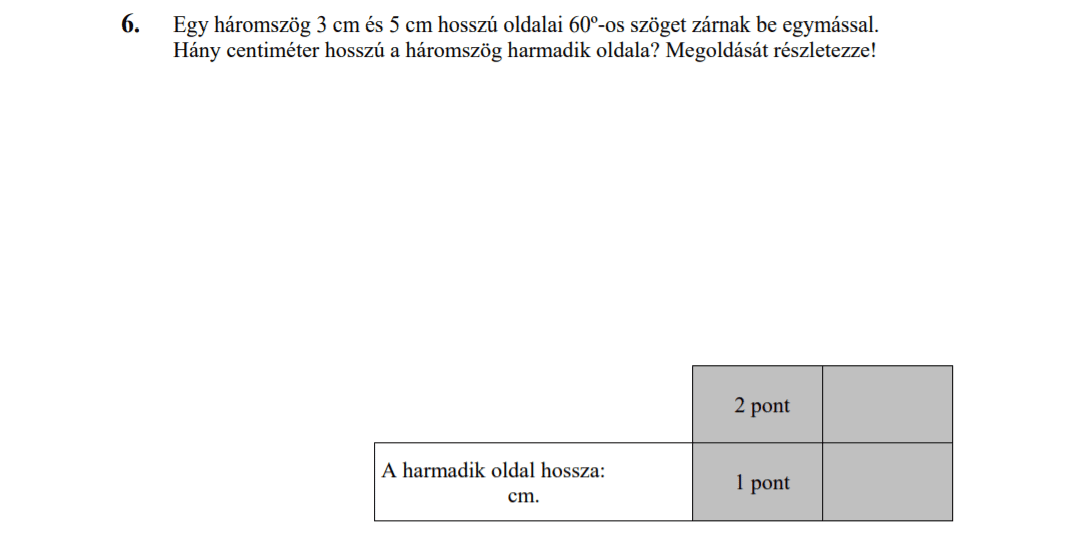

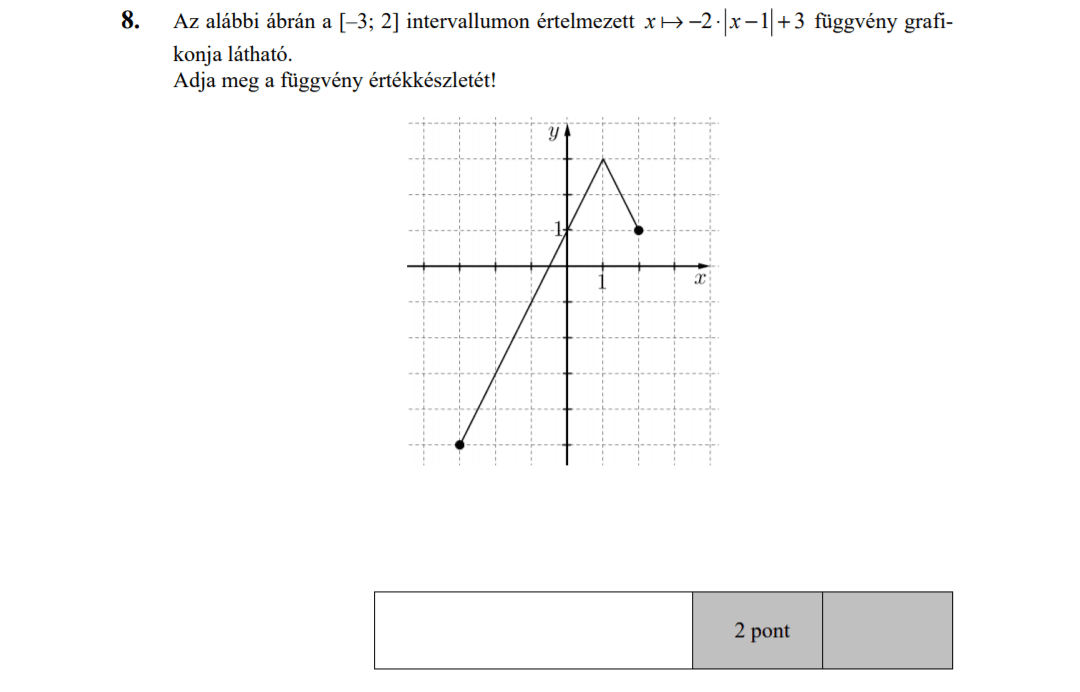

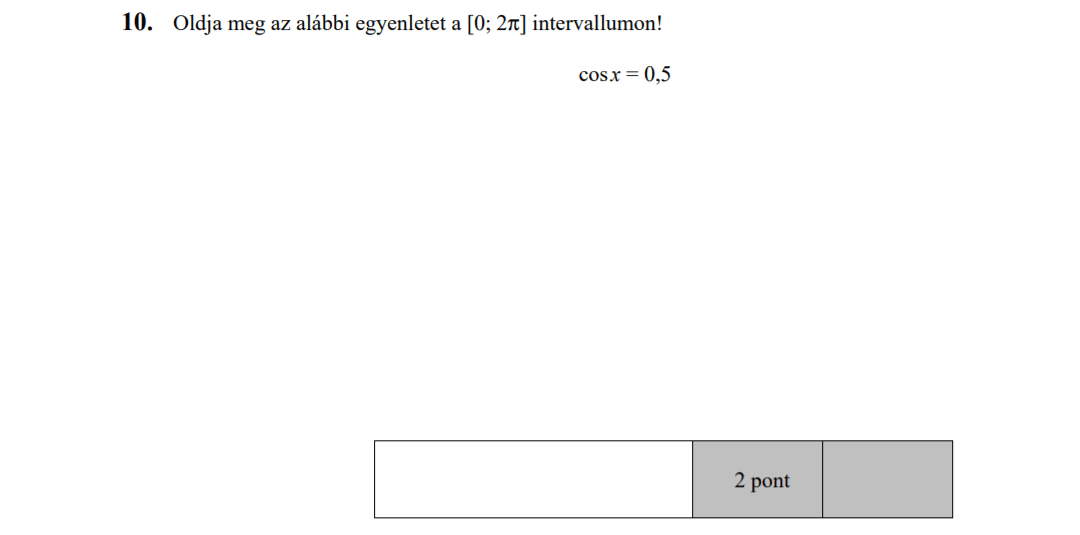

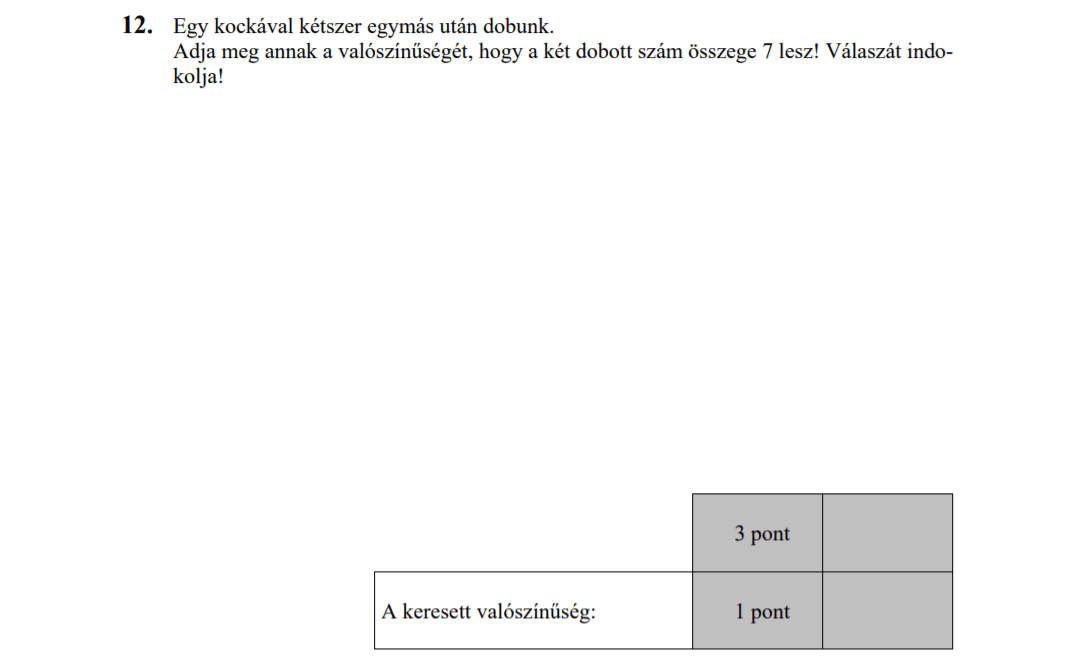
MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
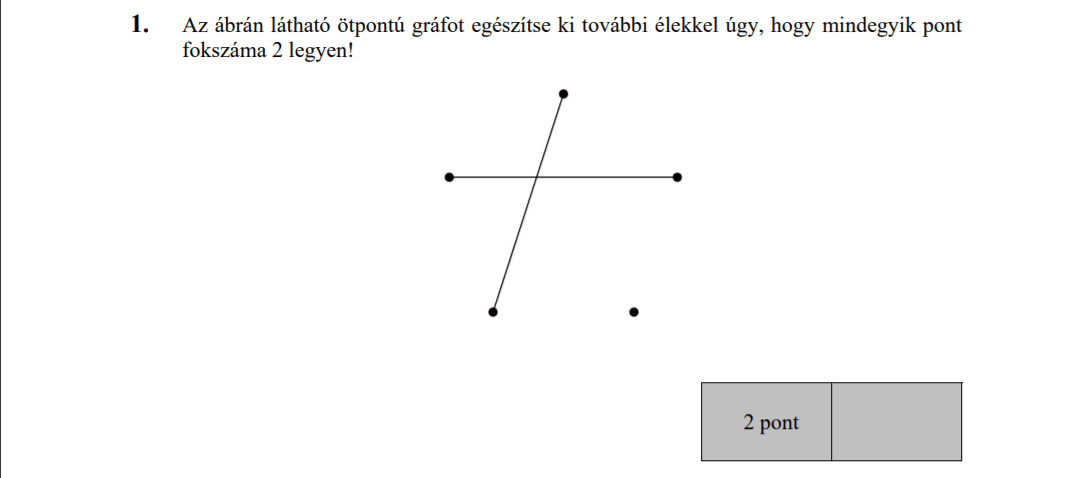
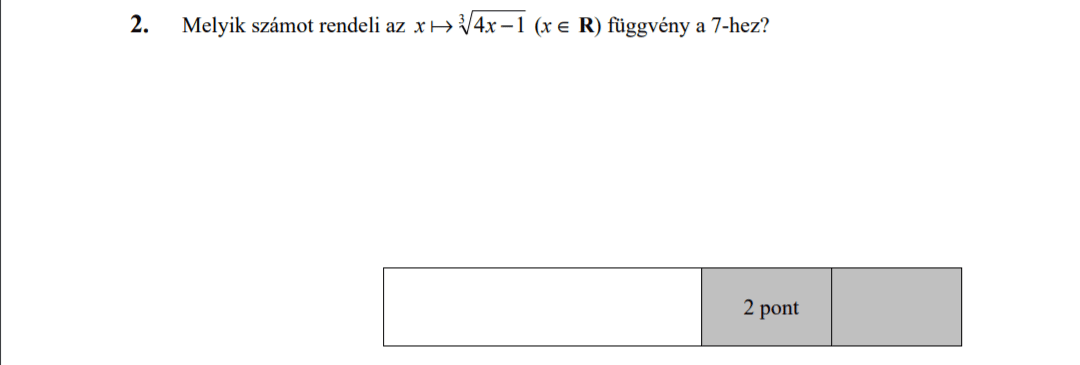
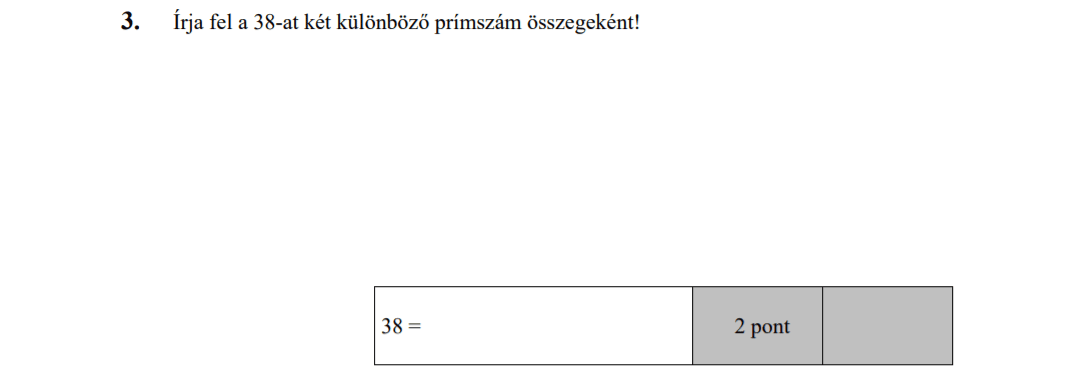


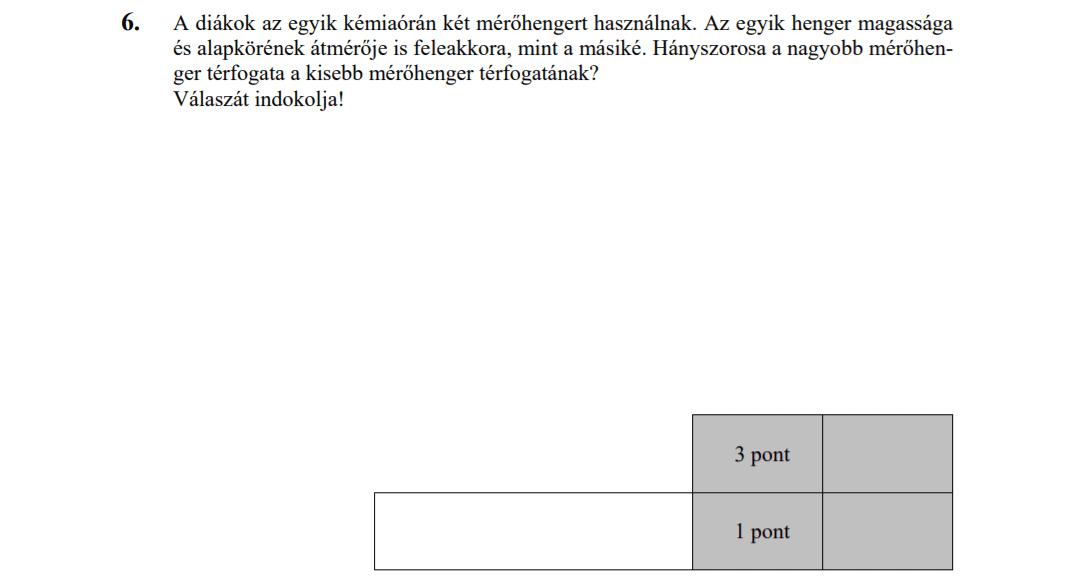
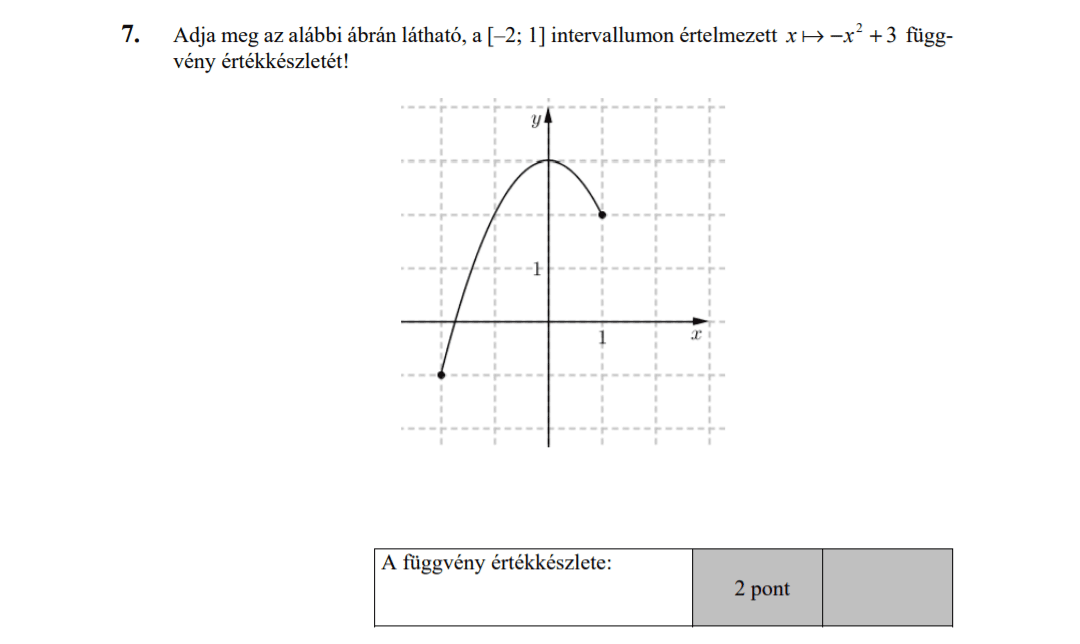

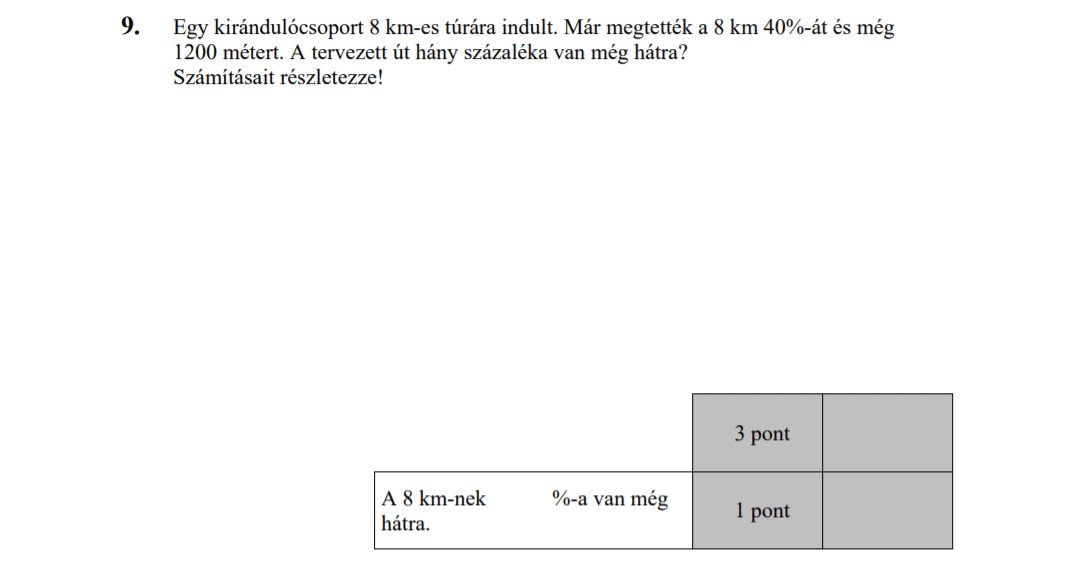
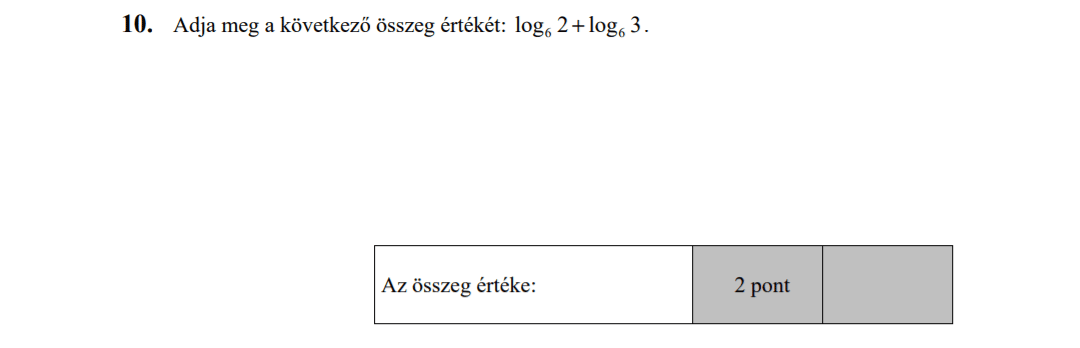

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






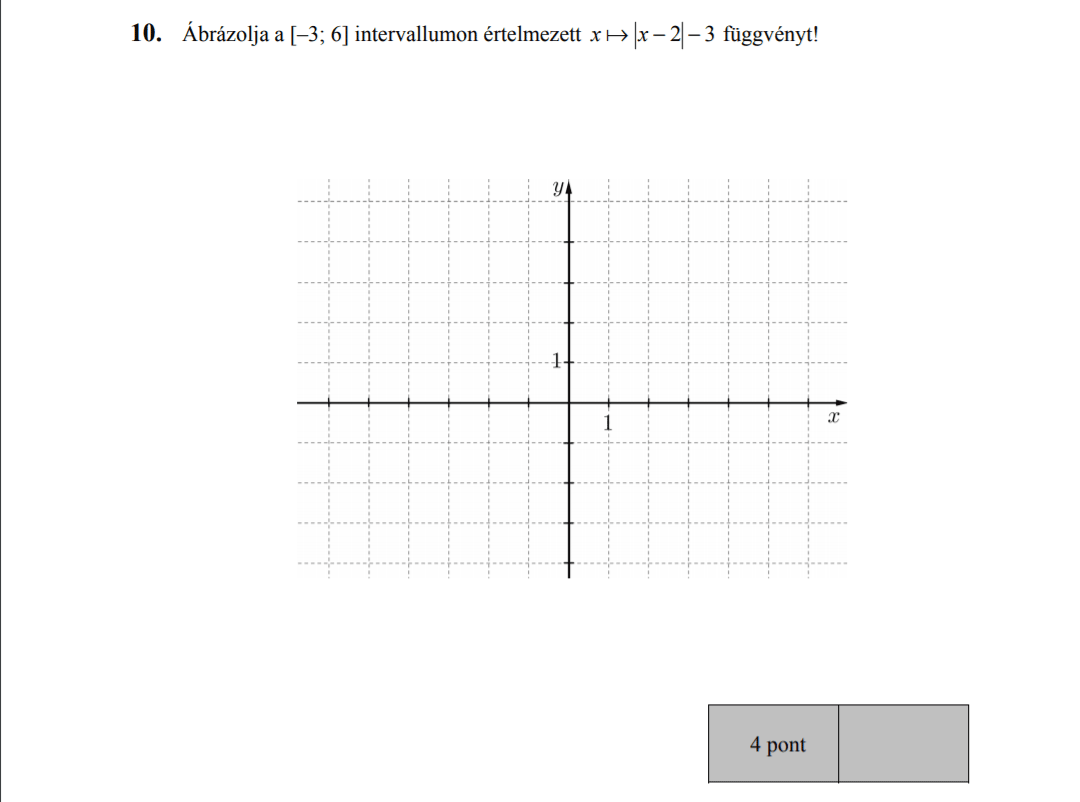

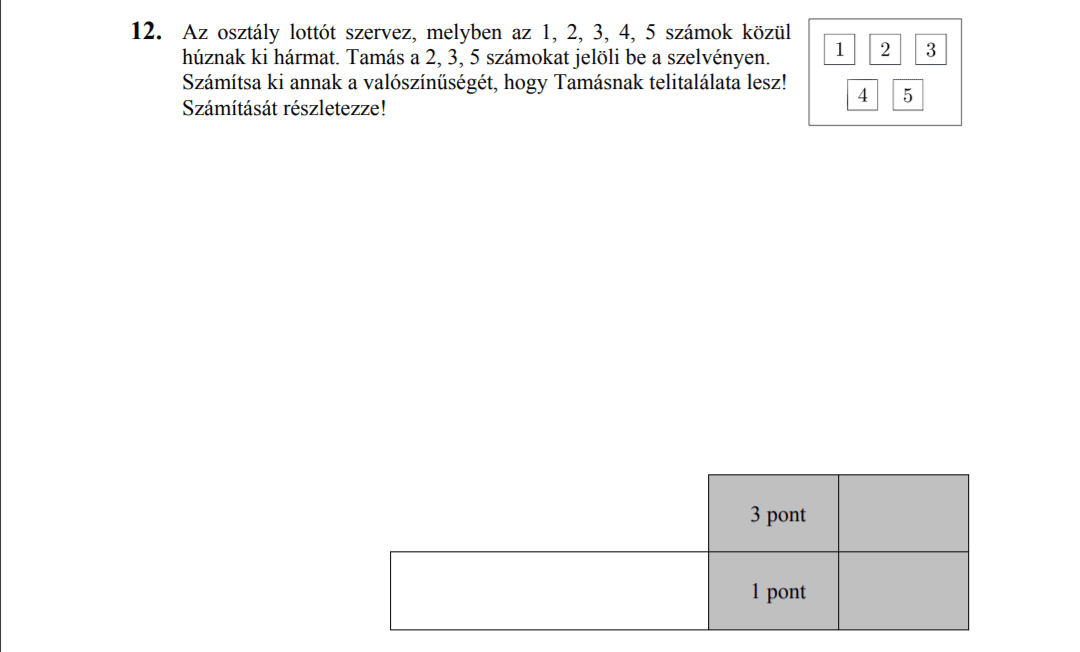
MÁSODIK RÉSZ

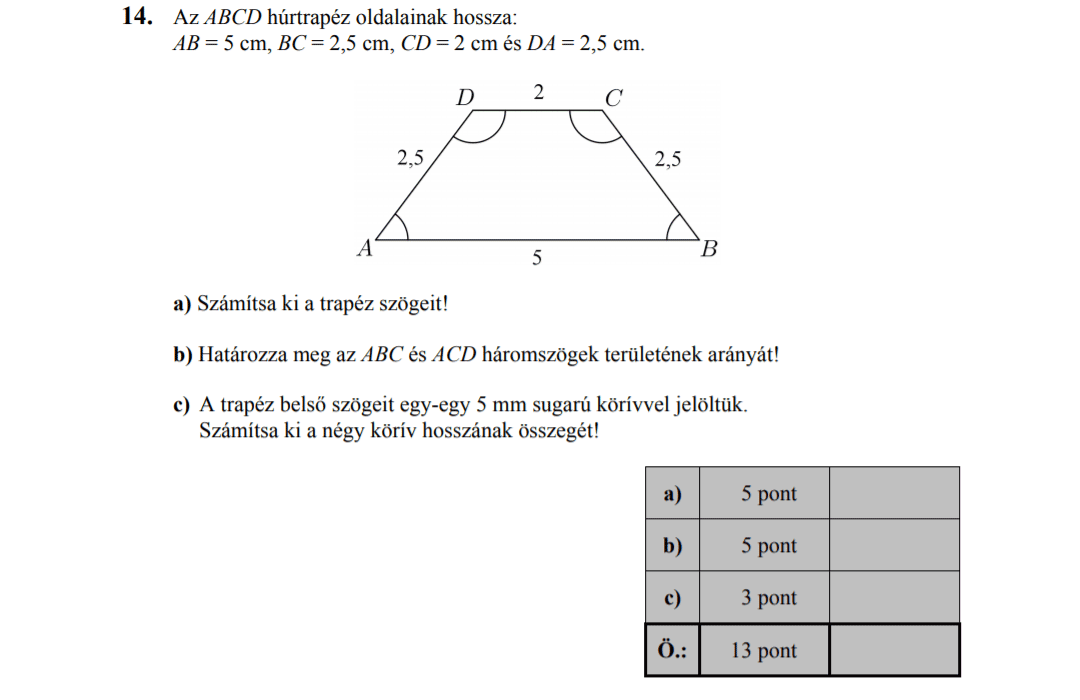

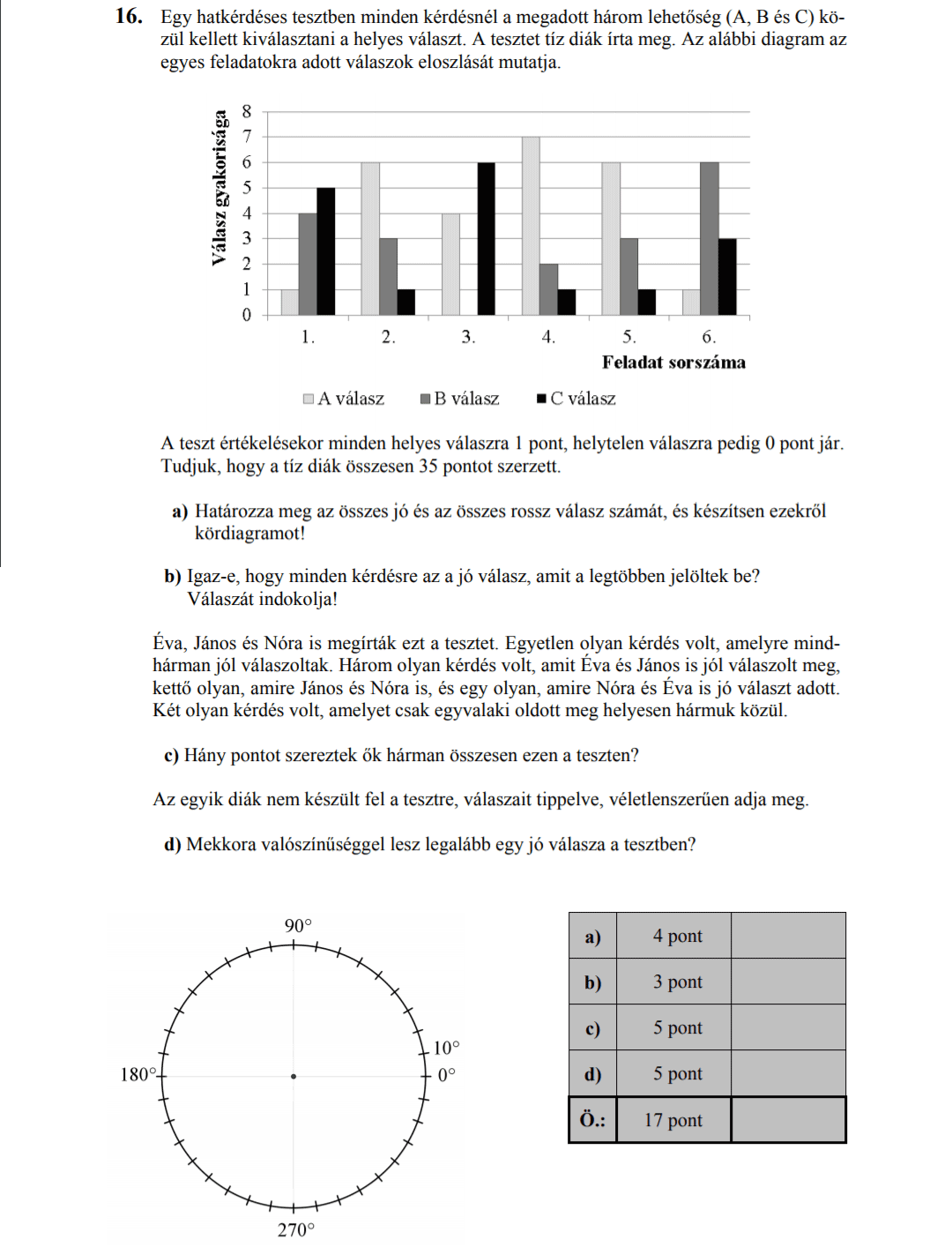


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

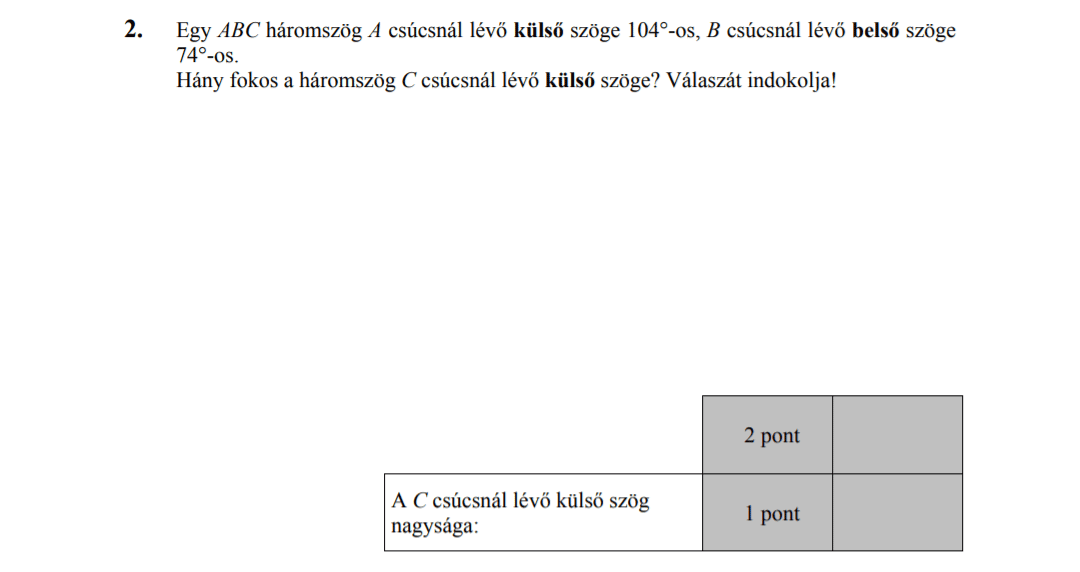





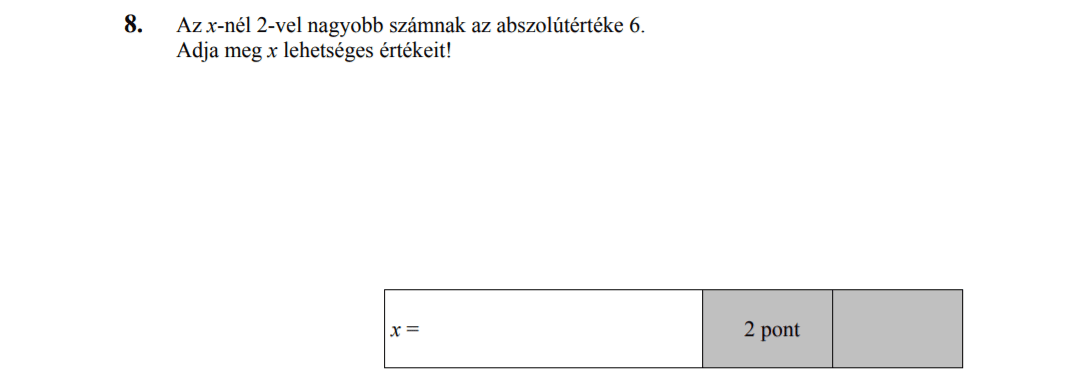

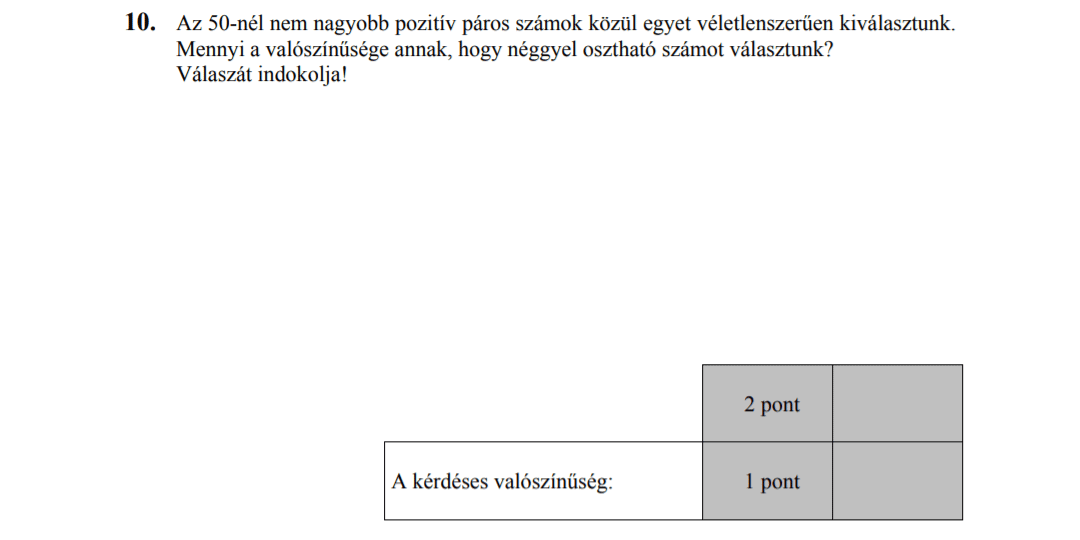


MÁSODIK RÉSZ

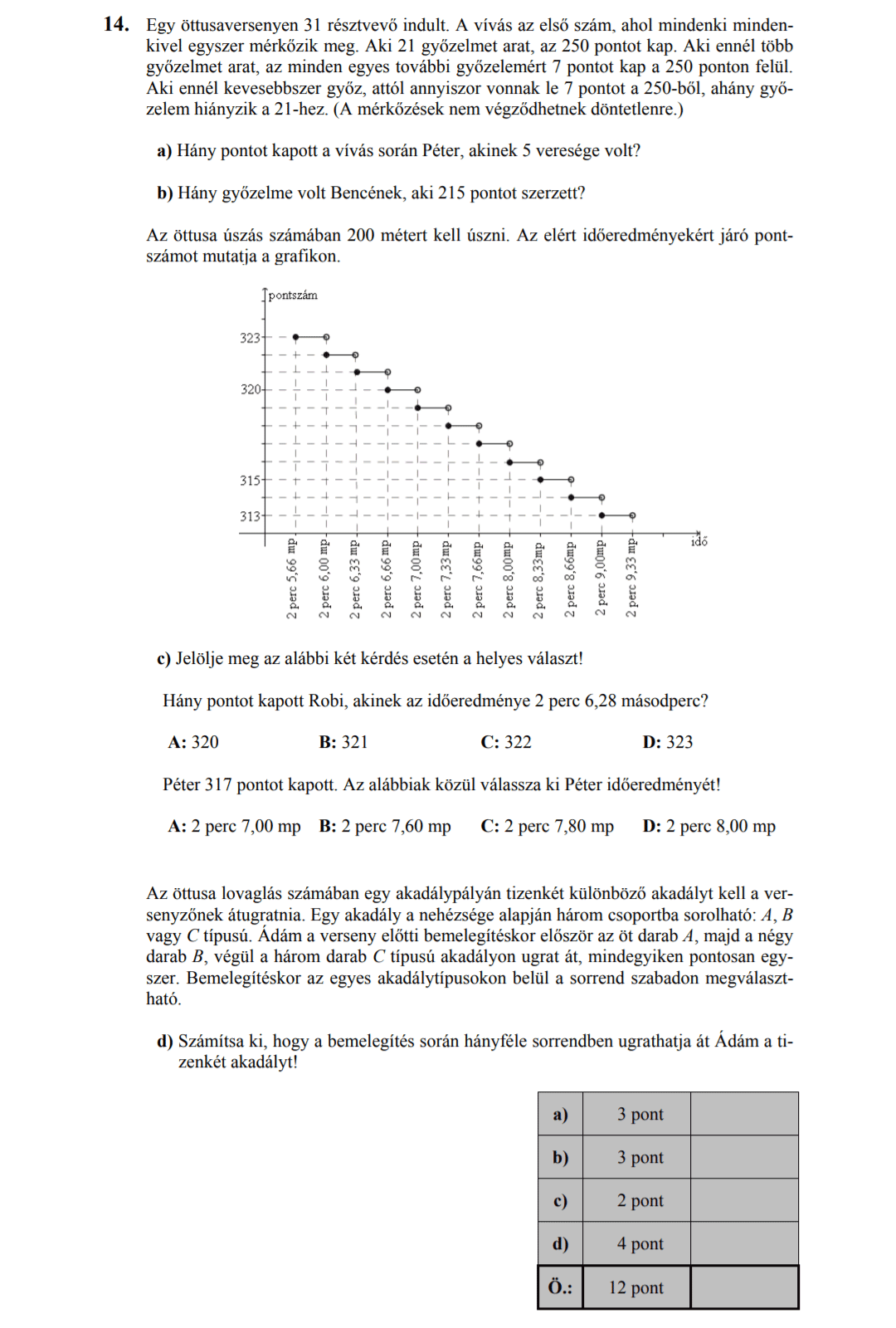
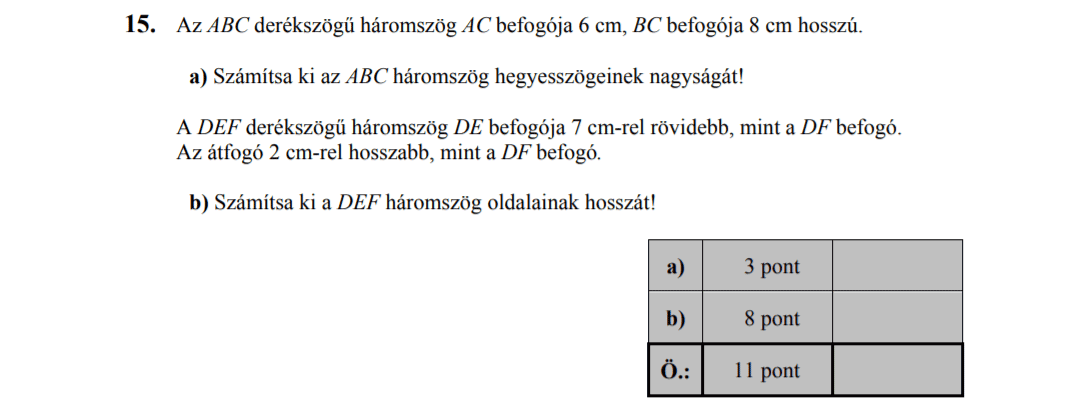



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

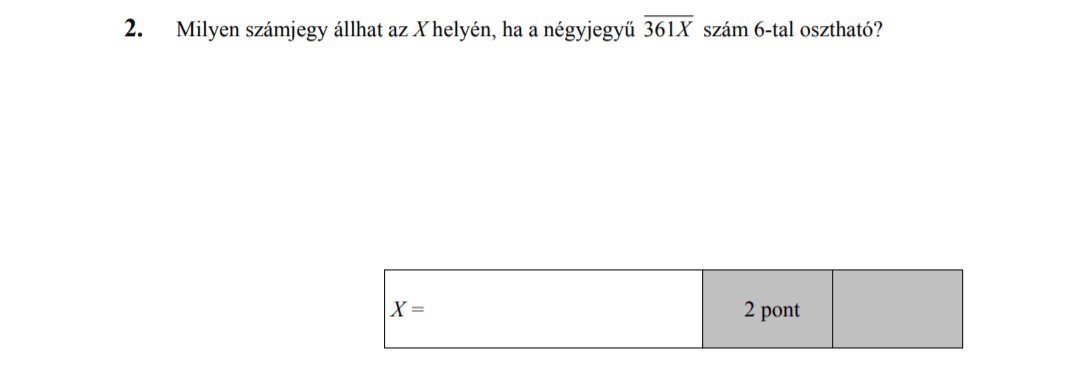



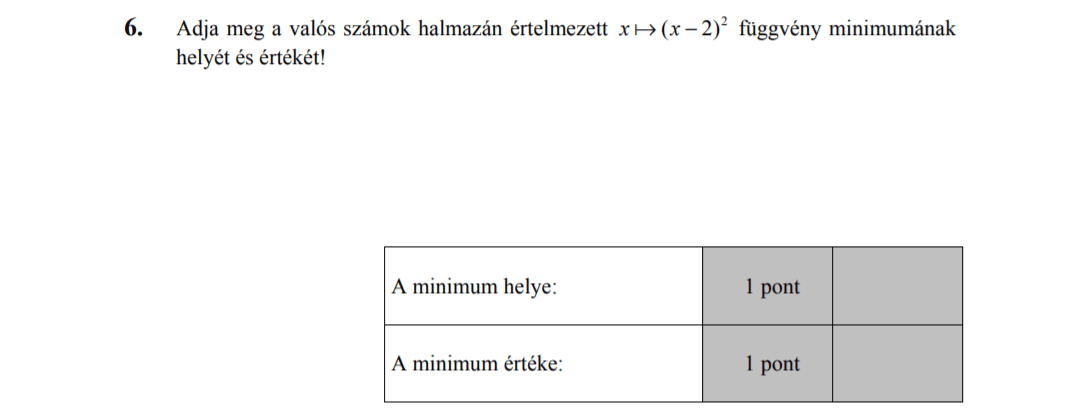

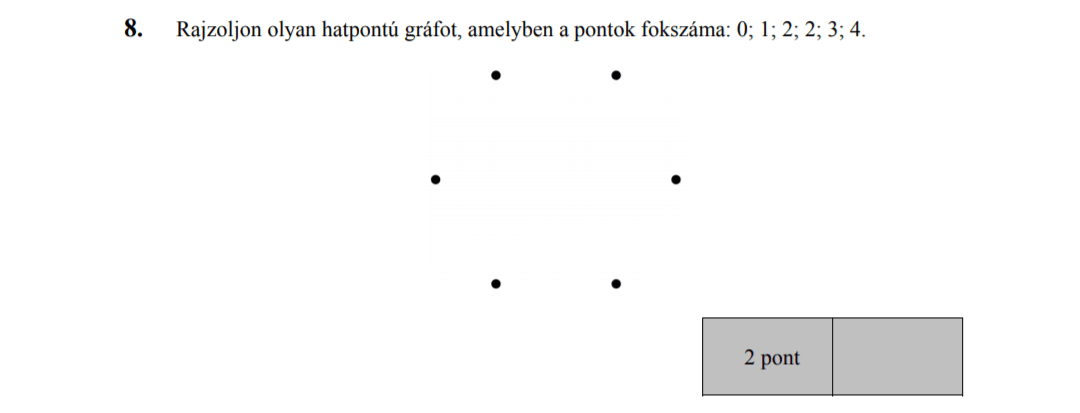


MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ




- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


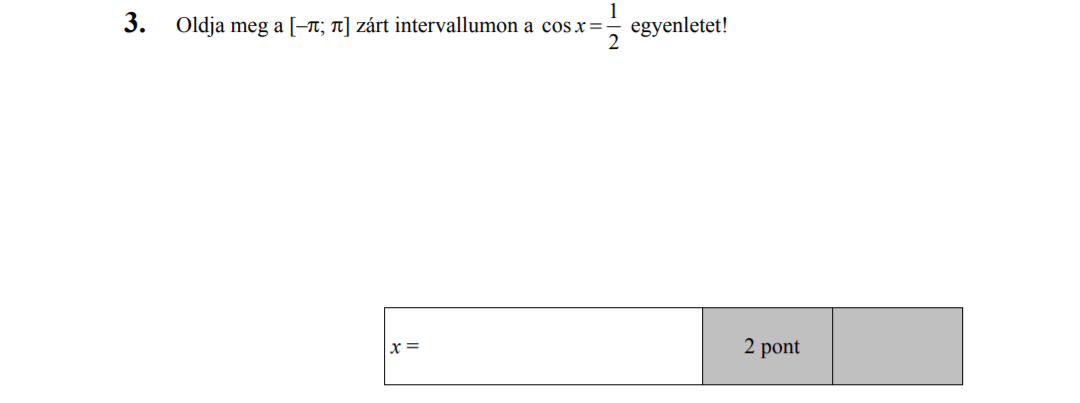


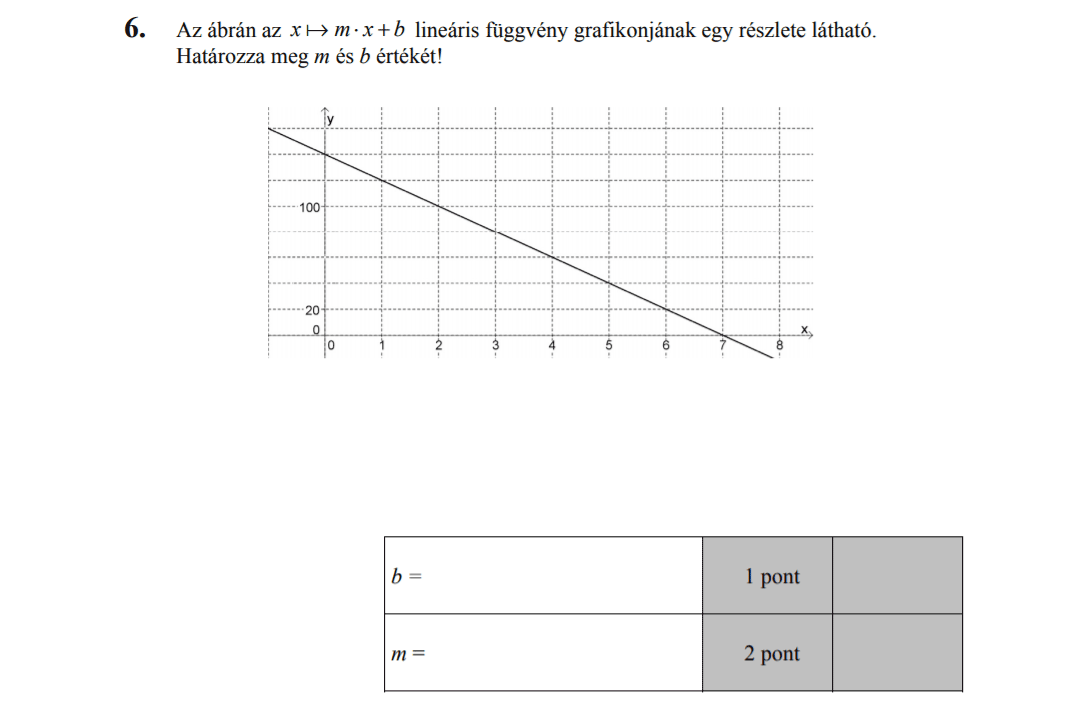



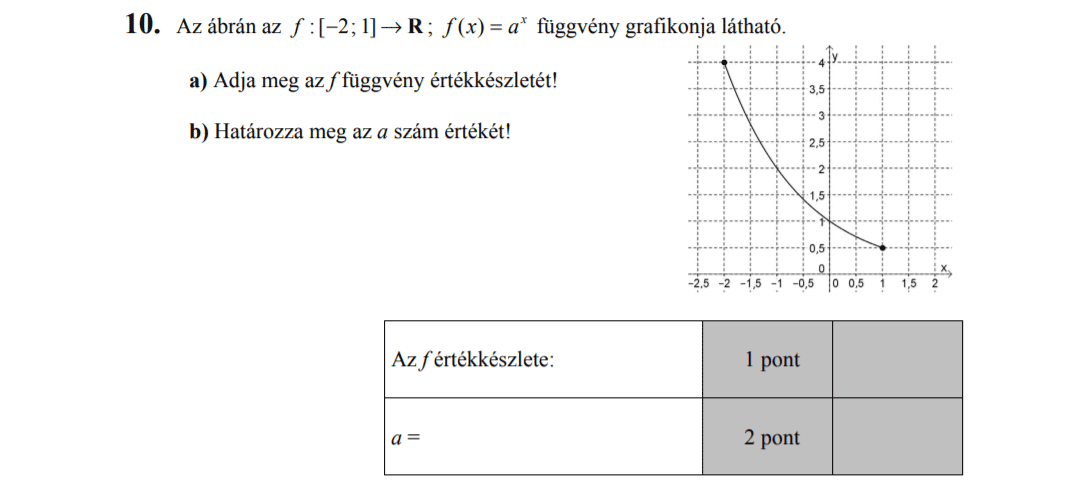

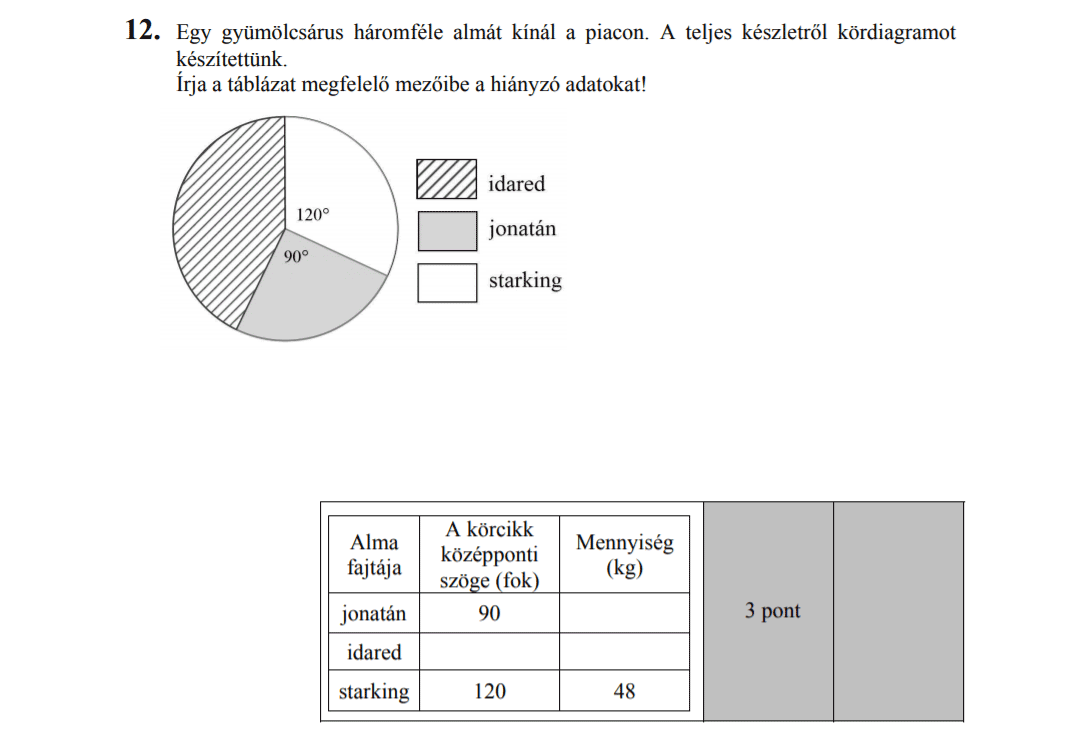
MÁSODIK RÉSZ





- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Oszthatóság
Az $a$ egész számnak a $b$ egész szám osztója, ha létezik olyan $q$ egész szám, hogy $a=b \cdot q$.
Maradékos osztás
Legyenek $a$ és $b$ természetes számok. Ekkor felírhatók
$a=q \cdot b + r \qquad 0<r<b$
Ahol $q$ és $r$ is természetes számok és $q$ az osztás hányadosa, $r$ pedig a maradék.
2-vel oszthatóság
Egy szám akkor osztható 2-vel, ha páros, azaz 0, 2, 4, 6, vagy 8-ra végződik.
3-mal oszthatóság
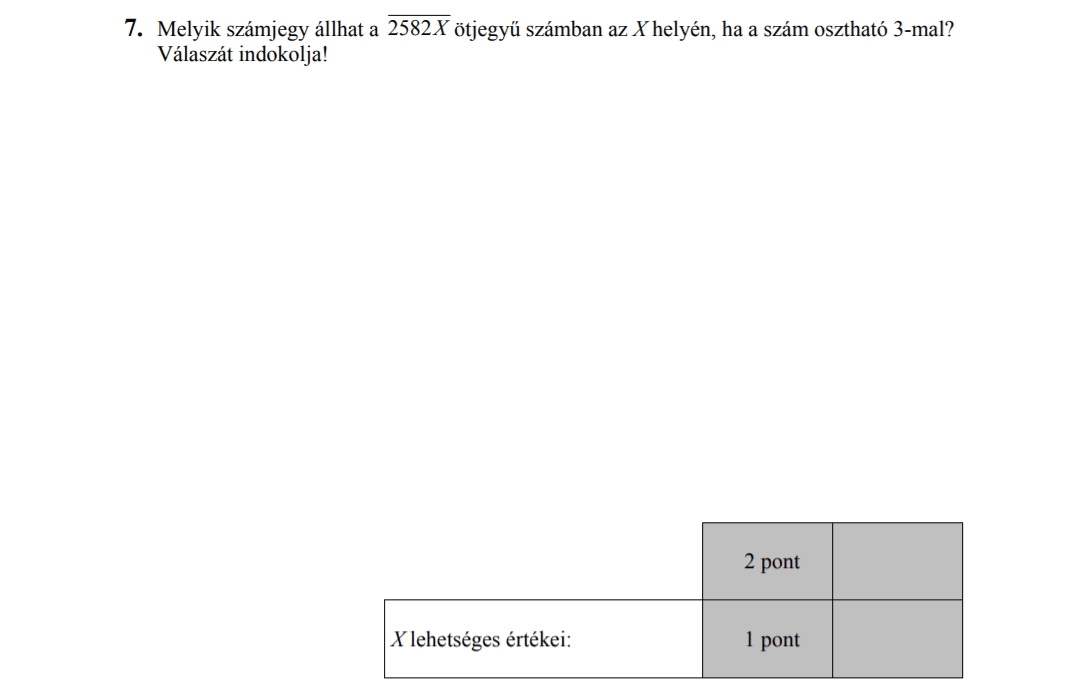
Egy szám akkor osztható 3-mal, ha a számjegyeinek összege osztható 3-mal.
4-gyel oszthatóság
Egy szám akkor osztható 4-gyel, ha az utolsó két jegyéből alkottot szám osztható 4-gyel.
5-tel oszthatóság
Egy szám akkor osztható 5-tel, ha az utolsó számjegye 0 vagy 5.
6-tal oszthatóság
6-tal azok a számok oszthatók, amik 2-vel és 3-mal is oszthatók.
Ezek éppen a 3-mal osztható páros számok.
9-cel oszthatóság
Egy szám akkor osztható 9-cel, ha a számjegyeinek összege osztható 9-cel.
10-zel oszthatóság
10-zel azok a számok oszthatók, amik 0-ra végződnek.
11-gyel oszthatóság
11-gyel akkor osztható egy szám, ha hátulról kezdve $+-+- \dots$ előjelekkel összeadjuk a számjegyeket, akkor az így kapott szám osztható 11-gyel.
Legnagyobb közös osztó
Az $a$ és $b$ szám legnagyobb közös osztója az a $d$ pozitív szám, amire $ d \mid a$ és $d\mid b$, és e közös osztók közül ez a legnagyobb.
Jelölés: $d=(a,b)$
Néhány oszthatósági szabály
Ha $ a \mid c$ és $ b \mid c$ és $(a,b)=1$ akkor $ab \mid c$
Ha $c \mid ab$ és $(a,c)=1$ akkor $c \mid b$
Prímek
Azokat az 1-től különböző pozitív egész számokat, amelyeknek az 1-en és önmagukon kívül nincsen más pozitív egész osztója, prímeknek nevezzük.
Szemléletesen a prímek az egész számok építőkockái. Vagyis a prímek segítségével tudjuk felépíteni az egész számokat. A 60 például így épül föl, hogy:
$ 60 = 2 \cdot 2 \cdot 3 \cdot 5 $
Itt a 2, a 3 és az 5 is prím, mert ezek már nem bonthatók kisebb építőkockákra. Az 1-et pedig azért nem tekintjük prímnek, mert a számok felépítésében nem sok hasznát vesszük, hiszen $ 1 \cdot 1 \cdot 1 \cdot 1 = 1 $
A legkisebb prím tehát a 2, és ez az egyetlen páros szám amelyik prím, hiszen az összes többi páros szám már osztható 2-vel. A 2 után következő prím a 3, aztán az 5, és a 7. A prímeket egy speciális módszerrel nagyon könnyű kiválogatni az egész számok közül. Ezt a módszert úgy hívják, hogy Eratoszthenész szitája és meg tudod nézni itt a kapcsolódó epizódban.
Számelmélet alaptétele
A nullától és az egytől különböző összes $n$ pozitív egész szám felbontható prímek szorzatára a sorrendtől eltekintve egyértelműen.
$ n = p_1^{\alpha_1} \cdot p_2^{\alpha_2} \cdot \dots \cdot p_k^{\alpha_k}$ ahol $k\in Z^{+}$
Itt $k$ a felbontásban szereplő különböző prímek száma.
Legkisebb közös többszörös (LKKT)
A legkisebb közös többszörös megtalálásának lépései:
- Elkészítjük a prímtényezős felbontást
- Vesszük az összes prímet a két prímtényezős felbontásból
- Mindegyik prím a nagyobbik kitevőt kapja.
a) Osztható-e 3-mal az 5728 és a 4758?
b) Osztható-e 4-gyel az 52742 és a 61524?
c) Osztható-e 6-tal a 3714?
d) Osztható-e 9-cel a 4326 és a 4257?
e) Osztható-e 11-gyel a 3718
a) Számoljuk ki a 108 és a 360 legnagyobb közös osztóját.
b) Számoljuk ki a 37 800 és 39 600 számok legnagyobb közös osztóját.
a) Számoljuk ki a 108 és 360 legkisebb közös többszörösét.
b) Számoljuk ki a 37 800 és a 39 600 számok legkisebb közös többszörösét.
