- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
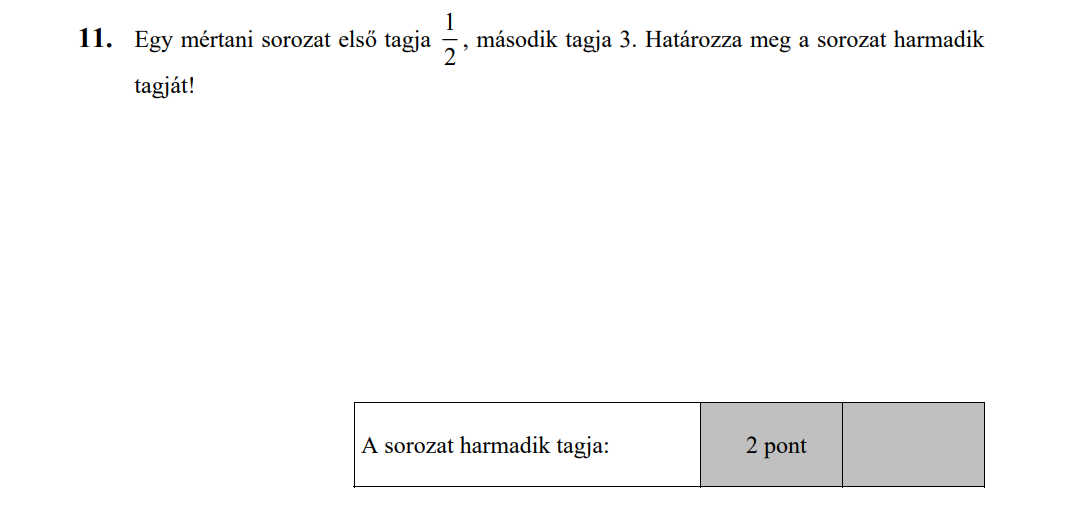
- Számtani és mértani sorozatok (16 pont)
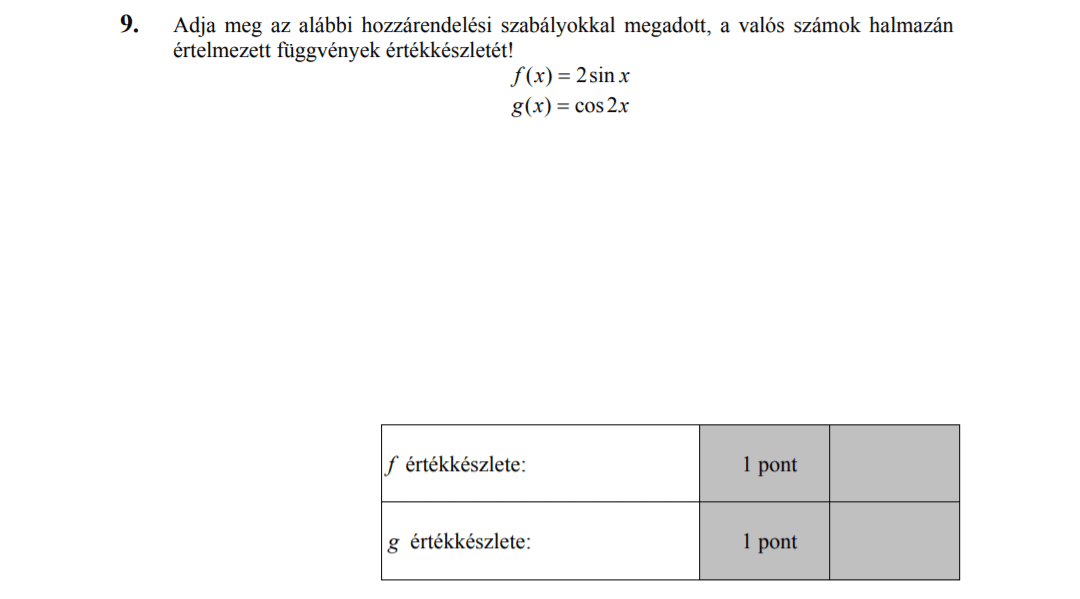
- Függvényekkel kapcsolatos feladatok (9,8 pont)
- Térgeometria (9,8 pont)
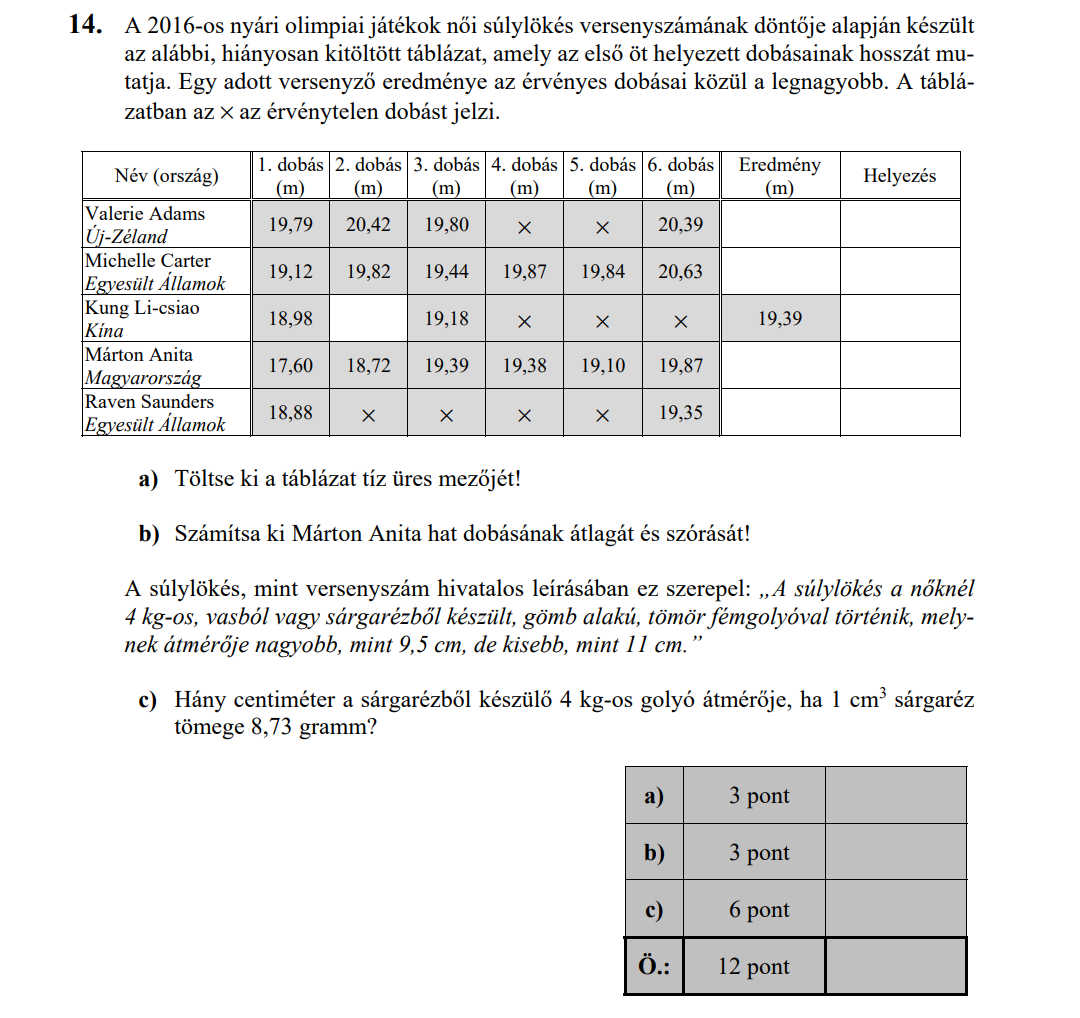
- Statisztika (9,3 pont)
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
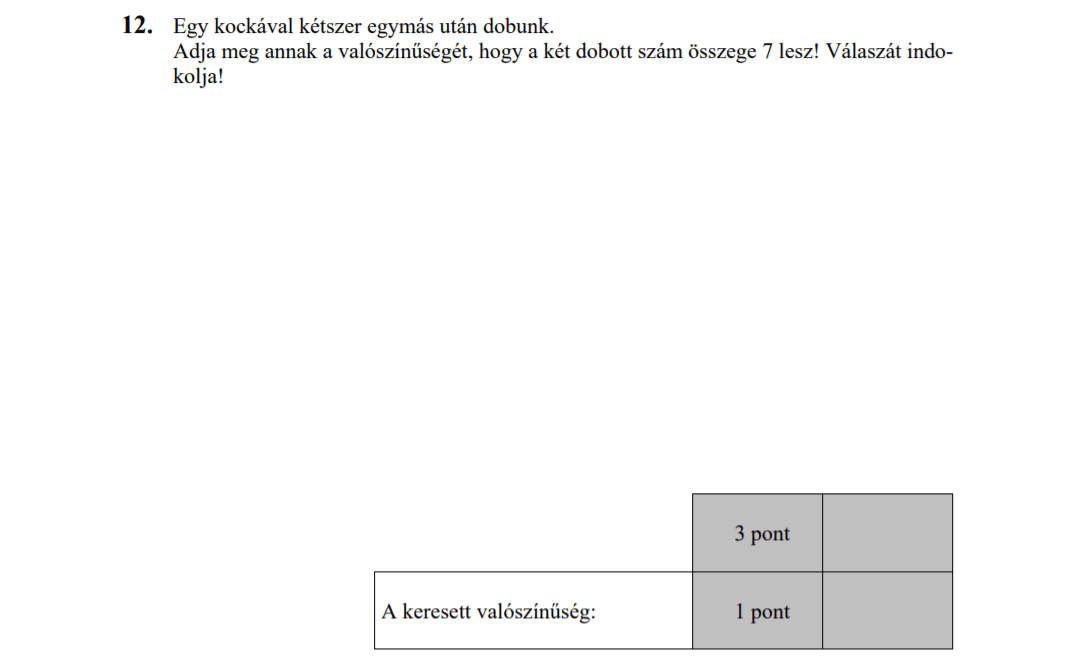
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
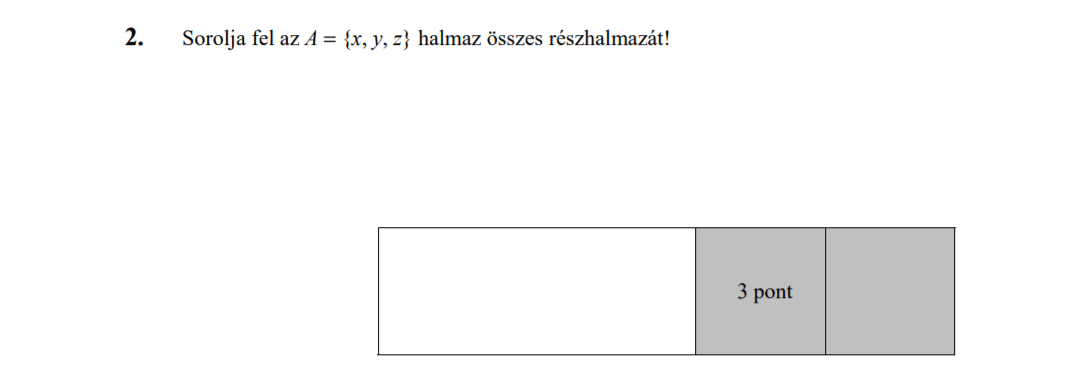
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
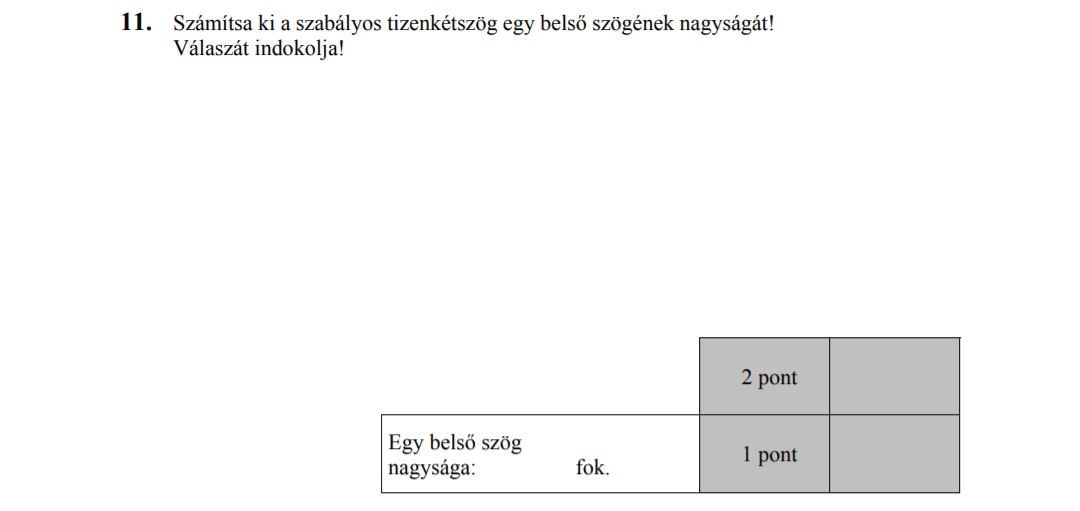
- Síkgeometria (4,5 pont)
- Százalékszámítás (3,8 pont)
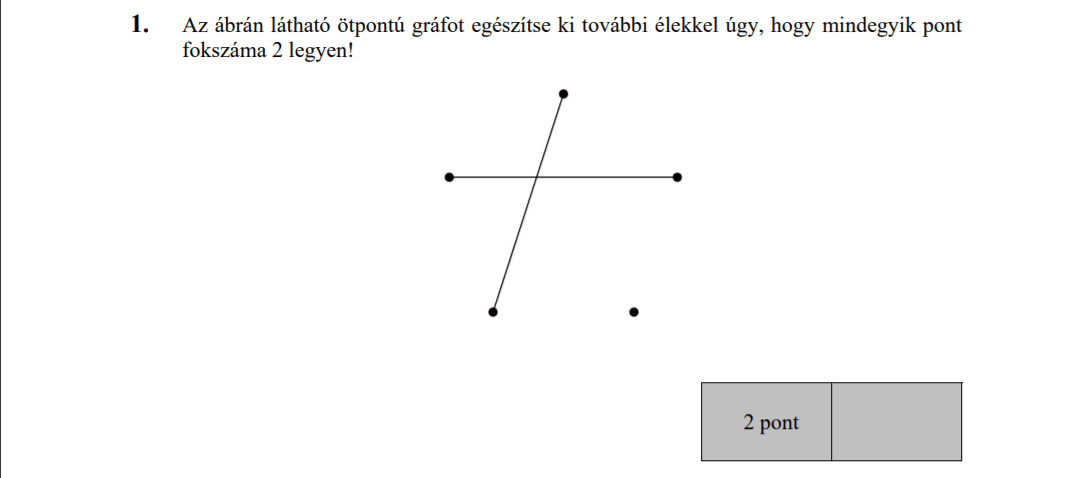
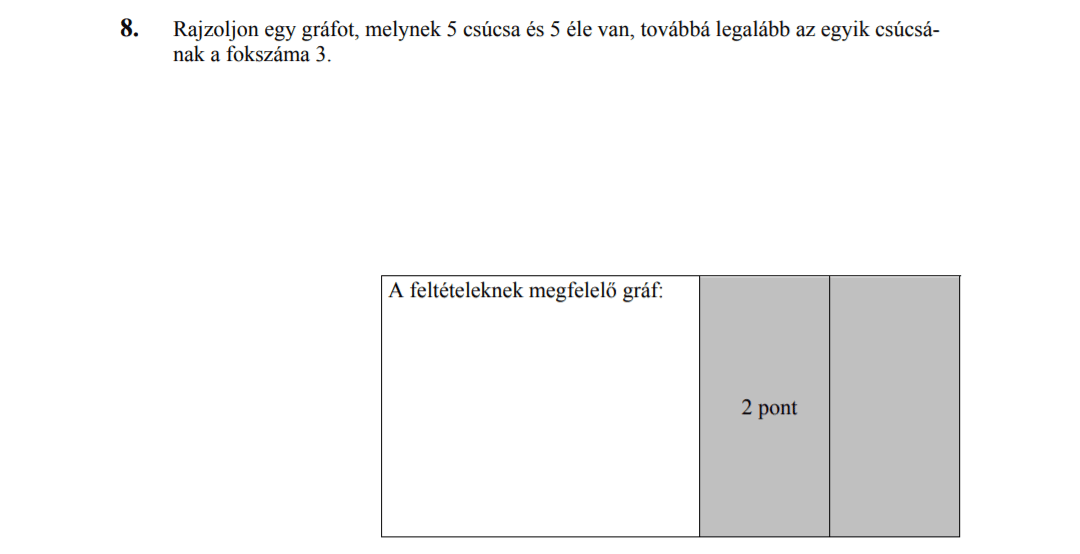
- Gráfok (3 pont)
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
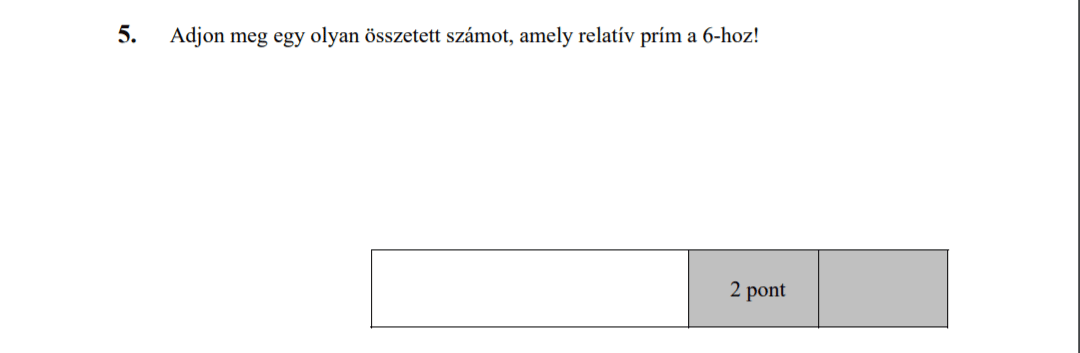
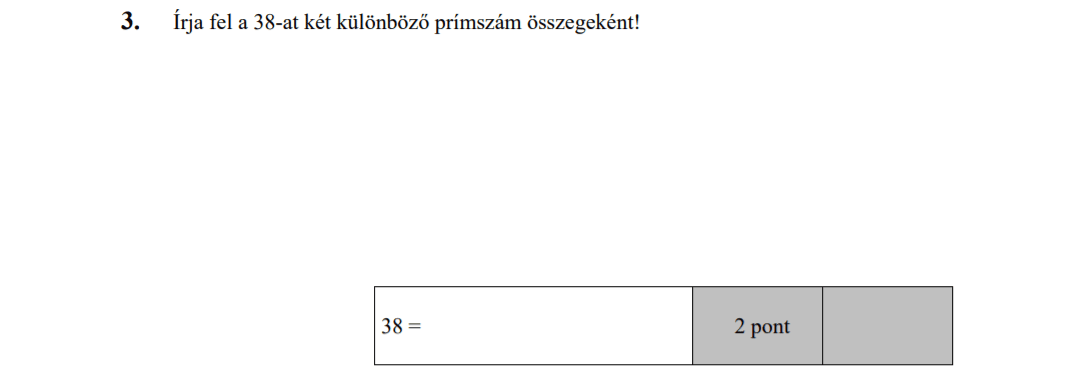
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Másodfokú egyenletek (3 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


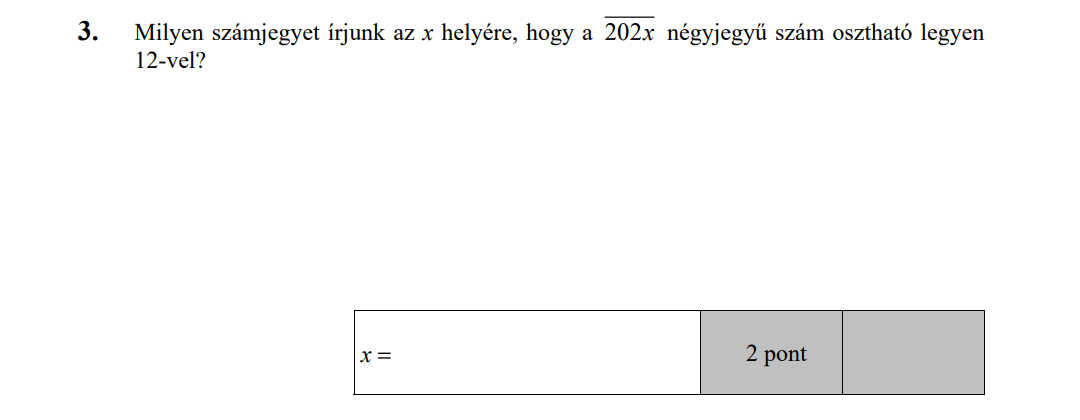
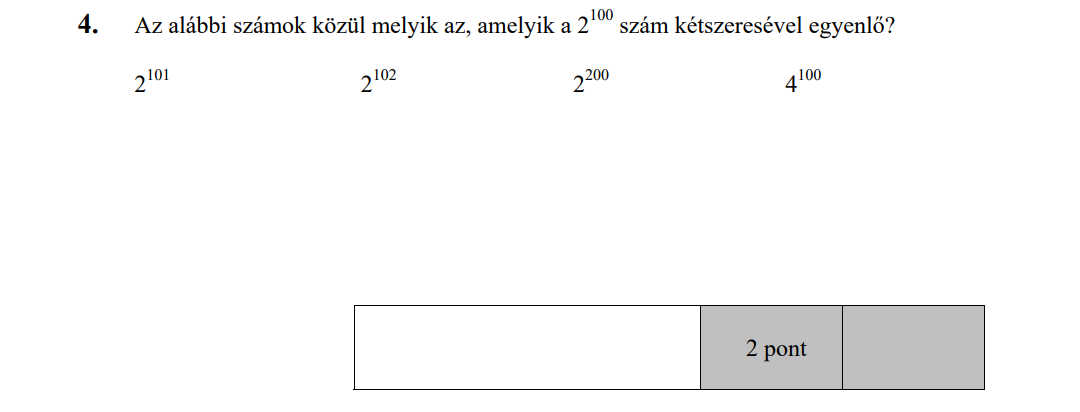



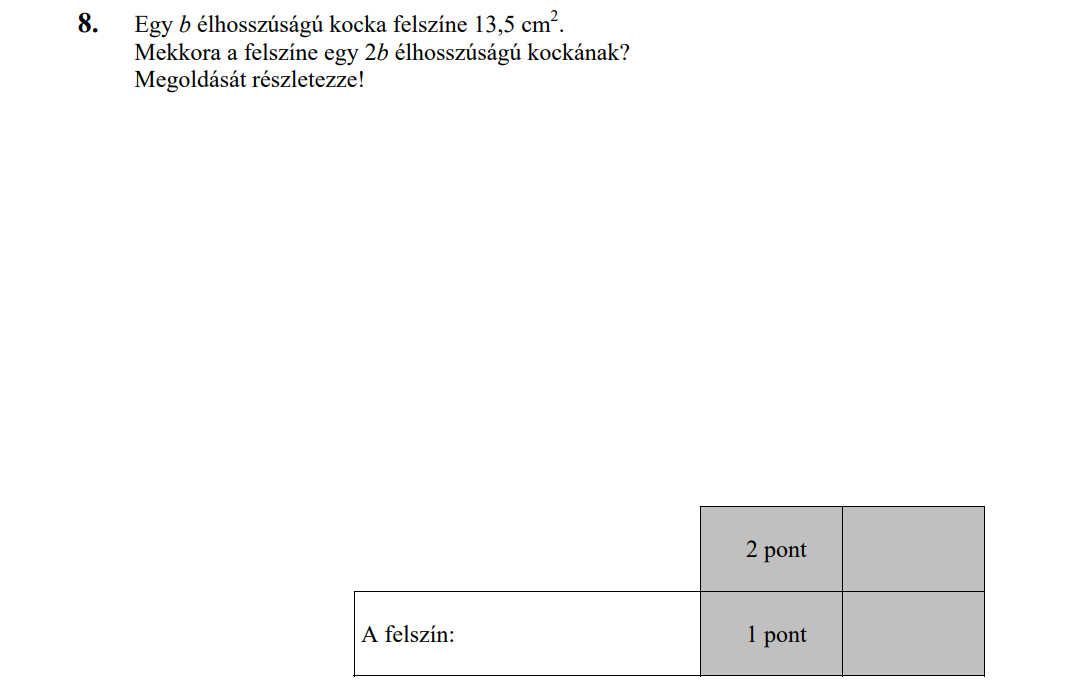




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
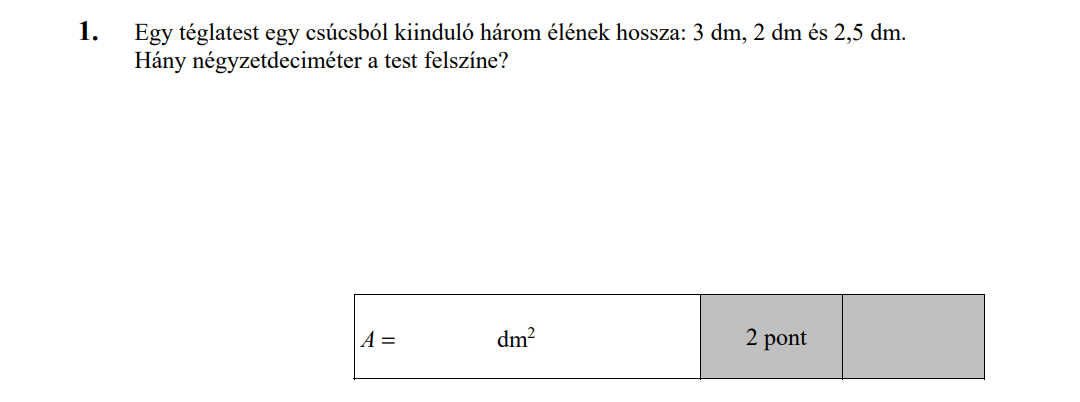
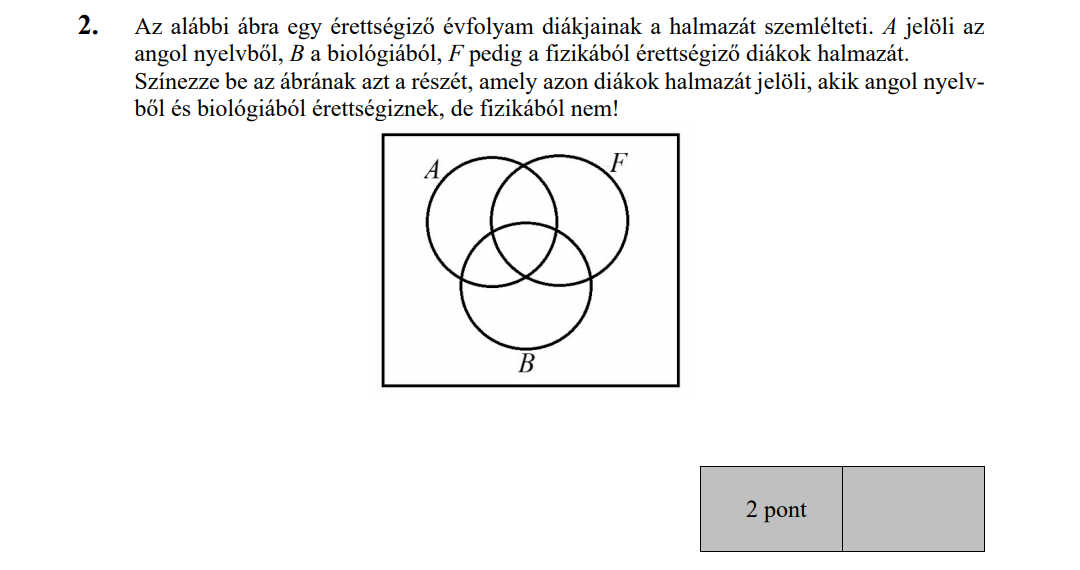

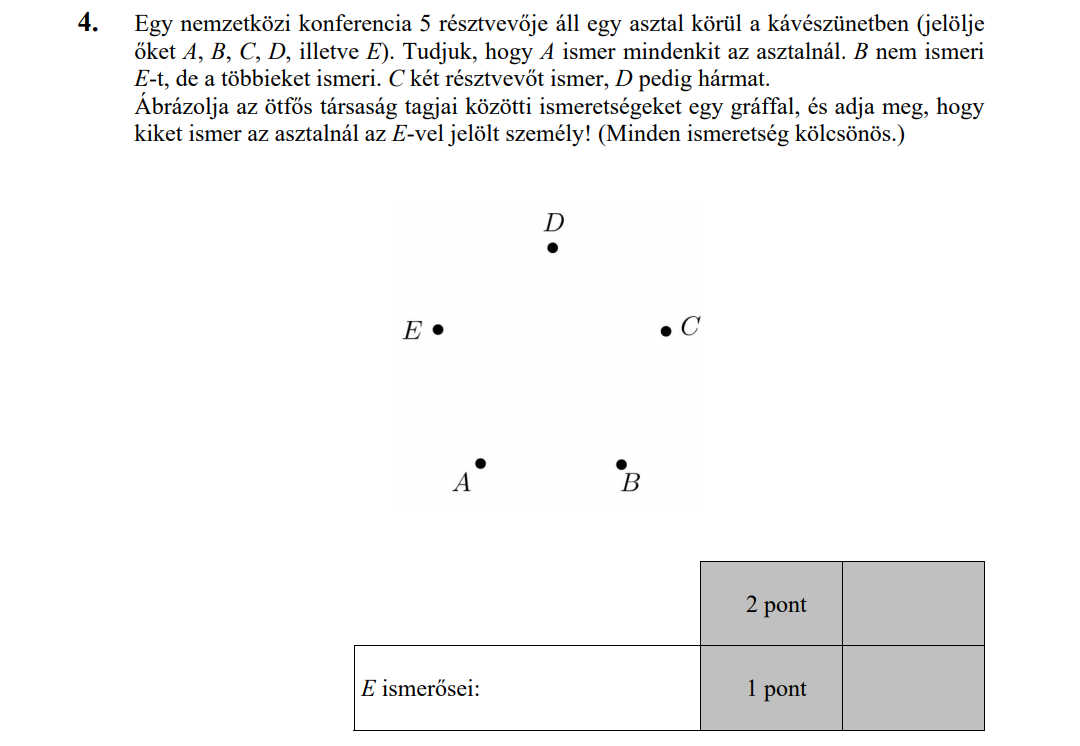

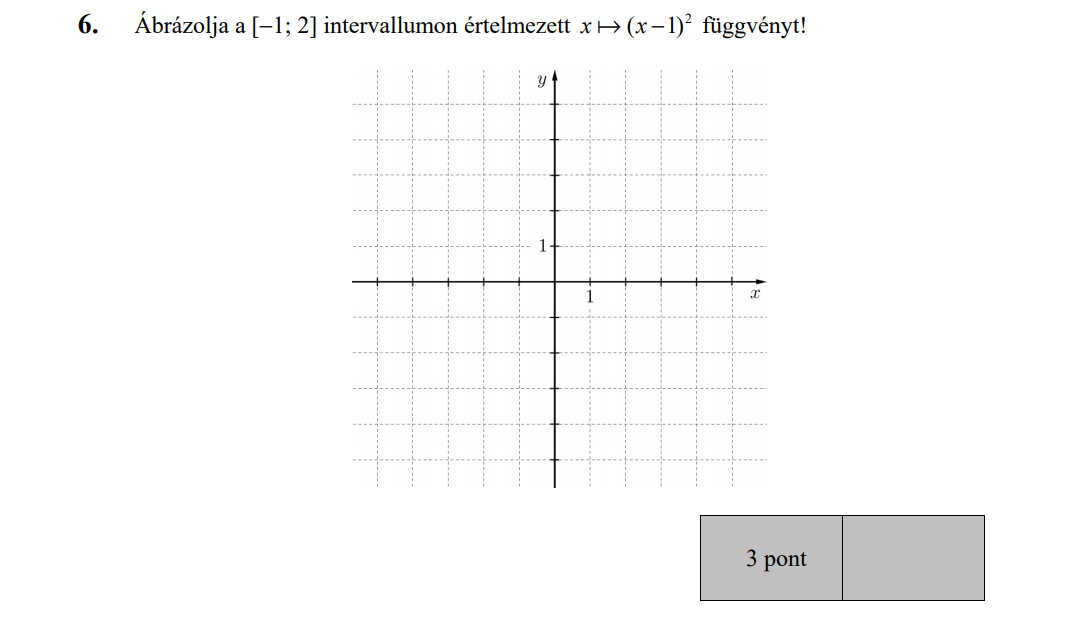



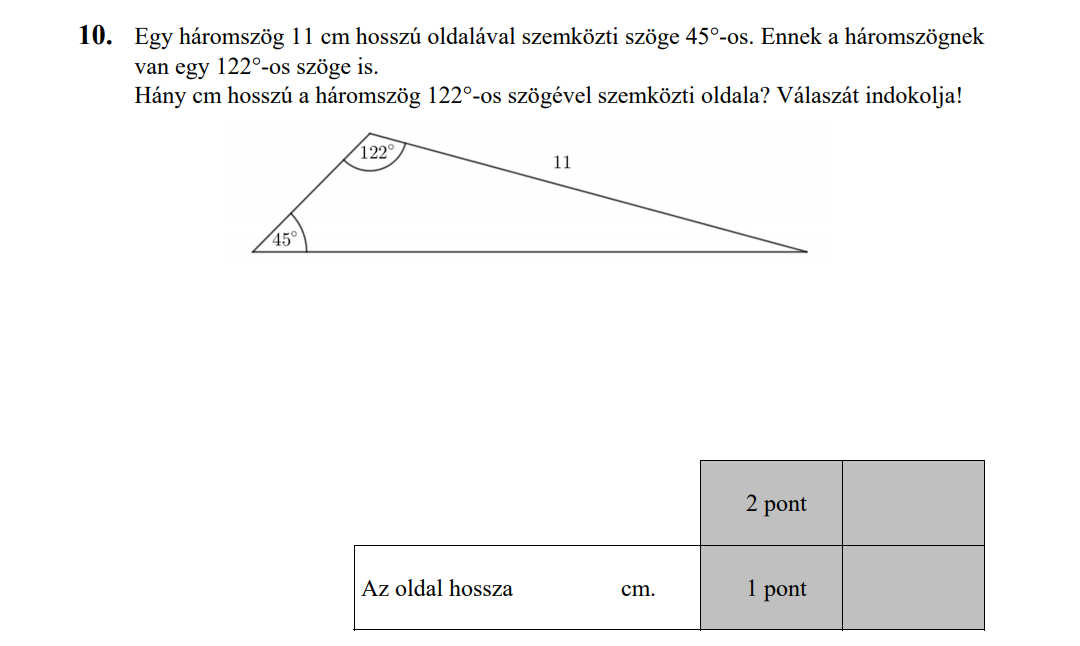

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



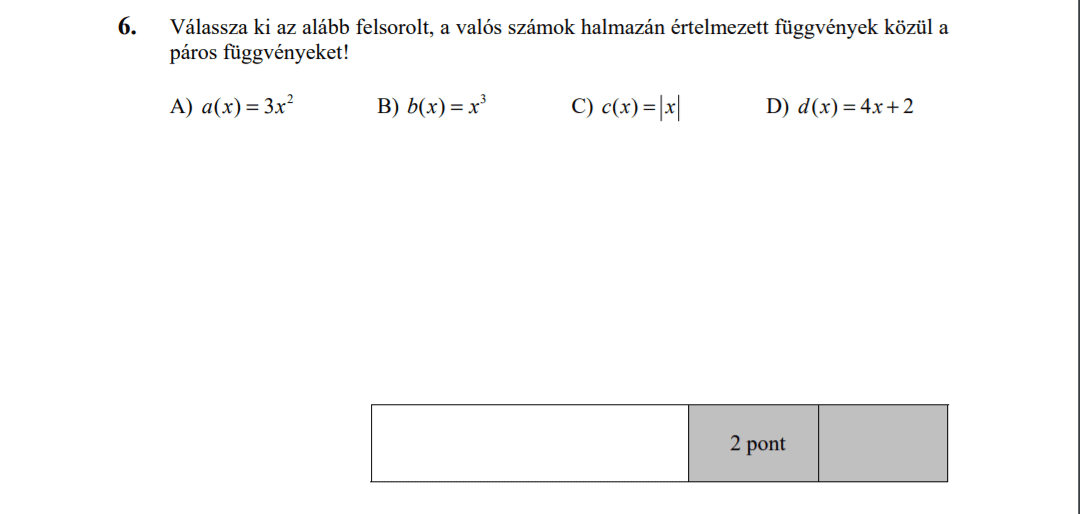
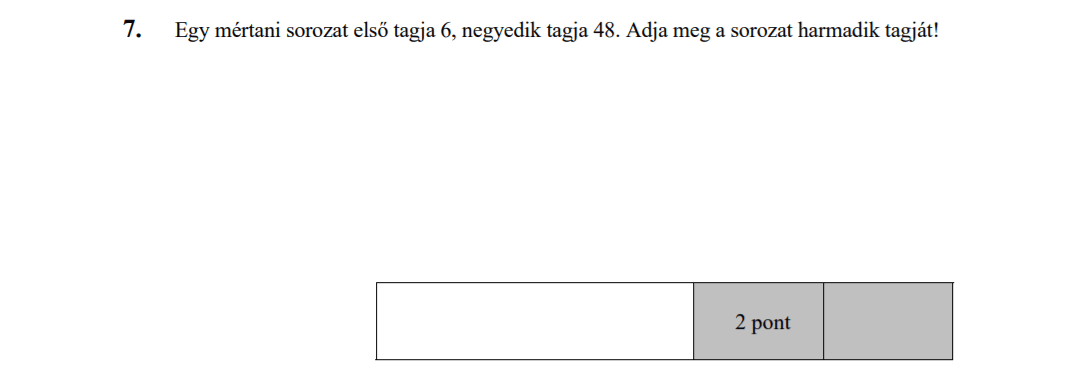



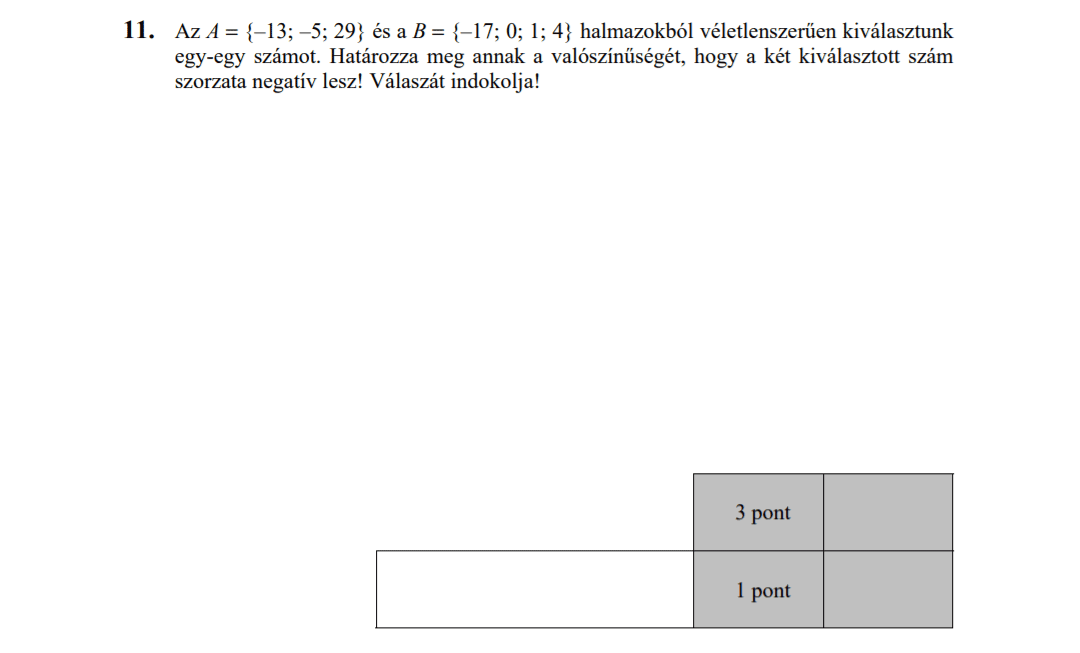

MÁSODIK RÉSZ


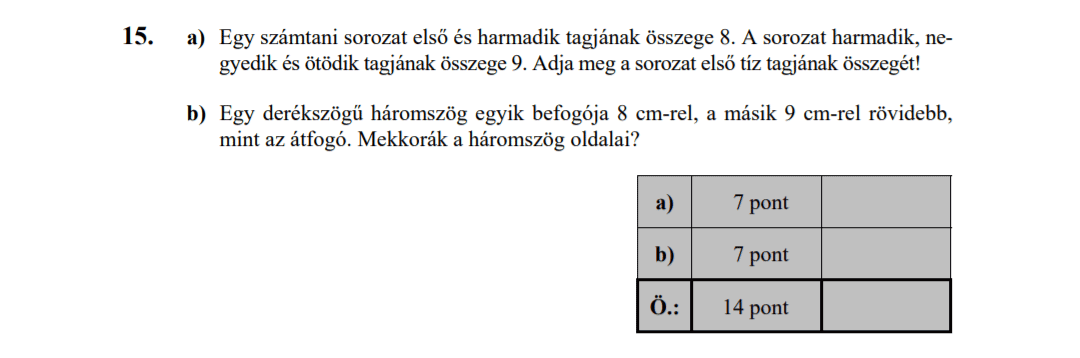



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






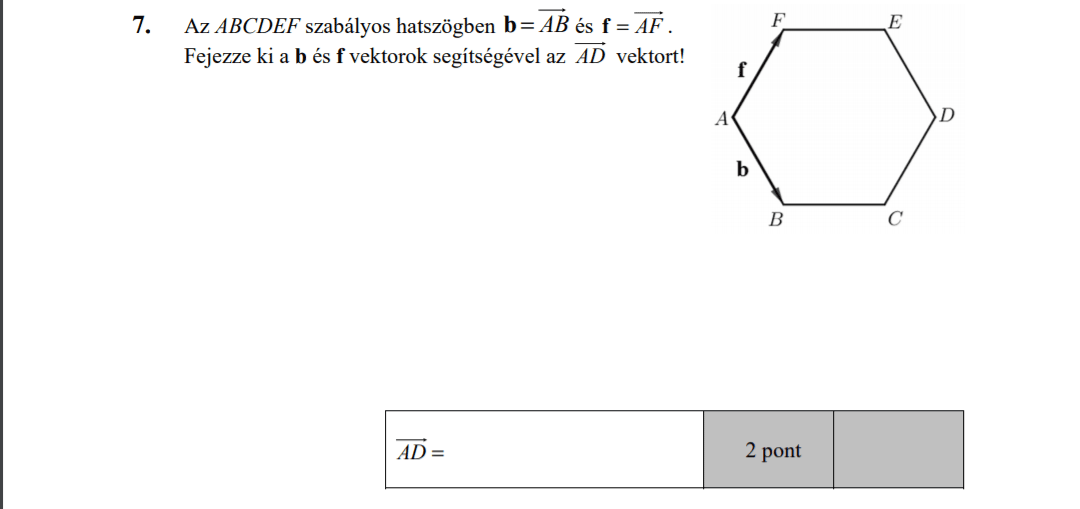



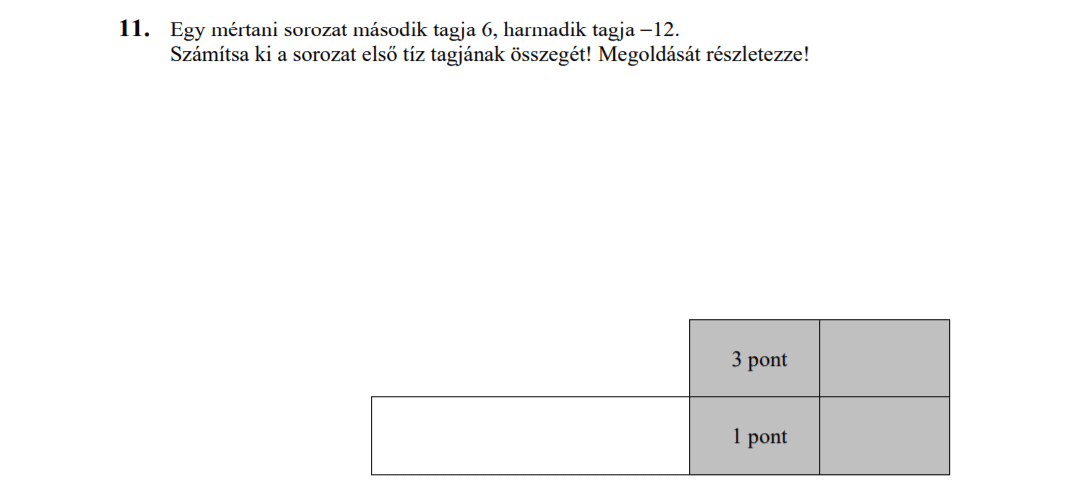

MÁSODIK RÉSZ

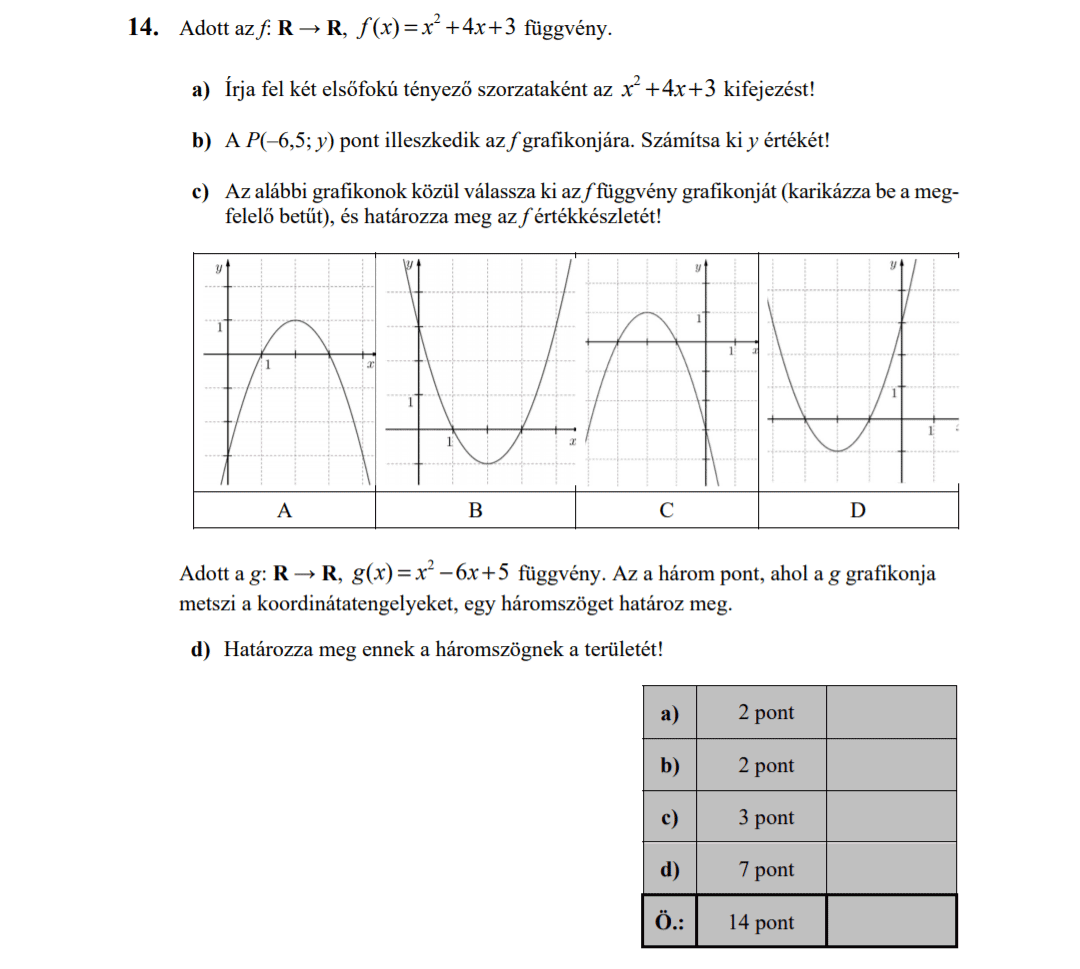




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



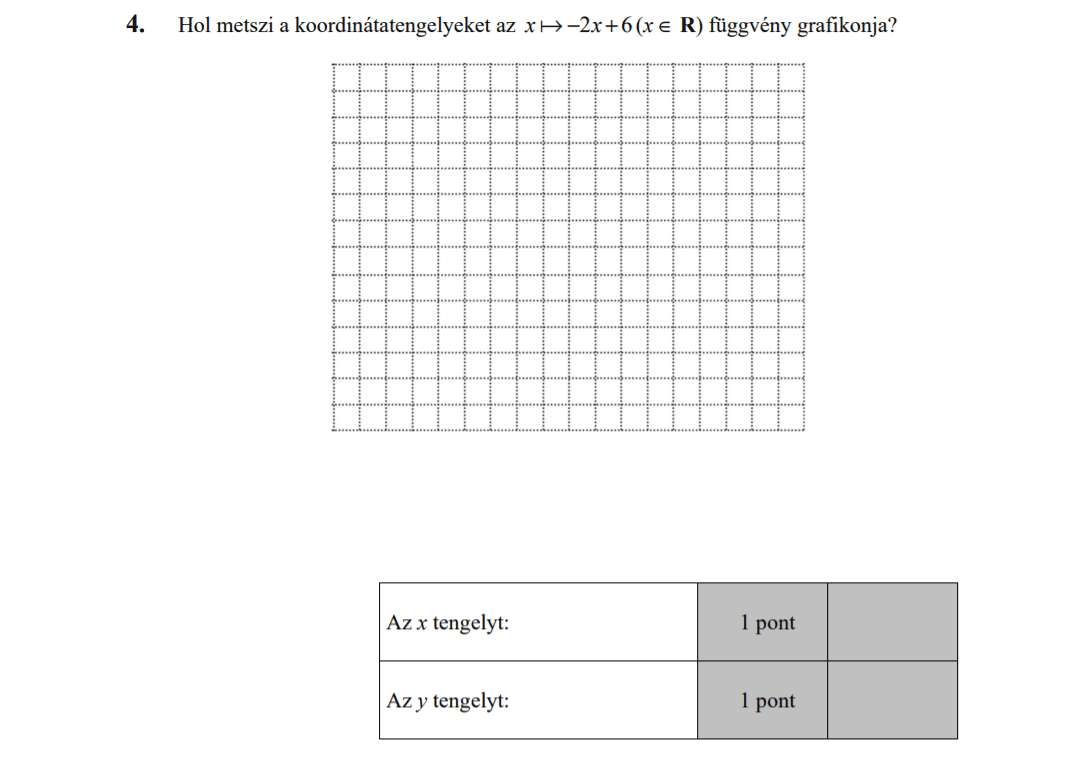







MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

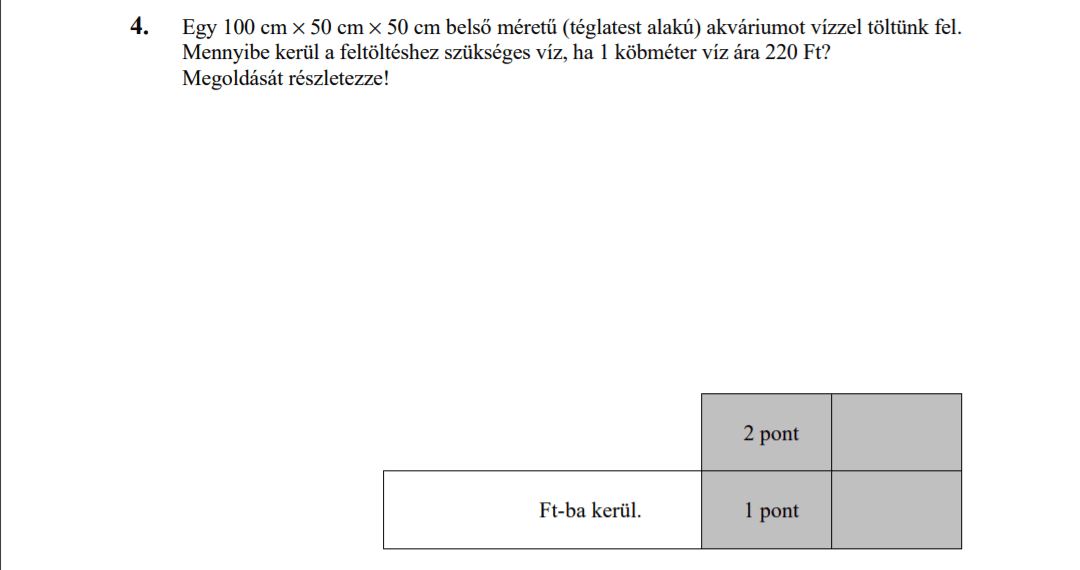
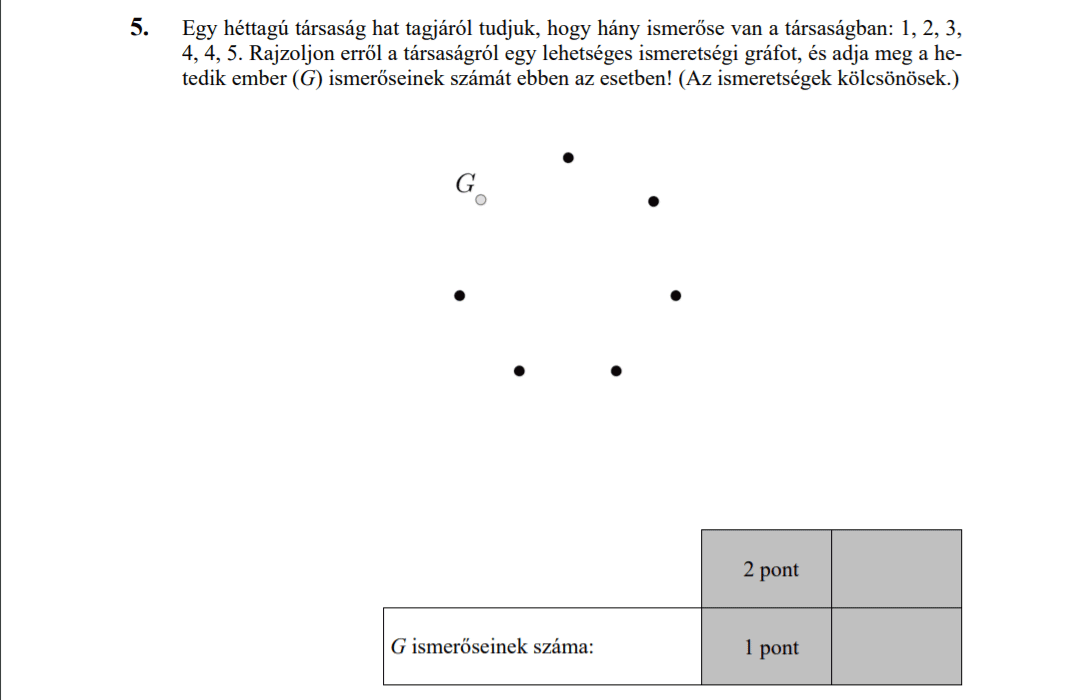







MÁSODIK RÉSZ
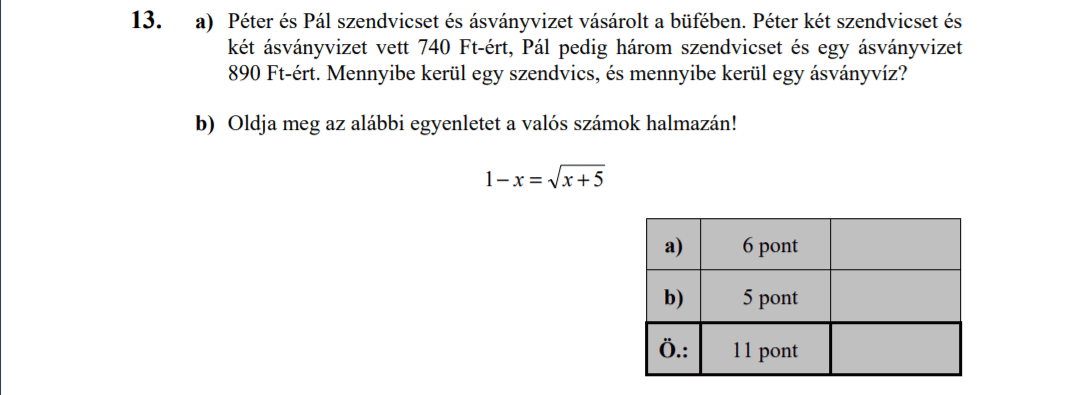
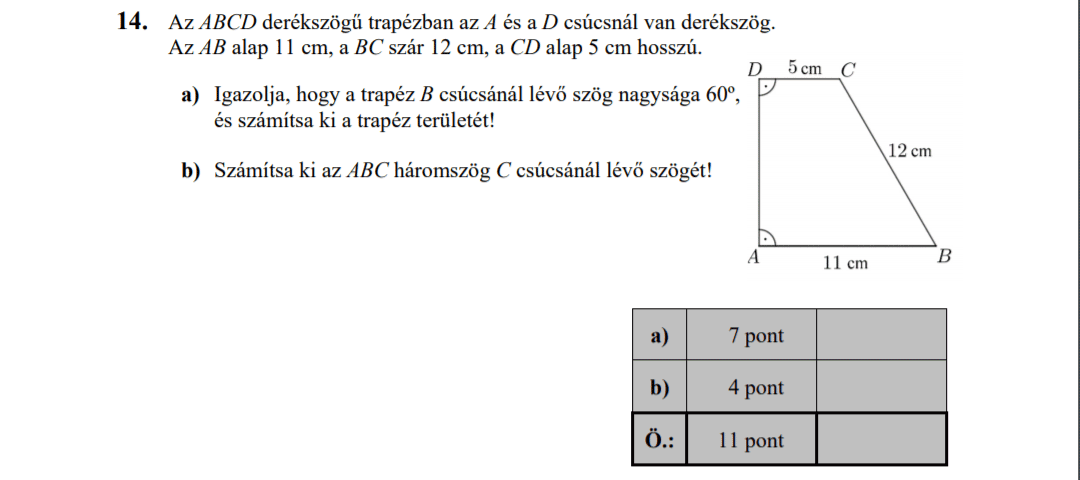

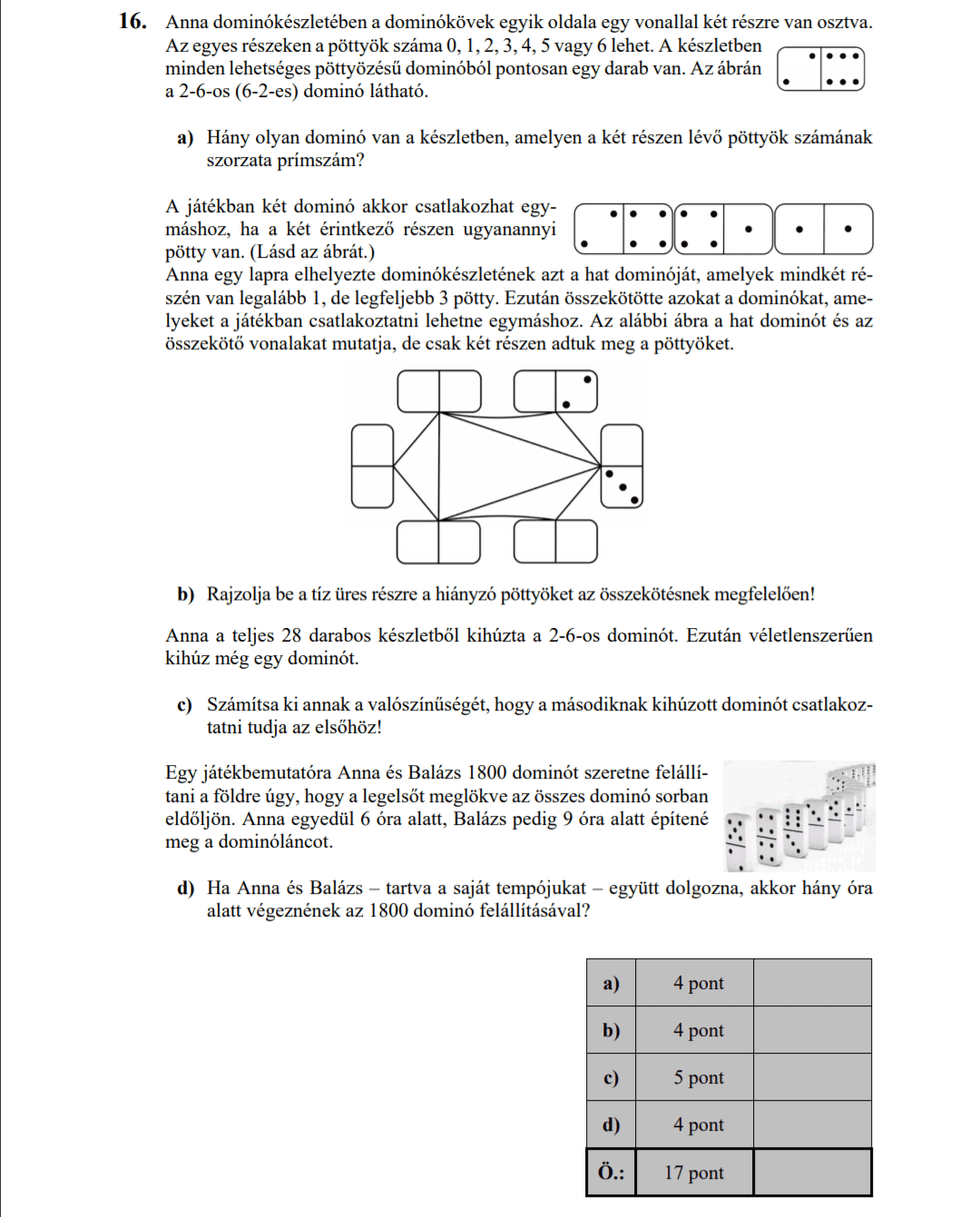


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




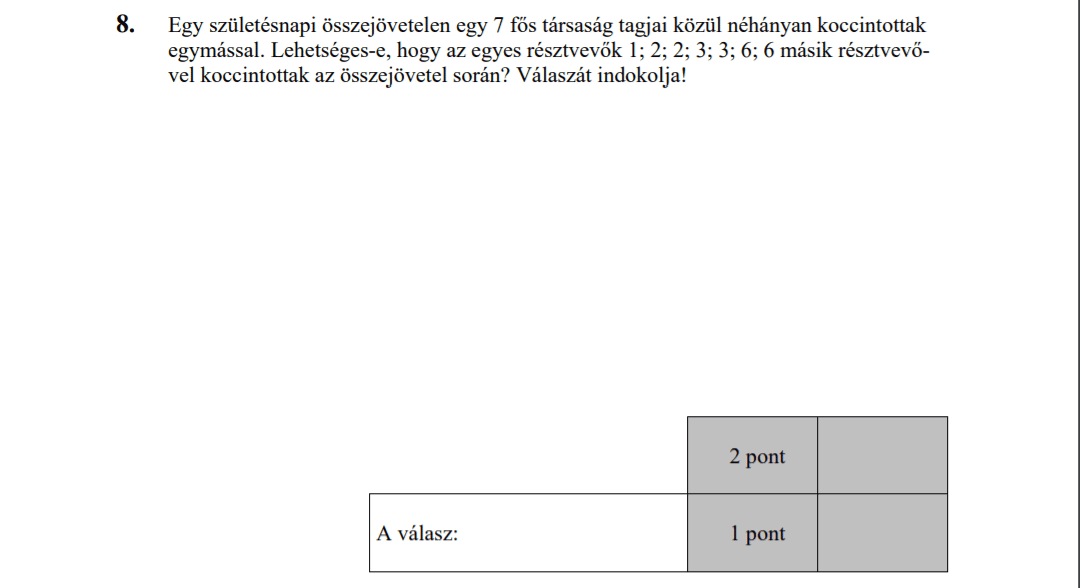



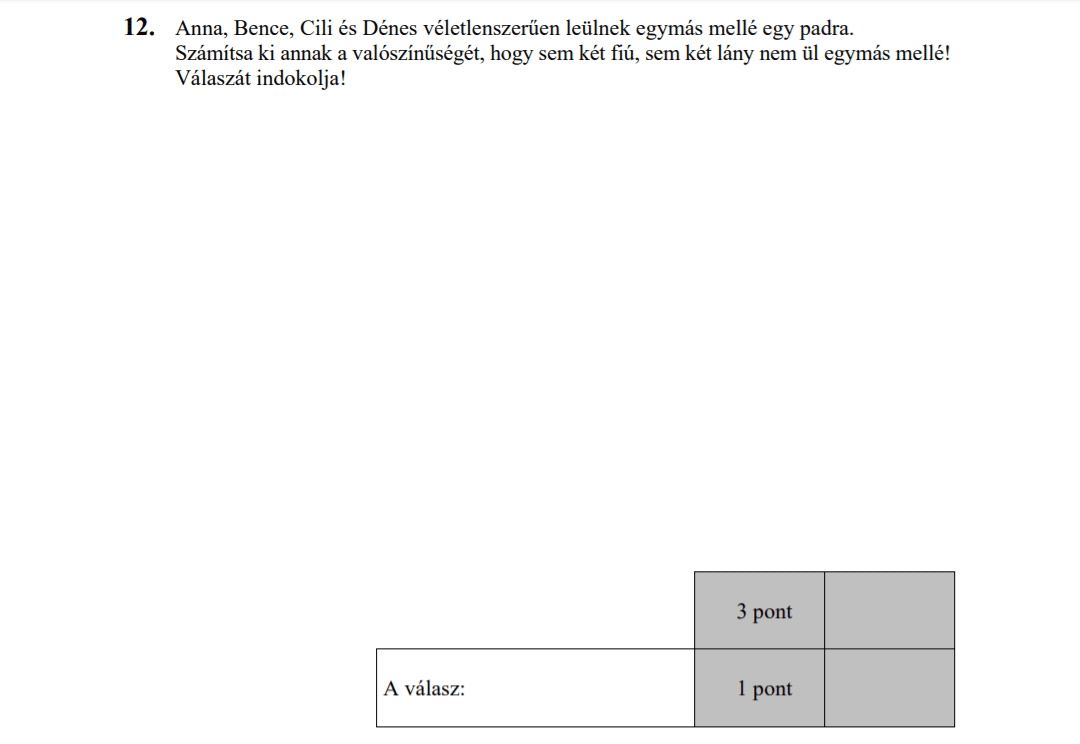
MÁSODIK RÉSZ

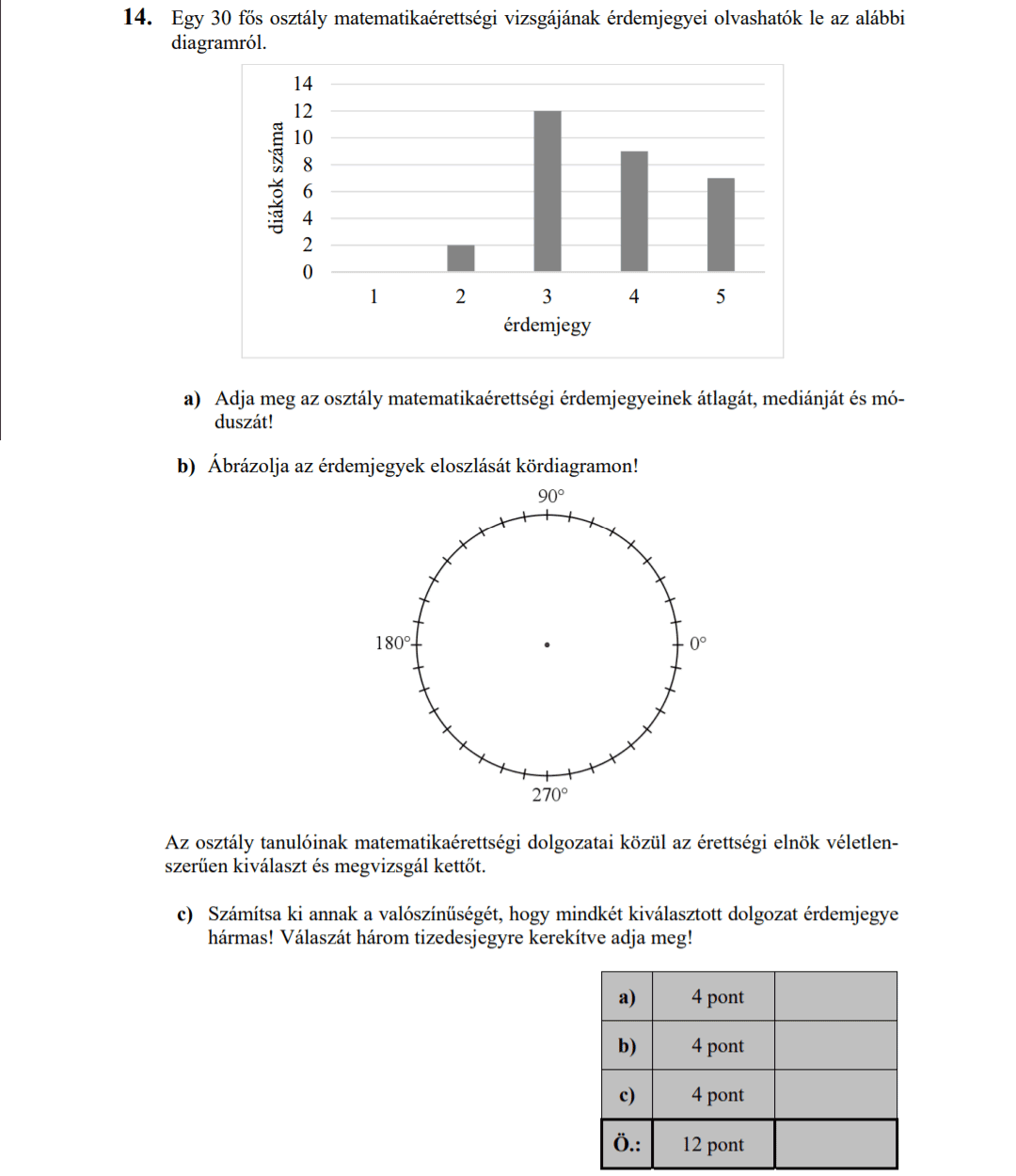
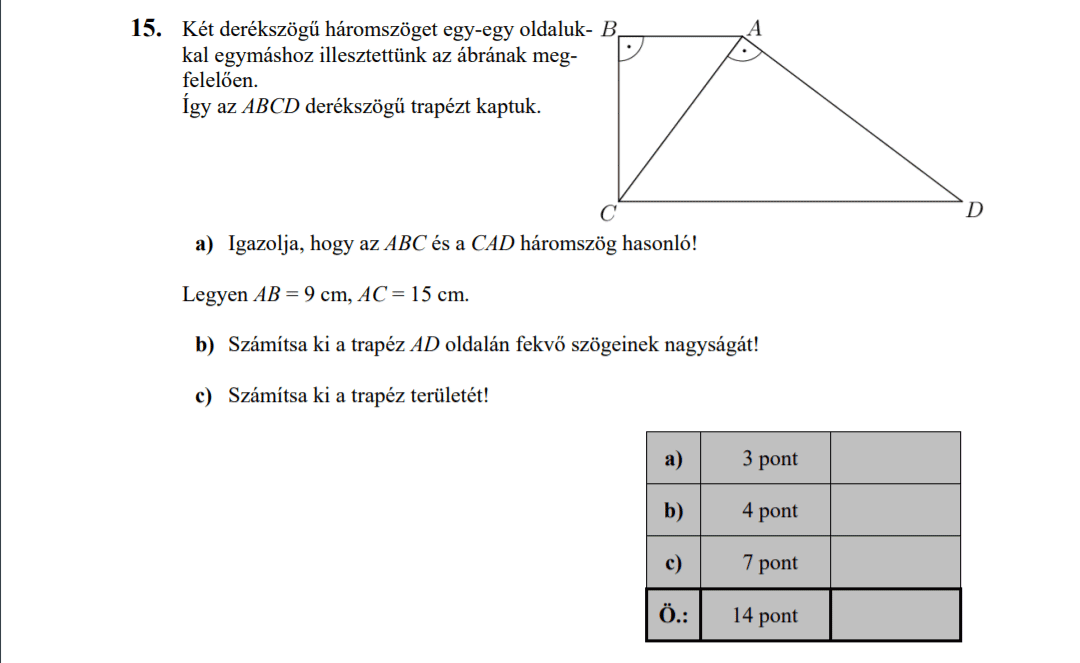



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


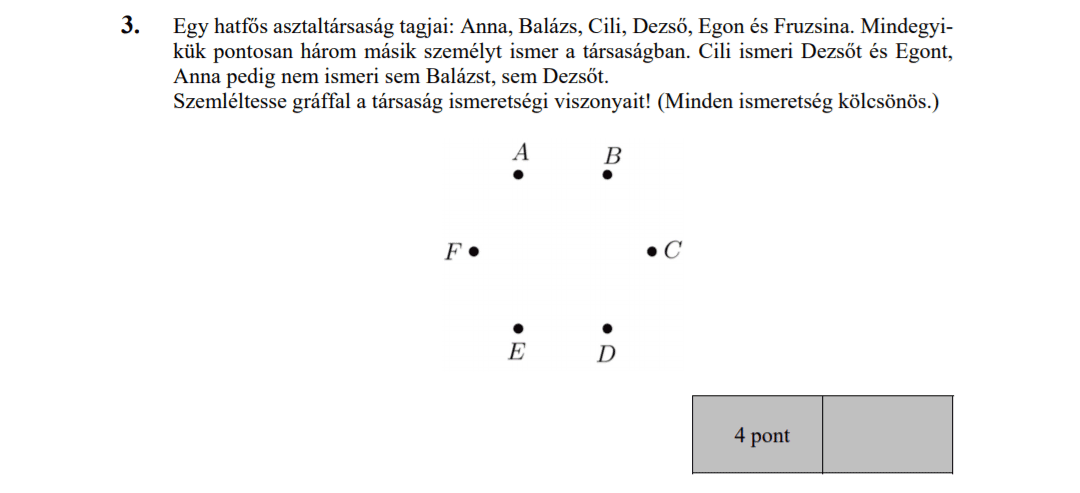


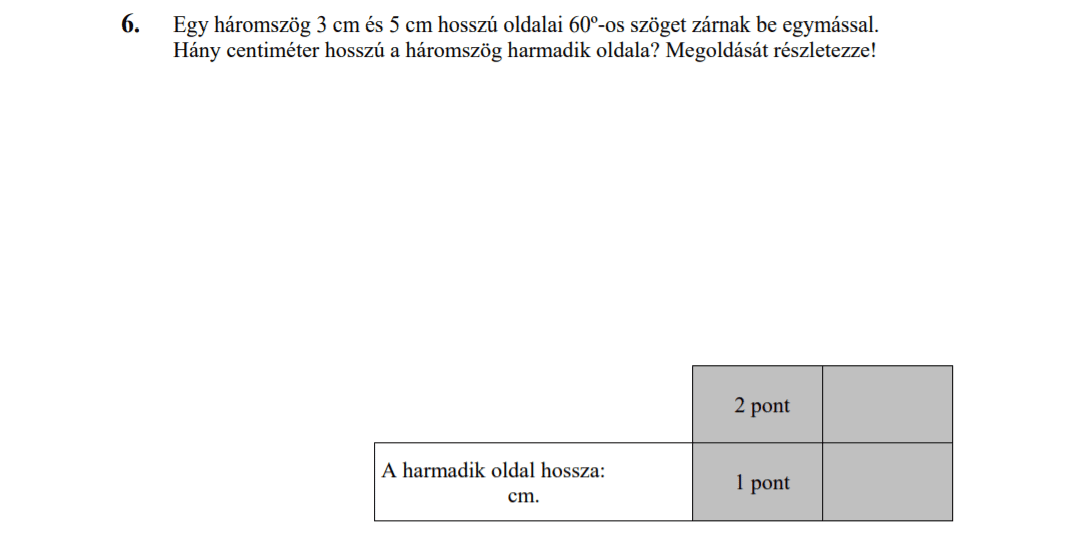

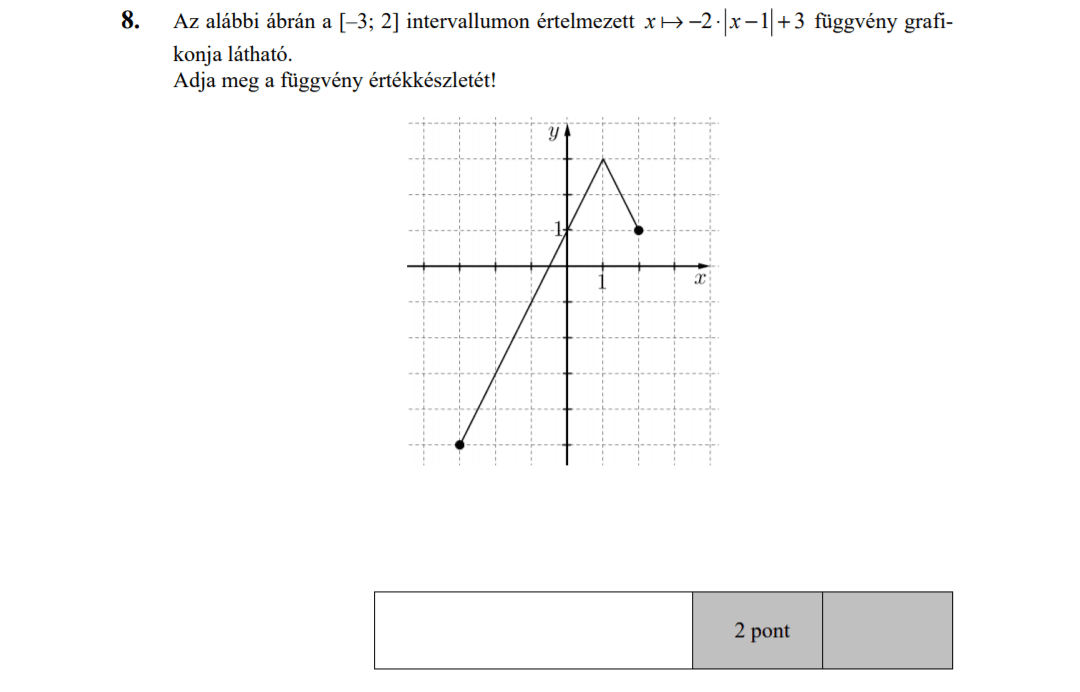

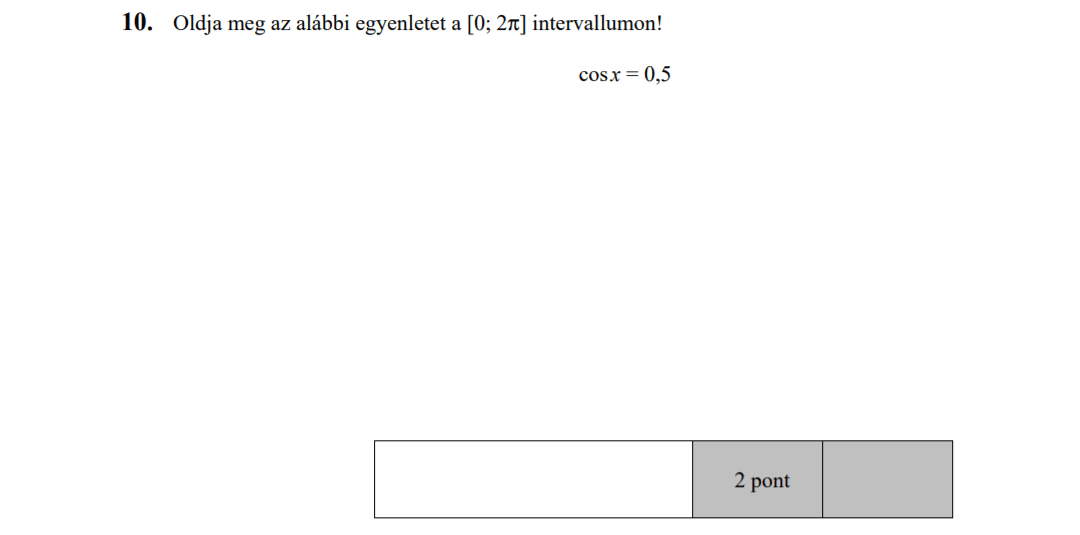

MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
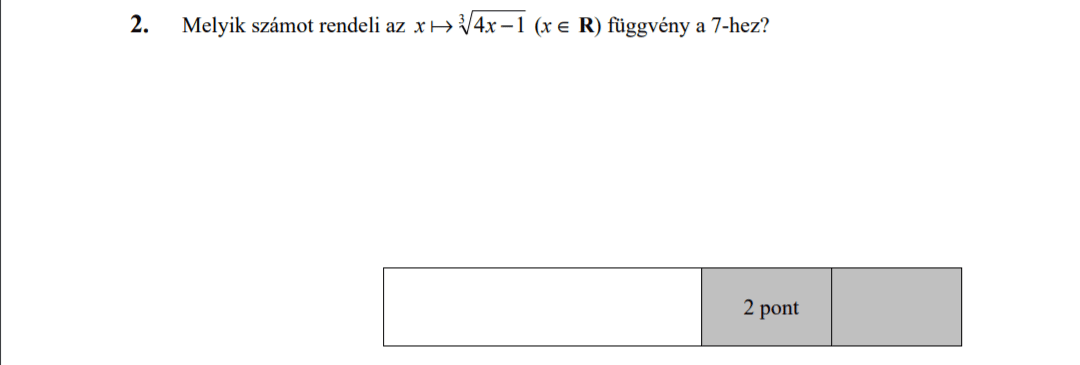


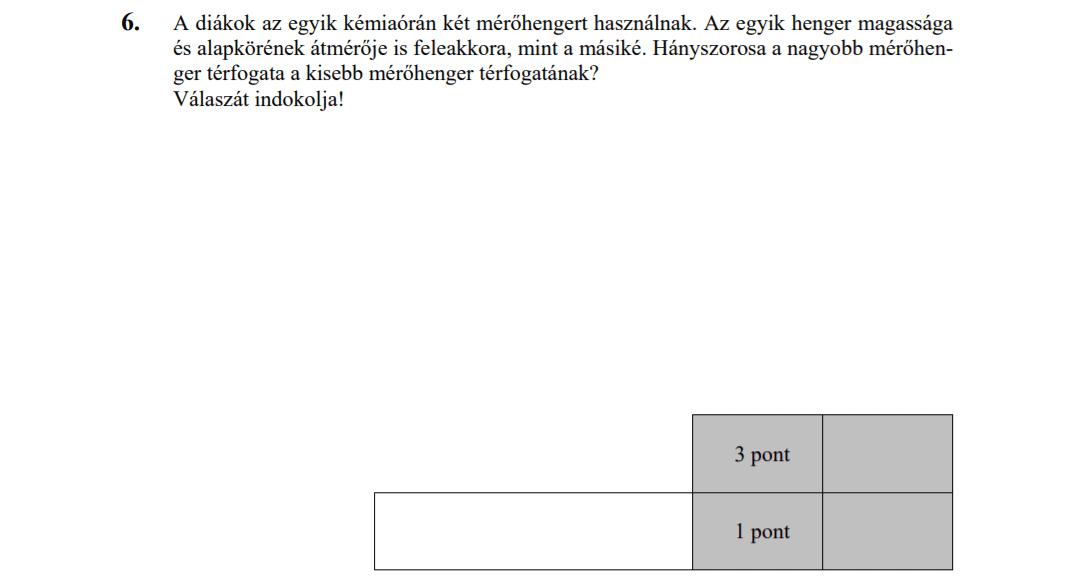
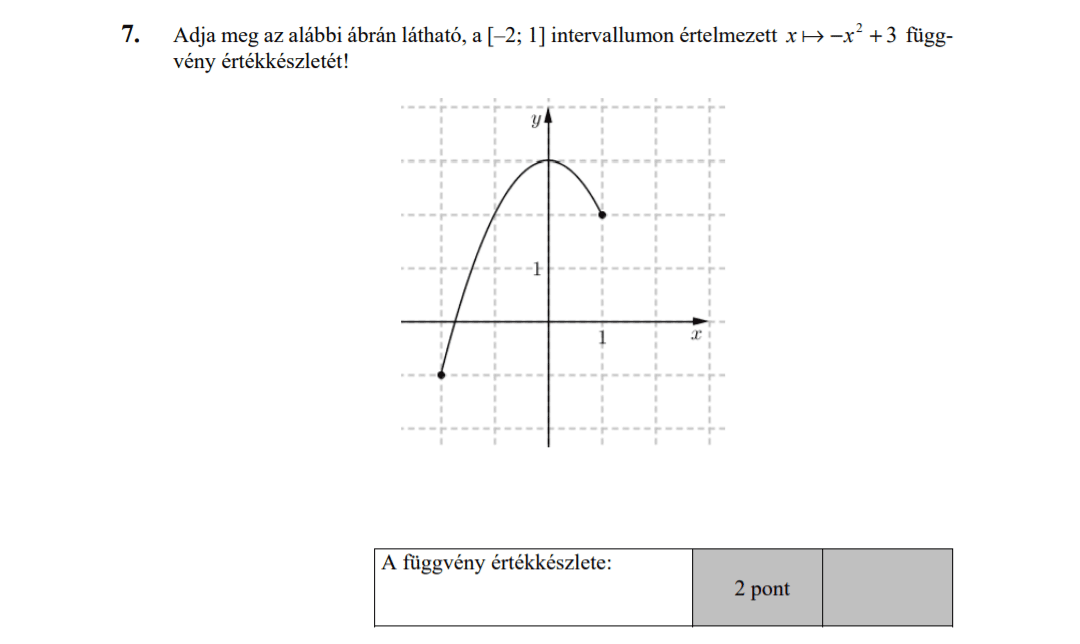

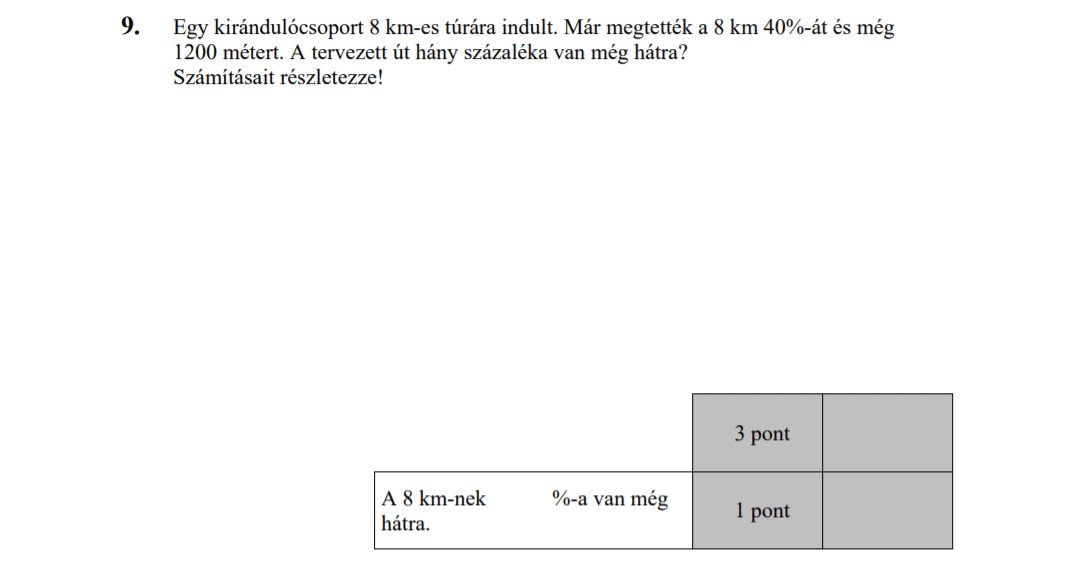
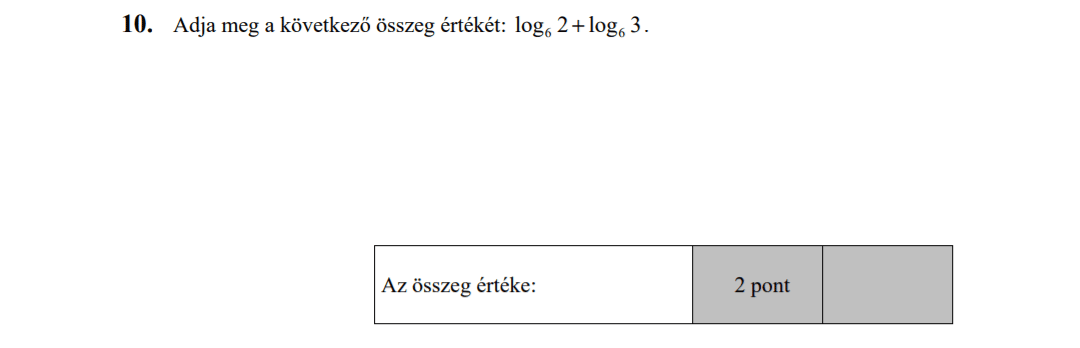
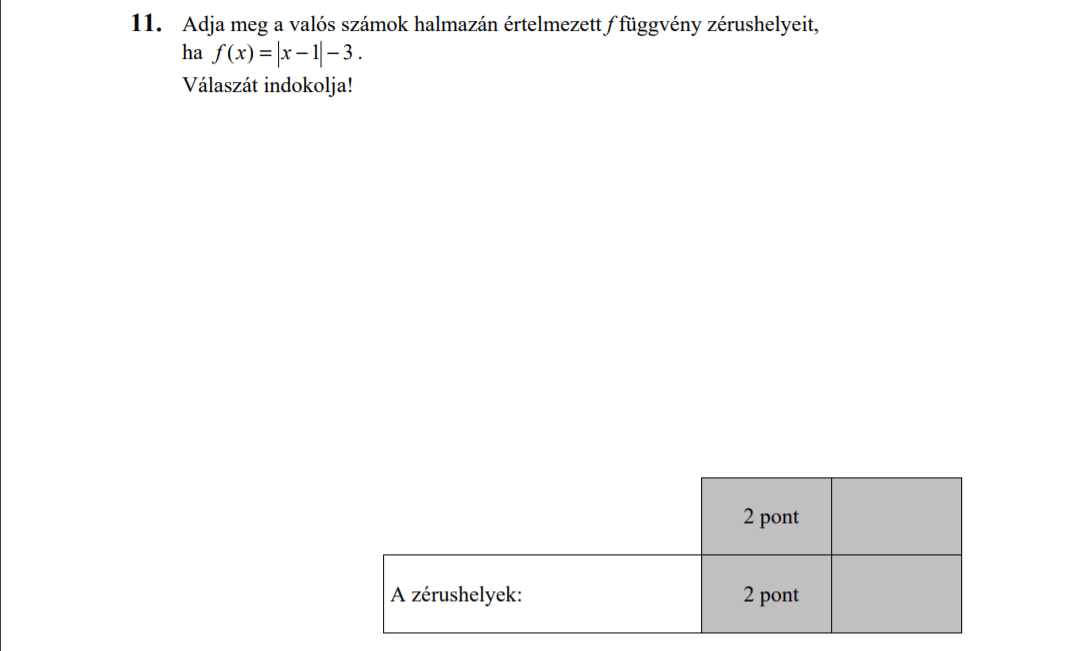

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
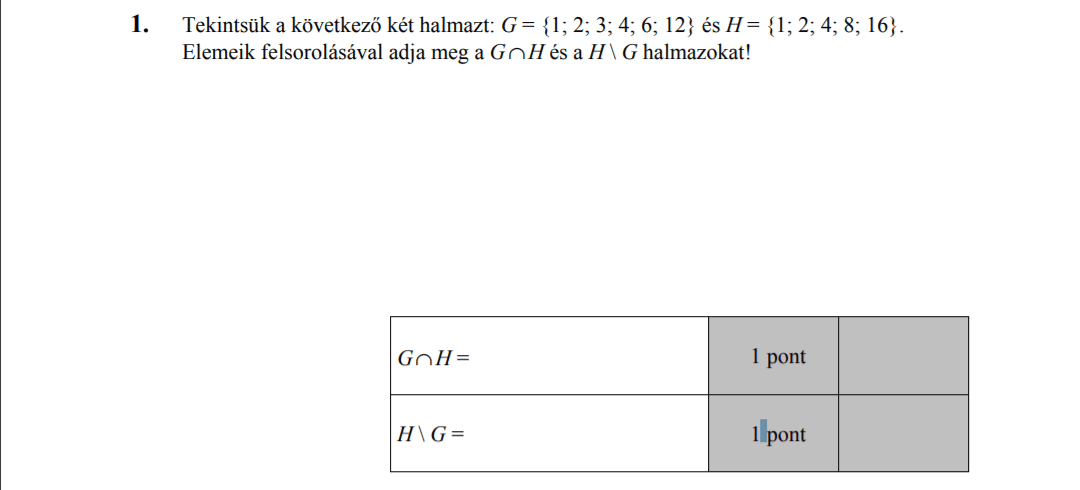



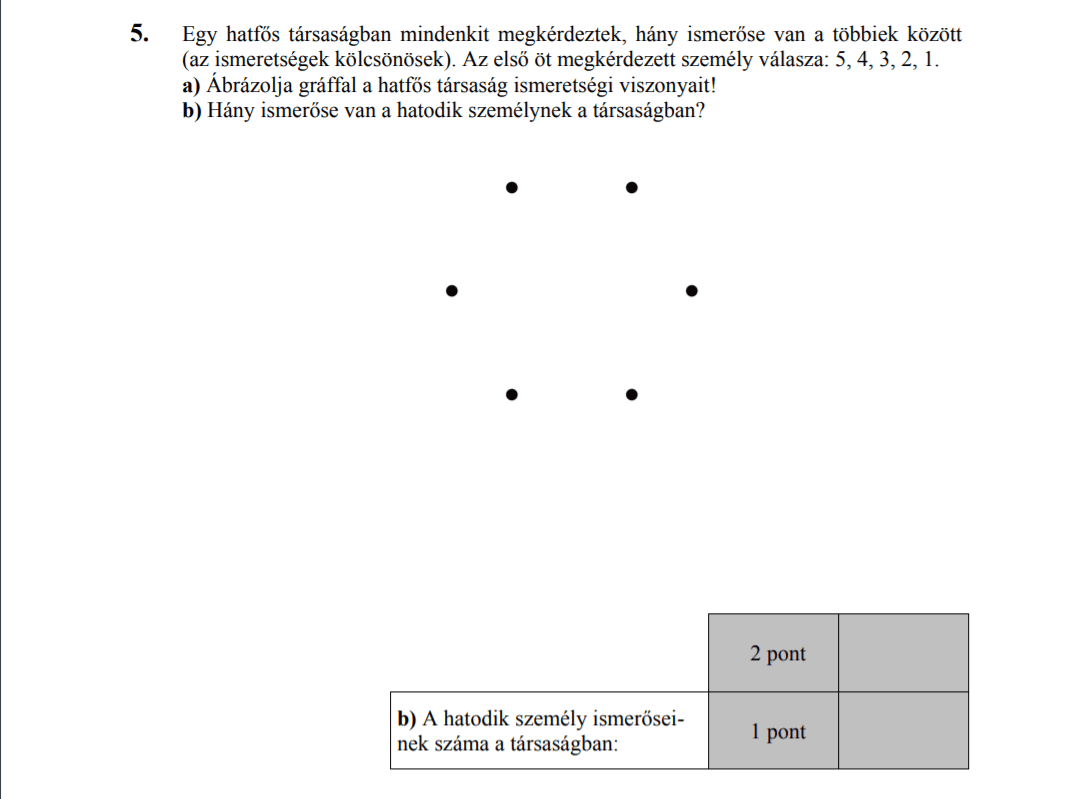


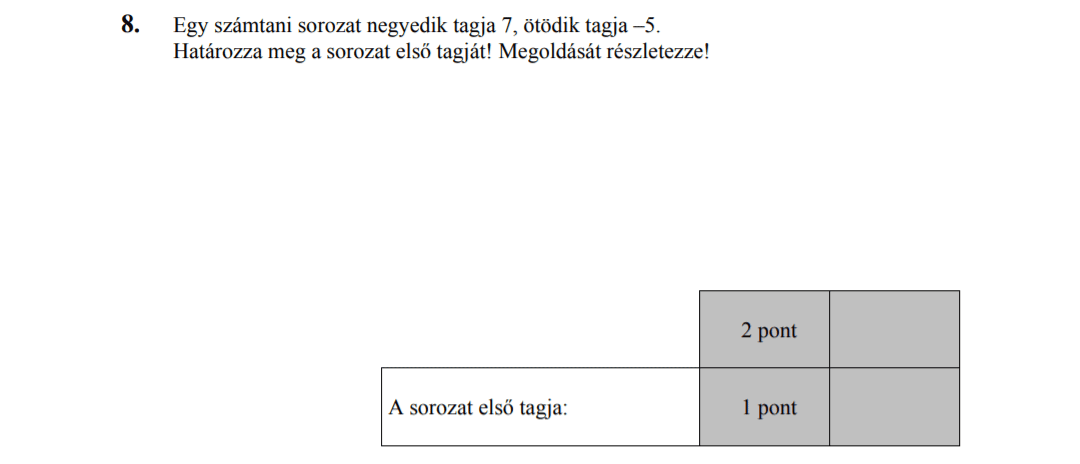

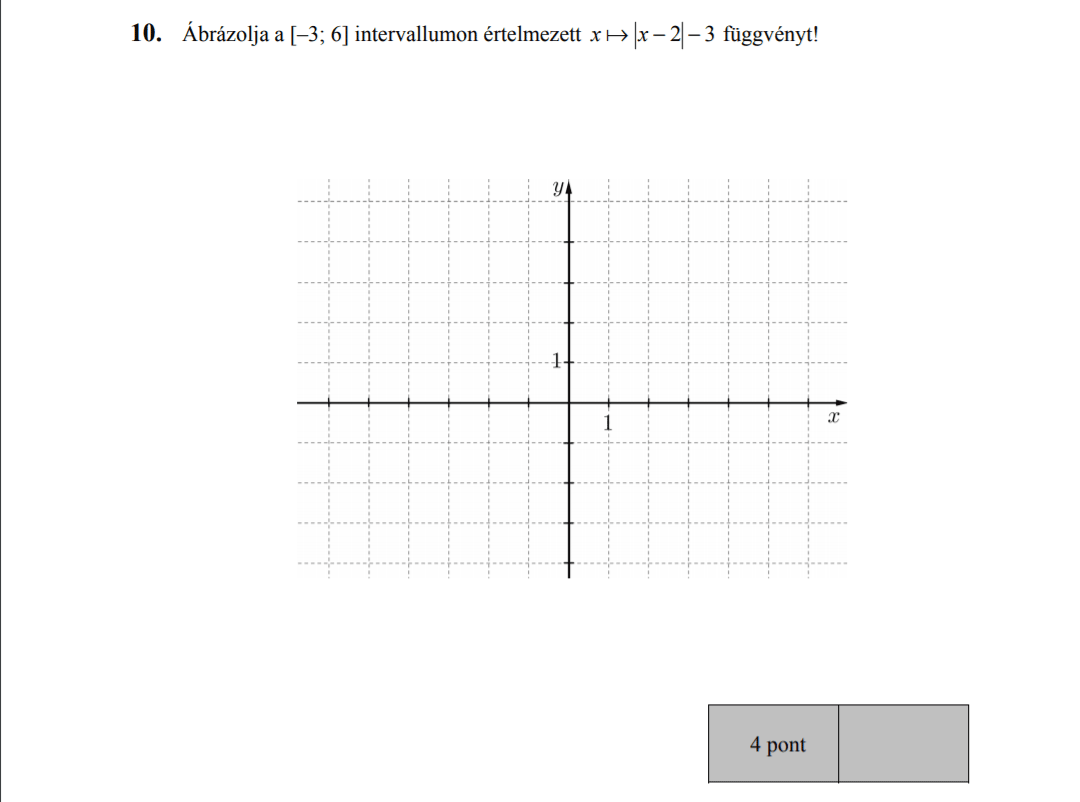

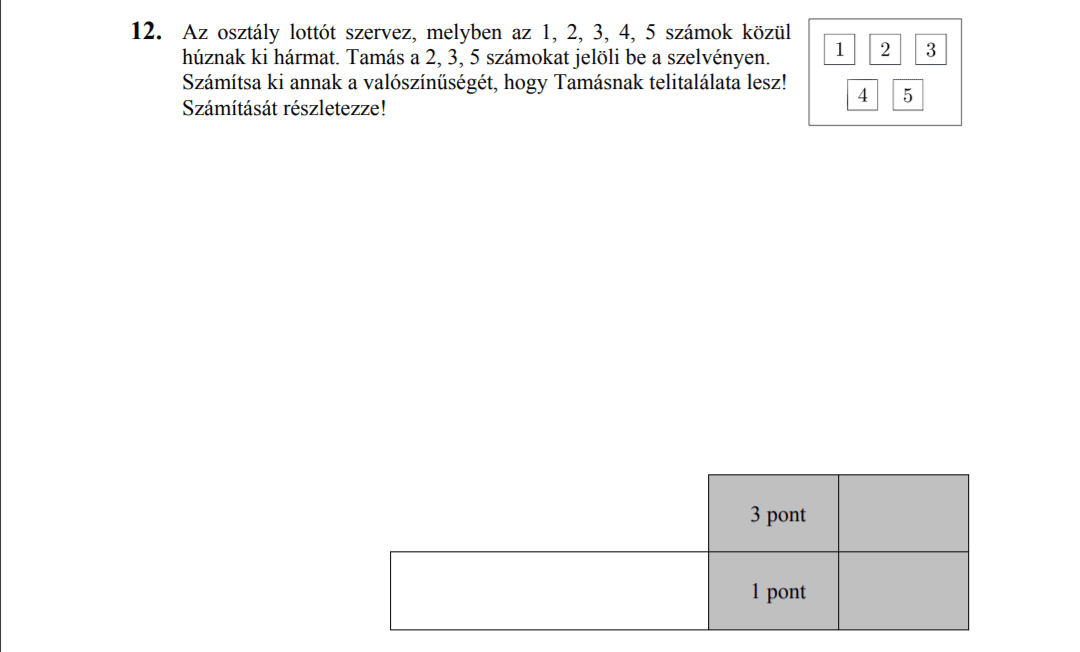
MÁSODIK RÉSZ

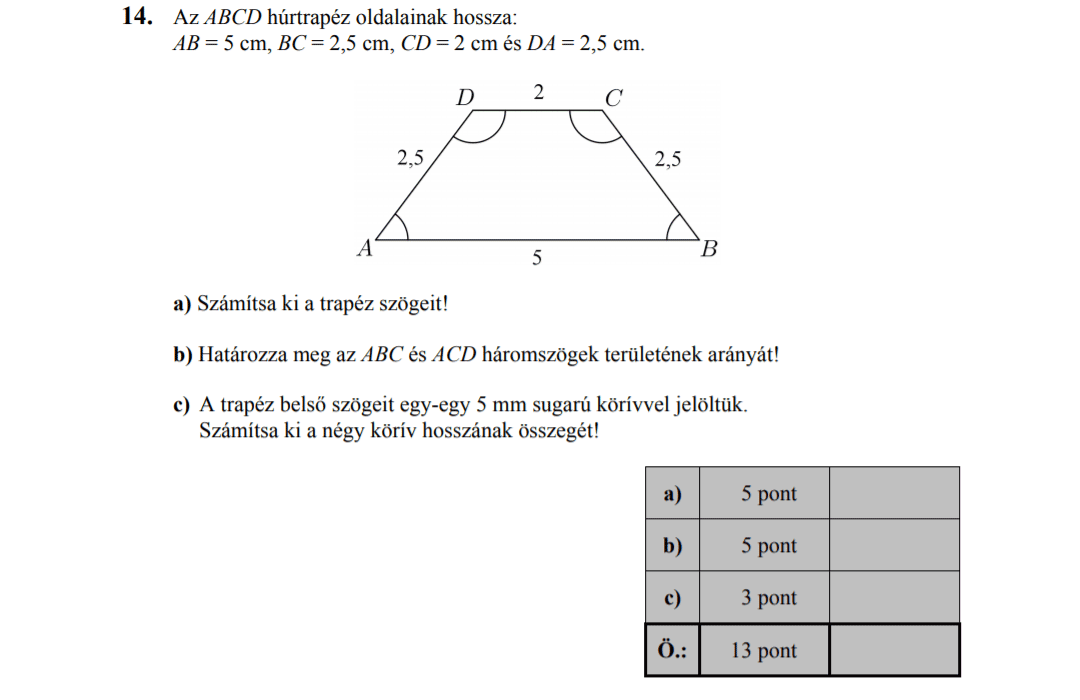

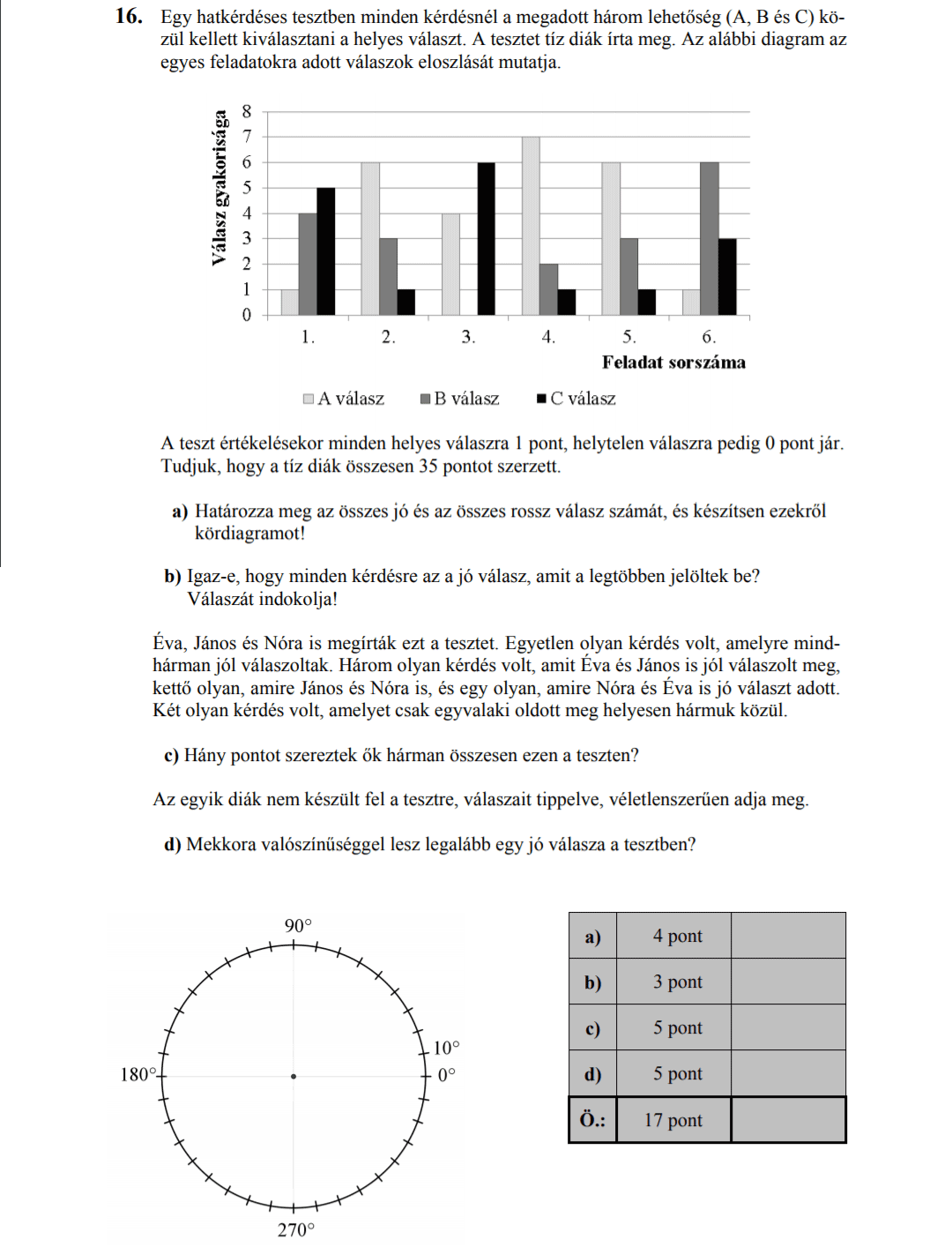


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

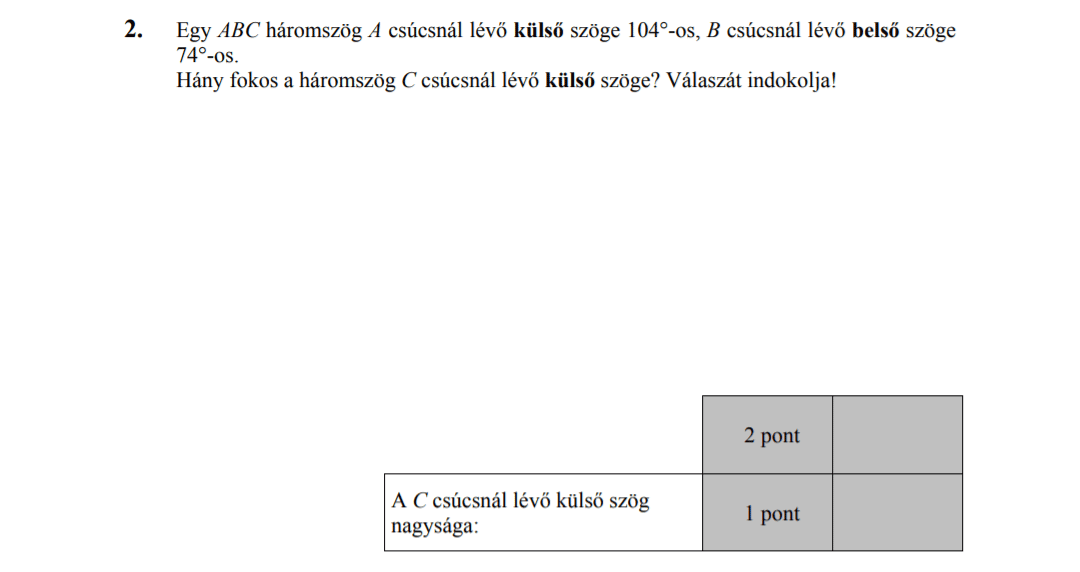





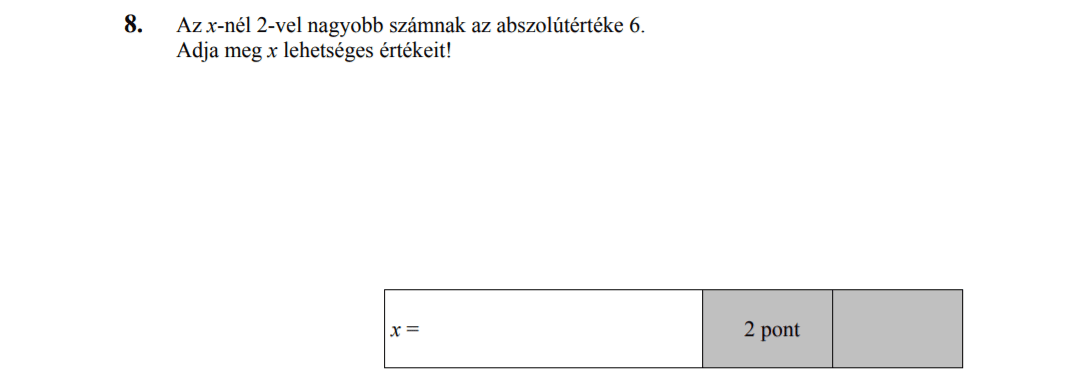

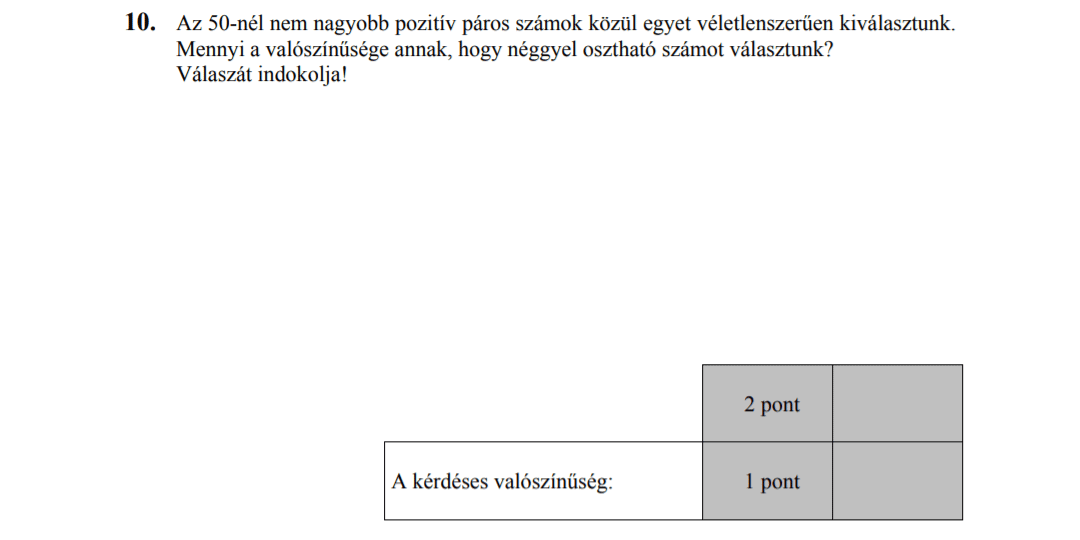


MÁSODIK RÉSZ

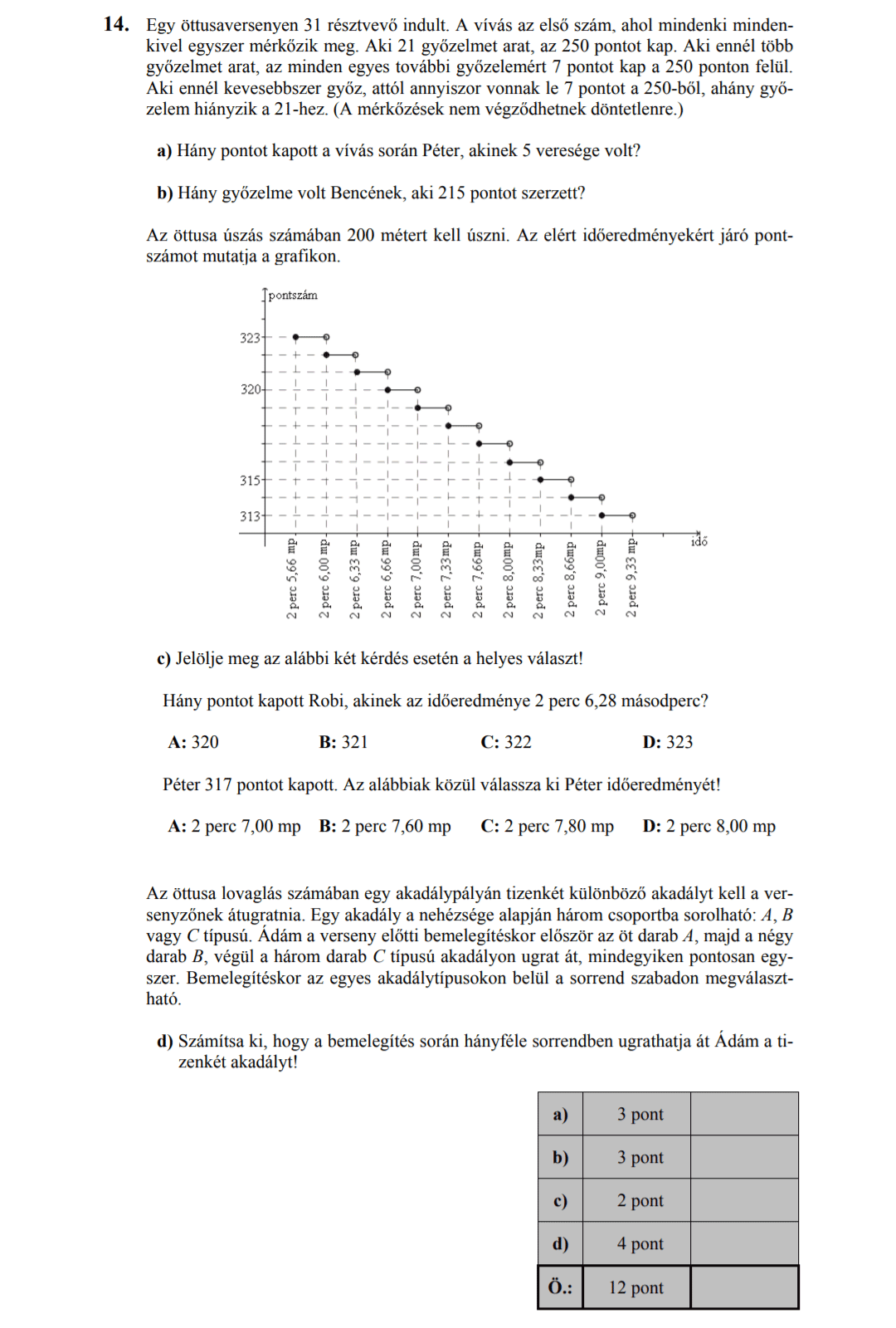
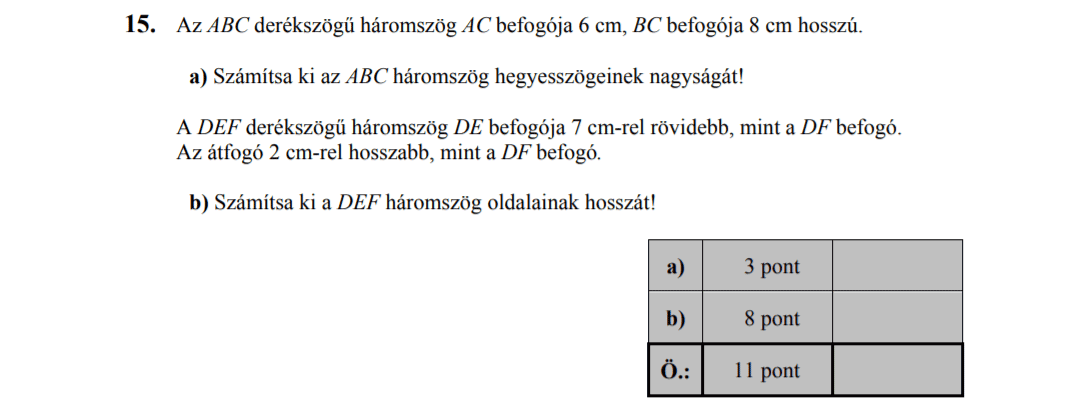



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

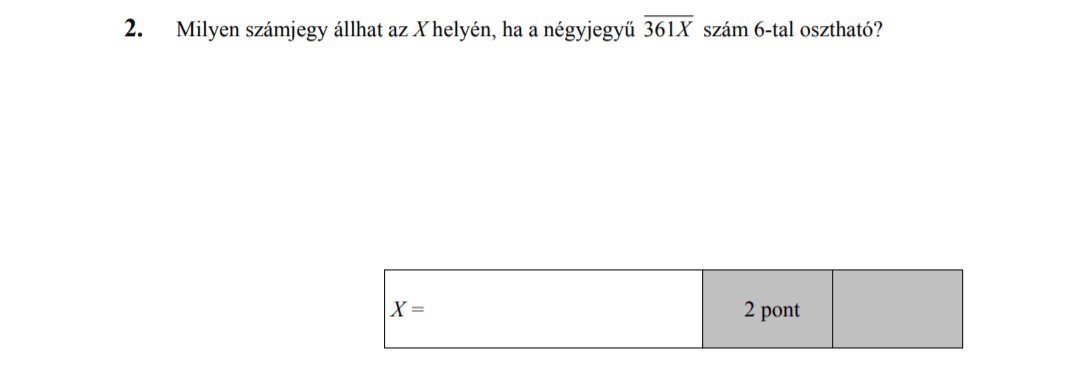



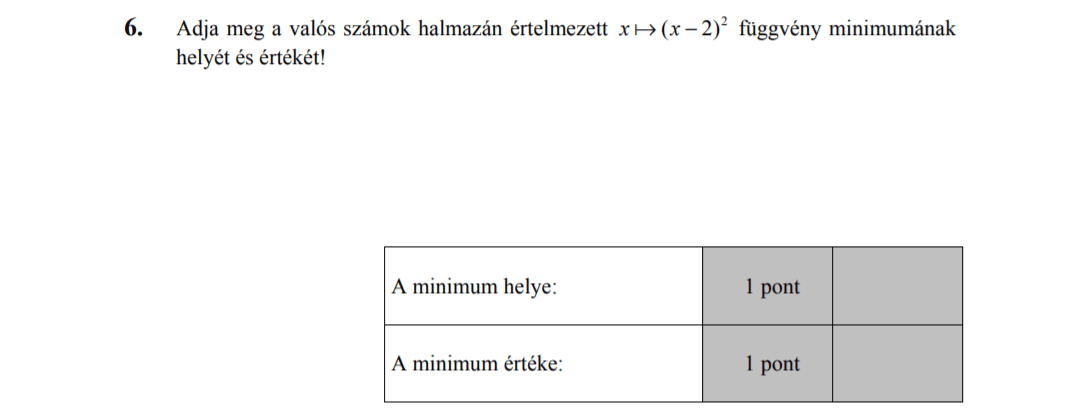

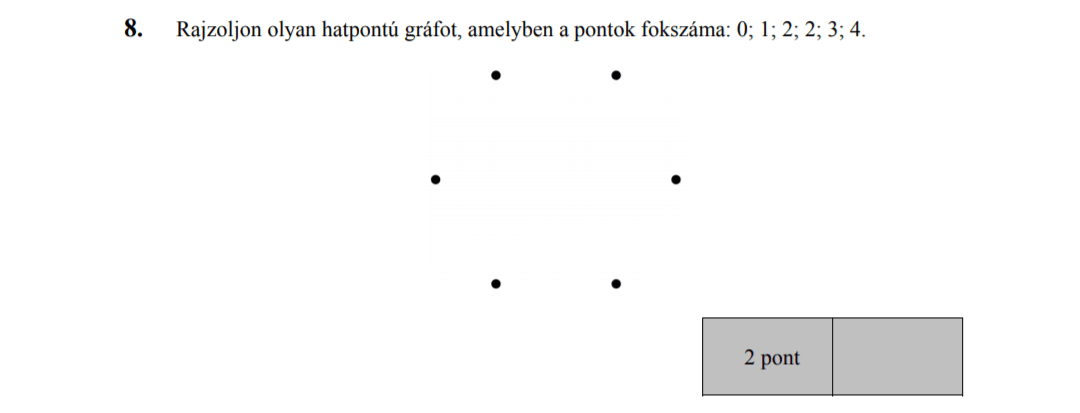


MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








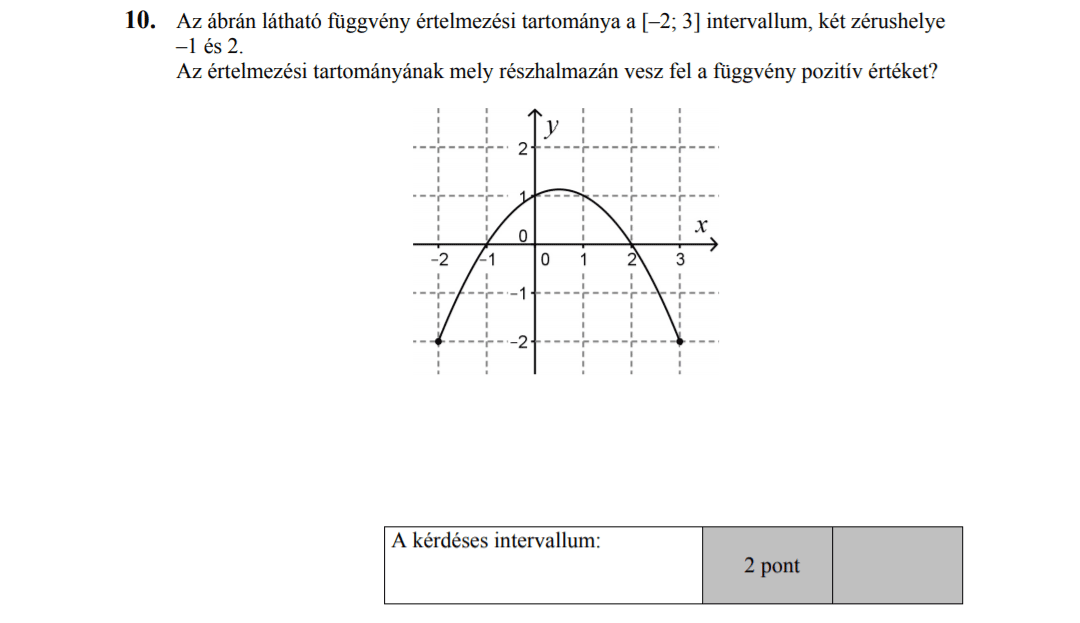


MÁSODIK RÉSZ


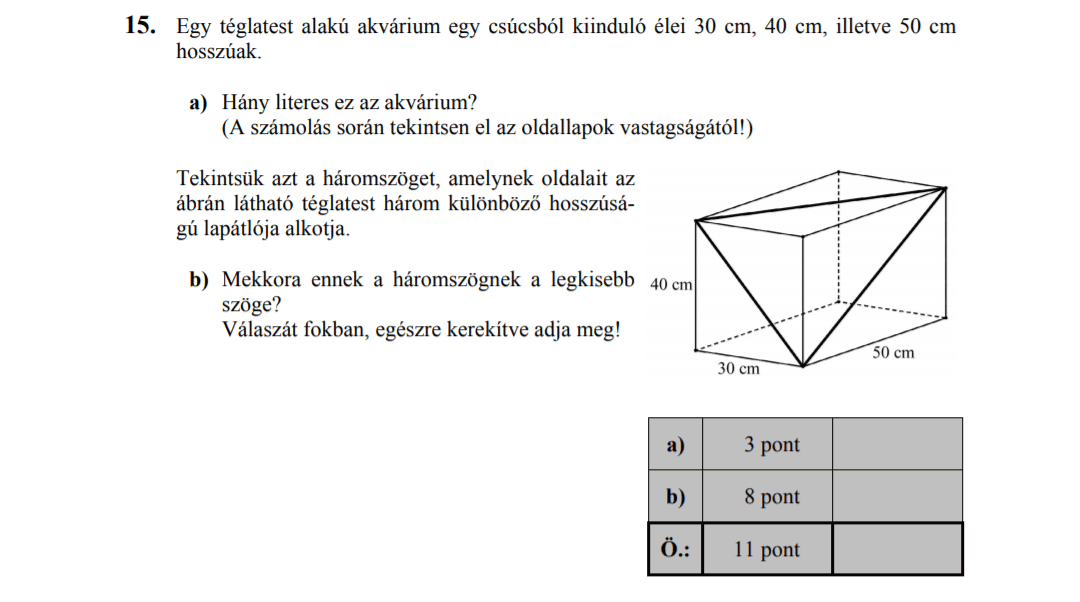

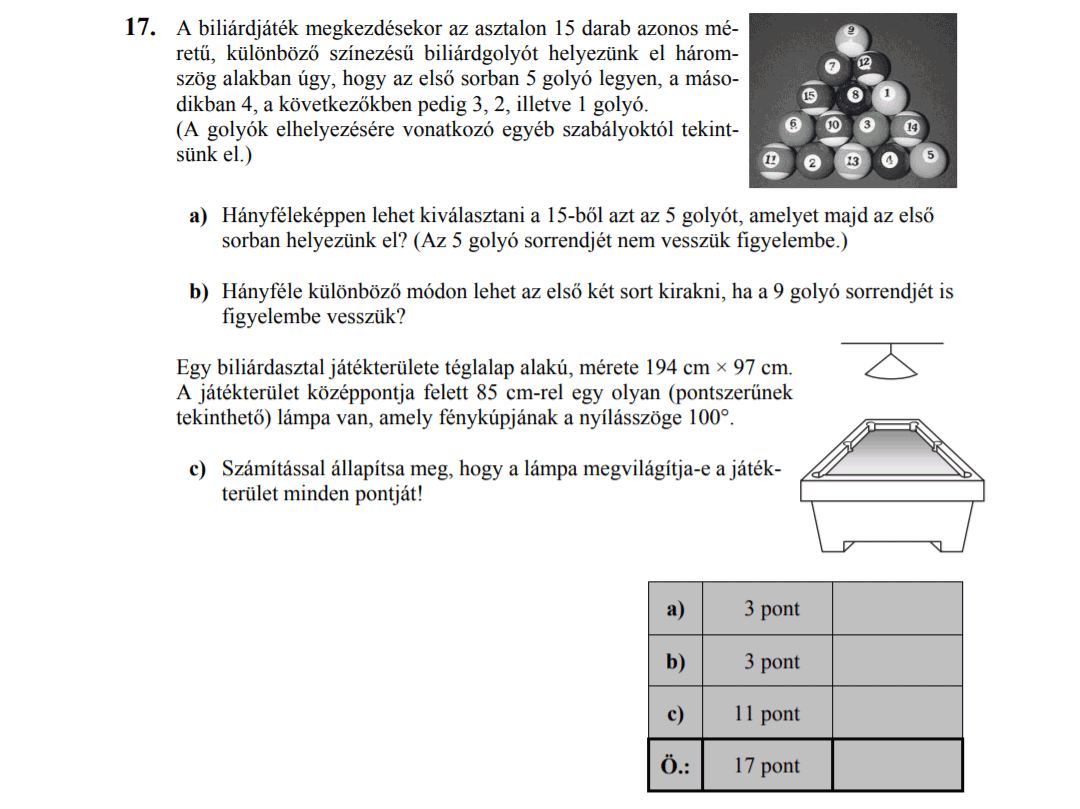

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


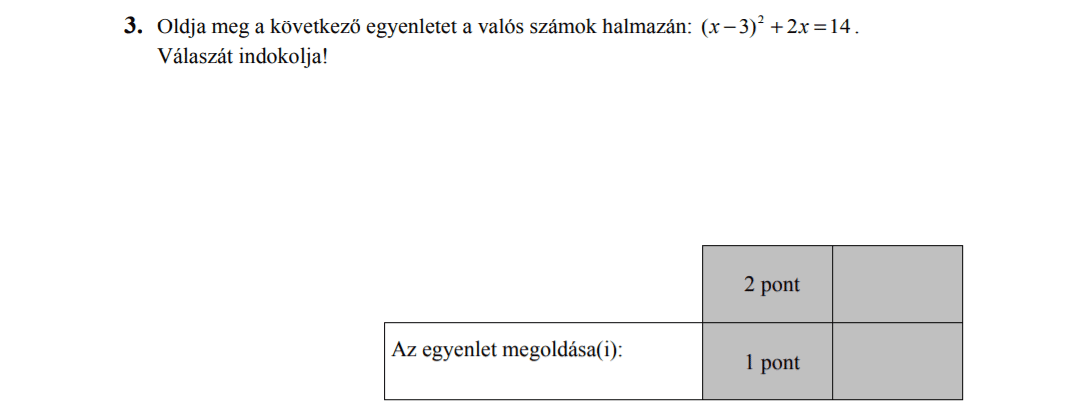


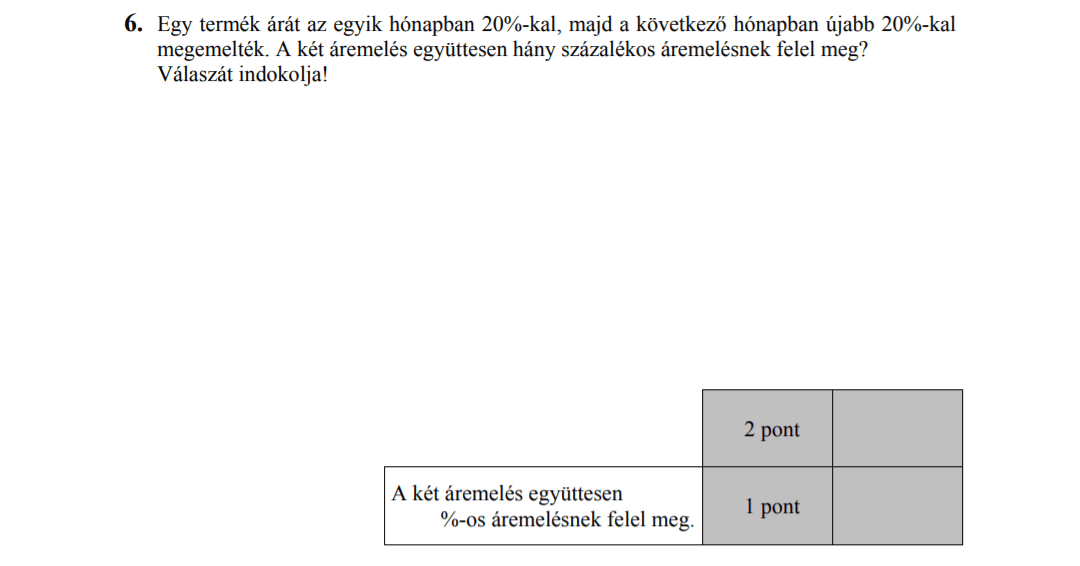
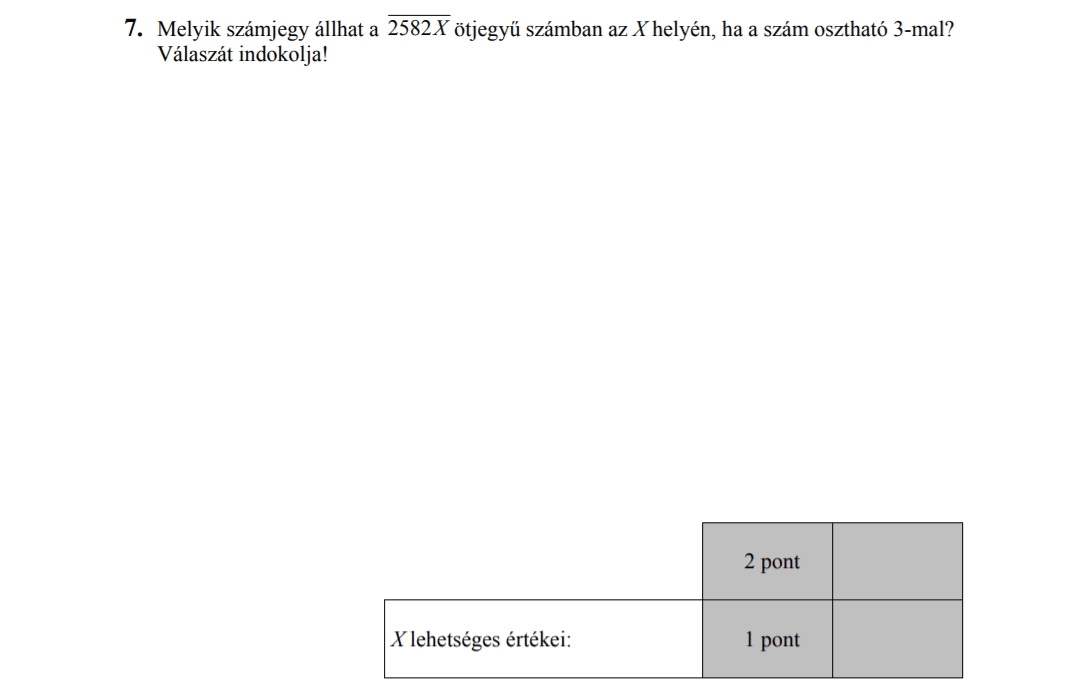
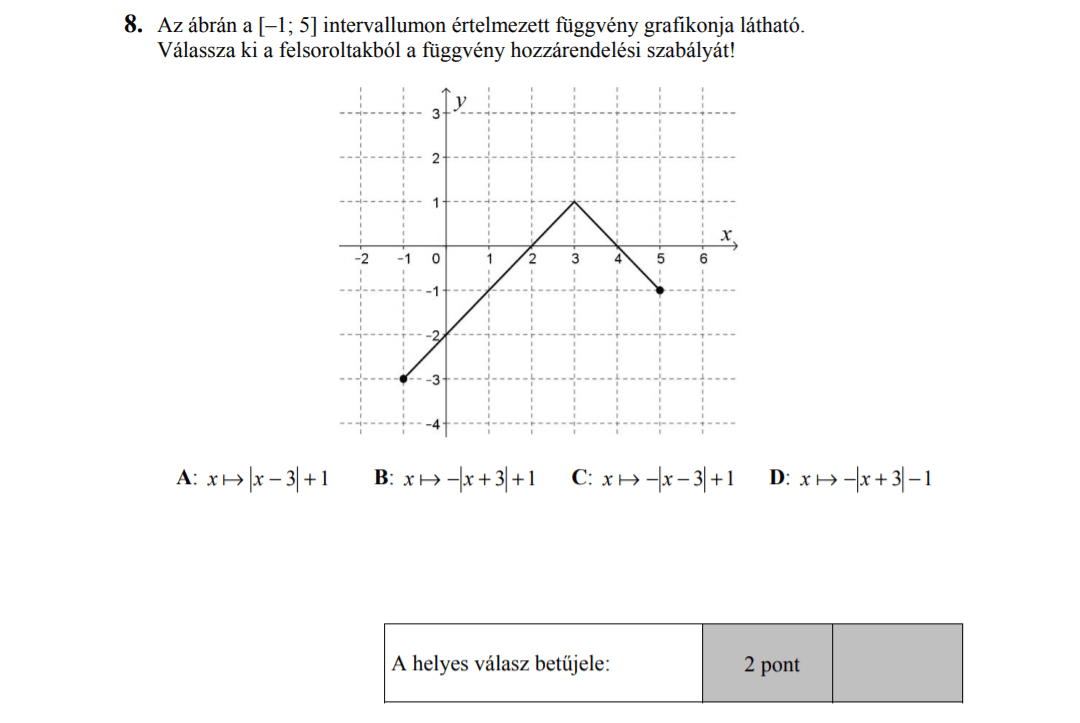


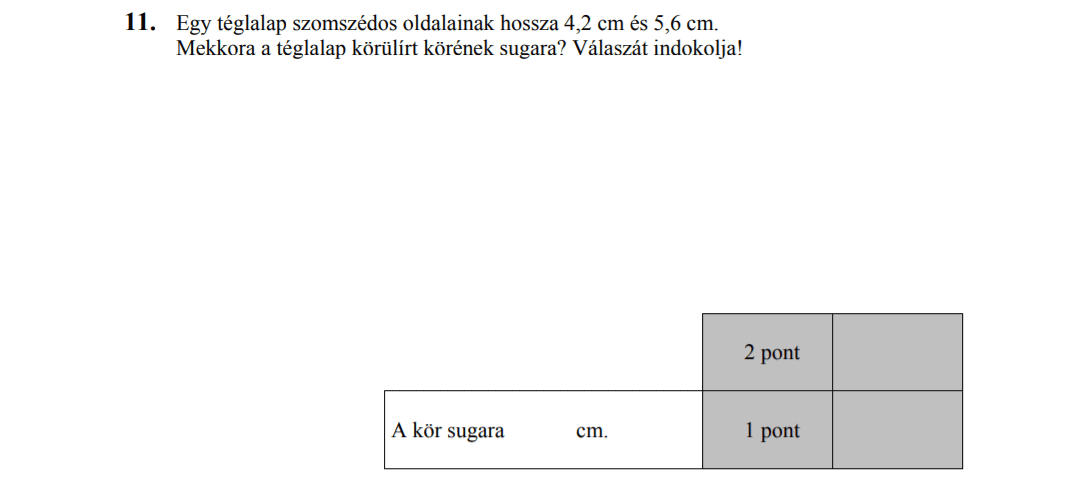

MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ

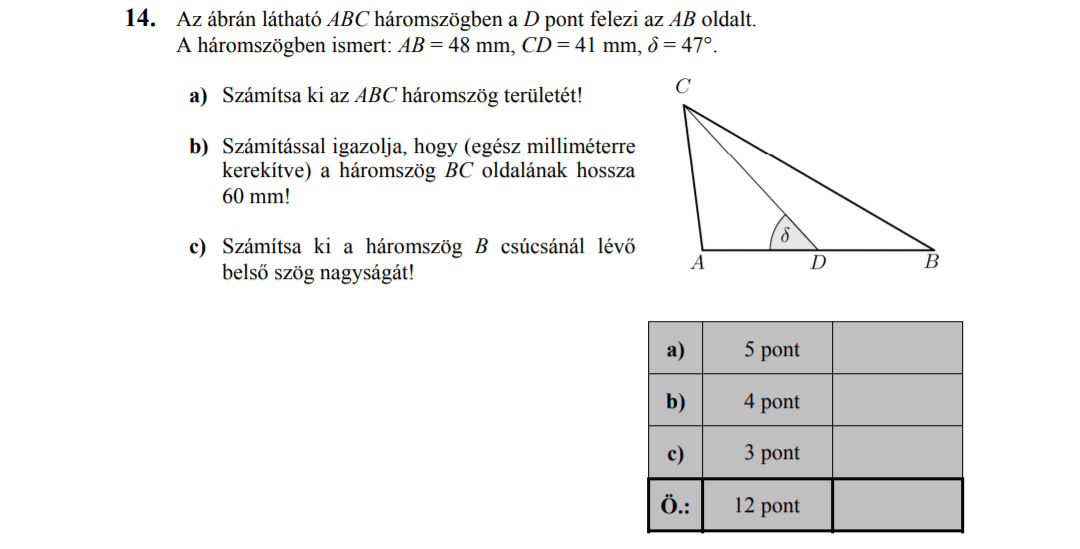




- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


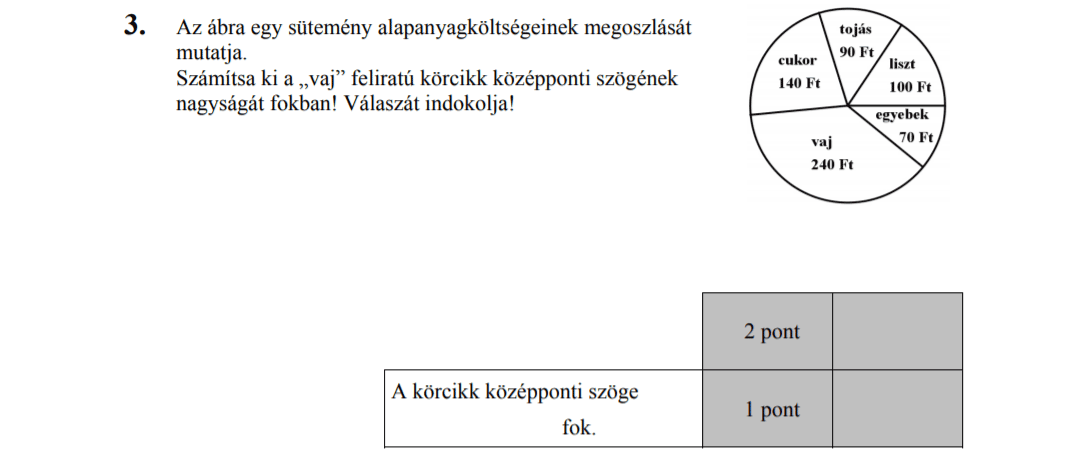
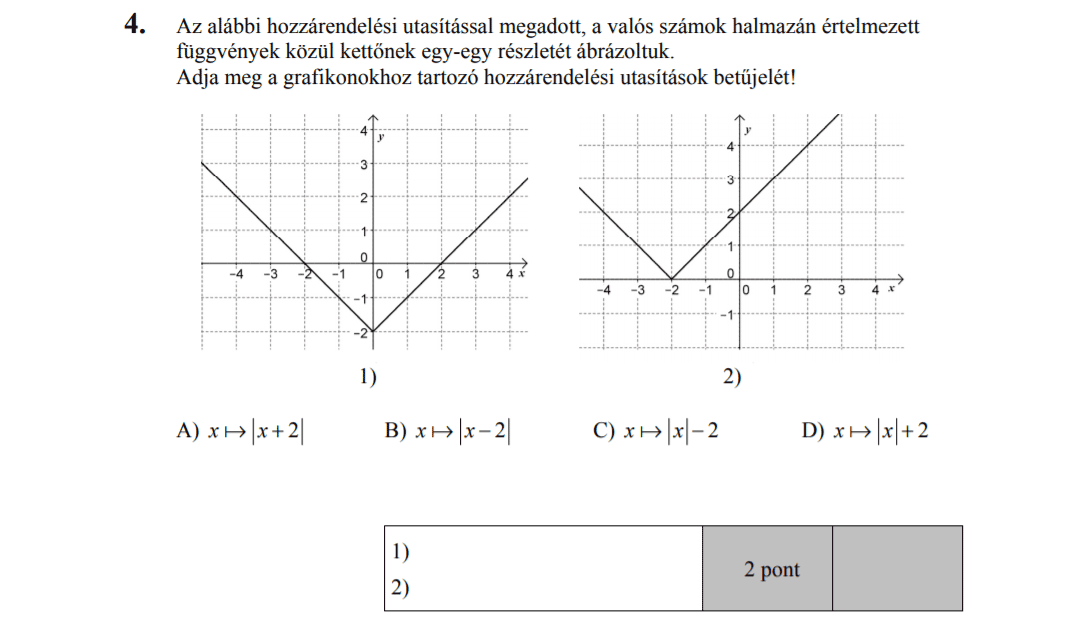
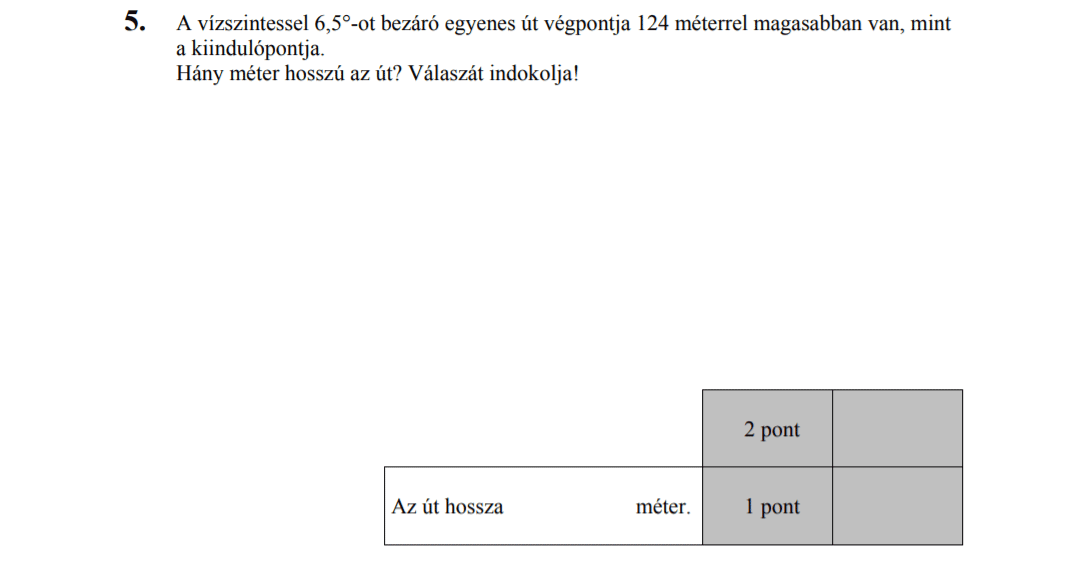

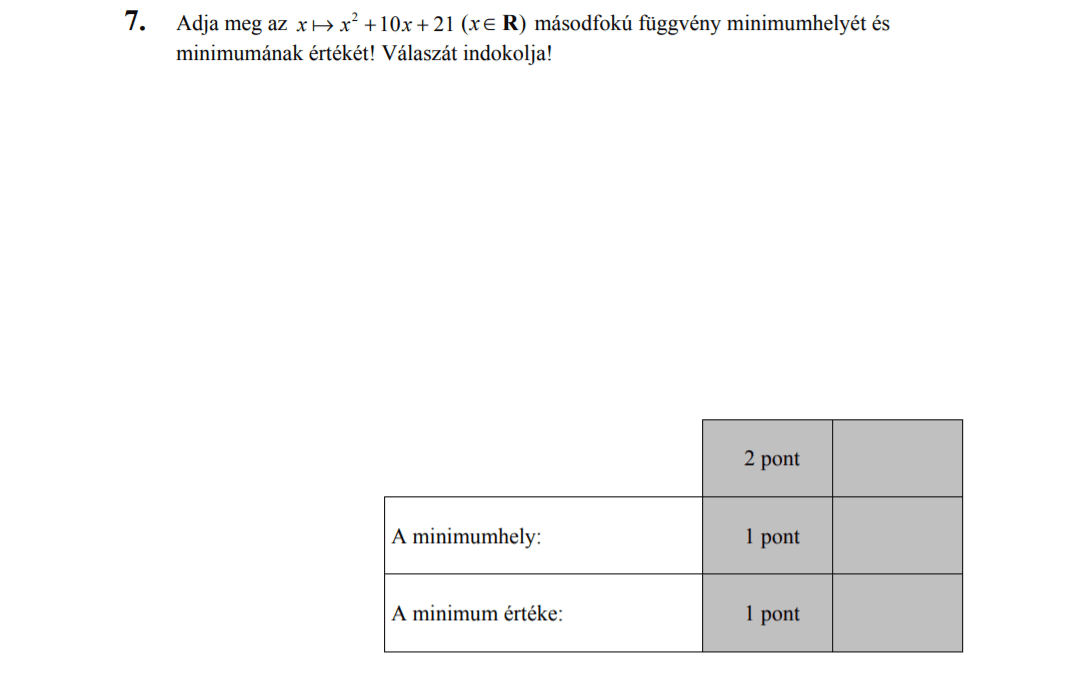



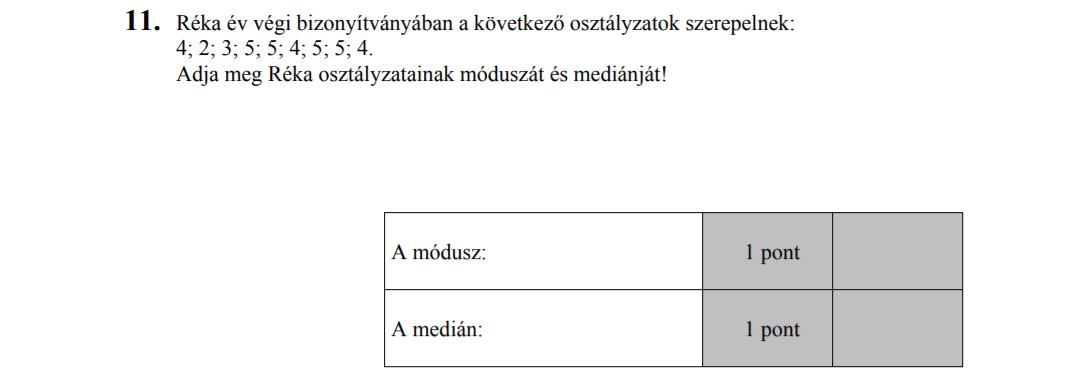

MÁSODIK RÉSZ





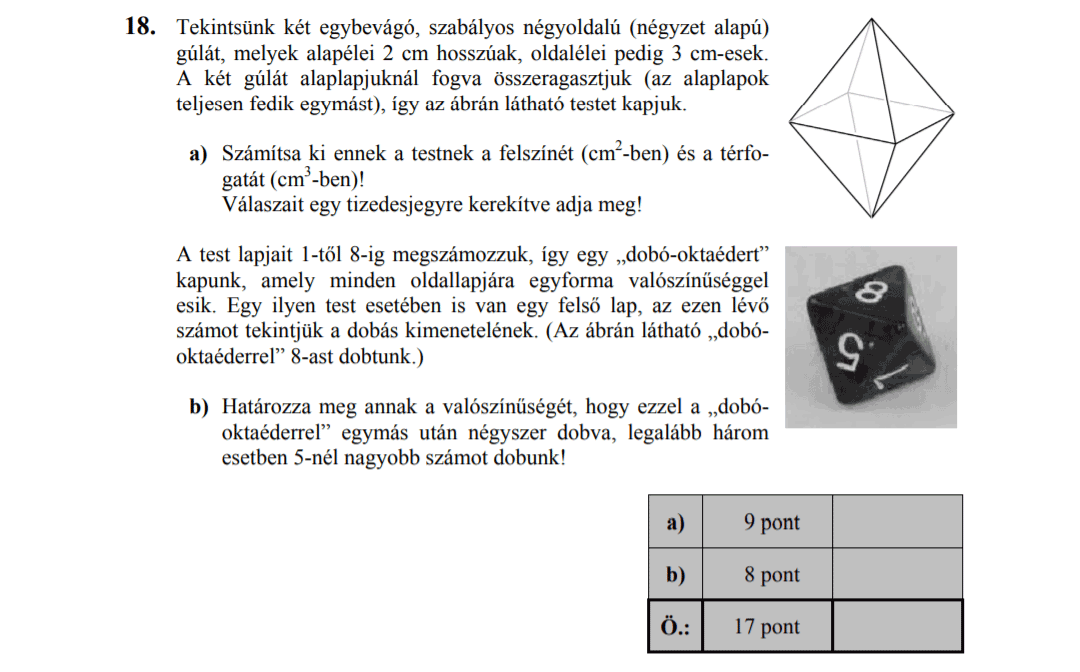
- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



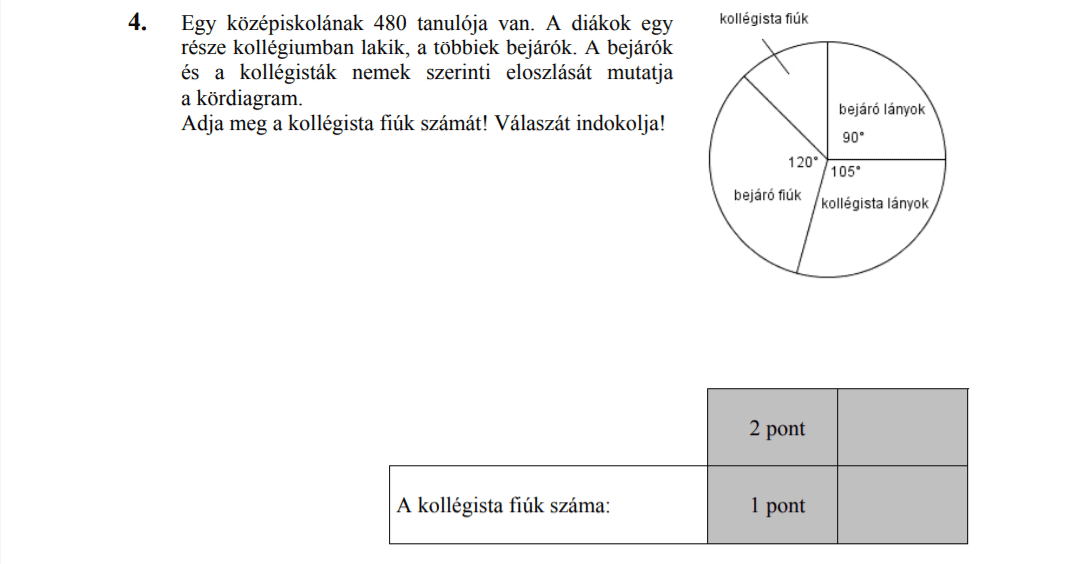





MÁSODIK RÉSZ






Elsőfokú egyenletek megoldása
A megoldás lényege, hogy gyűjtsük össze az $x$-eket az egyik oldalon, a másik oldalon pedig a számokat, a végén pedig leosztunk az $x$ együtthatójával.
Ha törtet is látunk az egyenletben, akkor az az első lépés, hogy megszabadulunk attól, mégpedig úgy, hogy beszorzunk a nevezővel.
Ha a tört nevezőjében $x$ is szerepel, akkor azzal kezdjük az egyenlet megoldását, hogy kikötjük, a nevező nem nulla.
Másodfokú egyenlet megoldóképlete
Ha a másodfokú egyenlet így néz ki:
\( a x^2 + bx + c = 0 \)
Akkor a megoldóképlet:
\( x_{1,2} = \frac{ -b \pm \sqrt{b^2-4ac} }{2a} \)
Diszkrimináns
A másodfokú egyenlet megoldóképletének gyök alatti részét nevezzük diszkriminánsnak.
\( D = b^2 -4ac \)
Ez dönti el, hogy a másodfokú egyenletnek hány valós megoldása lesz.
Ha a diszkrimináns nulla, akkor csak egy.
Ha a diszkrimináns pozitív, akkor az egyenletnek két valós megoldása van.
Ha pedig negatív, akkor az egyenletnek nincs valós megoldása.
Másodfokú egyenlet gyöktényezős alakja
Az $ax^2+bx+c=0$ alakú másodfokú egyenlet gyöktényezős alakja:
\( ax^2 + bx + c = a (x-x_1)(x-x_2) \)
Viète-formulák
A Viète-formulák nem valami titkós gyógyszer hatóanyag, hanem a másodfokú egyenlet gyökei és együtthatói közötti összefüggéseket írja le:
\( x_1 + x_2 = \frac{-b}{a} \qquad x_1 x_2 = \frac{c}{a} \)
Olyankor, amikor a másodfokú tag együtthatója 1, a Viète-formulák is egyszerűbbek:
\( x^2 + px + q = 0 \qquad x_1 + x_2 = -p \qquad x_1 x_2 = q \)
Oldd meg az alábbi egyenleteket.
a) \( 3x+2=12-2x \)
b) \( \frac{2x+1}{7} + x -2 = \frac{x+5}{4} \)
c) \( \frac{x+2}{x-5}=3 \)
d) \( \frac{x}{x+2} +3 = \frac{4x+1}{x} \)
Oldd meg az alábbi egyenleteket.
a) \( 3x^2-14x+8=0 \)
b) \( -2x^2+5x-3=0 \)
c) \( 4x + \frac{9}{x}=12 \)
d) \( x^2-6x+10=0 \)
Oldd meg az alábbi egyenleteket.
a) \( x^2+17x+16=0 \)
b) \( x^2+7x+12=0 \)
c) \( x^2-10x+20=0 \)
d) \( x^2-6x-16=0 \)
e) \( 3x^2-12x-15=0 \)
f) \( 4x^2+11x-3=0 \)
Alakítsd szorzattá.
a) \( x^2-6x-16=0 \)
b) \( x^2-7x+12=0 \)
c) \( 3x^2-14x+8=0 \)
Milyen \( A \) paraméter esetén van egy darab megoldása az egyenletnek?
a) \( x^2+2x+A=0 \)
b) \( x^2-Ax-3=0 \)
c) \( Ax^2+4x+1=0 \)
Milyen \( A \) paraméter esetén van egy darab megoldása az egyenletnek?
a) \( x^2+2x+A=0 \)
b) \( x^2-Ax-3=0 \)
c) \( Ax^2+4x+1=0 \)
Oldd meg az alábbi egyenleteket.
a) \( x^6-9x^3+8=0 \)
b) \( 4x^5-9x^4-63x^3=0 \)
c) \( x^9-7x^6-8x^3=0 \)
