- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
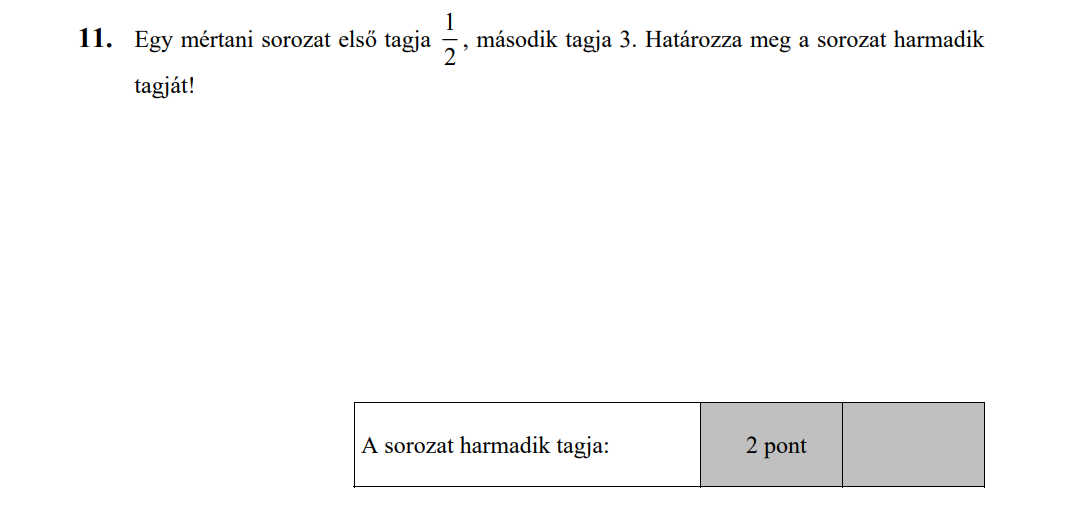
- Számtani és mértani sorozatok (16 pont)
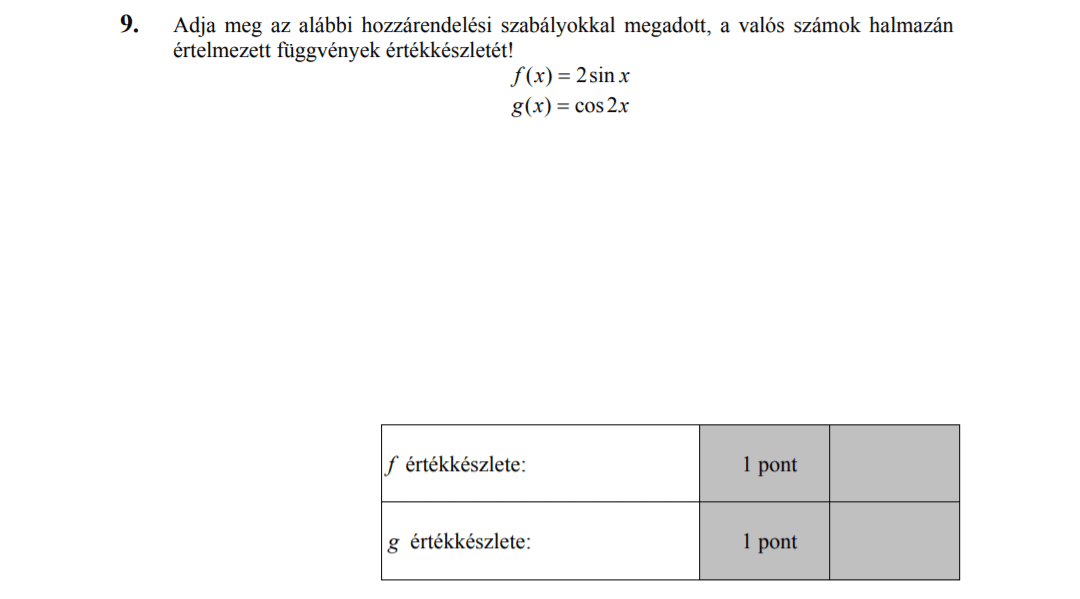
- Függvényekkel kapcsolatos feladatok (9,8 pont)
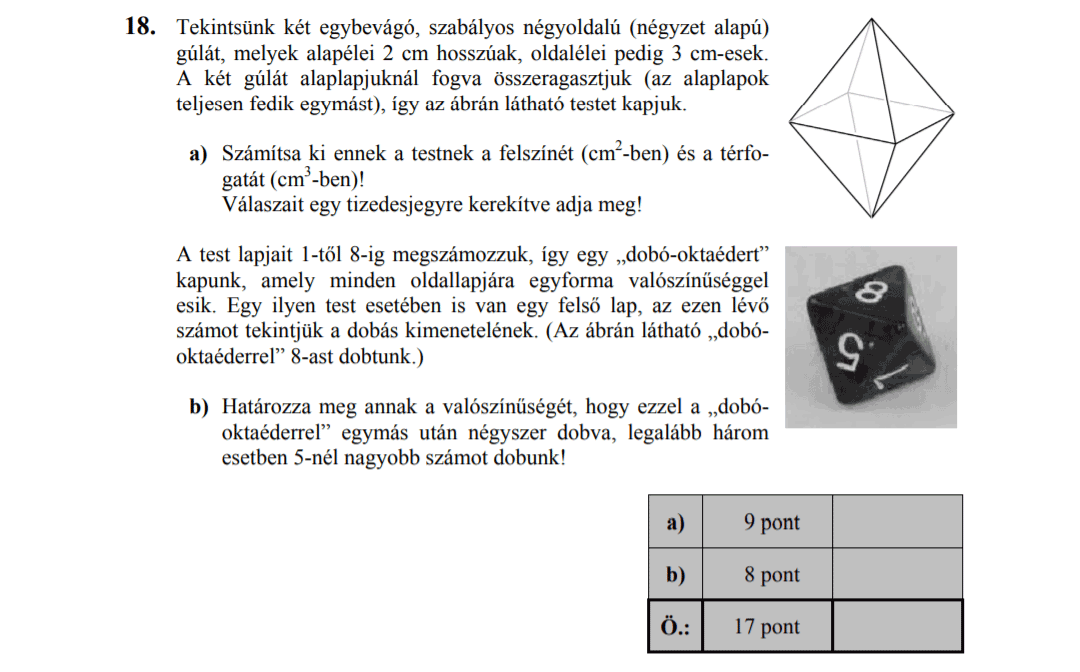
- Térgeometria (9,8 pont)
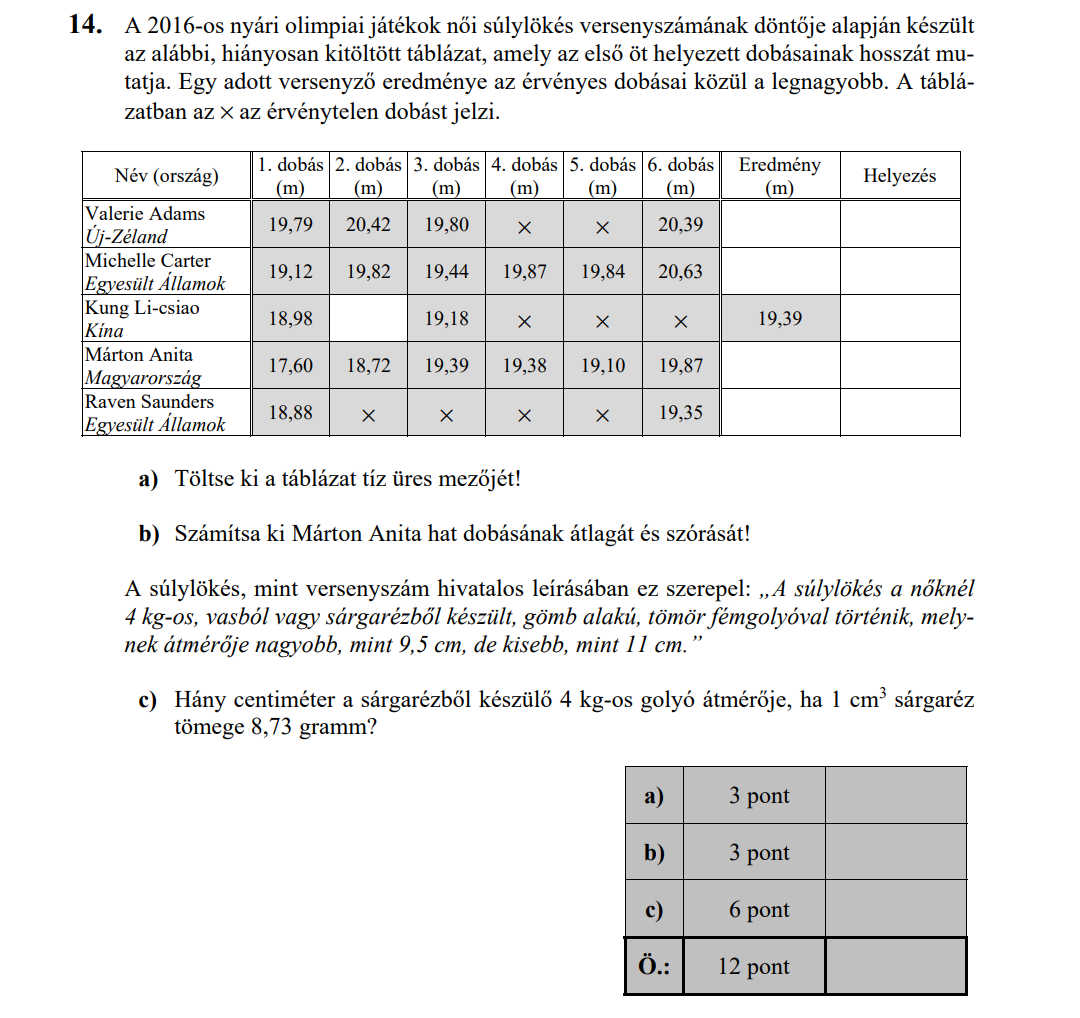
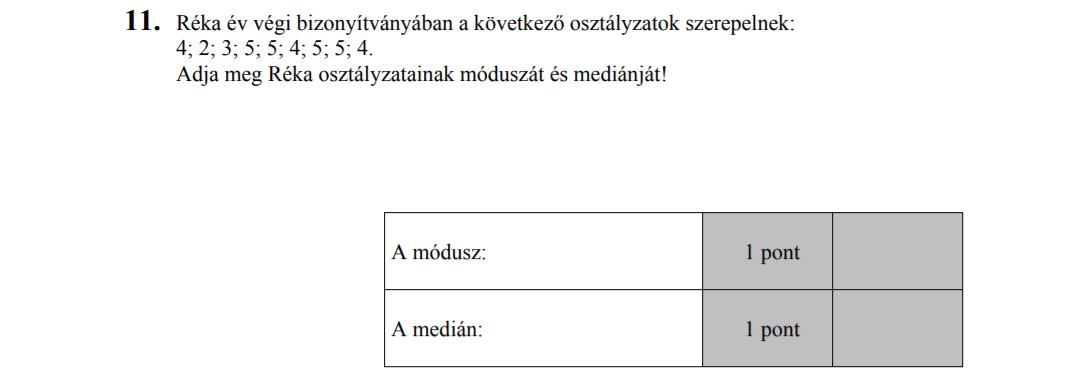
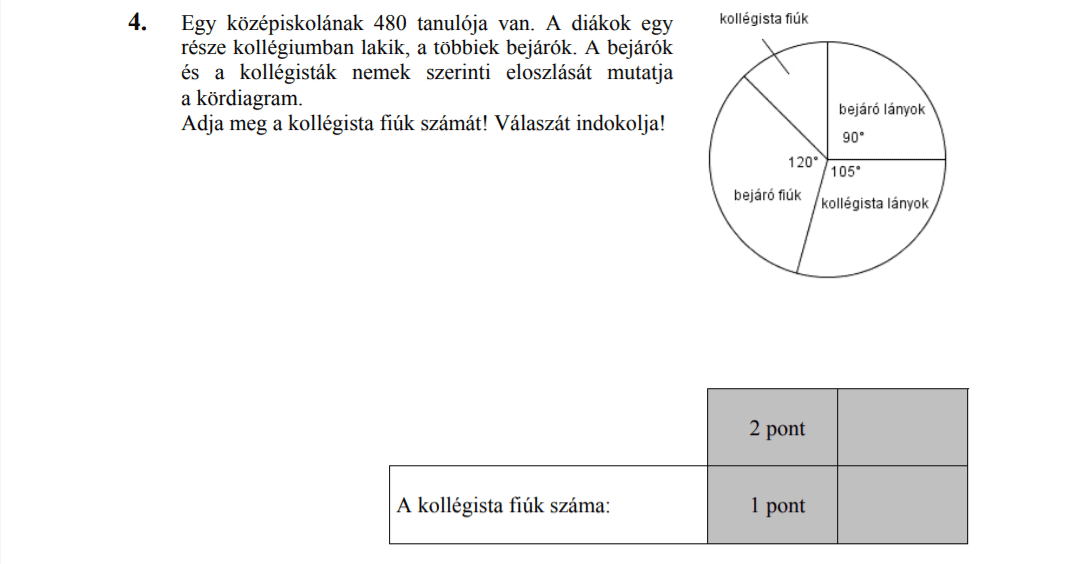
- Statisztika (9,3 pont)
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
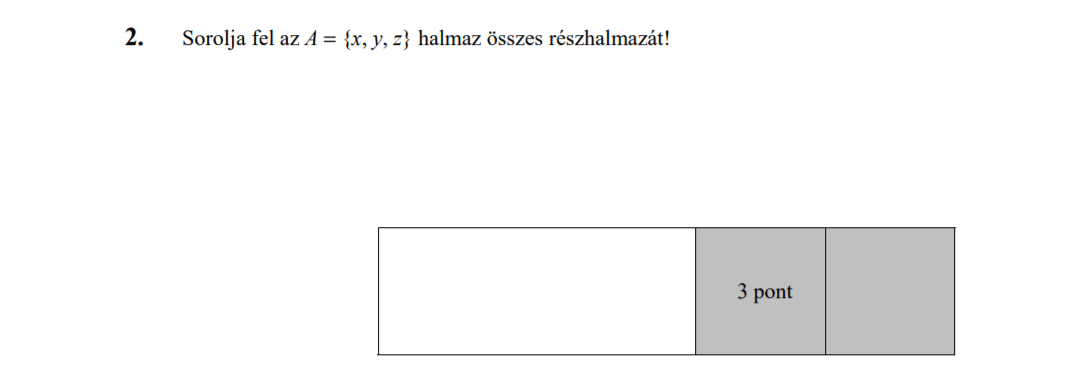
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
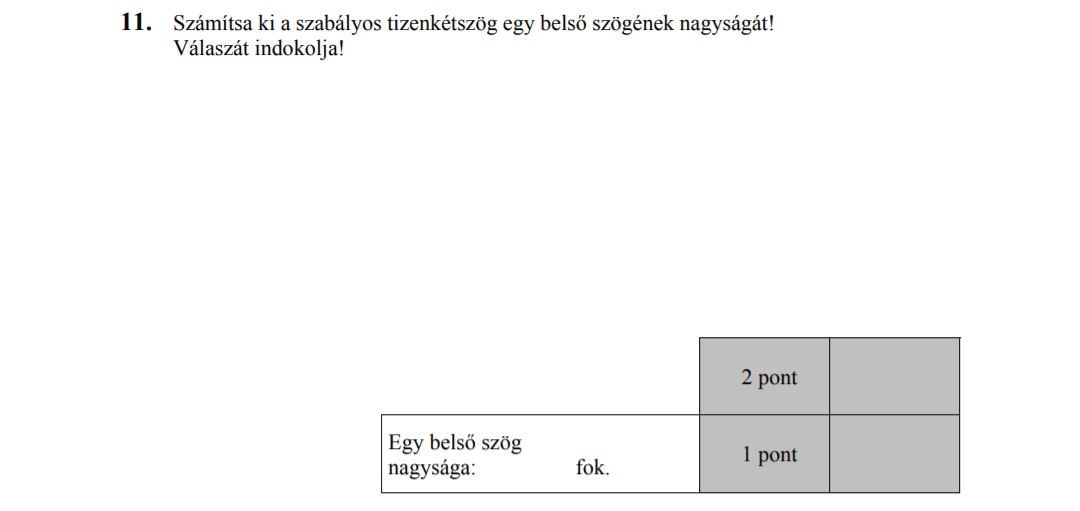
- Síkgeometria (4,5 pont)
- Százalékszámítás (3,8 pont)
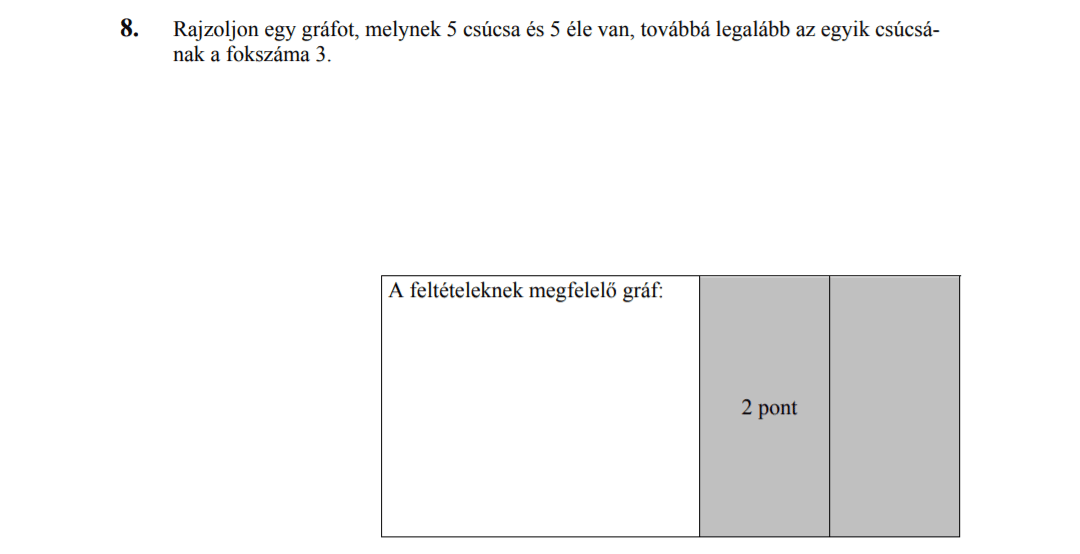
- Gráfok (3 pont)
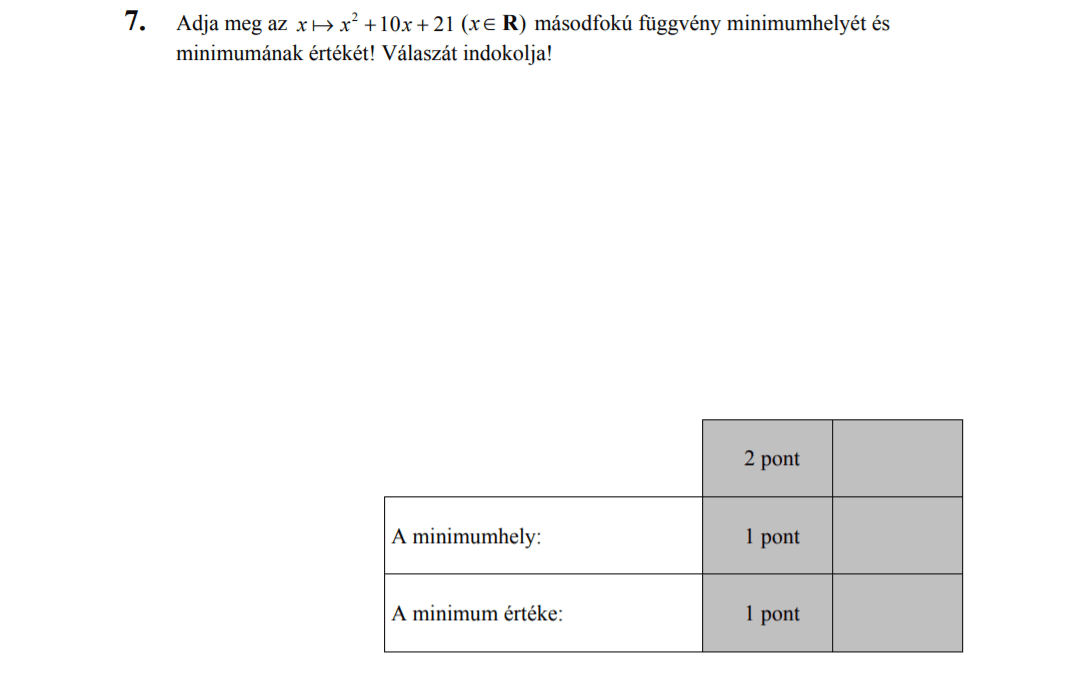
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
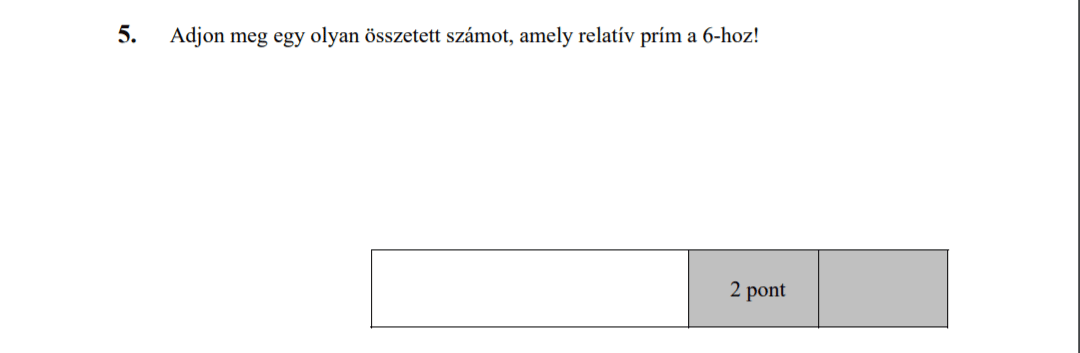
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
ÚJ! A várható érték
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


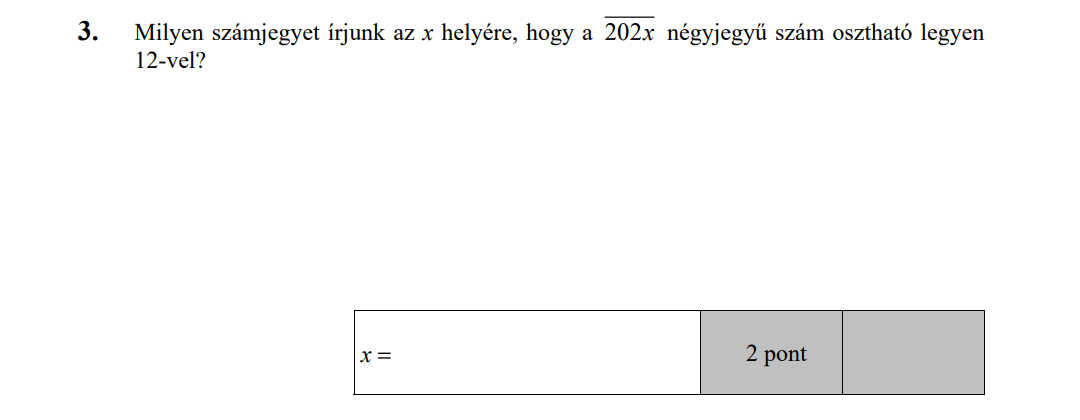
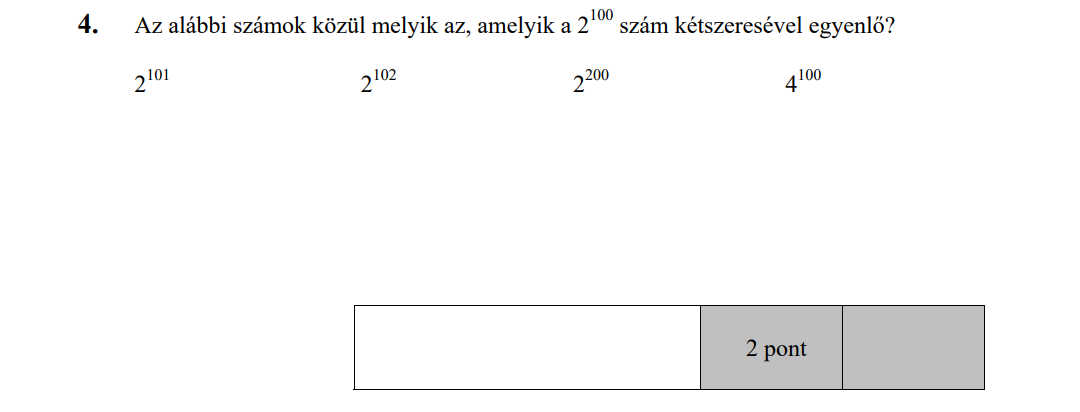



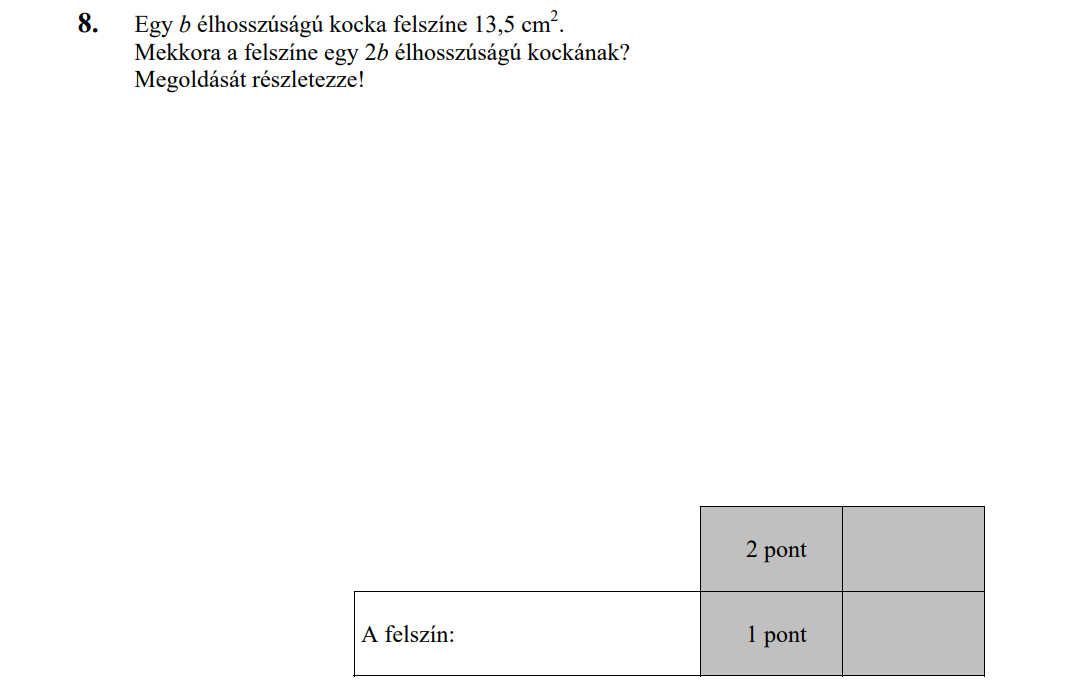




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
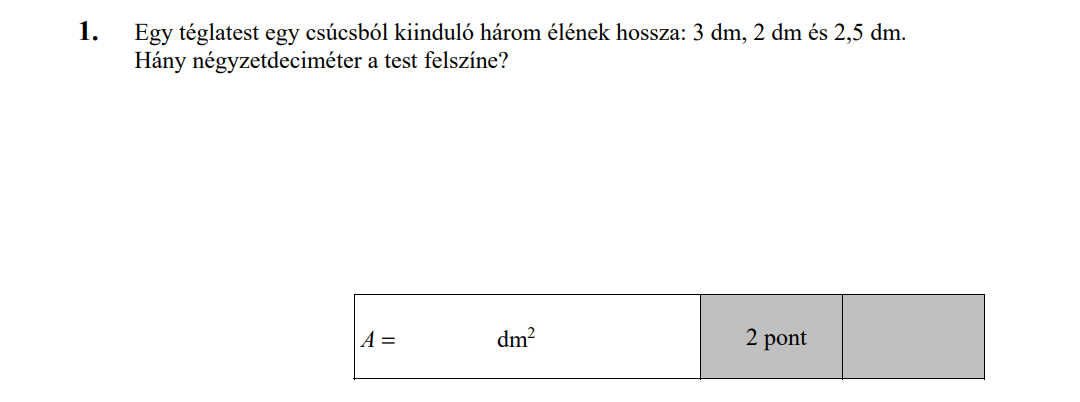
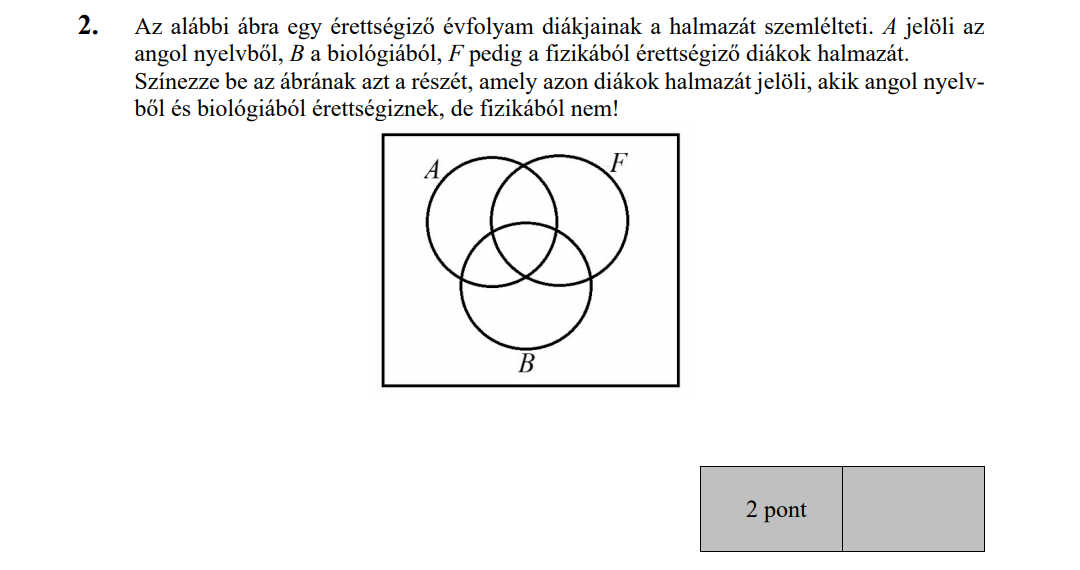

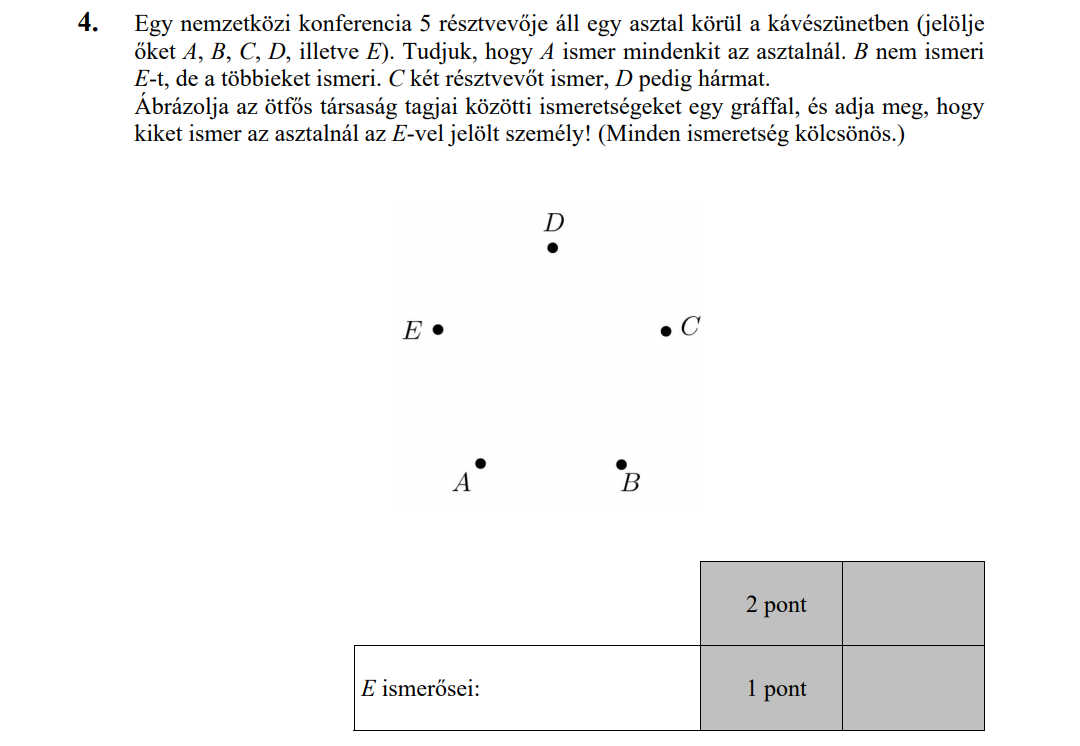

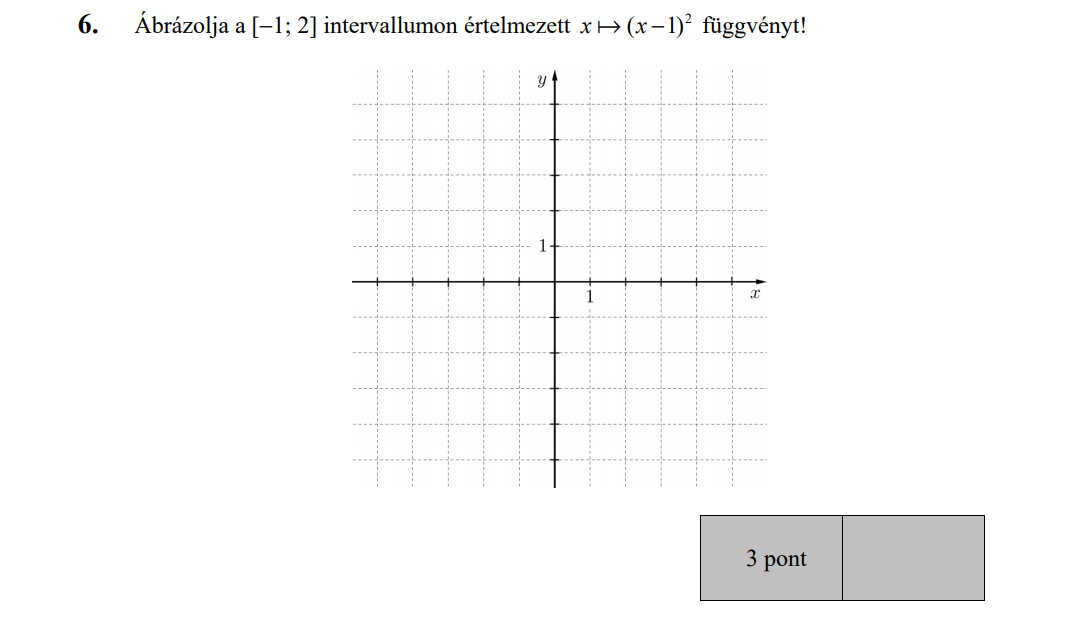



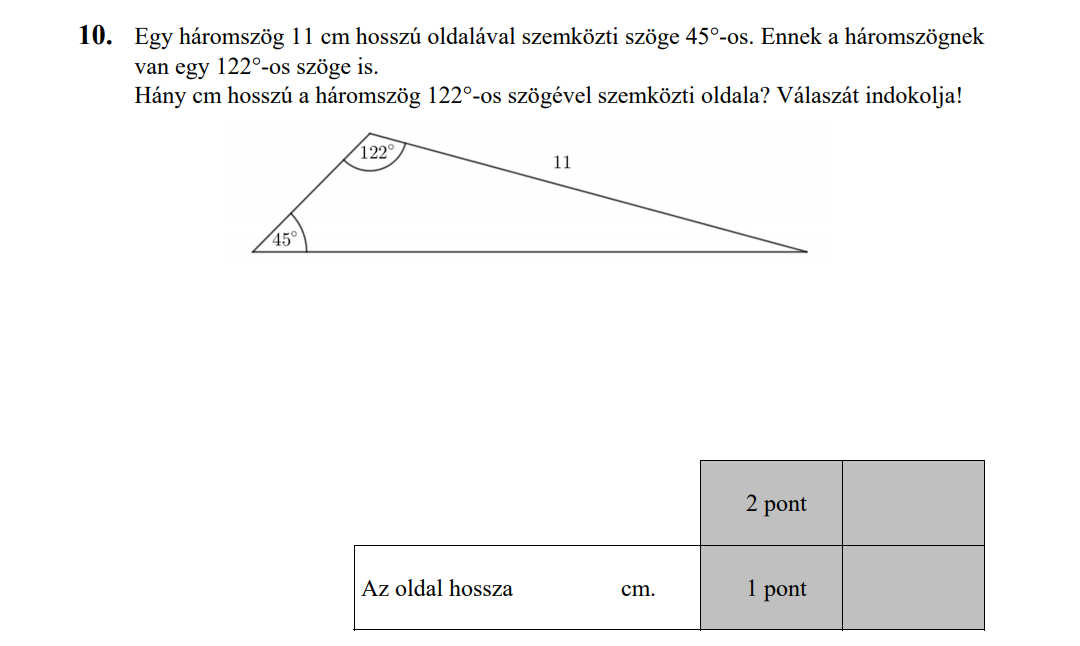

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



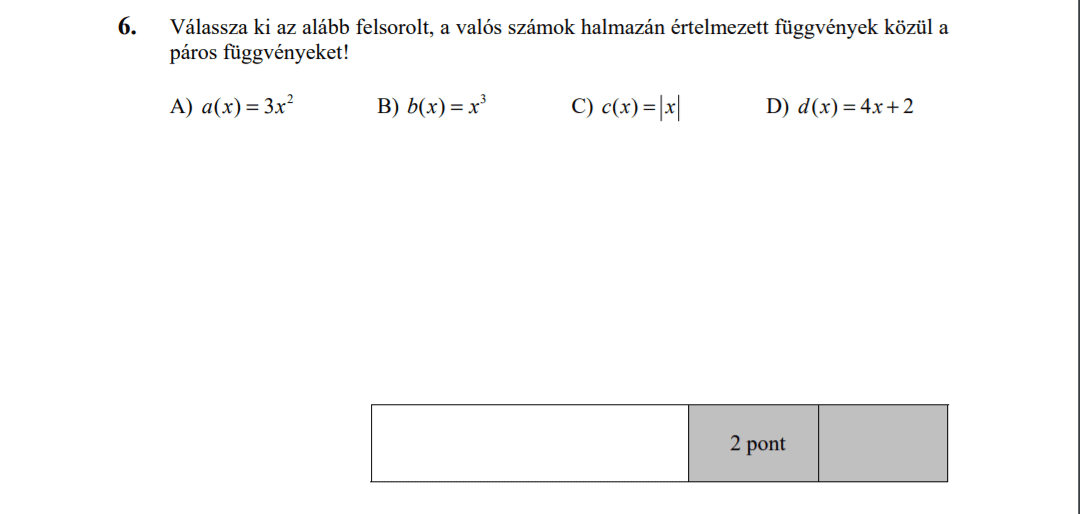
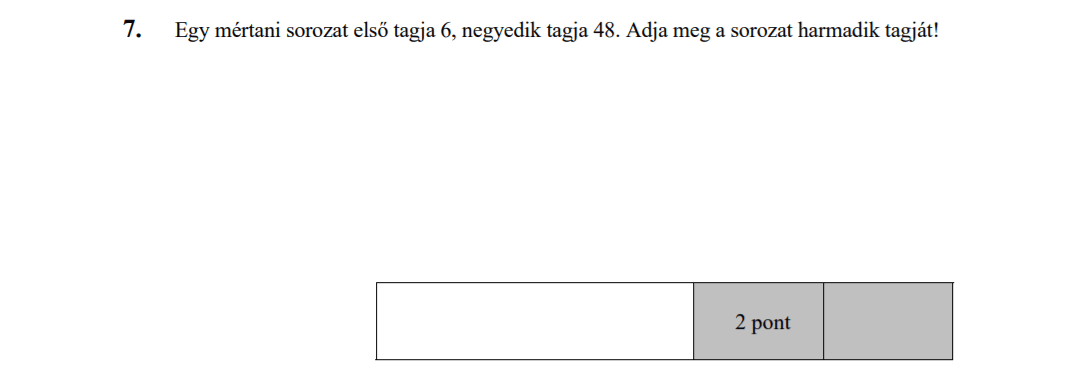



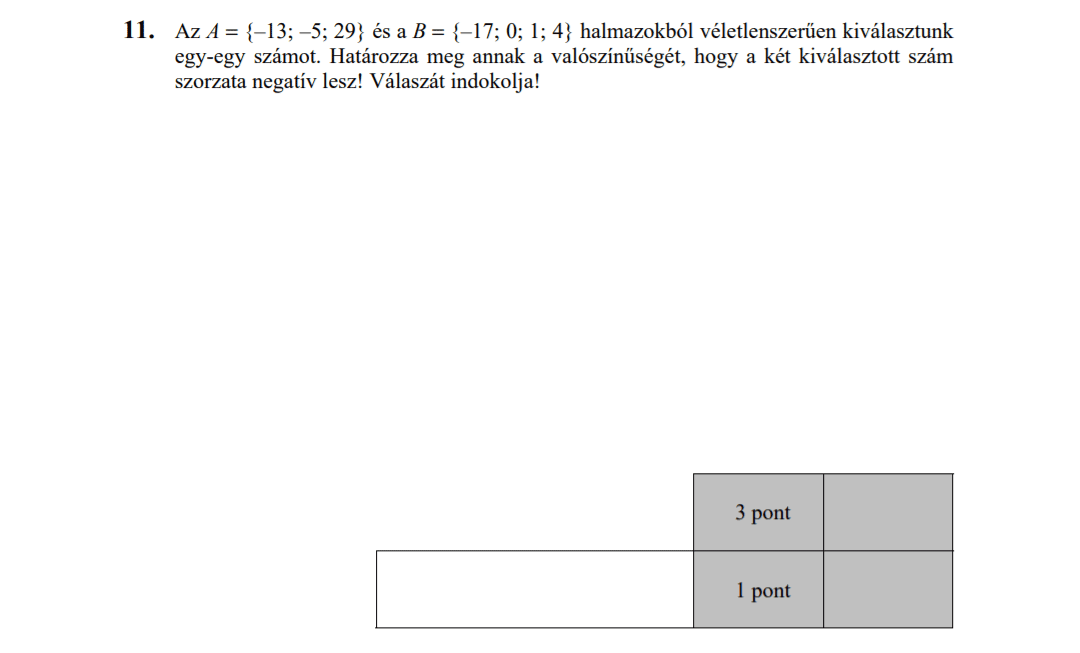

MÁSODIK RÉSZ


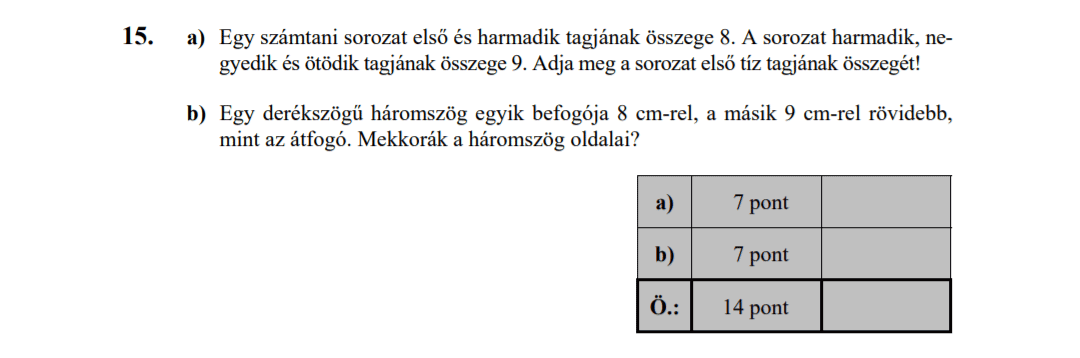



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






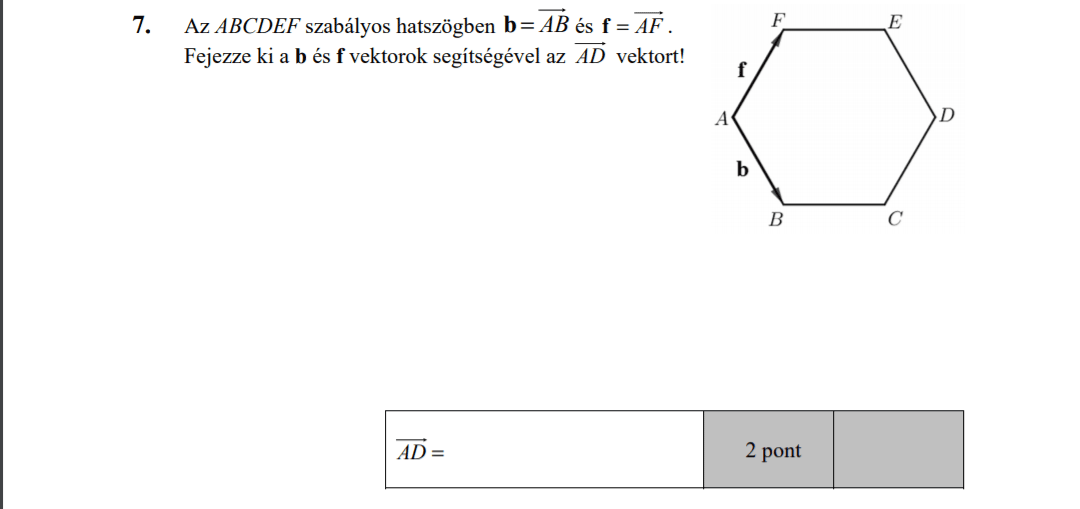



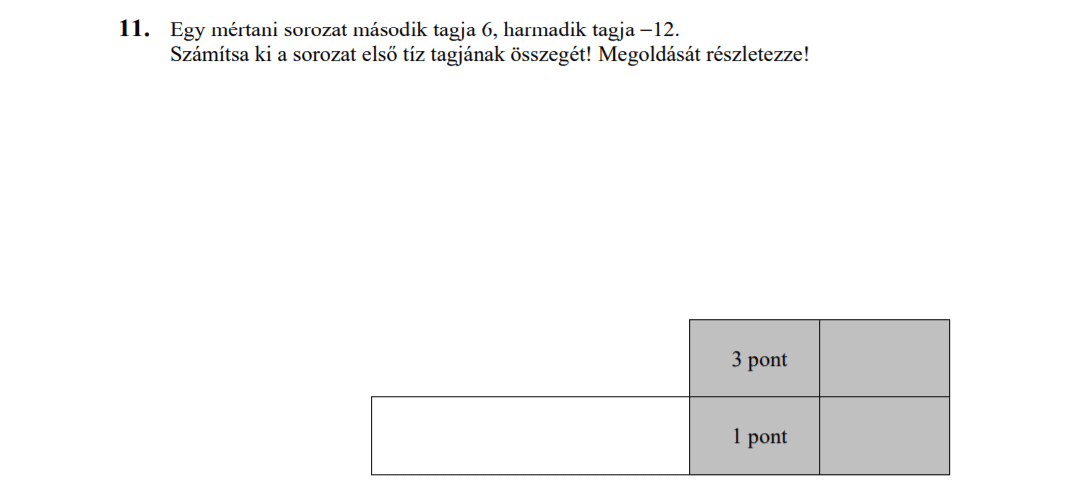

MÁSODIK RÉSZ

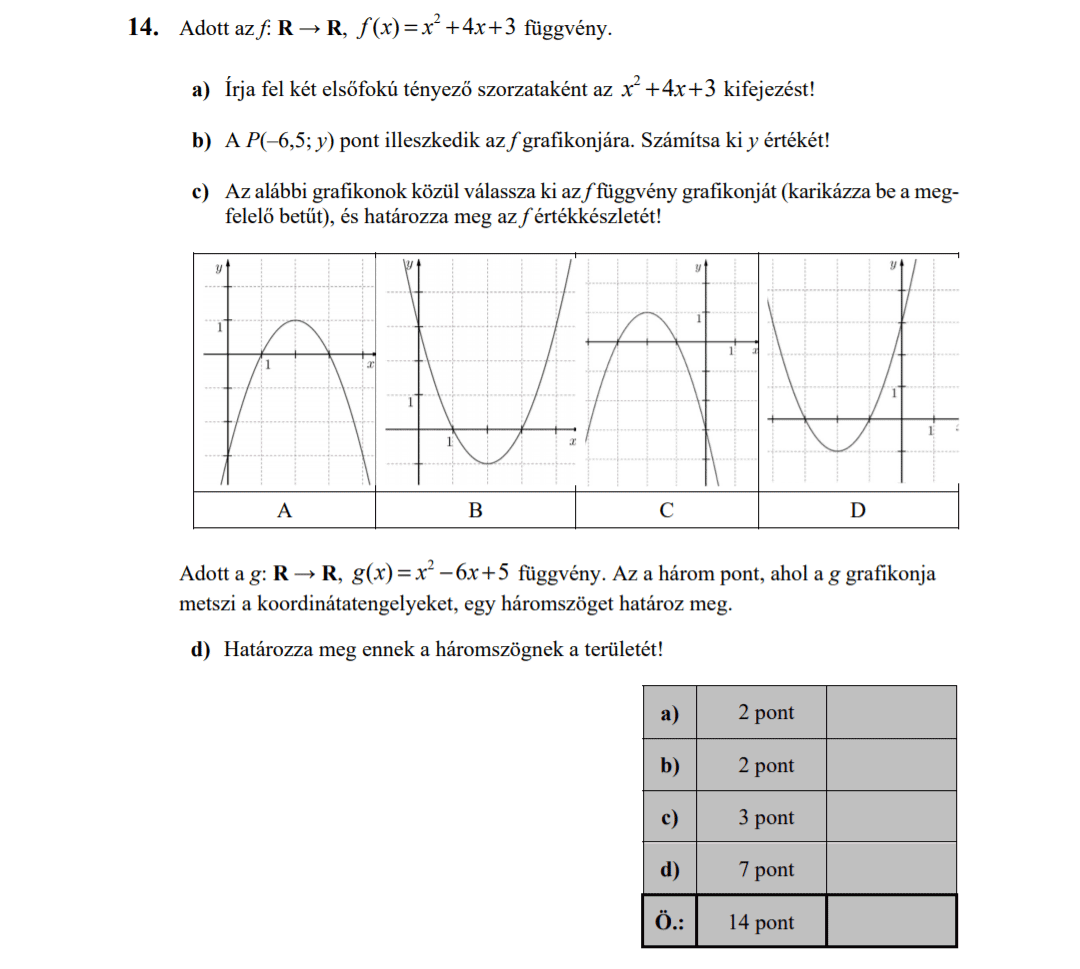




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



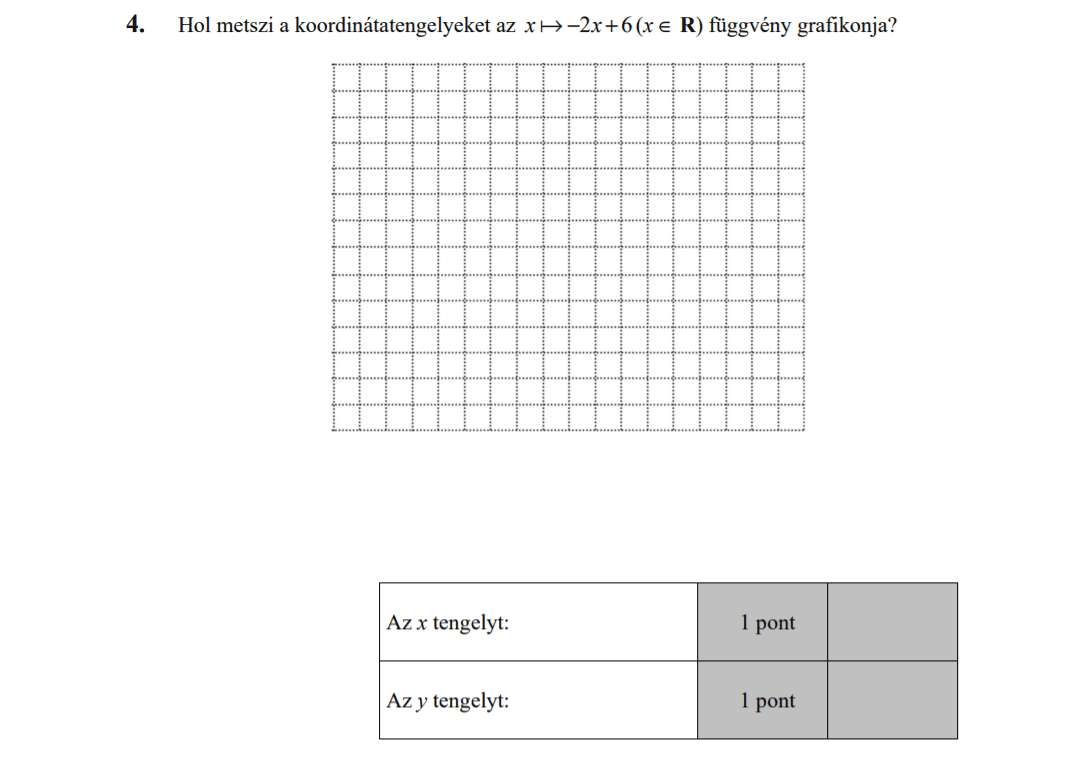







MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

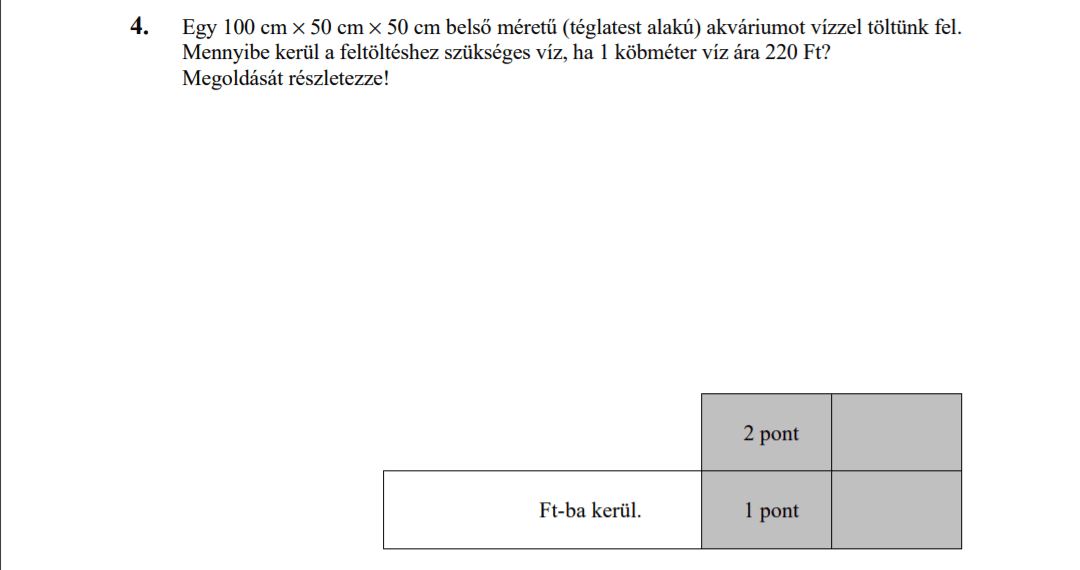
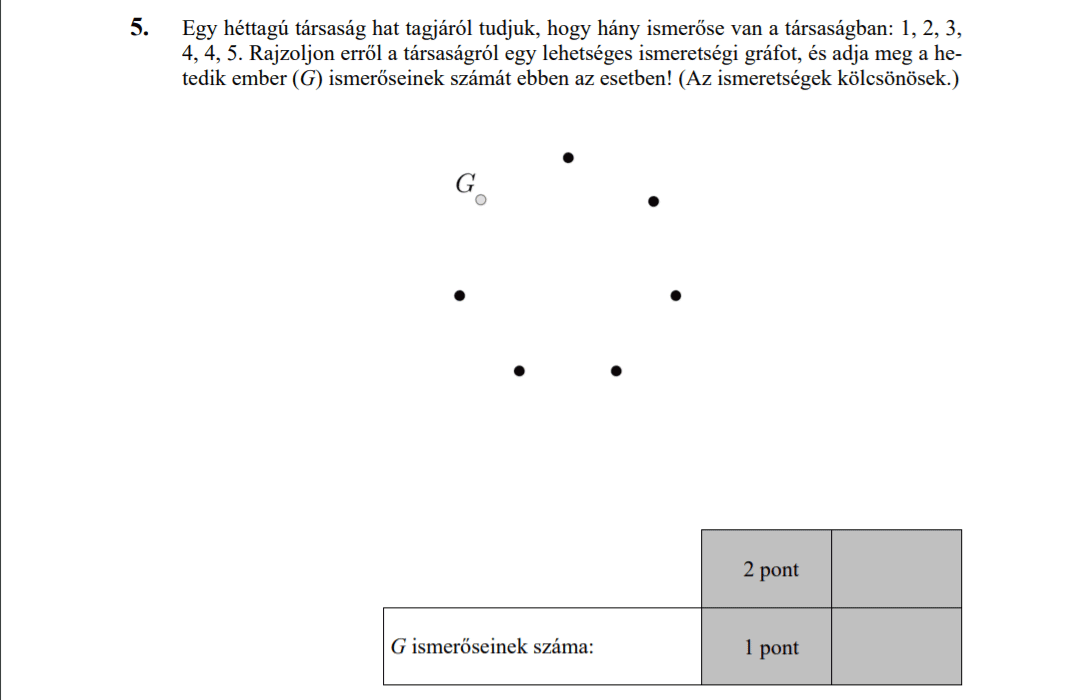







MÁSODIK RÉSZ
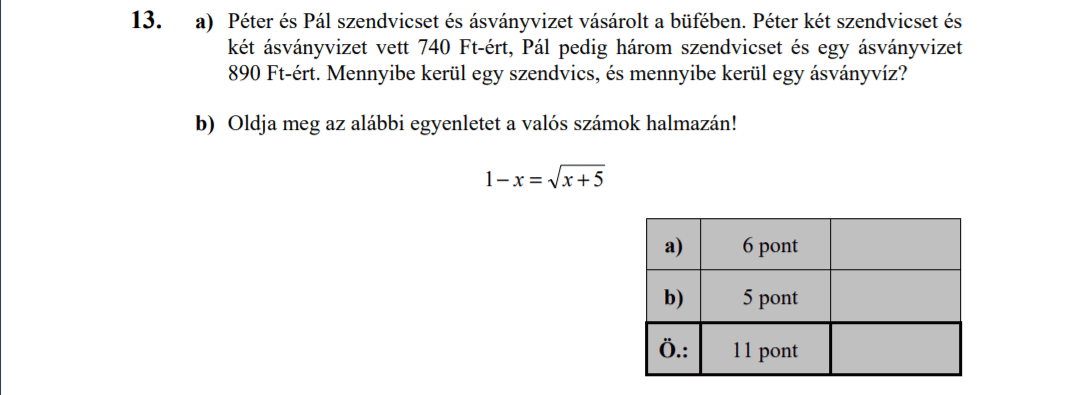
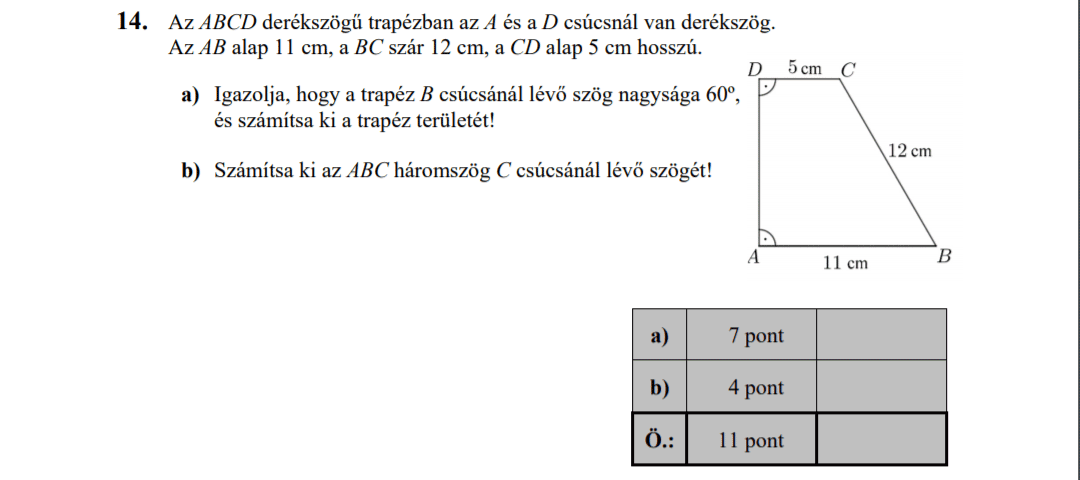

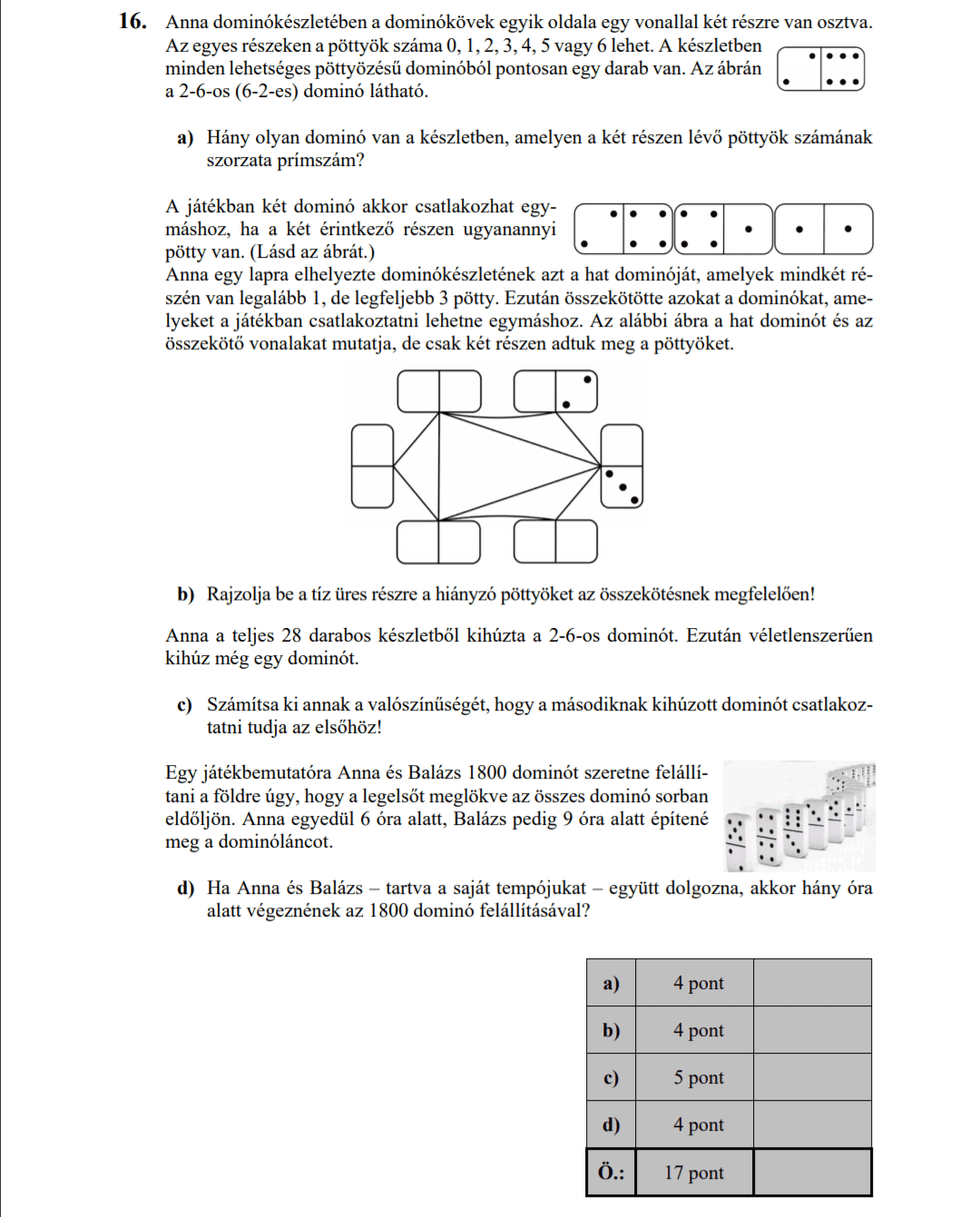


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




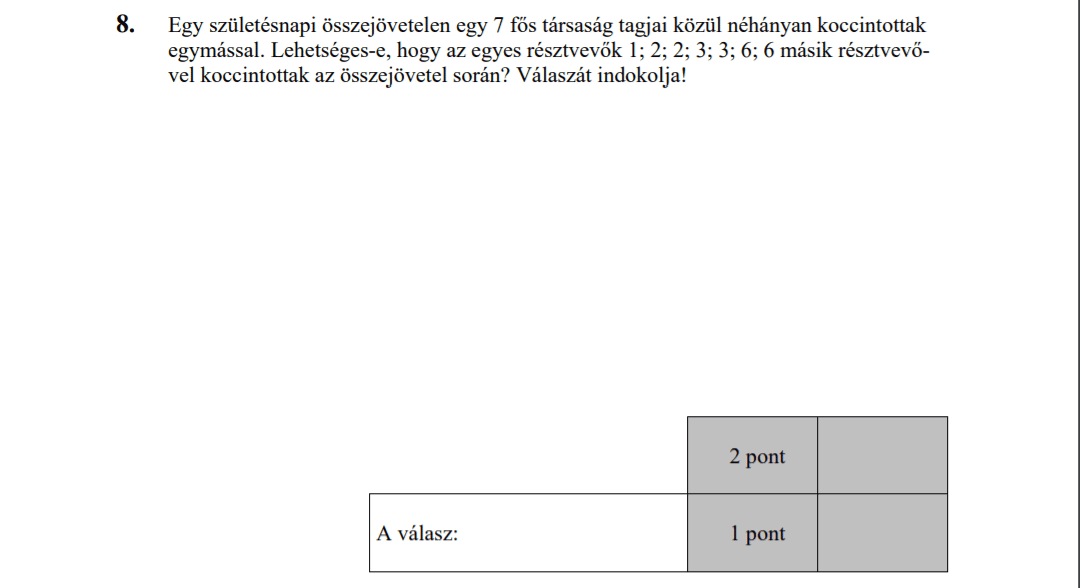



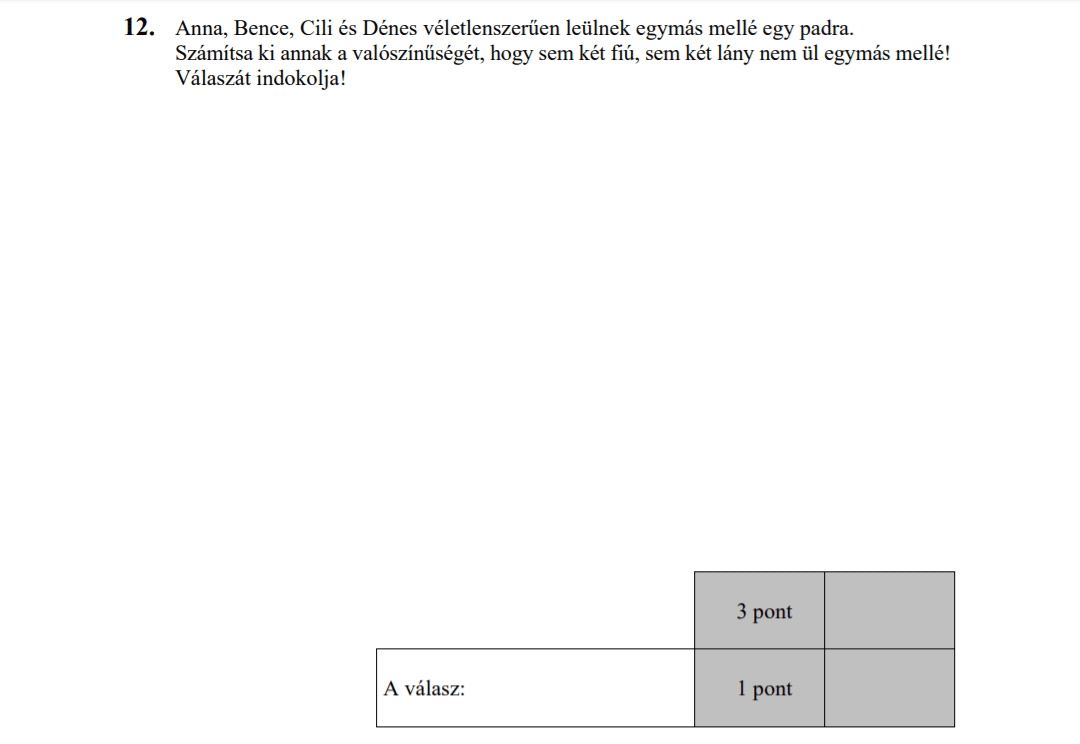
MÁSODIK RÉSZ

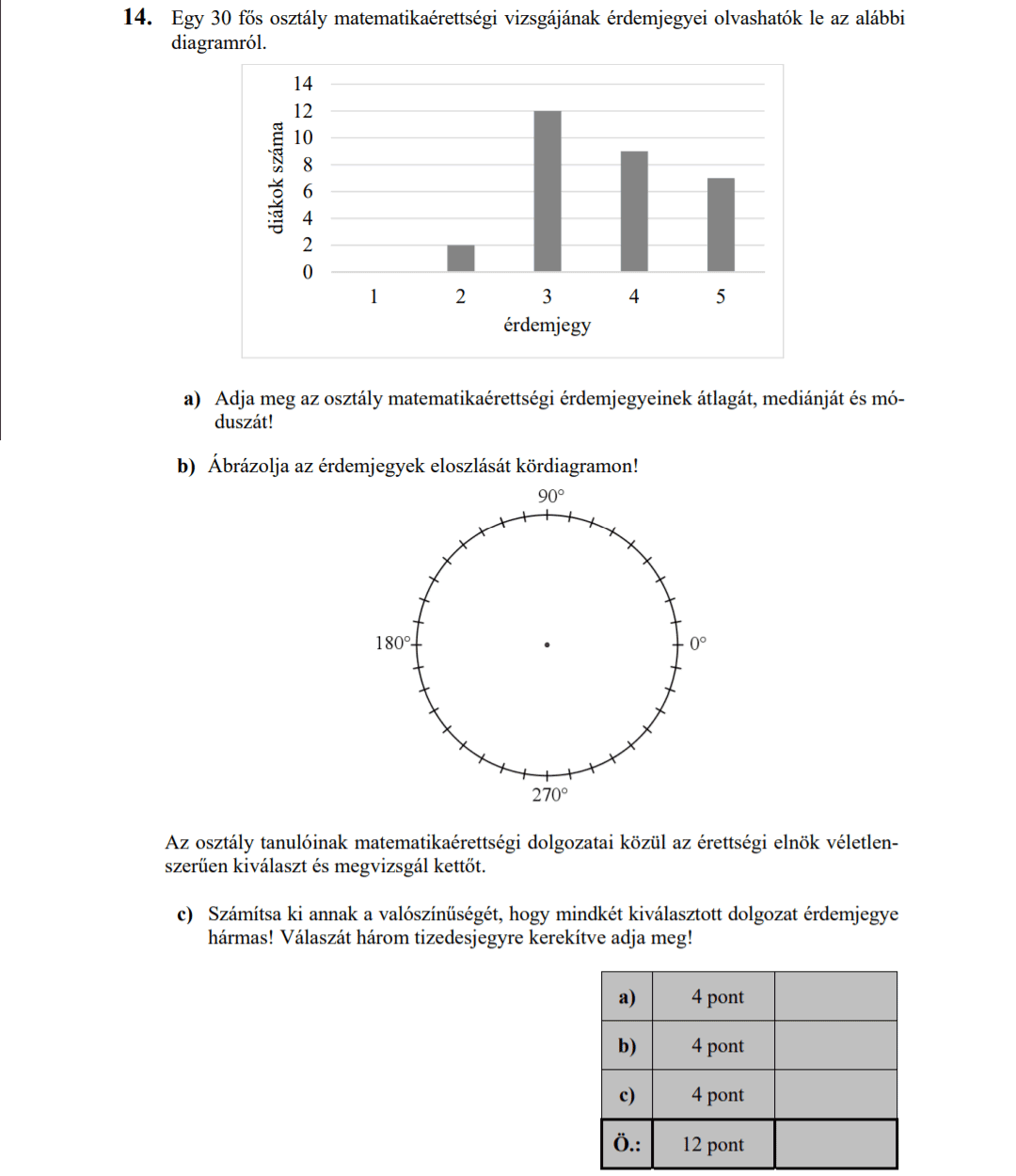
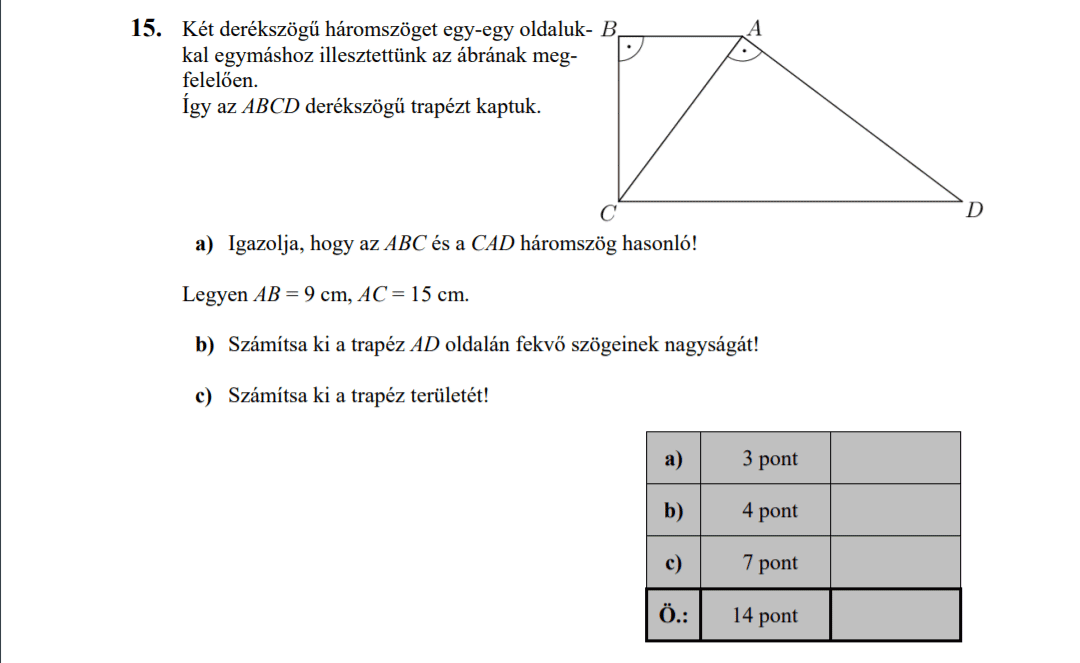



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


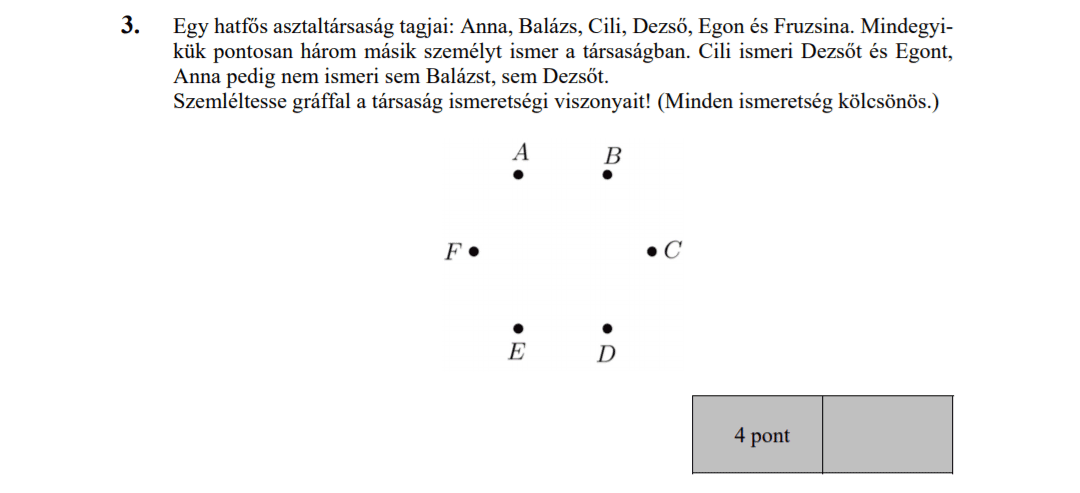


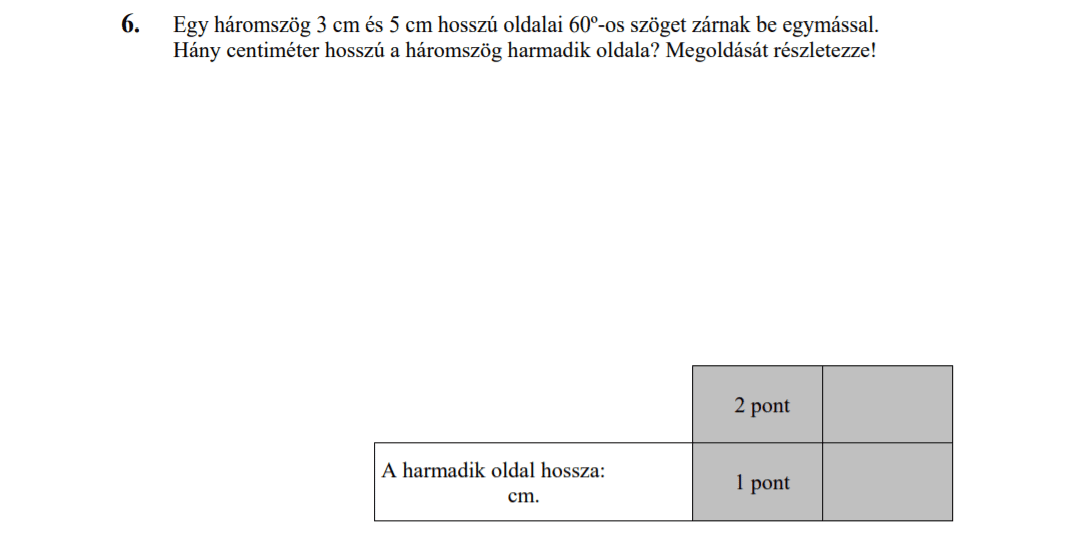

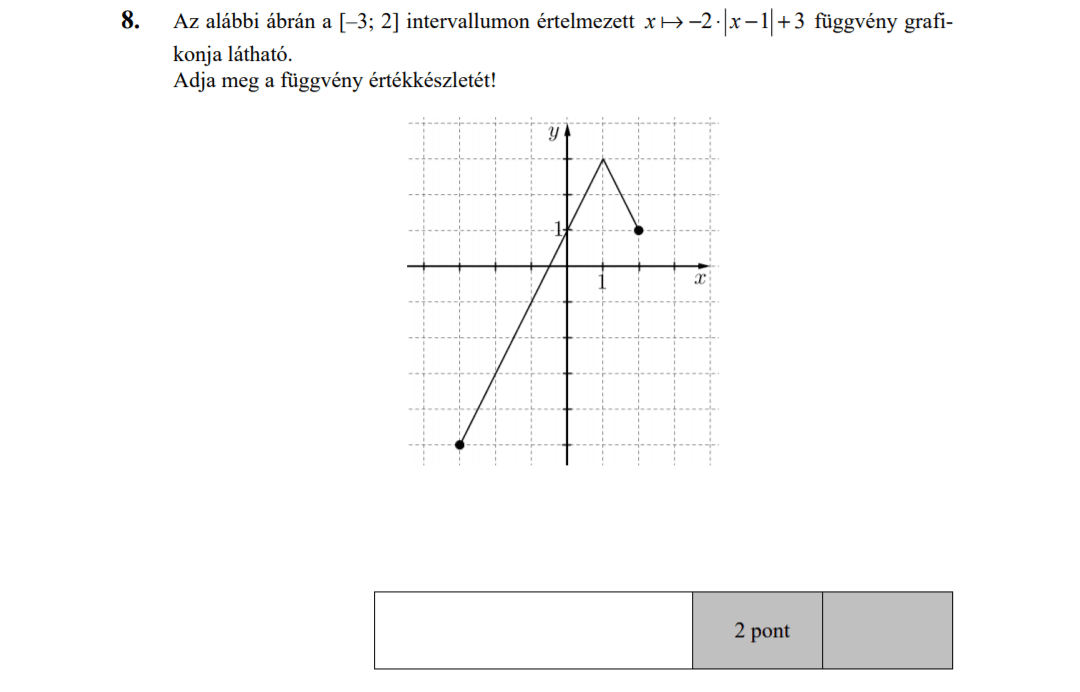

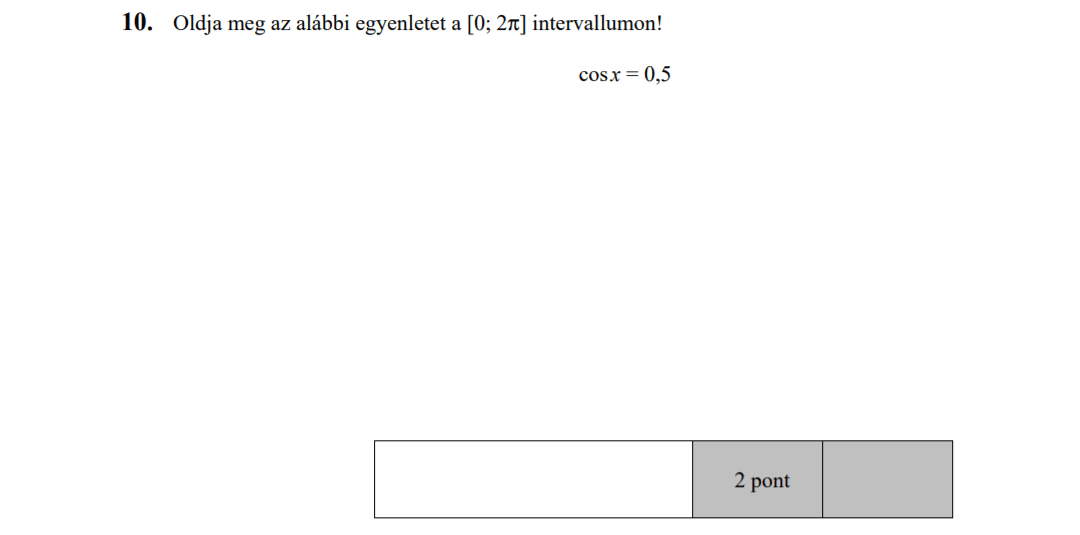

MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


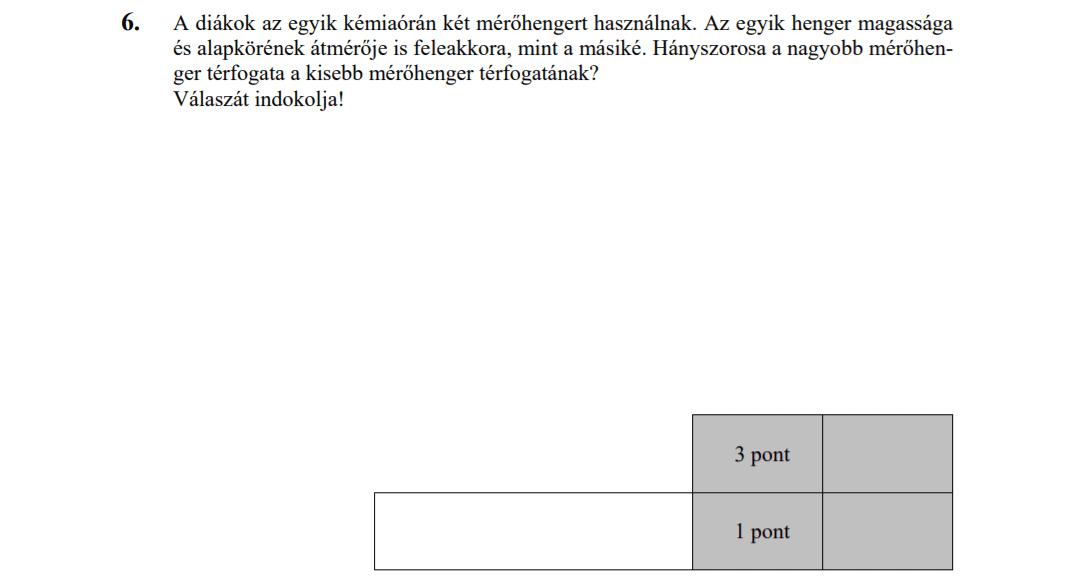
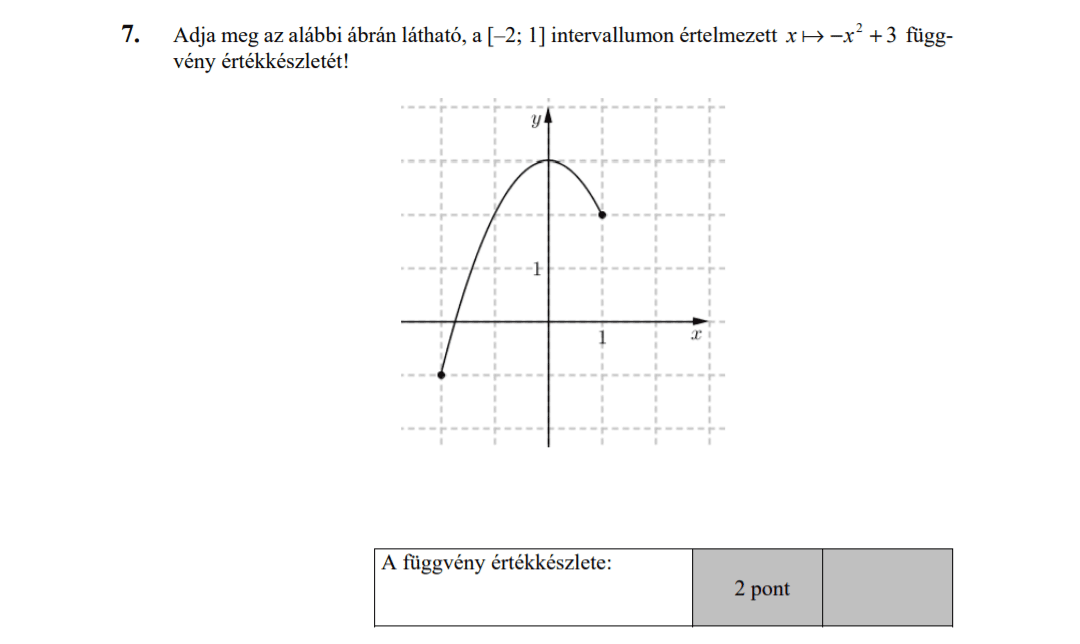

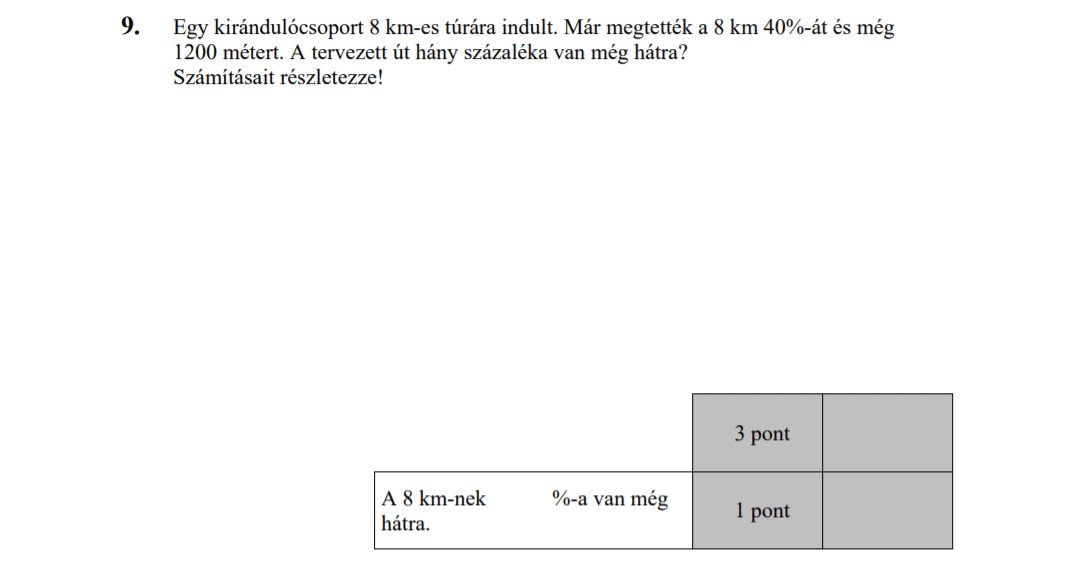
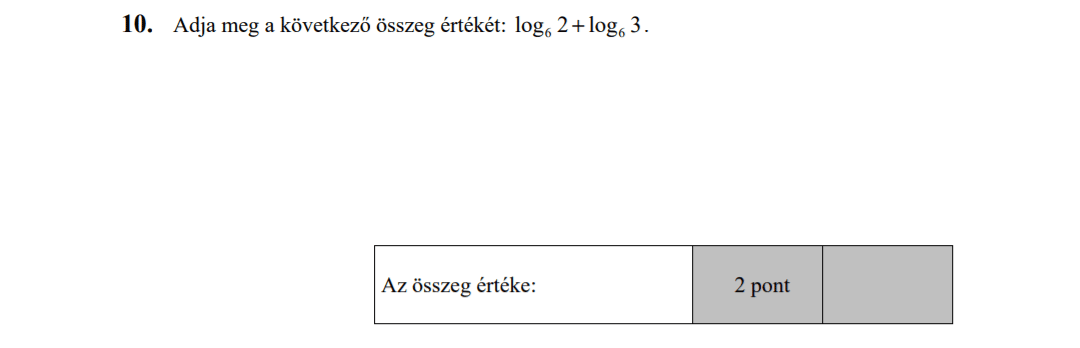

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






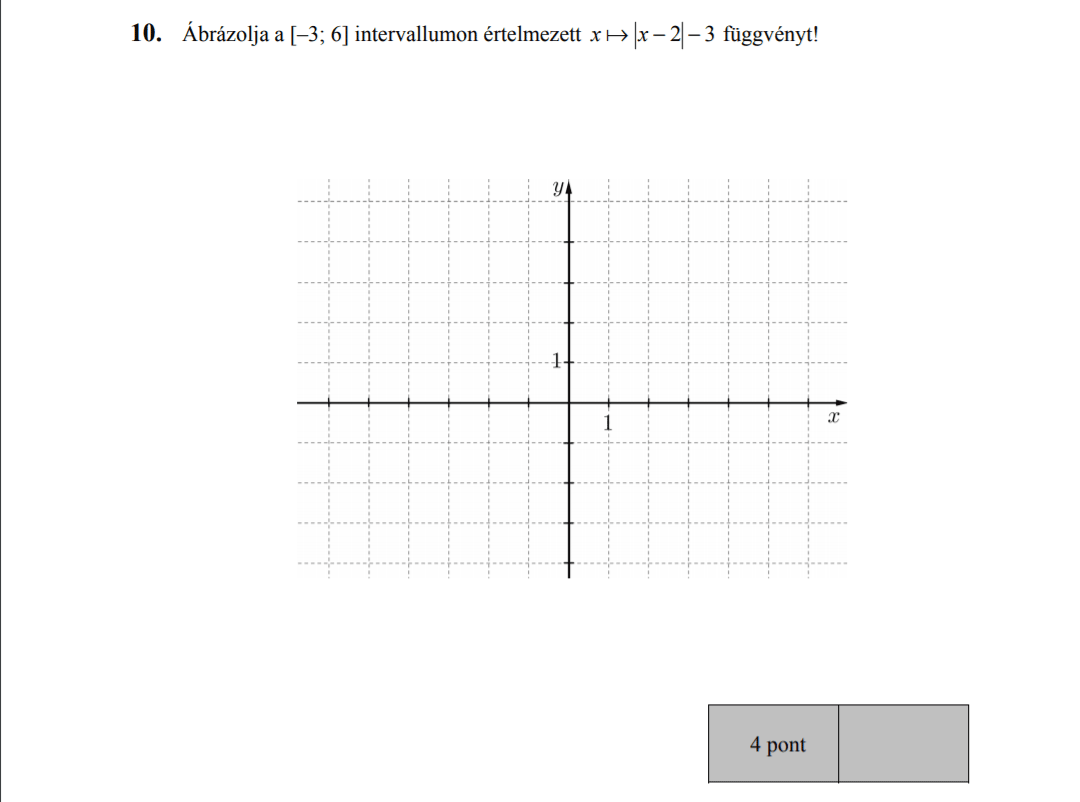

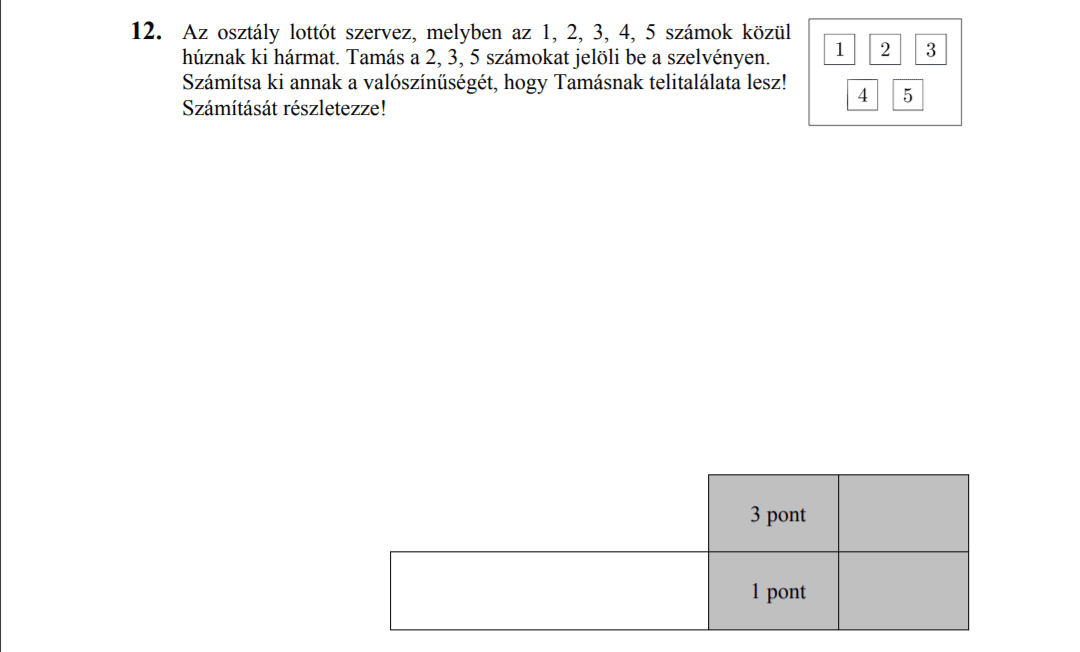
MÁSODIK RÉSZ

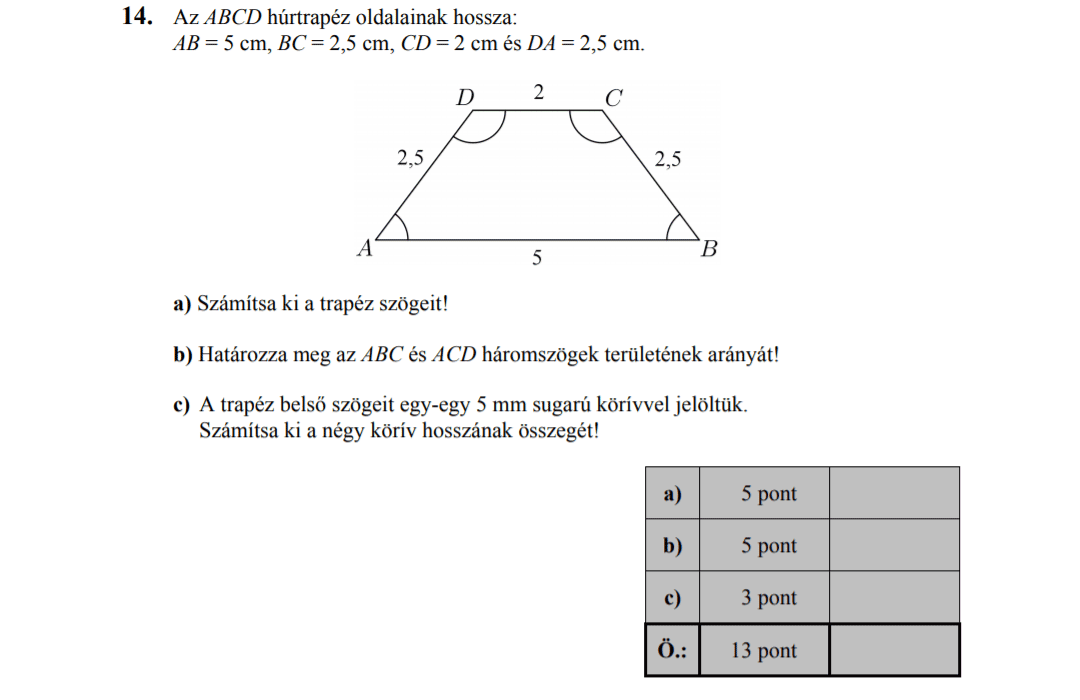

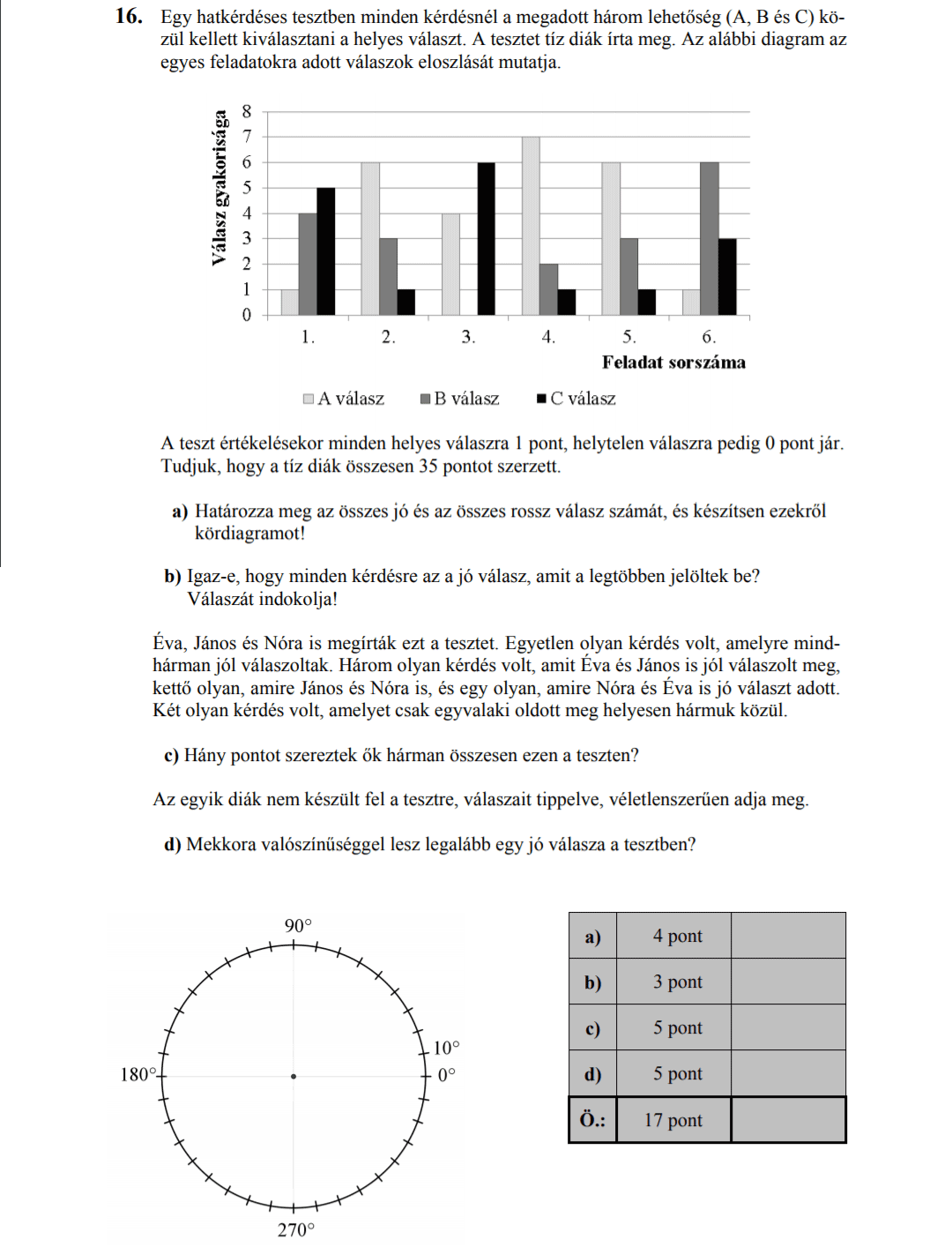


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

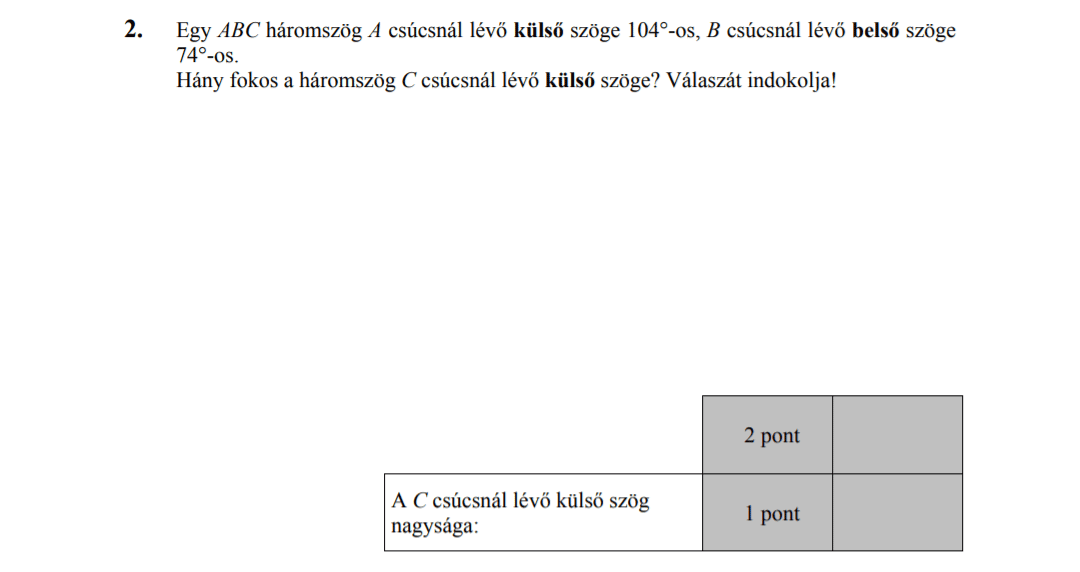





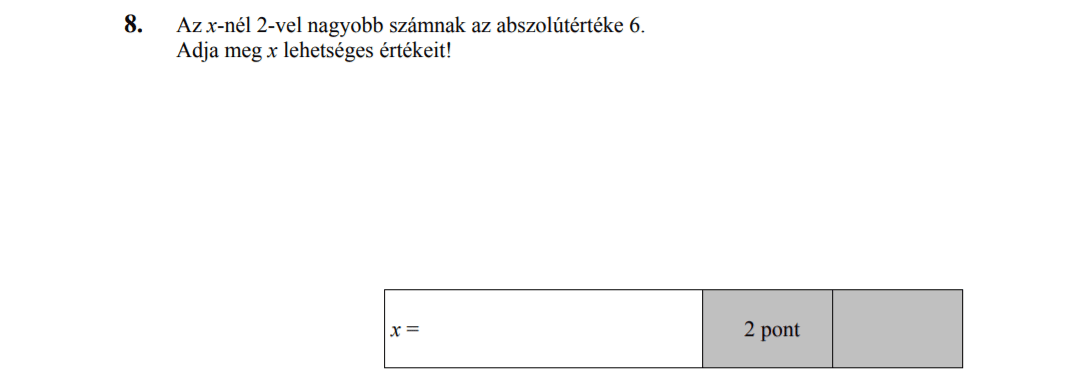

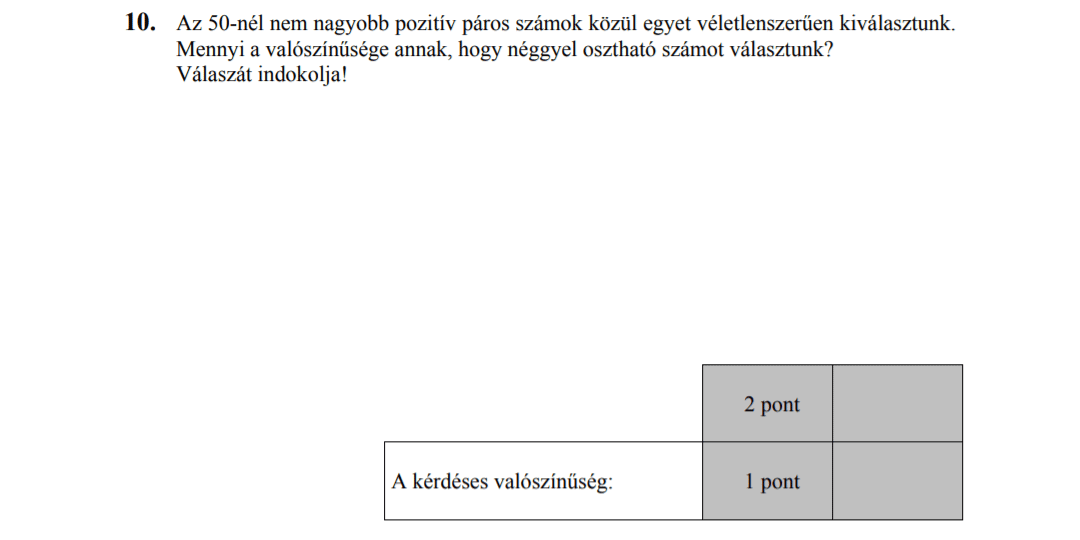


MÁSODIK RÉSZ

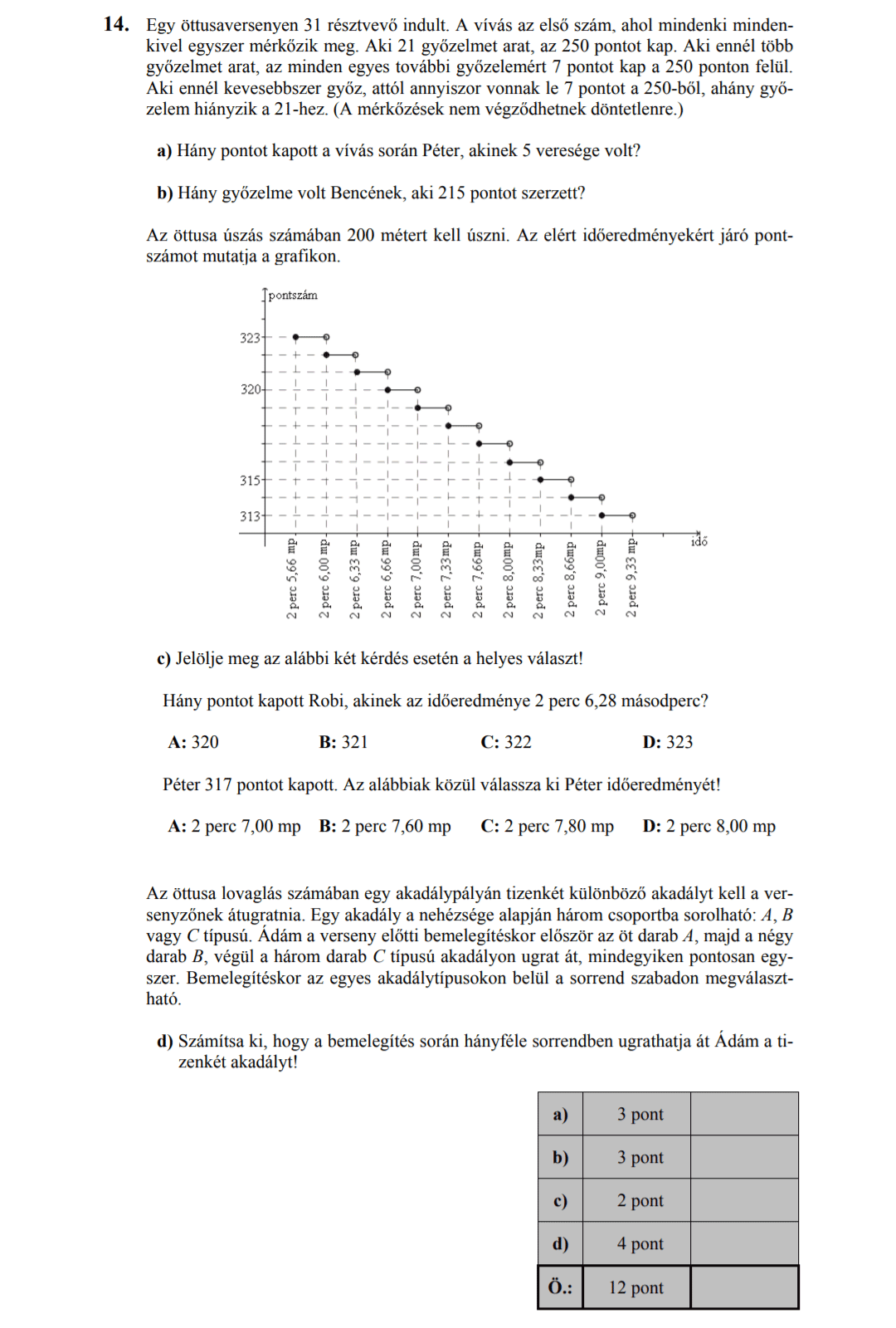
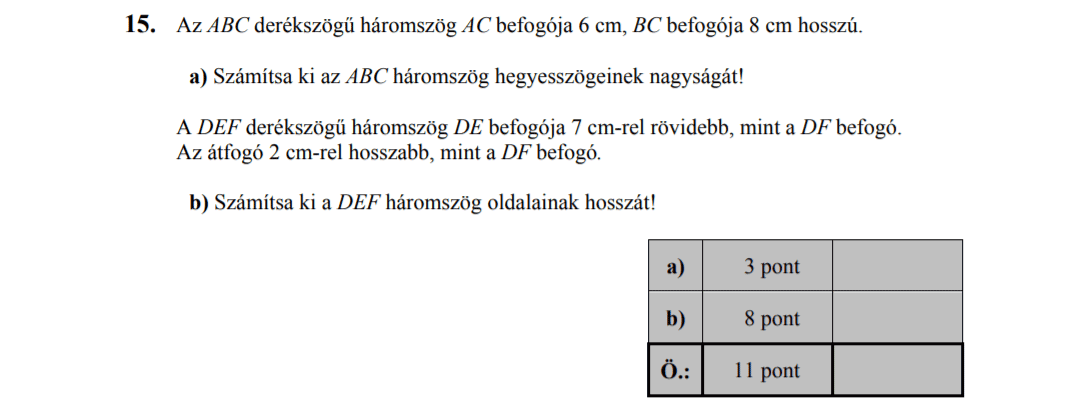



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

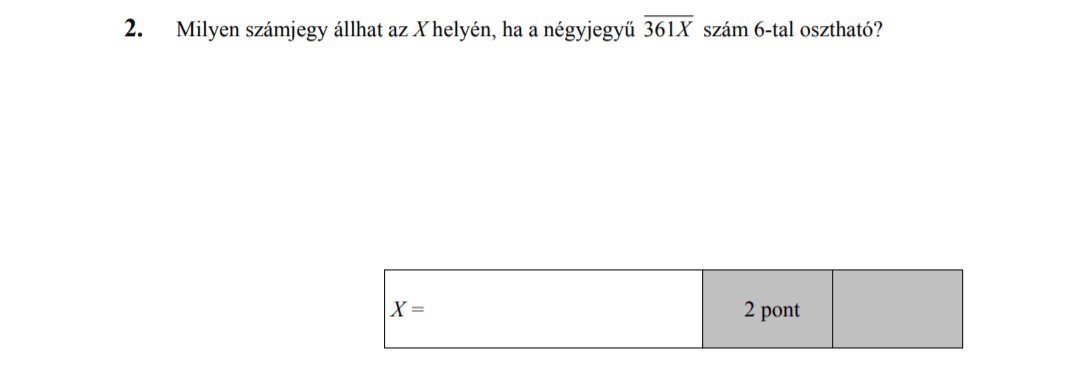



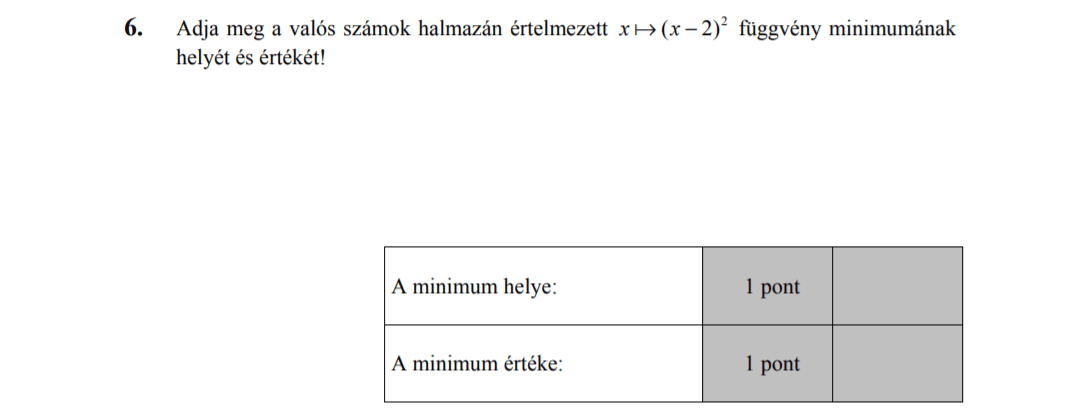

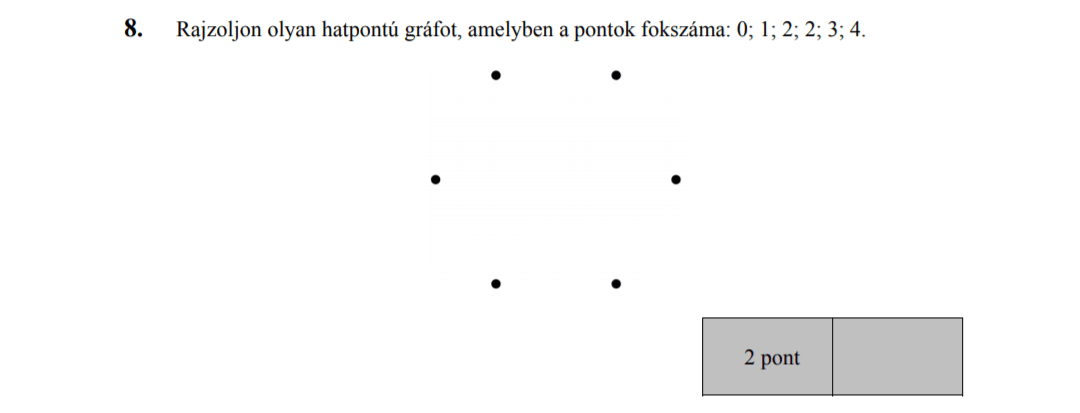


MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








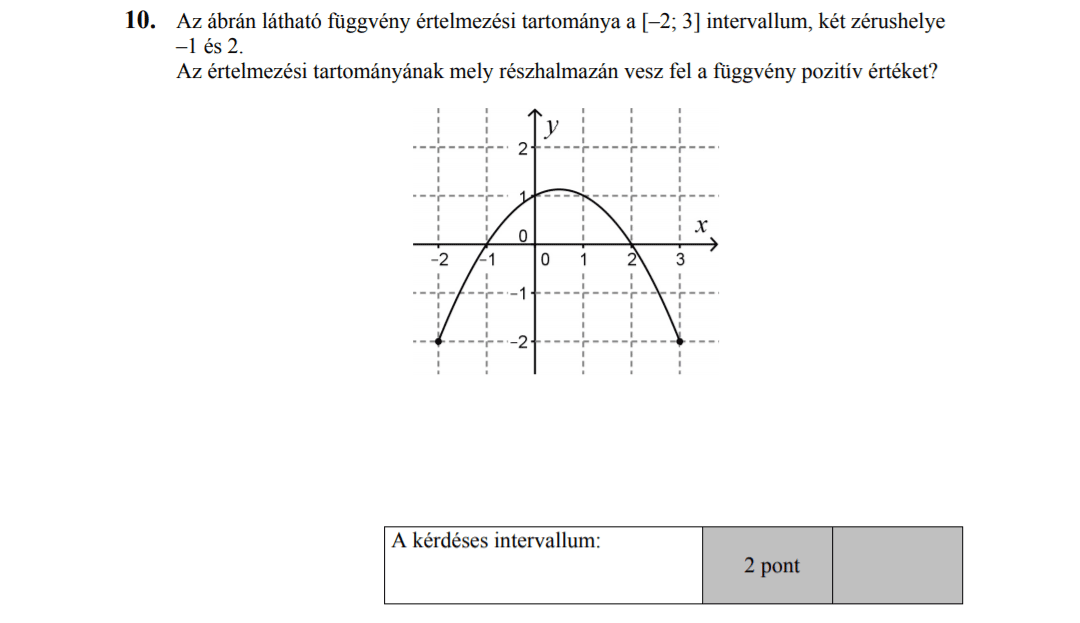


MÁSODIK RÉSZ


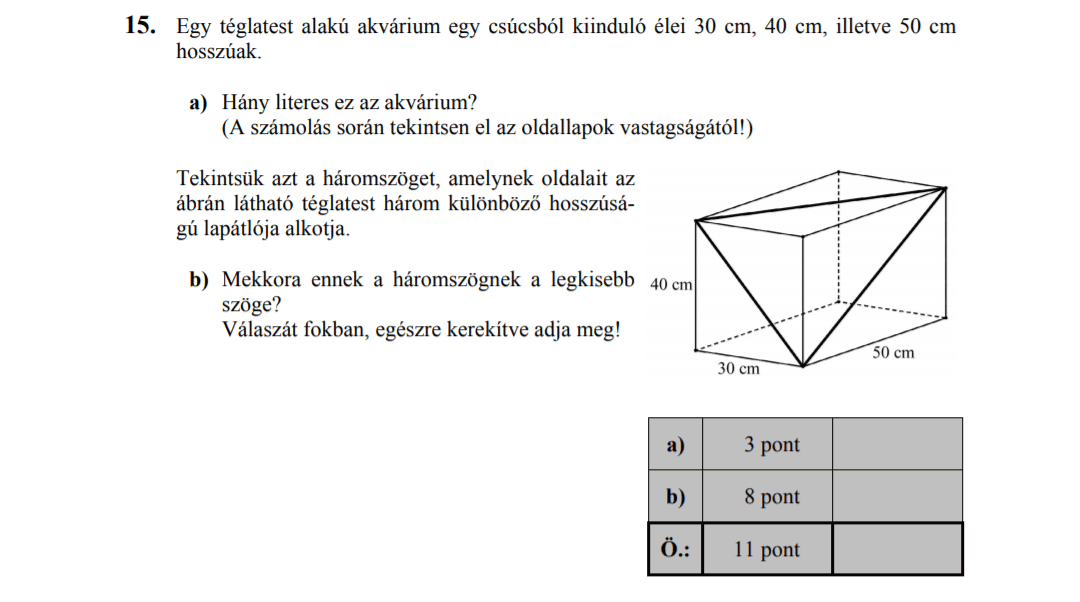

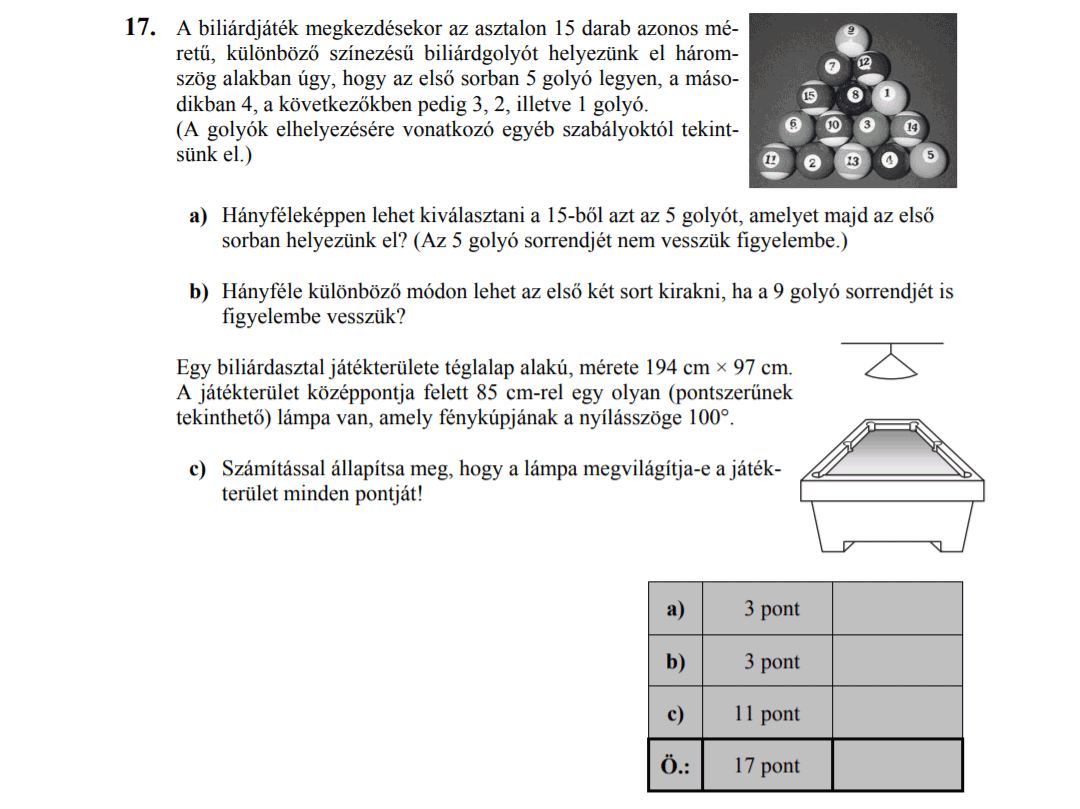

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


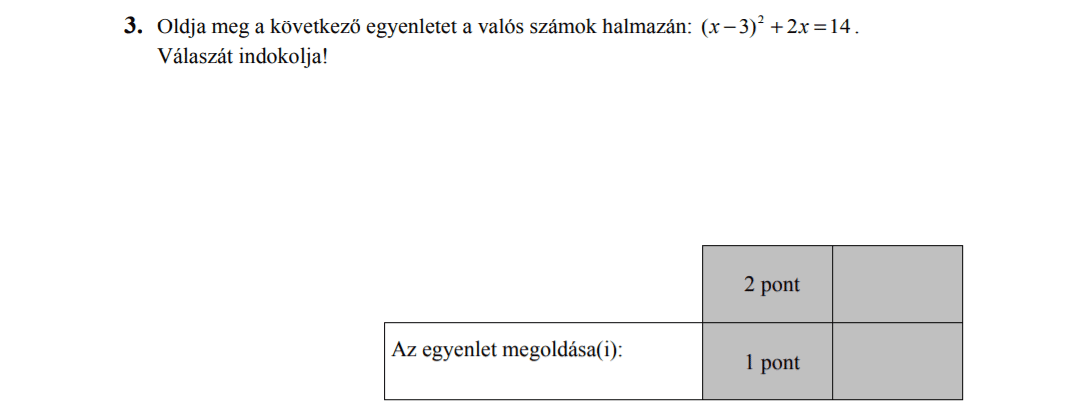





MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


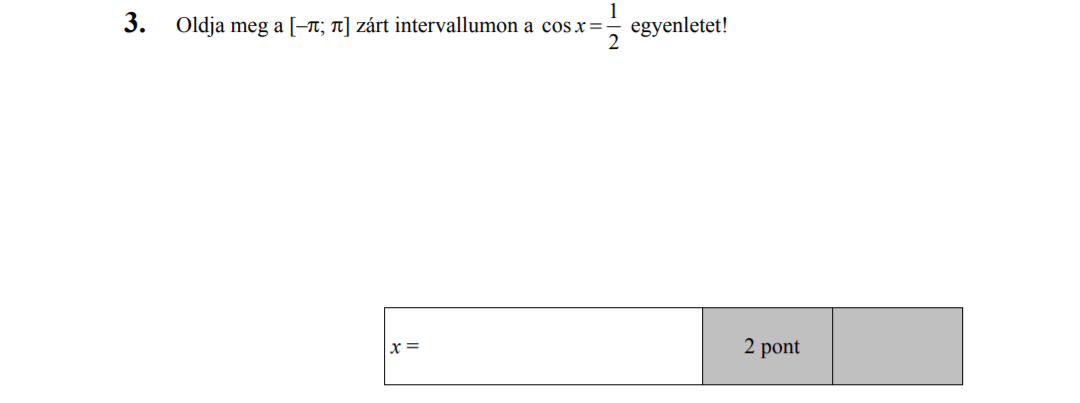


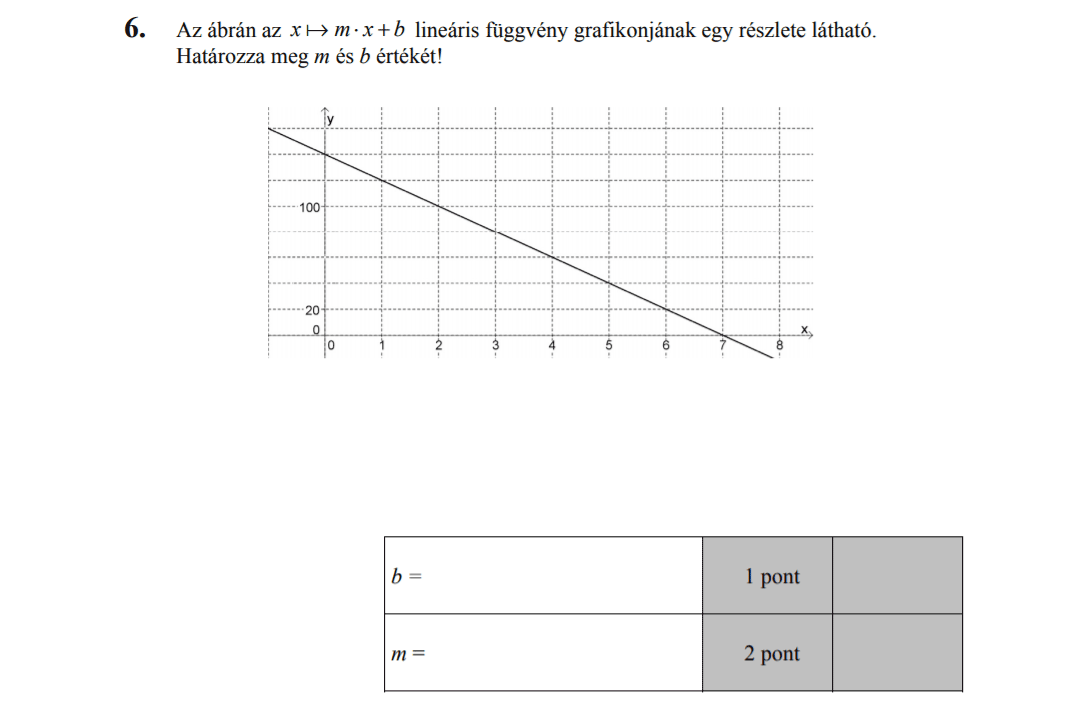



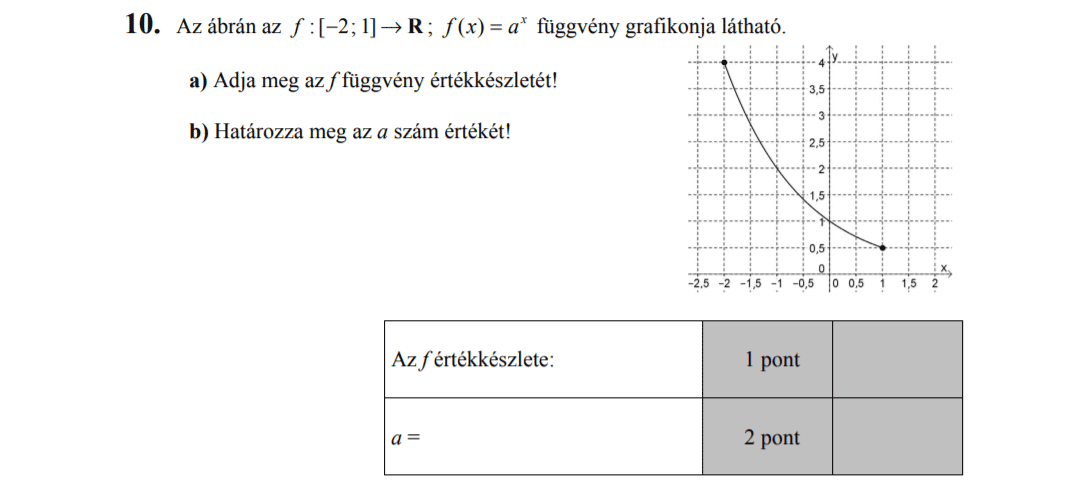

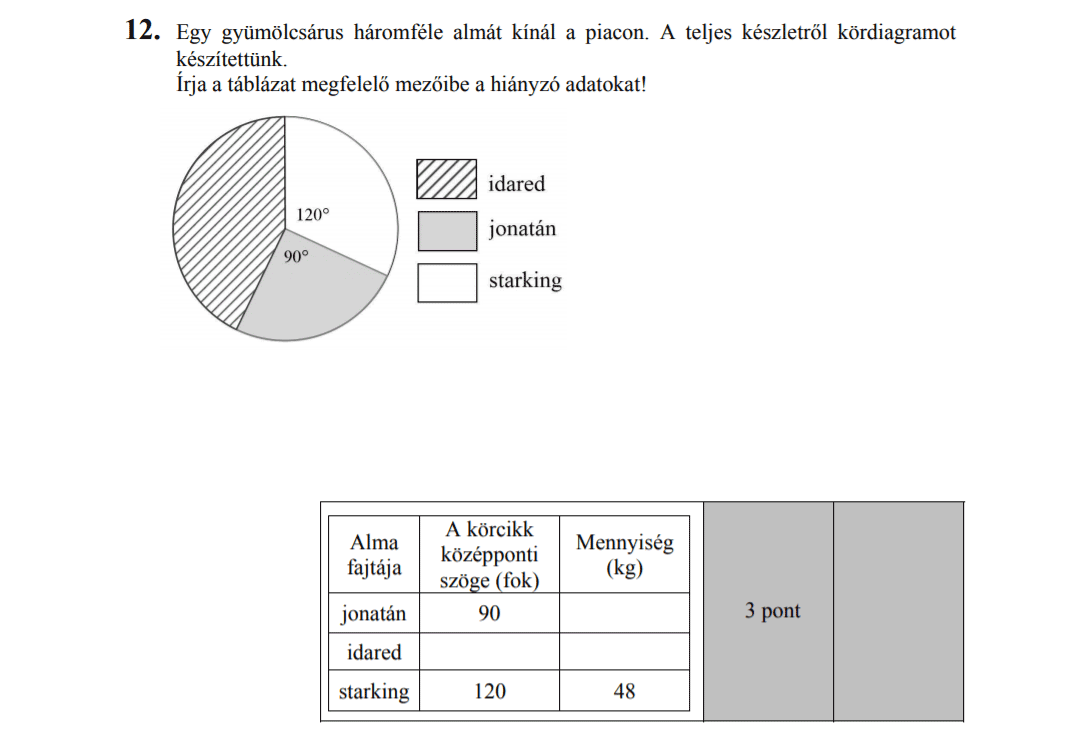
MÁSODIK RÉSZ

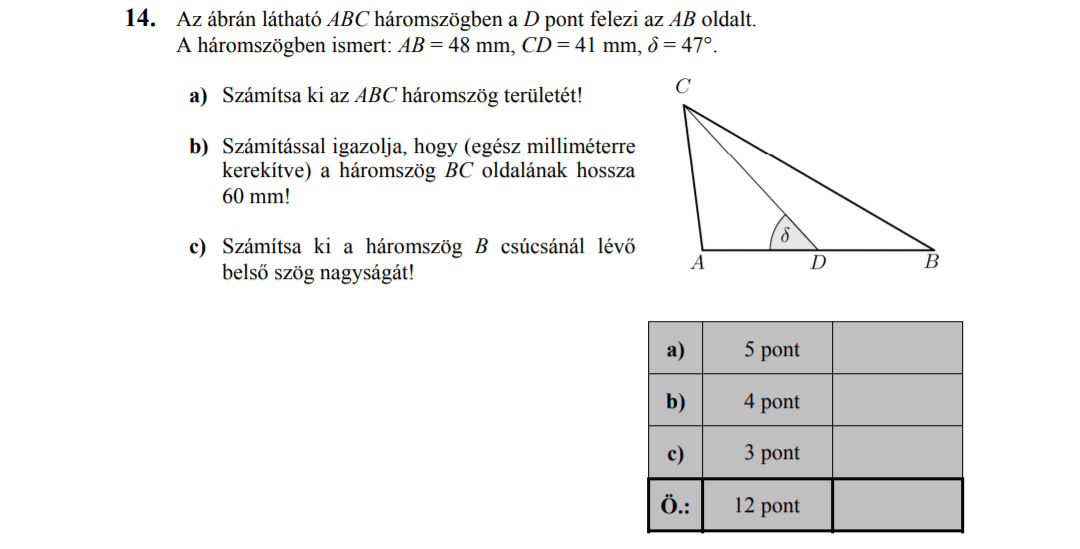




- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


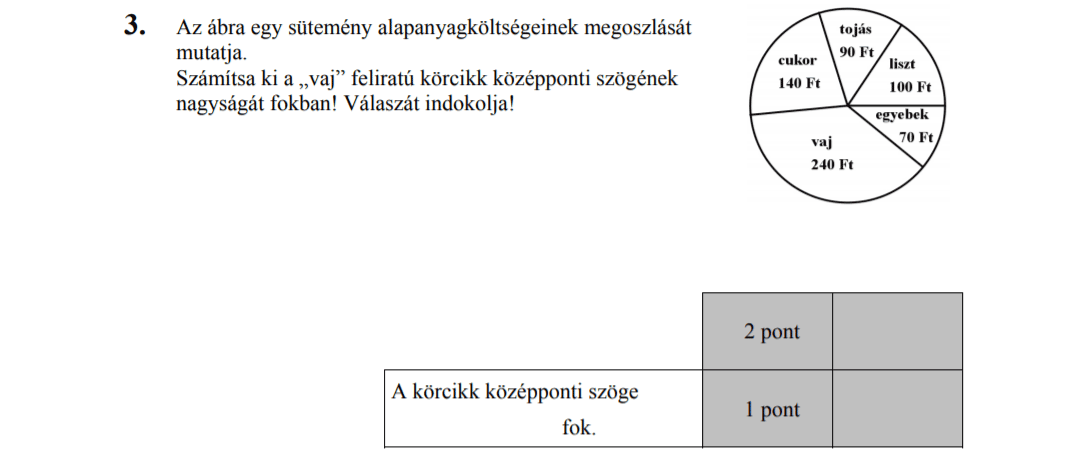
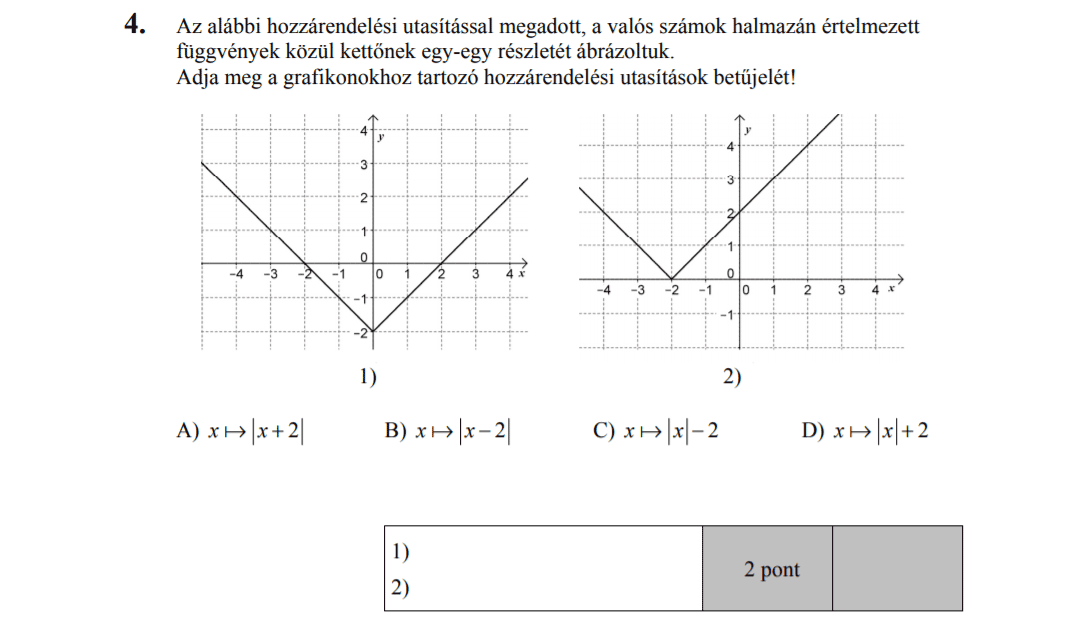
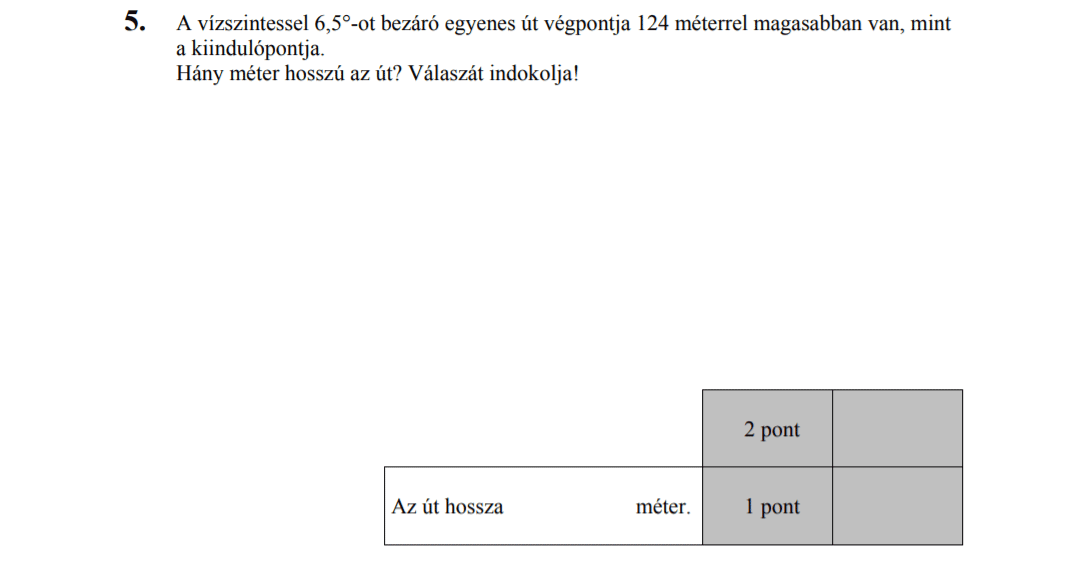





MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Várható érték
A várható érték jele $E(X)$ és ez nem más, mint egy esemény összes kimenetelének valószínűségekkel súlyozott átlaga.
A képlete:
\( E(X) = X_1 \cdot p_1 + X_2 \cdot p_2 + X_3 \cdot p_3 + \dots + X_n \cdot p_n = \sum X_i P(X_i) \),
ahol $X_i$ az i-edik kimenetel, $p_i$ pedig annak bekövetkezésének valószínűsége.
3 darab 10 dollárossal befektetési terveink vannak, egy rulett segítségével.
A terv a következő: felteszünk 10 dollárt a pirosra.
Ha nyer, akkor megdupláztuk a 10 dollárt és abbahagyjuk a játékot.
Namost, ha veszít, akkor újabb 10 dollárt teszünk a pirosra, és ha ezúttal nyerünk, akkor szintén abbahagyjuk a játékot.
Ha másodszorra sem nyerünk, akkor az utolsó 10 dollárost is felrakjuk a pirosra.
A kérdés az, várhatóan mennyi pénzünk lesz a tranzakció végén.
Egy vadrezervátumban 3 hím oroszlán él. Az illegális vadászat miatt 40% eséllyel 5 éven belül mindegyik elpusztul, 30% eséllyel 2 oroszlán pusztul el és 20% eséllyel egy.
Ha átköltöztetik az oroszlánokat egy biztonságosabb területre, akkor a tapasztalatok szerint az állatok harmada pusztul el a költöztetés miatt, a többiek életben maradnak. Átköltöztessük-e az oroszlánokat, ha azt szeretnénk, hogy 5 év múlva a lehető legtöbben legyenek?
Elemér és Huba egy dobókocka játékot játszanak. Huba annyi dollárt ad Elemérnek, amennyi a dobott szám kétszerese, Elemér pedig annyit ad Hubának, amennyi a dobott szám négyzete. Melyikünk kedvez a játék?
a) Egy dobókockával dobunk. Mennyi a dobott számok várható értéke?
b) Két dobókockával dobunk. Mennyi a dobott számok összegének várható értéke?
Az ötös lottón, egy hasábon 5 számot kell beikszelnünk 1-től 90-ig. Ha nulla vagy egy számot találunk el, akkor nem nyerünk semmit. Két találat esetén a nyeremény 700 Ft, hármas találatnál 10 ezer Ft, négyes esetén 789 ezer Ft, az ötös pedig 535 millió Ft-ot fizet. Mennyi a nyereményünk várható értéke?
Két kockával dobva mennyi a dobott számok nem kisebbikének várható értéke?
Egy sorsjegy 5% eséllyel nyerő, és kétféle nyeremény van, 2500 Ft és 50 000 Ft. A 2500 Ft-os nyerő sorsjegyből pontosan 24-szer annyi van, mint az 50 000 Ft-osból.
| 1 db sorsjegy nyereménye (Ft) | 0 | 2500 | 50 000 |
| nyeremény valószínűsége | 0,95 |
Töltsük ki a táblázat üres mezőit, majd számítsuk ki egy darab sorsjegy nyereményének várható értékét!
Egy dobókocka három lapján 3-as, két lapján 2-es, egy lapján 1-es szám van. Andi és Béla a következő játékot játsszák ezzel a dobókockával. Valamelyikük dob egyet a kockával. Ha a dobás eredménye 3, akkor Andi fizet Bélának $n$ forintot ($n>80$), ha a dobás eredménye 1, akkor Béla fizet $(n-80)$ forintot Andinak, ha pedig a dobás eredménye 2, akkor is Béla fizet Andinak $2(n-80)$ forintot. Mennyit fizet Béla Andinak az 1-es dobása esetén, ha ez a játék igazságos, azaz mindkét játékos nyereményének várható értéke 0?
