- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
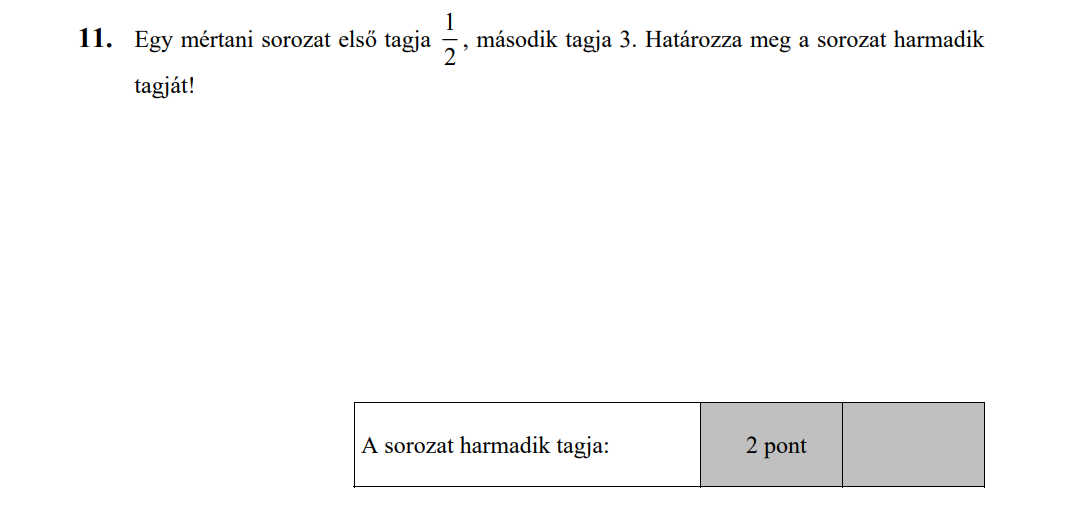
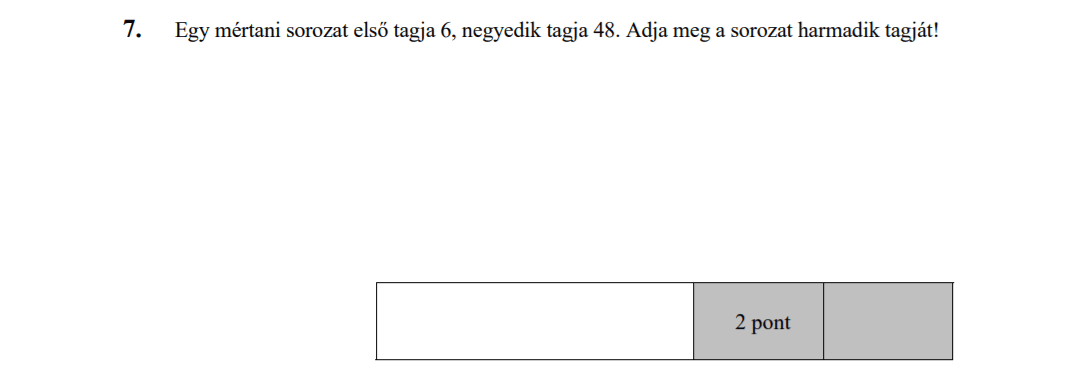
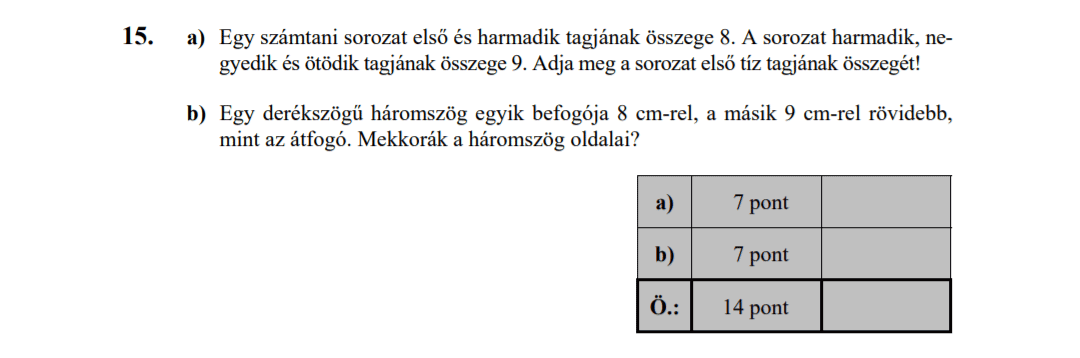
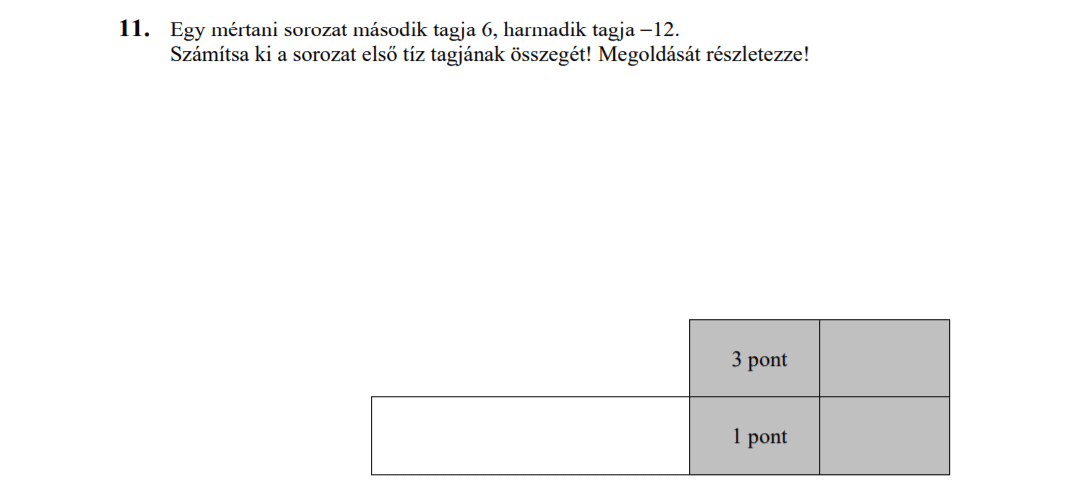
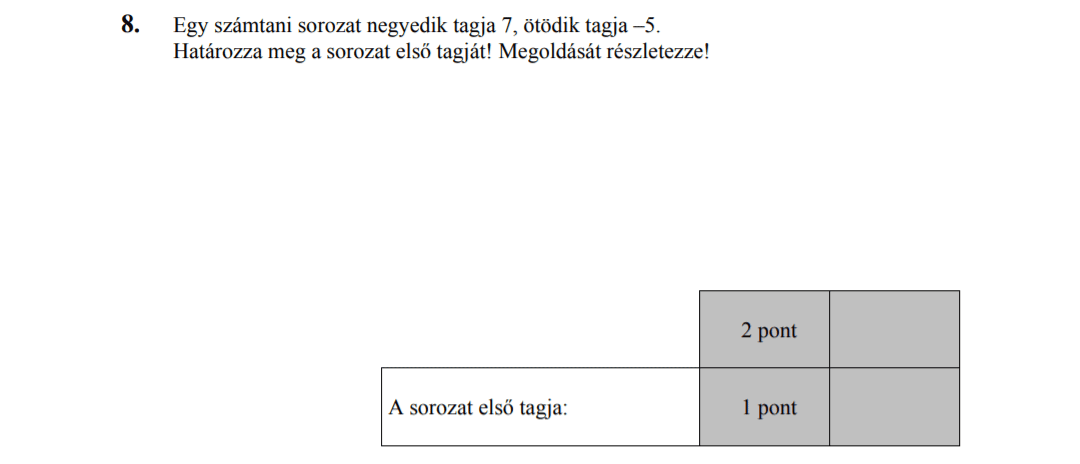
- Számtani és mértani sorozatok (16 pont)
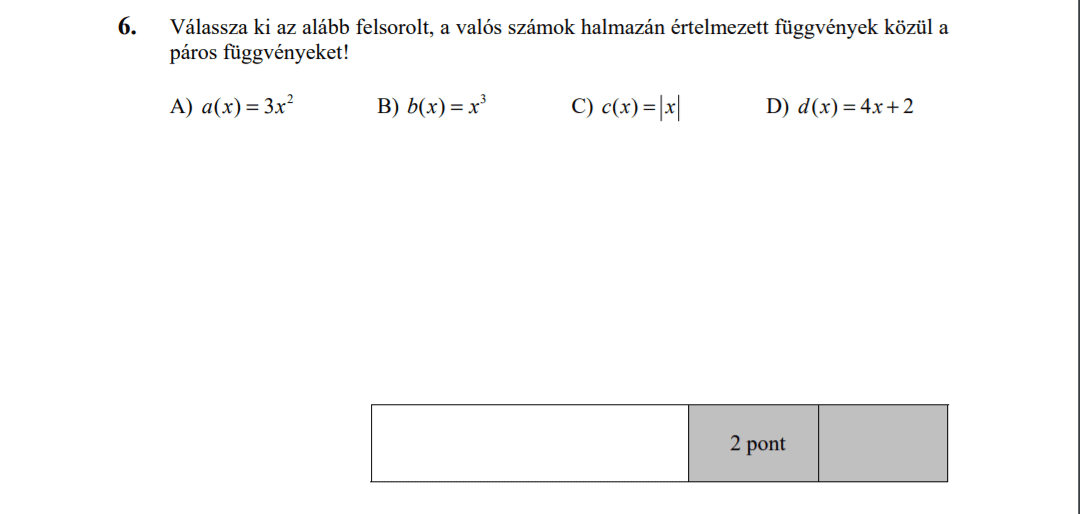
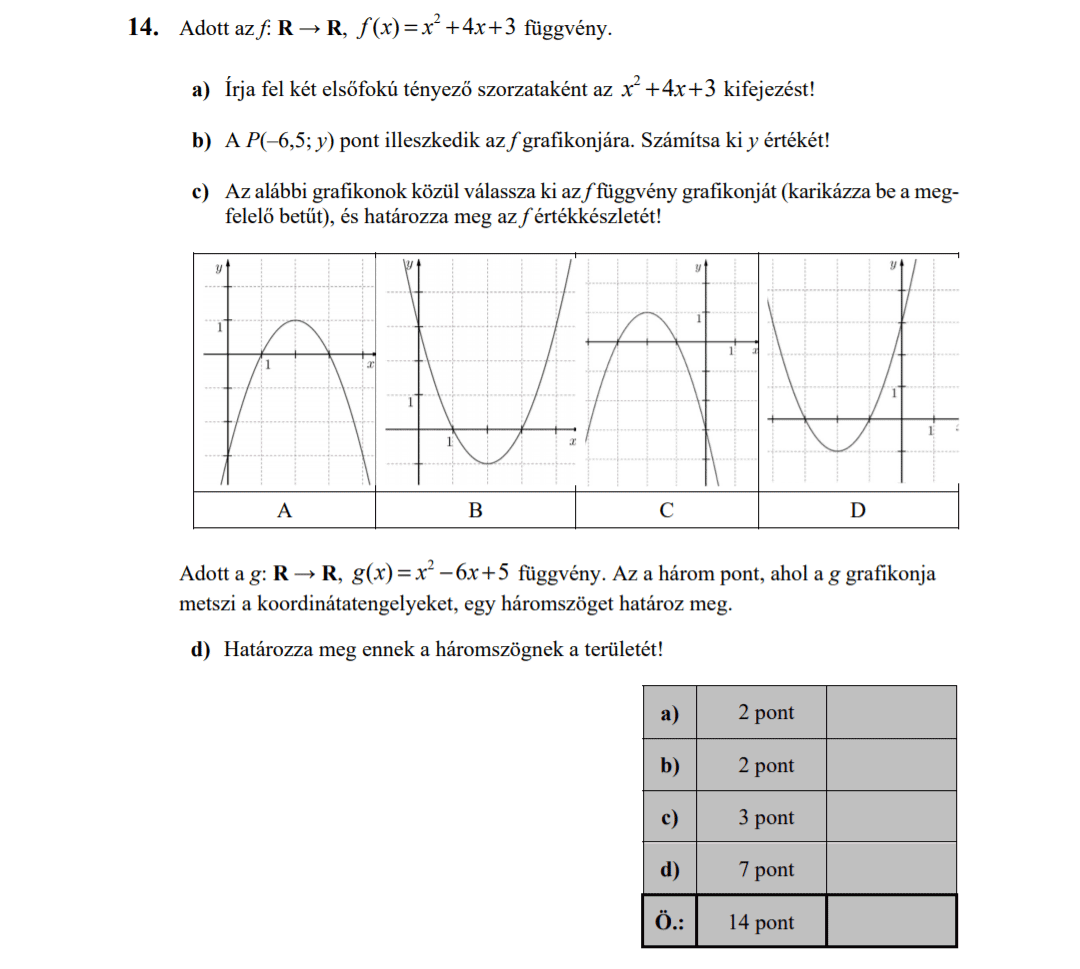
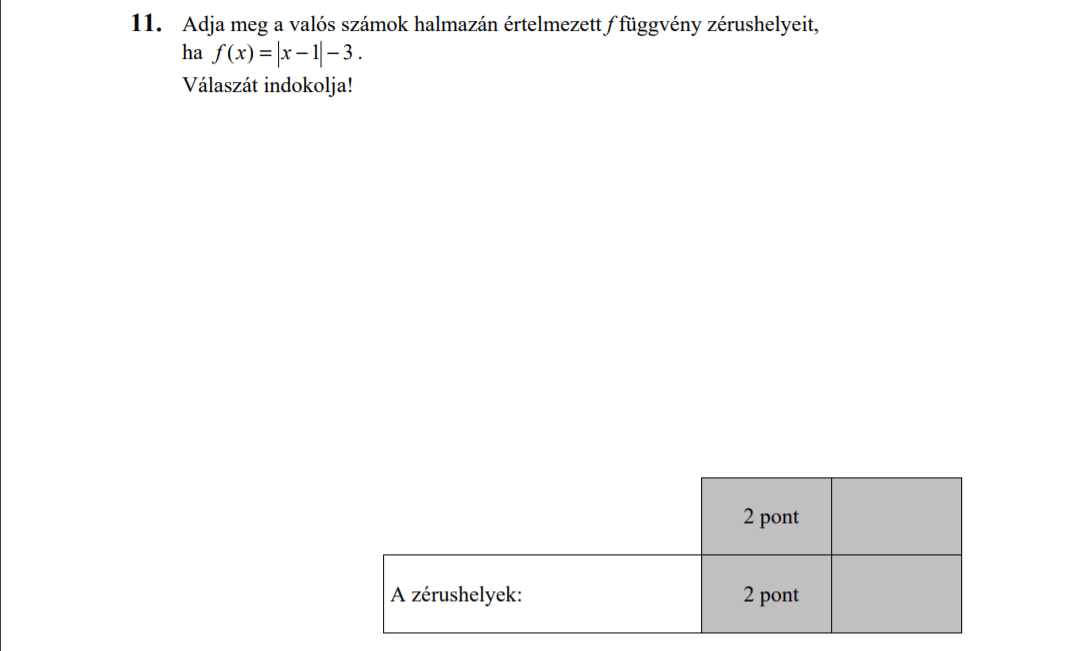
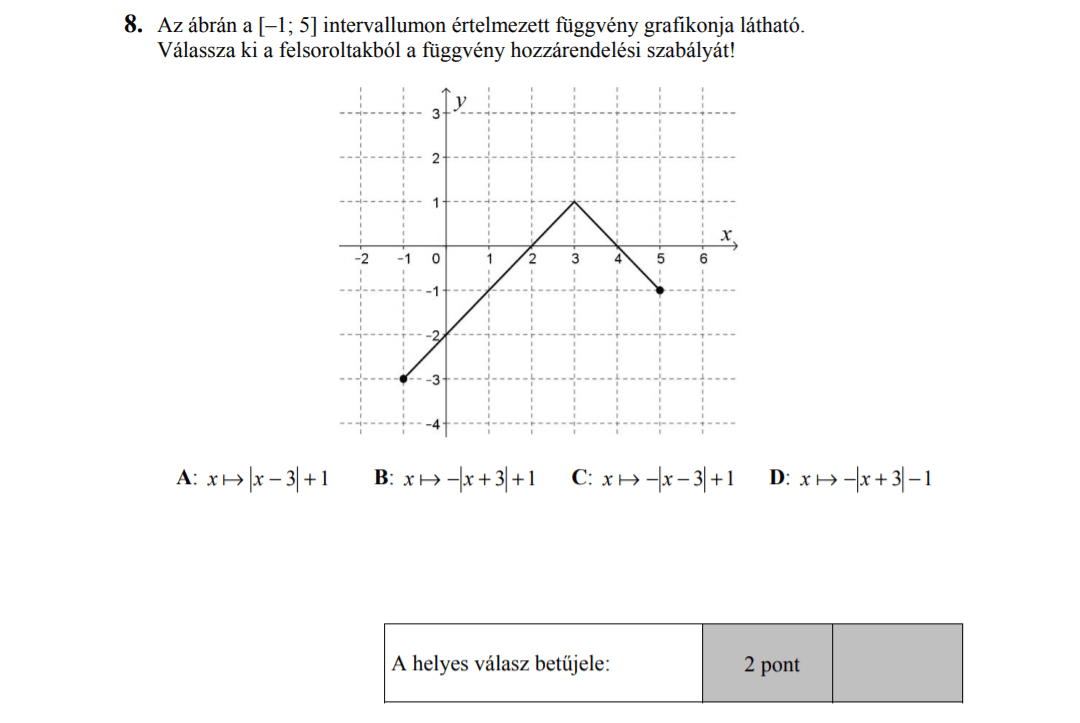
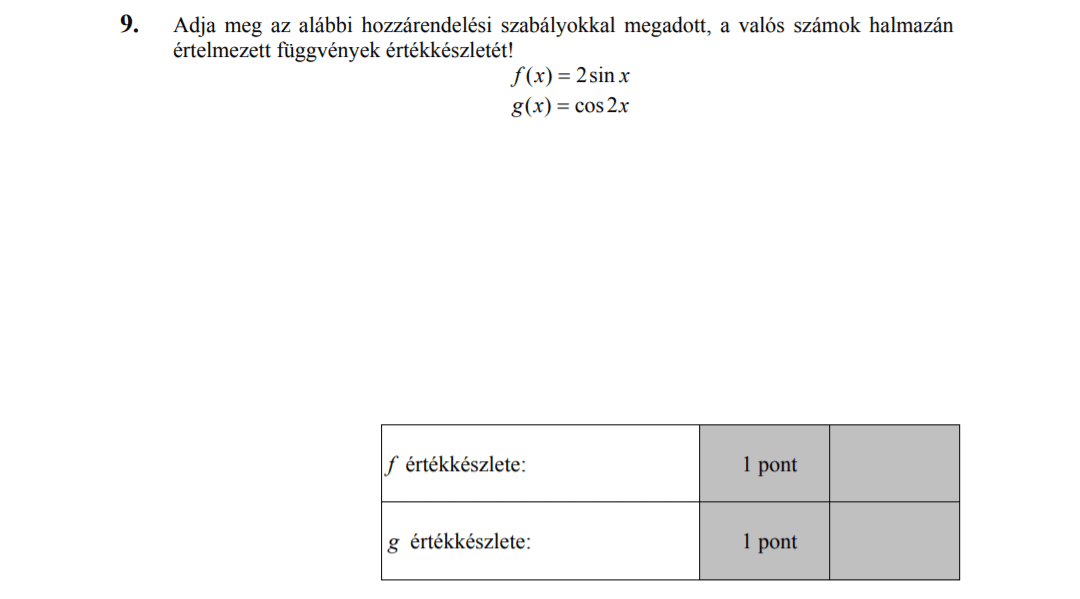
- Függvényekkel kapcsolatos feladatok (9,8 pont)
- Térgeometria (9,8 pont)
- Statisztika (9,3 pont)
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
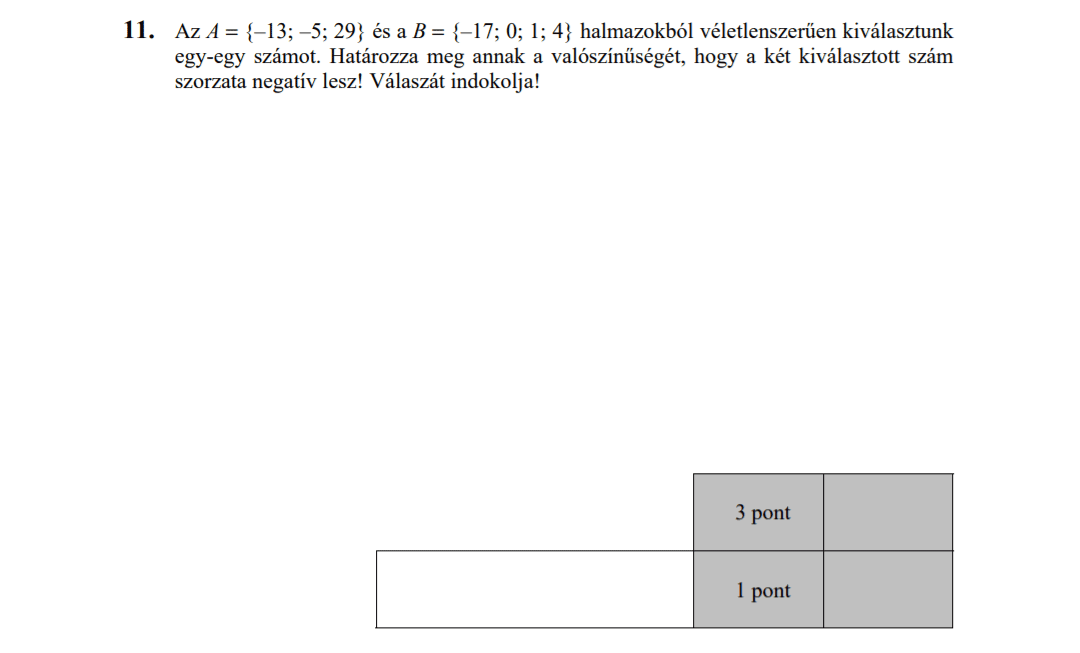
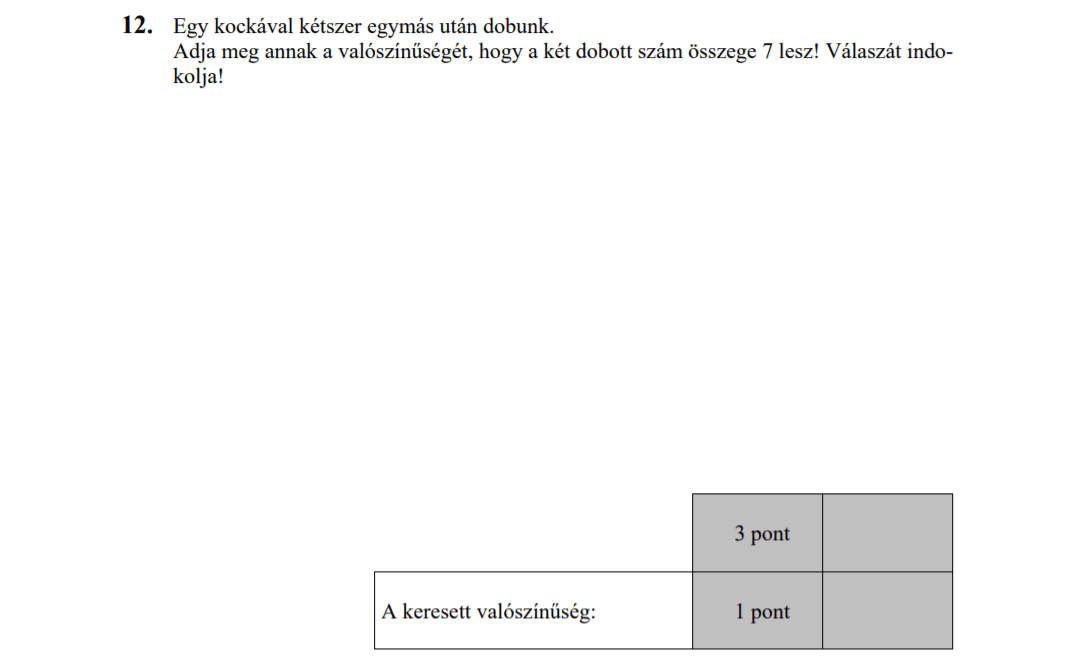
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
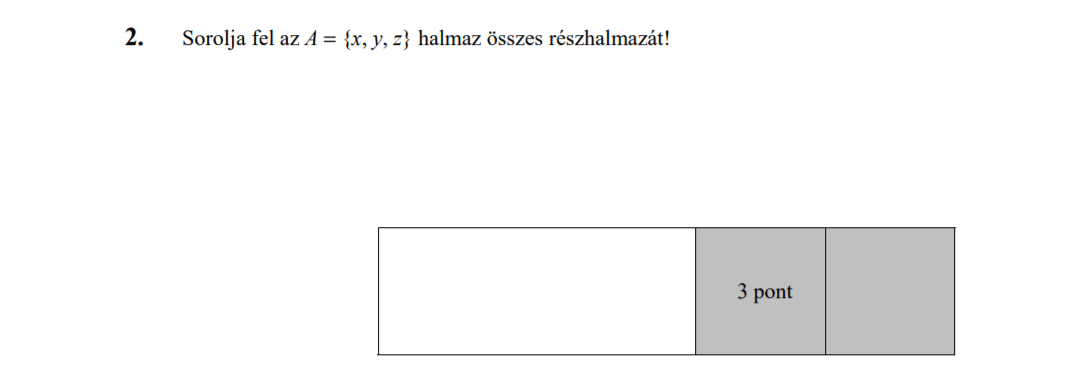
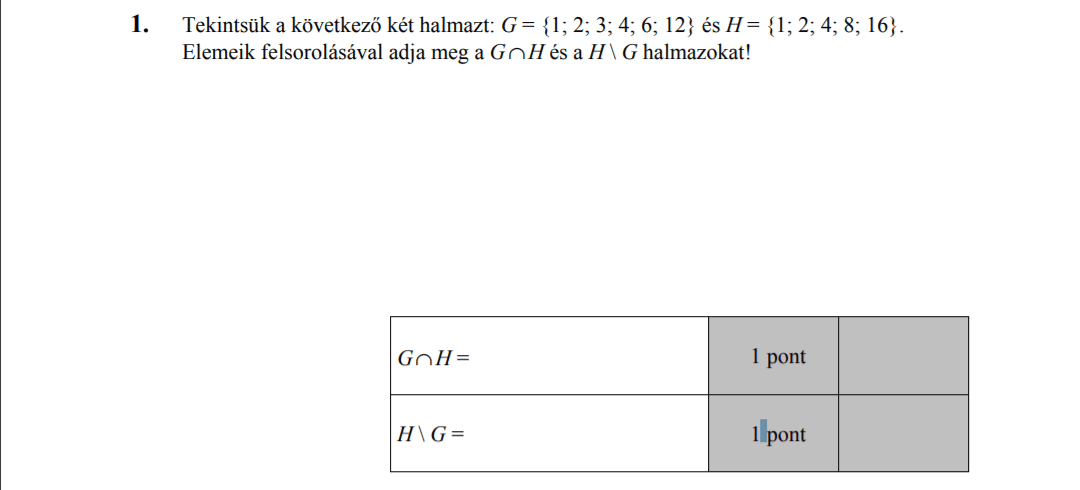
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
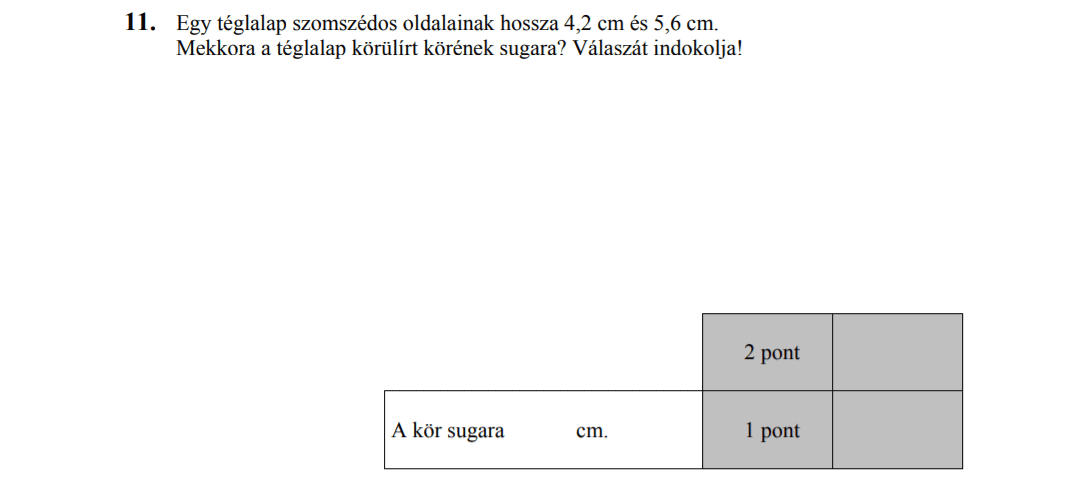
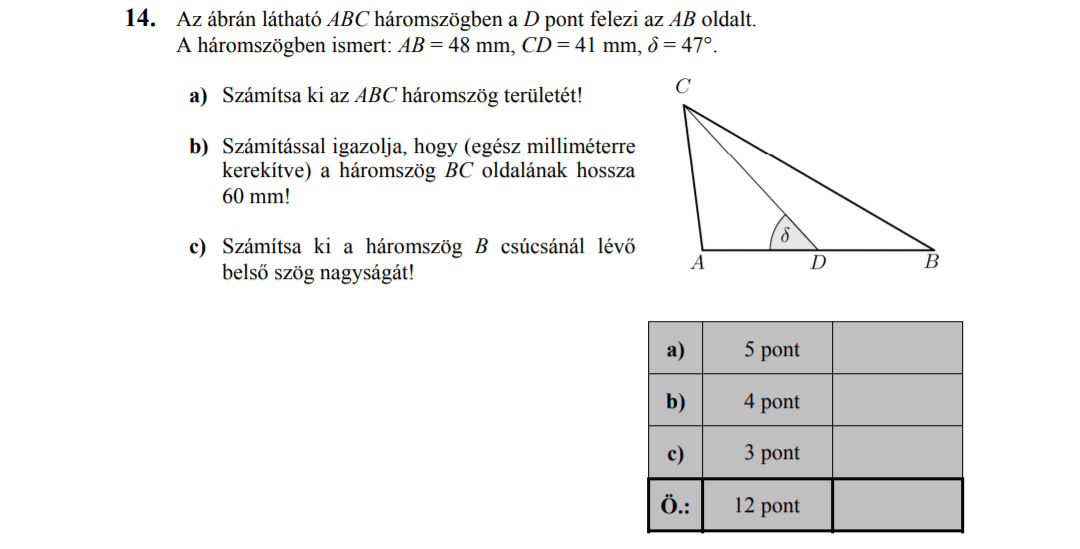
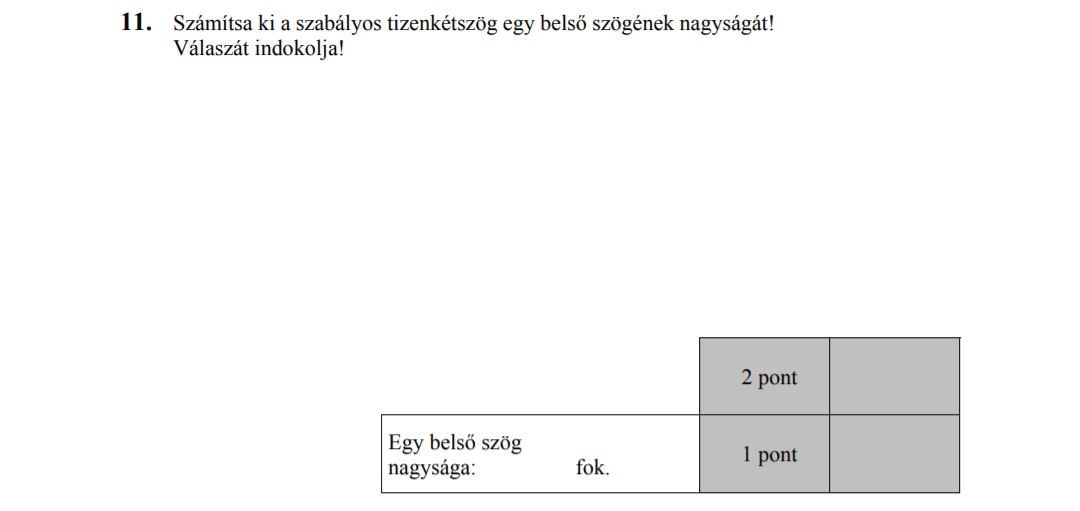
- Síkgeometria (4,5 pont)
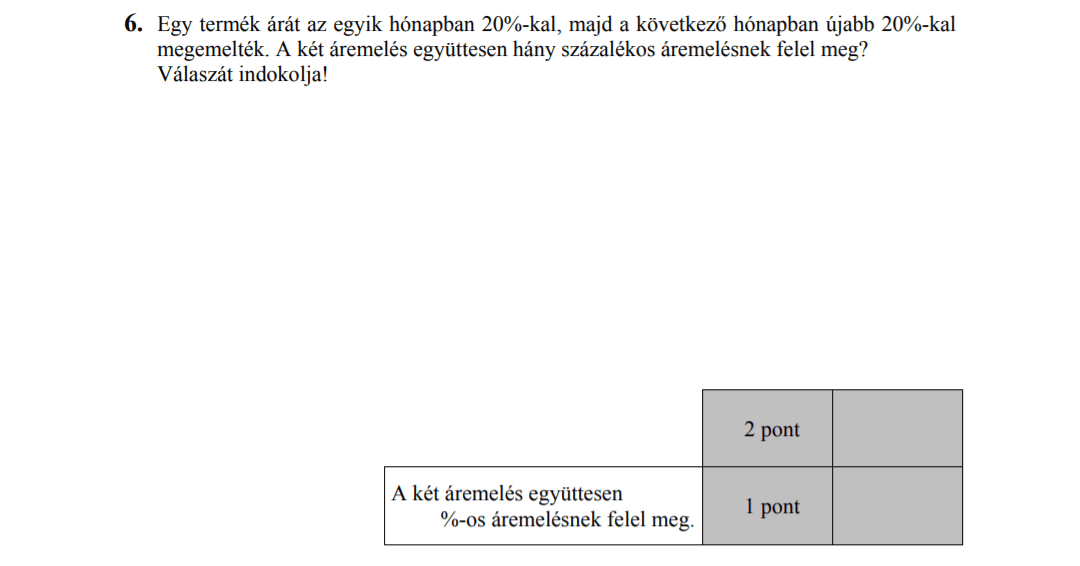
- Százalékszámítás (3,8 pont)
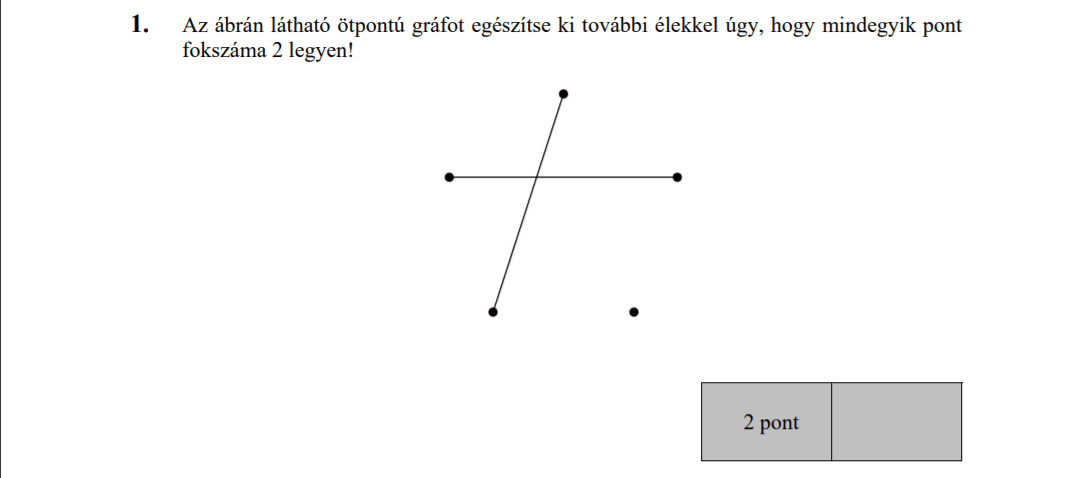
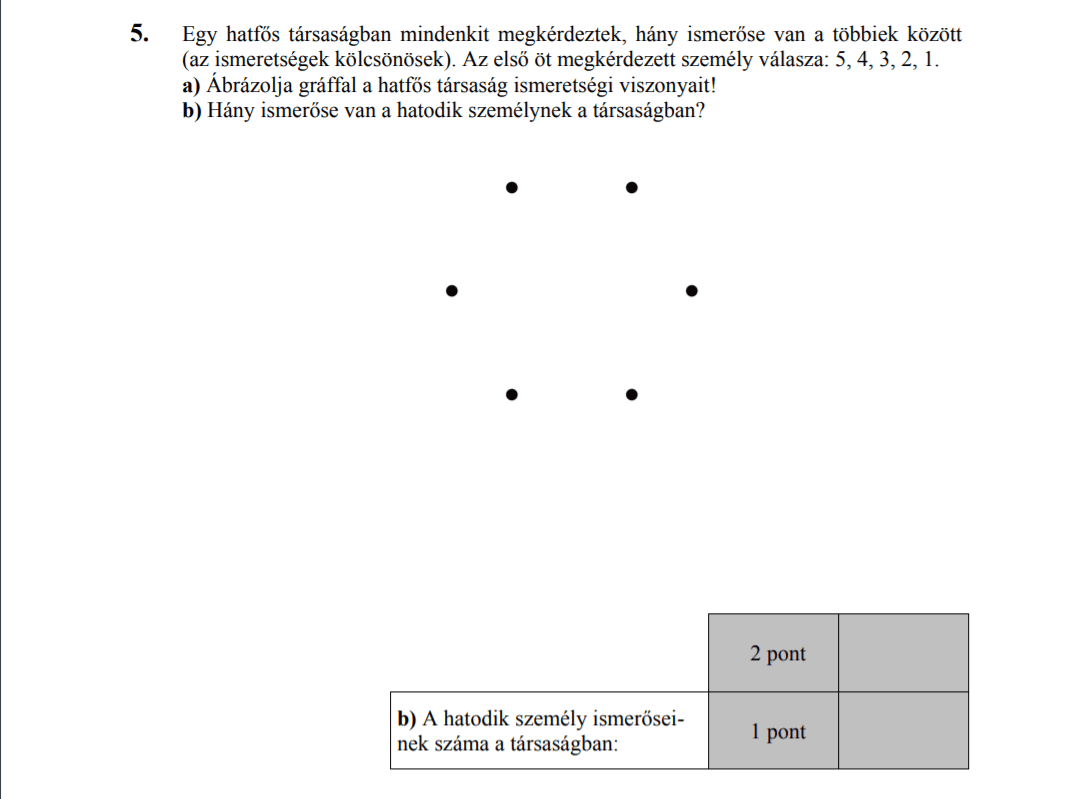
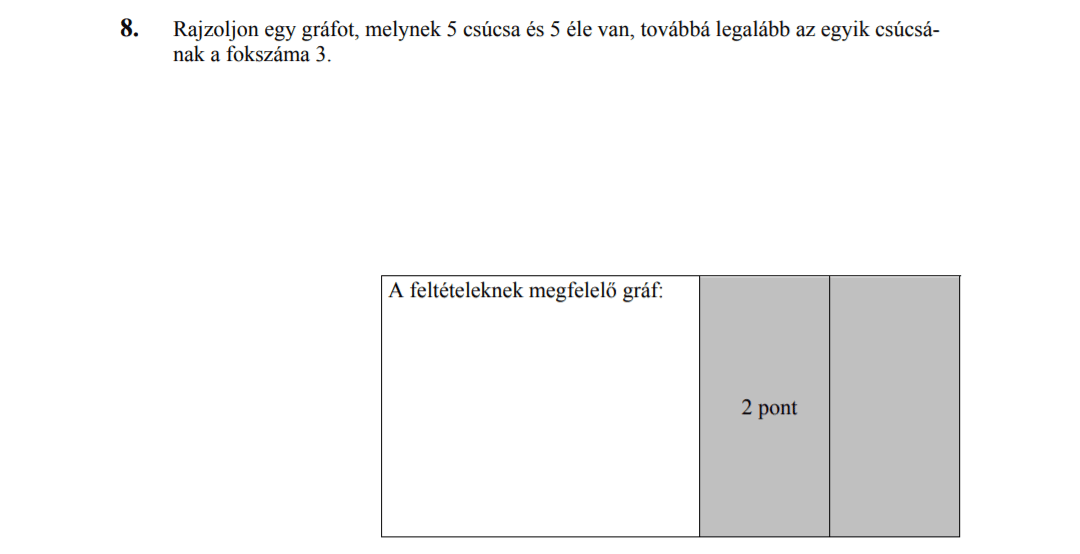
- Gráfok (3 pont)
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
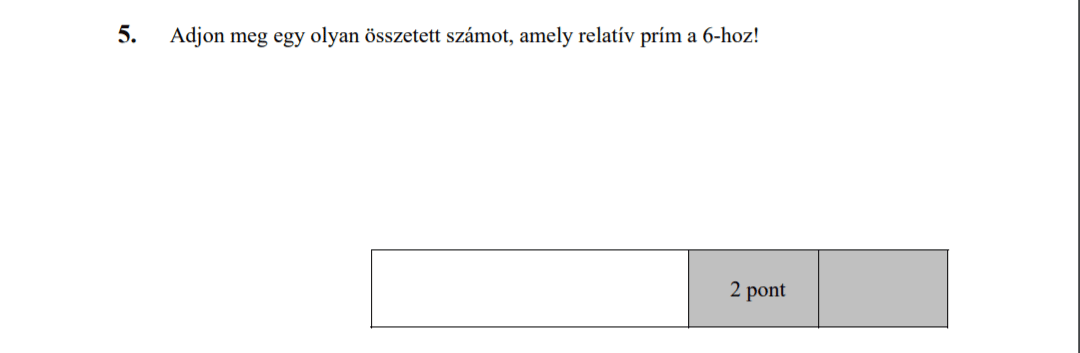
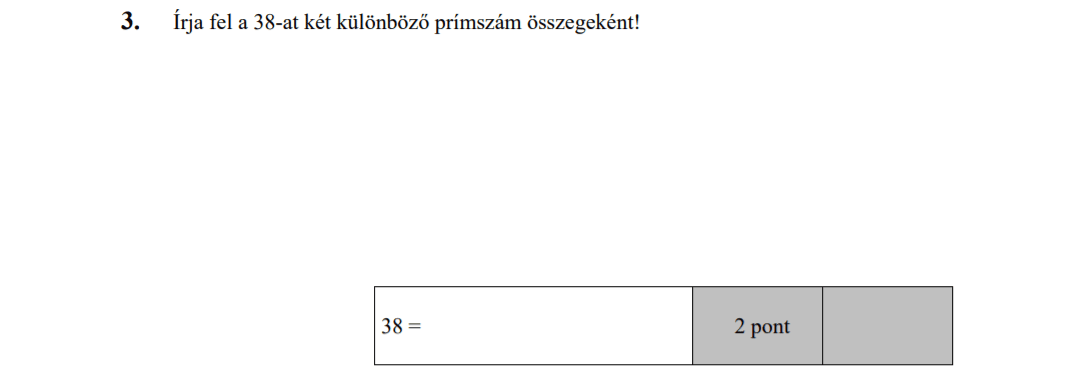
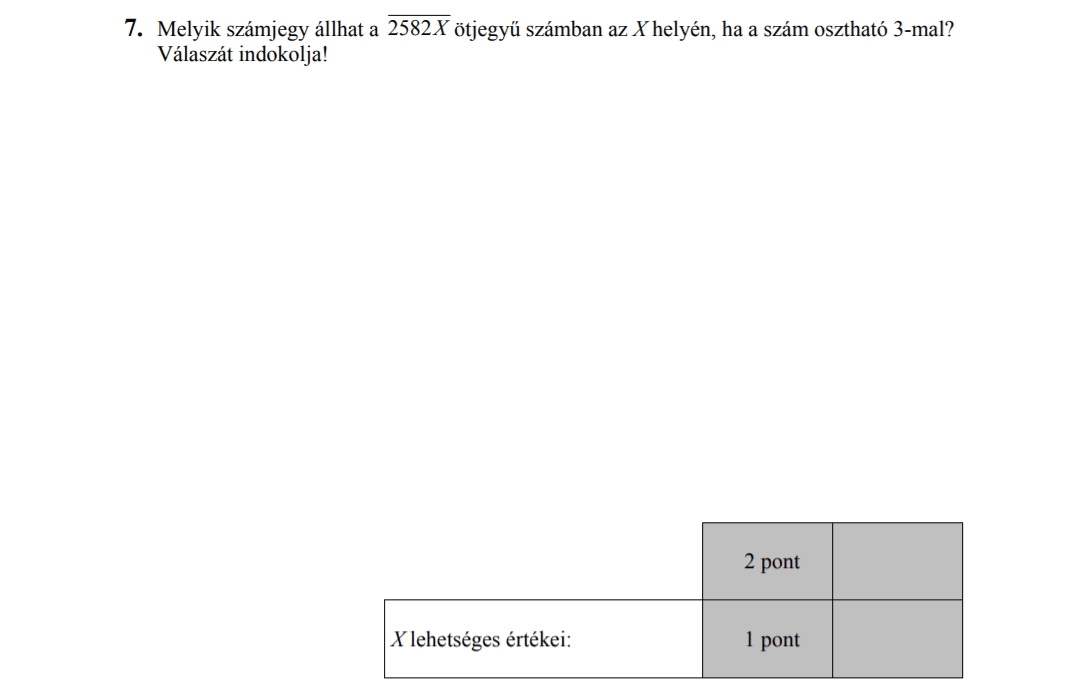
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
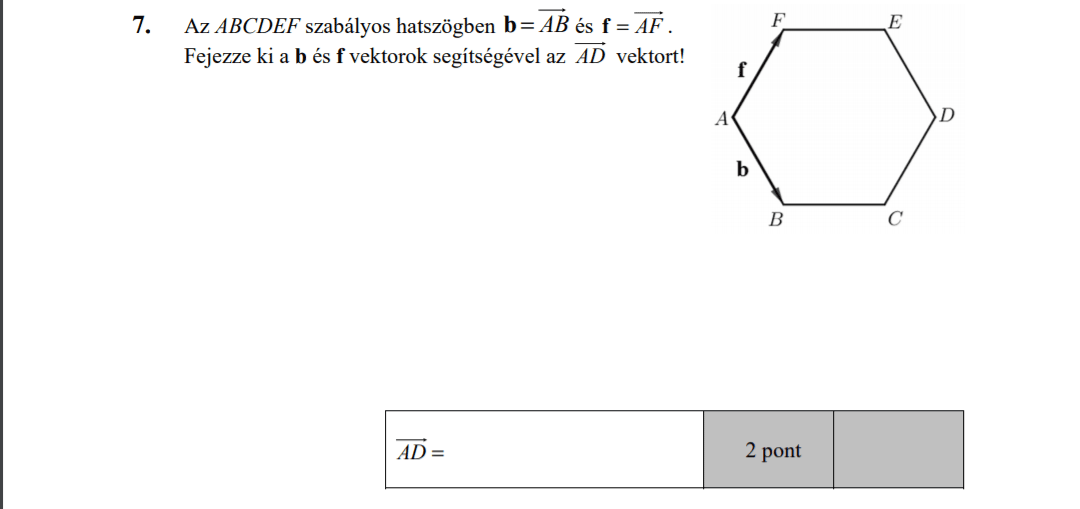
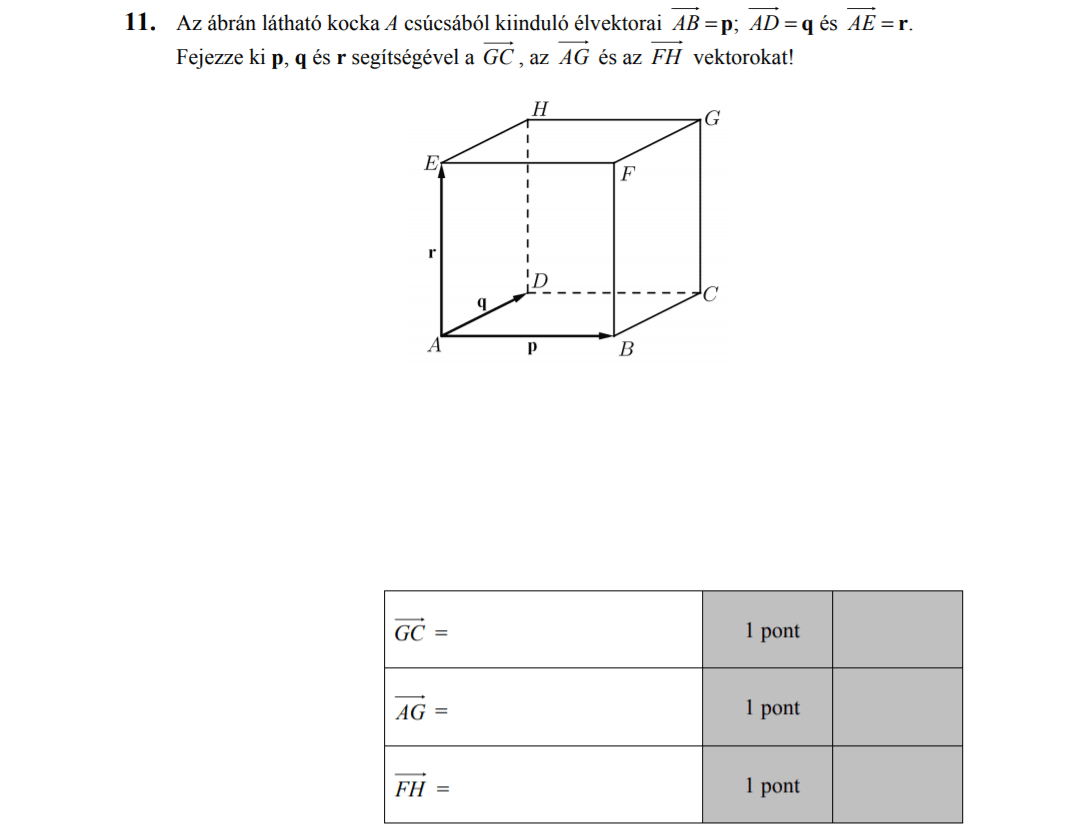
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Statisztika (9,3 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


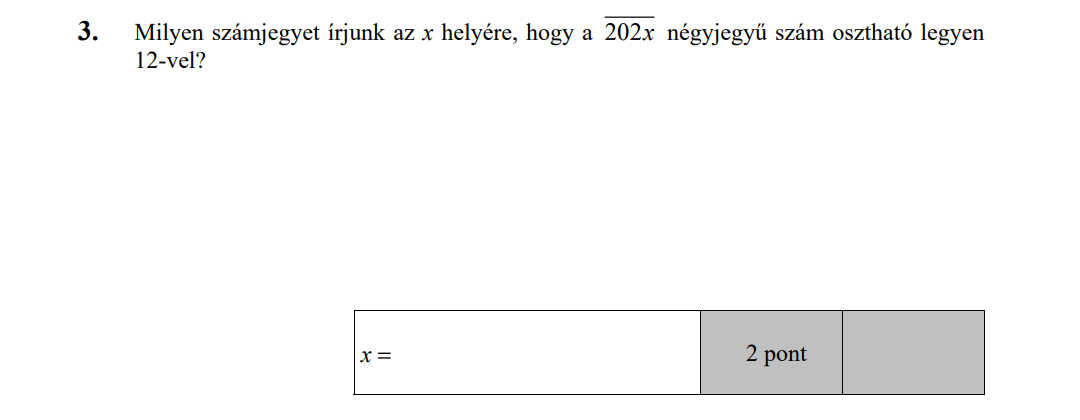
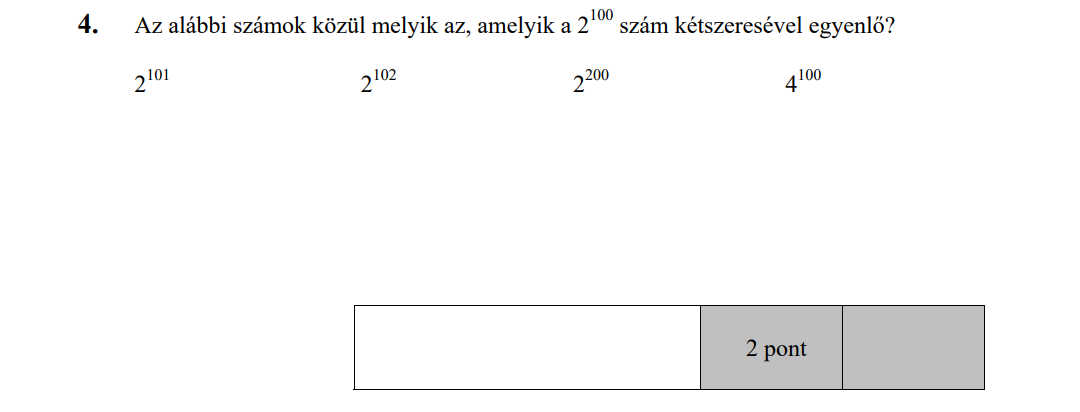



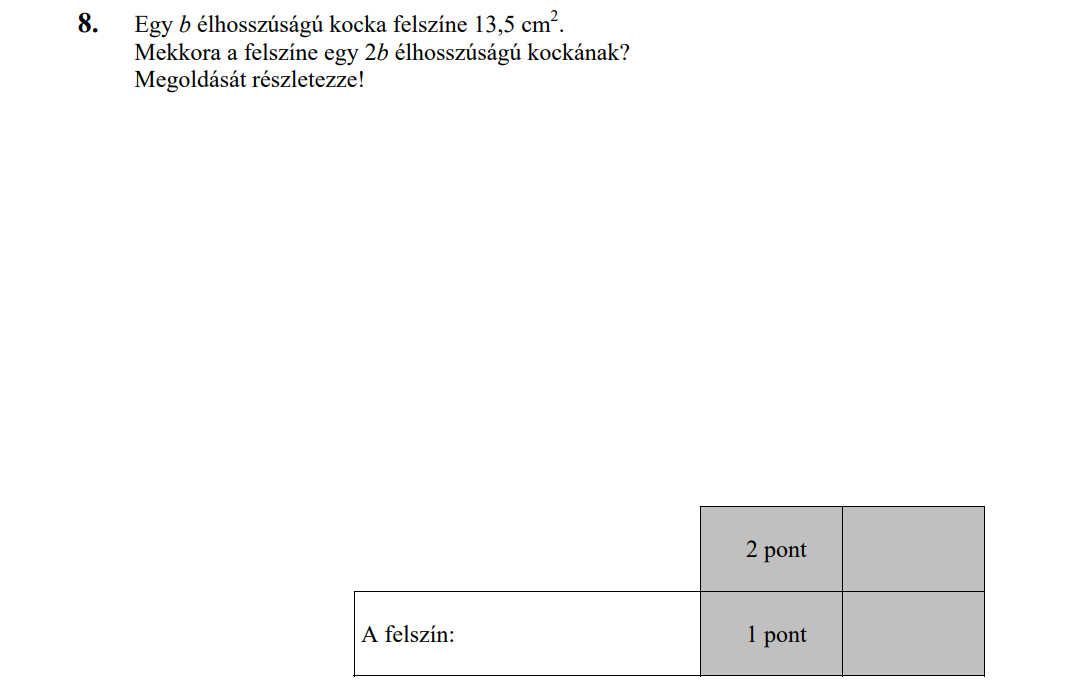




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
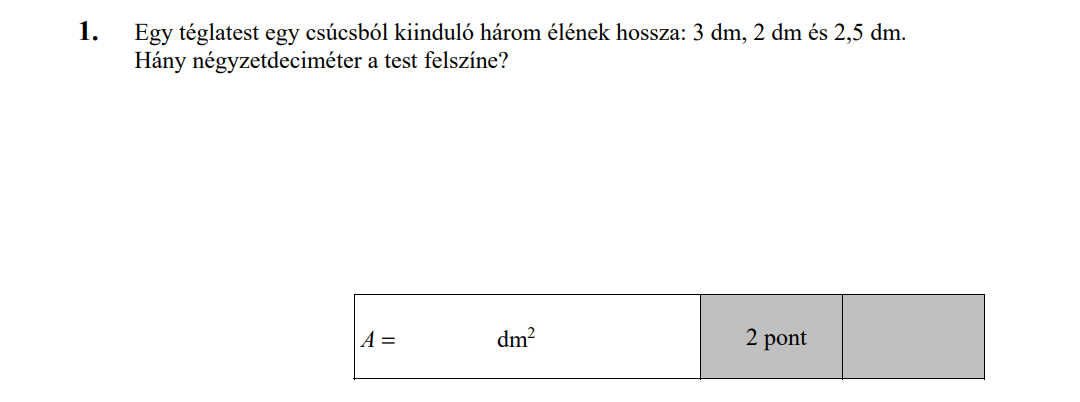
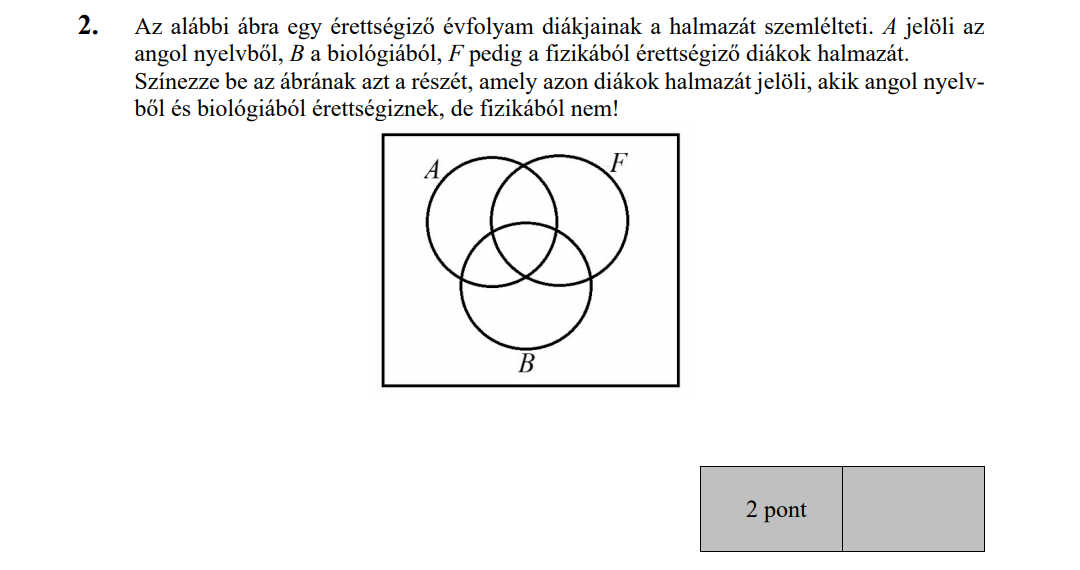

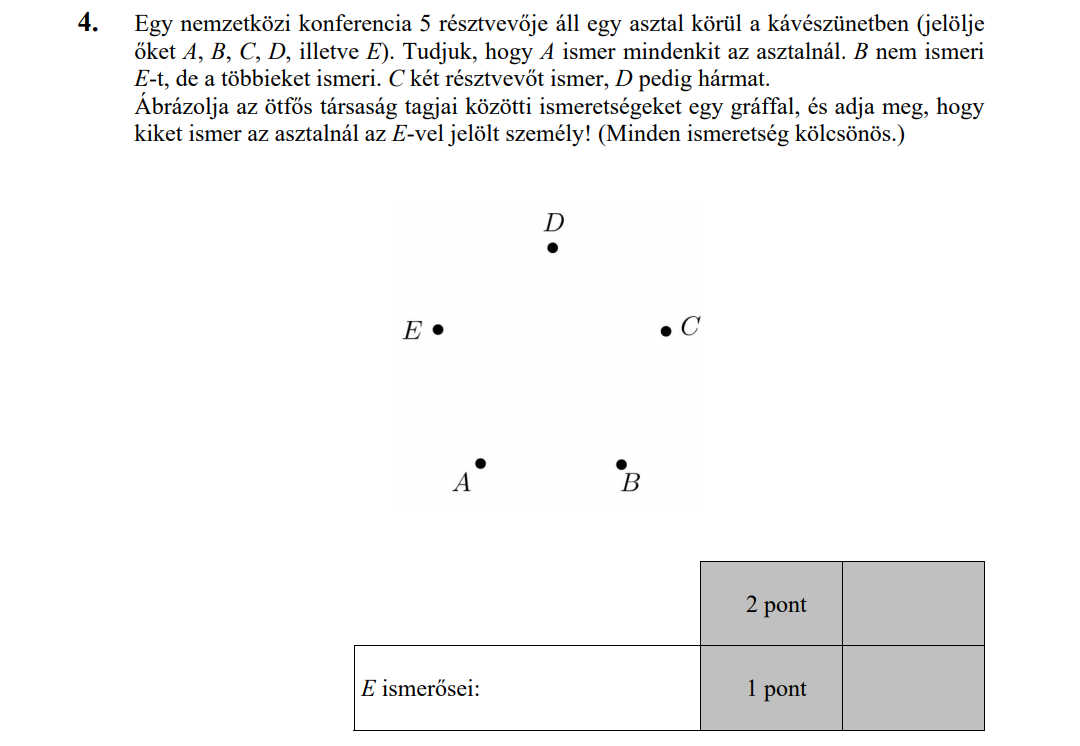

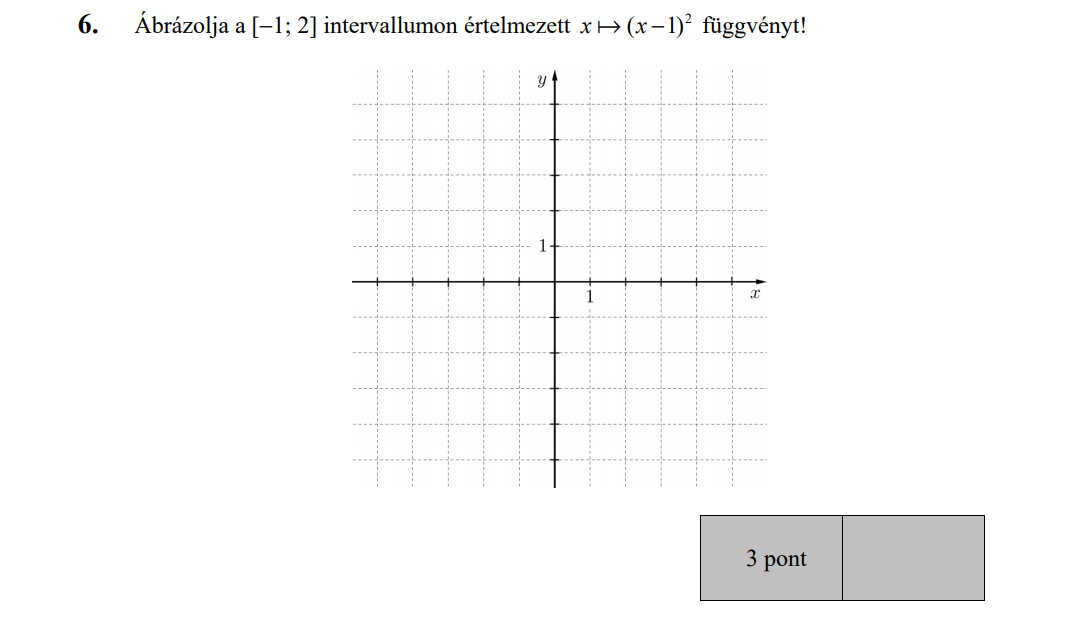



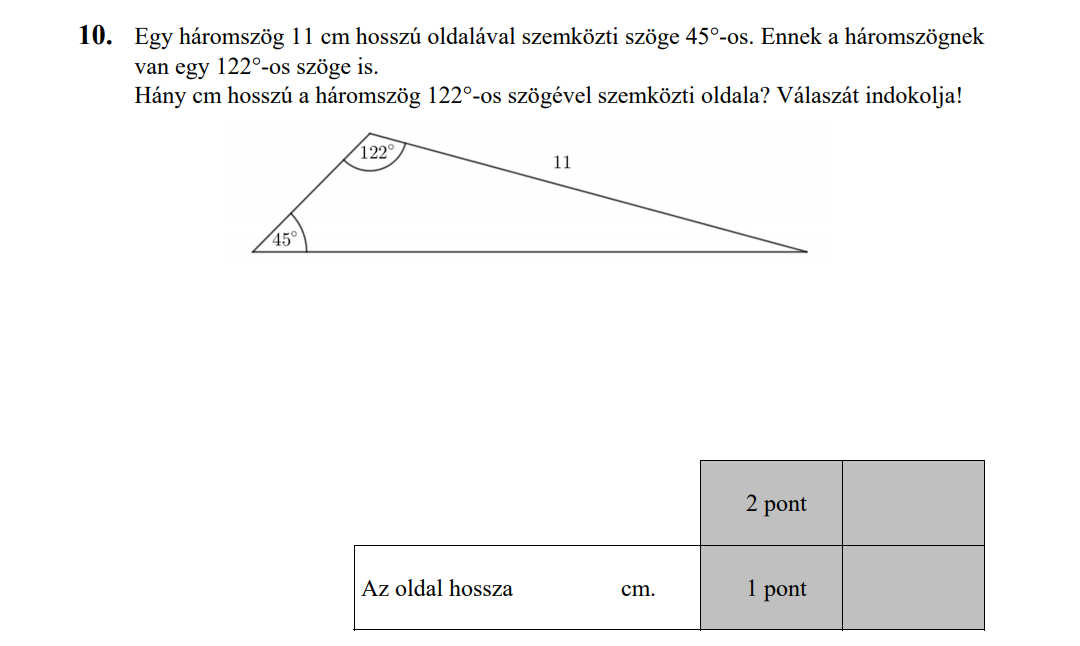

MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ





- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ

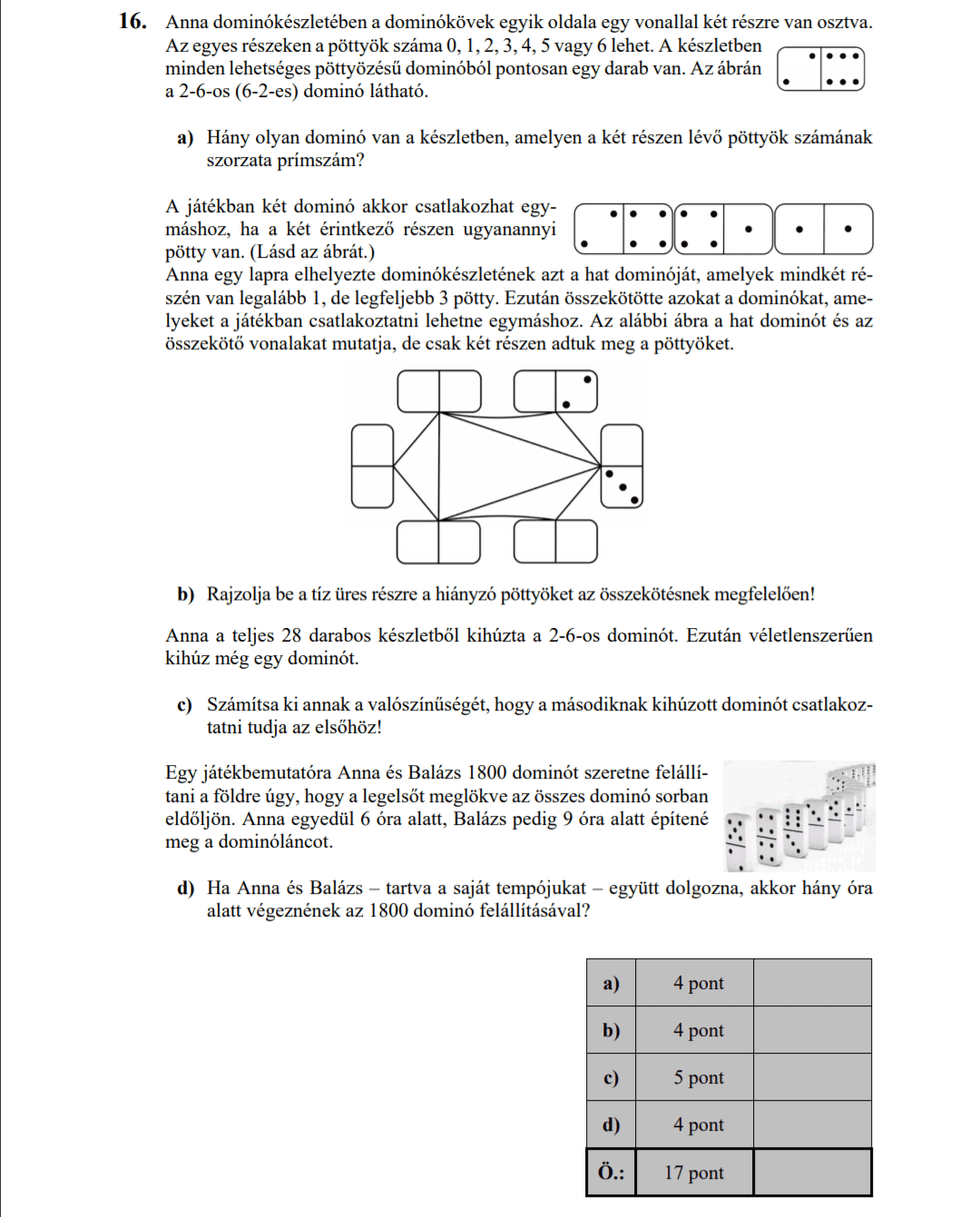


- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




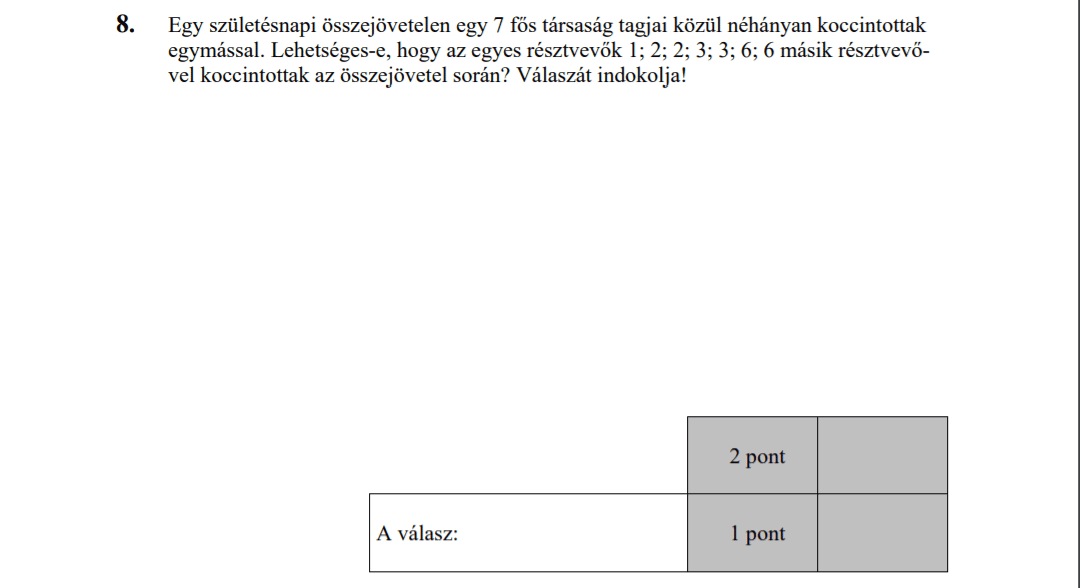



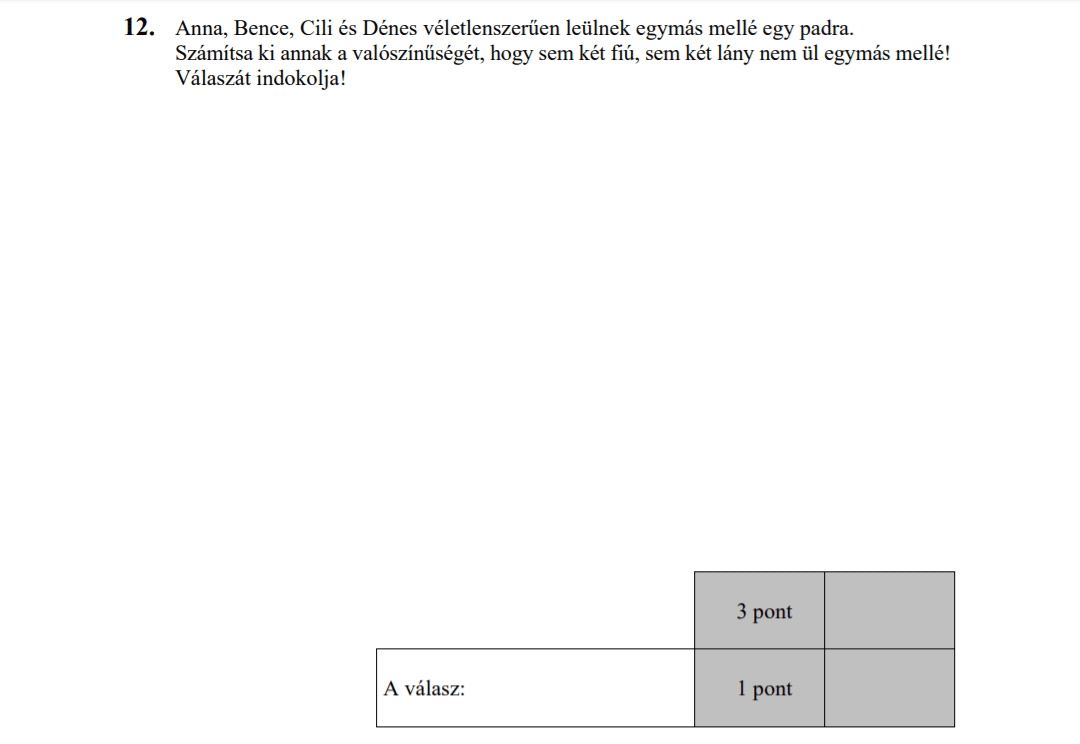
MÁSODIK RÉSZ

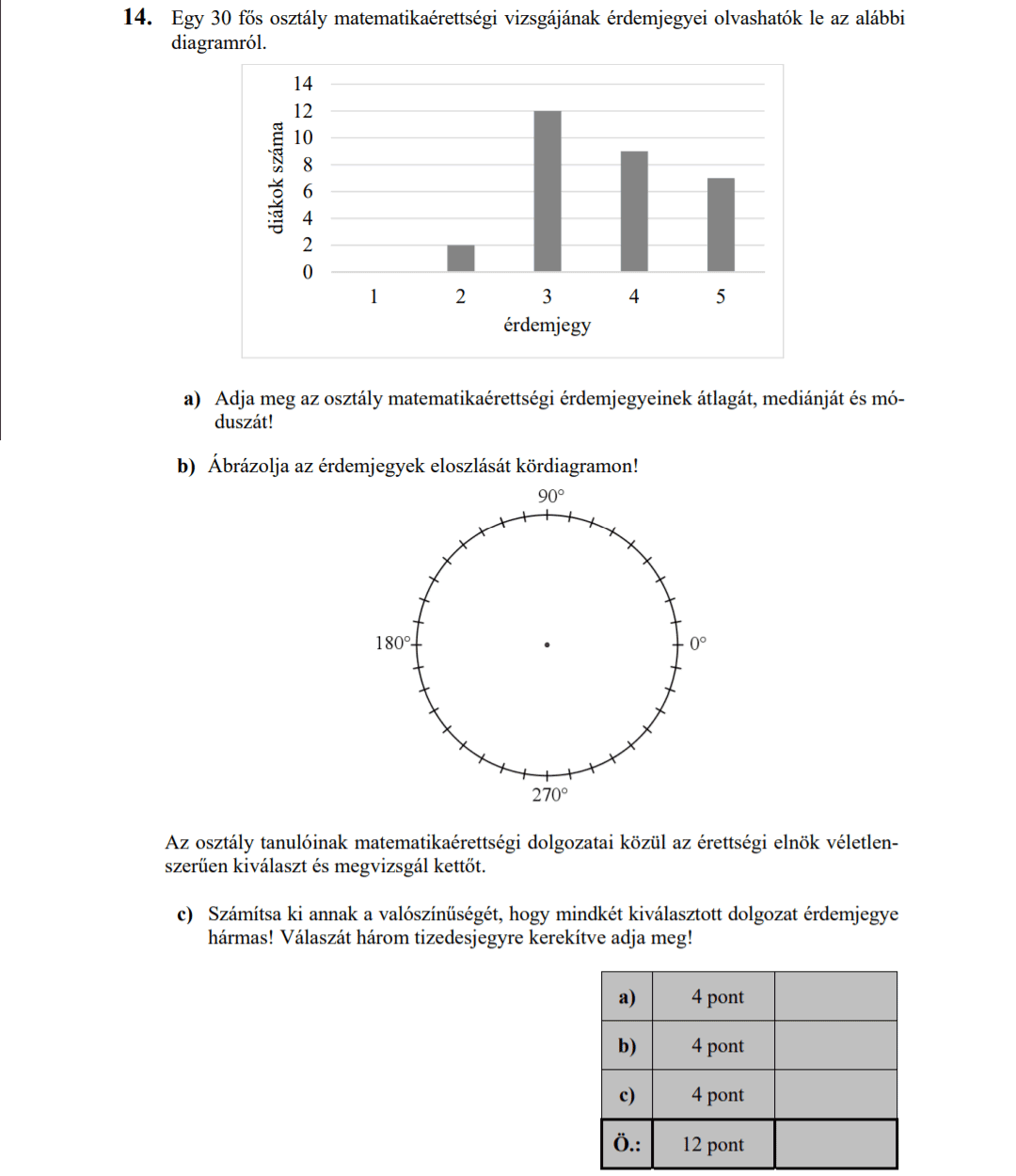
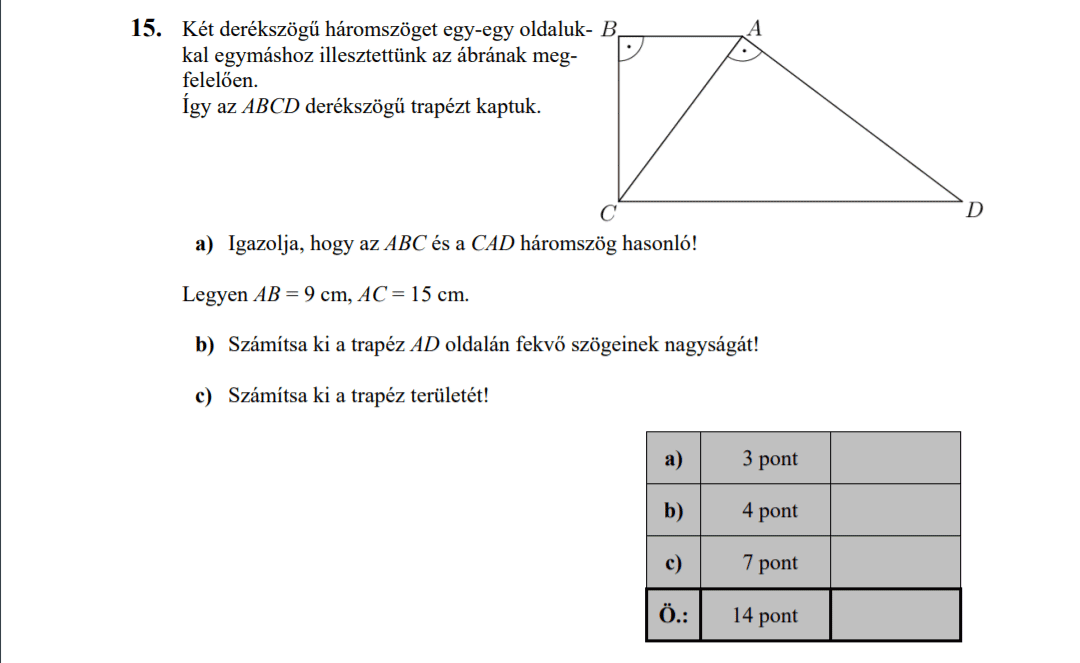



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


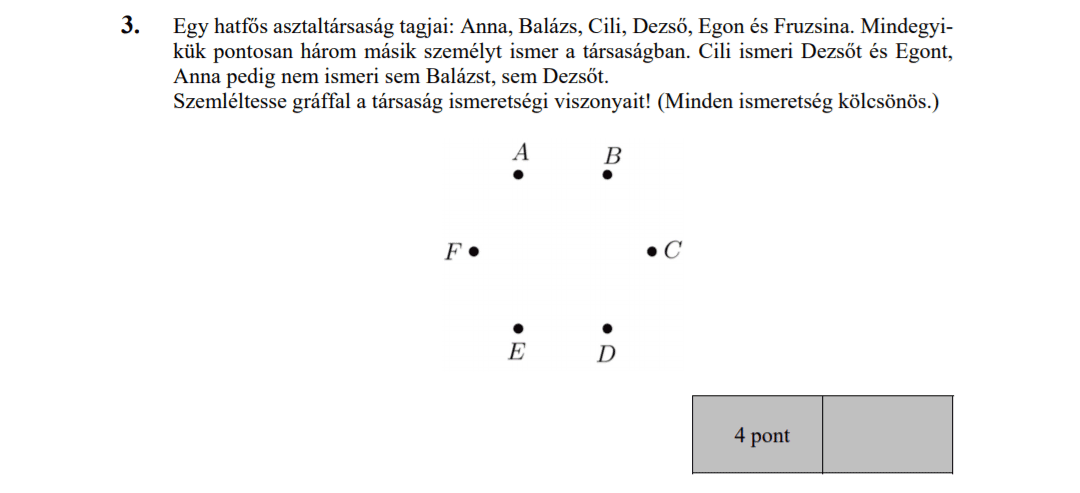


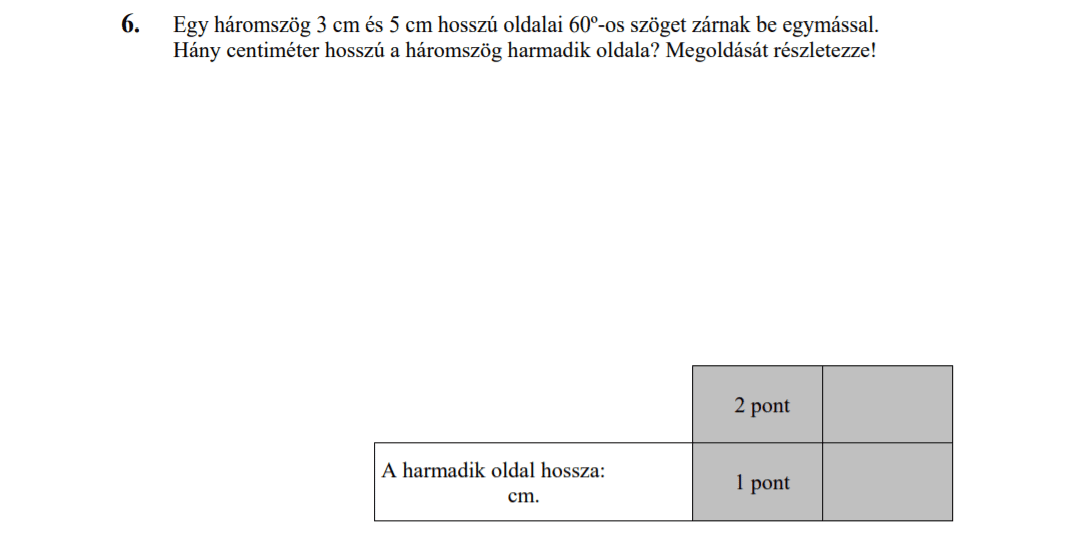

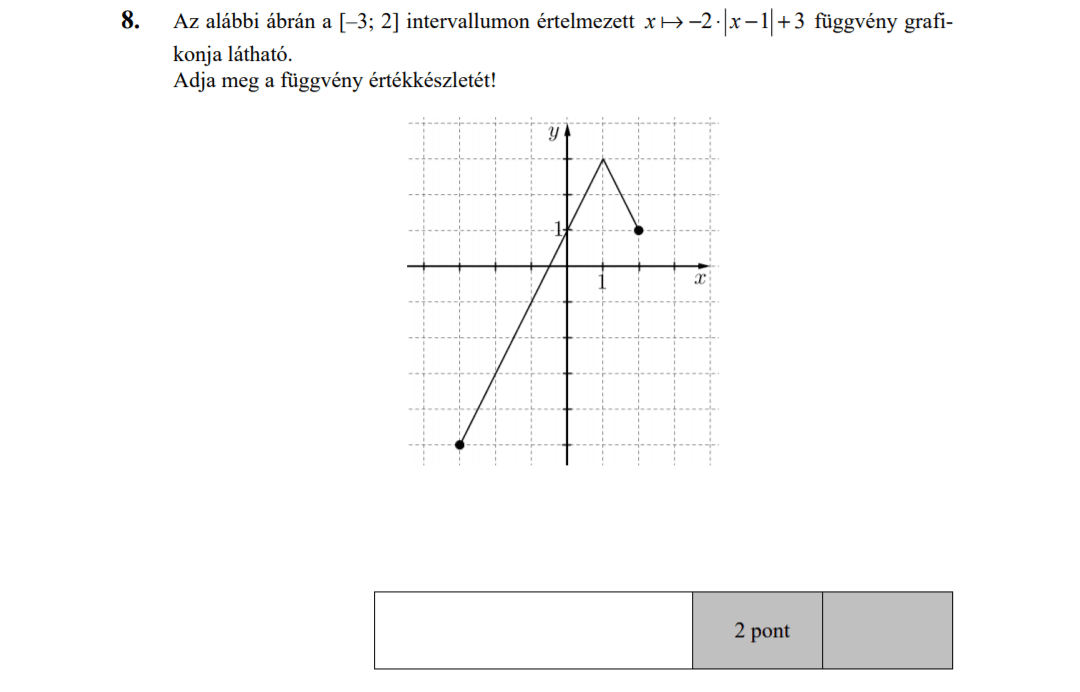

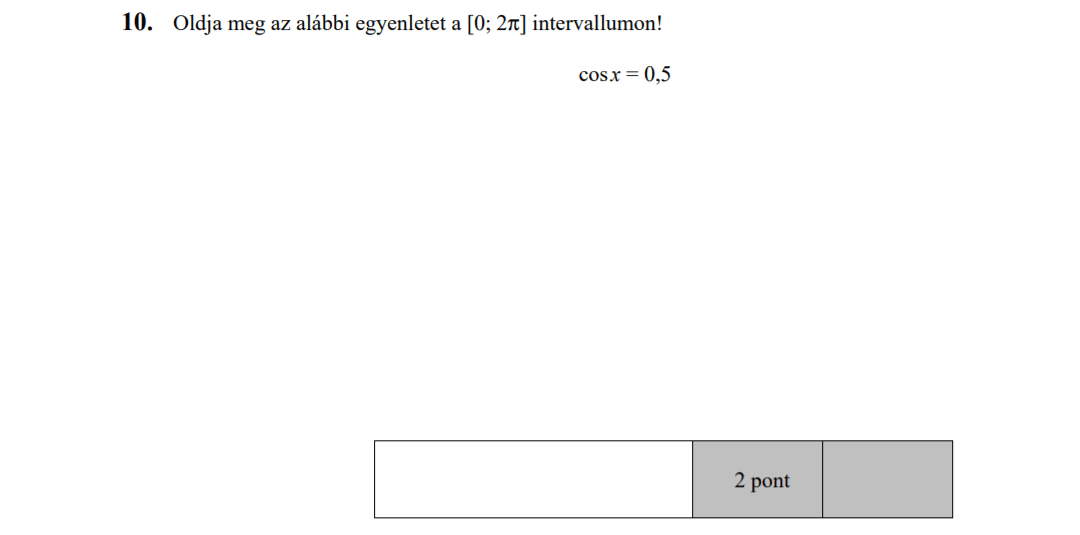

MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






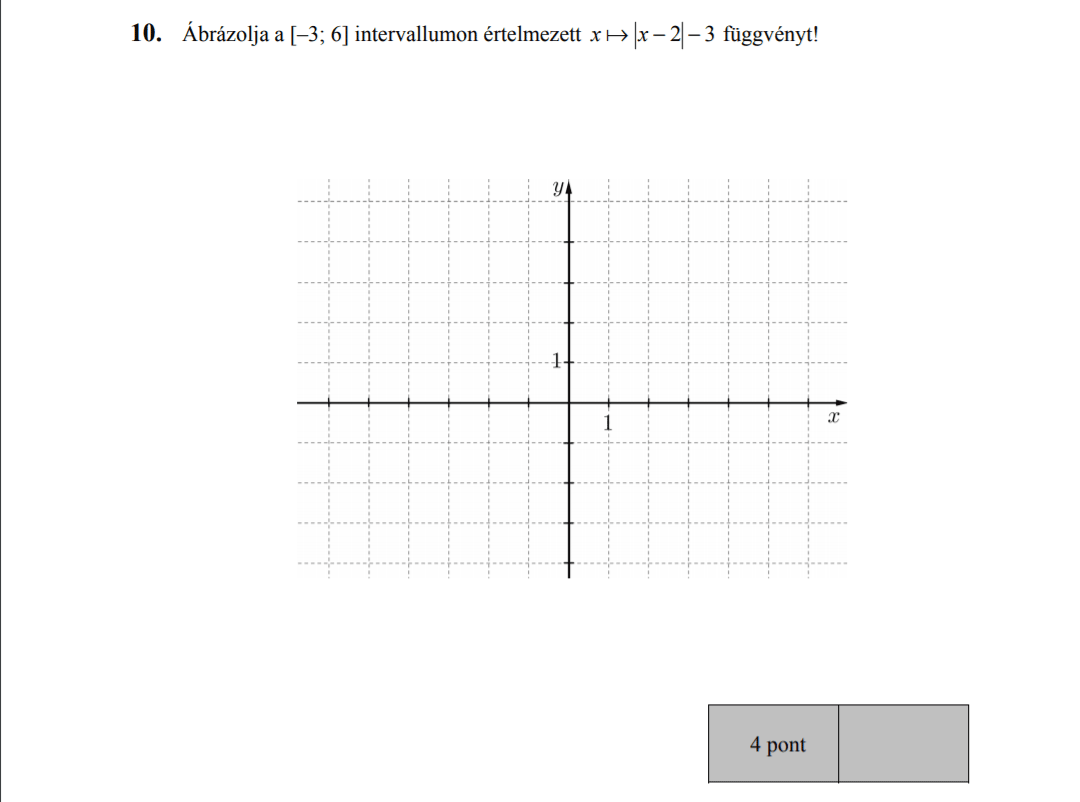

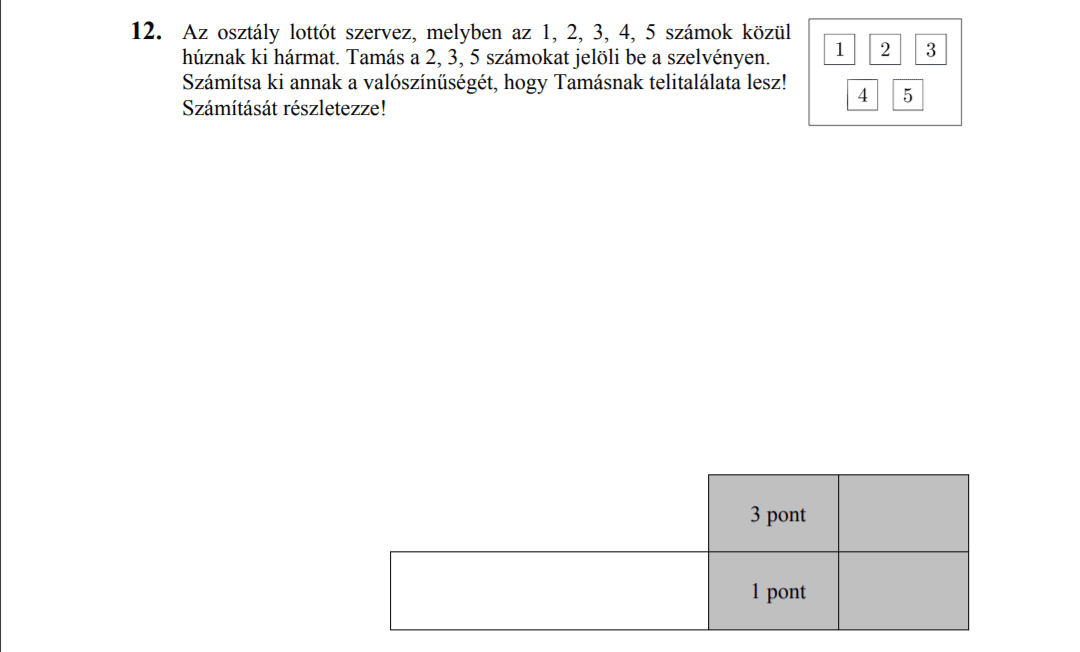
MÁSODIK RÉSZ

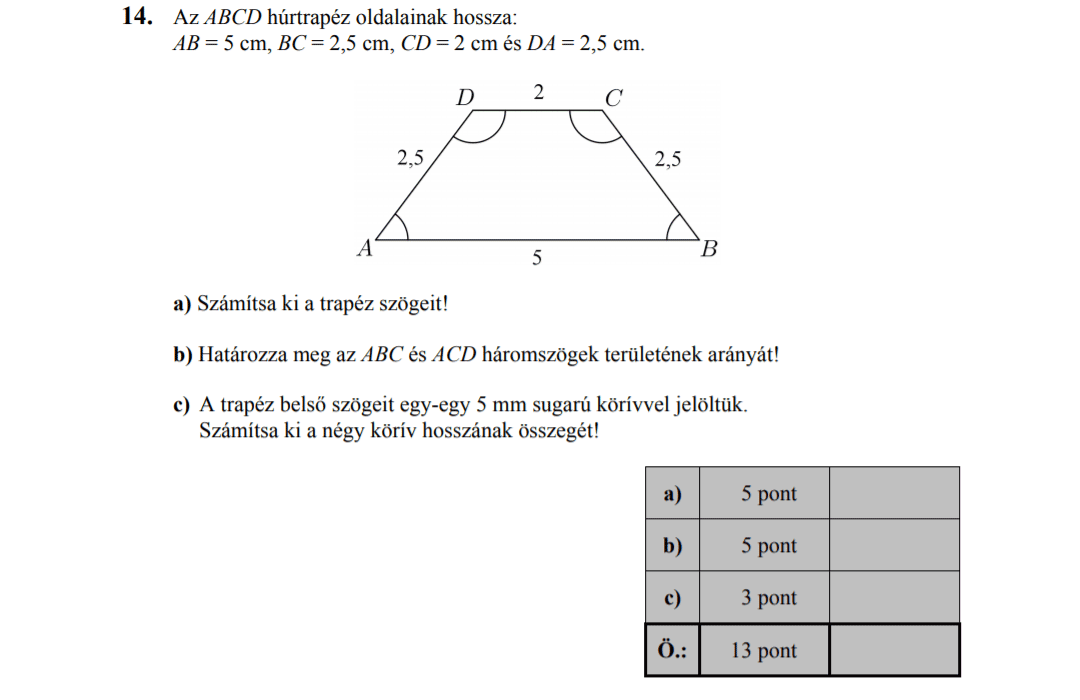

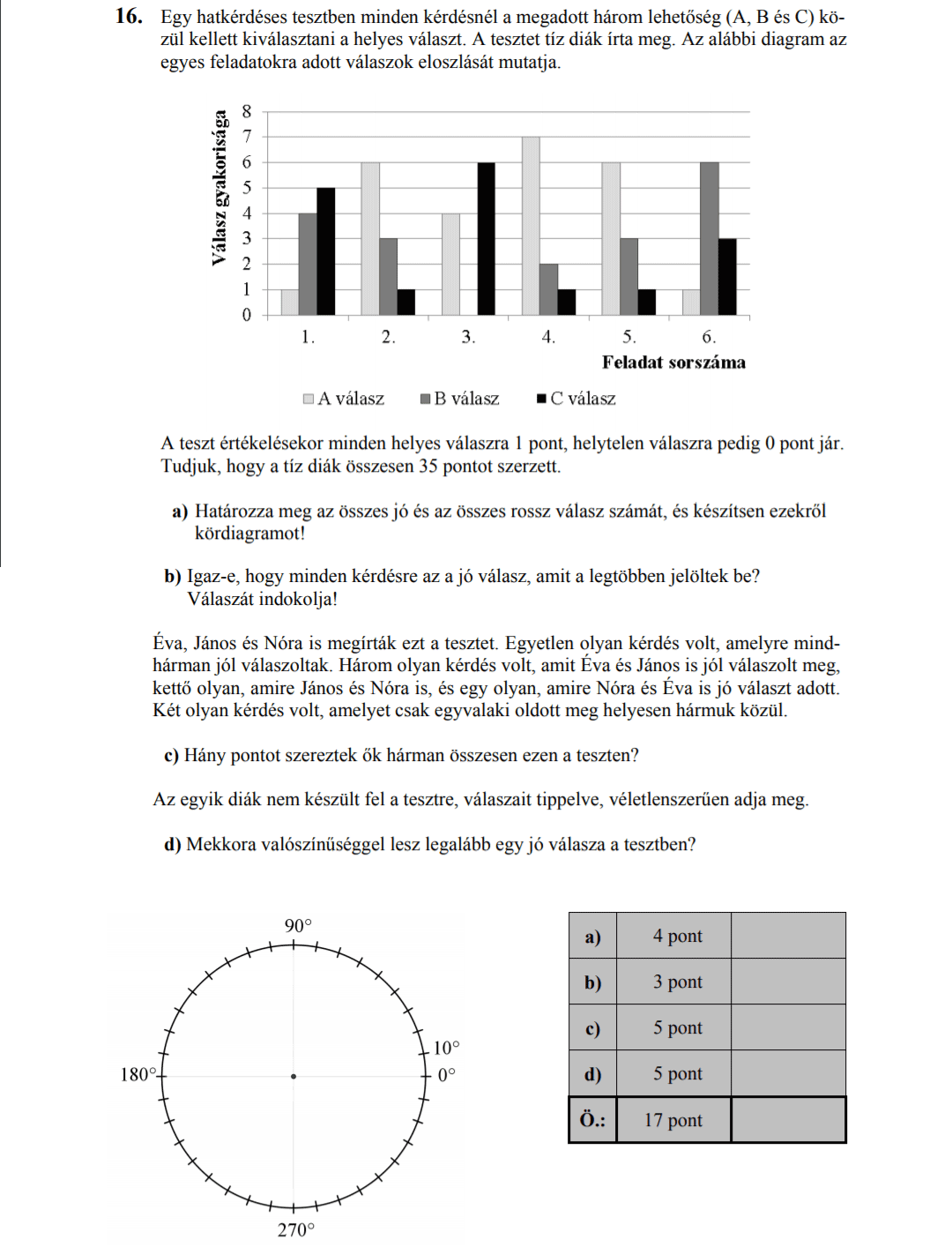


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ









MÁSODIK RÉSZ

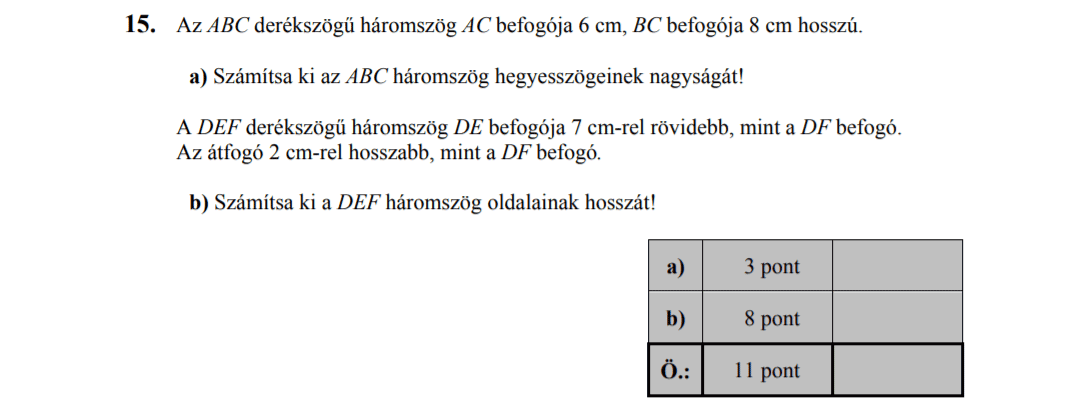



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

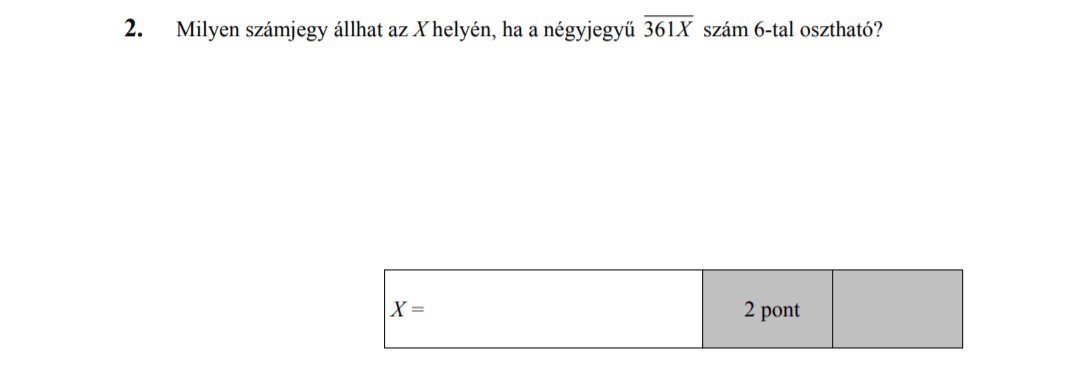



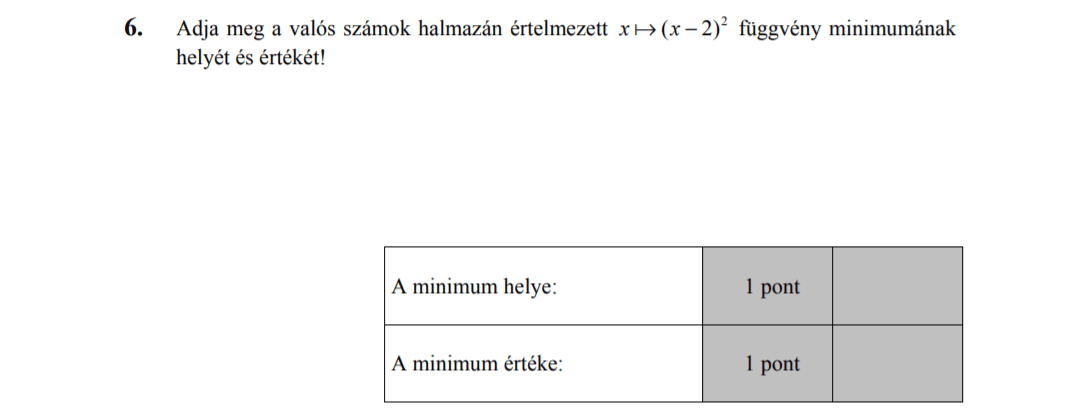

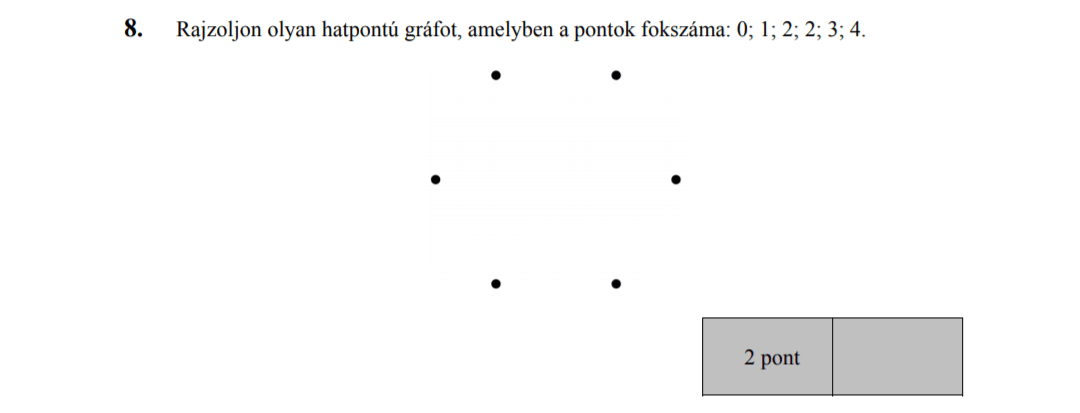


MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








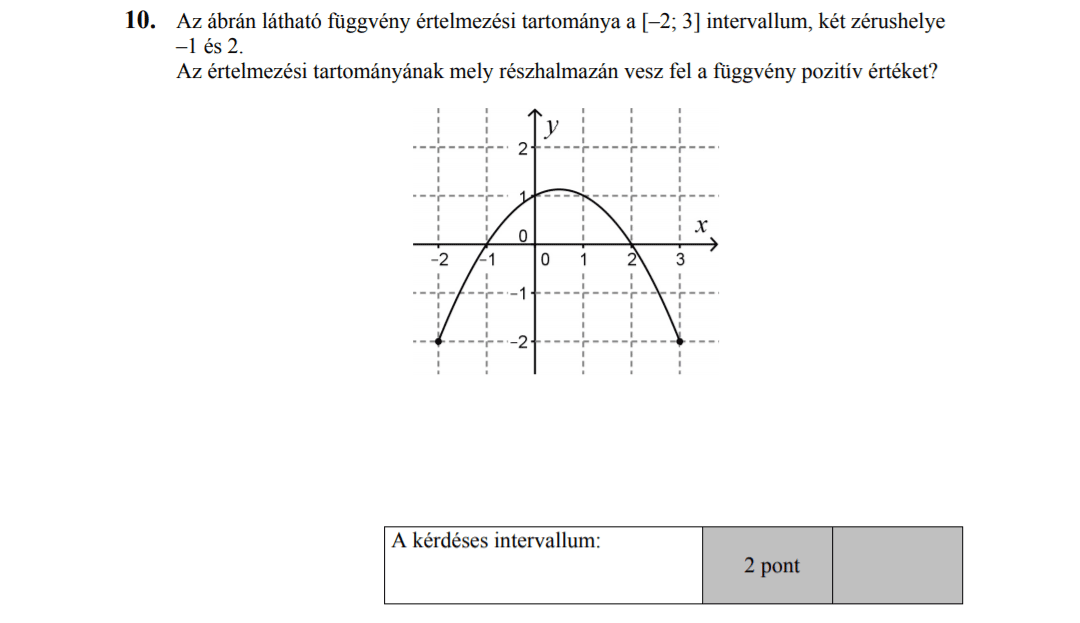


MÁSODIK RÉSZ


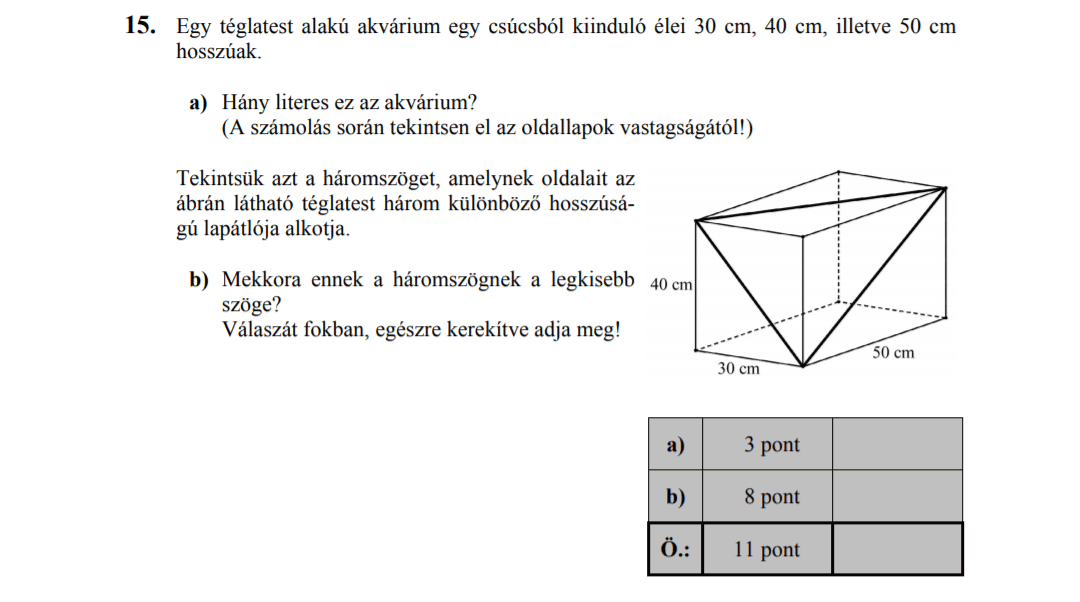

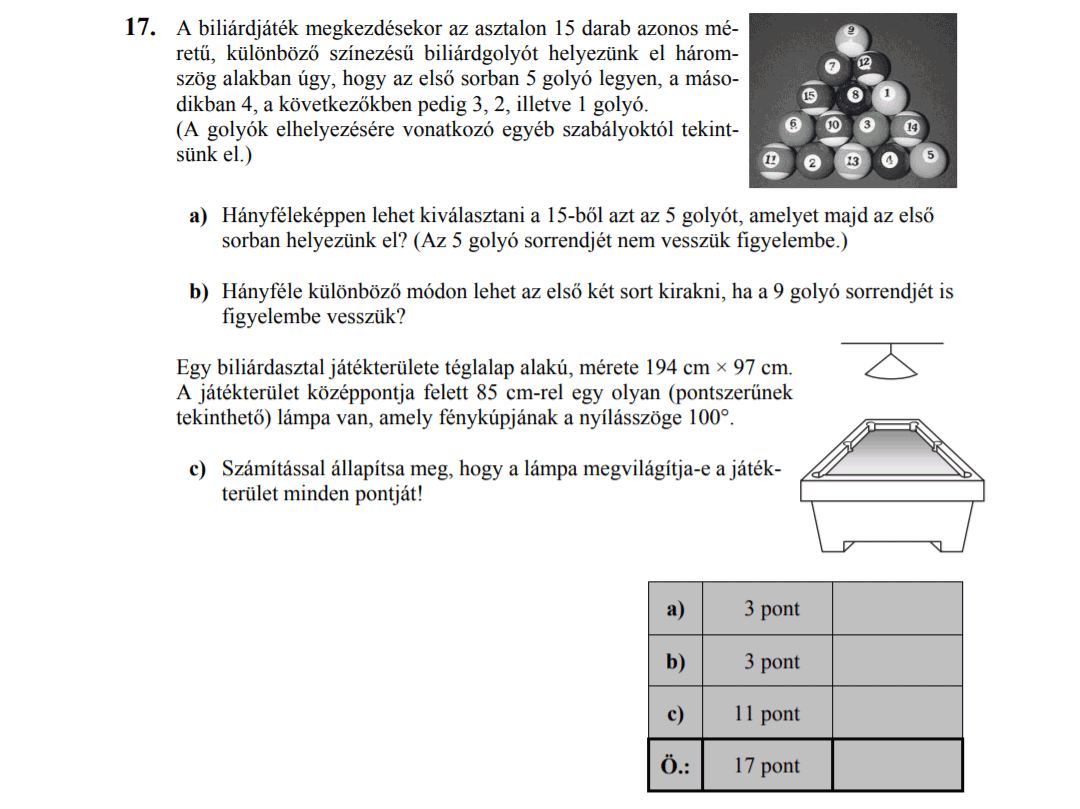

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


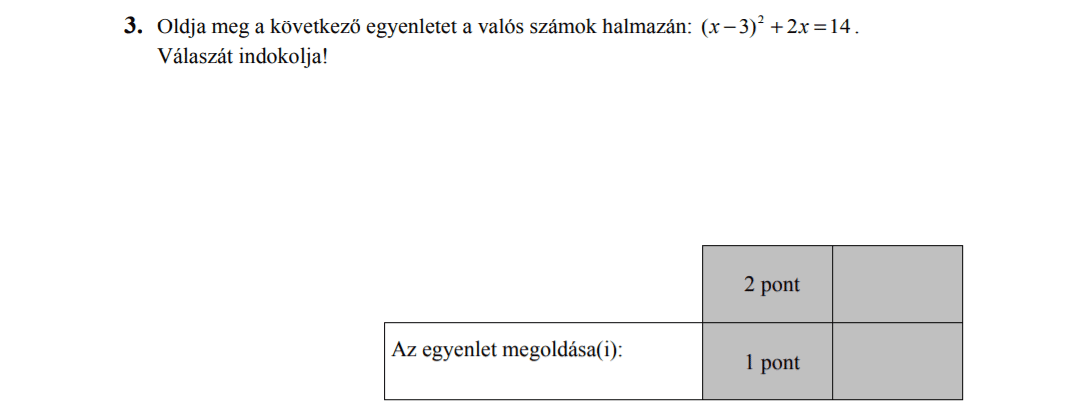





MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ





- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Módusz
Az adatsor legyakoribb értéke a módusz. Hogyha például Bob matekjegyei ezek:
2, 3, 1, 4, 1, 2, 2, 3, 5, 2, 3, 2, 3, 2, 4, 3, 2, 4, 2, 4
Akkor egyszerűen meg kell számolni, hogy melyikből van a legtöbb, és az a matekjegy lesz a módusz. Most 2-esből van a legtöbb, így Bob matekjegyeinek a módusza 2. A módusz jele Mo és így most Mo=2.
Léteznek olyan eloszlások is, amelyeknek több módusza van. Hogyha például Bob jegyei:
1, 2, 2, 3, 5, 3, 3, 4, 2
Itt 2-esből és 3-asból ugyanannyi van, mindkettőből 3 darab. Ez egy kétmóduszú eloszlás.
Medián
A medián a növekvő sorba rendezett adatsor középső értéke. Ha az adatsorban páros sok elem van, akkor nincs középső elem, ilyenkor a két középső elem átlagát vesszük.
Hogyha például Bob matekjegyei ezek:
2, 3, 1, 4, 1, 2, 2, 3, 5, 2, 3, 2, 3, 2, 4, 3, 2, 4, 2, 4
Akkor egyszerűen növekvő sorba kell rakni..
1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5
És aztán meg kell keresni melyik a középső. Most nincsen középső, mert páros sok elem van, így ilyenkor a két középen lévőt átlagoljuk:
1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5
Ezeknek az átlaga 2,5 vagyis a medián most 2,5. A medián jele Me, így Me=2,5
Átlag
Az átlagot úgy kapjuk meg, hogy az összes elemet összeadjuk, és aztán elosztjuk az elemek számával.
Jele: $\overline{x}$
Szórás
Az átlagtól való átlagos eltérés egyik legjobb mérőszáma a szórás. Hátránya, hogy egy kicsit ronda a szórás képlete. A szórást egy szigma nevű görög betűvel jelöljük.
\( \sigma = \sqrt{ \frac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+\dots+(x_n-\overline{x})^2}{n} } \)
Alsó kvartilis
Az adatsor első felének a felezőpontja az alsó kvartilis.
Az alsó kvartilis jele: $Q_1$
Felső kvartilis
Az adatsor második felének a felezőpontja a felső kvartilis.
A felső kvartilis jele: $Q_3$
Dobozdiagram, doboz-ábra (box plot)
A kvartilisek és a medián azt szemlélteti, hogyan oszlanak el az adatsorban szereplő adatok. Ezek segítségével készíthető el a doboz-ábra, vagy másnéven dobozdiagram. Szokás még sodrófa diagramnak is nevezni, és az angol elnevezést is gyakran használják, ami a box plot.
Egy sobarendezett adatsorban öt darab speciális negyedelőpontot fogunk használni. Az első az adatsor legkisebb értéke, ez a Q0 . Aztán a következő negyedelő az alsó kvartilis, ami Q1 utána jön a felezőpont vagyis a medián, ezt Me-vel és Q2-vel is jelöljük, végül a felső kvartilis, ami a Q3. Az adatsor legnagyobb értéke pedig Q4. A legnagyobb és a legkisebb érték különbsége a terjedelem, míg a két kvartilis különbségét félterjedelemnek vagy más néven interkvartilisnek hívjuk. Ezekből épül föl a doboz-ábra vagy másként dobozdiagram.
Előfordulhat, hogy az adatsorban kiugró értékek is szerepelnek. A kiugró érték az, ami az alsó kvartilisnál legalább a félterjedelem másfélszeresénél kisebb, vagy pedig a felső kvartilisnél legalább a félterjedelem másfélszeresénél nagyobb. Huh, ez elég bonyolultan hangzik. De valójában nagyon egyszerű, csak nézd meg kapcsolódó epizódot és kiderül.
Relatív szórás
A relatív szórás azt mondja meg, hogy a szórás az átlagnak hány százaléka:
\( V = \frac{\sigma}{\overline{X}} \)
Számítsuk ki Bob matekjegyeinek móduszát és mediánját.
Ezek a matek jegyek:
2, 3, 1, 4, 1, 2, 2, 3, 5, 2, 3, 2, 3, 2, 4, 3, 2, 4, 2, 4
Bob nem kedveli a kémiát.
Ezt a jegyei alapján bárki megállapíthatja.
2, 3, 3, 2, 3
Alfréd viszont rajong a kémia egyes területeiért... de csak azokért.
5, 5, 1, 1, 1
Számítsuk ki Bob és Alfréd jegyeinek átlagát és szórását.
a) Egy futóversenyen 10-en vesznek részt.
A futók eredményei (percben):
98, 73, 68, 92, 110, 75, 87, 96, 108, 130
Készítsünk doboz-ábrát az eredményekről.
b) A naprendszer bolygóinak aránya a Földhöz képest a következők:
| Merkúr | 0,06 |
| Mars | 0,12 |
| Vénusz | 0,82 |
| Föld | 1 |
| Uránusz | 14 |
| Neptunusz | 17 |
| Szaturnusz | 95 |
| Jupiter | 318 |
Készítsünk dobozdiagramot a bolygók tömegének eloszlásáról.
Egy futóversenyen 10-en vesznek részt.
A futók eredményei (percben):
98, 73, 68, 92, 110, 75, 87, 96, 108, 130
Készítsünk doboz-ábrát az eredményekről.
Egy futóversenyen több országból indultak versenyzők.
Íme, itt látható, hogy milyen eredményeket értek el, és melyik országból jöttek.
| Ország | Eredmény (percben) |
| Németország | 68 |
| Franciaország | 73 |
| Németország | 74 |
| Ausztria | 87 |
| Olaszország | 92 |
| Olaszország | 96 |
| Olaszország | 98 |
| Németország | 108 |
| Németország | 110 |
| Olaszország | 130 |
| Németország | 134 |
| Németország | 140 |
Ábrázoljuk a versenyzők nemzetiség szerinti eloszlását.
Egy futóversenyen 150 versenyző vett részt. A versenyzők eredményeit tartalmazza ez a táblázat
| Eredmény (perc) |
Versenyzők száma |
| 50-59 | 12 |
| 60-69 | 18 |
| 70-79 | 27 |
| 80-89 | 39 |
| 90-99 | 32 |
| 100-109 | 22 |
Számoljuk ki az átlagot, a szórást és a relatív szórást, valamint ábrázoljuk a verseny eredményét hisztogrammal.
a) Egy csoportban hatan írnak tesztet, a teszt eredménye 1-es, 2-es, 3-as, 4-es vagy 5-ös lehet. Tudjuk, hogy csak egy 3-as van és az átlag 4,5. Mik voltak az eredmények?
b) 11 darab nem negatív egész számról tudjuk, hogy egyetlen móduszuk a 2, mediánja 3, átlaga 4 és terjedelme 5. Adjunk meg a feltételnek eleget tevő 11 darab ilyen számot.
Egy vonat utasainak száma hétfőn 200, kedden 190, szerdán 90, csütörtökön 170. Hány utas volt pénteken, ha tudjuk, hogy az öt adat átlaga is szerepel az adatok között, és egyik nap sem utaztak 200-nál többen, sem pedig 90-nél kevesebben?
Egy vonat utasainak száma hétfőn 200, kedden 160, szerdán 90, csütörtökön 150. Hány utas volt pénteken, ha tudjuk, hogy az öt adat átlaga is szerepel az adatok között, továbbá az adatok egyetlen módusza nem egyenlő a mediánjukkal?
Egy városkában 30 szálloda üzemel. A szállodák között van kétcsillagos, háromcsillagos, négycsillagos és ötcsillagos is.
a) Számoljuk ki, hogy átlagosan hány csillagosak a szállodák a városkában. Adjuk meg a mediánt és a móduszt is.
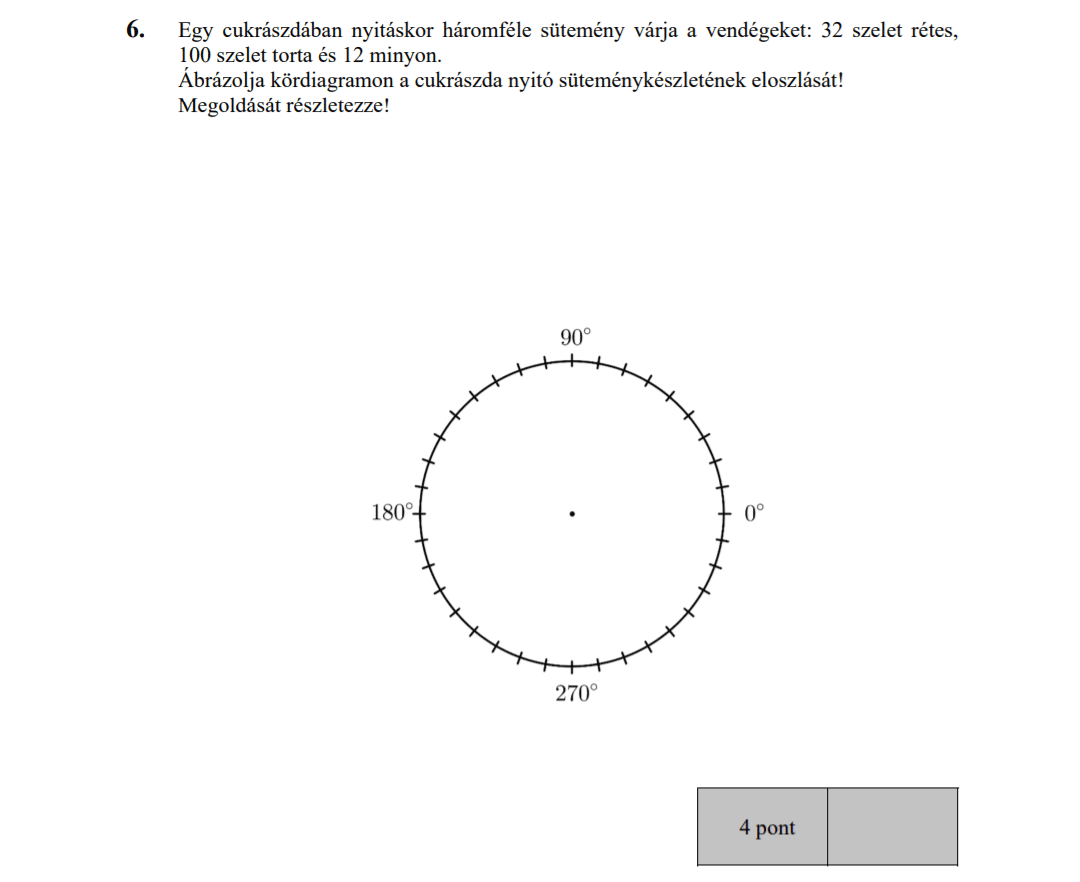
b) Ábrázoljuk kördiagramon a szállodák csillagok szerinti megoszlását.
| * | 0 |
| ** | 2 |
| *** | 12 |
| **** | 9 |
| ***** | 7 |
Egy tesztet 12 vizsgázó írja meg. A maximálisan elérhető pontszám 100, az eredmények pedig a következők: 56, 47, 60, 86, 71, 96, 55, 24, 76, 81, 72, 91
Készítsünk box plot diagramot.
Egy adathalmazról ezt a dobozdiagramot készítették.
a) Mennyi az alsó és felső kvartilis, a medián, és mekkora a terjedelem?
b) Adjunk meg egy olyan tizenkettő elemű adathalmazt, amiről egy ilyen dobozdiagram készülhetett.
Egy tesztet 12 vizsgázó írja meg. A maximálisan elérhető pontszám 100, az eredmények pedig a következők:
56, 47, 60, 86, 71, 96, 55, 24, 76, 81, 72, 91.
Készítsünk doboz-ábrát.
Egy piacon az almát egy olyan csomagolásban árulják, melynek felirata 5 kg \( \pm \) 10 dkg. A minőségellenőrzés során véletlenszerűen kiválasztanak 8 csomagot, és ezeket lemérik. Az almák árusítását csak akkor engedélyezik, ha egyik csomag tömege sem kisebb 4 kg 90 dkg-nál, és a mérési adatok 5 kg-tól mért átlagos abszolút eltérése nem haladja meg a 10 dkg-ot.
a) Engedélyezik-e az árusítást?
b) Határozzuk meg a mérési eredmények átlagát és szórását!
| Mérés sorszáma | 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. |
| mért tömeg (dkg) | 506 | 491 | 493 | 512 | 508 | 517 | 493 | 512 |
Egy 24 fős osztály matek érettségi eredményeit tartalmazza ez a táblázat.
| Osztályzat | 1 | 2 | 3 | 4 | 5 |
| Darabszám | 0 | 2 | 9 | 6 | 7 |
a) Mennyi a jegyek átlaga?
b) Mennyi a jegyek módusza, mediánja és terjedelme?
c) Készítsünk a matek érettségi eredményeiről dobozdiagramot.
30 napon keresztül vizsgálták, hogy egy úton naponta hány baleset történik.
| Balesetek száma | napok száma |
| 0 | 7 |
| 1 | 8 |
| 2 | 6 |
| 3 | 4 |
| 4 | 3 |
| 5 | 2 |
Számoljuk ki az átlagot, a szórást, a móduszt, a mediánt és ábrázoljuk a táblázat adatait oszlopdiagrammal.
Egy taxitársaságnál a telefonos rendeléstől a helyszínre érkezésig eltelt idő egy hét leforgása alatt az alábbi volt:
| Eltelt idő (perc) |
Esetek száma |
| 0-4 | 1654 |
| 5-9 | 2470 |
| 10-19 | 680 |
| 20-29 | 46 |
Számoljuk ki az átlagot, a szórást és a relatív szórást.
Bob nem túl jó matekból, viszont szeret rajzolni, így hát elhatározta, hogy ábrázolja a matekjegyeit egy grafikonon… Ezek a matekjegyek: És ez pedig Bob… Ezt a grafikont úgy hívjuk, hogy oszlopdiagram. Az egyik tengelyen vannak a matekjegyek… A másik tengelyen pedig az, hogy hány darab van belőlük. A diagramról lazán le tudjuk olvasni Bob matekjegyeit. Van két darab 1-ese… Hat darab 2-ese… Négy darab 3-asa… Két darab 4-ese… És egy 5-öse. Az oszlopdiagramról már messziről látni, hogy Bobnak leginkább 2-esei vannak. És az is látszik, hogy 5-ösből van a legkevesebb... De igaz-e vajon, hogy Bob matekjegyeinek több mint a fele 2-es? Na, ezt már nehezebb ránézésre megmondani. Meg kéne hozzá számolni, hogy hány darab 2-es van és hány jegy van összesen. Itt jön most egy másik diagram, amiről ez is ránézésre látszódni fog… Ezt úgy hívjuk, hogy kördiagram. Kell hozzá egy kör… Amit felosztunk annyi részre ahány matekjegye van Bobnak. A teljes kör 360 fok… Ezt kell felosztanunk 15 egyenlő részre… És most rajzoljuk be Bob matekjegyeit… A kördiagramon látszik, hogy Bobnak jó sok 2-ese van… De azért kevesebb, mint a jegyeinek a fele. Hogyha a darabszámokat is ráírjuk… Akkor a kördiagramból is pontosan kiderül, hogy hány darab van a különböző jegyekből. De most már ne rugózzunk tovább Bob matekjegyein… Beszélgessünk inkább az időjárásról. Íme, a következő 12 nap időjárása… Ábrázoljuk oszlopdiagramon és kördiagramon. Hát, reméljük, Bob szereti az esőt… Nézzük meg a kördiagramon, hogy milyen arányban fog esni. Úgy néz ki, hogy Bobnak csak a nyaralása felében fog kellene a napszemüveg… Sőt, igazán csak itt. Ez 4 nap a 12 napból… Vagyis a nyaralás harmada. De itt azért még lehet egy kis napsütés…
Ebben a táblázatban 12 nap időjárása látható a legkisebb és legnagyobb napi hőmérséklettel.
Nézzük meg, hogyan tudjuk ábrázolni az adatokat ebben a koordinátarendszerben.
Ábrázoljuk a következő 12 nap legkisebb és legnagyobb napi hőmérsékletét egy koordinátarendszerben.
Ez itt a koordinátarendszer…
És most nézzük, hogyan tudjuk ábrázolni az adatokat.
Kezdjük a napi legkisebb hőmérsékletekkel.
Ha egyszerűen csak berajzoljuk ezeket a koordinátarendszerbe…
Azt úgy hívjuk, hogy pontdiagram.
Egy kicsit izgalmasabb, hogyha a pontokat össze is kötjük…
Ezt vonaldiagramnak nevezzük.
Ugyanezt megcsinálhatjuk a napi legnagyobb hőmérsékletekkel is.
Itt jön a pontdiagram…
És ez a vonaldiagram.
Hogyha nem külön-külön ábrázoljuk a legkisebb és a legnagyobb hőmérsékleteket, hanem az egészet egyben…
Akkor hétfőn napközben emelkedni kezd a hőmérséklet…
Aztán éjszakára lehűl.
Másnap újra emelkedik…
Aztán megint csökken.
És így ezt a cikcakkos vonalat kapjuk a 12 nap hőmérsékleteivel.
A grafikonról lazán le tudjuk olvasni, hogy melyik nap van a leghidegebb…
És azt is, hogy melyik napon van a legmelegebb.
Végül itt jön egy beugratós kérdés…
Melyik nap volt a napi legmelegebb hőmérséklet a leghidegebb?
Vagyis most csak a pirosakat kell nézni…
Lássuk, hol a legkisebb…
Két ilyen nap is van.
És nézzük meg azt is, mikor volt a napi legkisebb hőmérséklet a legnagyobb…
És van itt még egy dolog…
Ezt az egészet ábrázolhatjuk oszlopdiagrammal is…
Mégpedig így, hogy minden nap két oszlopot használunk.
És a pöttyök nem is kellenek…
Ezt csoportosított oszlopdiagramnak nevezzük.
Itt van például egy ilyen diagram arról, hogy az iskolai színjátszó szakkörbe hány lány és hány fiú jár.
Ábrázoljuk ugyanezt vonaldiagrammal is.
És most itt az ideje, hogy fényt derítsünk néhány izgalmas kérdésre a színjátszó szakkörrel kapcsolatban…
Melyik hónapban volt a legtöbb, és mikor volt a legevesebb fiú a szakkörben?
Ez a vonaldiagramról már messziről látszik…
Januárban volt a legkevesebb fiú, éppen 10 darab.
És decemberben volt a legtöbb, amikor 40-en voltak.
Most nézzük, mi a helyzet a lányokkal…
A legtöbb lány itt volt novemberben, itt 30-an voltak.
A legkevesebb pedig itt, februárban.
Nem látszik valami jól, hogy pontosan hány lány volt februárban…
Az oszlopdiagramról ez talán könnyebb leolvasni.
Úgy tűnik, a halvány vonalkák kettesével vannak…
Így hát ez itt alighanem 18.
Vagyis februárban volt a legkevesebb lány, amikor 18-an voltak.
És most nézzük, mikor lett több a fiú, mint a lány…
Ezt a vonaldiagramról lehet a legegyszerűbben leolvasni.
Ahol a két grafikon metszi egymást…
Vagyis augusztusról szeptemberre haladta meg a fiúk száma a lányok számát.
És most lássuk, mire használhatnánk ezeket a diagramokat…
Ezt a felmérést egy vasúttársaság készítette arról, hogy az utasok hány százaléka szeret az emeletes vonatok felső szintjén utazni.
Úgy néz ki, hogy az utasok őrülten szeretnek az emeleten utazni…
De sajnos van itt valami, amit úgy hívnak, hogy csalás…
Ezek a kis vonalkák azt jelentik, hogy itt el van vágva a koordinátatengely.
És a helyzet valójában így néz ki.
Persze még így is többen vannak akik szeretnek az emeleten utazni…
De azért nem olyan sokkal.
Hogyha elkezdjük fölfelé tolni a vízszintes tengelyt….
Akkor egyre inkább az a kép alakul ki, hogy szinte miden utas az emeleten szeretne utazni.
Amikor ezeket a gyanús kis vonalakat látjuk egy diagramon, akkor készüljünk rá, hogy valaki éppen át akar minket verni…
De van itt valami, amit úgy hívnak, hogy csalás…
Ezek a kis vonalkák azt jelentik, hogy itt el van vágva a koordinátatengely.
A helyzet ugyanis valójában így néz ki.
A sárga oszlop tehát egyáltalán nem kétszer akkora, mint a kék.
Ha egy diagramon ezeket a gyanús kis vonalakat látjuk, akkor készüljünk rá, hogy valaki éppen át akar minket verni…
Sokan lesznek, akik ilyen diagramokkal akarnak minket átverni.
át akarnak verni…
A matekdolgozatban, a felvételin, az érettségin…
Na meg persze a reklámokban, és a politikai hirdetésekben.
Itt van például egy grafikon arról, hogy egy iskolában hányan utálják a matekot.
Úgy tűnik, decemberre csoda történt…
Már szinte alig van valaki, aki utálja a matekot.
És a decemberi csoda magyarázata…
Azért maradt még bőven, aki utálja a matekot…
Sőt, itt jön egy újabb trükk…
Hogyha egy kicsit összenyomjuk a grafikont…
Akkor még azt a látszatot is kelthetjük, hogy annyi csökkenés sem volt, amennyi tényleg volt.
Ez a diagram azt mutatja, hogy az egyik téli olimpián hány aranyérmet szerzett Ausztria, Svájc, Franciaország és Németország.
Igaz-e, hogy Svájc kétszer annyi aranyérmet szerzett, mint Ausztria?
Ez az oszlopdiagram arról szól, hogy egy 32 fős osztály tanulói hány ötöst kaptak magyarból. Bob kapta a legtöbb ötöst magyarból. Hány ötöst kapott Bob?
Ez a tengely azt mutatja, hogy egy tanulónak hány darab ötöse van…
Itt pedig az látszik, hogy hány darab ilyen tanuló van.
A legtöbb ötöst ez az egy darab tanuló kapta…
Ő kell, hogy legyen Bob.
És úgy néz ki, hogy 8 darab ötöse van Bobnak.
Az osztályban Lilinél és Miránál kevesebb ötöst nem kapott senki. Hány ötöst kapott összesen Lili és Mira? Hányan vannak még rajtuk kívül az osztályban, akik ilyen kevés ötöst kaptak?
A legkevesebb ötös 2 darab…
És ennyien vannak, akiknek csak 2 darab ötösük van.
Hatan.
8 db ötös
1 db tanuló
Úgy tűnik, hogy 192-en tanulnak franciát.
hat olyan diák van, akinek csak 2 darab ötöse van.
Közülük kettő Lili és Mira.
Mindkettőnek 2 darab ötöse van.
Ami összesen 4 darab.
És rajtuk kívül még 4-en vannak, akik ilyen kevés ötöst kaptak.
Végül számoljuk ki azt is, hogy hány ötöst kapott a 32 diák összesen.
Lássuk, mekkora középponti szög van a németeknél…
Egy ilyen körcikk 30 fokos…
És van belőle 5 darab…
Végül nézzük, mi van az olaszokkal.
Három cikkelyt foglalnak el az olaszok a 12 darabból…
Ez ránézésre is az egésznek a negyede, vagyis 25%.
De kiszámolhatjuk így is:
Így is kijön, hogy 25% tanul olaszt.
Egy 100 perces előadás három főszereplője Tom, Christoph és Emma. A diagram vízszintes szakaszai azt mutatják, hogy a 100 perc alatt a főszereplők mikor szerepeltek.
Hány percen keresztül szerepelt mindhárom főszereplő egyszerre? Ábrázoljuk oszlopdiagramon, hogy a három főszereplő mennyi ideig szerepelt az előadáson. Ábrázoljuk kördiagramon, hogy az előadás hány százalékában volt látható egy, kettő és mindhárom főszereplő.
Nézzük, mikor szerepelt mindhárom főszereplő…
Itt például igen.
