a) Számoljuk ki, hogy mennyi a térfogata és a felszíne ennek az építménynek, amit 6 darab 4 centis élhosszú kockából ragasztottunk össze.

b) Számoljuk ki, hogy mennyi a térfogata és a felszíne ennek az építménynek, amit 7 darab 3 centis élhosszú kockából ragasztottunk össze.

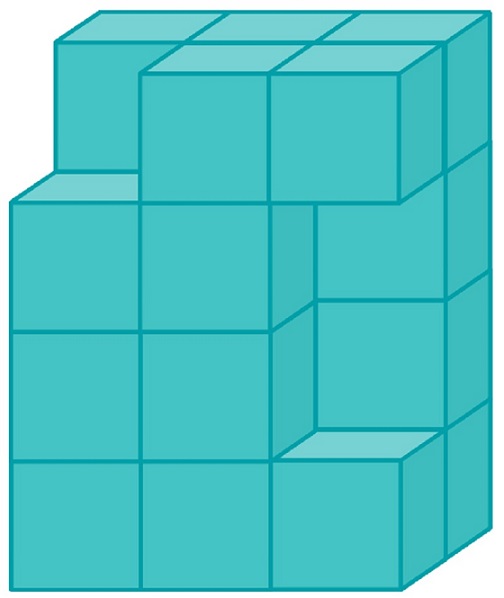
a) Kilenc darab egybevágó kockából raktuk össze ezt az építményt. Két szomszédos kocka egy-egy teljes lapjával van összeragasztva. Minden kocka élhossza 4 cm. Mekkora az így kapott test térfogata és felszíne?

b) Itt jön egy újabb izgalmas építmény, amit hét darab egybevágó kockából ragasztottunk össze. Két szomszédos kocka egy-egy teljes lapjával van összeragasztva. Minden kocka élhossza 5 cm. Mekkora a test térfogata és felszíne?

c) Most kilenc darab egybevágó kockánk van és egy kocka élhossza 3 centiméter. A kérdés a szokásos: mekkora az építmény térfogata és felszíne?

d) Hat darab egybevágó kockából raktuk össze ezt az építményt. Két szomszédos kocka egy-egy teljes lapjával van összeragasztva. Minden kocka élhossza 4 cm. Mekkora az így kapott test térfogata és felszíne?

e) Egy nagy, tömör téglatestet állítottunk össze egybevágó kockákból, majd az ábrán látható módon kivettünk belőle három darab kockát. Az így kapott test legrövidebb éle 2 cm hosszú. Mekkora a test térfogata és felszíne?
a) Számítsuk ki a kocka élhosszúságát, ha a felszíne $6 \; dm^2$.
b) Számítsuk ki a kocka élhosszúságát, ha térfogata $8 \; cm^3$
a) Mekkora annak a kockának a térfogata, amelynek felszíne $54\; cm^2$?
b) Mekkora annak a kockának a felszíne, amelynek térfogata $27 \; cm^3$?
Az alábbi táblázatban egy kocka élének hosszát, valamint felszínének és térfogatának nagyságát adtuk meg. Töltsük ki a hiányzó adatokat.
|
élhosszúság $a$ |
felszín $A$ |
térfogat $V$ |
| $8 \; cm$ | ||
| $24 \; dm^2$ | ||
| $125 \; m^3$ |
a) Egy téglatest két különböző élének hossza $8 \; cm$ és $9\; cm$.
Mekkora a harmadik élének hossza, ha térfogata $114 \; cm^3$?
b) Egy téglatest két különböző élének hossza $4 \; cm$ és $6 \; cm$.
Mekkora a harmadik élének hossza, ha a felszíne $68\; cm^2$?
Egy pizzás doboz 5 cm magas, 35 cm széles és 40 cm hosszú. Mekkora a térfogata és a felszíne?
Egy pizzás doboz 5 cm magas, 35 cm széles és 40 cm hosszú. Mekkora a térfogata és felszíne?
a) Számoljuk ki, hogy mennyi a térfogata és a felszíne ennek az építménynek, amit 6 darab 4 centis élhosszú kockából ragasztottunk össze.

b) Számoljuk ki, hogy mennyi a térfogata és a felszíne ennek az építménynek, amit 7 darab 3 centis élhosszú kockából ragasztottunk össze.

a) Kilenc darab egybevágó kockából raktuk össze ezt az építményt. Két szomszédos kocka egy-egy teljes lapjával van összeragasztva. Minden kocka élhossza 4 cm. Mekkora az így kapott test térfogata és felszíne?

b) Itt jön egy újabb izgalmas építmény, amit hét darab egybevágó kockából ragasztottunk össze. Két szomszédos kocka egy-egy teljes lapjával van összeragasztva. Minden kocka élhossza 5 cm. Mekkora a test térfogata és felszíne?

c) Most kilenc darab egybevágó kockánk van és egy kocka élhossza 3 centiméter. A kérdés a szokásos: mekkora az építmény térfogata és felszíne?

d) Hat darab egybevágó kockából raktuk össze ezt az építményt. Két szomszédos kocka egy-egy teljes lapjával van összeragasztva. Minden kocka élhossza 4 cm. Mekkora az így kapott test térfogata és felszíne?

e) Egy nagy, tömör téglatestet állítottunk össze egybevágó kockákból, majd az ábrán látható módon kivettünk belőle három darab kockát. Az így kapott test legrövidebb éle 2 cm hosszú. Mekkora a test térfogata és felszíne?

a) Az alábbi ábrán látható testet öt darab egybevágó négyzetes oszlopból ragasztottuk össze. (A ragasztási felületek teljes négyzetek.)
i) Hány $cm^2$ az ábrán látható test felszíne?
ii) Hány $cm^3$ az ábrán látható test térfogata?

b) Öt darab egybevágó négyzetes oszlopból ragasztottuk össze az ábrán látható testet. Az így kapott test leghosszabb éle 9 cm, a legrövidebb éle 1 cm hosszú.
i) Hány cm hosszúak a négyzetes oszlopok $a$ és $b$ élei?
ii) Hány $cm^2$ az ábrán látható test felszíne?

a) Az alábbi ábrán látható testet négy darab egybevágó négyzetes oszlopból ragasztottuk össze. (A ragasztási felületek teljes négyzetek.)
A négyzetes hasábok éleinek hossza 2 cm és 5 cm.
Mekkora az ábrán látható test felszíne és térfogata?
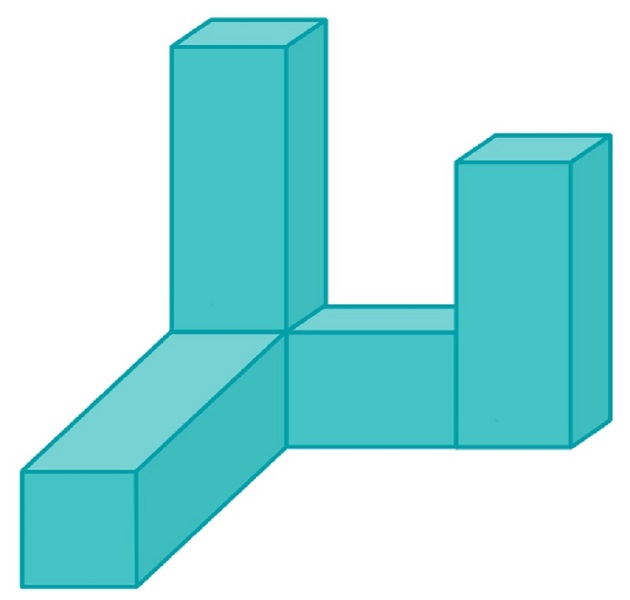
b) Az alábbi ábrán látható testet négy darab egybevágó négyzetes oszlopból ragasztottuk össze. (A ragasztási felületek teljes négyzetek.)
A négyzetes hasábok éleinek hossza 2 cm és 4 cm.
Mekkora az ábrán látható test felszíne és térfogata?

a) Négy darab egybevágó négyzetes oszlopból ragasztottuk össze az ábrán látható testet.
A négyzetes hasábok éleinek hossza 1 cm és 4 cm.
Mekkora az ábrán látható test térfogata és felszíne?

b) Három darab egybevágó négyzetes hasábból ragasztottuk össze az ábrán látható testet.
Az így kapott test leghoszabb éle 7 cm, a legrövidebb éle 2 cm hosszú.
i) Hány cm hosszúak a négyzetes hasábok élei?
ii) Hány $cm^2$ egy négyzetes hasáb felszíne?
iii) Hány $cm^2$ az ábrán látható test felszíne?

a) Egy kocka és két darab egybevágó négyzetes hasáb összeragasztásával építettük meg az ábrán látható testet.
i) Hány cm hosszúak a négyzetes hasáb élei (a és b)?
ii) Mekkora az ábrán látható test térfogata és felszíne?

b) Kilenc darab olyan egybevágó négyzetes hasábunk van, amelyekből egy nagy kockát ragaszthatnánk össze. Az ábrán az látható, amikor már csak az utolsó hasáb hiányzik a kockából.
Az ábrán látható test térfogata $192\; cm^3$.
Hány centiméter hosszúak a négyzetes hasáb élei (a és b)?

a) 27 darab egybevágó kockából építettük föl a nagy kockát. Az így kapott nagy kocka egyik oldalán kivettük a középső kis kockát, és ugyanezt megcsináltuk a nagy kocka átellenes oldalánál is. A megmaradt építmény így 25 darab kockából áll. Mekkora az építmény térfogata és felszíne, hogyha a leghosszabb éle 12 centiméter?

b) Megint 27 darab egybevágó 4 cm élhosszúságú kockából építettük föl a nagy kockát. Az így kapott nagy kocka egyik sarkából kiveszünk egy kis kockát. A megmaradt építmény így 26 darab kockából áll. Mekkora az építmény felszíne?

c) 27 darab egybevágó 5 cm élhosszúságú kockából építettük föl a nagy kockát. Az így kapott nagy kockának minden sarkából kiveszünk egy kis kockát. A megmaradt építmény így 19 darab kockából áll. Mekkora az építmény felszíne?

a) Öt darab egybevágó 5 centiméteres élhosszúságú kockából ragasztottuk össze ezt a keresztet. A ragasztási felületek mindig teljes négyzetek. Mekkora az így kapott test felszíne?
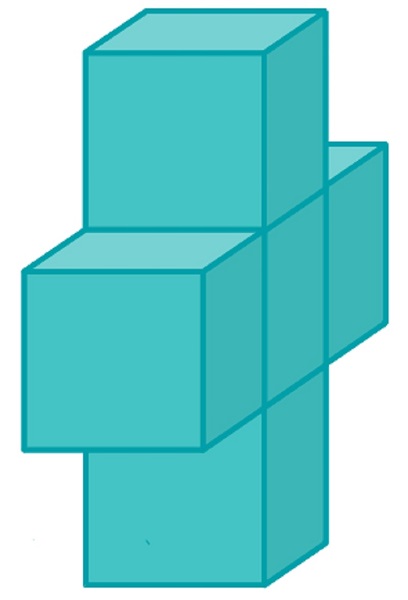
b) 10 darab egybevágó 5 centiméteres élhosszúságú kockából ragasztottuk össze az ábrán látható kereszt alakú építményt. A ragasztási felületek mindig teljes négyzetek. Az építmény középső része 6 darab egymáshoz ragasztott kockából áll, a felső és az alsó része 2-2 darab kockából. Mekkora a test felszíne?

c) 27 darab egybevágó 4 cm élhosszúságú kockából építünk föl egy nagy kockát. Az így kapott nagy kockának minden oldalán kivettük a középső kockát. Így összesen 6 darab kockát távolítottunk el. Mekkora a megmaradt test felszíne?

d) 18 darab egybevágó 5 cm-es élhosszú kockából építettünk föl egy hasábot, majd a hasáb belsejéből két kockát eltávolítottunk az ábrán látható módon. A megmaradt építmény így 16 darab egybevágó kockából áll. Mekkora az építmény felszíne?

27 darab egybevágó 5 cm élhosszúságú kockából építünk föl egy nagy kockát. Az így kapott nagy kockának minden oldalán kivettük a középső kockát, végül pedig a nagy kocka belsejében lévő középső kockát is eltávolítottuk. Mekkora a megmaradt test térfogata és felszíne?

