- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
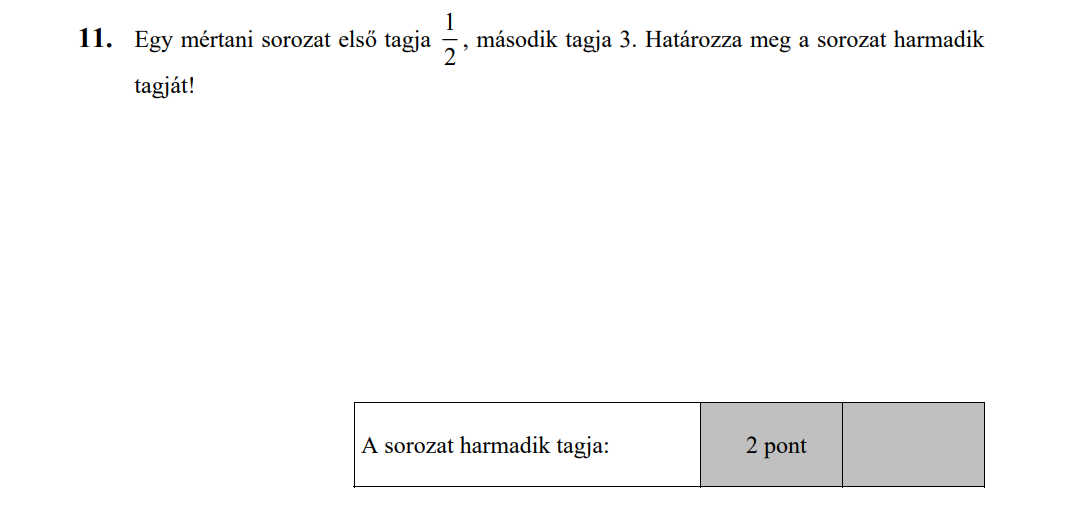
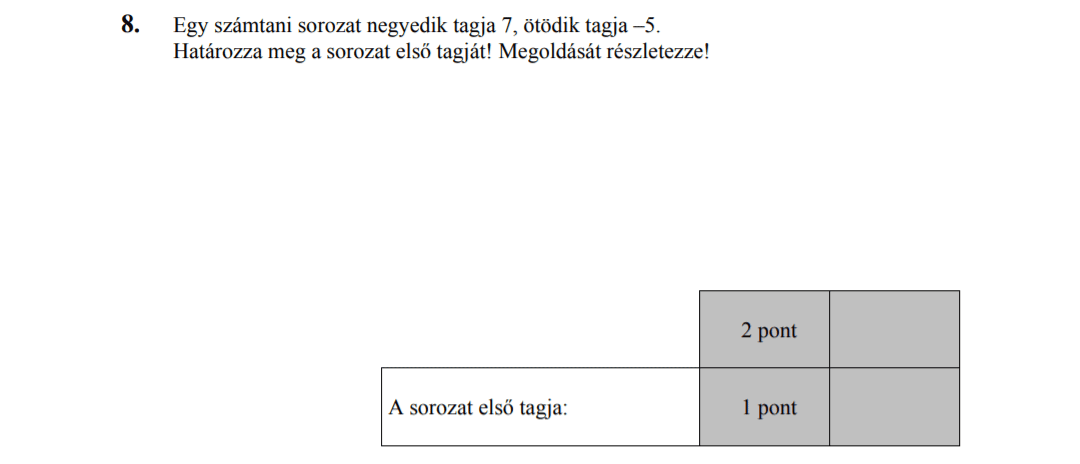
- Számtani és mértani sorozatok (16 pont)
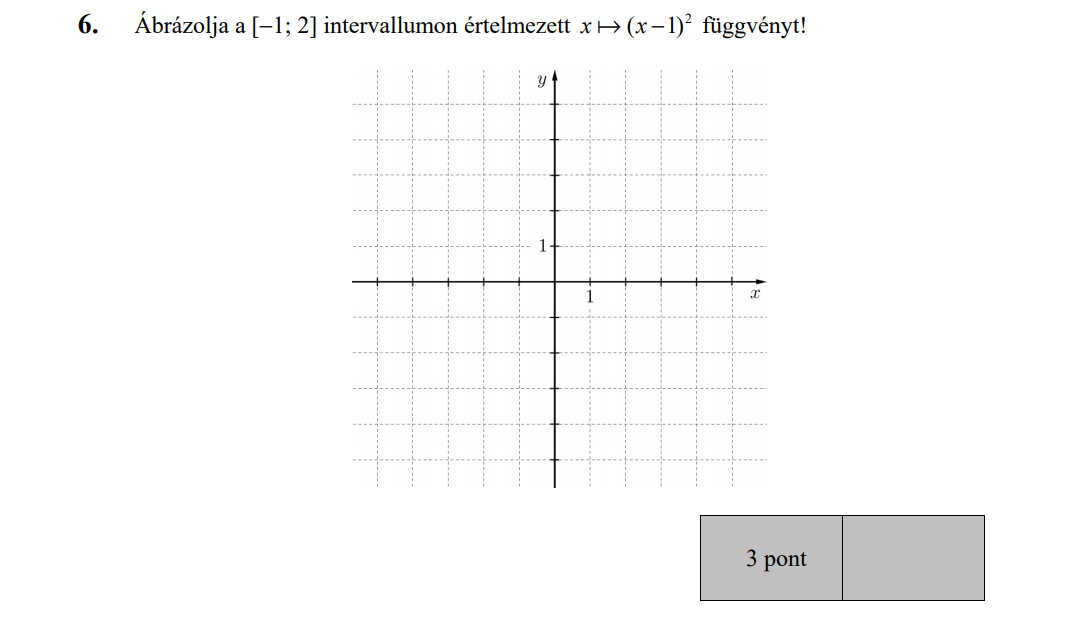
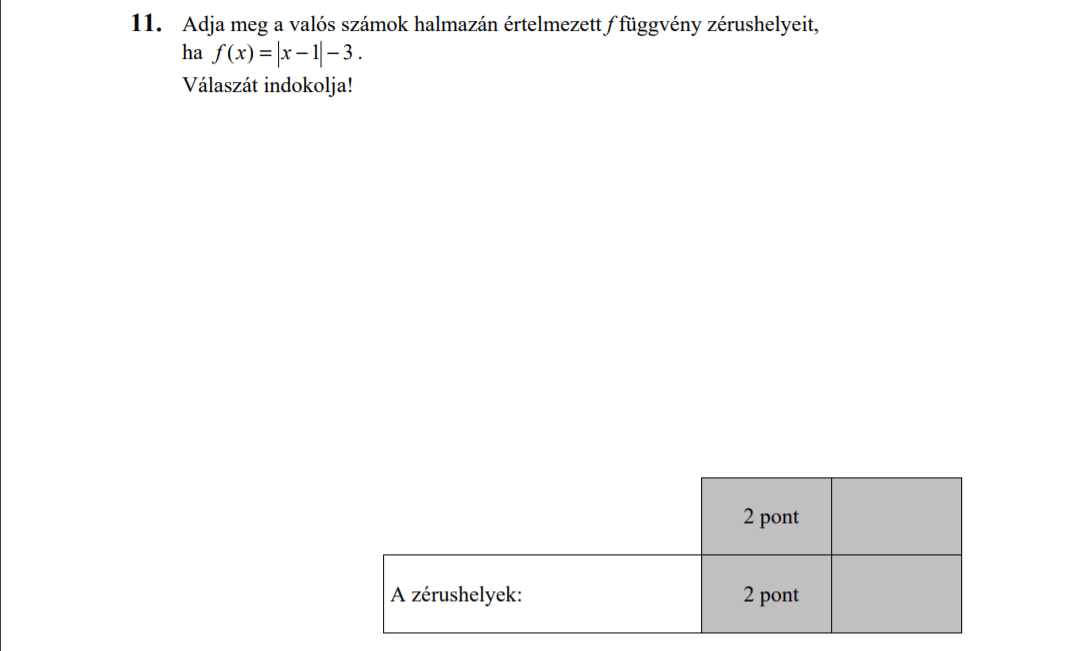
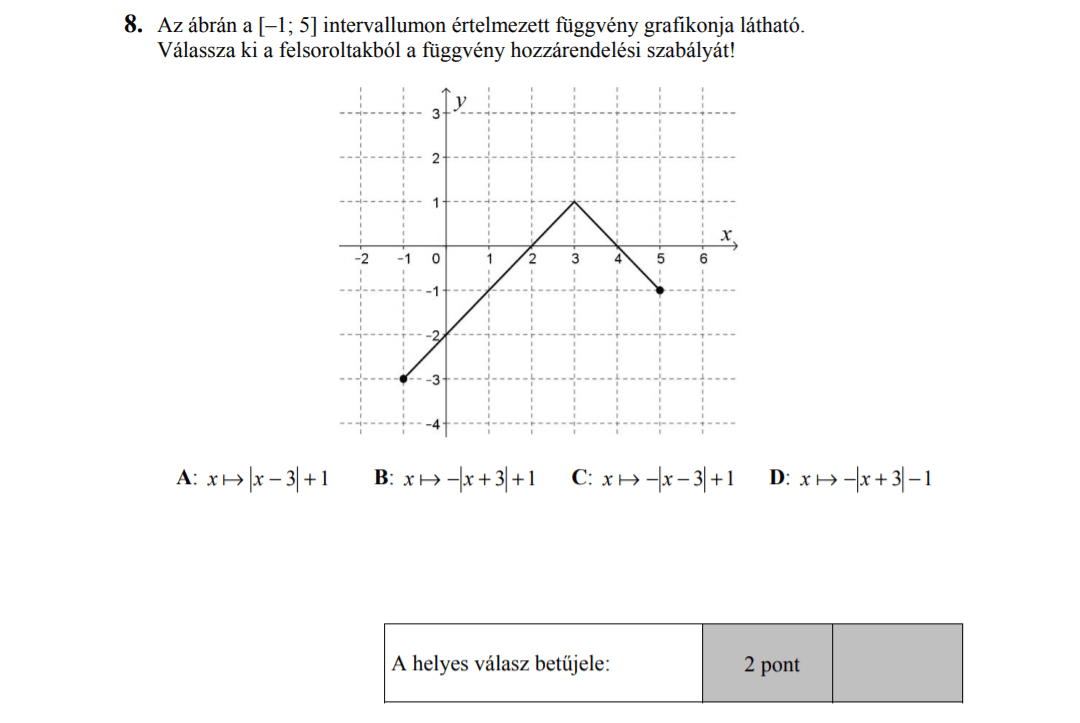
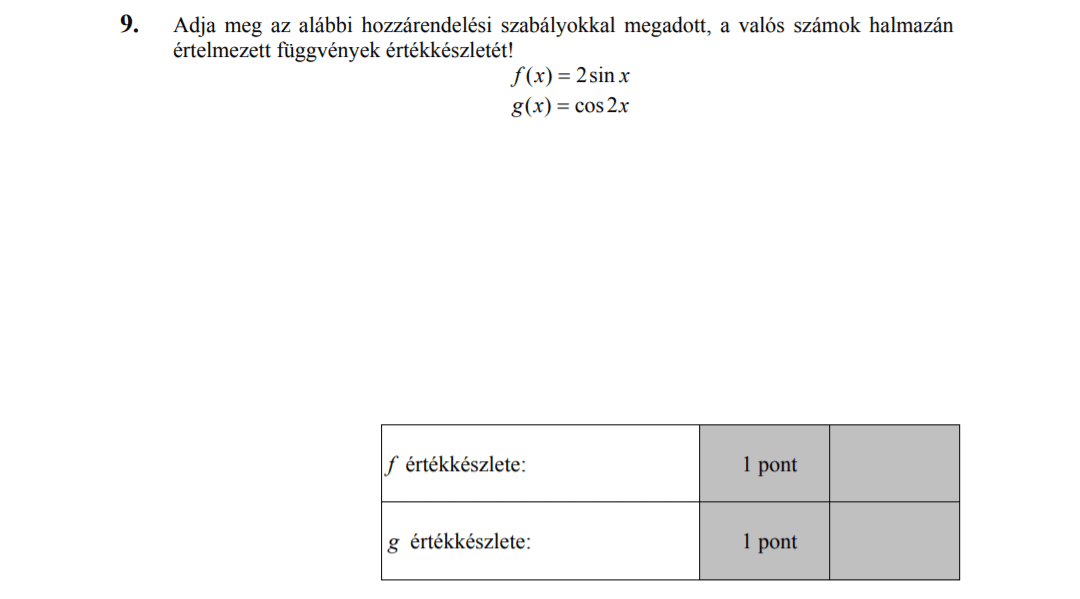
- Függvényekkel kapcsolatos feladatok (9,8 pont)
- Térgeometria (9,8 pont)
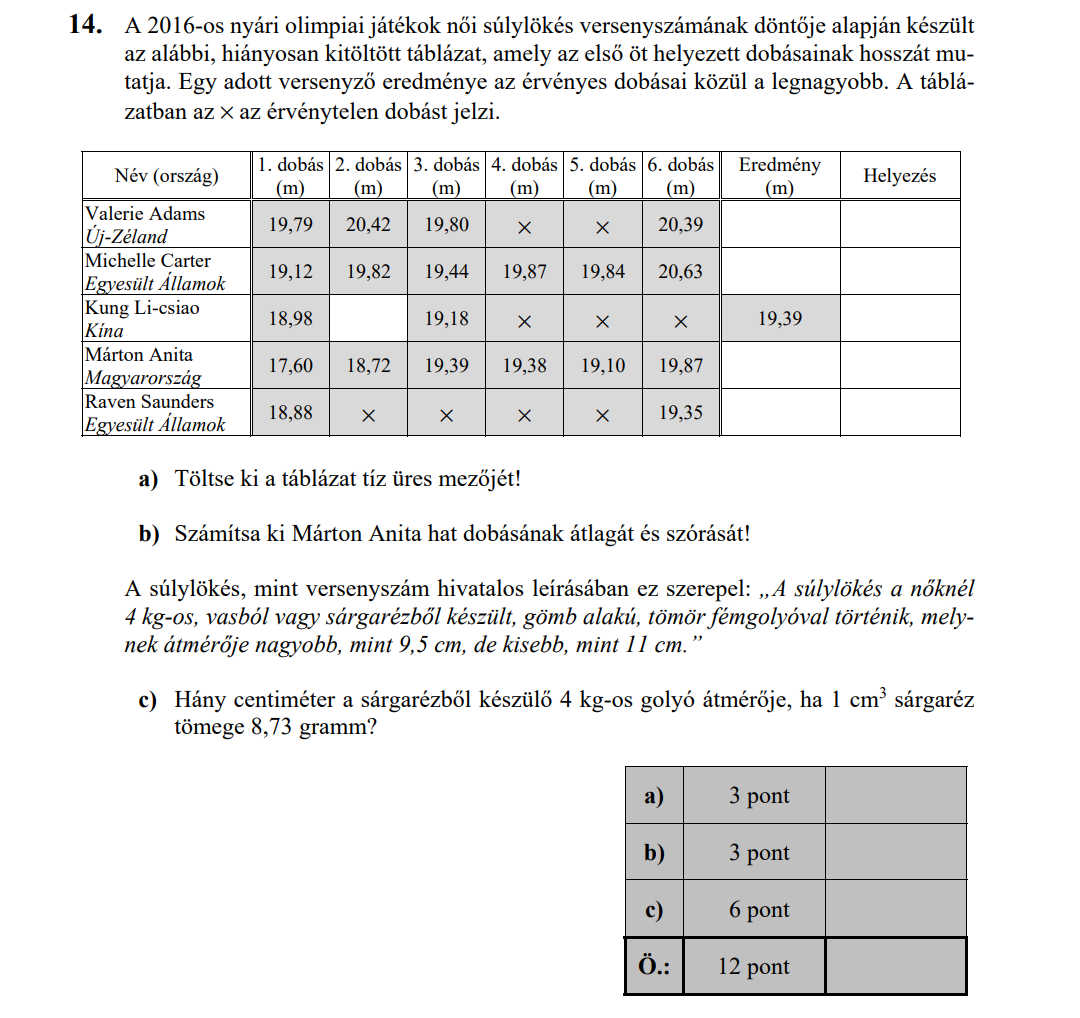
- Statisztika (9,3 pont)
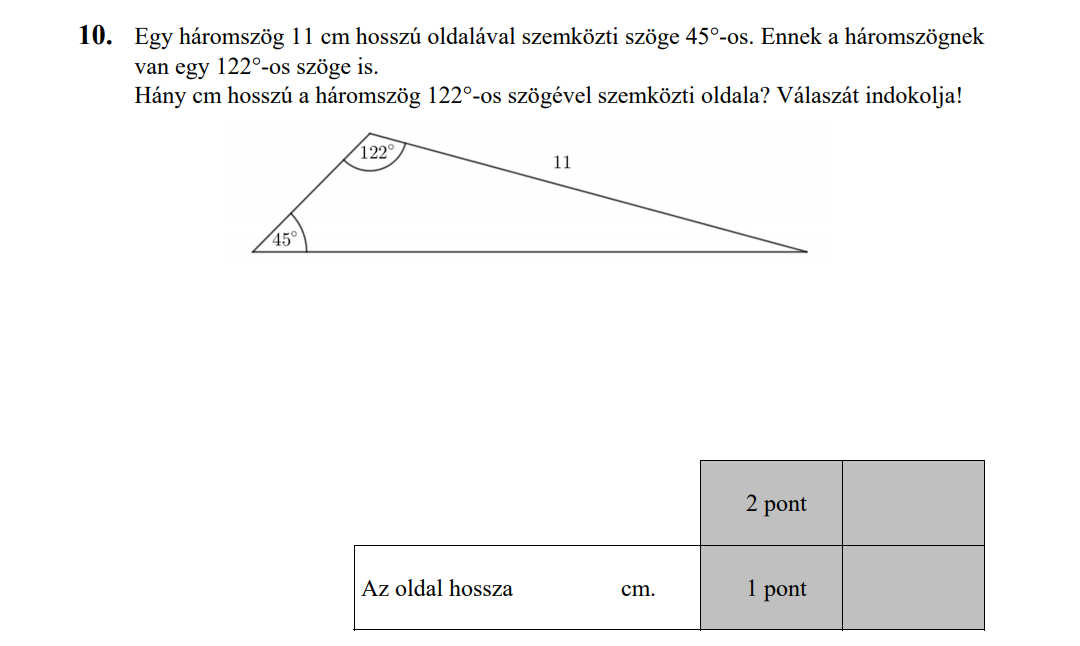
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
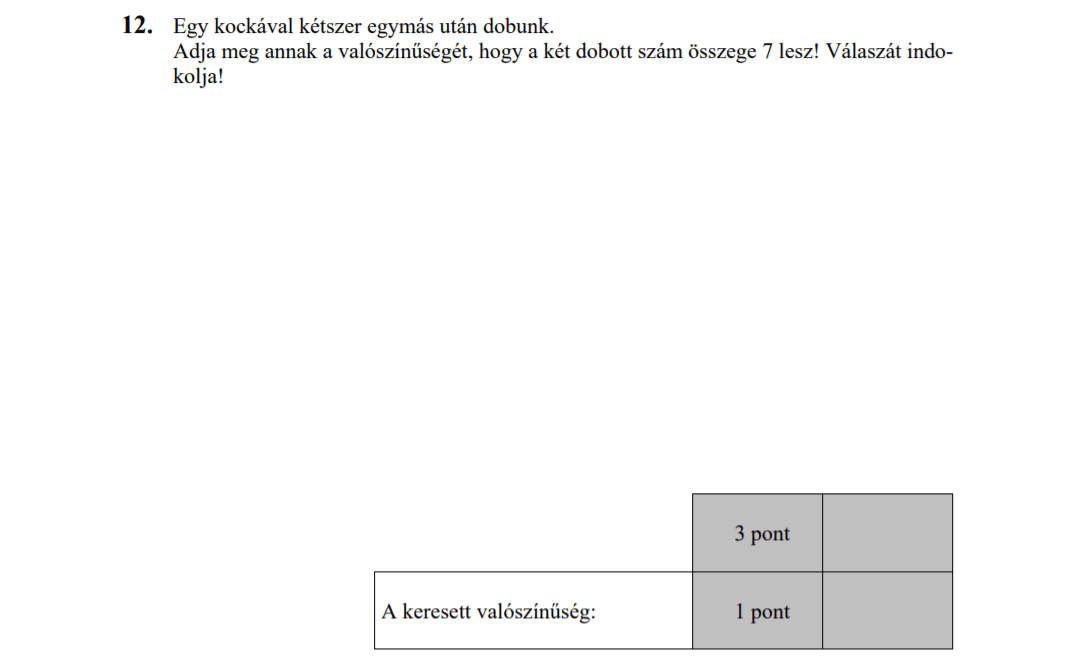
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
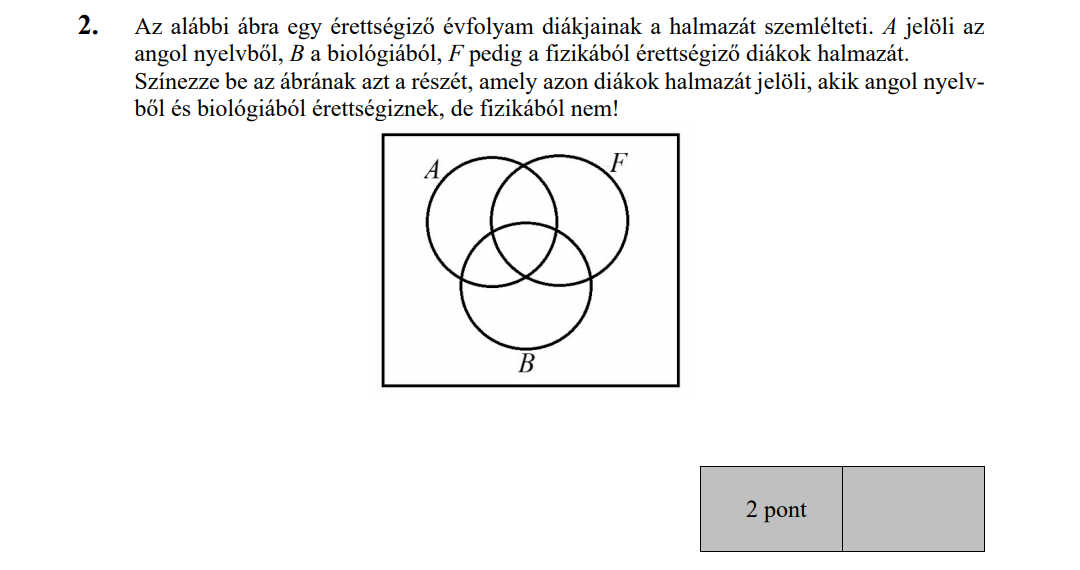
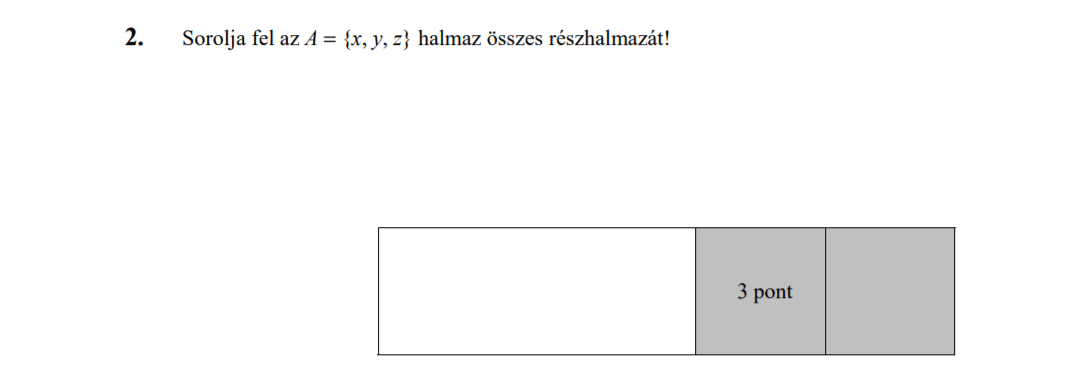
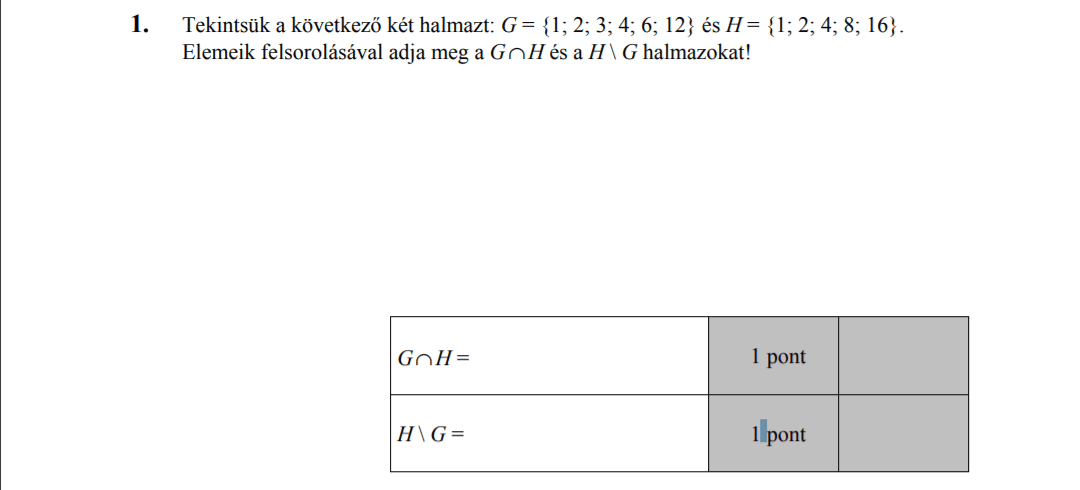
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
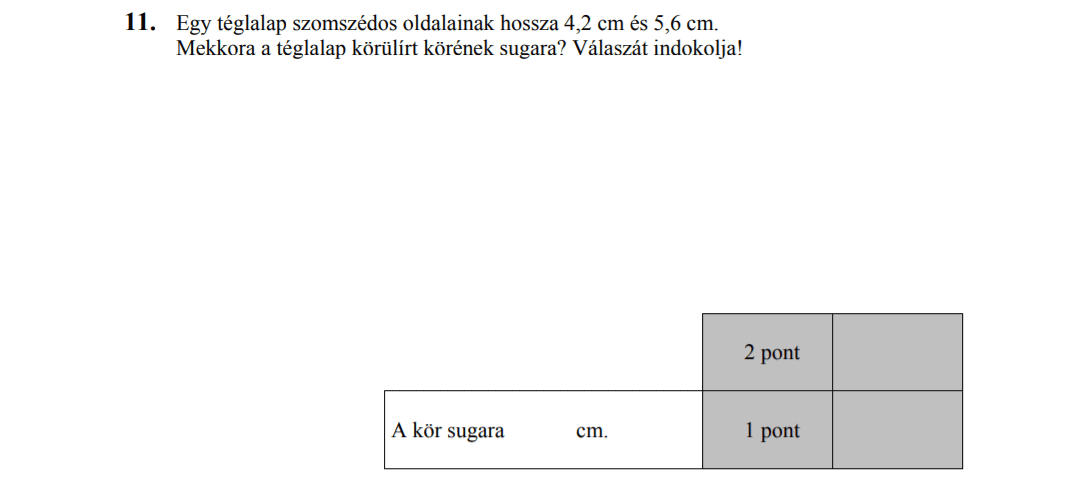
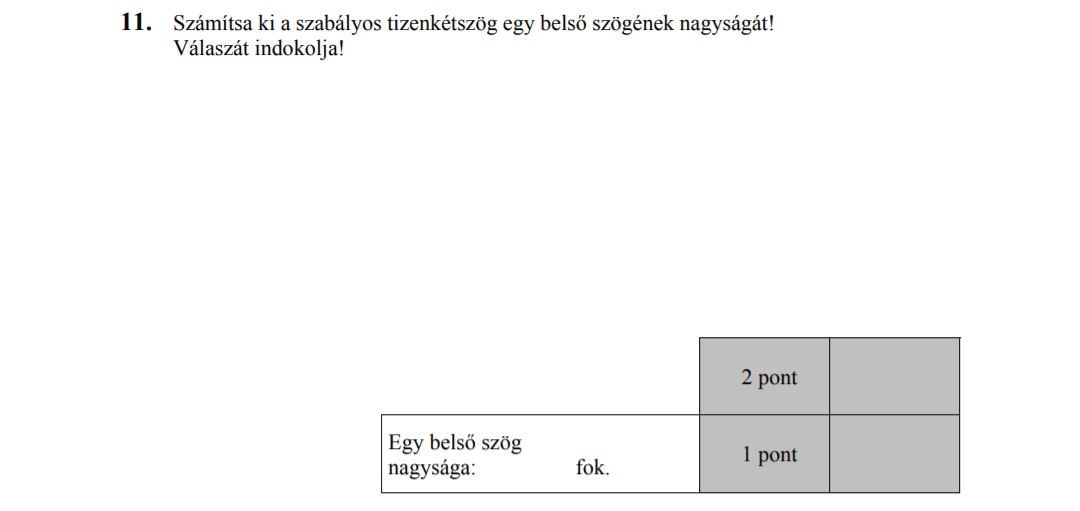
- Síkgeometria (4,5 pont)
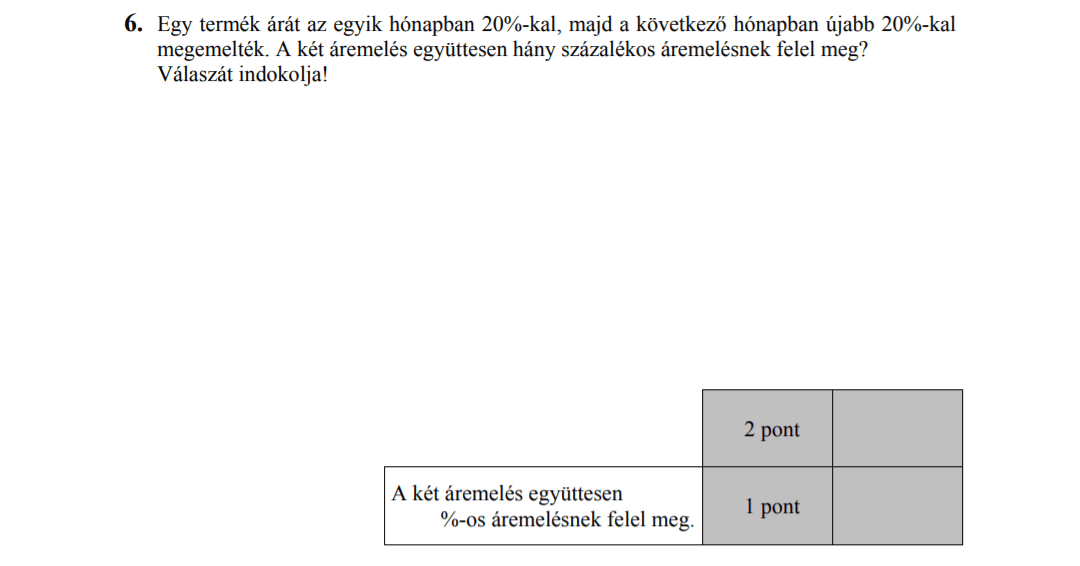
- Százalékszámítás (3,8 pont)
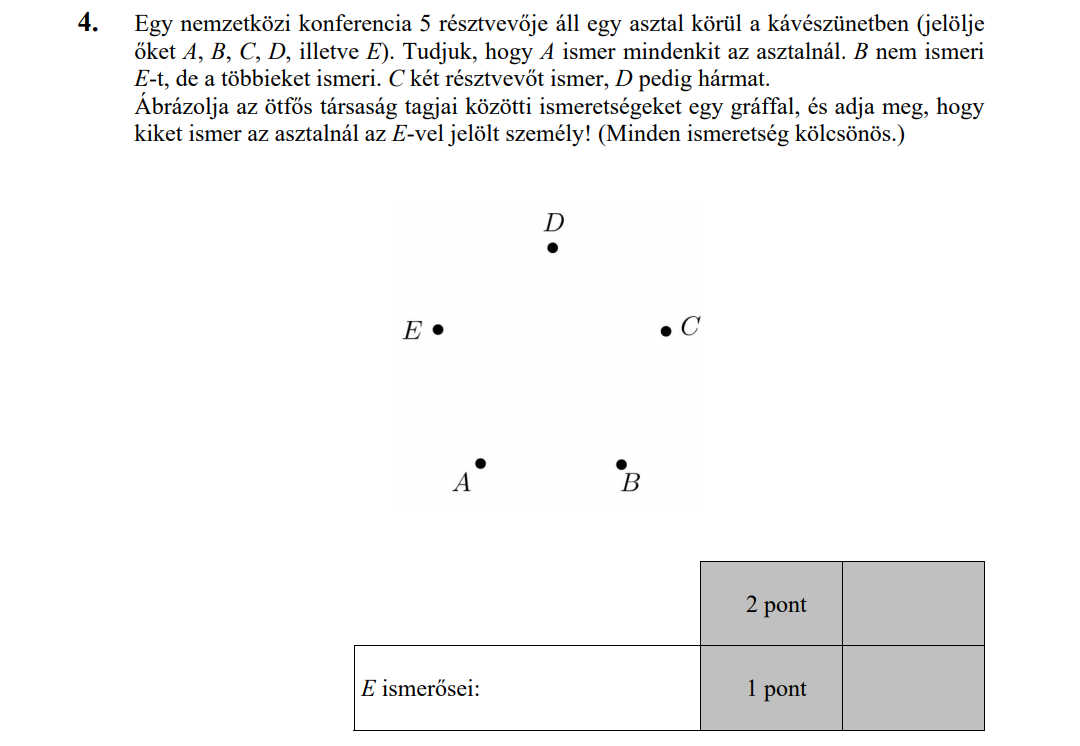
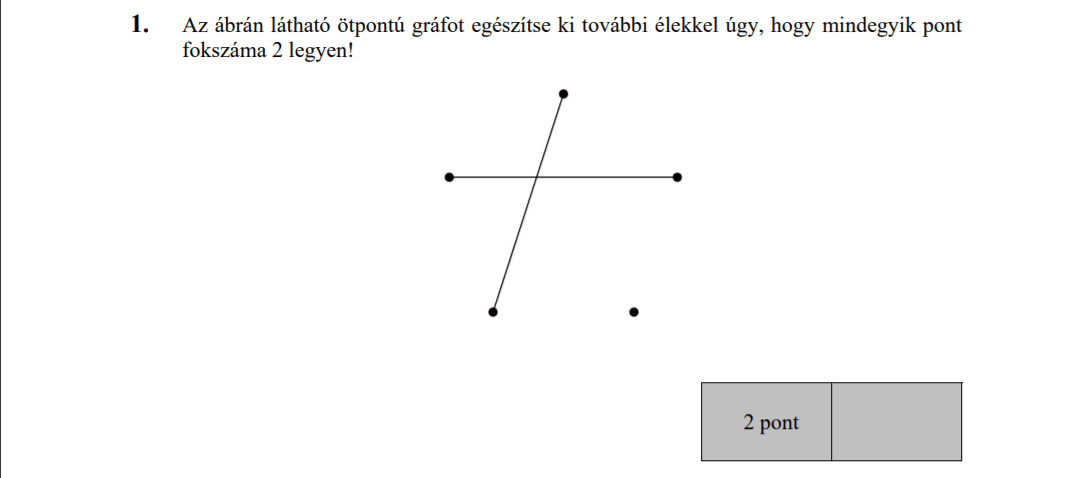
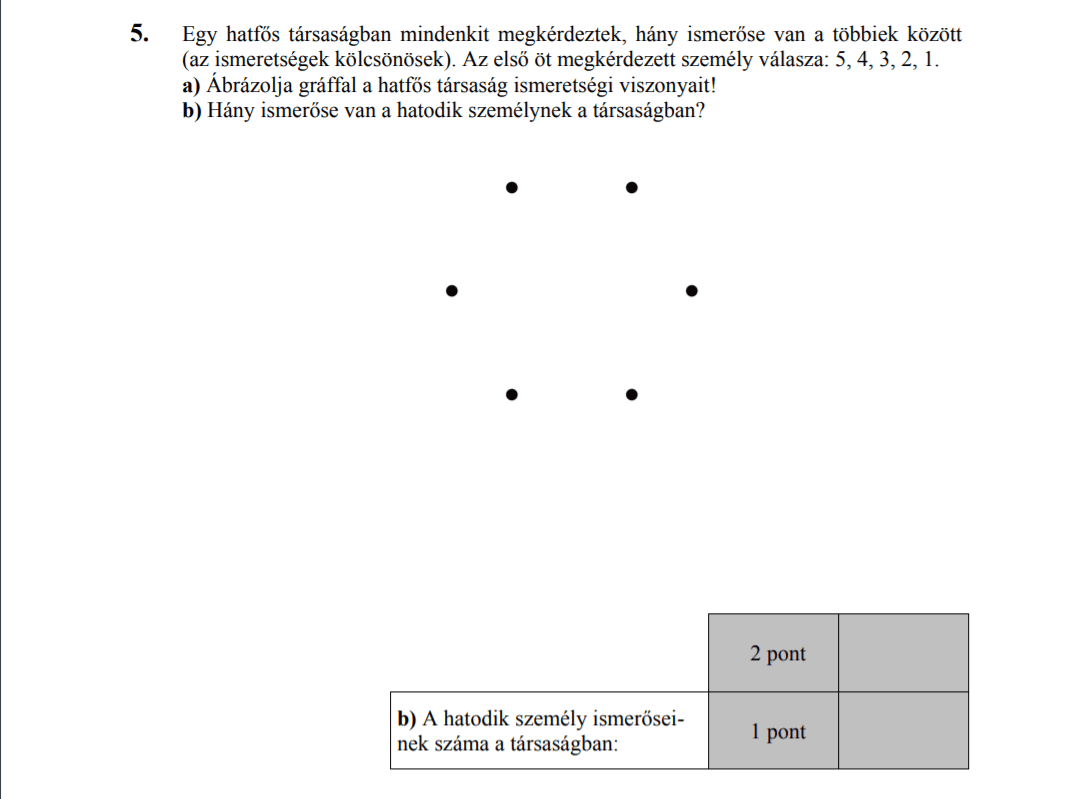
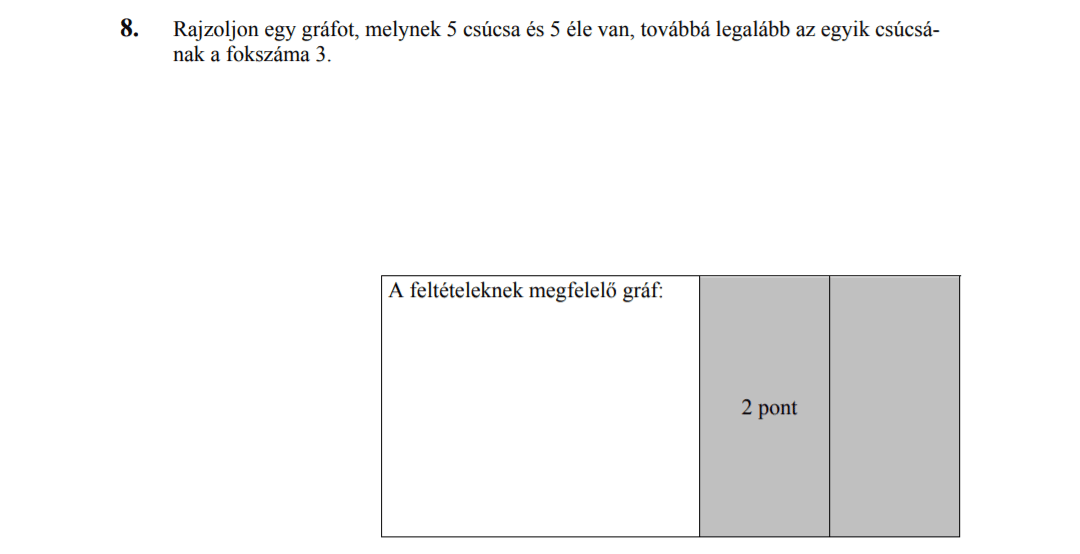
- Gráfok (3 pont)
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
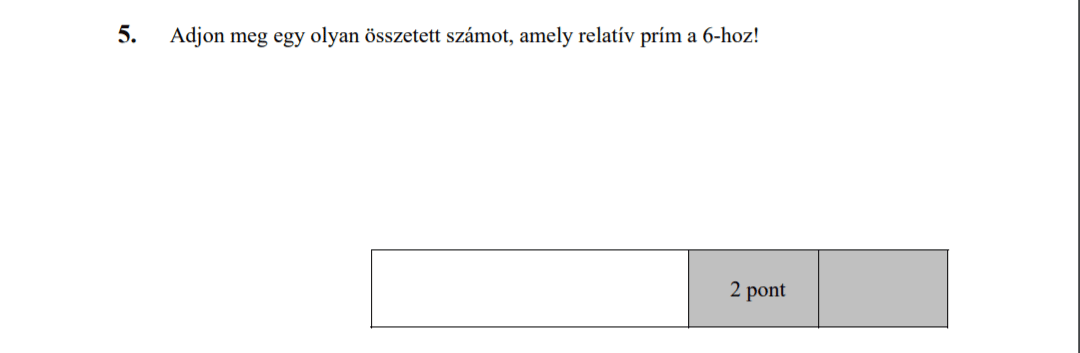
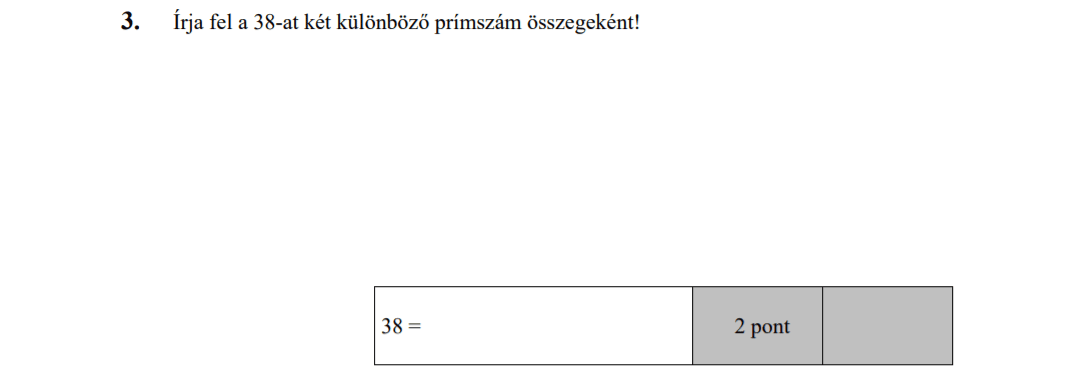
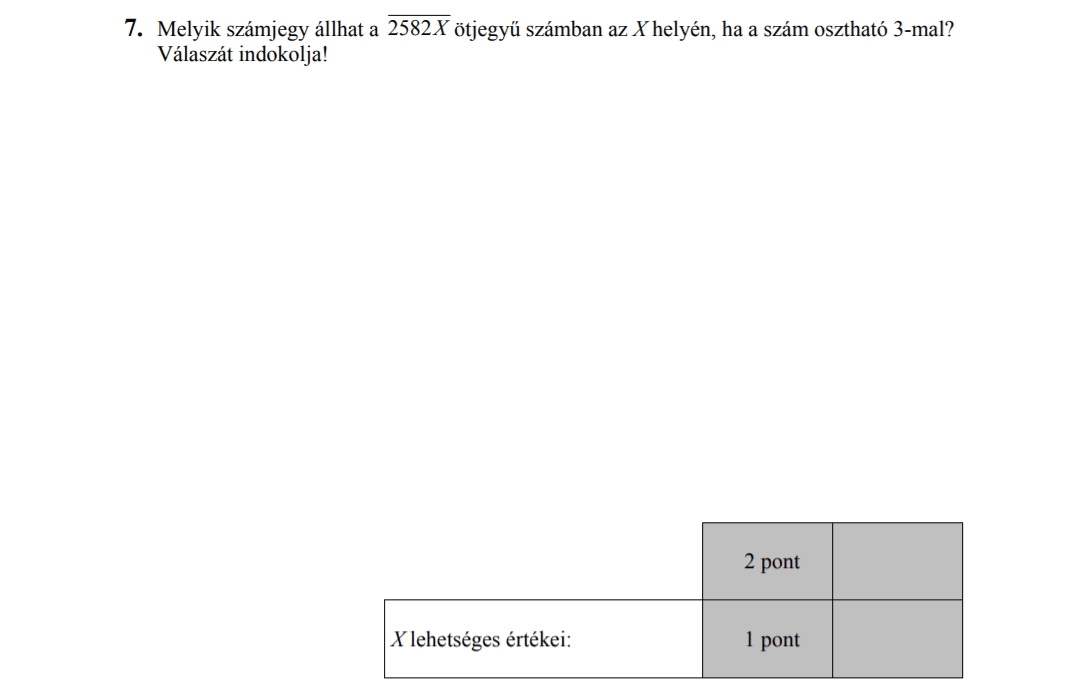
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Koordinátageometria (2,8 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


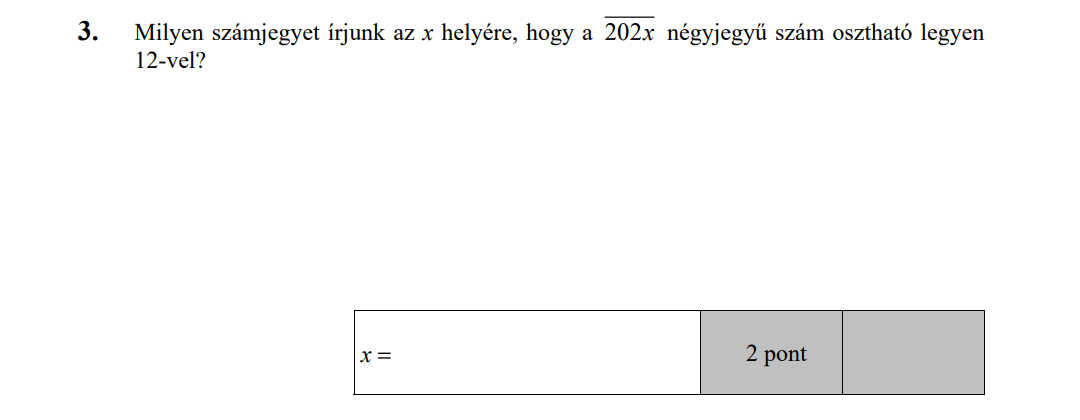
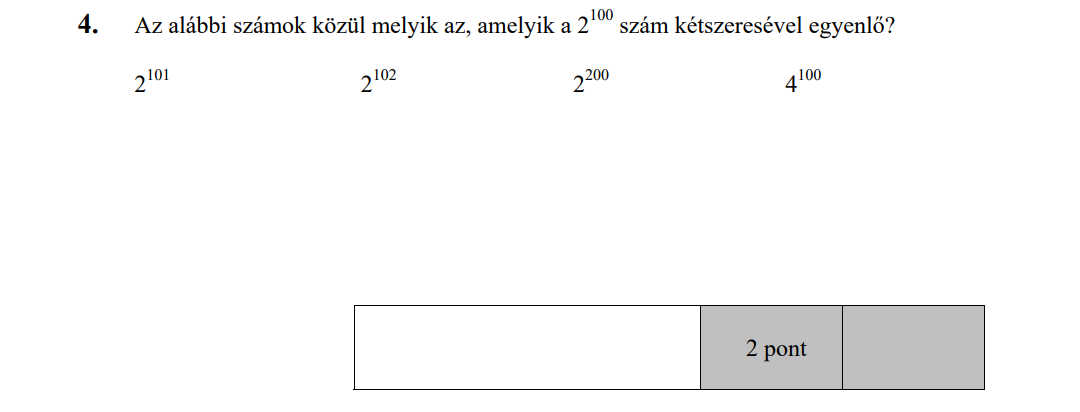



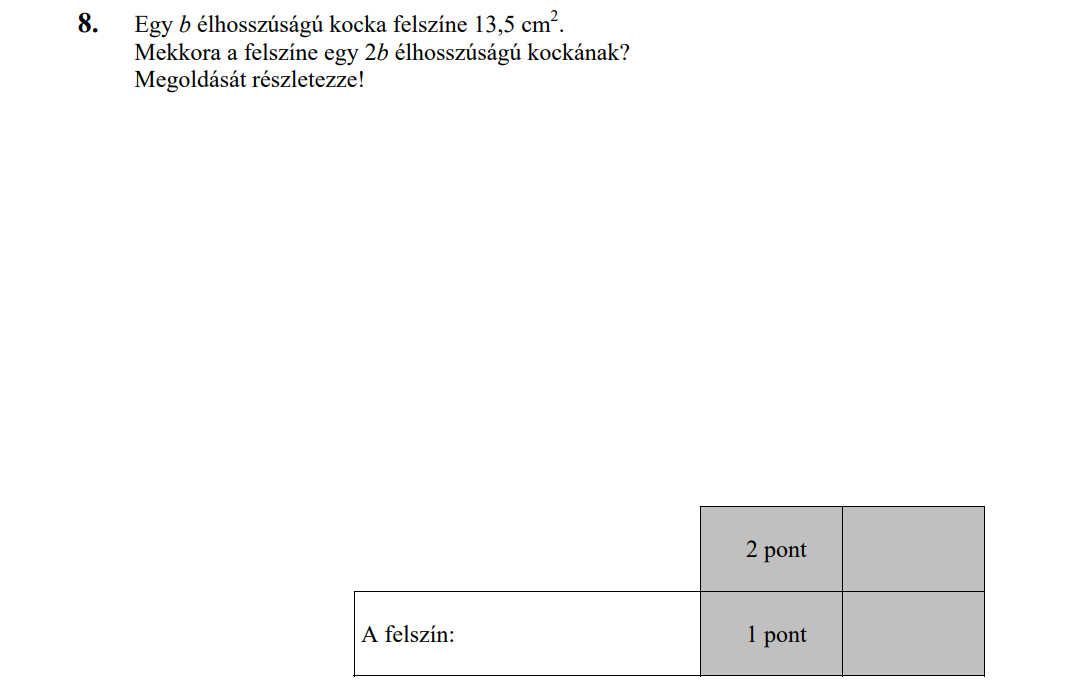




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
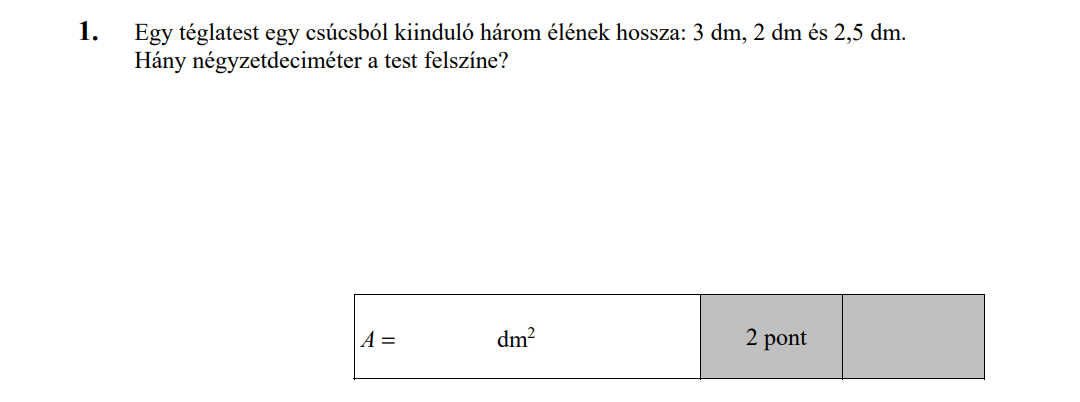






MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



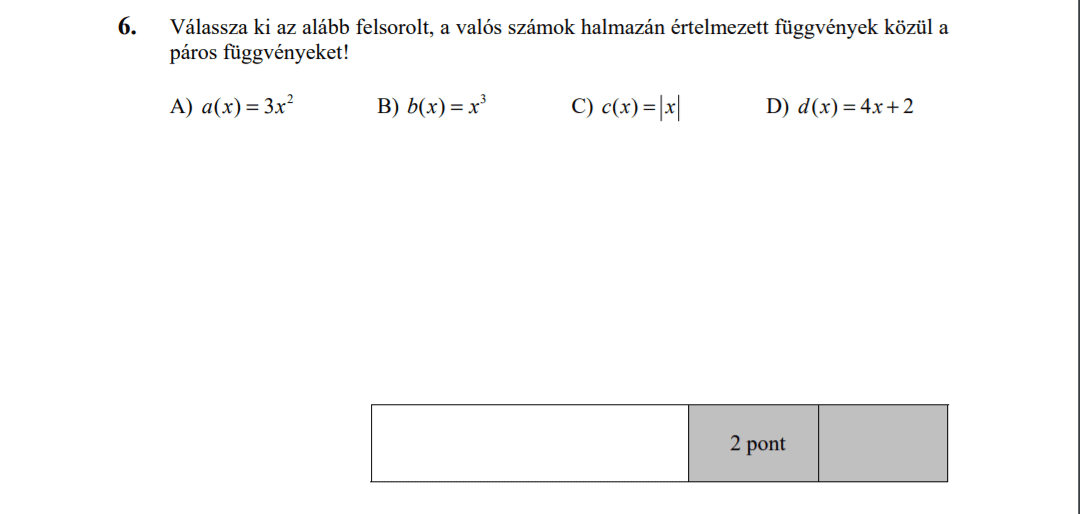
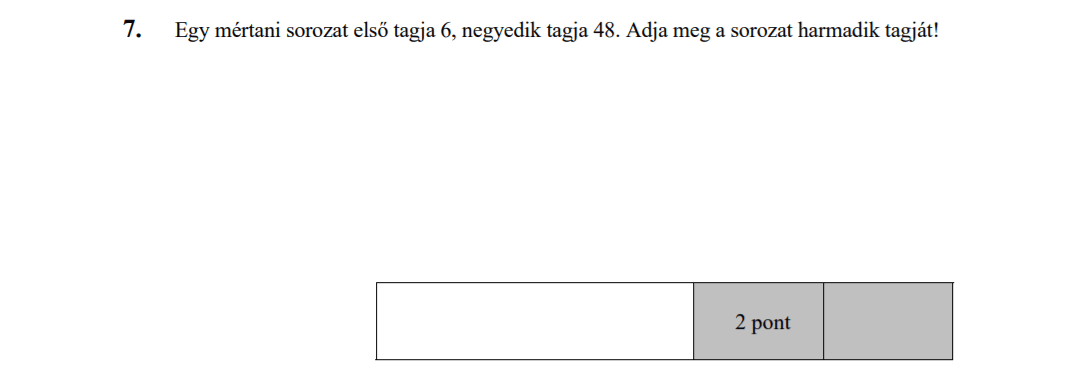



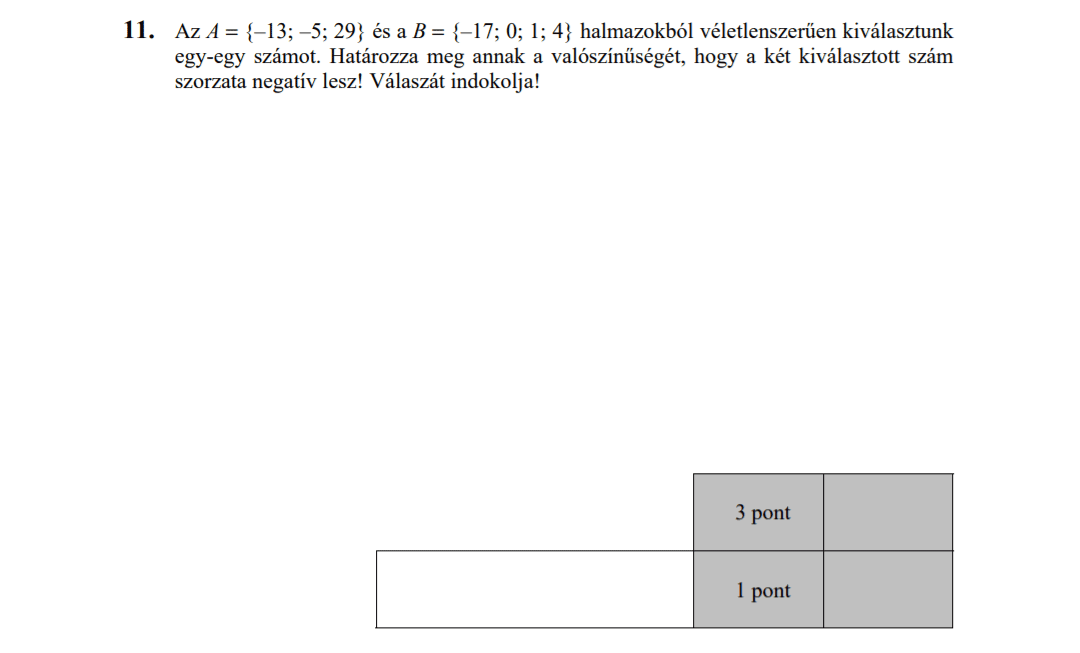

MÁSODIK RÉSZ


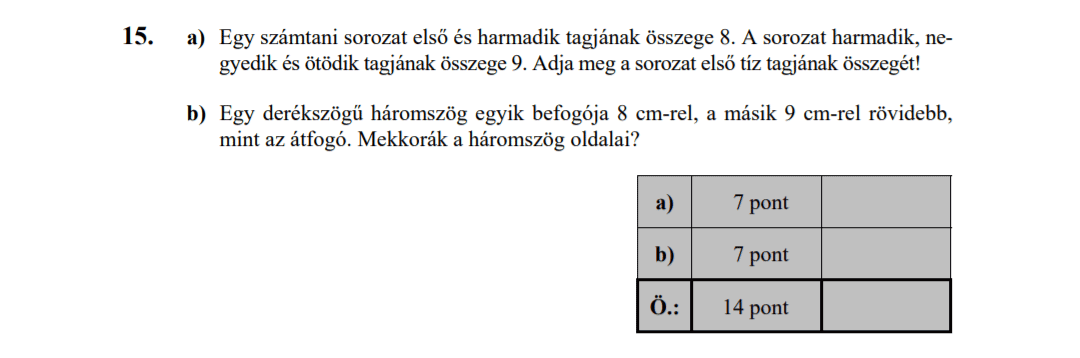



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






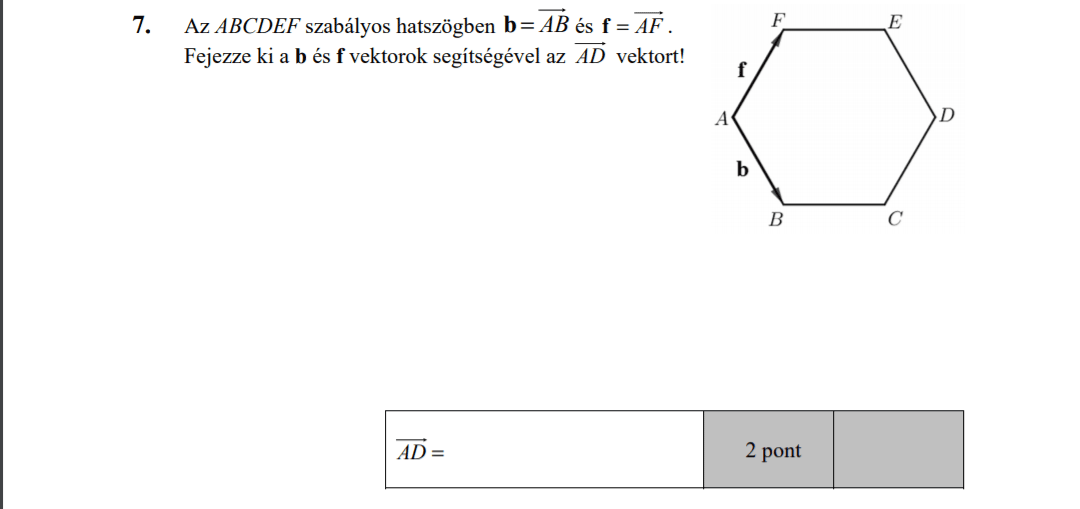



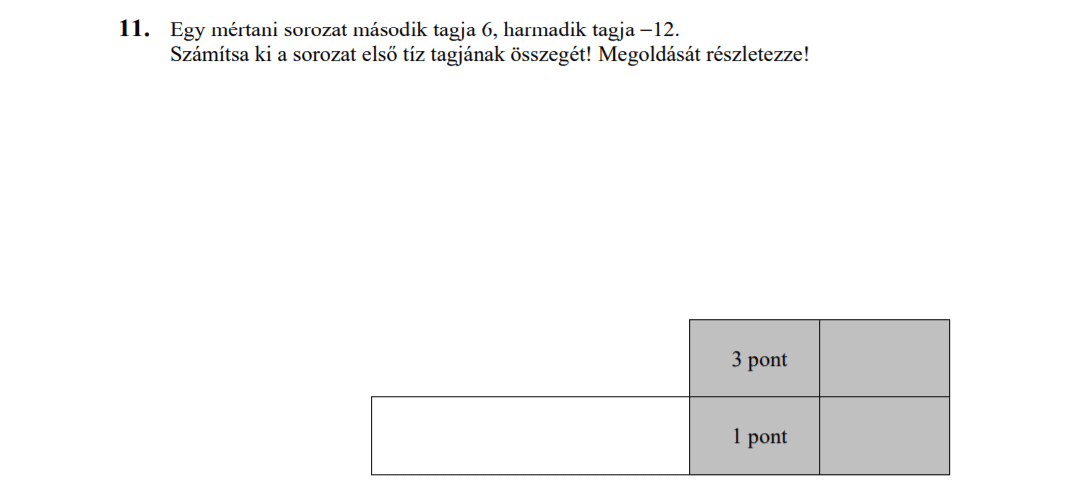

MÁSODIK RÉSZ

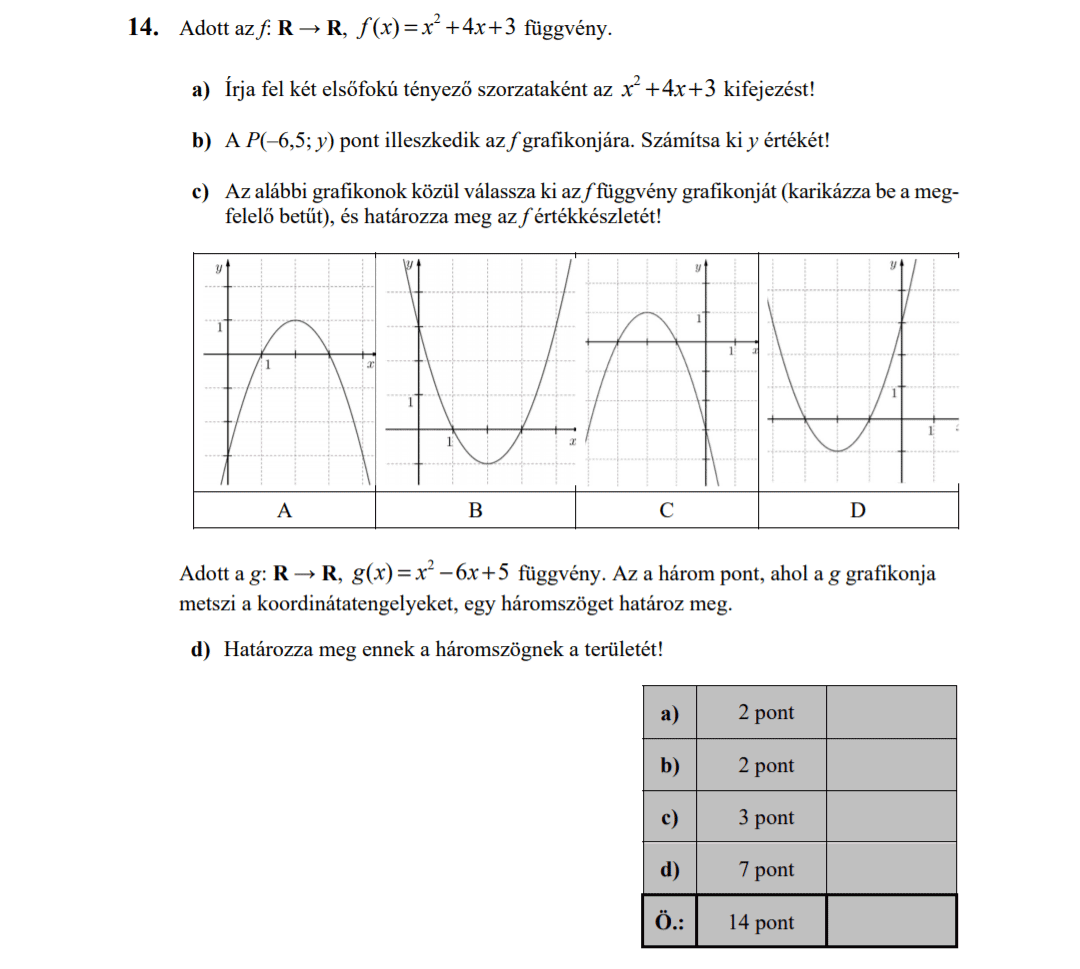




- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



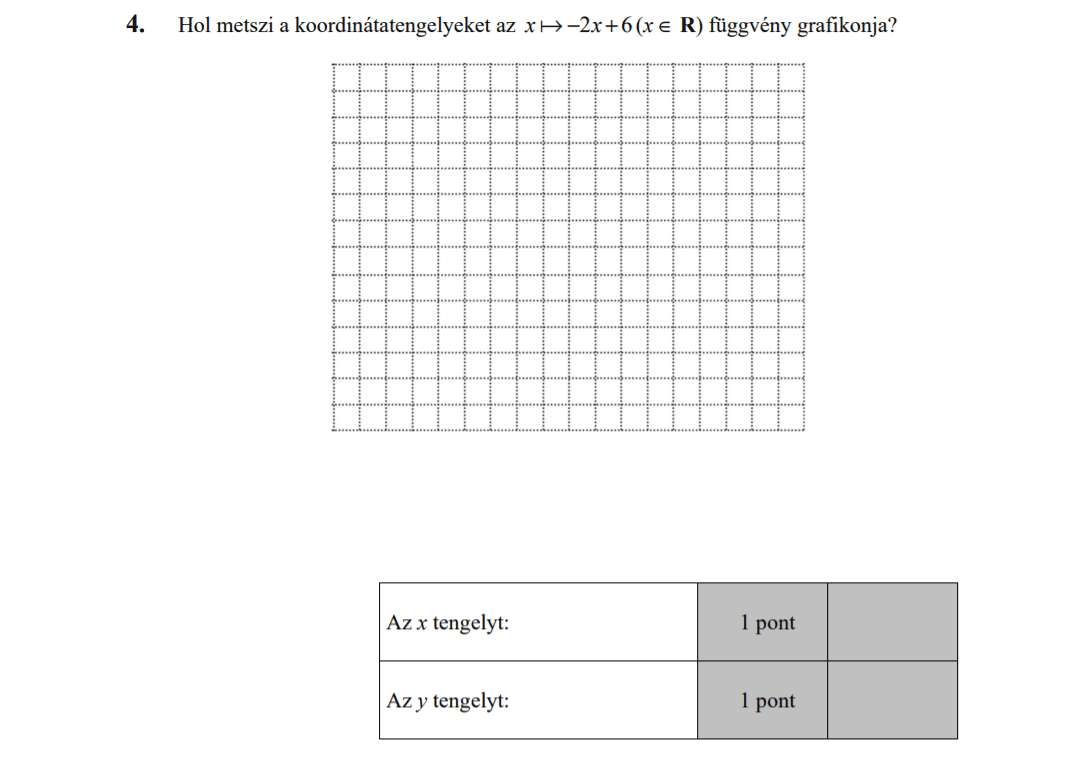







MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

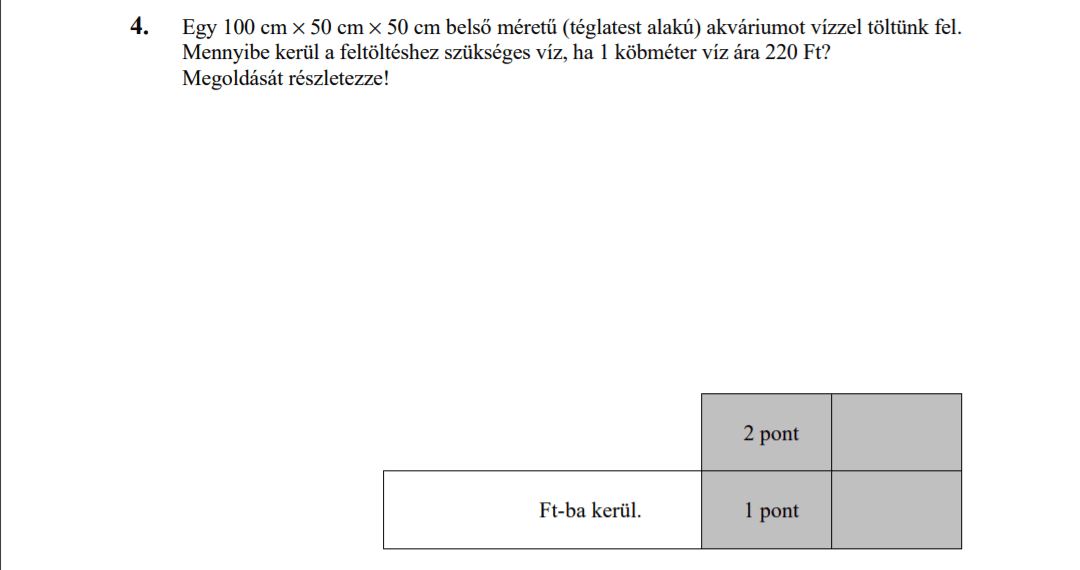
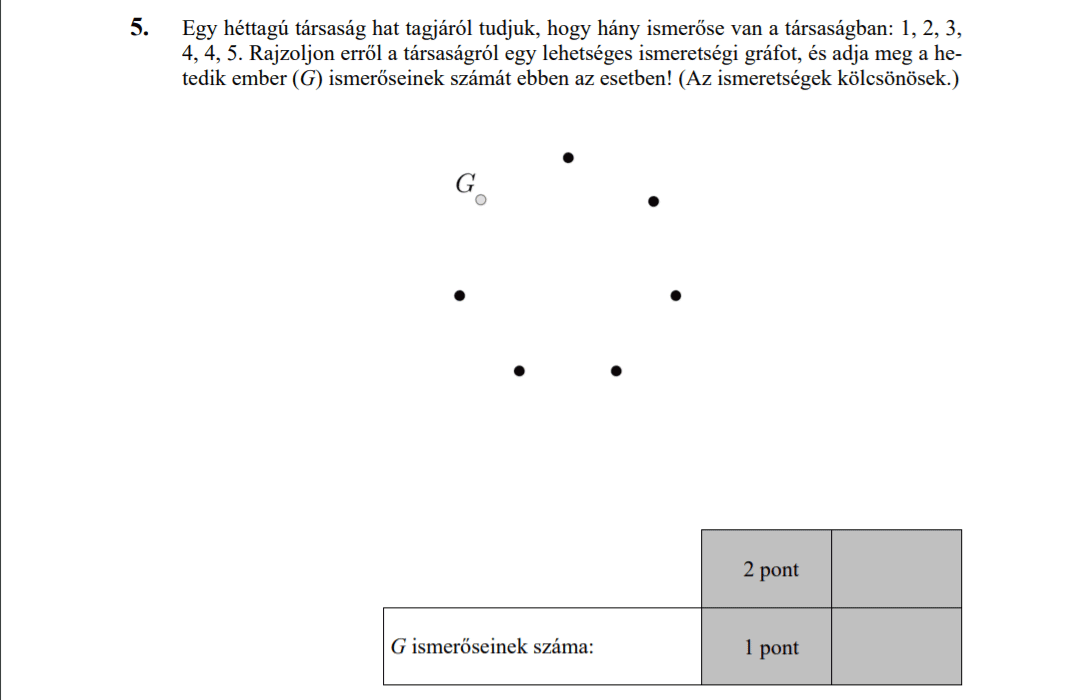







MÁSODIK RÉSZ
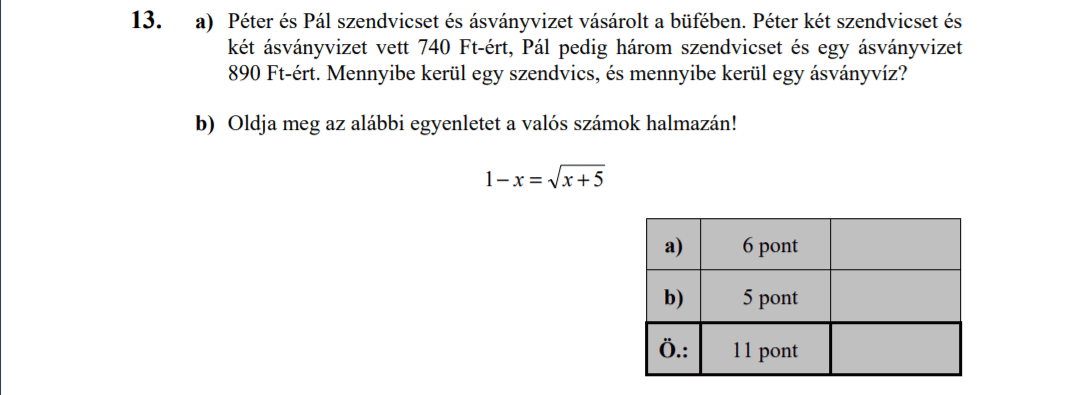
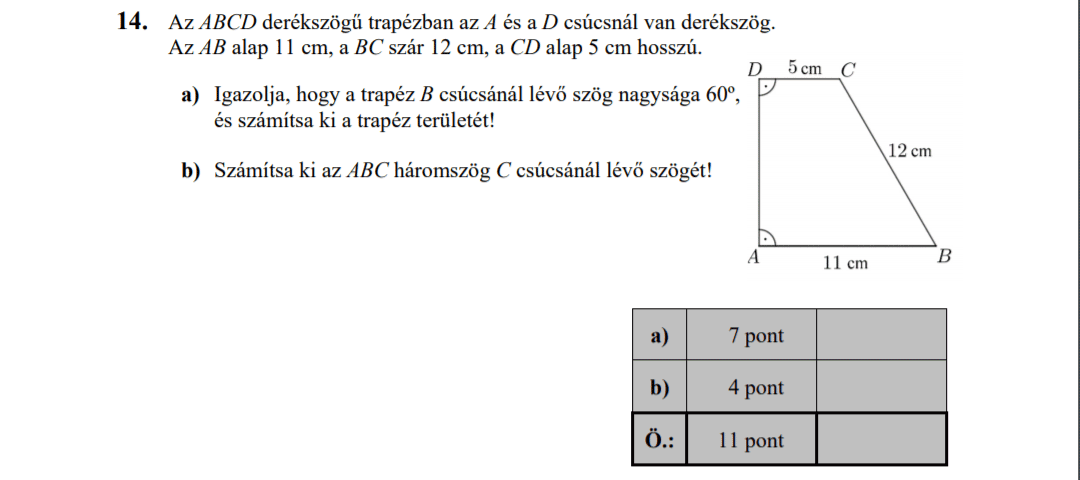



- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




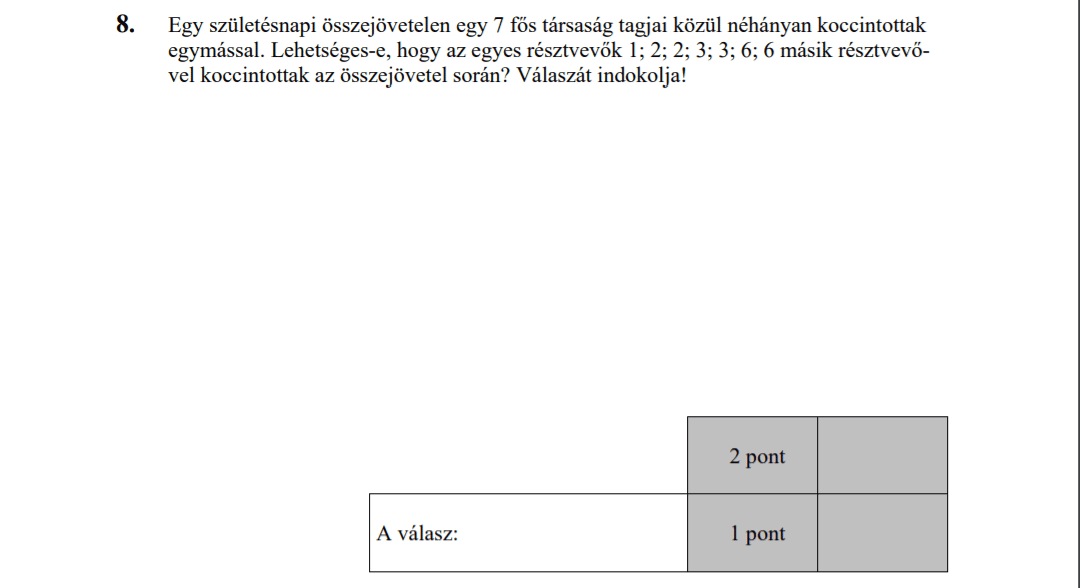



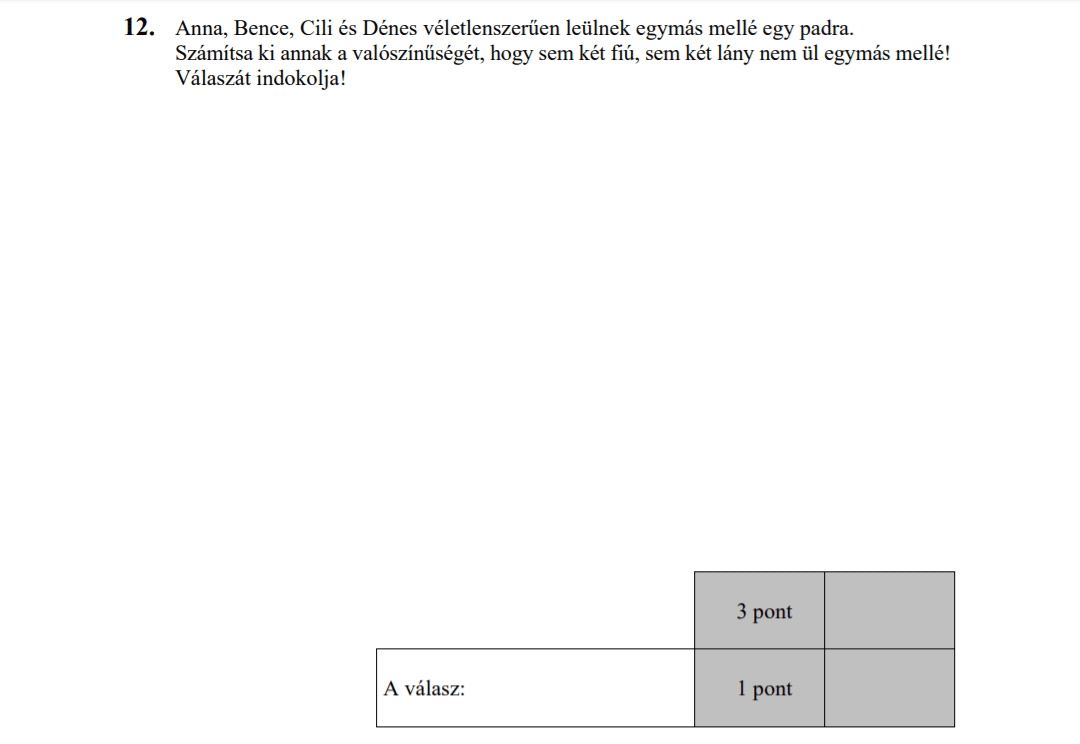
MÁSODIK RÉSZ

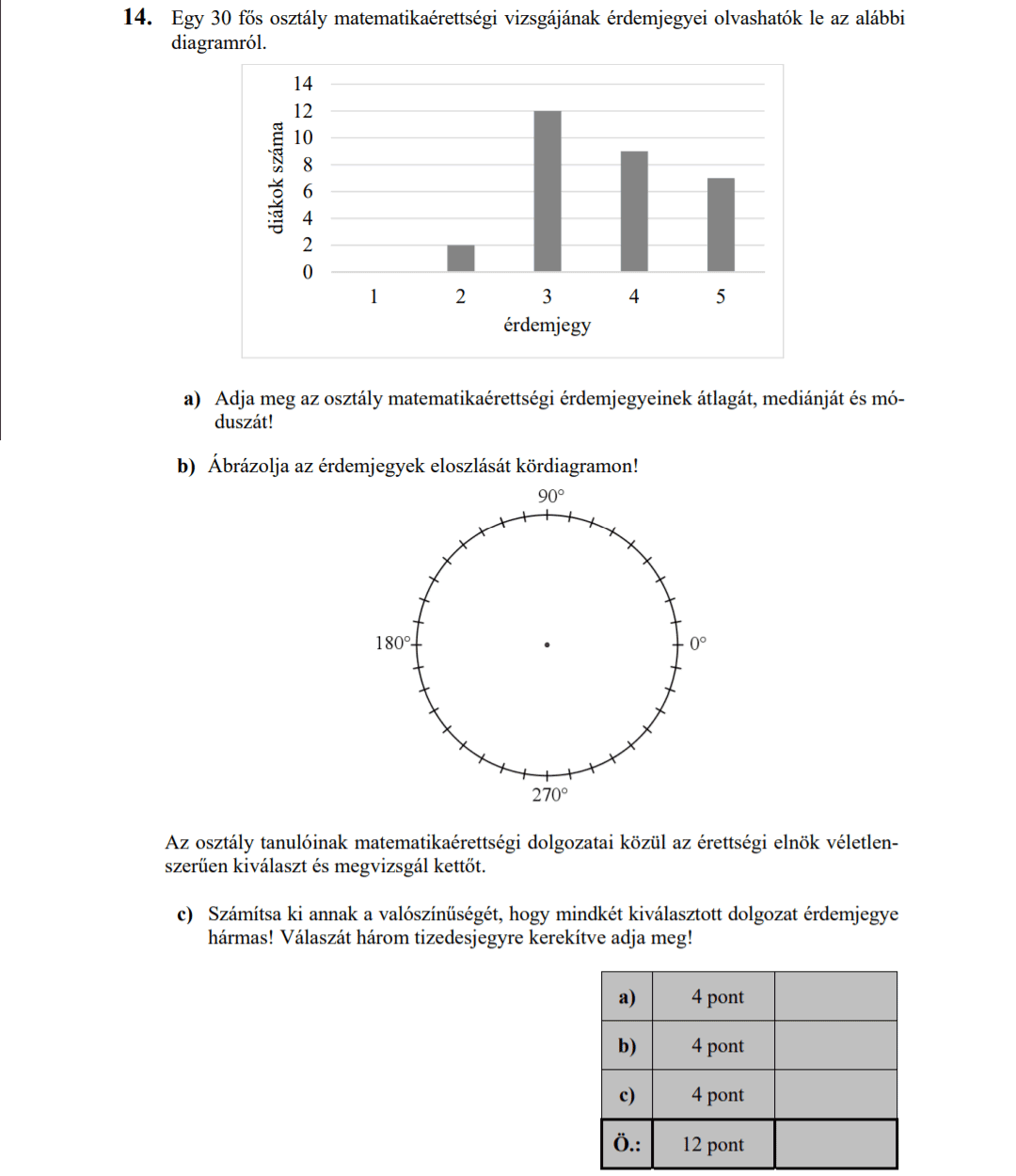
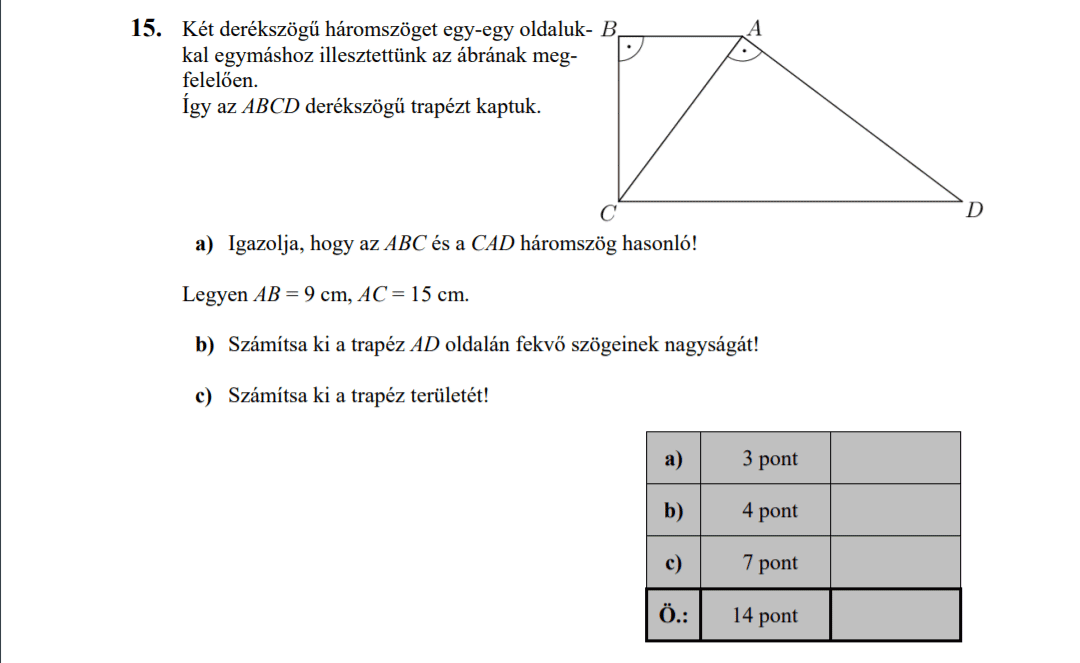



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


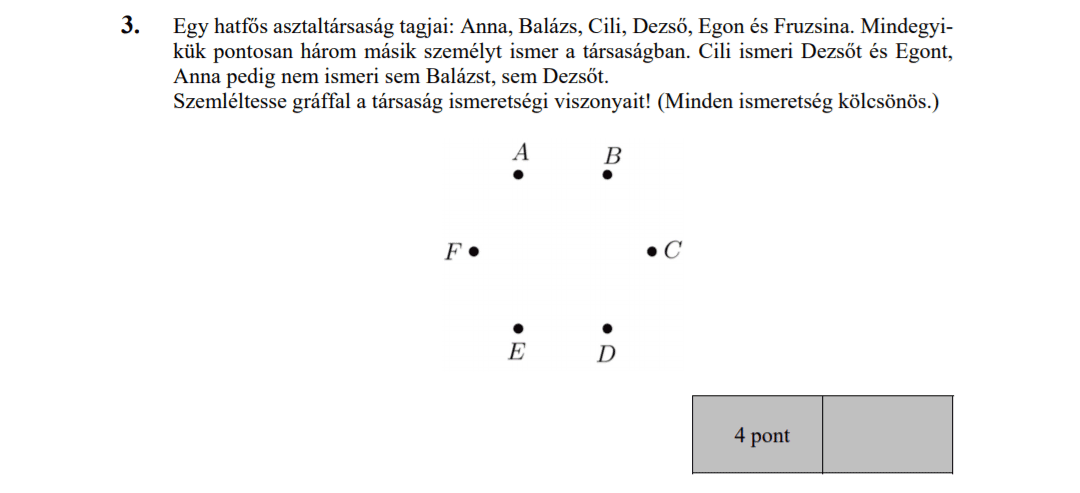


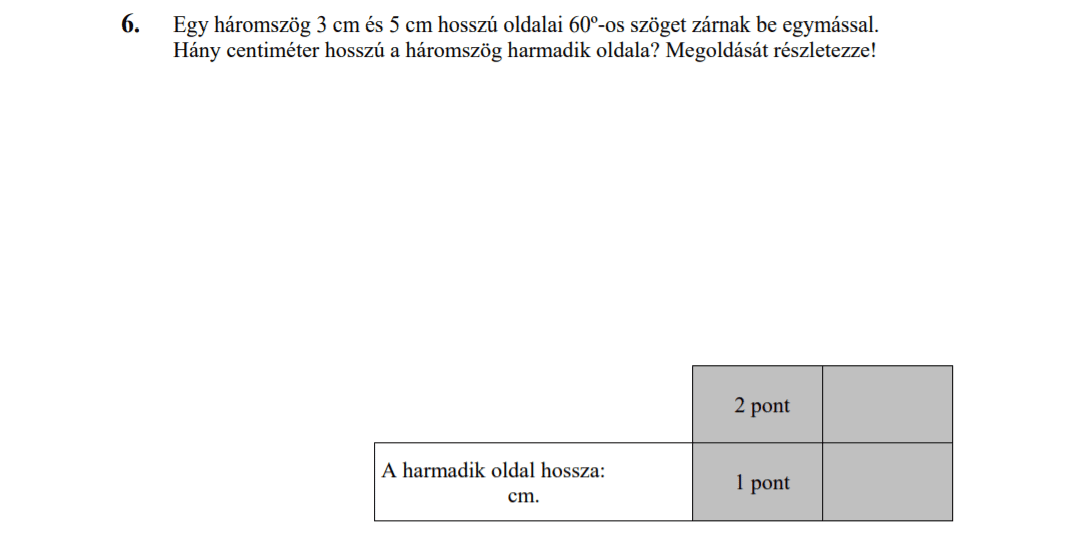

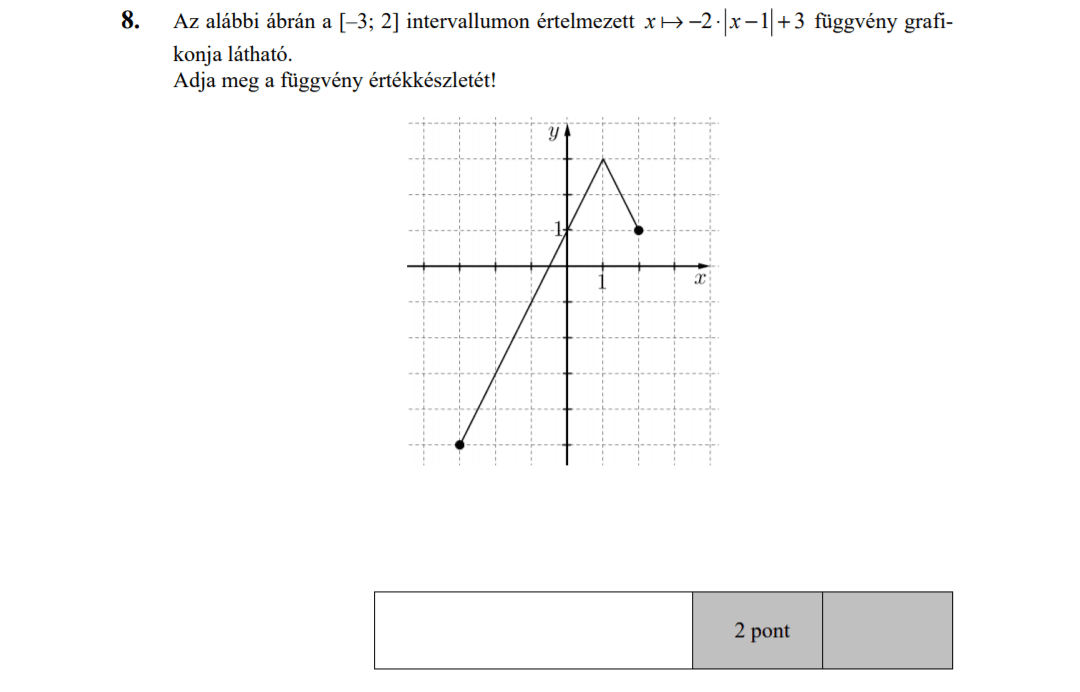

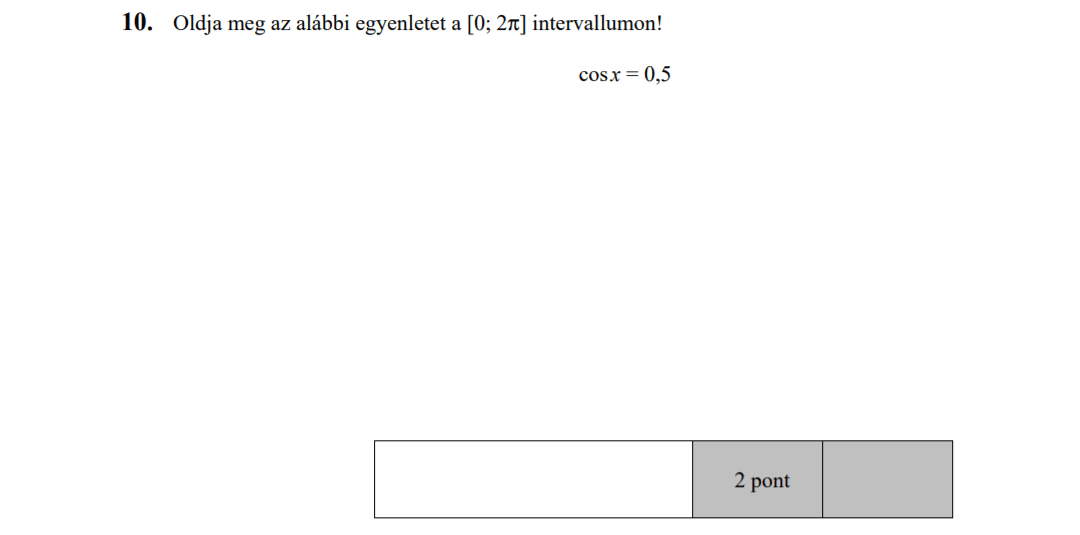

MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
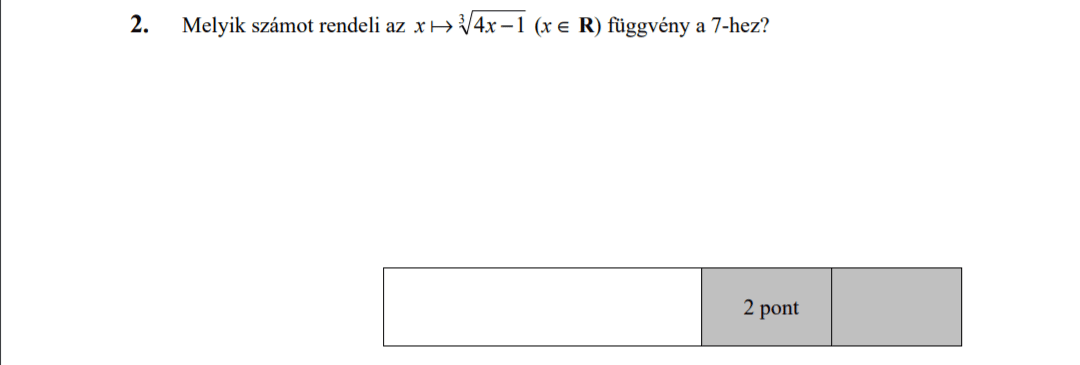


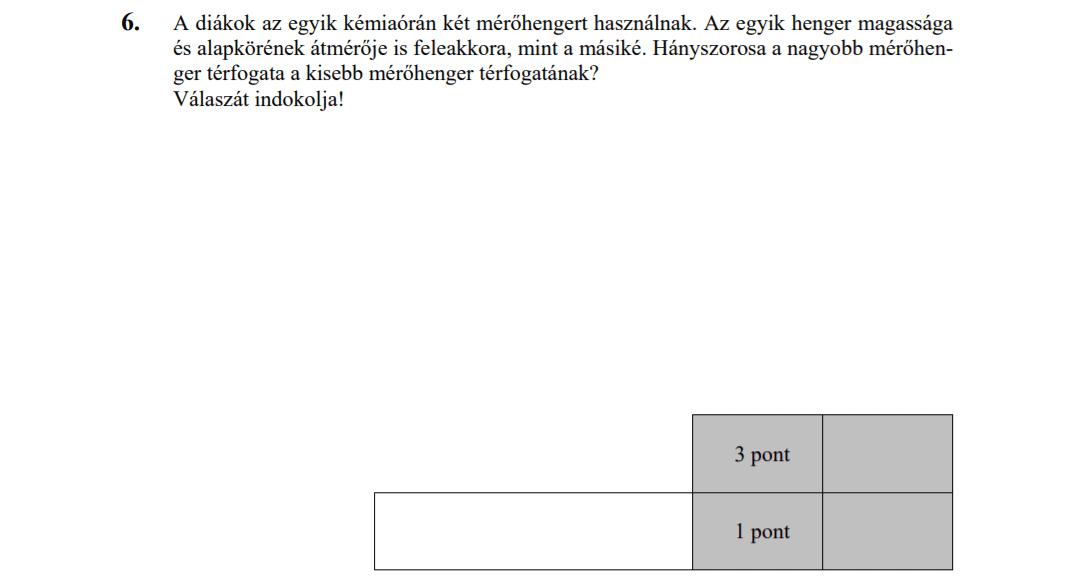
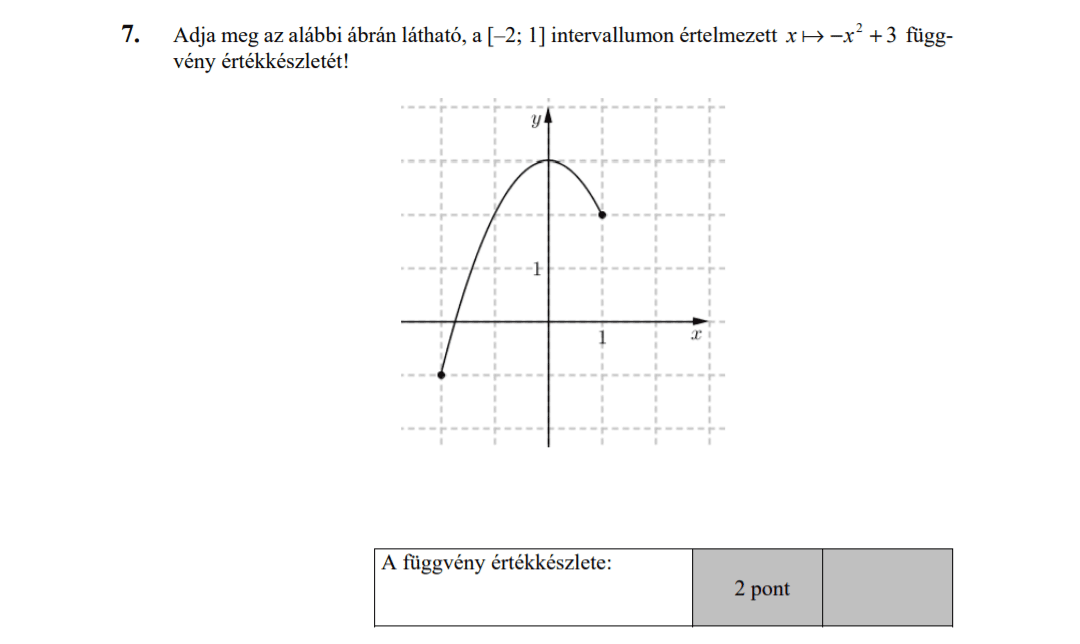

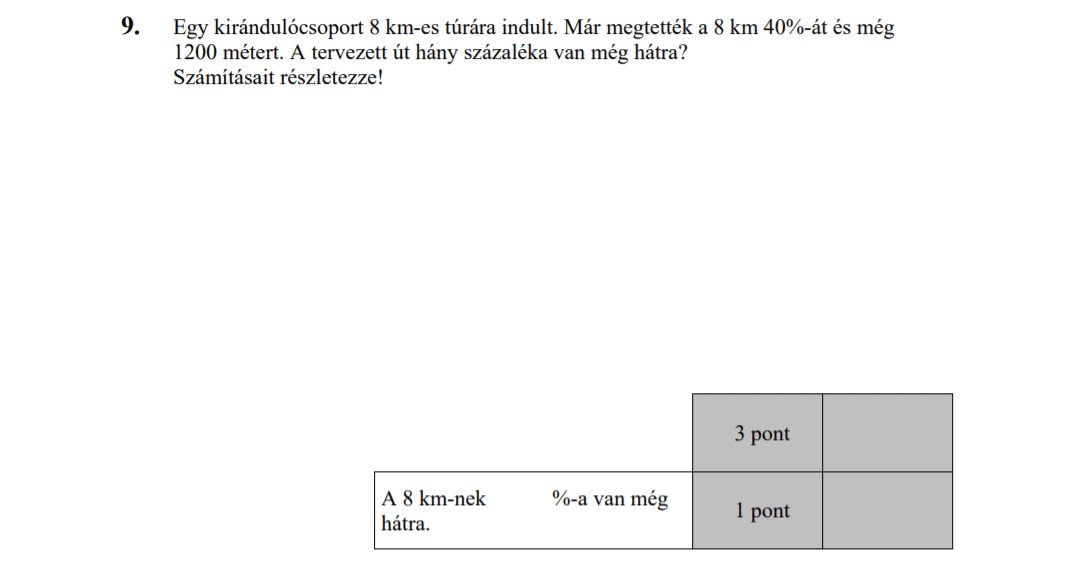
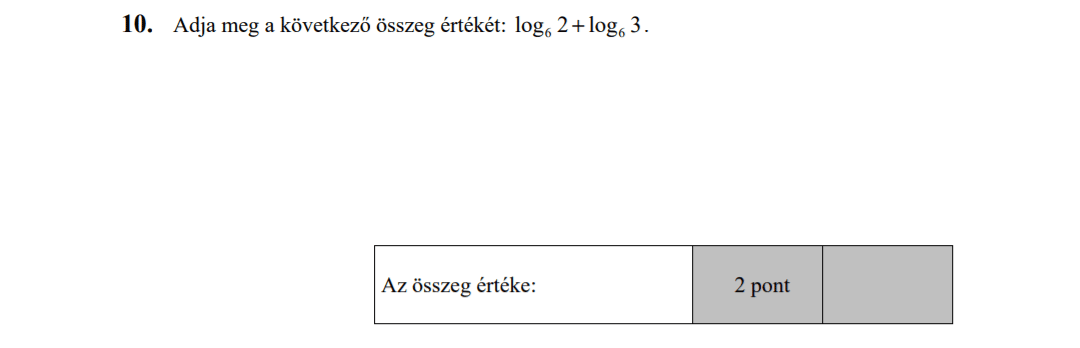

MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






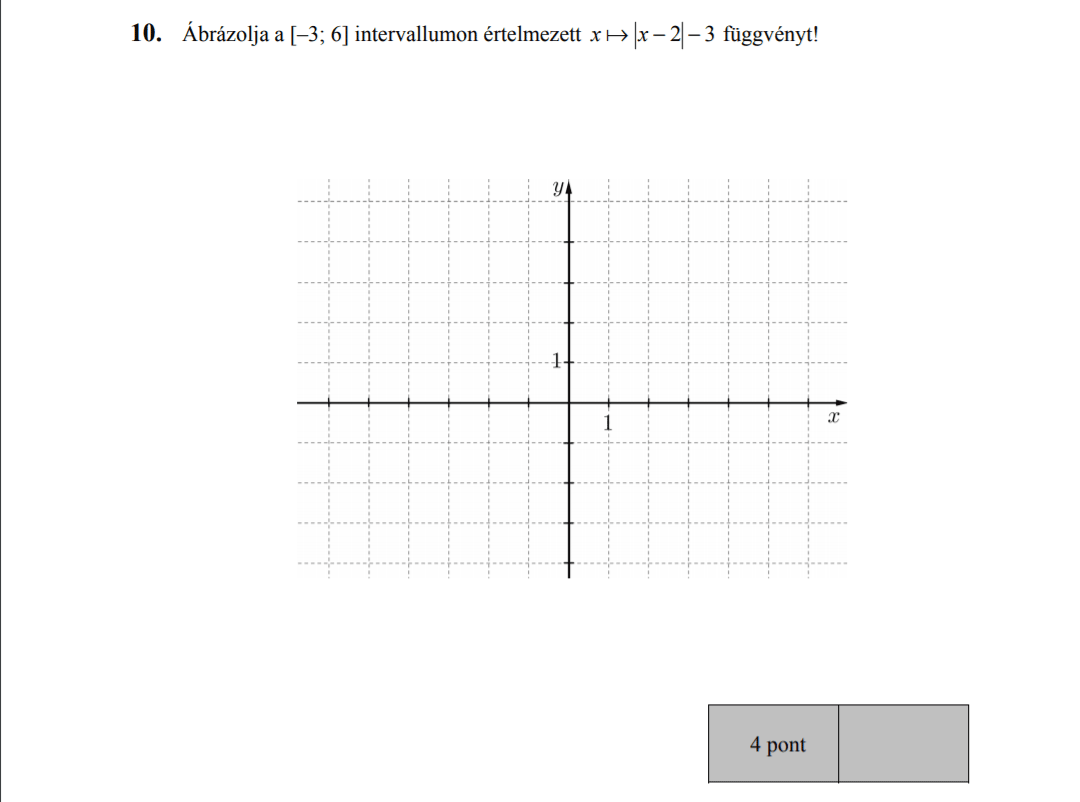

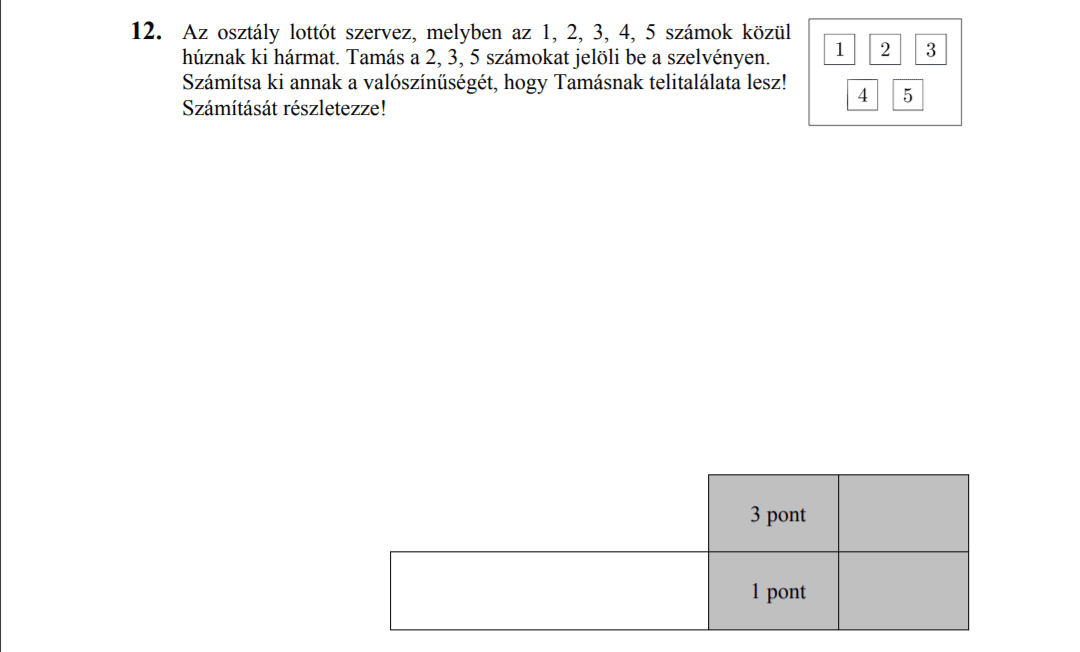
MÁSODIK RÉSZ

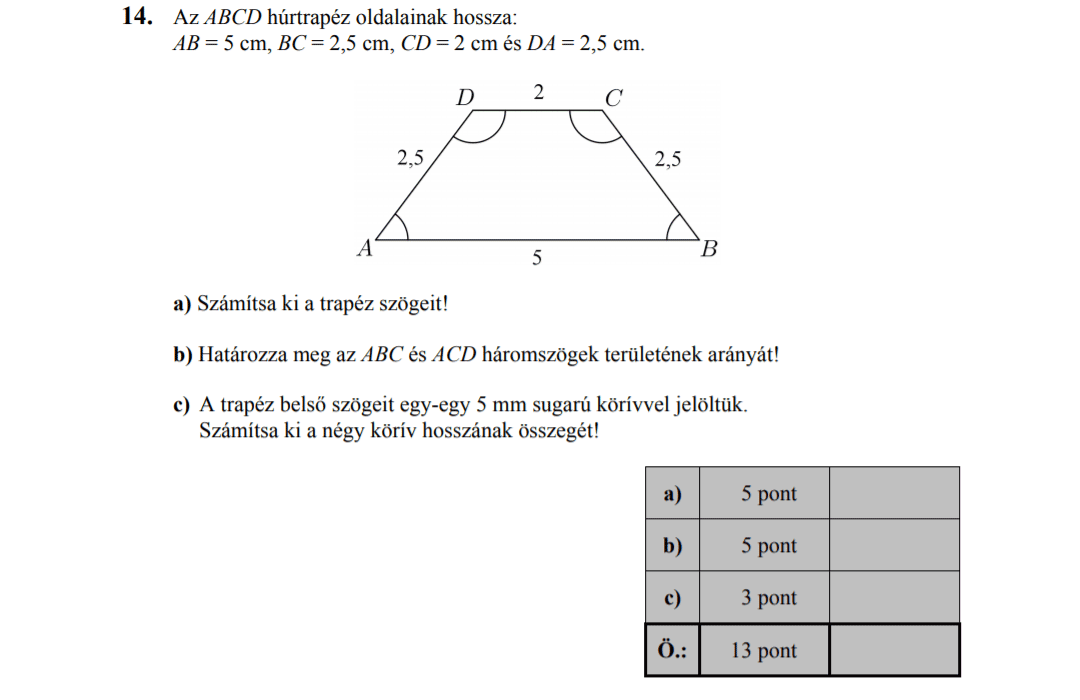

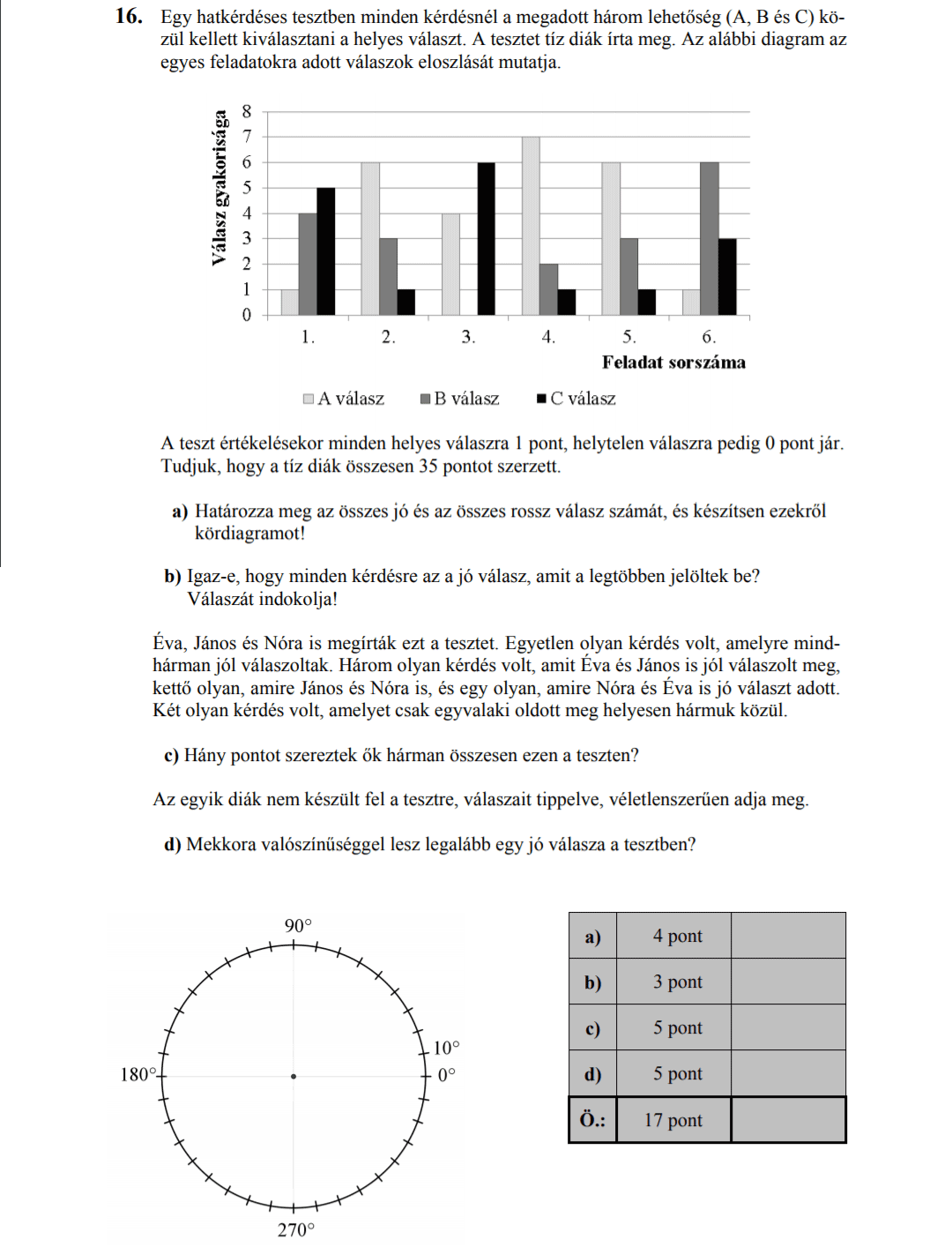


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

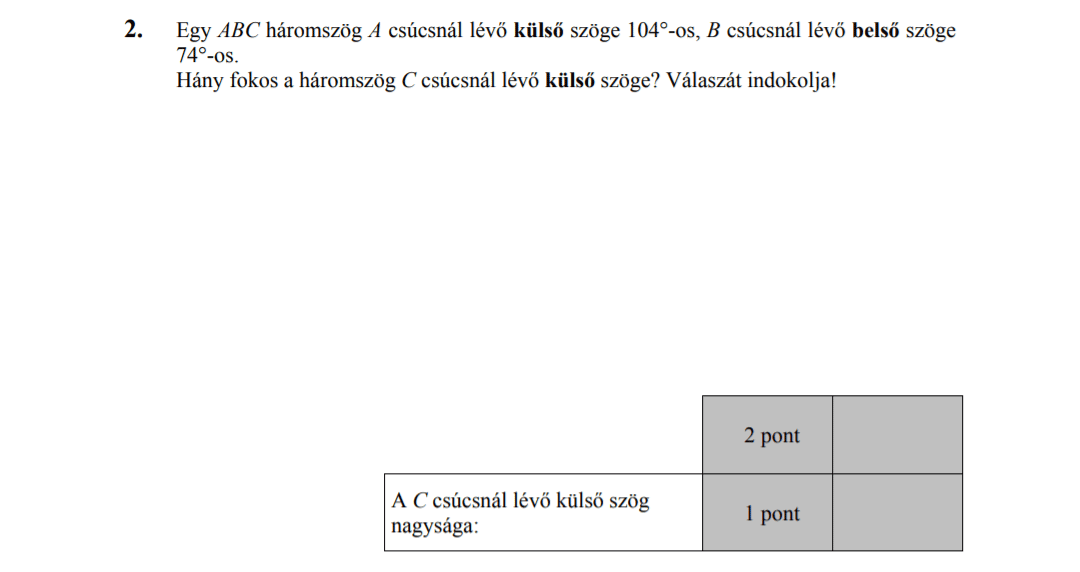





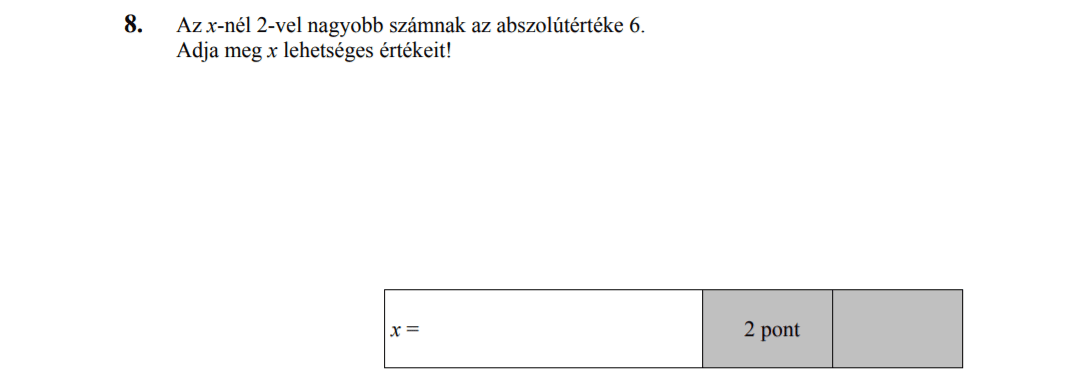

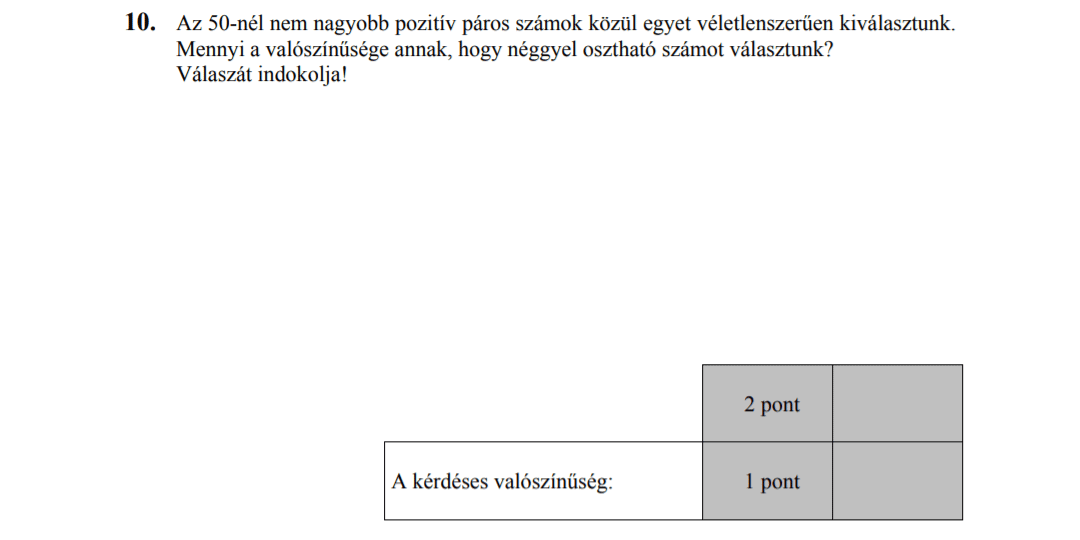


MÁSODIK RÉSZ

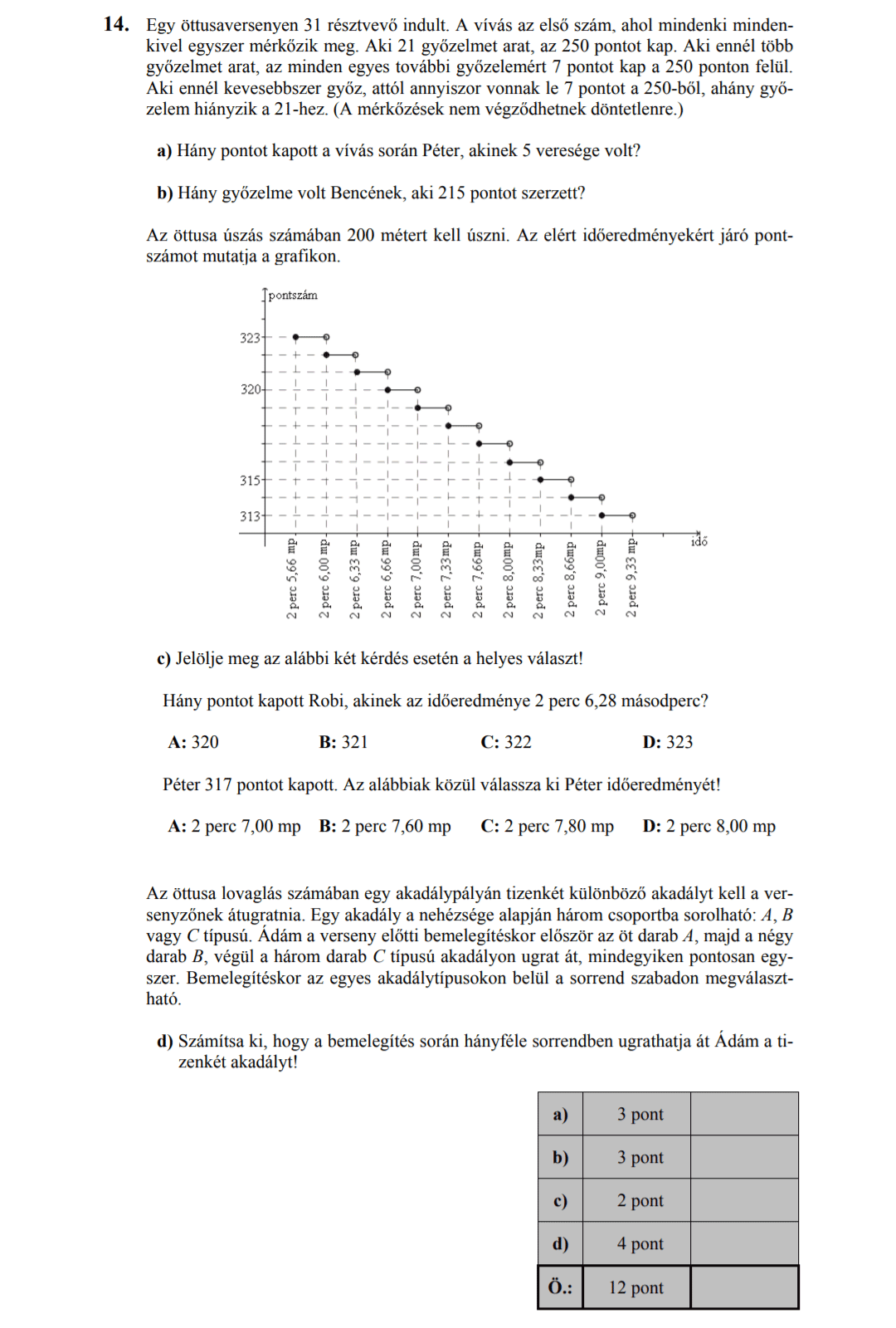
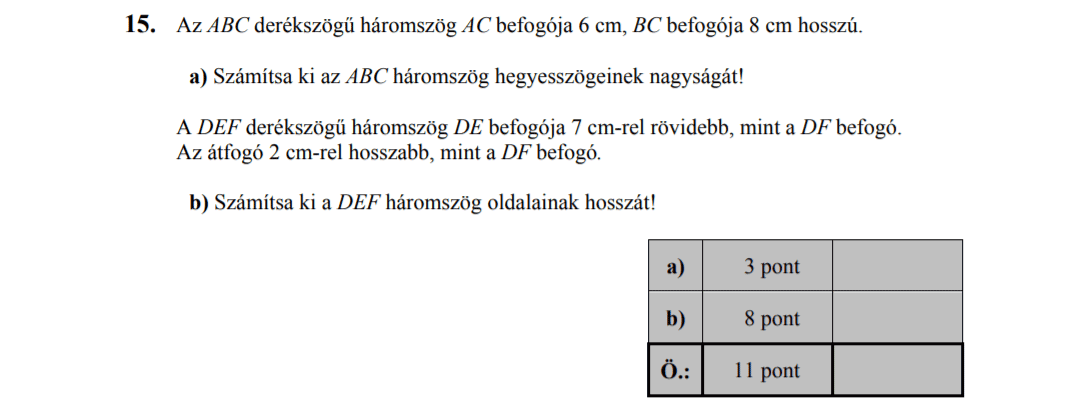



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

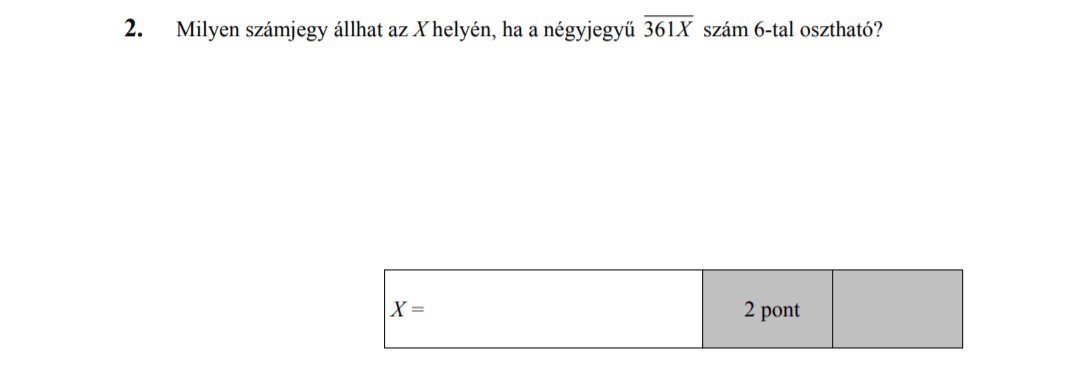



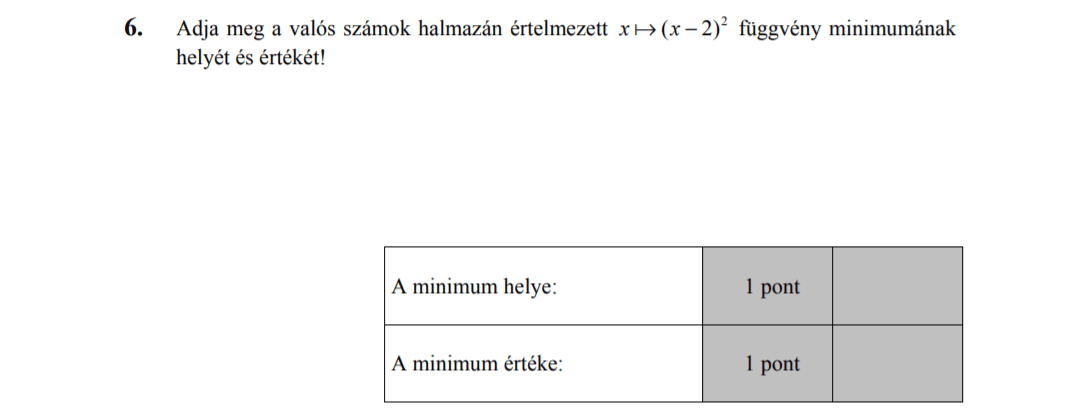

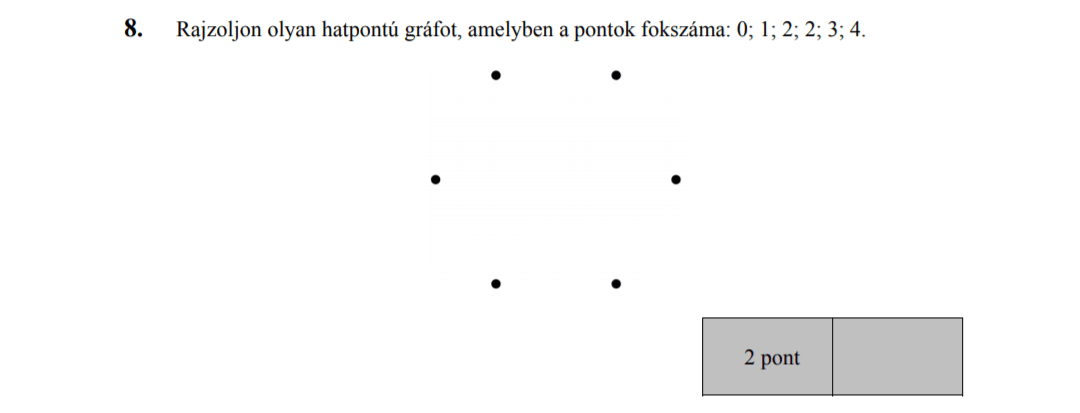


MÁSODIK RÉSZ





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








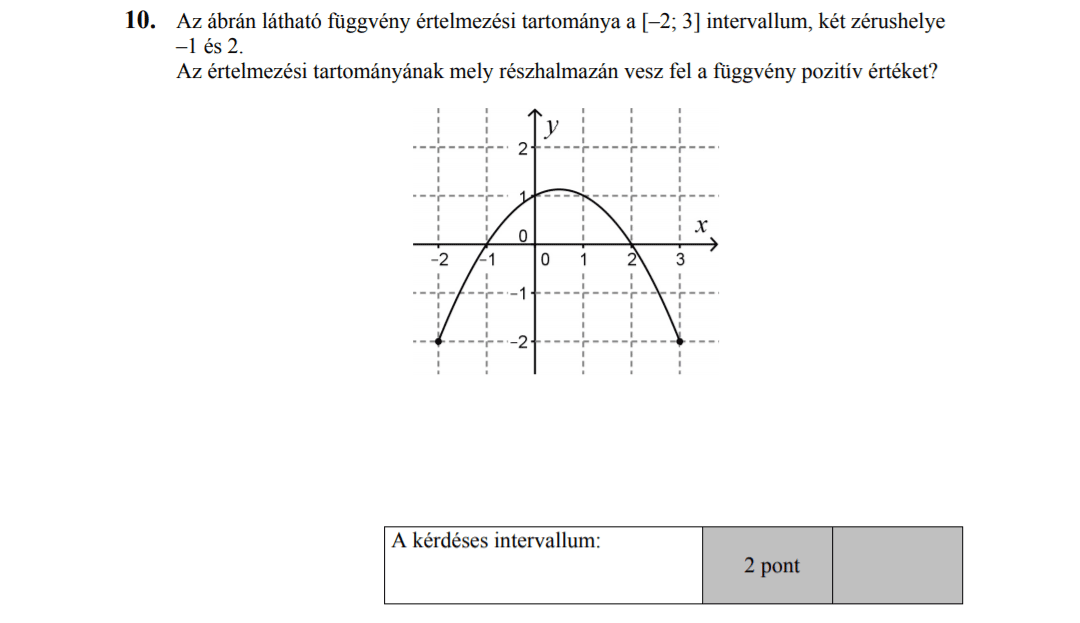


MÁSODIK RÉSZ


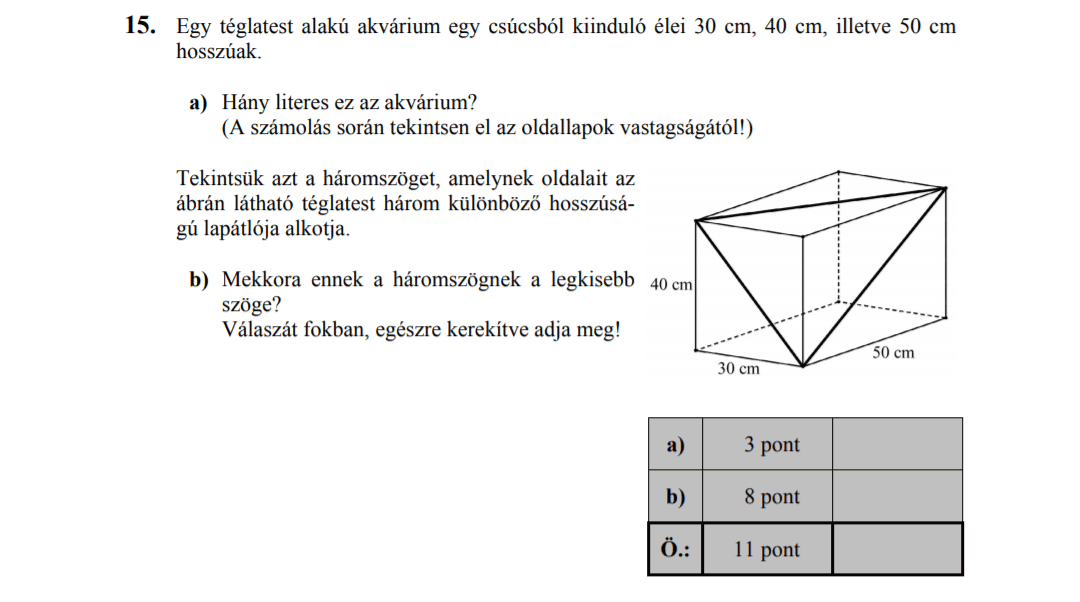

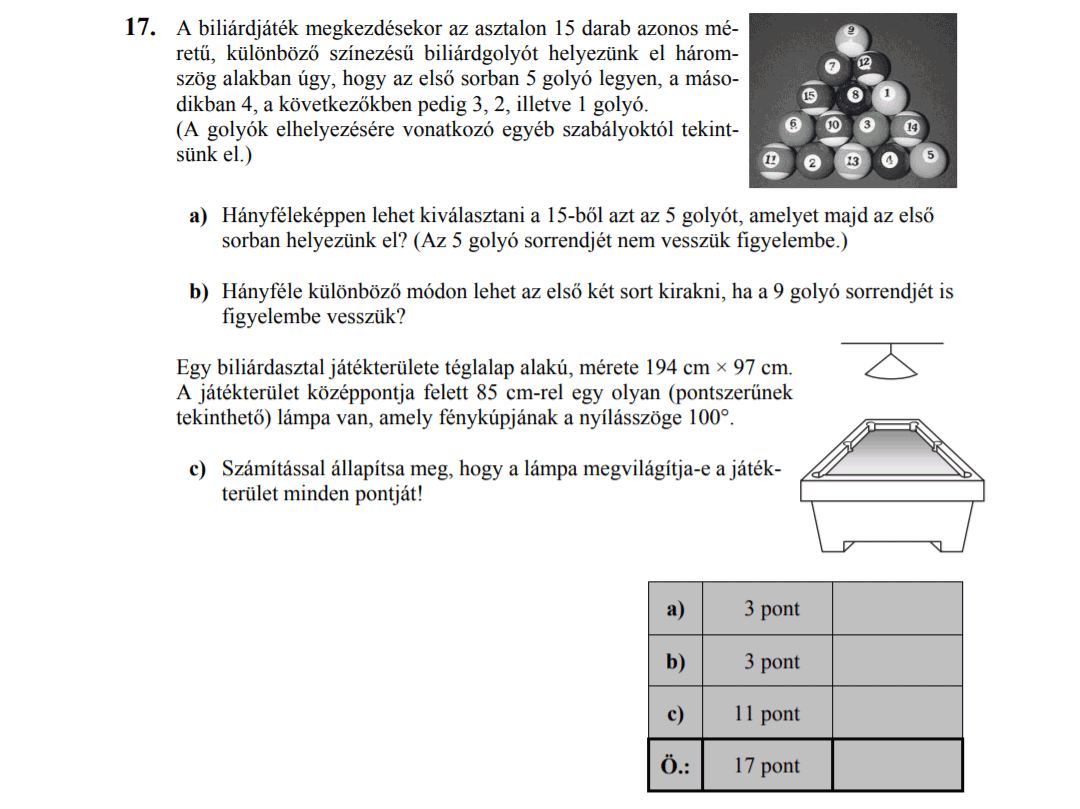

- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


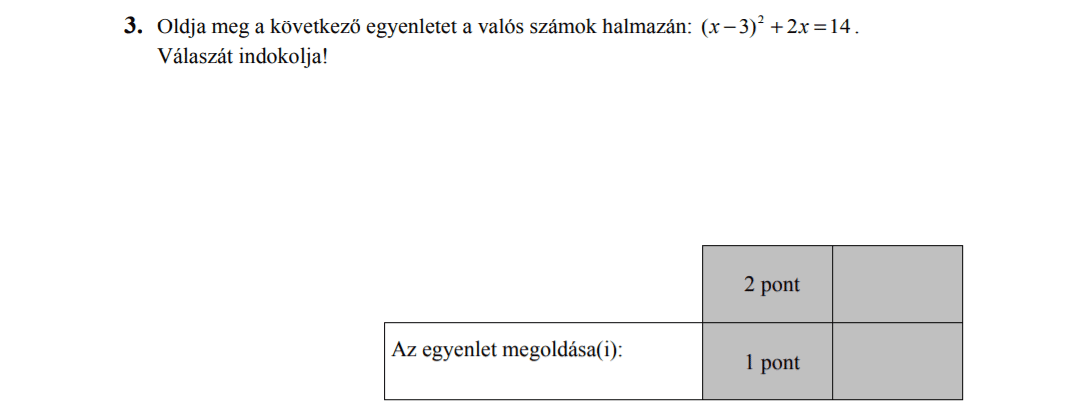





MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ





- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Kör egyenlete
$C(u,v)$ középpontú és $r$ sugarú kör egyenlete:
\( (x-u)^2 + (y-v)^2 = r^2 \)
Van két pont a koordináta-rendszerben: $A(2,4)$ és $B(5,2)$.
a) Mik az $\vec{AB}$ vektor koordinátái?
b) $\underline{a}+\underline{b}=?$
c) Mi az $AB$ szakasz felezőpontja?
d) $\underline{a}$ vektor hossza?
e) $\vec{AB}$ vektor hossza?
f) $AB$ szakasz hossza?
Írjuk fel annak az egyenesnek az egyenletét, ami átmegy az $A(1,2)$ és $B(6,5)$ pontokon.
a) Van két egyenes: $y=\frac{2}{3}x+1$ és $x+2y=6$. Számoljuk ki az egyenes $P$ metszéspontját.
b) Van két egyenes: $y=2x+4$ és $y=2x-2$. Számoljuk ki az egyenes $P$ metszéspontját.
c) Írjuk föl annak az egyenesnek az egyenletét, amelyik párhuzamos az $y=4x+5$ egyenletű egyenessel, és átmegy a $P(3,1)$ ponton.
Az $ABC$ háromszög csúcsai: $A(-4,-2)$, $B(2,2)$, $C(-4,4)$
Írjuk fel a $C$ csúcson átmenő magasságvonal egyenesének egyenletét!
a) Ábrázoljuk azt a kört, aminek az egyenlete: $ (x-1)^2 + (y-2)^2 = 9 $
b) Ábrázoljuk azt a kört, aminek az egyenlete: $ (x+1)^2+(y-2)^2=9$ és döntsük el, hogy a $P(1,5)$ és a $Q(2,2)$ pontok a körhöz képest hol helyezkednek el.
a) Egy kör középpontja a $K(4,2)$ pont, és a kör átmegy a $P(1,3)$ ponton. Mekkora a kör sugara? Írjuk fel a kör egyenletét, és döntsük el, hogy a $Q(3,5)$ pont rajta van-e a körön.
b) Egy derékszögű háromszög három csúcsa: $A(6,1)$, $B(-2,3)$, $C(3,-2)$ és a C csúcsnál derékszög van.
- Írjuk föl a $C$ csúcson átmenő súlyvonal egyenletét.
- Írjuk föl a háromszög köré írható körének egyenletét.
Hogyan kell $m$ értékét megválasztani úgy, hogy az $y=mx+4$ egyenes áthaladjon a $2x-y+1=0$ és az $y=x+5$ egyenesek metszéspontján?
Már mutatjuk is, hogyan számoljuk ki két egyenes metszéspontjának koordinátáit, és hogyan tudunk rávenni egy y=mx+b alakú egyenest, hogy menjen át ezen a metszésponton.
Itt ez a koordinátarendszer, és benne néhány pont.
Az A pontnak az x koordinátája 2, az y pedig 4.
A B pont koordinátái 1 és 2…
És ez pedig a C.
Mindhárom pont ugyanazzal a különleges képességgel rendelkezik…
Egy olyan kulcs birtokában vannak, amely képes kinyitni az univerzum titkos ajtóit.
Nem, ezzel mégsem rendelkeznek, viszont azt tudják, hogy az y koordinátájuk az x-nek a kétszerese.
Azért ez is valami…
Azok a pontok, amik azt tudják, hogy az y koordinátájuk az x-nek a kétszerese, egy egyenesen helyezkednek el.
Ezen az egyenesen itt.
És ez pedig az egyenes egyenlete:
Hogyha egy pont rajta van az egyenesen…
Akkor a koordinátáit az egyenes egyenletébe helyettesítve az teljesül.
Olyankor viszont, amikor a pont nincs rajta az egyenesen…
A koordinátáit az egyenes egyenletébe helyettesítve az nem teljesül.
Itt egy másik egyenes…
És két dolgot érdemes róla tudni.
Az egyik, hogy milyen meredeken megy…
Ezt meredekségnek hívjuk, és így jön ki:
A másik dolog, amit érdemes tudni, hogy hol metszi a függvény grafikonja az y tengelyt.
Ezt úgy hívjuk, hogy tengelymetszet, és a jele b.
És ez pedig az egyenes egyenlete.
Pontosabban az egyenes egyenletének a meredekséges alakja.
Próbáljuk is ki ezt a képletet erre az egyenesre itt.
Ezt hívjuk az egyenes egyenletének.
Azok az egyenesek, amelyeknek a meredeksége egyforma, egymással párhuzamosak.
Nézzük meg például, hogy mi lesz annak az egyenesnek az egyenlete, ami ezzel párhuzamos, és átmegy a P(3,2) ponton.
Hát, az biztos, hogy a meredeksége 2…
A P ponton pedig akkor megy át, hogyha a pont koordinátáit az egyenes egyenletébe helyettesítve az teljesül.
És most nézzük, hogyan tudjuk felírni annak az egyenesnek az egyenletét, ami átmegy ezeken a pontokon…
A meredekséggel kezdjük…
Itt jön az egyenes egyenlete:
Itt jön most egy másik egyenes:
Most pedig még el kell intéznünk, hogy menjen át az A ponton.
Sőt, a B ponton is át kéne mennie…
Hogyha a meredekség már megvan, a két pont közül elég az egyiket behelyettesíteni…
Az mindegy, hogy melyiket.
Feldobhatunk például egy érmét, és ha fej, akkor az A-t helyettesítjük be, ha írás, akkor a B-t.
De az izgalmak még csak most jönnek…
Ez itt egy egyenes…
És két dolgot érdemes róla tudni.
Az egyik, hogy milyen meredeken megy, ezt hívjuk meredekségnek…
A másik dolog, amit érdemes tudni, hogy hol metszi az y tengelyt.
Itt jön aztán egy másik egyenes…
Aminek az egyenlete:
Számoljuk ki az egyenesek metszéspontjának koordinátáit.
A metszéspontot hívjuk mondjuk P-nek.
Ennek a P pontnak van egy különleges tulajdonsága.
Egyszerre van rajta mindkét egyenesen.
Vagyis egyszerre kell teljesülnie mindkét egyenletnek.
Hát igen, ezt úgy hívják, hogy egyenletrendszer.
Meg is vannak a metszéspont koordinátái.
Nézzük meg ezeket az egyeneseket is…
Számoljuk ki a metszéspontjuk koordinátáit.
Az egyik egyenesünk meredeksége 2…
És a másik egyenes meredeksége is 2…
Ezek egyforma meredek egyenesek.
Vagyis egymással párhuzamosak.
És így nincs metszéspontjuk.
Ezt jó tudni, épp most spóroltuk meg egy egyenletrendszer megoldását…
Ha két egyenes egyenlete
ezek pontosan akkor párhuzamosak, ha
Írjuk föl annak az egyenesnek az egyenletét, amelyik párhuzamos az y=4x+5 egyenletű egyenessel, és átmegy a P(3,1) ponton.
Készítsünk egy rajzot…
Ehhez a feladathoz egy ilyen rajz is bőven elég…
A keresett egyenes egyenlete:
Akkor lesz párhuzamos a másik egyenessel, ha a meredekségeik egyenlők…
És akkor megy át a P ponton, ha a koordinátáit behelyettesítve az egyenletbe, az teljesül.
Most pedig nézzük, hogy két egyenes mikor lesz egymásra merőleges…
Ezzel folytatjuk…
Itt van ez az egyenes, aminek a meredeksége 2 és az y tengelyt 1-nél metszi…
És az egyenlete…
Hogyha ezt a kis háromszöget itt elforgatjuk 90 fokkal…
Akkor a meredekség ez lesz…
Ez a két egyenes éppen egymásra merőleges.
És az összes többi is, aminek a meredeksége -1/2.
A dolog minden egyenesre igaz.
Két egyenes pontosan akkor merőleges egymásra, ha a meredekségeik szorzata -1.
De azért van még itt egy kis csalás.
Létezik ugyanis egy olyan egyenes, aminek nincs meredeksége.
A függőleges egyenesnek…
Az y tengellyel párhuzamos egyenesek egyenlete:
Az x tengellyel párhuzamos egyenesek egyenlete pedig:
Ezeknek egyébként van meredekségük…
Mégpedig a meredekség nulla.
És most lássuk, mire használhatnánk mindezt, jóra vagy rosszra…
Ez a három pont egy háromszög három csúcsa.
Írjuk föl a C csúcson átmenő magasságvonal egyenesének egyenletét.
Hogyha ránk törnek a régi emlékek…
Hogy mi is volt egy háromszögben a magasságvonal…
A C csúcson átmenő magasságvonal az AB oldal egyenesére bocsájtott merőleges.
Ez itt az AB oldal egyenese…
És ez pedig a C-n átmenő merőleges.
Kezdjük azzal, hogy írjuk föl az AB oldal egyenes egyenletét.
Nézzük, mekkora a meredekség:
A b-t úgy kapjuk meg, hogy veszünk egy olyan pontot, ami rajta van az egyenesen…
És a koordinátáit behelyettesítjük az egyenes egyenletébe.
Itt van, mondjuk ez a pont.
A magasságvonal erre merőleges lesz…
Így hát a meredekségek szorzata:
Itt jön a magasságvonal egyenlete:
Ez akkor fog átmenni a C csúcson, ha behelyettesítve a C csúcs koordinátáit az egyenlet teljesül.
Egy kör középpontja a pont, és a kör átmegy a ponton. Mekkora a kör sugara? Írjuk fel a kör egyenletét, és döntsük el, hogy a pont rajta van-e a körön.
A kör sugara éppen ekkora…
A K pontnak és a P pontnak a távolsága.
Itt is jön a távolságképlet:
Itt van ez az egyenes, aminek a meredeksége 2 és az y tengelyt 1-nél metszi…
És most jöhet a kör egyenlete:
Nézzük aztán, mi a helyzet a Q ponttal…
Hát, ez valahol itt van…
Így ránézésre rajta van a körön.
Egy kissé precízebben, akkor van rajta a Q pont a körön, ha a koordinátáit a kör egyenletébe helyettesítve az teljesül.
A Q pont tehát rajta van a körön.
Egy derékszögű háromszög három csúcsa:
A derékszög a C csúcsnál van.
Írjuk föl a C csúcson átmenő súlyvonal egyenletét
Írjuk föl a háromszög köré írható körének egyenletét.
Íme, a háromszög…
És ez pedig a súlyvonal.
Hogyha egy hipnózis segítségével felidézzük az általános iskolás emlékeinket…
Különösen azokat a részeket, amik a súlyvonalakkal kapcsolatosak…
Akkor talán bevillan egy kép, hogy a súlyvonal a háromszög egyik csúcsát a szemközti oldal felezőpontjával összekötő szakasz.
Ez tehát egy felezőpont.
És a szakasz felezőpontjának koordinátái:
A súlyvonal egyenlete innen már sima ügy.
Egy olyan egyenes egyenletét keressük, ami átmegy a C és a D ponton.
A b-t úgy kapjuk meg, hogy a C vagy a D pont koordinátáit behelyettesítjük.
Az mindegy, hogy melyiket.
Legyen mondjuk a C.
Meg is van a súlyvonal egyenlete.
És most nézzük a háromszög köré írható kör egyenletét.
Egy újabb hipnózis…
Ezúttal Thalész…
A derékszögű háromszögek köré írható köre a Thalész-kör.
Aminek a középpontja az átfogó felezőpontja.
A kör sugara pedig…
Az A és D pontok távolsága.
Vagy épp a B és D pontok távolsága.
Vagy a C és D pontok távolsága.
Mindegyik ugyanakkora.
És itt jön a kör egyenlete:
