- ÚJ! Kvartilisek és dobozdiagram (box plot)
- ÚJ! A geometriai valószínűség
- ÚJ! A várható érték
- ÚJ! Kamatos kamat, törlesztőjáradék, gyűjtőjáradék
- ÚJ! Számrendszerek
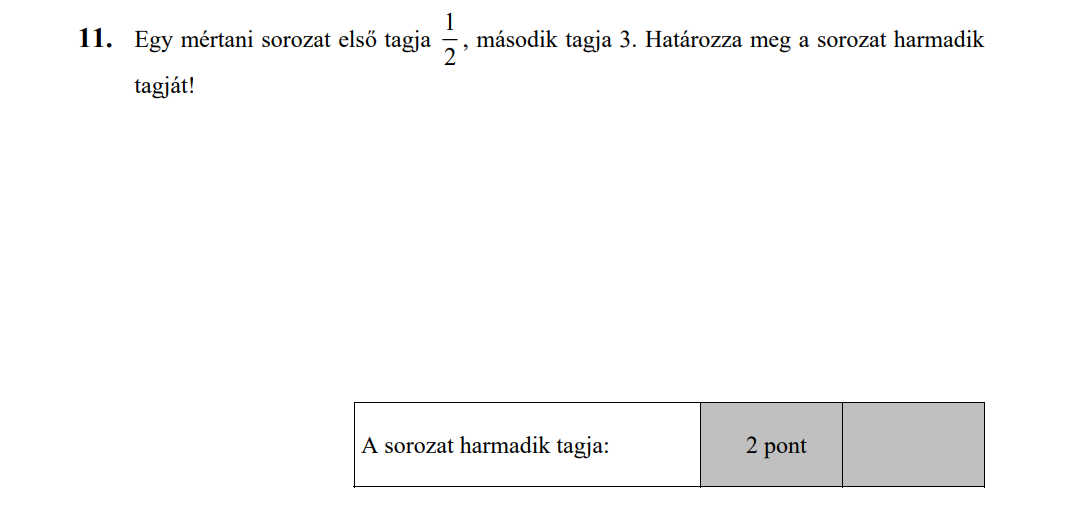
- Számtani és mértani sorozatok (16 pont)
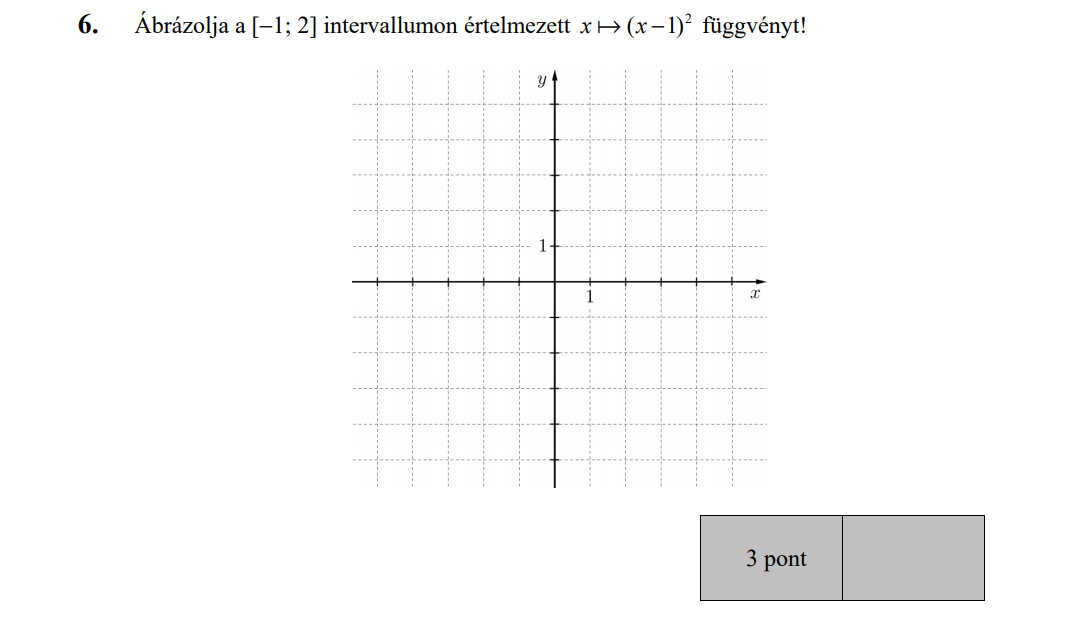
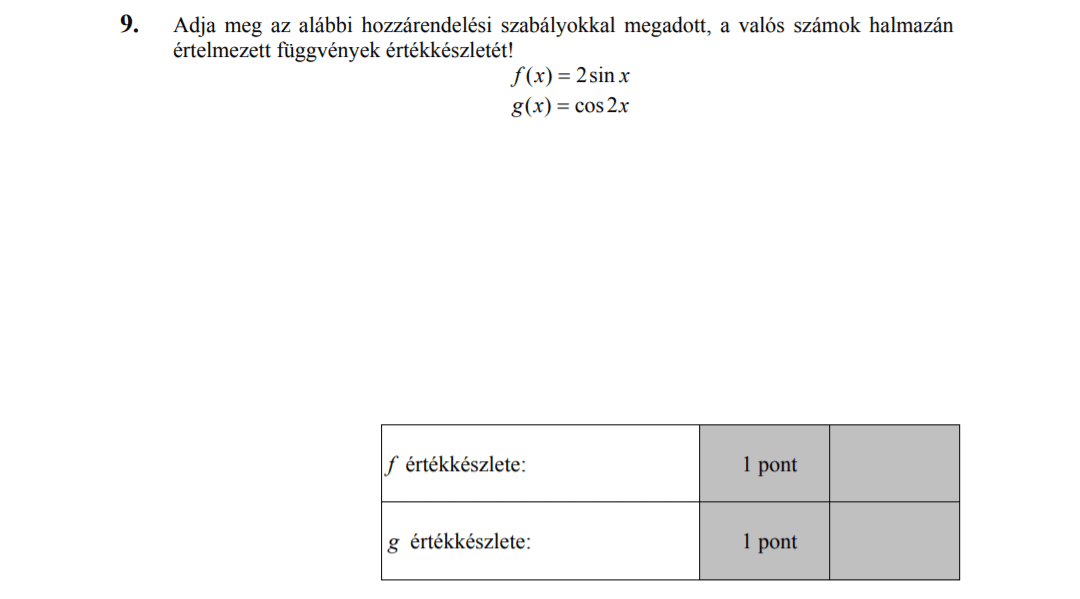
- Függvényekkel kapcsolatos feladatok (9,8 pont)
- Térgeometria (9,8 pont)
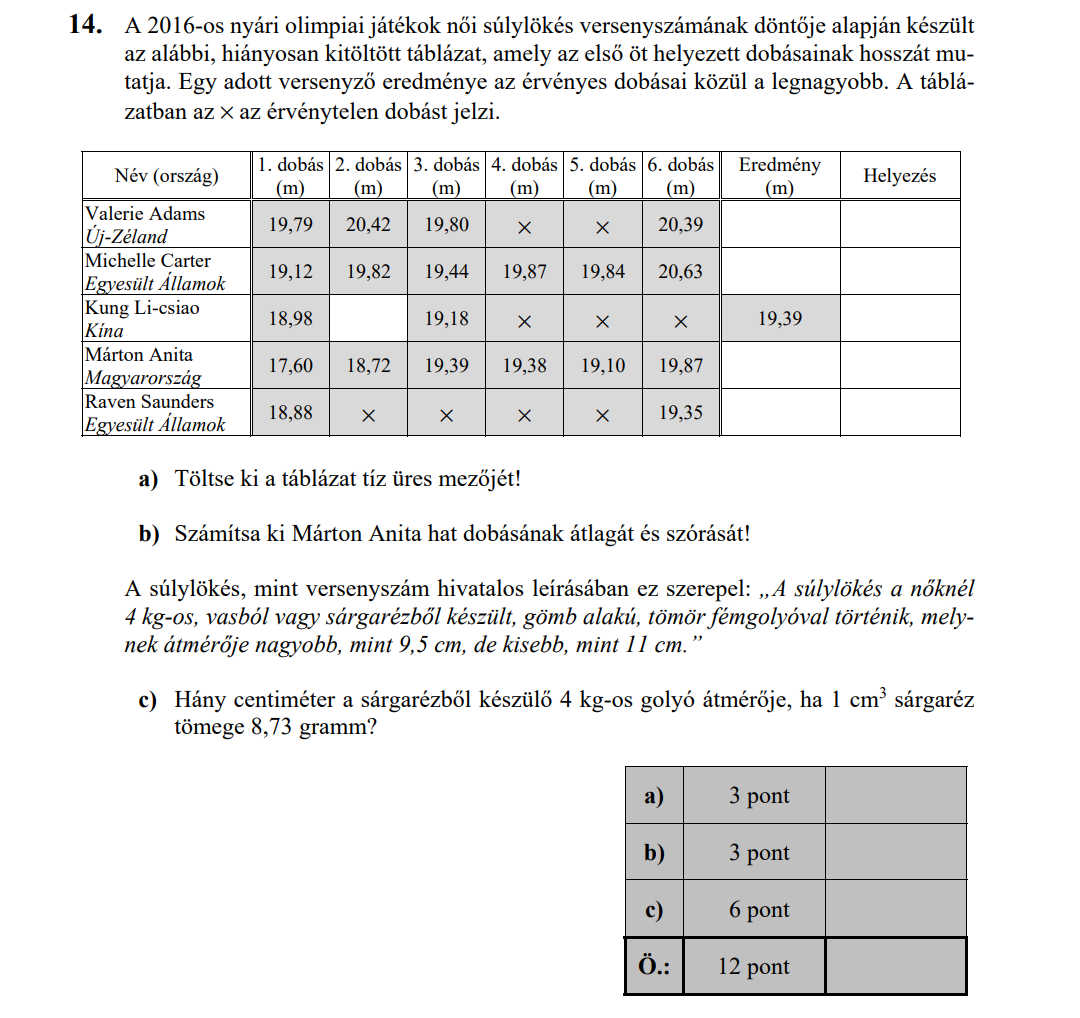
- Statisztika (9,3 pont)
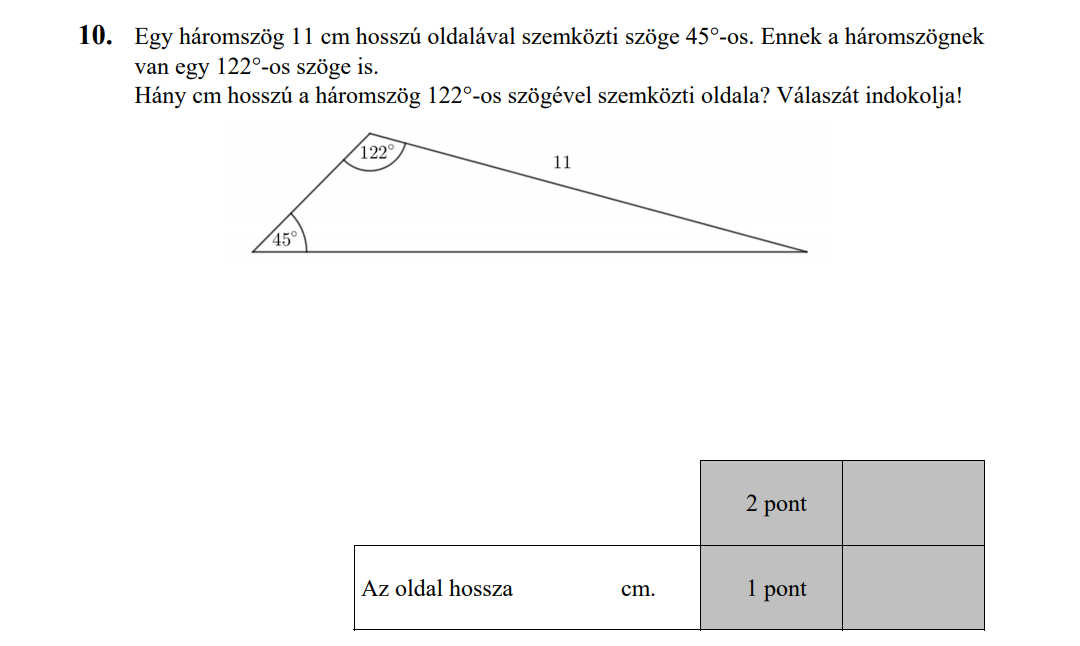
- Trigonometria, szinusztétel, koszinusztétel (9,3 pont)
- Valószínűségszámítás (9,1 pont)
- Szöveges feladatok (7,4 pont)
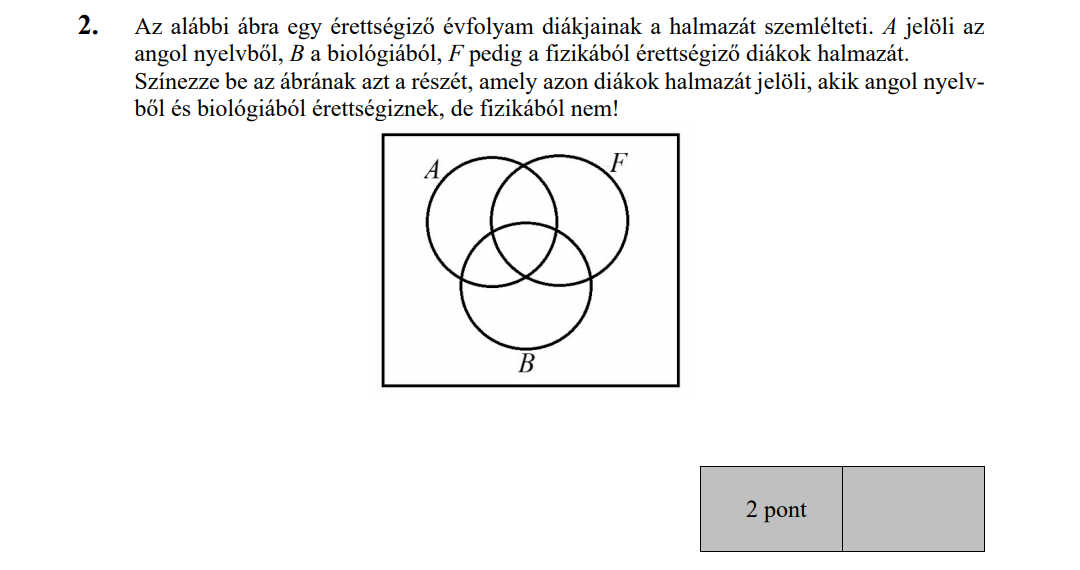
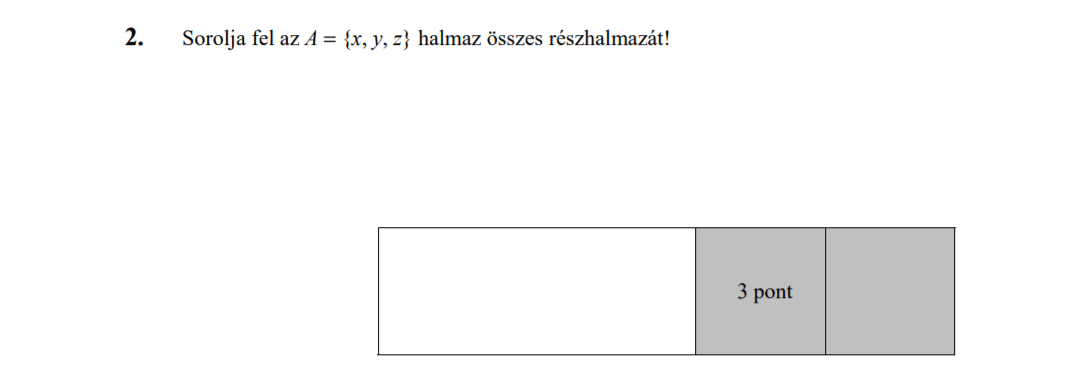
- Halmazok (6 pont)
- Kombinatorika (5,9 pont)
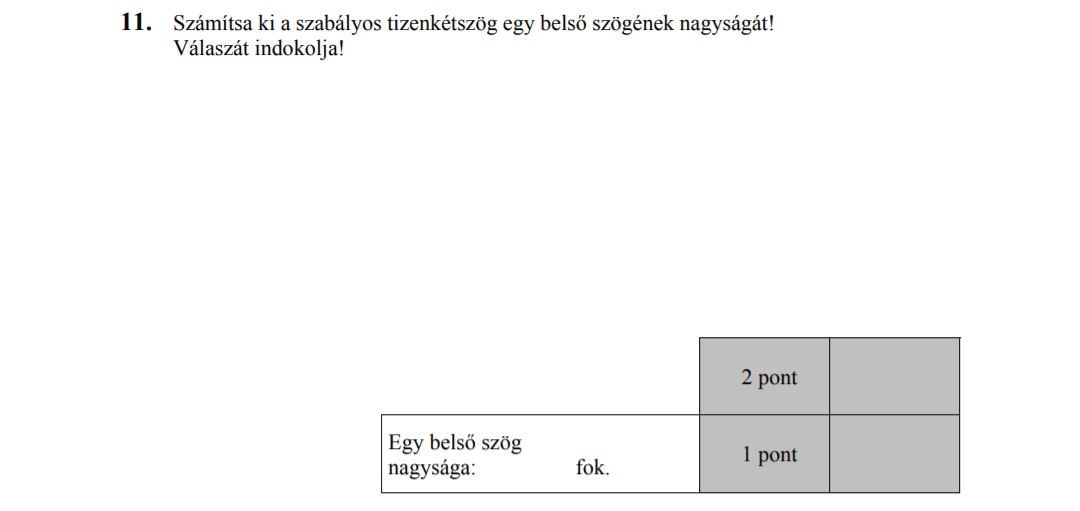
- Síkgeometria (4,5 pont)
- Százalékszámítás (3,8 pont)
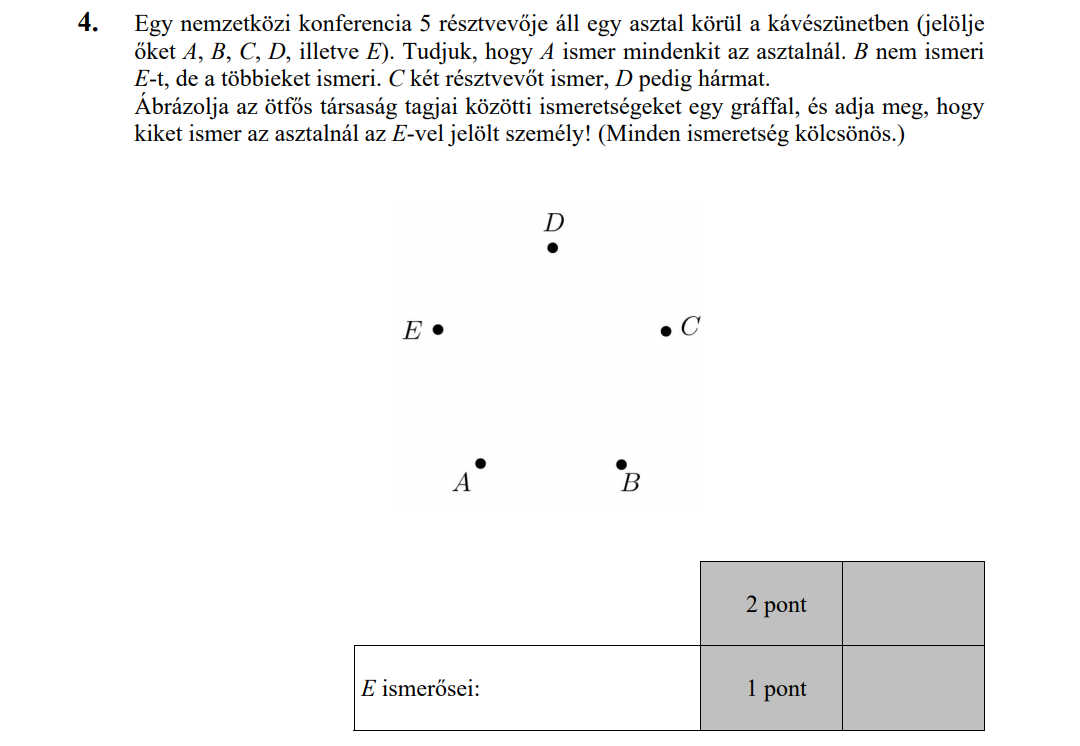
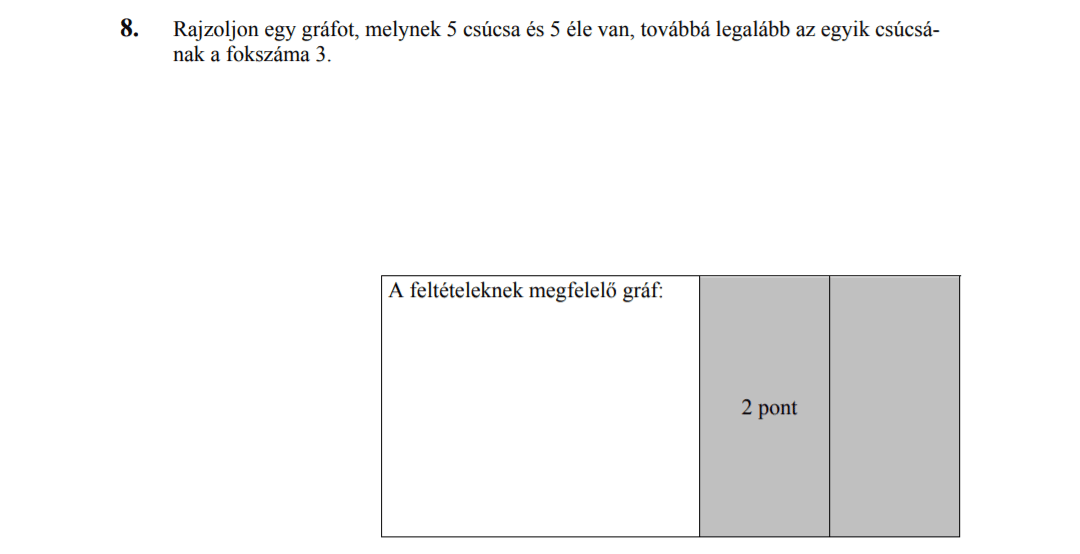
- Gráfok (3 pont)
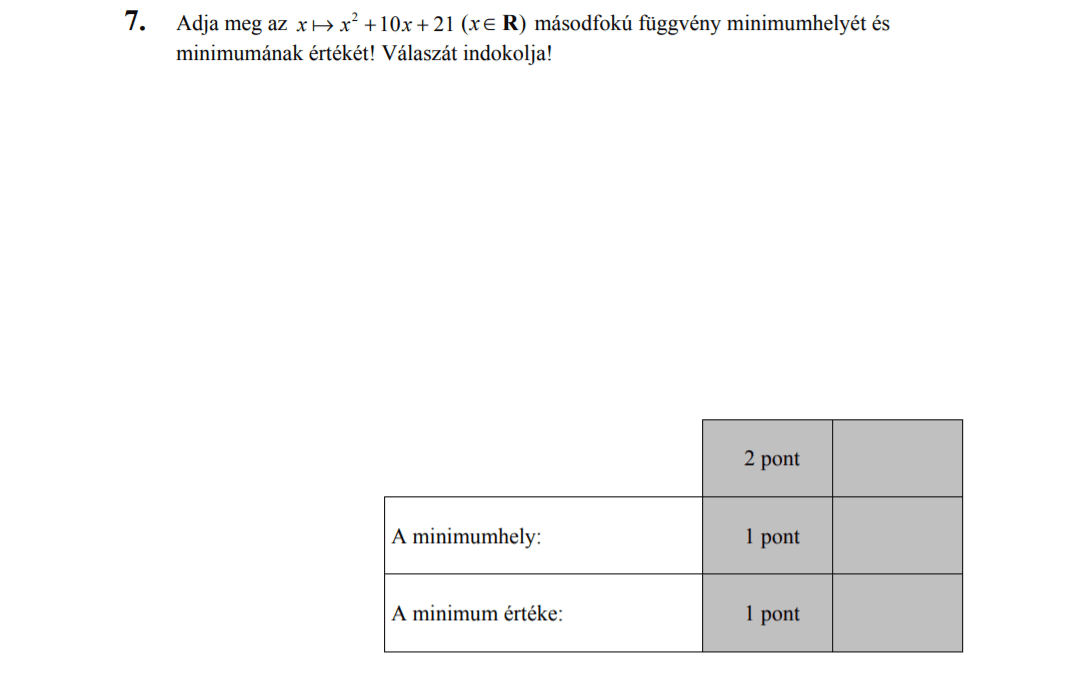
- Másodfokú egyenletek (3 pont)
- Koordinátageometria (2,8 pont)
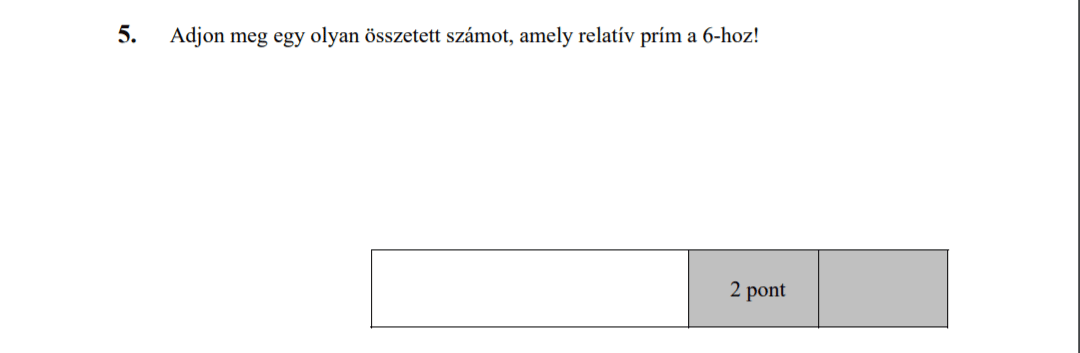
- Számelmélet (2,6 pont)
- Hatványozás, exponenciális egyenletek (1,4 pont)
- Egyenlőtlenségek (0,5 pont)
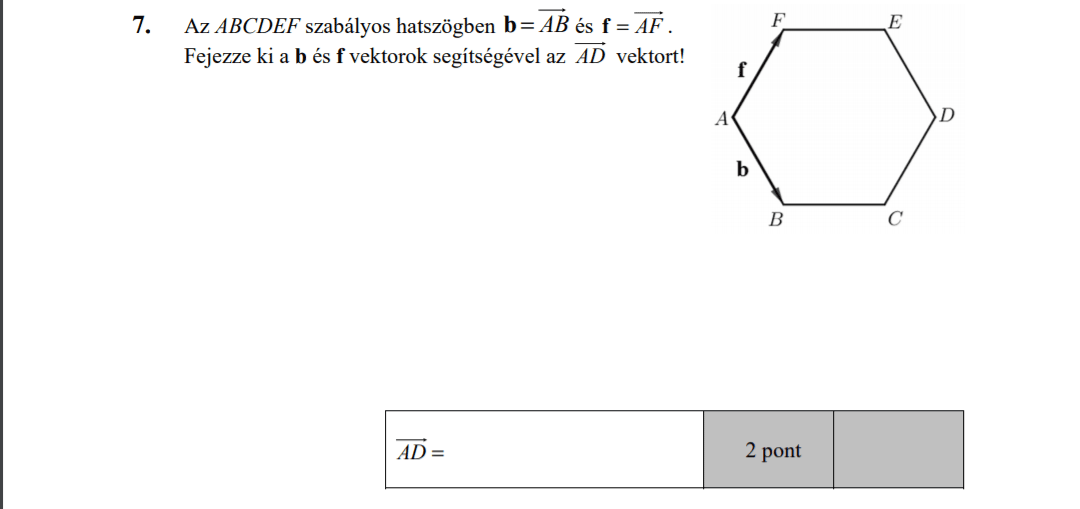
- Vektorok (0,7 pont)
- Algebra, nevezetes azonosságok
- Egyenletrendszerek
- Bizonyítási módszerek, matematikai logika
- A Pitagorasz-tétel
- Gyökös azonosságok és gyökös egyenletek
- Hatványozás, hatványazonosságok, normálalak
- Logaritmus, logaritmus használata szöveges feladatokban
- Mértékegységek és mértékegység-átváltás
- Pontok, egyenesek, síkok, szögek, a geometria alapjai
- Síkidomok, háromszögek, négyszögek, sokszögek
- Egybevágósági transzformációk
Kombinatorika (5,9 pont)
Válaszd ki, hogy melyik év középszintű érettségi feladataival szeretnél gyakorolni.
- 2020 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


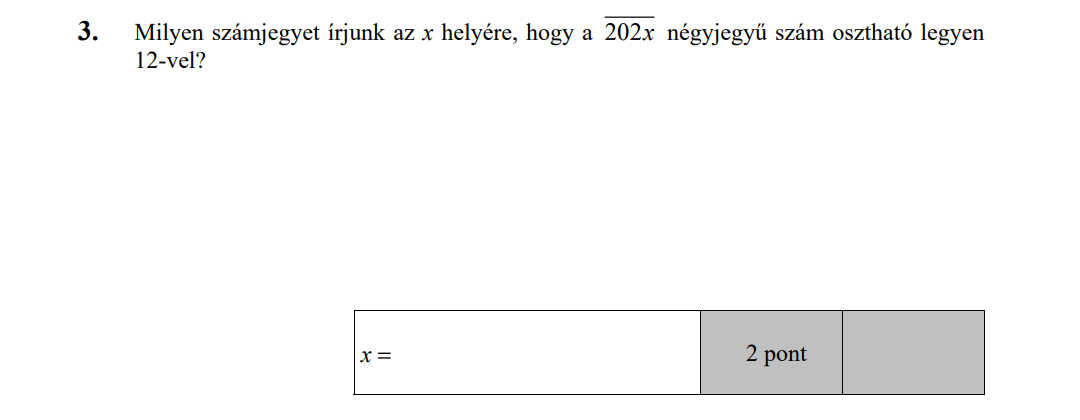
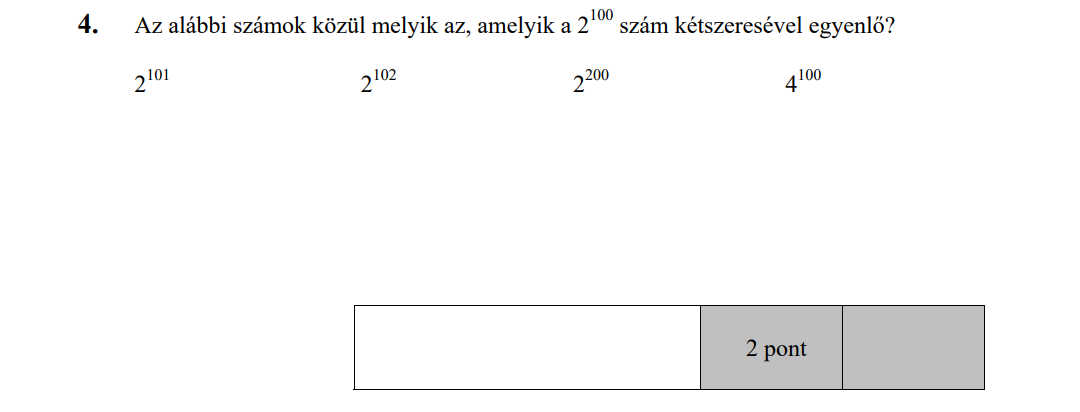



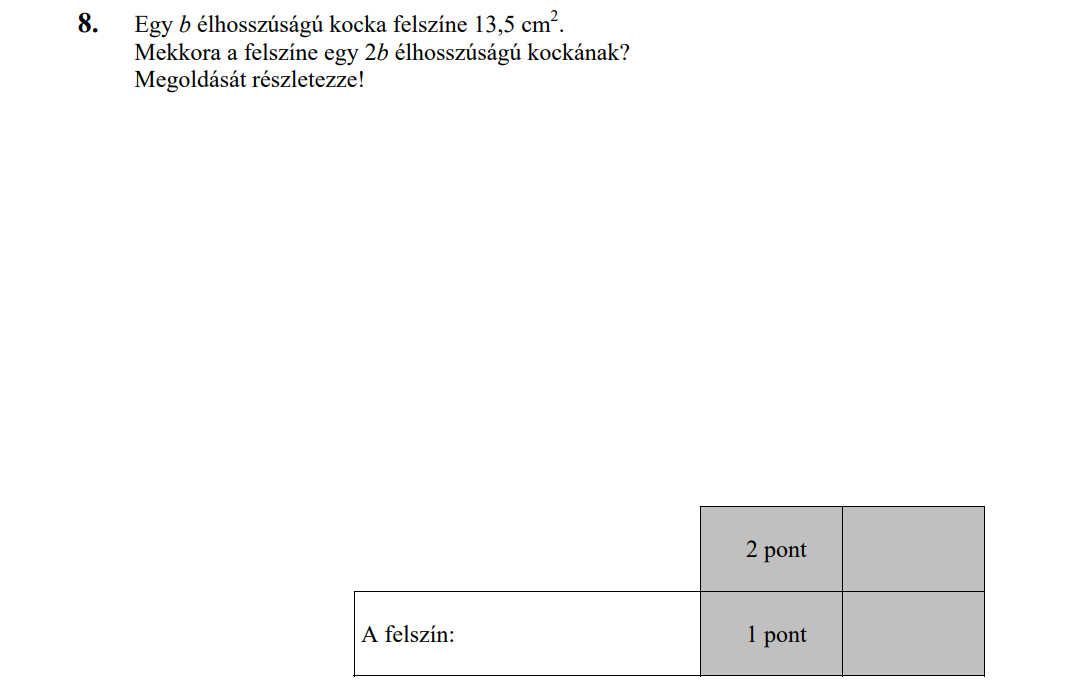




MÁSODIK RÉSZ






- 2020 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ
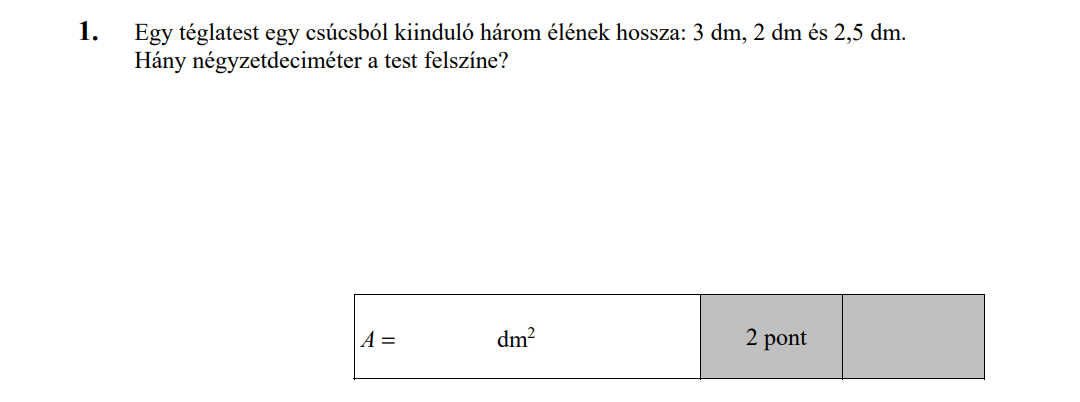






MÁSODIK RÉSZ





- 2019 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ



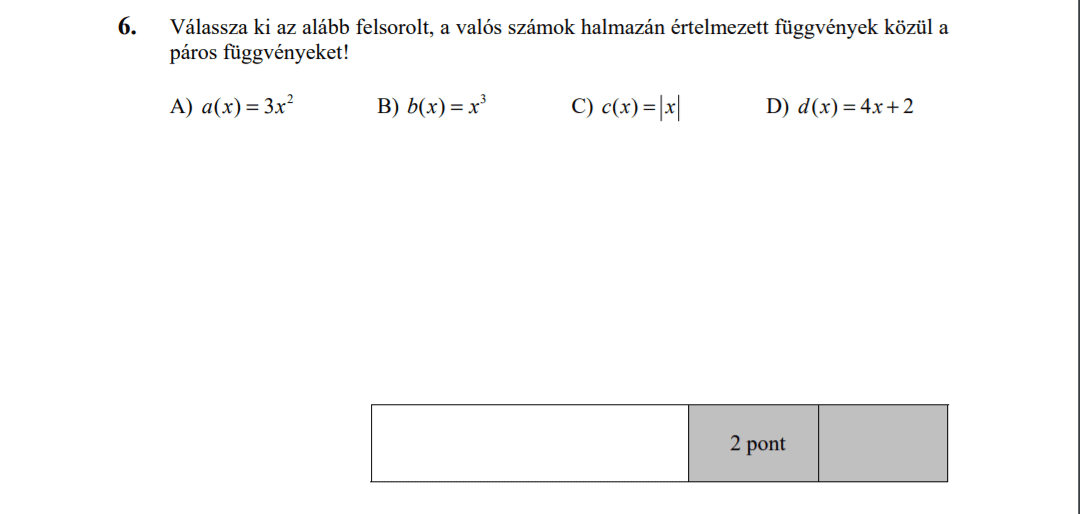
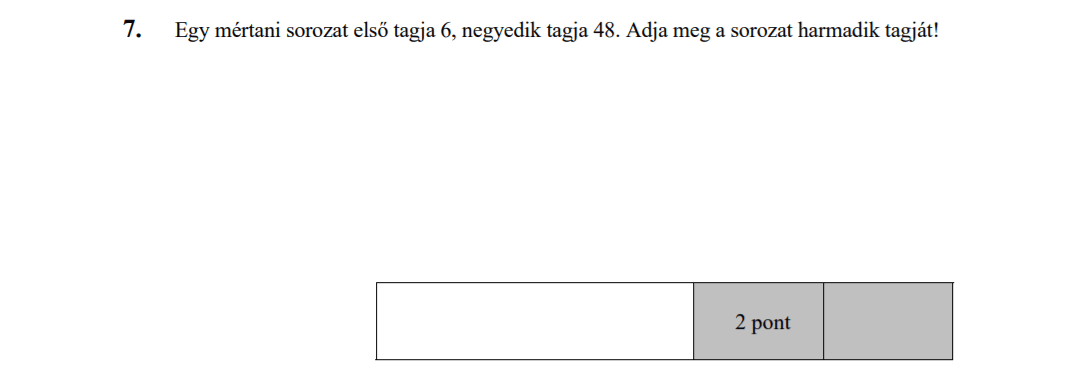



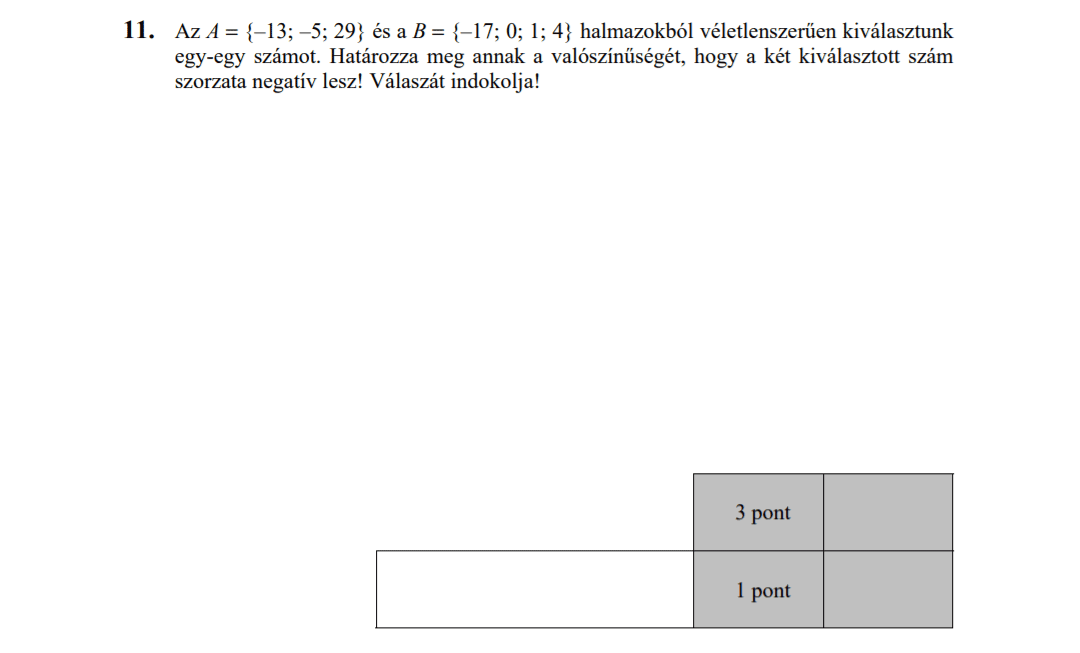

MÁSODIK RÉSZ


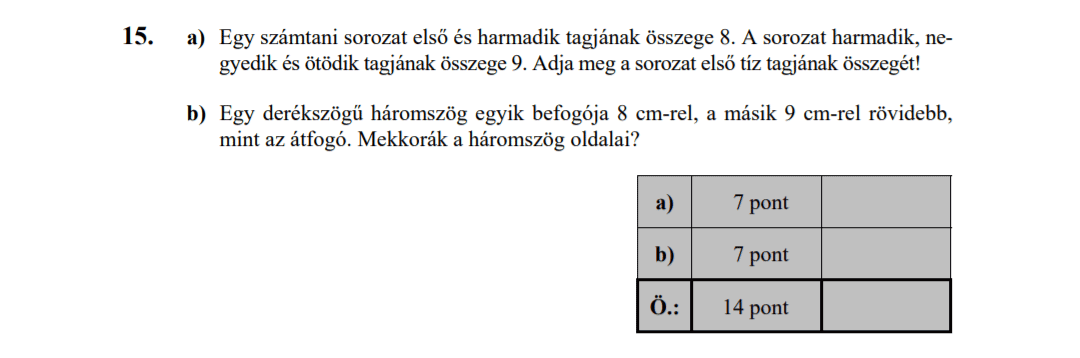



- 2019 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ





- 2018 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ










MÁSODIK RÉSZ





- 2018 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

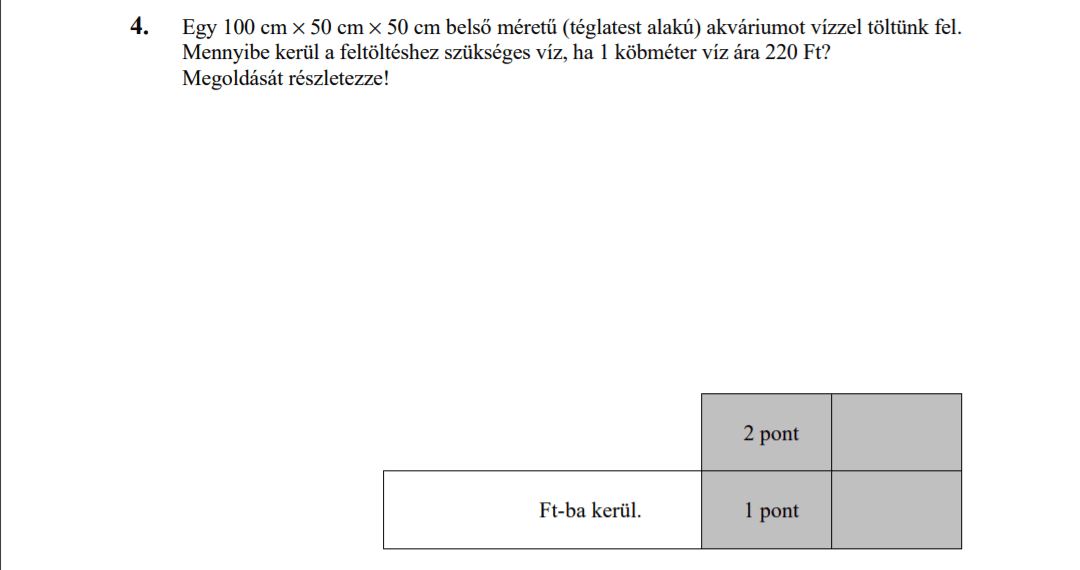
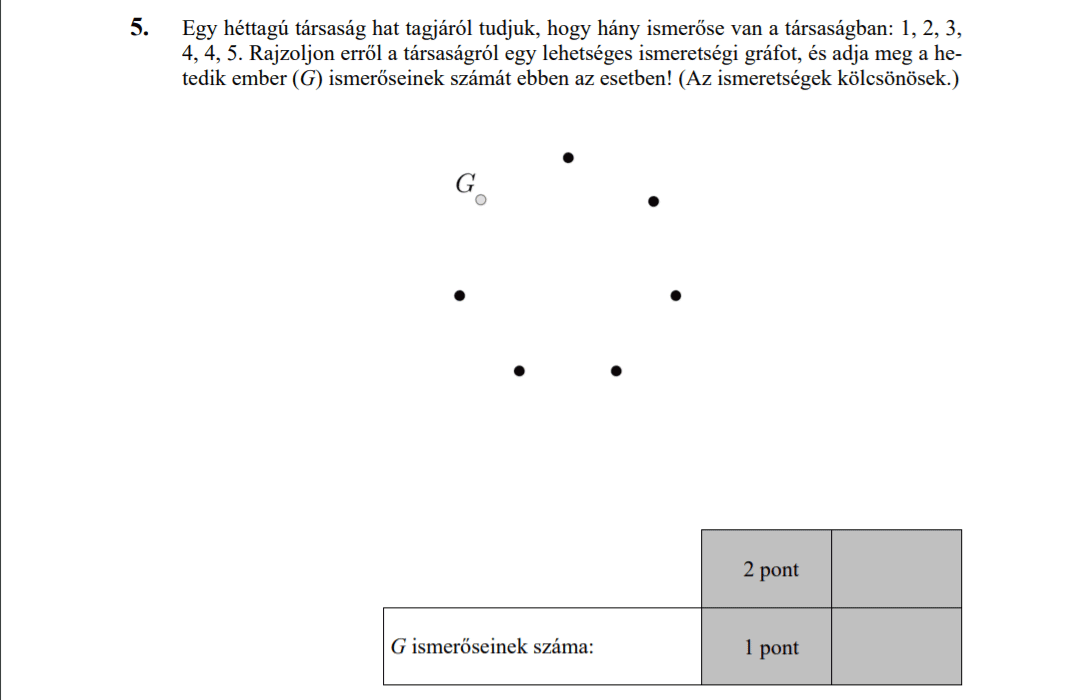







MÁSODIK RÉSZ
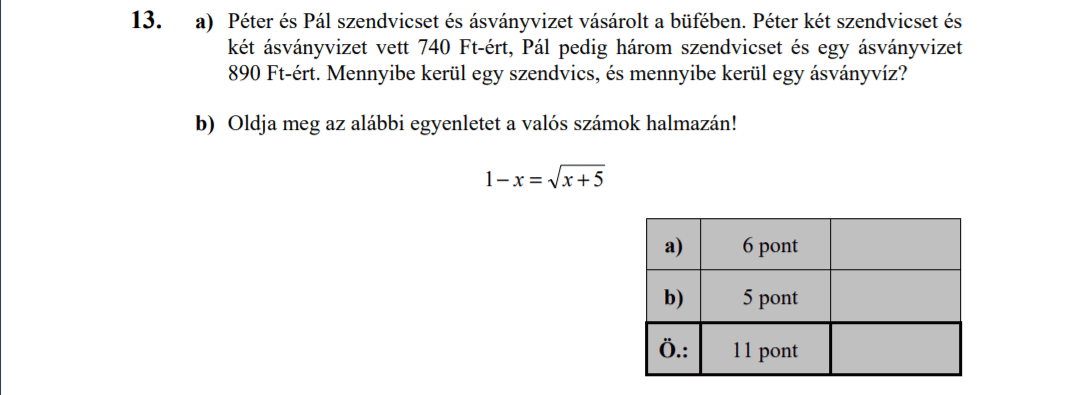
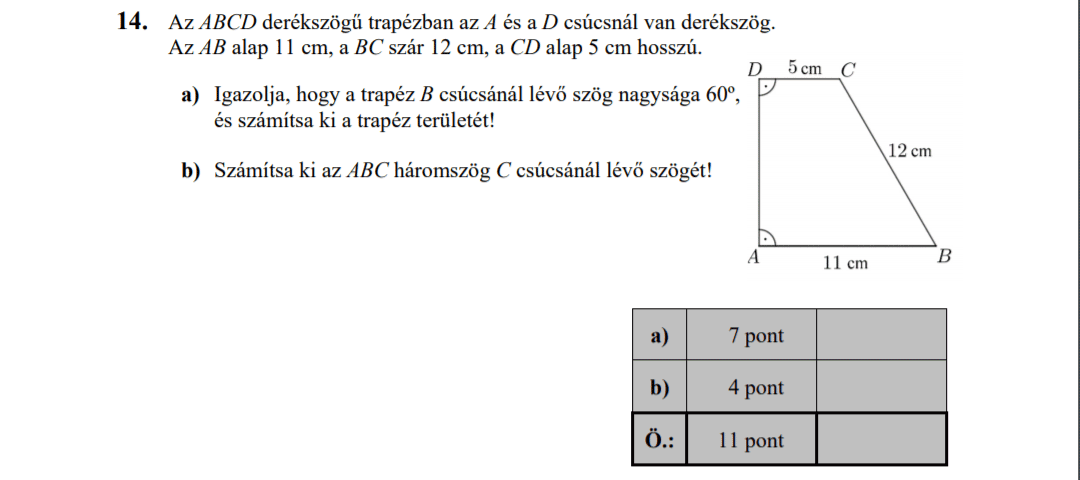



- 2017 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




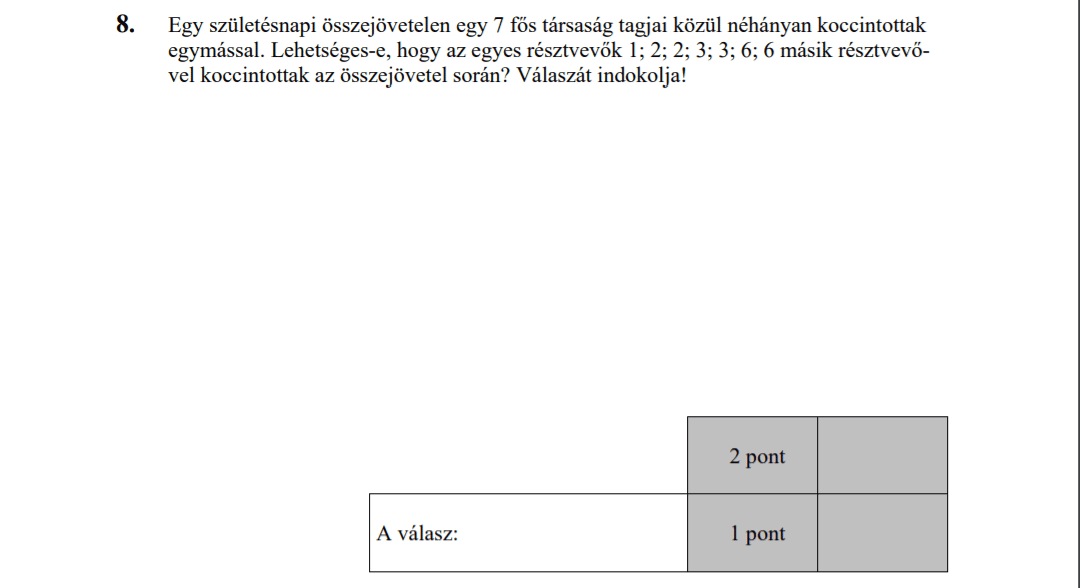



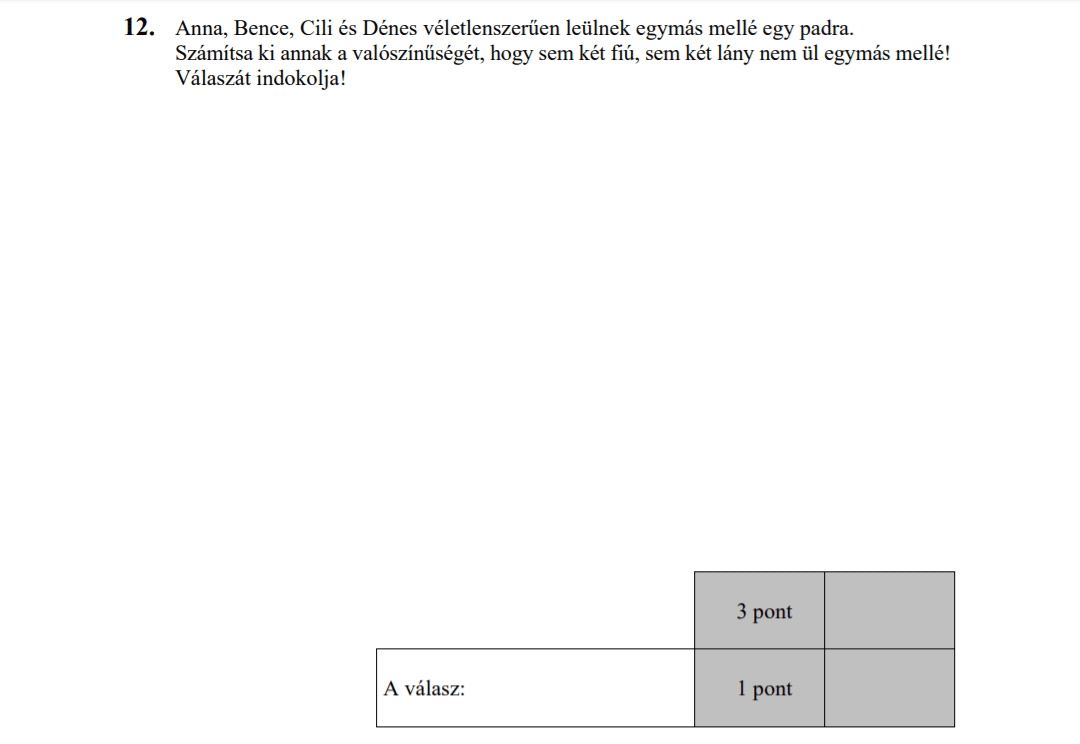
MÁSODIK RÉSZ

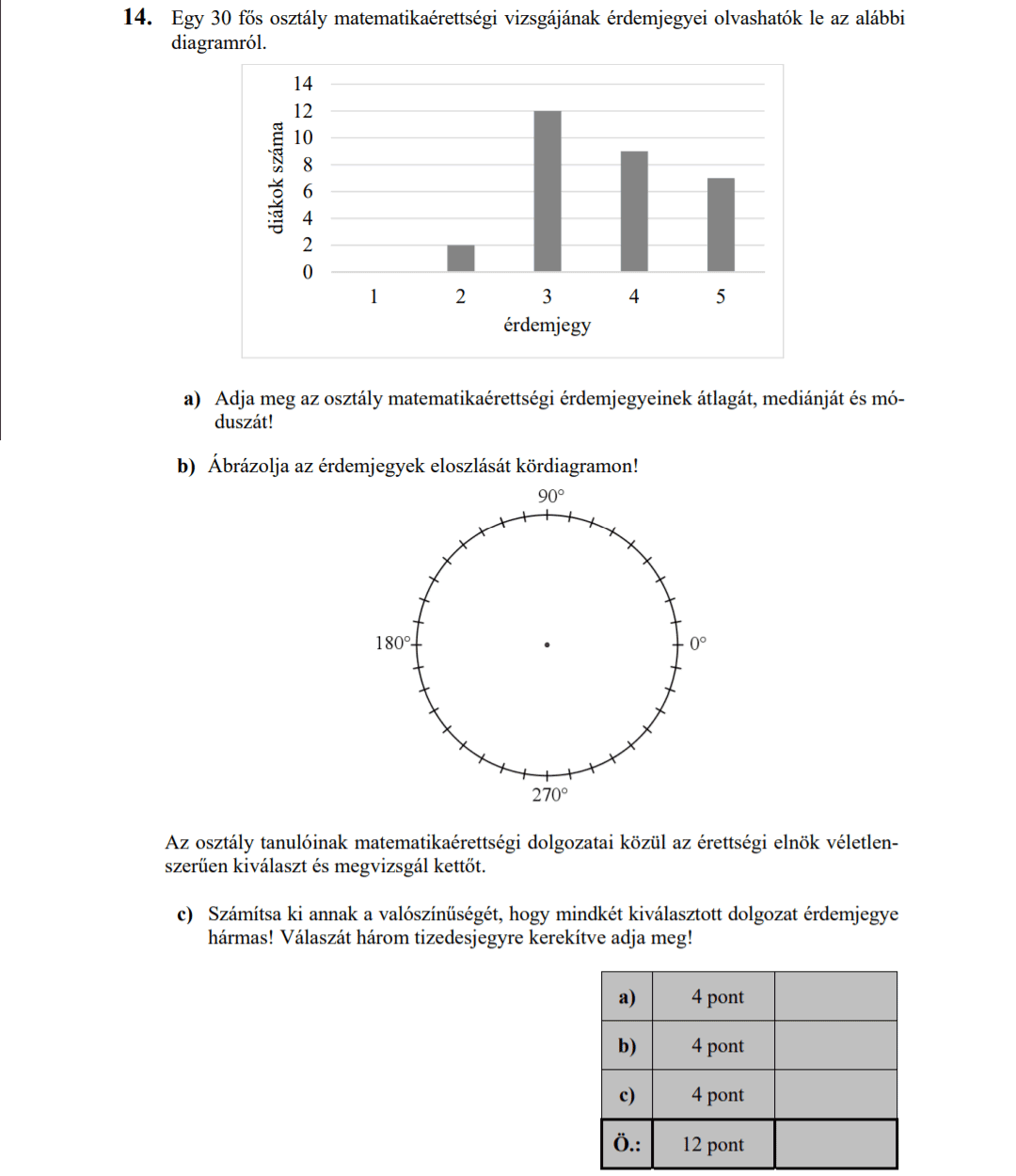
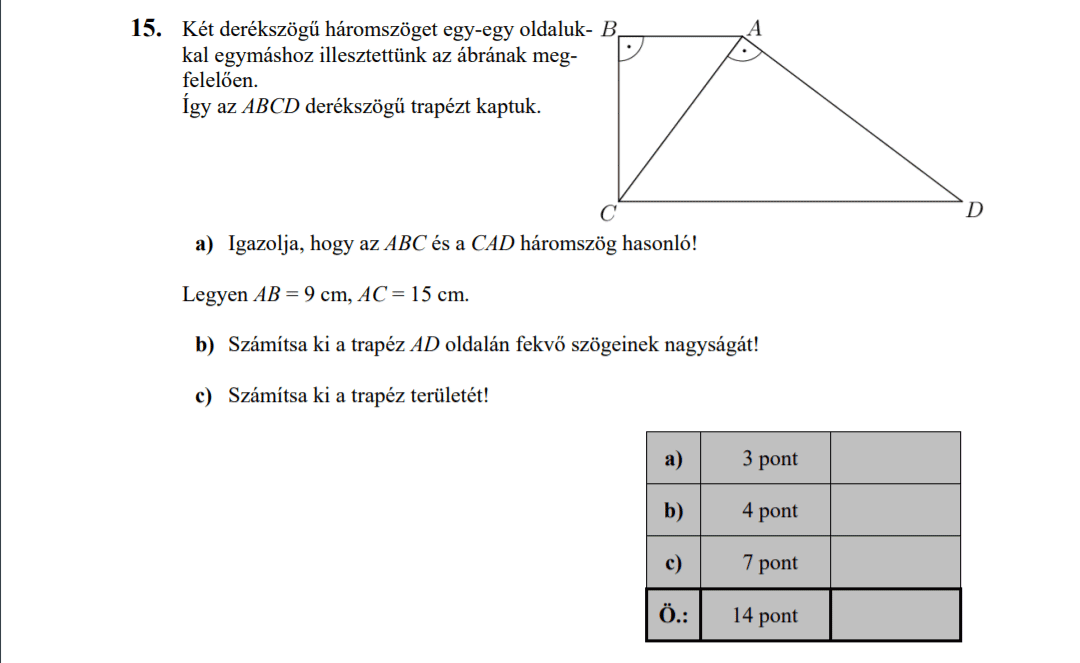



- 2017 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ






- 2016 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




MÁSODIK RÉSZ






- 2016 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ






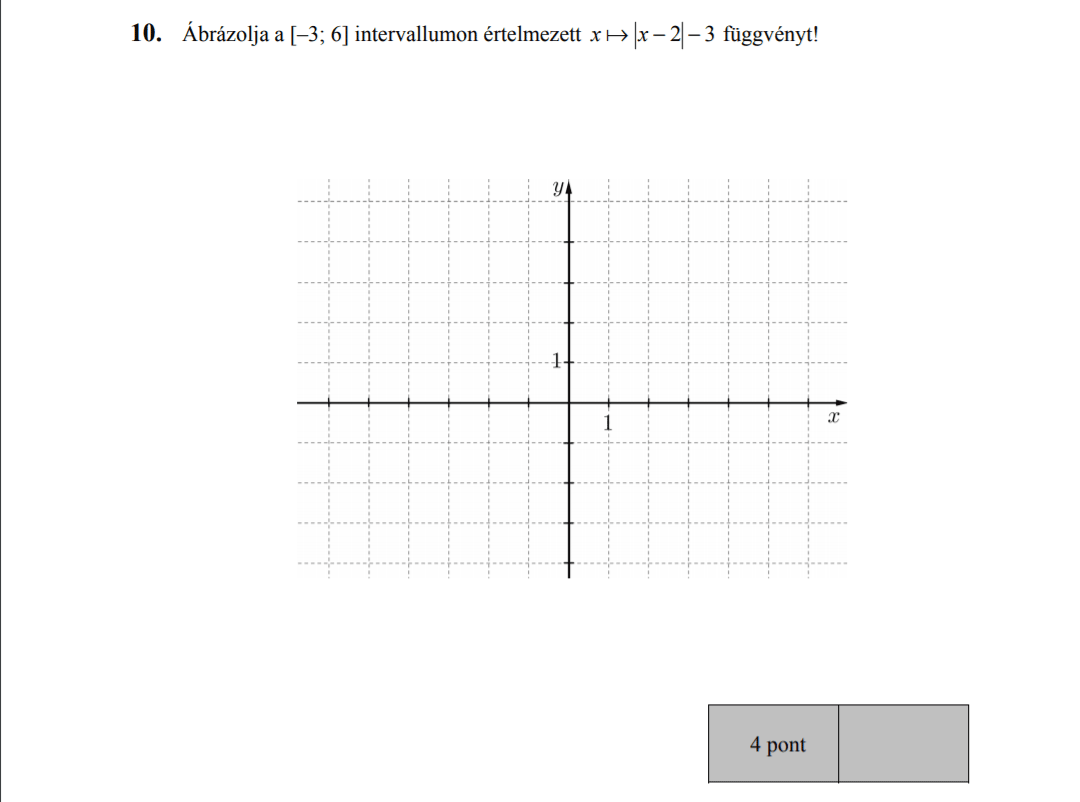

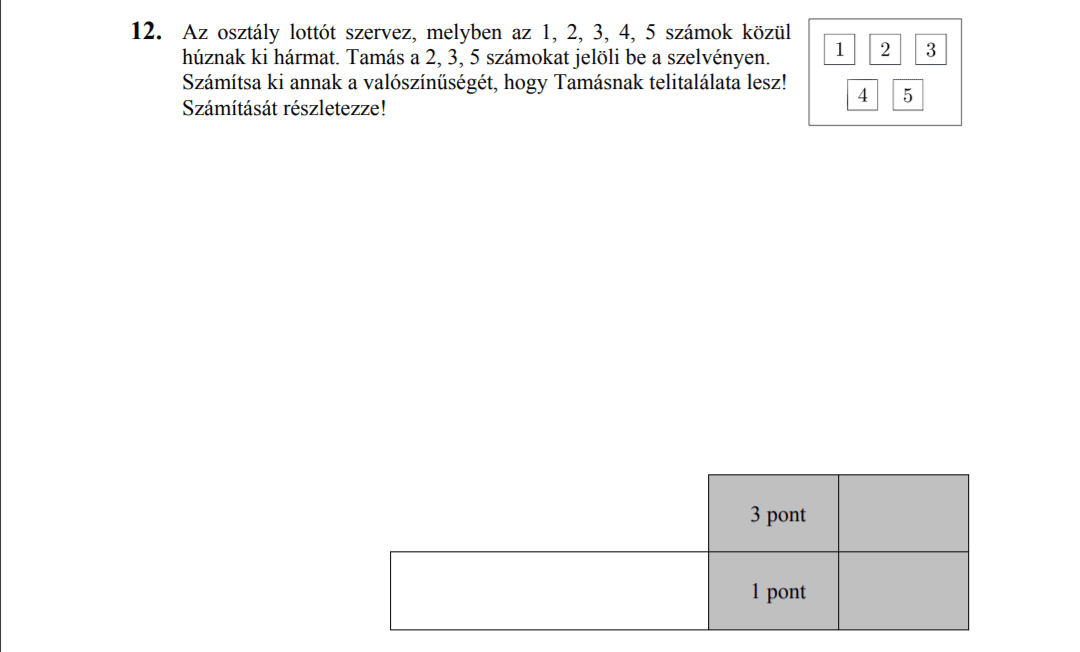
MÁSODIK RÉSZ

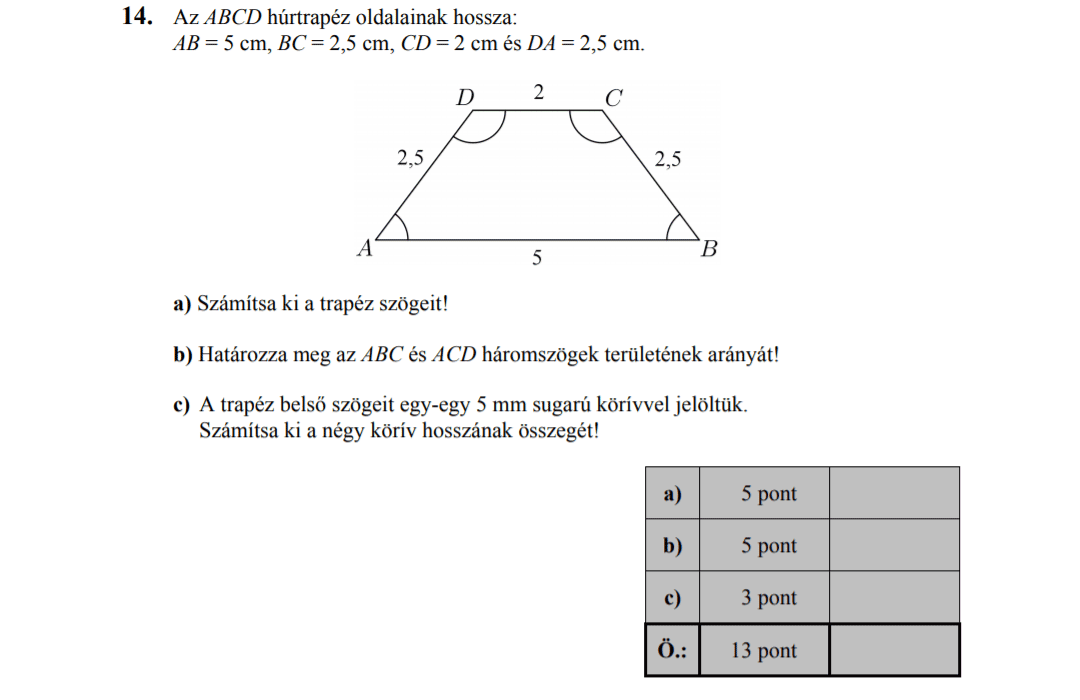

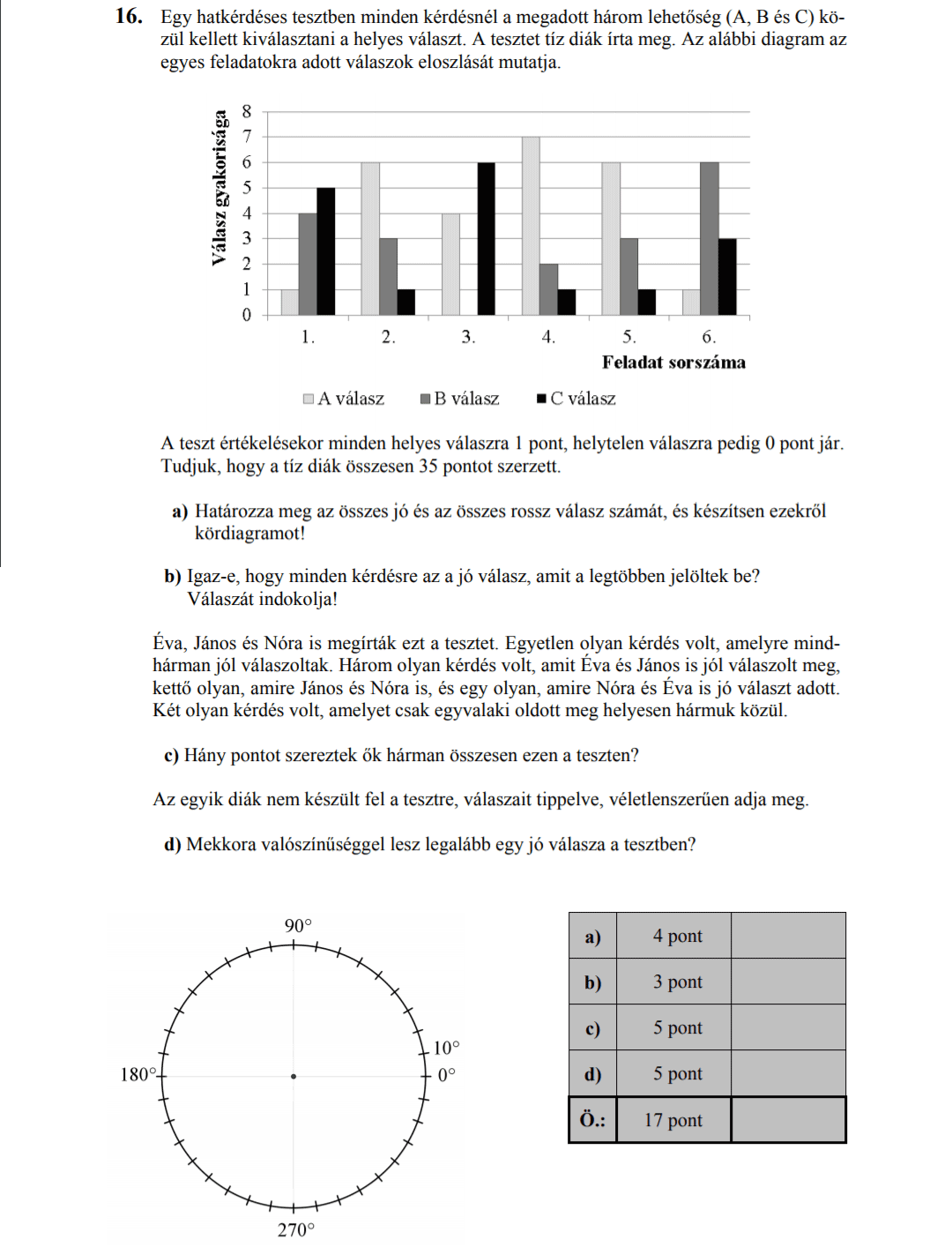


- 2015 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ

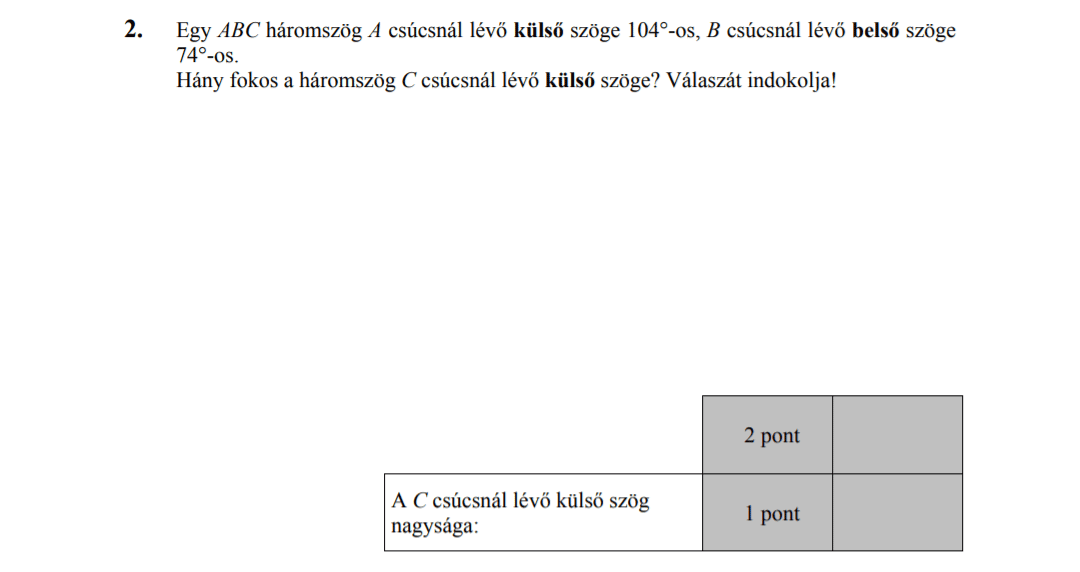





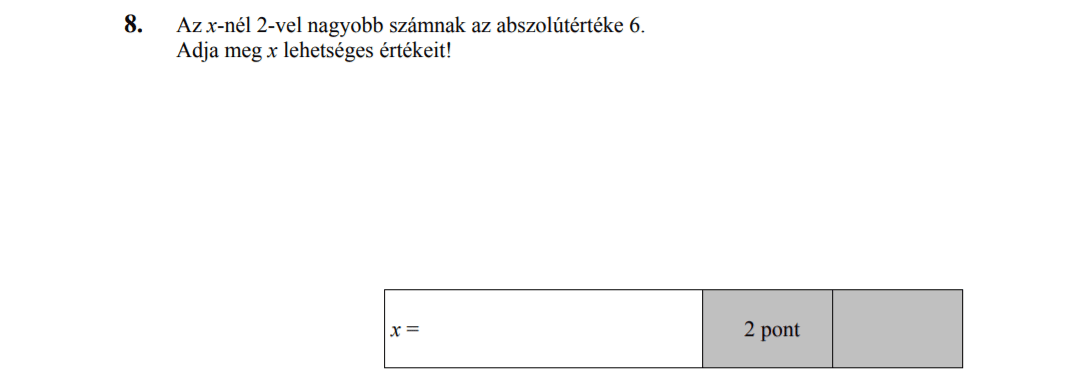

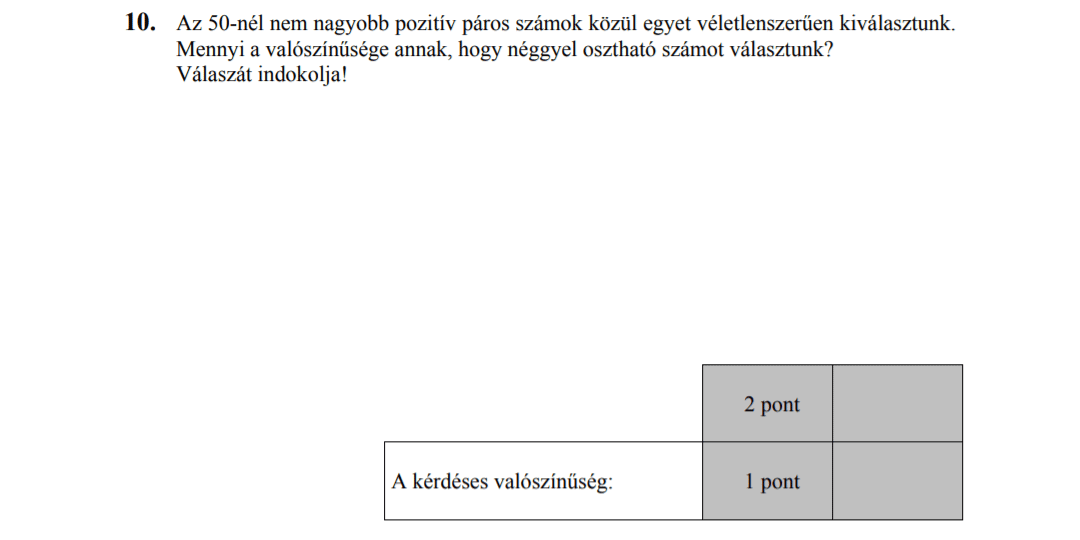


MÁSODIK RÉSZ

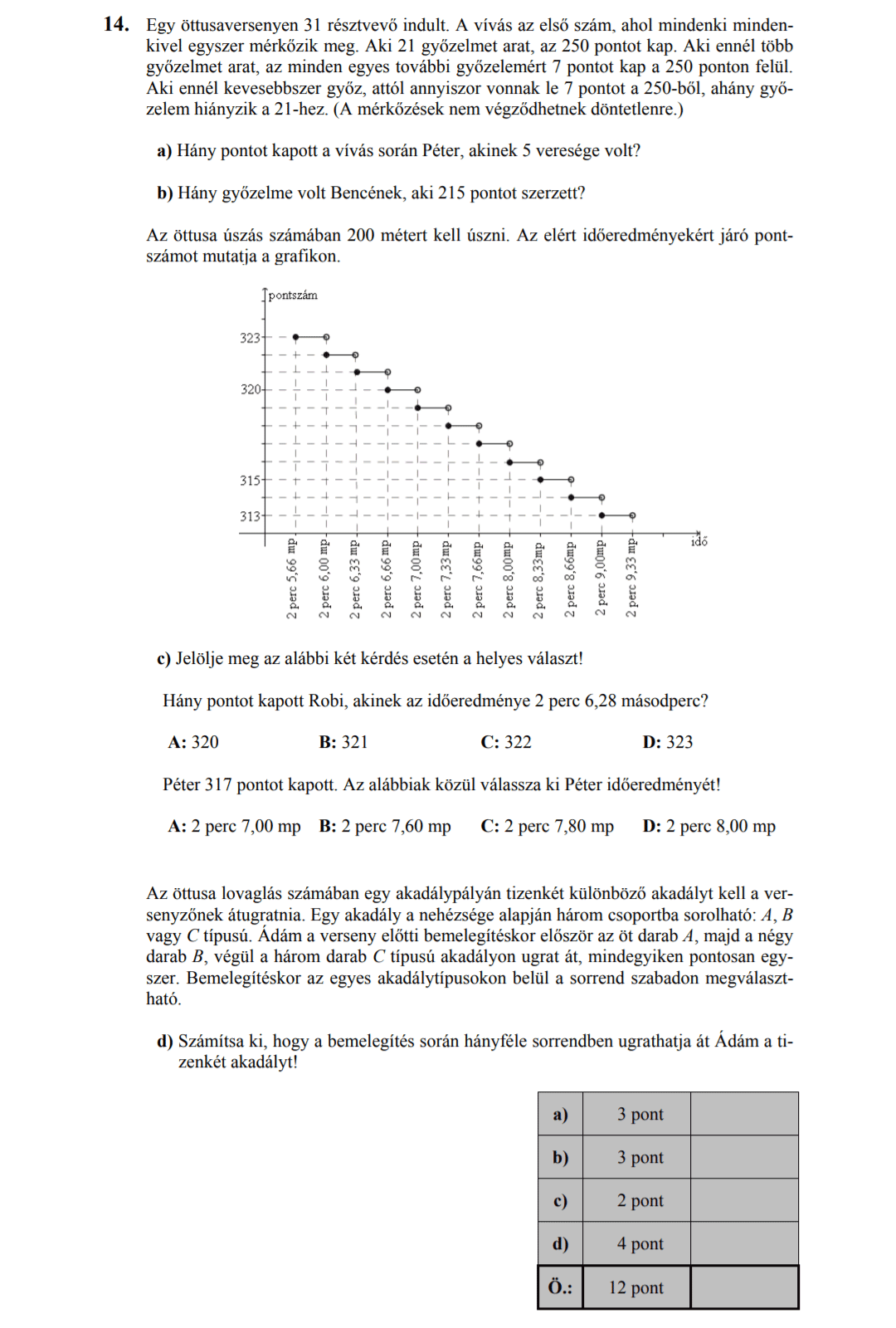



- 2015 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







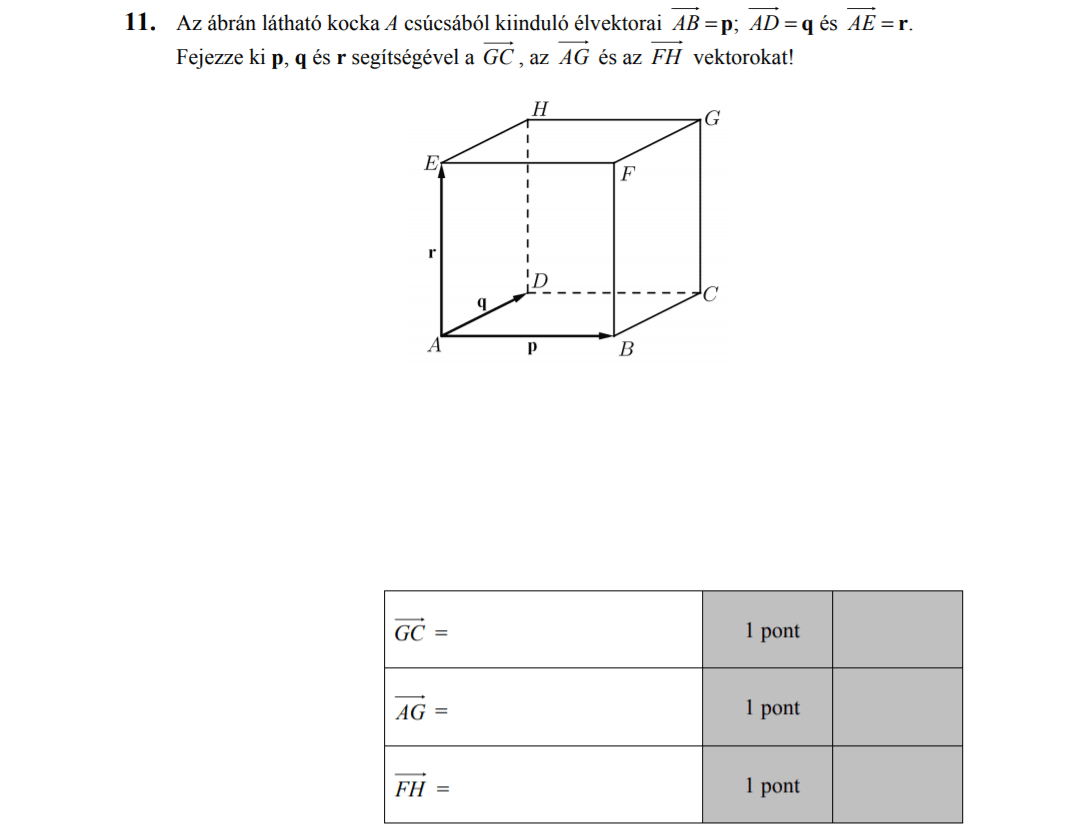
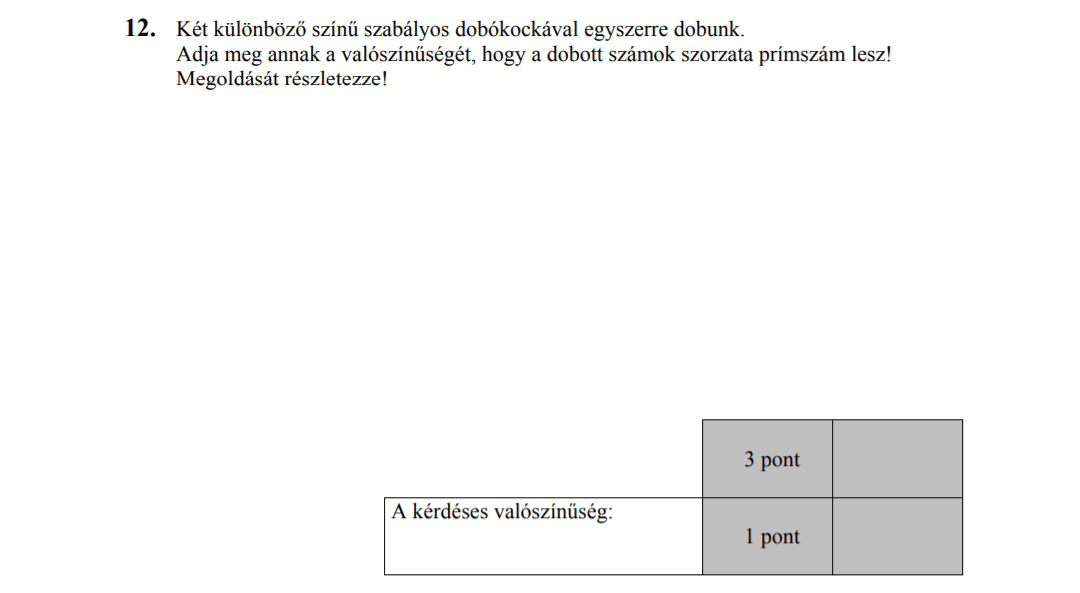
MÁSODIK RÉSZ
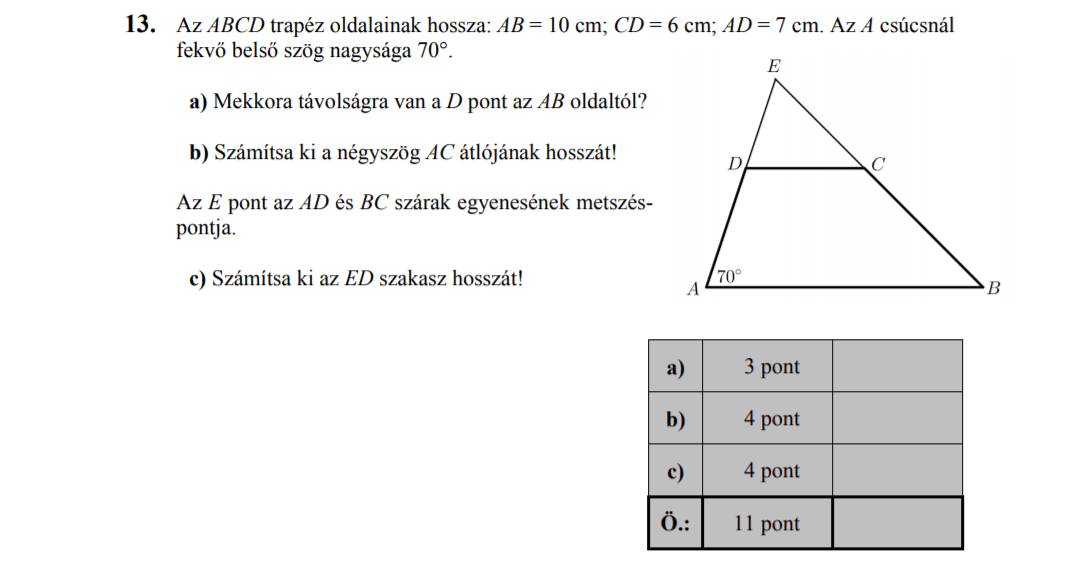





- 2014 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ


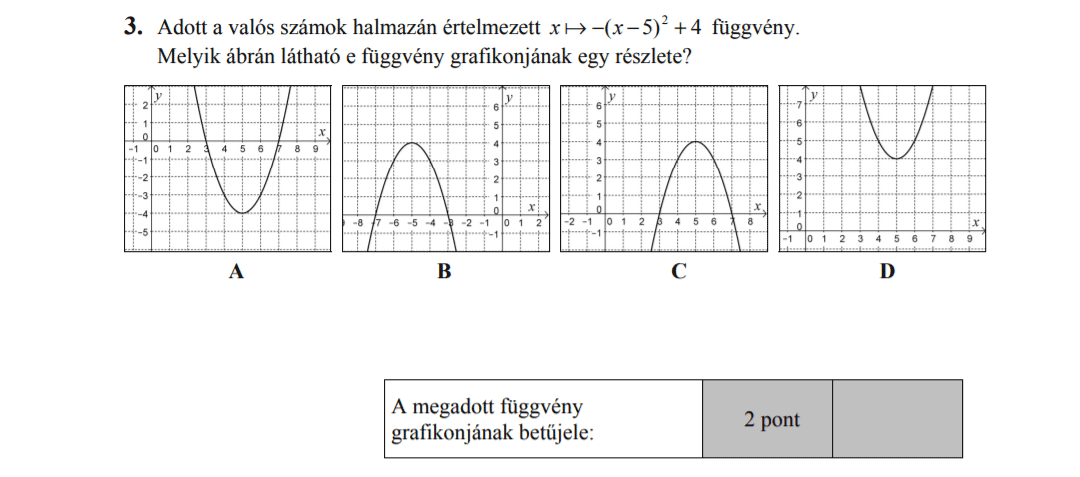








MÁSODIK RÉSZ




- 2014 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ




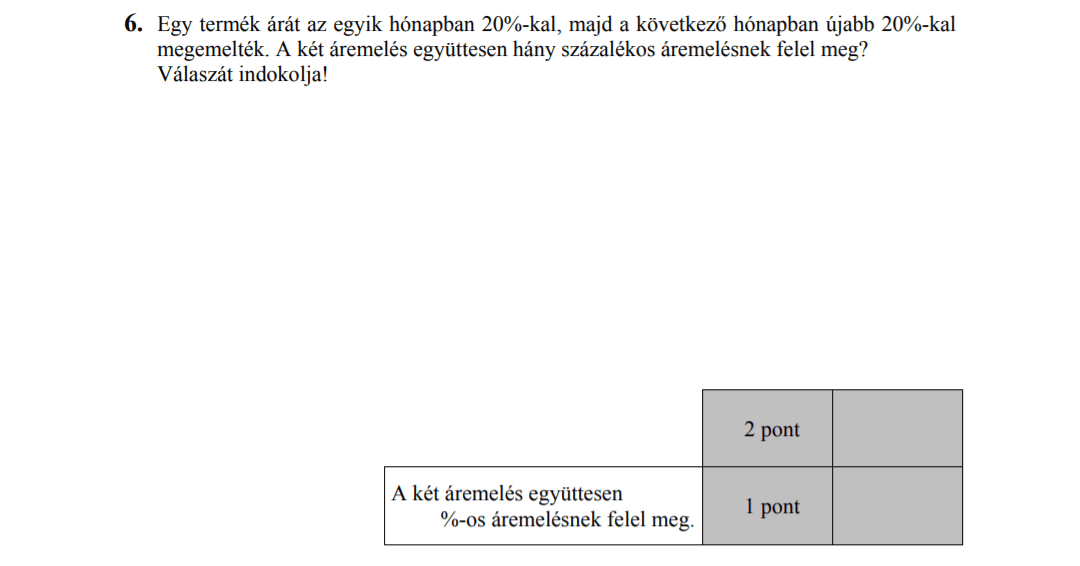
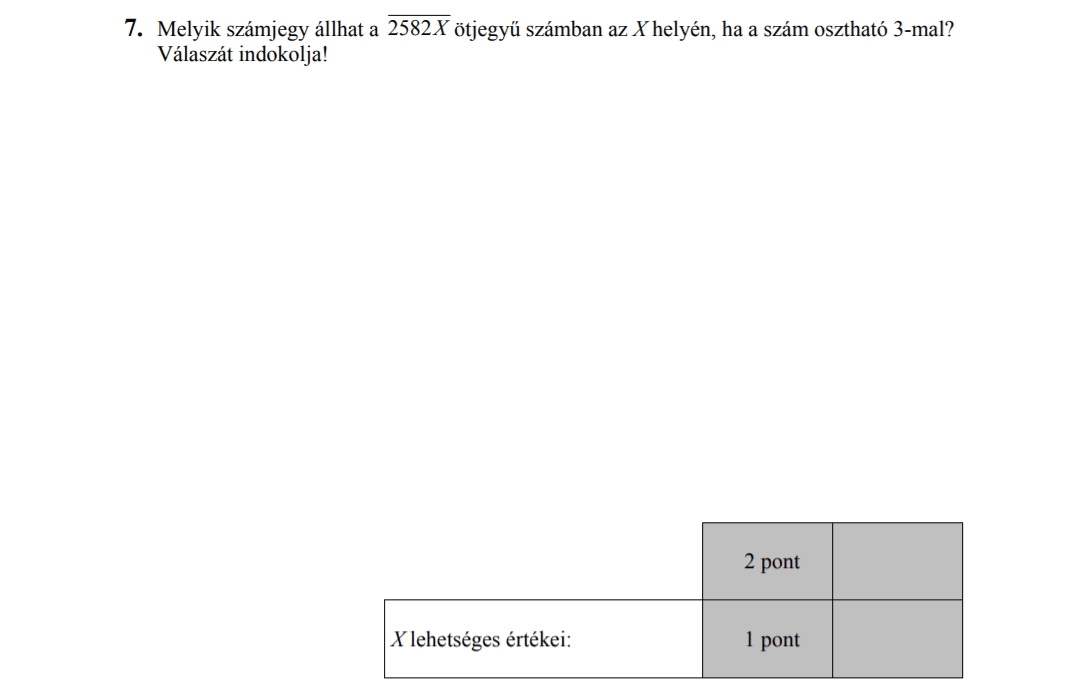
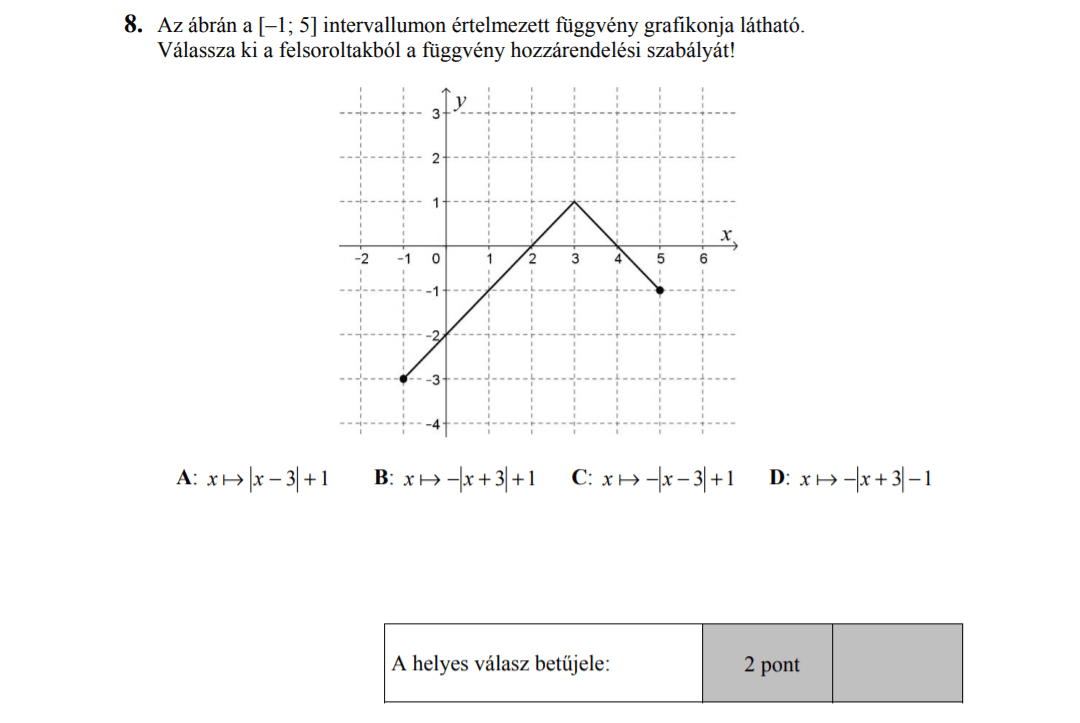


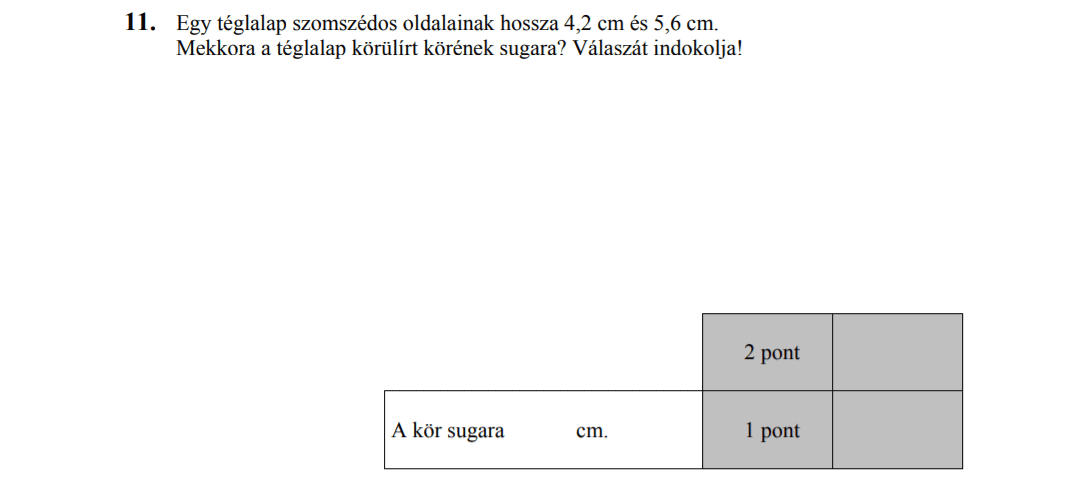

MÁSODIK RÉSZ






- 2013 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ





- 2013 MÁJUSI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ







MÁSODIK RÉSZ





- 2012 OKTÓBERI MATEK ÉRETTSÉGI FELADATOK
-
ELSŐ RÉSZ








MÁSODIK RÉSZ






Ismétlés nélküli permutáció
Egy adott $n$ elemű halmaz elemeinek egy ismétlés nélküli permutációján az $n$ különböző elem egy sorba rendezését értjük.
$n$ darab különböző elem permutációinak száma:
\( 1 \cdot 2 \cdot 3 \cdot \dots \cdot n = n! \)
Faktoriális
$n$ faktoriálisán az $n$-nél kisebb vagy egyenlő pozitív egész számok szorzatát értjük.
$n! = n \cdot (n-1) \cdot (n-2) \cdot \dots 3 \cdot 2 \cdot 1 $
pl.:
$4!=4\cdot 3\cdot 2 \cdot 1 = 24 $
$5!=5\cdot 4\cdot 3\cdot 2 \cdot 1 = 120 $
$1!=1$
Továbbá definíció szerint $0!=1$.
Ismétlés nélküli variáció
Ha $n$ db. egymástól különböző elem közül kiválasztunk $k$ ($k \leq n$) db.-ot úgy, hogy a kiválasztott elemek sorrendje is számít, akkor az $n$ elem $k$-ad osztályú ismétlés nélküli variációját kapjuk.
$n$ darab különböző elemből kiválasztott $k$ darab elem variációinak száma:
\( n \cdot (n-1) \cdot (n-2) \cdot \dots \cdot (n-k+1) = \frac{n!}{(n-k)!} \)
Ismétlés nélküli kombináció
Ha $n$ különböző elem közül kiválasztunk $k$ ($k \leq n$) db.-ot úgy, hogy a kiválasztott elemek sorrendjére nem vagyunk tekintettel, akkor $n$ elem $k$-ad osztályú ismétlés nélküli kombinációját kapjuk.
$n$ darab különböző elem közül kiválasztott $k$ darab elem kombinációinak száma:
\( \binom{n}{k} = \frac{ n!}{ k! (n-k)!} \)
Ismétléses permutáció
Ha $n$ elem között van $k_1, k_2, \dots, k_r$ egymással megegyező, akkor az elemek egy sorba rendezését ismétléses permutációnak nevezzük.
$n$ elem közötti $k_1, k_2, \dots, k_r$ egymással megegyező ismétléses permutációinak száma:
\( \frac{n!}{k_1! \cdot k_2 \cdot \dots \cdot k_r!} \)
Ismétléses variáció
Ha $n$ db. egymástól különböző elem közül kiválasztunk $k$ db.-ot úgy, hogy a kiválasztott elemek sorrendje is számít és ugyanazt az elemet többször is választhatjuk, akkor az $n$ elem $k$-ad osztályú ismétléses variációját kapjuk.
Az $n$ elem $k$-ad osztályú ismétléses variációk száma: $n^k$.
Ciklikus permutáció
Ha kör alakban helyezünk el $n$ különböző elemet és azok sorrendjét vizsgáljuk, akkor ciklikus permutációról beszélünk.
$n$ darab különböző elem ciklikus permutációinak száma $\frac{n!}{n} = (n-1)!$
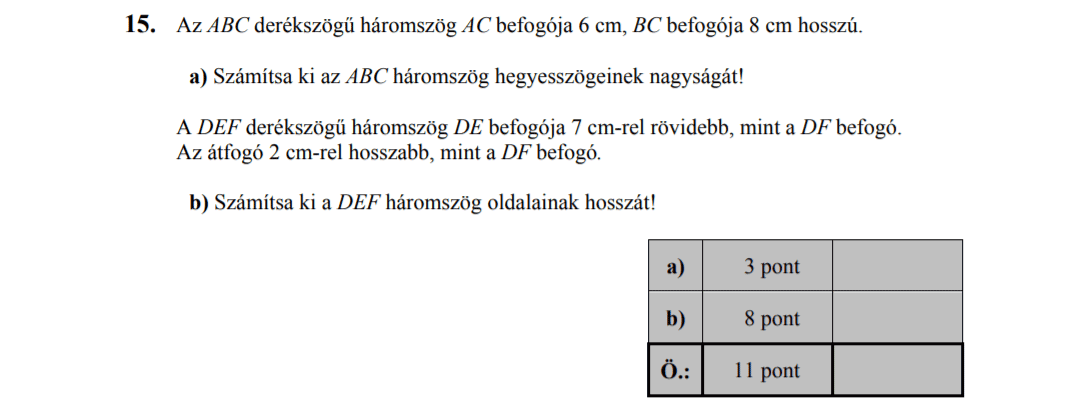
a) Egy futóverseny döntőjében 3 versenyző ér célba leghamarabb. Hányféle sorrendben érkezhetnek be?
b) Egy másik futóversenyen 6-an kerültek a döntőbe. Hányféle sorrendben érkezhetnek célba?
c) Egy másik futóversenyen 6-an kerültek a döntőbe. Hányféle sorrend lehet, ha tudjuk, hogy a svájci versenyző ér először célba?
d) Egy másik futóversenyen 6-an kerültek a döntőbe. Hányféle sorrend lehet, ha tudjuk, hogy a svájci versenyző a negyedik?
e) Egy másik futóversenyen 6-an kerültek a döntőbe. Hány olyan sorrend van, amikor a német az első és a francia a negyedik?
f) Egy másik futóversenyen 6-an kerültek a döntőbe. Hányféleképp érhet célba a legjobb három versenyző?
a) Hányféleképp érhet célba hét versenyzőből a legjobb három?
b) Itt vannak ezek a számjegyek: 1 2 3 4 5 6 7 8 9.
Hányféle ötjegyű számot tudunk készíteni belőlük, ha minden számjegyet csak egyszer használhatunk föl?
Hány olyan ötjegyű számot tudunk készíteni belőlük, amiben a harmadik számjegy 7-es, ha minden számjegyet csak egyszer használhatunk föl?
Hány olyan ötjegyű számot tudunk készíteni belőlük, amiben a harmadik számjegy páros, ha minden számjegyet csak egyszer használhatunk föl?
a) Bob őrülten rajong a modern művészetekért, és elhatározza, hogy festeget egy kicsit... Minden festményét két színnel készíti el, a színeket pedig 9 lehetséges szín közül választja ki. Hányféleképpen tud két színt kiválasztani?
b) Bob 36 darab képe közül 4-et kiállítanak egy múzeumban. Hányféleképp lehet kiválasztani a 36 darab kép közül azt a 4-et amit kiállítanak?
c) Egy másik kiállítás megnyitóján 24 festő volt jelen, akiknek a képeit kiállították. A megnyitón a 24 festő mindegyike mindegyik másik festővel koccint. Hány koccintás történt?
a) Hányféleképpen ülhet le öt ember egymás mellé a padon?
b) Hányféleképpen ülhet le öt ember közül három egymás mellé a padon?
c) Hányféleképpen választhatunk ki öt ember közül hármat?
d) Hányféle hatjegyű szám alkotható az 1, 2, 3, 4, 5, 6 számjegyekből, ha mindegyiket csak egyszer használhatjuk fel? És ha mindegyik számjegyet többször is felhasználhatjuk?
e) Egy buszon 20-an utaznak, és az öt megállója során végül minden utas leszáll. Hányféleképpen tehetik ezt meg?
f) Egy nyereményjátékon 20 ember között kisorsolnak 5 ajándékot. Hányféleképpen lehetséges ez, ha a nyeremények különbözőek, és egy ember csak egyet kaphat?
a) Hányféleképpen ülehet le öt ember egy kerek asztal köré?
b) Az 1, 1, 1, 2, 3, 4, 4 számjegyek sorrendjének variálásával 7 jegyű számokat készítünk. Hányféle ilyen szám van? Hány ilyen páros szám van?
c) A 0, 1, 2, 3, 4, 5, 6 számjegyek felhasználásával 4 jegyű számokat készítünk úgy, hogy egy jegyet akárhányszor felhasználhatunk. Hányféle ilyen szám van? Hány ilyen páros szám van? Hány ilyen 10-zel osztható szám van?
d) A 0, 1, 2, 3, 4, 5, 6 számjegyek felhasználásával 4 jegyű számokat készítünk úgy, hogy egy jegyet csak egyszer használhatunk. Hányféle ilyen szám van? Hány ilyen páros szám van? Hány ilyen 10-zel osztható szám van?
a) Tíztagú társaság raftingolni indul egy ötszemélyes egy háromszemélyes és egy kétszemélyes csónakkal. Hányféleképpen ülhetnek a csónakba, ha a csónakokon belül a helyek között nem teszünk különbséget? Mi a helyzet akkor, ha két adott ember egy csónakba akar kerülni?
b) A 1, 2, 3, 4, 5, 6, 7, 8, 9 számjegyek felhasználásával 4 jegyű számokat készítünk úgy, hogy egy jegyet csak egyszer használhatunk. Hány olyan szám keletkezik, amelyben két páros és két páratlan számjegy szerepel?
b) A 1, 2, 3, 4, 5, 6, 7, 8, 9 számjegyek felhasználásával 4 jegyű számokat készítünk úgy, hogy egy jegyet csak egyszer használhatunk. Hány olyan szám készíthető amiben szerepel a 9-es számjegy?
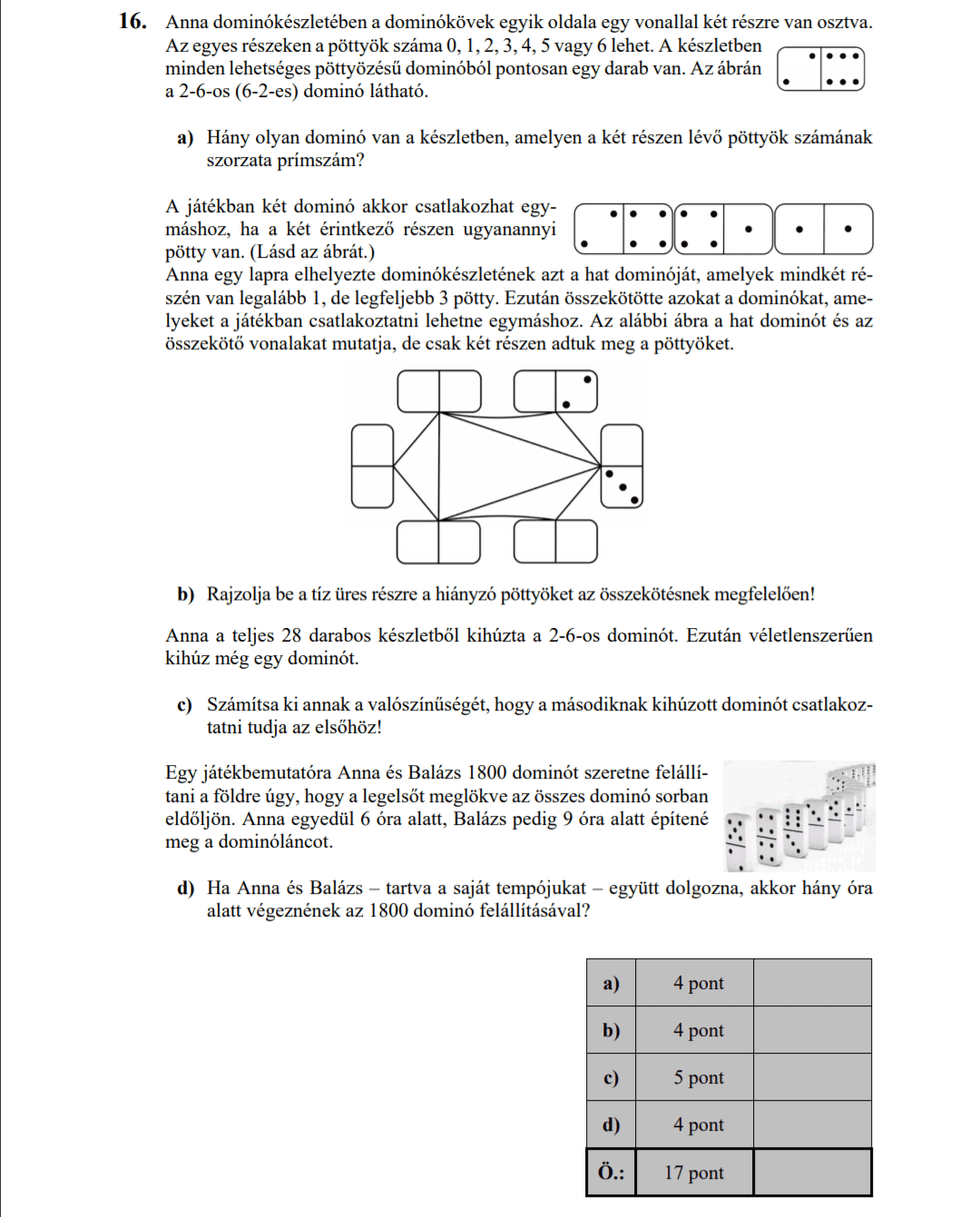
a) Egy dominókészlet azonos méretű dominókból áll. Minden dominó egyik oldala egy vonallal két részre van osztva. Az egyes részeken elhelyezett pöttyök száma 0-tól 6-ig bármi lehet. Minden lehetséges párosításnak léteznie kell, de két egyforma nem lehet egy készletben. Hány darabból áll egy dominókészlet?
b) Egy állatkert beszerez 4 hím és 5 nőstény oroszlánt, melyeket egy kisebb és egy nagyobb kifutóban kívánnak elhelyezni a következő szabályok mindegyikének betartásával:
1) Háromnál kevesebb oroszlán egyik kifutóban sem lehet.
2) A nagyobb kifutóba több oroszlán kerül, mint a kisebbikbe.
3) Mindkét kifutóban hím és nőstény oroszlánt is el kell helyezni.
4) Egy kifutóban sem lehet több hím, mint nőstény.
Hányféleképpen helyezhetik el a 9 oroszlánt a két kifutóban?
Színezzük ki Svájcot és a vele határos országokat úgy, hogy két szomszédos ország nem lehet egyforma színű. Hányféleképpen lehet így szinezni?
Egy 8 fős baráti társaság vonattal utazik nyaralni. Útközben szeretnének beszélgetni, ezért két egymás melletti négyes blokkba szeretnének ülni, ahol asztal is van.
a) Hányféleképpen tudnak leülni egy kocsin belül?
b) Hányféleképpen tudnak leülni úgy, hogy Anna és Bálint egymással szemben és ablak mellé üljenek?
c) Hányféleképpen tudnak leülni úgy, hogy Anna és Bálint egymás mellett, és Anna ablak mellett üljön?
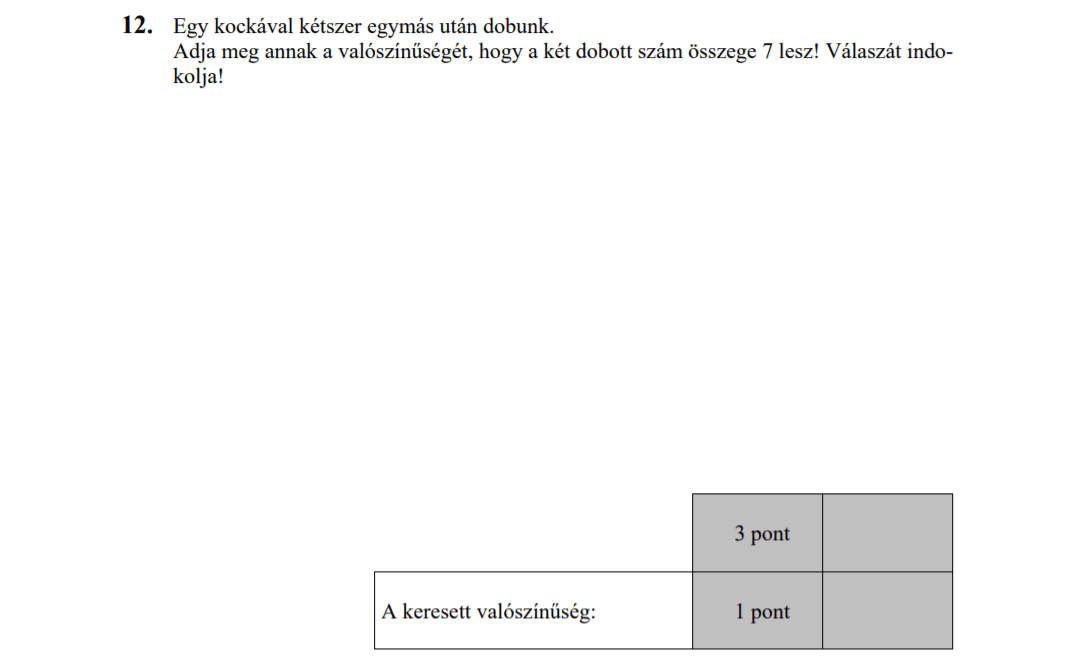
Van öt különböző színű dobókockánk, egy sárga, egy piros, egy kék, egy zöld és egy rózsaszín. Sorban egymás után mindegyik dobókockával egyet dobunk.
a) Hányféle sorrendben tudunk dobni a kockákkal úgy, hogy nem a piros kockával kezdünk?
b) Hányféle olyan dobás lehetséges, hogy nem a piros kocka az első és a sárga az utolsó?
c) Hányféle olyan dobás lehetséges, ahol a dobott pontokat is figyelembe vesszük, az első dobás 4-es, az utolsó dobás pedig a piros kockával történik?
Van 3 kék, 3 zöld, 3 sárga és 3 piros színű dobókockánk. Hányféleképpen tudunk kiválasztani közülük 4 kockát úgy, hogy
a) három különböző színű kocka legyen?
b) két különböző színű kocka legyen?
Egy 8 fős baráti társaság vonattal utazik nyaralni. Mivel kicsit későn vették meg a vonatjegyet, olyan hely már nincs, ahol mind a 8-an együtt utazhatnának. Háromfős, kétfős és egyfős helyek vannak még szabadon. Egyedül egyikük sem szeretne utazni, ezért hármas és kettes csoportokban ülnek le a megmaradt helyekre. Hányféleképpen tudnak ilyen csoportokat alkotni?
a) Egy sífutóveresenyen 8-an vesznek részt, mindegyikük más-más országból.
a) A cél előtt nem sokkal már látszik, hogy az utolsó helyen a dán versenyző fog végezni, az első három helyen a svájci, a francia és a norvég fog osztozni, az olasz pedig a negyedik lesz. Hányféleképpen érhetnek célba a versenyzők?
b) Hányféleképpen érhet célba a 8 versenyző, ha annyit tudunk, hogy nem a svájci fog nyerni, viszont nem is a svjáci az utolsó?
Egy konferenciára öt országból érkeznek résztvevők, Svájcból, Franciaországból, Ausztriából, Németországból és Oroszországból. Egy szállodában négy résztvevő száll meg, és amikor megérkezik, kiteszik az országának megfelelő zászlót a szállodára (ha esetleg két résztvevő is ugyanabból az országból érkezik, akkor is csak egy zászlót tesznek ki). Hányféleképpen tudják kitenni a zászlókat, ha a zászlók sorrendje nem számít?
Tíz különböző szín felhasználásával hányféle különböző 6 cikkelyből álló esernyő készíthető, ahol
a) minden cikkely más színű?
b) két szín ismétlődik felváltva?
c) az egyik szín kétszer szerepel, de nem szomszédos cikkelyen, a többi szín csak egyszer?
Egy társaságban van 5 férfi és 5 nő. Hányféleképpen tudnak leülni egy kör alakú asztal köré, ha
a) férfiak és nők felváltva ülnek?
b) az egyik férfi mindenképpen egy adott nő mellett szeretne ülni?
c) két ember a társaságban semmiképpen nem szeretne egymás mellett ülni?
d) férfiak és nők felváltva ülnek és egy férfi semmiképpen nem szeretne egy adott nő mellett ülni.
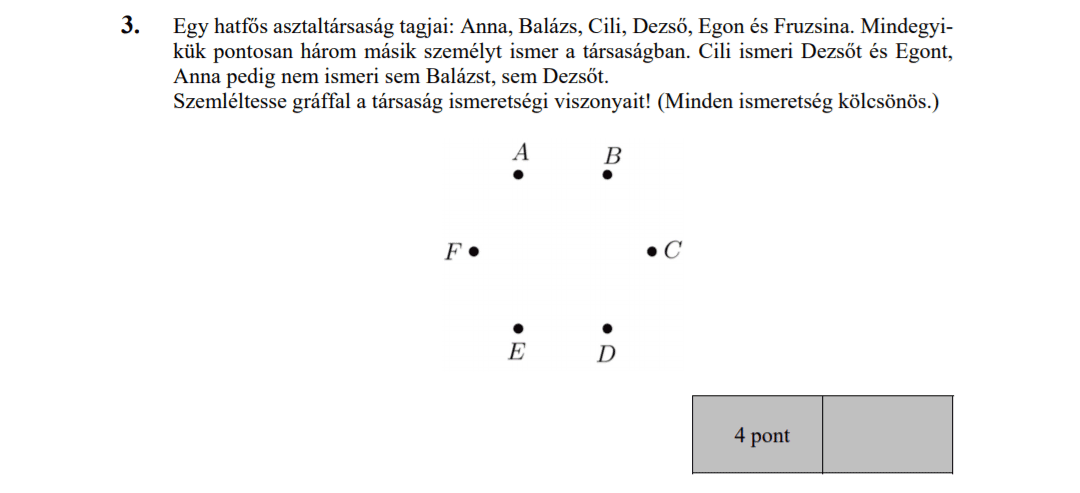
Egy nyomozás során egy hattagú társaság (A, B, C, D, E, F) tagjait 3 fős csoportokban hallgatják ki. Minden olyan 3 fős csoport kihallgatását megszervezik, amelyben A és B együtt nincs jelen. Összesen hány ilyen csoportos kihallgatást kell szervezni?
Egy séf új ízek kitalálásán kísérletezik. Az ételek ízesítéséhez hatféle fűszer áll rendelkezésére: keserű, savanyú, édes, sós, csípős és fanyar. Hányféleképp ízesítheti az ételeket, hogyha a hatból három- vagy négyféle fűszert szeretne használni, de az édes és keserű nem szerepelhet egyszerre?
A 0, 1, 2, 3, 4, 5, 6, 7 számjegyek felhasználásával leírtuk az összes különböző számjegyből álló négyjegyű számot. Hány olyan van ezek között, amelyben a számjegyek összege 16?
Anna, Laura, Hanna és Zoé együtt mentek moziba. Mozijegyük négy egymás melletti helyre szólt.
a) Hányféle sorrendben ülhetnek le a négy egymás melletti helyre?
b) Hányféle sorrendben ülhetnek le a négy egymás melletti helyre, ha Anna és Laura nem ültek egymás mellé?
c) A mozi után beültek egy pizzériába egy kerek asztal köré. Hányféleképp ülhettek le?
Hányféle különböző számot kaphatunk a 222 335 szám számjegyeinek felcserlésével?
Hány olyan háromjegyű szám képezhető az 1, 2, 3, 4, 5 számjegyekből, amelyikben csupa különböző számjegyek szerepelnek?
Hány olyan háromjegyű szám képezhető az 1, 2, 3, 4, 5 számjegyekből, amelyikben csupa különböző számjegyek szerepelnek?
A szóbeli érettségi vizsgán egy osztály 35 tanulója közül az első csoportba öten kerülnek. Hányféle sorrendben felelhet történelemből az 5 kiválasztott diák?
Hány 5-tel osztható ötjegyű szám alkotható a 0, 1, 2, 3, 4, 5 számjegyek felhasználásával?
Hány 4-gyel osztható hétjegyű szám alkotható az 1, 2, 3, 4, 5 számjegyek felhasználásával?
Itt az ideje, hogy készítsünk egy rövid kombinatorikai összefoglalót. Kiderül, hogy mi az a permutáció, kombináció, variáció, sőt, ami még ennél is fontosabb, az is kiderül, hog mikor melyiket kell használni. Van n darab elem mindet kiválasztjuk kiválasztunk közülük k darabot a sorrend számít a sorrend nem számít PERMUTÁCIÓ n darab különböző elem permutációinak száma: mese: Hányféleképpen ülhet le öt ember egymás mellé egy padon? Permutációból van ismétléses permutáció és ismétlés nélküli permutáció. Most az ismétlés nélküli permutációt nézzük, az ismétléses permutáció egy másik epizódban lesz. VARIÁCIÓ n darab különböző elemből kiválasztott k darab elem permutációinak száma: Hányféleképpen ülhet le öt ember közül három egymás mellé egy padon? Variációból is van ismétléses variáció és ismétlés nélküli variáció. Most az ismétlés nélküli variációval foglalkozunk, de egy másik epizódban jön az ismétléses variáció is. KOMBINÁCIÓ n darab különböző elem közül kiválasztott k darab elem kombinációinak száma: Kombinációból csak az ismétlés nélküli kombinációval fogunk foglalkozni, de azzal nagyon. Hányféleképpen választhatunk ki öt ember közül hármat? Most pedig nézzünk néhány feladatot. Hányféle hatjegyű szám alkotható az 1,2,3,4,5,6 számjegyekből, ha mindegyiket csak egyszer használhatjuk? Az első helyre még bármelyik számjegyet tehetjük… A következő helyre már csak ötfélét. És így tovább… Most nézzük, mi történik akkor, ha vannak a számjegyek közt egyformák. Hány hatjegyű szám alkotható ezekből? Az elv ugyanaz, mint az előbb. És mivel most vannak köztük egyformák… ezért sokkal kevesebb eset lesz. Osztani kell az egyforma elemek faktoriálisaival. Ezt hívjuk ismétléses permutációnak. Lássuk, mi történik akkor, ha nem az összes elemet permutáljuk, csak a kiválasztott elemeket. Készítsünk ötjegyű számokat úgy, hogy egy számjegyet csak egyszer használhatunk. Ha úgy készítünk ötjegyű számokat, hogy minden számjegyet többször is használhatunk… Ezt ismétléses variációnak hívjuk. Az ismétléses variáció meglehetősen alattomos feladatokban is fel szokott bukkanni. Egy buszon 20-an utaznak, és az öt megállója során végül minden utas leszáll. Hányféleképpen tehetik ezt meg? Nos, itt vannak a megállók: Az első megállónál bárki leszállhat, ami húszféle utas. A második megállóban szintén bárki leszállhat, így ez is 20. Namost, ha az első megállóban leszállnak például 4-en… Akkor a másodikban már nem tudnak 20-an leszállni, mert nincs is annyi ember a buszon. De mivel fogalmunk sincs, hányan szállnak le az első megállóban, ezért nem tudjuk milyen számot írjunk a második megállóhoz. Jegyezzük meg, hogy ha egy kombinatorika feladatot nem tudunk megoldani, akkor inkább keressünk egy másik feladatot. Ja, nem. Ne ezt jegyezzük meg… Ha egy kombinatorika feladatot nem tudunk megoldani, akkor fordítsuk meg a hozzárendelést. megálló utas Szóval, itt vannak az utasok: És az első utas leszállhat ötféle helyen… a második utas is leszállhat ötféle helyen, és így tovább. Végül itt jön még egy izgalmas ügy. Egy nyereményjátékon 20 ember között kisorsolnak 5 ajándékot. Hányféleképpen lehetséges ez, ha a)A nyeremények különbözőek, és egy ember csak egyet kaphat? Az első embernek adhatunk ötféle ajándékot. A másodiknak már csak négyfélét… De van itt egy kis gond. Egyáltalán nem biztos, hogy az első ember kapott ajándékot. És, ha nem kapott, akkor a második ember ötfélét kaphat. Megint jönnek a kérdőjelek. És ez bizony nem jó jel… Úgyhogy fordítsuk meg a hozzárendelést. ember nyeremény Az első nyereményt adhatjuk 20-féle embernek. A második nyereményt már csak 19-nek. És így tovább… b)A nyeremények különbözőek, de egy ember többet is kaphat? Az első nyereményt adhatjuk 20-féle embernek. És az összes többit is. c)A nyeremények egyformák, de egy ember csak egyet kaphat? Az első nyereményt adhatjuk 20-féle embernek. Csakhogy itt most nincs első nyeremény. Mert mindegyik nyeremény egyforma. Ezért nem számít a nyeremények sorrendje. Az egyforma ajándékok miatt nem számít a sorrend. Vagyis ez egy kombináció lesz, ahol 20 emberből választunk ki 5 embert. Ezt számológéppel az nCr gomb lenyomásával tudjuk kiszámolni:
Ha egy kombinatorika feladatot nem tudunk megoldani, akkor fordítsuk meg a hozzárendelést. megálló utas Szóval, itt vannak az utasok: És az első utas leszállhat ötféle helyen… a második utas is leszállhat ötféle helyen, és így tovább. Végül itt jön még egy izgalmas ügy. Egy nyereményjátékon 20 ember között kisorsolnak 5 ajándékot. Hányféleképpen lehetséges ez, ha a)A nyeremények különbözőek, és egy ember csak egyet kaphat? Az első embernek adhatunk ötféle ajándékot. A másodiknak már csak négyfélét… De van itt egy kis gond. Egyáltalán nem biztos, hogy az első ember kapott ajándékot. És, ha nem kapott, akkor a második ember ötfélét kaphat. Megint jönnek a kérdőjelek. És ez bizony nem jó jel… Úgyhogy fordítsuk meg a hozzárendelést. ember nyeremény Az első nyereményt adhatjuk 20-féle embernek. A második nyereményt már csak 19-nek. És így tovább… b)A nyeremények különbözőek, de egy ember többet is kaphat? Az első nyereményt adhatjuk 20-féle embernek. És az összes többit is. c)A nyeremények egyformák, de egy ember csak egyet kaphat? Az első nyereményt adhatjuk 20-féle embernek. Csakhogy itt most nincs első nyeremény. Mert mindegyik nyeremény egyforma. Ezért nem számít a nyeremények sorrendje. Az egyforma ajándékok miatt nem számít a sorrend. Vagyis ez egy kombináció lesz, ahol 20 emberből választunk ki 5 embert. Ezt számológéppel az nCr gomb lenyomásával tudjuk kiszámolni: Egy dominókészlet azonos méretű dominókból áll. Minden dominó egyik oldala egy vonallal két részre van osztva. Az egyes részeken elhelyezett pöttyök száma 0-tól 6-ig bármi lehet. Minden lehetséges párosításnak léteznie kell, de két egyforma nem lehet egy készletben. Hány darabból áll egy dominókészlet? Íme, épp itt van egy dominó a készletből. Az első fontos észrevétel, hogy ha megfordítjuk... attól ez még ugyanaz a darab dominó marad. A második fontos észrevétel, hogy vannak olyan dominók is, amiket eszünkbe se jut megfordítani. Mert mindkét oldaluk egyforma. Most nézzük, melyikből hány darab van. Ezekből van 7 darab… Ezek meg itt olyanok, hogy az egyik mezőben nem ugyanaz a szám van, mint a másikban. A felső szám még 0-tól 6-ig bármi lehet, ez összesen 7-féle lehetőség, az alsó viszont nem lehet ugyanolyan, mint a felső, ezért az csak 6-féle. De valójában csak fele ennyi eset van, mert bármelyiket megfordítva ugyanazt a dominót kapjuk. Több váratlan fordulat már nincs, a készlet 21+7=28 darab dominóból áll.
Még mindig a középiskolai matek felelevenítésével foglalkozunk, ahol elvileg mindenki tanult valószínűségszámítást és kombinatorikát. De csak elvileg, éppen ezért teljesen az alapoktól kezdünk és nem építünk a középiskolai matematika tanulmányokra. Tíztagú társaság raftingolni indul egy ötszemélyes egy háromszemélyes és egy kétszemélyes csónakkal.
Hányféleképpen ülhetnek a csónakokba, ha a csónakokon belül a helyek között nem teszünk különbséget?
Mi a helyzet akkor, ha két adott ember egy csónakba akar kerülni?
Ilyenkor az szokott lenni, hogy egynek vesszük őket…
Így aztán 9 elemet kell elhelyezni.
Csak hát az a baj, hogy ha ezt az 5 elemet választjuk…
akkor az hat ember és nem férnek el.
Hát jó, akkor válasszunk csak 4-et, hogy biztosan beférjenek.
Csak hát az a baj, hogy ha ezt a 4 elemet választjuk…
akkor az tényleg csak 4 ember, vagyis marad egy üres hely.
Úgy tűnik sehogyan sem akar ez kijönni.
A problémát az okozza, hogy két embert egynek vettünk.
Az „egynek vesszük” elv tökéletesen jól működik olyankor, amikor csak sorba akarjuk rakni az elemeket.
De nem működik olyankor, amikor kiválasztunk.
Ilyenkor esetekre kell bontani.
Hány olyan szám keletkezik, amelyben két páros és két práratlan számjegy szerepel?
Először kiválasztjuk a számjegyeket…
aztán sorba rakjuk.
Hány olyan szám készíthető amiben szerepel a 9-es számjegy?
Az előző módszer itt is működik.
Egy másik jó ötlet, hogy vesszük az összes esetet…
és levonjuk belőle azokat amikor nincs 9-es.
Egy állatkert beszerez 4 hím és 5 nőstény oroszlánt, melyeket egy kisebb és egy nagyobb kifutóban kívánnak elhelyezni a következő szabályok mindegyikének betartásával: 1) Háromnál kevesebb oroszlán egyik kifutóban sem lehet. 2) A nagyobb kifutóba több oroszlán kerül, mint a kisebbikbe. 3) Mindkét kifutóban hím és nőstény oroszlánt is el kell helyezni. 4) Egyik kifutóban sem lehet több hím, mint nőstény. Hányféleképpen helyezhetik el a 9 oroszlánt a két kifutóban? (Az oroszlánokat megkülönböztetjük egymástól) Hát ez nagyon izgalmasnak tűnik. Itt vannak a kifutók, a kisebbik meg a nagyobbik. Lássuk, melyikbe hány oroszlán kerülhet. Mindkét helyre legalább 3 oroszlán kell, és a nagyobb kifutóba több. Ez például jó. És ez is. Más lehetőség nincs, mert a nagyobb kifutóban több oroszlánnak kell lenni. Két verzió van tehát, ezeket kéne most megvizsgálni. Kezdjük ezzel. Jönnek az oroszlánok. Most már a 3-as számú oroszlántartási szabálynak is megfelelünk. Ez fantasztikus. Végül itt jön a 4-es szabály. És most jön a legizgalmasabb rész. Amikor név szerint kiválasztjuk az oroszlánokat. Ide a 4 hímből kell 1, és az 5 nőstényből pedig 3. Ha pedig ide kiválasztottuk az oroszlánokat, akkor a másikba megy az összes többi. Az első esetben tehát 40 lehetőség van. A második eset az lesz, amikor a kisebb kifutóban 4 oroszlán van. az egyik kifutóba kiválasztottuk az oroszlánokat, akkor a másikba megy a maradék. Mondjuk, átterelünk egy nőstényt. Ajjaj, ez nem lesz jó. Akkor legyen inkább egy hím… A 4 hímből teszünk ide 2-t, és az 5 nőstényből is 2-t. A második esetben60 lehetőség van. Így tehát összesen 100-féleképpen helyezhetjük el az oroszlánokat. Csodás, hogy ma ezt is megtudtuk. Egy 52 lapos francia kártyából kihúzunk 5 lapot. Mi a valószínűsége, hogy az első és a harmadik lap ász? kedvező eset összes eset Kezdjük az összes esettel. Az 52 lap közül választunk ki 5 darabot. A kérdés az, hogy számít-e a sorrend vagy nem. Mivel a szövegben ilyenek vannak, hogy első lap, meg harmadik lap, a jelek szerint számít a sorrend. Most lássuk a kedvező eseteket. Az első lap ász, ez négyféle lehet. A következő lap elvileg bármi lehet a maradék 51 lapból. Aztán a harmadik lapnak megint ásznak kell lennie. Lássuk csak hány ász van még. Fogalmunk sincs. Ha ugyanis a második helyre is ászt raktunk, akkor már csak kettő. De ha a második helyre nem, akkor három. Ez bizony probléma. A kedvező eset számolásánál mindig a kívánsággal kell kezdeni. Most tehát azzal, hogy az első lap ász és a harmadik lap is ász. Utána jöhetnek a többi lapok. Van még 50 darab lap a második helyre. Aztán még 49 és 48. Mi a valószínűsége, hogy csak az első és a harmadik lap ász? Most is számít a sorrend. Az összes eset ugyanannyi,mint az előbb. Lássuk mi van a kedvezőkkel. Megint a kívánsággal kezdünk. De most csak ez a két ász van, tehát a második lap nem lehet ász. Így csak 48 féle lehet. Aztán 47 és 46. Mi a valószínűsége, hogy a lapok közt két ász lesz? Itt nem számít a sorrend ezért kombinációt használunk. A 4 ászból ki kell húznunk kettőt. Aztán pedig kell még 3 lap ami már nem ász. Hát ez remek. Végül nézzünk meg még egy feladatot. Egy kosárlabdacsapat 9 játékosból áll, közülük öten vannak egyszerre a pályán. Mekkora a valószínűsége, hogy a két legjobb játékos egyszerre van a pályán? A kiválasztás sorrendje nem számít, csak az, hogy kiket választunk a pályára. Így aztán kombinációra lesz szükség. Nézzük mennyi eset van összesen. A 9 játékosból kell kiválasztanunk ötöt. A kedvező amikor a két legjobb a pályán van, vagyis őket mindenképp kiválasztjuk, és még hármat. Mi a valószínűsége, hogy a két legjobb játékos közül csak az egyik van a pályán? Az összes eset itt is ugyanannyi. A kedvező pedig amikor a két legjobb játékosból választunk egyet és a többi tehetségtelen amatőr közül még négyet.
Tíz különböző szín felhasználásával hányféle különböző 6 cikkelyből álló esernyő készíthető, ahol
a) minden cikkely más színű?
b) két szín ismétlődik felváltva?
c) az egyik szín kétszer szerepel, de nem szomszédos cikkelyen, a többi szín csak egyszer?
Ez egy nagyon egyszerű kérdés. Nézzünk meg két különböző megoldást is.
Az egyik megoldás, hogy elkezdjük kiosztani a színeket…
Az első helyre még bármelyik szín kerülhet.
Aztán a következő helyre már csak kilencféle…
és így tovább.
Mivel pedig az esernyő kör alakú…
ezért el kell osztani a cikkelyek számával.
A másik megoldás egy nagyon hasznos ötletet tartalmaz, amit érdemes megjegyezni, mert később még jól jöhet.
A hasznos ötlet úgy szól, hogy először kiválasztunk…
ilyenkor még nem számít a sorrend…
aztán sorba rakunk.
Ebben az esetben csak két színt választunk ki.
45 lehetőség van kiválasztani a két színt.
Viszont kénytelenek vagyunk felváltva rakosgatni, tehát csak egyféle sorrend van.
Válasszuk ki a színeket.
Van a dupla szín…
és még 4 másik.
Ezeket kell szépen körben lerakni.
Az összes eset…
Ez egy ismétléses permutáció.
Ráadásul ciklikus permutáció.
Tehát osztani kell még az esernyő cikkelyeinek a számával.
Most levonjuk belőle a rossz eseteket.
Amikor a két sárga egymás mellett van.
Jön a szokásos „egynek vesszük” trükk.
Ez akkor 5 elem ciklikus permutációja.
Na, ez is megvan.
Ennyi lehetőség van körberakni a színeket úgy, hogy a két azonos szín nincs egymás mellett.
És a megoldás pedig…
