Középiskolai matek kurzusunkban 400-nál is több epizódon keresztül nézheted végig a 9. osztálytól egészen a 12. osztályig a teljes középiskolai matekot. Közülük 71 epizód ingyenesen is elérhető, ezeket témakörök szerint gyűjtöttük össze. Éppen itt is jönnek:
01 Műveletek és a műveleti sorrend
04 Törtek egyszerűsítése, algebrai törtek
06 Algebrai műveletek gyakorlása
07 Gyökös kifejezések azonos átalakításai
09 Binomiális tétel és binomiális együtthatók
10 Az értelmezési tartomány (miért nem osztunk nullával?)
01 Halmazok, metszet, unió, és egyebek
01 Minden amit a gráfokról tudni érdemes
01 Oszthatóság, maradékos osztás
02 Legnagyobb közös osztó, relatív prímek
01 Függvények ábrázolása, függvénytranszformációk
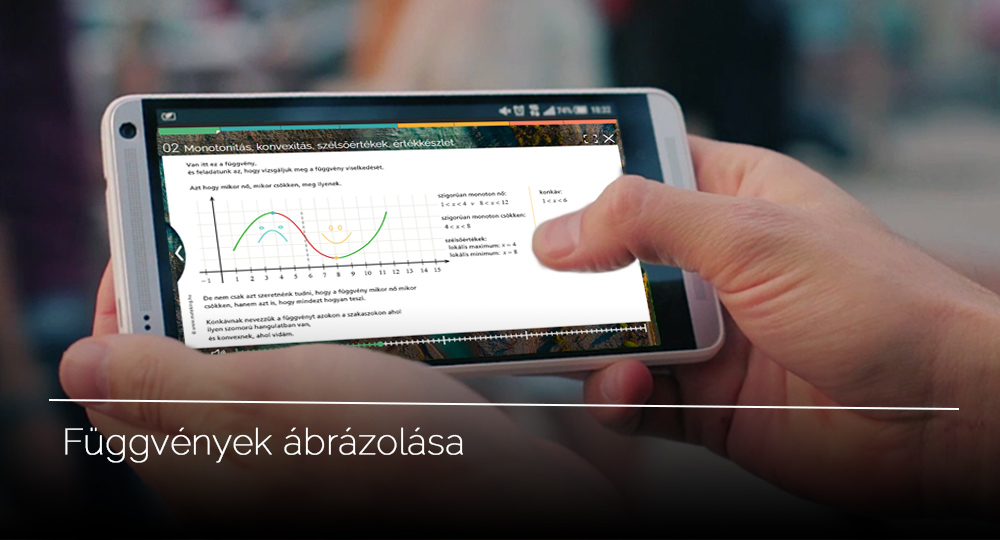
02 Monotonitás, konvexitás, szélsőértékek, értékkészlet
03 A másodfokú függvény ábrázolása
01 Elsőfokú egyenletek megoldása
02 A másodfokú egyenlet és a megoldóképlet
03 Másodfokú egyenletek megoldása
01 Hogyan oldjunk meg egyenlőtlenségeket?
02 Törtes egyenlőtlenségek megoldása: a számegyenes
01 Térelemek, pontok, egyenesek, síkok
02 Háromszögek nevezetes pontjai, vonalai

01 Elsőfokú egyenletrendszerek
01 Mi az az abszolútérték? Abszolútértékes egyenletek
01 Gyök, köbgyök, gyökös azonosságok
02 Gyökös azonosságokkal megoldható feladatok
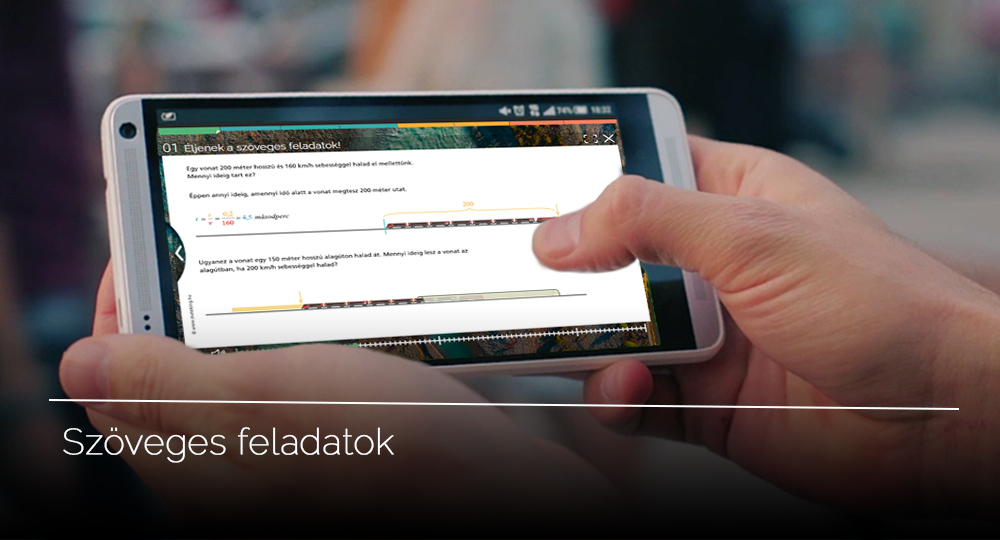
01 Mozgással kapcsolatos szöveges feladatok
01 Párhuzamos szelők tétele, középpontos hasonlóság
01 Szinusz, Koszinusz derékszögű háromszögekben
01 Permutáció, variáció, kombináció: nagy kombinatorikai összefoglaló
01 Hatványazonosságok, az exponenciális függvény
02 Exponenciális egyenletek megoldása, szöveges feladatok
01 Mi az a logaritmus? A logaritmus azonossága, egyenletek
02 Szinusz, koszinusz, trigonometrikus egyenletek
01 Másodfokú függvények viselkedésével kapcsolatos feladatok
01 Vektorok összeadása, hossza, skaláris szorzata, és 90°-os forgatása
02 Az egyenes egyenlete, egyenesek metszéspontja
01 A százalékszámítás, százalékszámítás feladatok
01 Gúlák, hasábok, kúpok, hengerek, térfogat és felszín
02 Független és kizáró események
03 Újabb remek valószínűségszámítás feladatok
01 A várható érték és a szórás
01 Konvergens sorozatok definíciója és a küszöbindex kiszámolása
01 Tanulj meg deriválni 10 perc alatt
01 A teljes függvényvizsgálat lépései
01 A függvény grafikonjához húzott érintő egyenlete